Impact of Climate Change on the Frequency of Dynamic Breakup Events and on the Risk of Ice-Jam Floods in Quebec, Canada
Abstract
1. Introduction
2. Background
3. Methodology
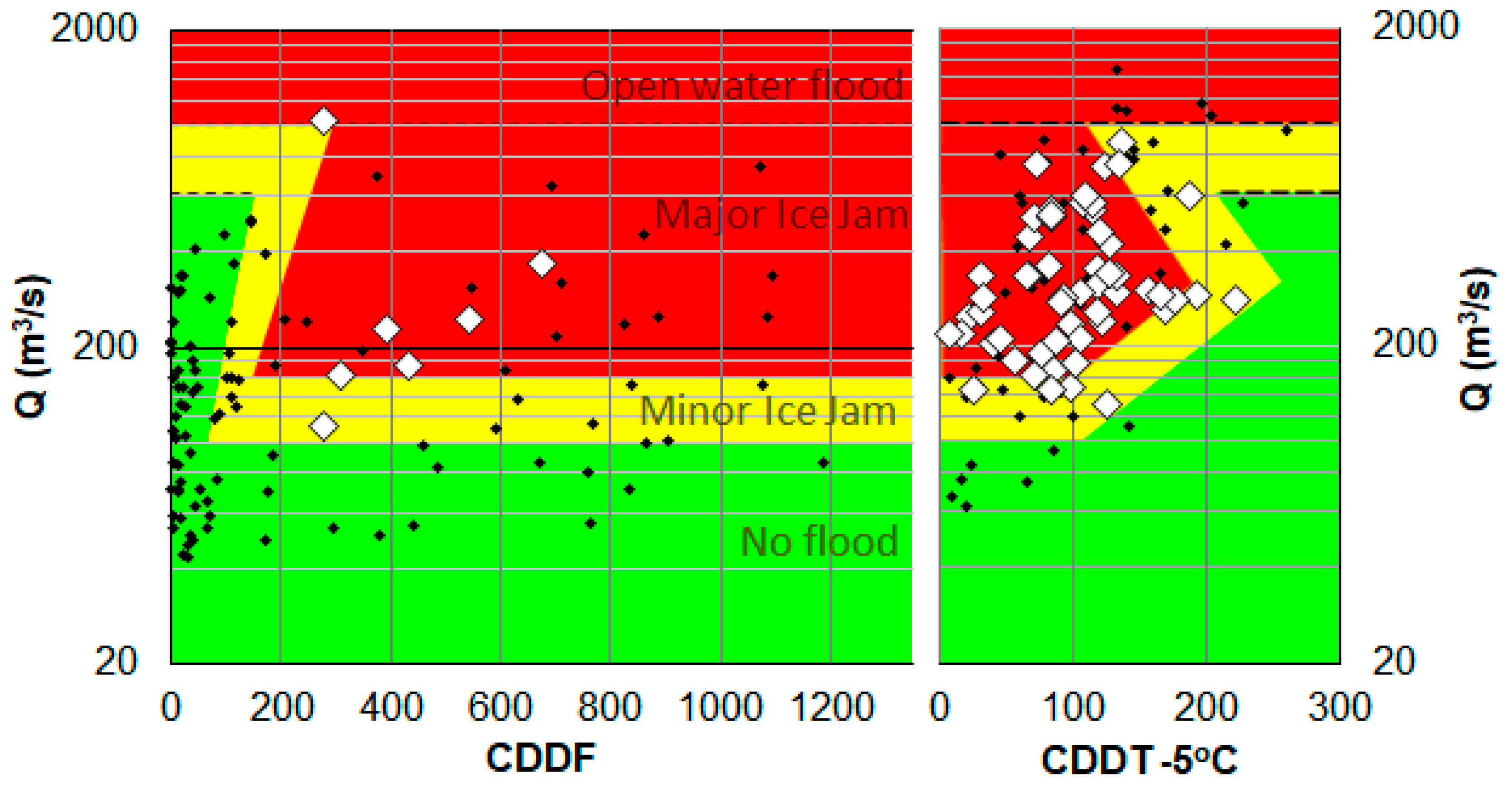
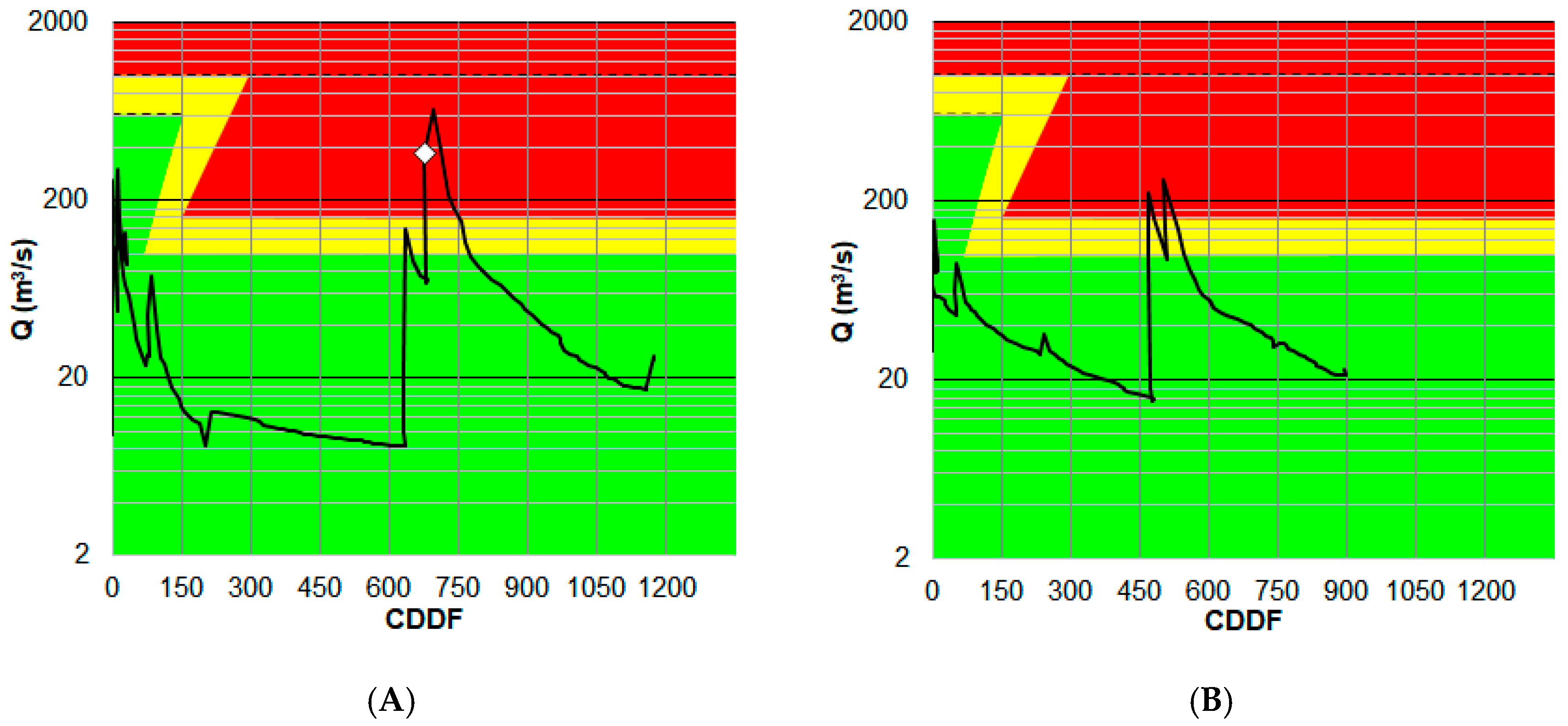
3.1. Historical Data and Breakup Models
- When a (partial or complete) breakup event was closely (in terms of CDDF or CDDT-5) followed by an equal or lower second runoff event, this second peak was discarded as it would not generate additional ice movements that could cause flooding.
- When there was insufficient ice produced (less than 100 to 200 CDDF, depending on the river) since the last partial or complete winter breakup event to generate any significant ice jam.
- When there was enough melting (generally more than 50 CDDT-5) after a partial spring breakup event to considerably reduce the probability of a significant ice jam.
3.2. Future Climate
3.3. From Ice-Jam Flood Frequency to Ice-Jam Flood Risk
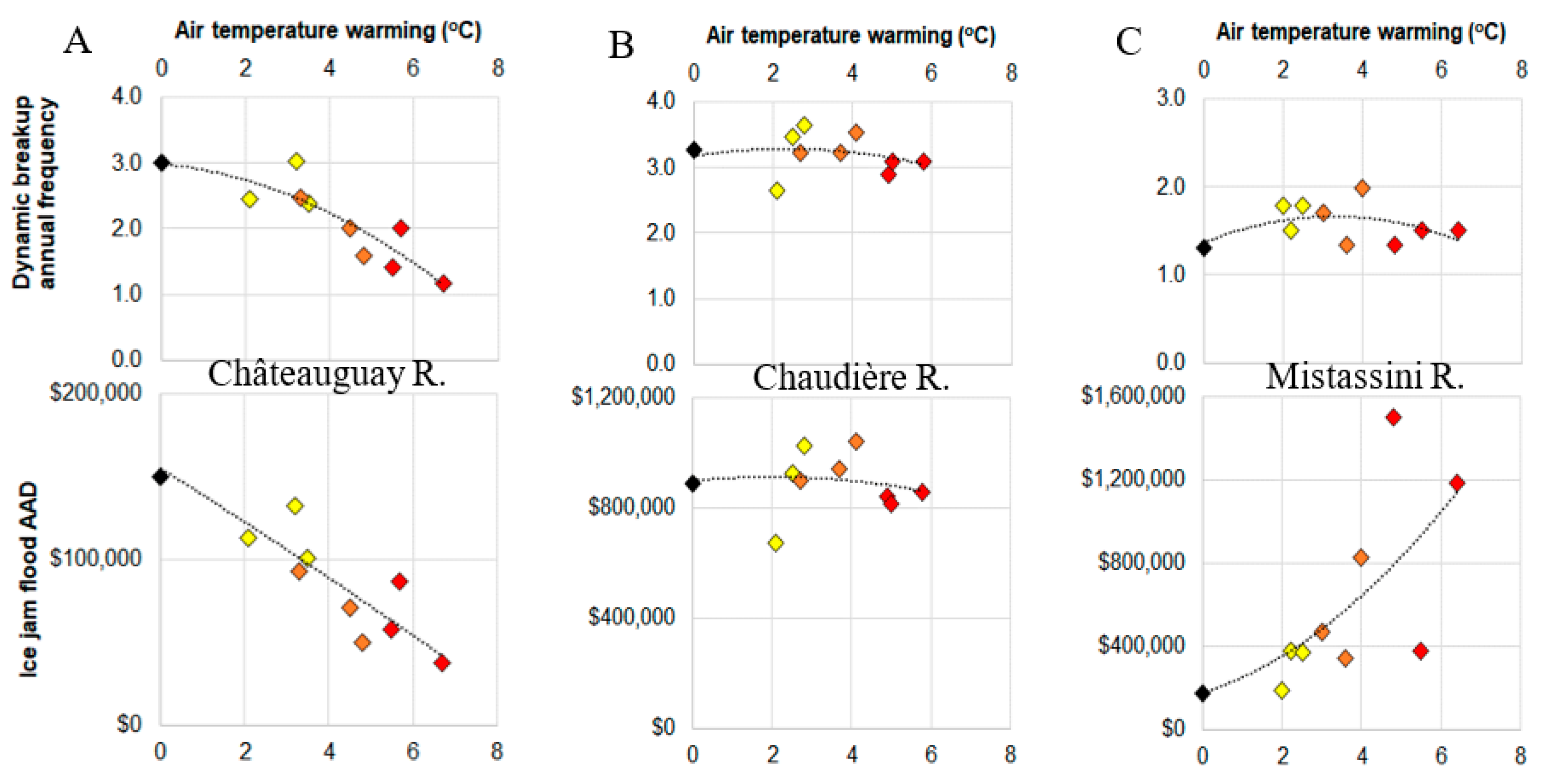
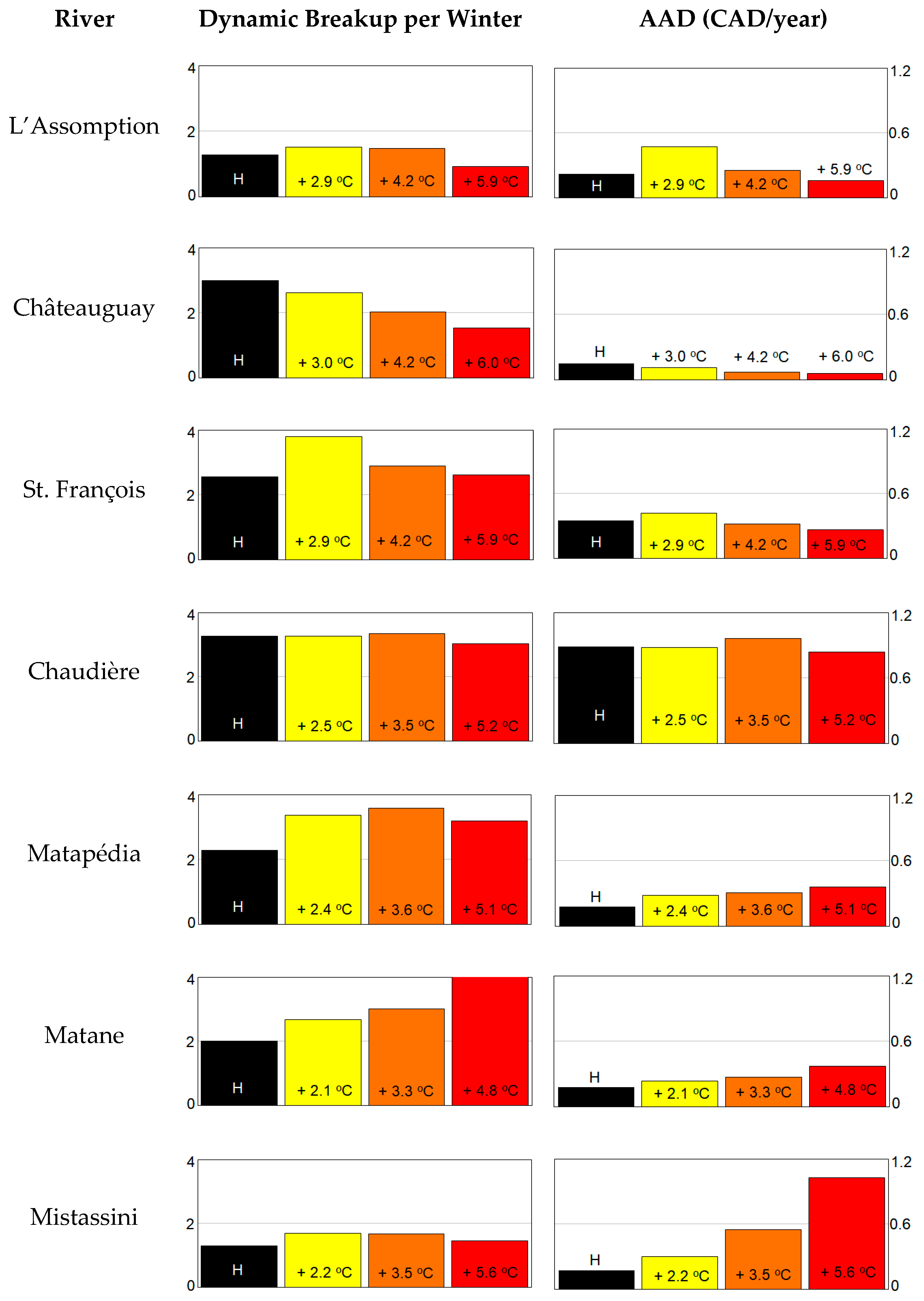
4. Results
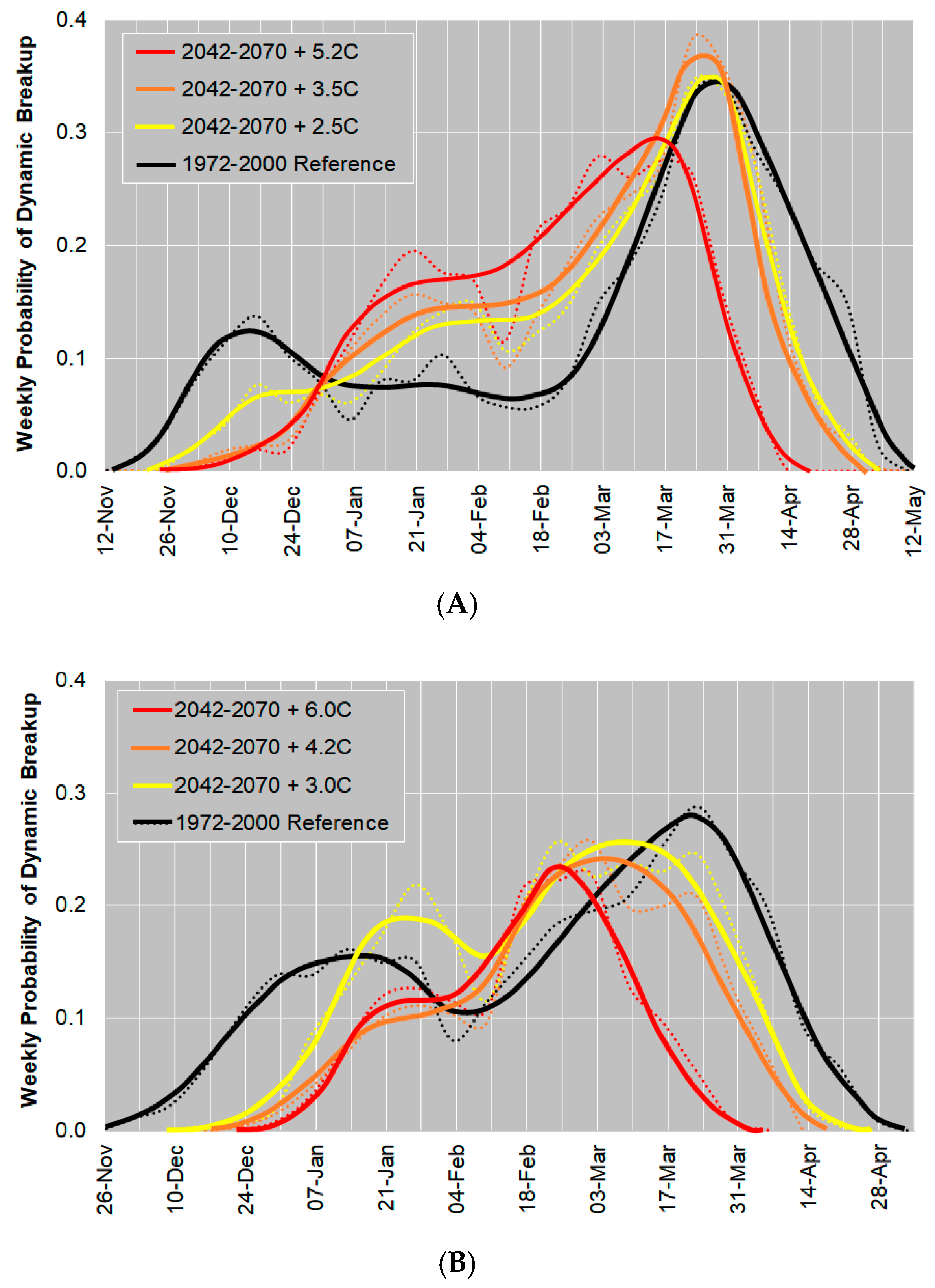
4.1. Evolution in the Winter Distribution of Dynamic Breakup Events
4.2. Evolution in the Probability and Risk of Dynamic Breakup Events
5. Discussion
5.1. Meaning of the Results
5.2. Relative Success of the Methodology
5.3. Transferability of the Results
5.3.1. Hydrology
5.3.2. Weather
5.3.3. Ice Processes
5.3.4. Morphology
5.3.5. Watershed Evolution
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gerard, R.L.; Davar, K.S. Introduction. In River Ice Jams; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 1995; Chapter 1. [Google Scholar]
- Beltaos, S. Overview of the Breakup Process. In River Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 3. [Google Scholar]
- Beltaos, S. Ice Jams. In River Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 7. [Google Scholar]
- Turcotte, B.; Burrell, B.; Beltaos, S. The Impact of Climate Change on Breakup Ice Jams in Canada: State of Knowledge and Research Approaches. In Proceedings of the 20th CGU HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, Canada, 10–12 July 2019. [Google Scholar]
- She, Y.T.; Andrishak, R.; Hicks, F.; Morse, B.; Stander, E.; Krath, C.; Keller, D.; Abarca, N.; Nolin, S.; Tanekou, F.N.; et al. Athabasca River ice jam formation and release events in 2006 and 2007. Cold Reg. Sci. Technol. 2009, 55, 249–261. [Google Scholar] [CrossRef]
- White, K.D. Breakup Ice Jam Forecasting. In River Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 10. [Google Scholar]
- Turcotte, B.; Morse, B. River-ice breakup forecast and annual risk distribution in a climate change perspective. In Proceedings of the 18th CGU-HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Quebec City, QC, Canada, 18–20 August 2015. [Google Scholar]
- Carr, M.; Vuyovich, C.M.; Tuthill, A.M. Benefit Analysis of Ice Control Structures in Oil City, Pennsylvania. ASCE J. Cold Reg. Eng. 2017, 31, 05016003. [Google Scholar] [CrossRef]
- Tuthill, A.M. River Ice Control. In River Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 13. [Google Scholar]
- Burrell, B.C. Mitigation. In River Ice Jams; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 1995; Chapter 7. [Google Scholar]
- Beltaos, S.; Burrell, B.C. Climatic Aspects. In River-Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 12. [Google Scholar]
- Beltaos, S.; Prowse, T.D. River-ice hydrology in a shrinking cryosphere. Hydrol. Process. 2009, 23, 122–144. [Google Scholar] [CrossRef]
- Milburn, D. The Ice Cycle of Canadian Rivers. In River-Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 2. [Google Scholar]
- Bush, E.; Lemmen, D.S. (Eds.) Canada’s Changing Climate Report; Government of Canada: Ottawa, ON, Canada, 2019; p. 444. [Google Scholar]
- Beltaos, S.; Burrell, B.C. Climatic change and river-ice breakup. Can. J. Civ. Eng. 2003, 30, 145–155. [Google Scholar] [CrossRef]
- Vincent, L.A.; Zhang, X.; Brown, R.D.; Feng, Y.; Mekis, E.; Milewska, E.J.; Wan, H.; Wang, X.L. Observed Trends in Canada’s Climate and Influence of Low-Frequency Variability Modes. J. Clim. 2015, 28, 4545–4560. [Google Scholar] [CrossRef]
- Magnuson, J.J.; Robertson, D.M.; Wynne, R.H.; Benson, B.J.; Livingstone, D.M.; Arai, T.; Assel, R.A.; Barry, R.D.; Card, V.; Kuusisto, E.; et al. Ice cover phenologies of lakes and rivers in the Northern Hemisphere and climate warming. Science 2000, 289, 1743–1746. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, S. Winter Hydrometry: Real-time data issues. In Proceedings of the 12th CGU-HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Edmonton, AB, Canada, 19–20 June 2003. [Google Scholar]
- De Rham, L.; Dibike, Y.; Beltaos, S.; Peters, D.; Bonsal, B.; Prowse, T.D. A Canadian River Ice Database from National Hydrometric Program Archives. Earth Syst. Sci. Data Discuss 2020. [Google Scholar] [CrossRef]
- Anctil, F.; Parent, A.-C. Pour des mesures de conservation et d’utilisation efficace de l’eau adaptables aux changements climatiques pour le bassin versant du Fleuve Saint-Laurent. In Plan D’action sur Les Changements Climatiques 2006–2012; Université Laval: Quebec City, QC, Canada, 2012; p. 191. (In French) [Google Scholar]
- Carr, M.L.; Gaughan, S.P.; George, C.R.; Mason, J.G. CREEL’s Ice Jam Database: Improvements and Updates. In Proceedings of the 18th CGU-HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Quebec City, QC, Canada, 18–20 August 2015. [Google Scholar]
- Daly, S.F. (Retired, U.S. Army Corps of Engineers, Cold Regions Research and Engineering Laboratory, Hanover, NH, USA). Personal communication, 2020.
- Garver, J.I. Ice Jam flooding on the lower Mohawk River and the 2018 mid-winter ice jam event. In Proceedings of the 2018 Mohawk Watershed Symposium, Union College, NY, USA, 23 March 2018; Volume 10, pp. 13–18. [Google Scholar]
- Garver, J.I. The 2019 mid-winter ice jam event on the lower Mohawk River, New York. In Proceedings of the 2019 Mohawk Watershed Symposium, Union College, NY, USA, 22 March 2019; Volume 11, pp. 12–17. [Google Scholar]
- Carr, M.L.; Vuyovich, C.M. Investigating the effects of long-term hydro-climatic trends on Midwest ice-jam events. Cold Reg. Sci. Technol. 2014, 106–107, 66–81. [Google Scholar] [CrossRef]
- Pietroniro, A.; Fortin, V.; Kouwen, N.; Neal, C.; Turcotte, R.; Davison, B.; Verseghy, D.; Soulis, E.D.; Caldwell, R.; Evora, N.; et al. Development of the MESH modelling system for hydrological ensemble forecasting of the Laurentian Great Lakes at the regional scale, Hydrol. Earth Syst. Sci. 2007, 11, 1279–1294. [Google Scholar] [CrossRef]
- Lindenschmidt, K.-E. RIVICE—A Non-Proprietary, Open-Source, One-Dimensional River-Ice Model. Water 2017, 9, 314. [Google Scholar] [CrossRef]
- Das, A.; Rokaya, P.; Lindenschmidt, K.-E. Assessing the impact of climate change on ice jams long the Athabasca River at Fort McMurray, Alberta, Canada. In Proceedings of the 19th CGU-HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Whitehorse, YT, Canada, 9–12 July 2017. [Google Scholar]
- Das, A.; Rokaya, P.; Lindenschmidt, K.-L. Ice-Jam Flood Risk Assessment and Hazard Mapping under Future Climate. J. Water Resour. Plann. Manag. 2020, 146, 40220029. [Google Scholar] [CrossRef]
- Rokaya, P.; Morales-Marín, L.; Bonsal, B.; Wheater, H.; Lindenschmidt, K.-L. Climatic effects on ice phenology and ice-jam flooding of the Athabasca River in western Canada. Hydrol. Sci. J. 2019, 64, 1265–1278. [Google Scholar] [CrossRef]
- Marsh, C.B.; Pomeroy, J.W.; Wheater, H.S. The Canadian Hydrological Model (CHM) v1.0: A multi-scale, multi-extent, variable-complexity hydrological model—Design and overview. Geosci. Model Dev. 2020, 13, 225–247. [Google Scholar] [CrossRef]
- Gaborit, É.; Fortin, V.; Xu, X.; Seglenieks, F.; Tolson, B.; Fry, L.M.; Hunter, T.; Anctil, F.; Gronewold, A.D. A hydrological prediction system based on the SVS land-surface scheme: Efficient calibration of GEM-Hydro for streamflow simulation over the Lake Ontario basin. Hydrol. Earth Syst. Sci. 2017, 21, 4825–4839. [Google Scholar] [CrossRef]
- Craig, J.R.; Brown, G.; Chlumsky, R.; Jenkinson, R.W.; Jost, G.; Lee, K.; Mai, J.; Serrere, M.; Sgro, N.; Shafii, M.; et al. Flexible watershed simulation with the Raven hydrological modelling framework. Environ. Model. Softw. 2020, 129, 104728. [Google Scholar] [CrossRef]
- Fortin, J.P.; Turcotte, R.; Massicotte, S.; Moussa, R.; Fitzback, J.; Villeneuve, J.P. A Distributed watershed model compatible with remote sensing and GIS data. Part 1: Description of the model. J. Hydrol. Eng. Am. Soc. Civ. Eng. 2001, 6, 91–99. [Google Scholar]
- U.S. Army Corps Engineers (USACE). HEC-RAS River Analysis System, Hydraulic Reference Manual; CPD-69; U.S. Army Corps Engineers (USACE): Washington, DC, USA, 2016.
- Aaltonen, J.; Huokuna, M. Flood mapping of river-ice breakup jams in River Kyrönjoki delta. In Proceedings of the 19th CGU-HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Whitehorse, YT, Canada, 9–12 July 2017. [Google Scholar]
- Carson, R.; Beltaos, S.; Groeneveld, J.; Healy, D.; She, Y.; Malenchak, J.; Morris, M.; Saucet, J.-P.; Kolerski, T.; Shen, H.T. Comparative testing of numerical models of river ice jams. Can. J. Civ. Eng. 2011, 38, 669–678. [Google Scholar] [CrossRef]
- Tolszczuk-Leclerc, S.; Muise, P.; Gauthier, Y. Proposal for a National Ice Jam Database Model. In Proceedings of the CGU HS Committee on River Ice Processes and the Environment 20th Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, Canada, 14–16 May 2019. [Google Scholar]
- Bonnifait, L. Développement de courbes submersion-dommages pour l’habitat résidentiel québécois. Master’s Thesis, Université du Québec INRS-ÉTÉ, Quebec City, QC, Canada, 2005. [Google Scholar]
- Bilello, M.A. Maximum Thickness and Subsequent Decay of Lake, River and Fast Sea Ice in Canada and Alaska; Report 80-6; U.S. Army, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1980; p. 160. [Google Scholar]
- Centre d’expertise hydrique du Québec (CEHQ). Atlas hydroclimatique du Québec Méridional—Impact des Changements Climatiques sur Les Régimes de Crue, D’étiage et D’hydraulicité à L’horizon 2050; Ministère de l’Environnement et de la Lutte contre les Changements Climatiques: Quebec City, QC, Canada, 2015; p. 81.
- Mpelasoka, F.S.; Chiew, F.H.S. Influence of rainfall scenario construction methods on runoff projections. J. Hydrometeorol. 2009, 10, 1168–1183. [Google Scholar] [CrossRef]
- Beltaos, S.; Burrell, B.C. Hydroclimatic aspects of ice jam flooding near Perth-Andover, New Brunswick. Can. J. Civ. Eng. 2015, 42, 686–695. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Shook, K.; Fang, X.; Brown, T.; Marsh, C. Development of a Snowmelt Runoff Model for the Lower Smoky River, Centre for Hydrology Report: Report No. 13; Centre for Hydrology, University of Saskatchewan: Saskatoon, SK, Canada, 2013. [Google Scholar]
- Burrell, B.C. Introduction. In River Ice Breakup; Beltaos, S., Ed.; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2008; Chapter 1. [Google Scholar]
- Nolin, S.; Pelletier, P.; Groux, F. Stress-Resistance Approach to Assess the Ice-Jam Flood Risk. In Proceedings of the 20th CGU HS CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, USA, 10–12 July 2019. [Google Scholar]
- Turcotte, B.; Morse, B. A global river ice classification model. J. Hydrol. 2013, 507, 134–148. [Google Scholar] [CrossRef]
- Prowse, T.D. River ice processes. In River Ice Jams; Beltaos, S., Ed.; Water Resources Publications: Highland Ranch, CO, USA, 1995; Chapter 2. [Google Scholar]
- Turcotte, B.; Morse, B.; Anctil, F. Impacts of precipitation on the cryologic regime of stream channels. Hydrol. Process. 2012, 26, 2653–2662. [Google Scholar] [CrossRef]
- Ashton, G.D.; Beltaos, S. Thermal growth of ice cover. In River Ice Formation; Beltaos, S., Ed.; Committee on River Ice Processes and the Environment, Canadian Geophysical Union, Hydrology Section: Edmonton, AB, Canada, 2013; Chapter 8. [Google Scholar]
- Hicks, F.E.; Cui, W.; Ashton, G.D. Heat Transfer and Ice Cover Decay. In River-Ice Breakup; Beltaos, S., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 2008; Chapter 4. [Google Scholar]
- De Munck, S.; Gauthier, Y.; Bernier, M.; Chokmani, K.; Légaré, S. River predisposition to ice jams: A simplified geospatial model. Nat. Hazards Earth Syst. Sci. 2017, 17, 1033–1047. [Google Scholar] [CrossRef]
- Beltaos, S. Freezeup jamming and formation of ice cover. In River Ice Formation; Beltaos, S., Ed.; Committee on River Ice Processes and the Environment, Canadian Geophysical Union, Hydrology Section: Edmonton, AB, Canada, 2013; Chapter 7. [Google Scholar]
- Turcotte, B.; Morse, B.; Bergeron, N.E.; Roy, A.G. Sediment transport in ice-affected rivers. J. Hydrol. 2011, 409, 561–577. [Google Scholar] [CrossRef]
- Beltaos, S.; Doyle, P.E. Ice jam mitigation using setback dikes: Cold River at Merritt, B.C. J. Cold Reg. Eng. 1996, 10, 190–206. [Google Scholar] [CrossRef]
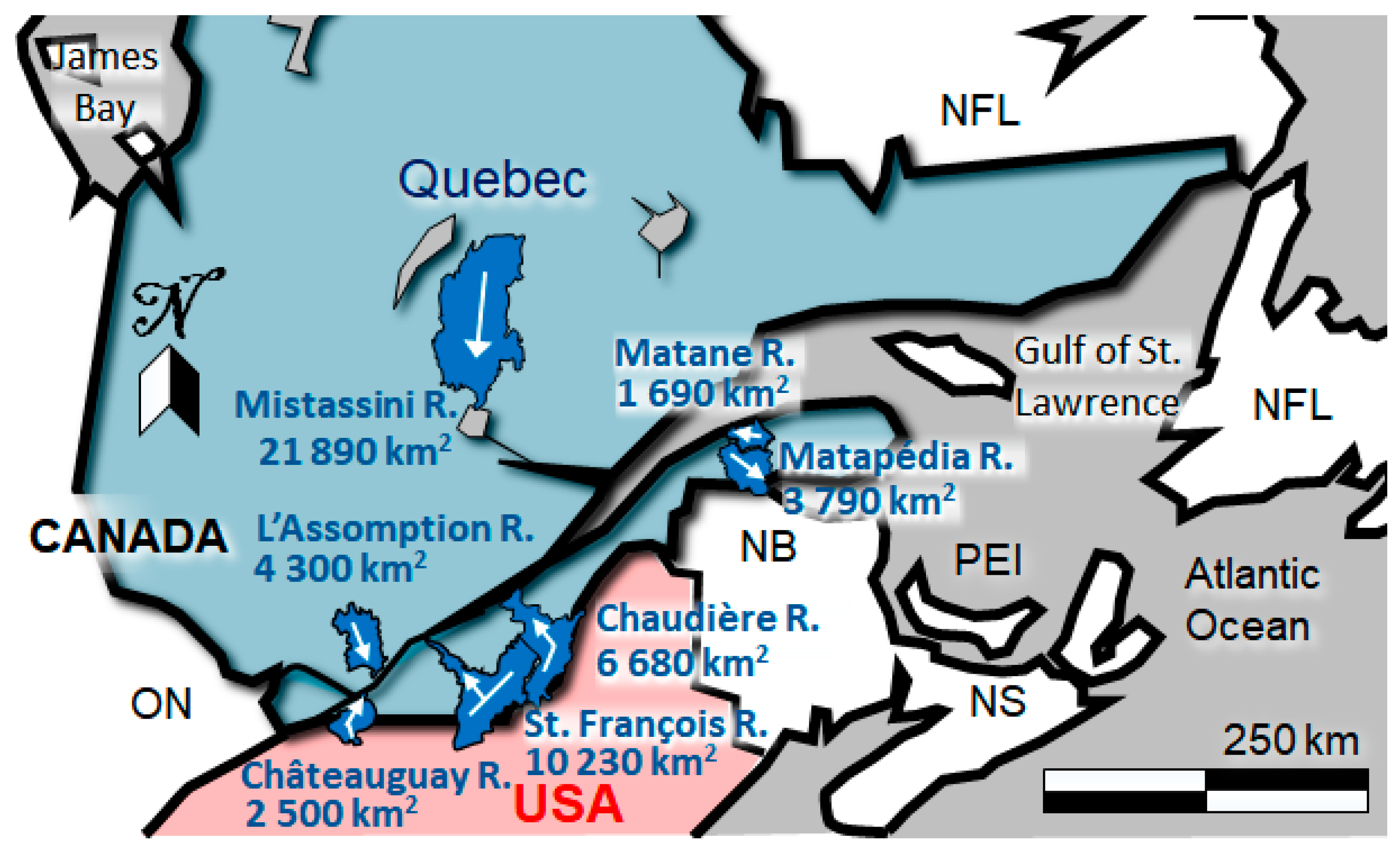
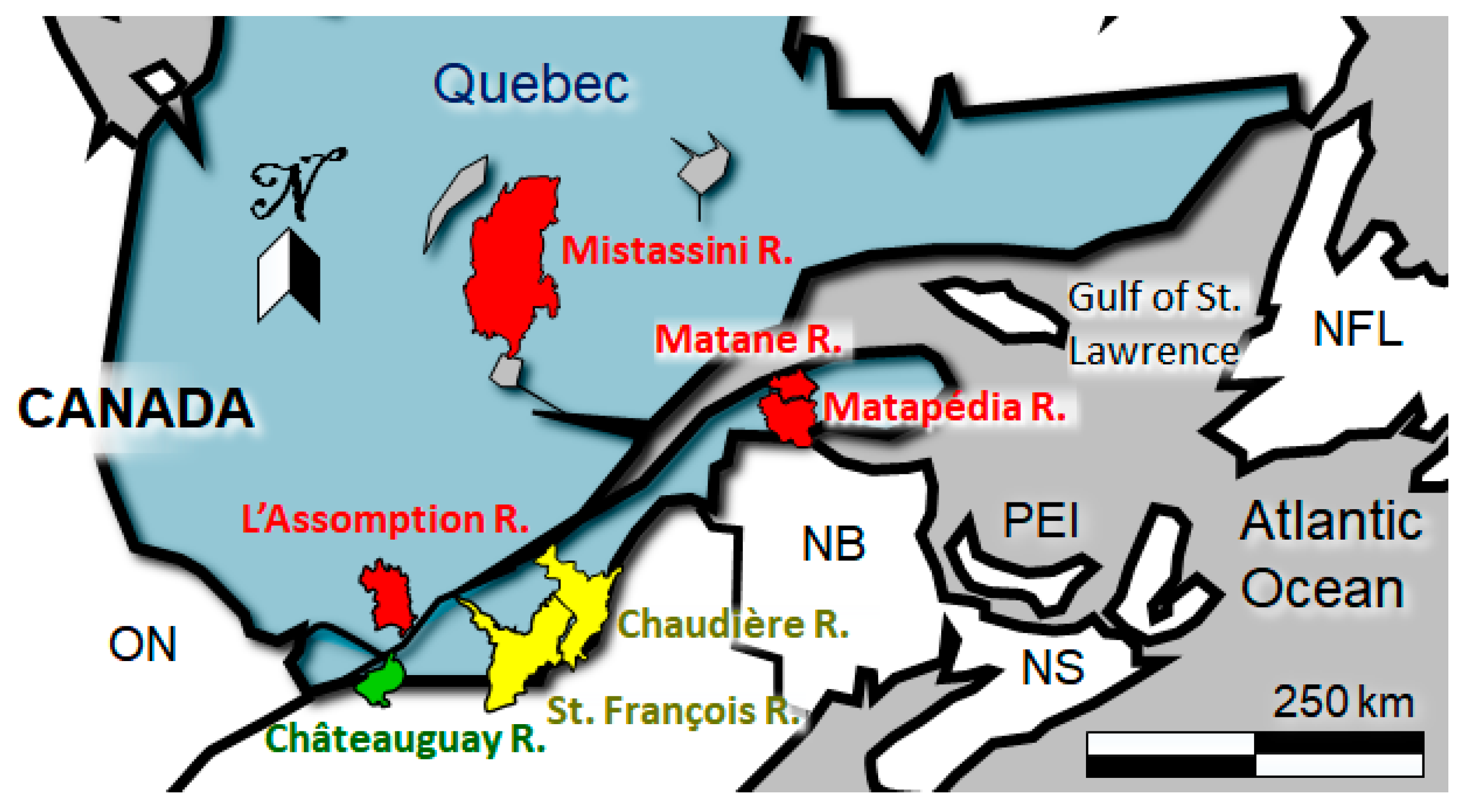
| River | River Extent (km) | Average Slope | Upstream and Downstream Municipality | Federal Meteorological Station ID | Provincial Hydrometric Station ID | Peak Flow Factor |
|---|---|---|---|---|---|---|
| L’Assomption | 100 | 0.19% | St. Côme to Joliette | 7014160 | 052219 | 1.10 |
| Châteauguay | 60 | 0.05% | Huntington to Châteauguay | 702S006 | 030905 | 1.15 |
| St. François | 200 | 0.12% | Weedon to Pierreville | 7022160 | 030208 | 1.15 |
| Chaudière | 150 | 0.16% | St. Ludger to St. Lambert | 7028754 | 023429 | 1.25 |
| Matapédia | 70 | 0.19% | Causapscal to Matapédia | 7051200 | 011509 | 1.05 |
| Matane | 30 | 0.12% | St. René de Matane to Matane | 7057395 | 021601 | 1.15 |
| Mistassini | 70 | 0.12% | Notre-Dame-De-Lorette to Dolbeau-Mistassini | 7065960 | 062102 | 1.05 |
| Rivers | Breakup Threshold | Total Winter and Spring Runoff Events | Selected Breakup Events | Frequency (Breakup Events/Year) |
|---|---|---|---|---|
| L’Assomption | 35 m3/s | 173 | 37 | 1.3 |
| Châteauguay | 80 m3/s | 350 | 87 | 3.0 |
| St. François | 300 m3/s | 568 | 74 | 2.6 |
| Chaudière | 100 m3/s | 338 | 95 | 3.3 |
| Matapédia | 40 m3/s | 143 | 66 | 2.3 |
| Matane | 40 m3/s | 289 | 58 | 2.0 |
| Mistassini | 300 m3/s | 202 | 38 | 1.3 |
| Emission Scenario | Projected Rise in Winter and Spring Air Temperatures | |
|---|---|---|
| Climate Model | Representative Concentration Pathway | |
| MPI-ESM-LR | RCP 4.5 | 2.1–3.0 °C |
| ACCESS1-3 | RCP 4.5 | |
| CMCC-CMS | RCP 4.5 | |
| MPI-ESM-LR | RCP 8.5 | 3.3–4.0 °C |
| BNU-ESM | RCP 8.5 | |
| CMCC-CMS | RCP 8.5 | |
| MIROC5 | RCP 8.5 | 4.8–6.0 °C |
| MIROC-ESM-CHEM | RCP 4.5 | |
| MIROC-ESM-CHEM | RCP 8.5 | |
| River | Total Winter and Spring Runoff Events | Selected Breakup Events |
|---|---|---|
| L’Assomption | 919 | 253 |
| Châteauguay | 2833 | 537 |
| St. François | 2387 | 434 |
| Chaudière | 3011 | 839 |
| Matapédia | 721 | 334 |
| Matane | 852 | 283 |
| Mistassini | 1148 | 356 |
| Value or Equation of the Damage Associated with a Dynamic Breakup Event (CAD) | Confirmed vs. Potential AAD Ratio | ||
|---|---|---|---|
| River | Yellow Zone | Red Zone | |
| L’Assomption | 5600 | 8875 (Q) − 890,000 | 81% |
| Châteauguay | 26,500 | 265,000 | 28% |
| St. François | 20,000 | 0.26 (Q2) + 73.5 (Q) − 100,000 | 42% |
| Chaudière | 10,000 | 1.97 (Q2) + 1107.1 (Q) − 500,000 | 16% |
| Matapédia | 1010.5 (Q) − 50,000 | 24% | |
| Matane | 190,500 | 47% | |
| Mistassini | 2.2016 (10−20) (Q7.978) | 24% | |
| 0 | 0.721 (Q2) − 770.6 (Q) + 200,000 | 17% | |
| 25,000 | 250,000 | 28% | |
| River | Historical AAD (CAD/Year) |
|---|---|
| L’Assomption | 220,000 |
| Châteauguay | 150,000 |
| St. François | 350,000 |
| Chaudière | 890,000 |
| Matapédia | 180,000 |
| Matane | 180,000 |
| Mistassini | 180,000 |
| Total (7 rivers) | 2,150,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turcotte, B.; Morse, B.; Pelchat, G. Impact of Climate Change on the Frequency of Dynamic Breakup Events and on the Risk of Ice-Jam Floods in Quebec, Canada. Water 2020, 12, 2891. https://doi.org/10.3390/w12102891
Turcotte B, Morse B, Pelchat G. Impact of Climate Change on the Frequency of Dynamic Breakup Events and on the Risk of Ice-Jam Floods in Quebec, Canada. Water. 2020; 12(10):2891. https://doi.org/10.3390/w12102891
Chicago/Turabian StyleTurcotte, Benoit, Brian Morse, and Gabriel Pelchat. 2020. "Impact of Climate Change on the Frequency of Dynamic Breakup Events and on the Risk of Ice-Jam Floods in Quebec, Canada" Water 12, no. 10: 2891. https://doi.org/10.3390/w12102891
APA StyleTurcotte, B., Morse, B., & Pelchat, G. (2020). Impact of Climate Change on the Frequency of Dynamic Breakup Events and on the Risk of Ice-Jam Floods in Quebec, Canada. Water, 12(10), 2891. https://doi.org/10.3390/w12102891




