1. Introduction
In Western Europe only, more than 300,000 sites whose aquifer need be remediated have been identified [
1]. In Italy, 12,482 sites under regional jurisdiction, together with 41 sites under national jurisdiction (Site of National Interest, SIN), are currently subjected to administrative proceedings [
2].
Groundwater contamination in industrial sites is mainly due to leakages from plants or tanks and to the incorrect disposal of untreated wastes on soils. In general, the main pollutants found in groundwater are aromatic hydrocarbons (e.g., Benzene, Toluene, Ethylbenzene and Xylene, BTEX compounds) and chlorinated hydrocarbons (e.g., Tetrachloroethylene, Trichloroethylene) present also as Non-Aqueous Phase Liquids (NAPLs, [
3,
4,
5]), as well as heavy metals.
A correct and thorough definition of the Conceptual Site Model (CSM) of the polluted area, obtained by organizing all of the available data and information about the contamination and the hydrogeological setting and the potential targets, is crucial to select the most appropriate remediation technique. Currently, many remediation techniques are available, classified according to where the contaminated matrix is treated (in situ, on site or off site) and how the contamination removal is achieved (physical, chemical, or biological) [
6].
Each technology has its own advantages and disadvantages that need to be carefully evaluated during the remediation process design by means of a cost–benefit analysis considering the whole service life of the project; it is essential to verify if a certain technology is sufficiently efficient and economically and socially sustainable in a long-term perspective. Pump and treat systems (P&T) are among ex situ chemical–physical treatments.
The P&T technology is based on a simple principle: the contaminated water is removed from the aquifer by means of wells or trenches and then sent to a specific treatment plant using physical, chemical, or biological processes to reduce the concentrations below the desired level [
7]. Such systems act as a hydraulic barrier for groundwater flow, avoiding the spreading of contamination outside the contaminated site boundaries (often considered as a constraint), while helping the aquifer remediation. Thanks to their versatility [
8,
9,
10,
11,
12], many P&T applications can be found in Italy and worldwide. For instance, in many Italian SIN, more than one active hydraulic barrier operates. However, if the hydraulic containment can be easily reached, the complete groundwater clean-up is not feasible in many sites. Particular P&T systems are currently implemented: [
13] demonstrated that pulsed pumping can achieve similar contaminant removal for a given amount of time as continuous pumping while pumping less water; [
14] studied a system of pumping wells coupled to injecting wells and demonstrate that the proper configuration of wells, varying the flow rate value many times during the year and collecting corresponding groundwater responses, is equivalent to conducting a large-scale hydraulic tomography survey, with minimal additional costs. Nagheli et al. [
15] studied, by means of an equation-based particle swarm optimization and genetic algorithm, the optimization of pumping and injecting wells in a multilayer configuration. These innovative improvements were devised to try to overcome the limits shown by the P&T system. Indeed, Cohen [
16] highlighted that the efficiency of a P&T system is often compromised by many factors, from the contaminant types to the site characteristics, so that in the US, during the 1990s, it was hard to reach the remediation objectives within a reasonable time frame, that is, less than 10 years [
17]. In many sites, the concentrations detected in the extracted water diverged from the theoretical concentrations, revealing two typical phenomena called “tailing” and “rebound”. As time proceeds, the decline in the rate of contaminant concentrations in groundwater slow (tailing effect) and the residual concentrations reach an asymptotic value above the remediation objective. Moreover, concentrations can increase again (rebound effect) as the P&T system is turned off, after temporarily reaching the concentration objective. Tailing and rebound can be caused by several physical and chemical processes and can complicate the remediation efforts at a site, depending on the chemical–physical characteristics of the contaminant treated, the aquifer material, and the groundwater [
17]. The main factors influencing such effects are NAPL dissolution, contaminant desorption, precipitate dissolution, back diffusion, and groundwater velocity variations [
16,
17,
18,
19,
20,
21,
22,
23]. Therefore, a site characterization able to identify the site-specific conditions (hydrogeological complexity, contaminant distribution, and governing transport phenomena) is essential to allow for setting up models to estimate the clean-up time frame.
In order to evaluate correctly the global costs and the time feasibility of a P&T system in comparison to other possible treatments, an evaluation of the time needed to achieve the remediation objectives is necessary [
24]. Although P&T is a long-established technique, a general formulation to assess the remediation time is not yet available. In literature, different formulations exist with different complexity, depending on the transport processes and the contaminant considered. The formulations range from the evaluation of the number of pore volumes that are necessary to flush in order to reach the clean-up target concentrations [
16,
25], numerical models set up for site-specific conditions or specific processes [
26,
27,
28,
29], and numerical models coupled with genetic algorithms [
30,
31,
32,
33,
34,
35,
36,
37].
Generally, as the model complexity increases, the number and the type of parameters also increase, as well as the time and the effort needed to set up the model. Moreover, most of the numerical codes used to simulate groundwater flow and solute transport are not freely available and require a specific know-how to be implemented and results interpreted correctly. Therefore, in the present paper, analytical models were evaluated to verify whether they can provide reasonable results in both a P&T system design phase and in the performance evaluation of an existing system. When the transport phenomena are driven by advection and sorption, the batch flushing model [
38] is noteworthy. In this model, the physical process of water renewal due to a pumping system is simulated by means of a subsequent series of flushing stages with clean water in sufficient quantity to fill the pore volume within a given portion of the aquifer. The batch flushing model was applied to the Lone Pine Superfund site in the US, where a simple aquifer system exists and the contamination was due to dissolved chlorinated solvents [
39]. The batch flushing model becomes more effective when coupled with particle tracking analysis, although it involves numerical simulations [
40]. Another interesting analytical approach is the advection–dispersion–retardation (ADR) model developed by [
41], where clean water flows through the contaminated area and the resulting contaminant flushing within the control volume is simulated using an adjusted version of the Ogata–Banks equation. This model can be applied when the diffusion phenomenon is negligible in the transport processes. Nevertheless, in most contaminated sites, the remediation time depends on matrix diffusion processes. Matrix diffusion was widely studied by [
20,
42,
43,
44], which by means of contaminant numerical transport models showed how this phenomenon is the cause of long clean-up times when low hydraulic conductivity zones are present. In cases where fine sediments are present and matrix diffusion is a relevant mechanism, the square root model (SRM) and the Dandy–Sale model (DSM) [
21,
45,
46,
47], as implemented in the Matrix Diffusion Toolkit (a freeware Microsoft Office-based tool) [
48], can be used to assess the performance of the P&T in the long-term.
In this paper, some available methodologies to assess the remediation time of a P&T system were applied to a real field case and to a synthetic case. Analytical and easy to implement solutions were chosen depending on the contamination transport phenomena occurring at the site; the batch flushing model, the ADR model, and the SRM were applied both to the field case and benchmark case. Some ad hoc numerical models were implemented only for the benchmark case (in MODFLOW/MT3DMS (version 2000, United States Geological Survey, Reston, VA, USA)) in order to study the back diffusion role on clean-up time, since low hydraulic conductivity zones are often present in real cases. The numerical simulation results allowed for the verification of the back diffusion effects and to validate the analytical SR model approach.
2. Case Studies
2.1. Field Case
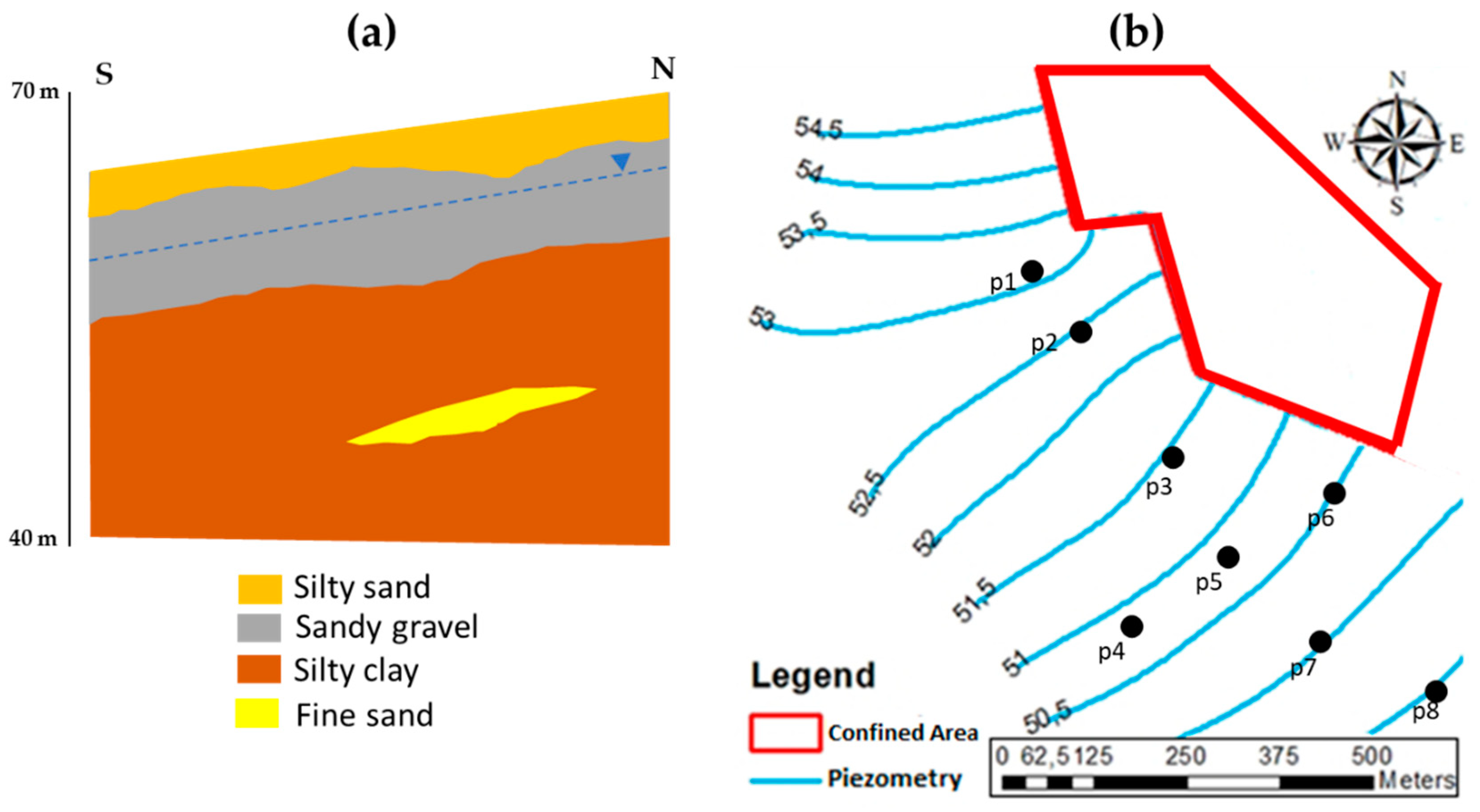
The first case study refers to a former chemical industry, located in Italy, that from the early 1960s until 1990 manufactured PVC (polyvinyl chloride), chlorine, and sodium hydroxide, among others. After site decommissioning, the site characterization activities carried out highlighted a high groundwater contamination due to chlorinated hydrocarbons (mainly 1,1-dichloroethylene or 1,2-dichloroethylene or vinyl chloride). This fact led to the implementation of a physical source control measure in a portion of the contaminated area.
The site stratigraphy can be described as follows:
- (1)
Sandy silts and fine silty sands with an average thickness of about 3–5 m and of brown-light brown color;
- (2)
Sandy gravels in a sandy or silty-sandy matrix, of gray light brown color, with an average thickness of about 5–10 m;
- (3)
Silty clays of gray-light blue color with an average thickness greater than 50 m, with thin sandy layers.
The silty clay layer acts as a base for groundwater, the latter being mainly hosted in the sandy gravel unit; the shallow silty sandy layer is an unsaturated (or vadose) zone, since no groundwater flow is present. The data recorded during several piezometric and analytical field campaigns allowed definition of the hydrogeological setting and groundwater quality. The flow is mainly directed towards North North West-South South East, where a river is located.
Figure 1a shows the site stratigraphy while
Figure 1b shows the piezometric map obtained by interpolating the hydraulic head values measured in the piezometers; the map shows only the piezometers relevant from a contamination point of view; the other points used for the piezometric interpolation are not represented.
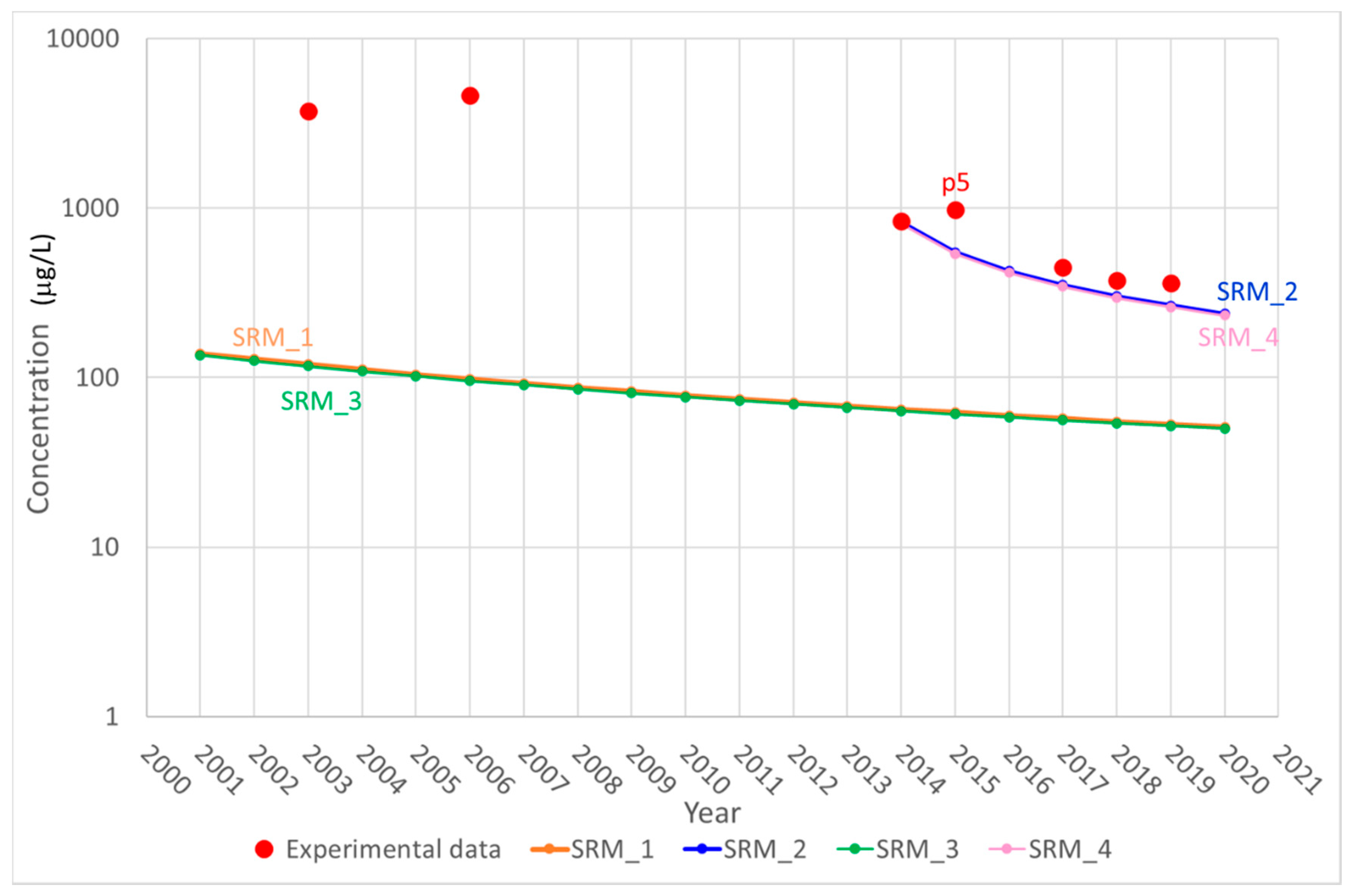
Despite the physical source control implementation near the monitoring wells p1, p2, p3, p5, p7, and p8 (see
Figure 1), concentrations of 1,1-DCE, 1,2-DCE, and VC exceeding regulatory limits were continuously observed. Comparing the contaminant distributions over time in each piezometer, no decrease in the detected concentrations was observed, but a fluctuation around an average value. Based on the site characterization analyses, the presence of an active source (probably active for many years) is likely assumed in the proximity of p1; therefore, the aquifer contamination can be supposed to be in a steady-state condition. For the sake of simplicity, the analyses discussed in this paper refer to one contaminant only, 1,2-DCE, whose groundwater remediation limit is 60 μg/L, according to the Italian regulation. The analysis was specifically focused on 1,2-DCE because the concentrations were higher than the legal limit, unlike 1,1-DCE and VC, whose concentrations were just above the legal limit. The maximum 1,2-DCE concentration in the last 20 years was 20,000 μg/L, measured in piezometer p2 in 2006.
Table 1 shows the average values of the parameters implemented in the analytical model calculations. K
d represents the distribution coefficient, which for hydrophobic, nonpolar organic contaminants is derived from:
where K
oc is the organic carbon partition coefficient for 1,2-DCE and f
oc is the organic carbon content of the aquifer. Both parameters can be obtained from laboratory analyses of core material and literature sources. The retardation factor is linked to the lithology and is calculated as:
where
is the bulk density and θ the porosity.
Seepage velocities vary according to the different hydraulic condition implemented. In one case, the unperturbed aquifer conditions with a hydraulic gradient of 0.44% were simulated, whereas in the second case, the hydraulic gradient (equal to 0.45%), calculated considering the whole length of the contaminated area, was slightly influenced by a hypothetical hydraulic barrier made up of eight wells (total withdrawal of 20 m3/s) located on a 300 m line between piezometers p4 and p6, approximately 320 m downgradient of p2.
2.2. Synthethic Case
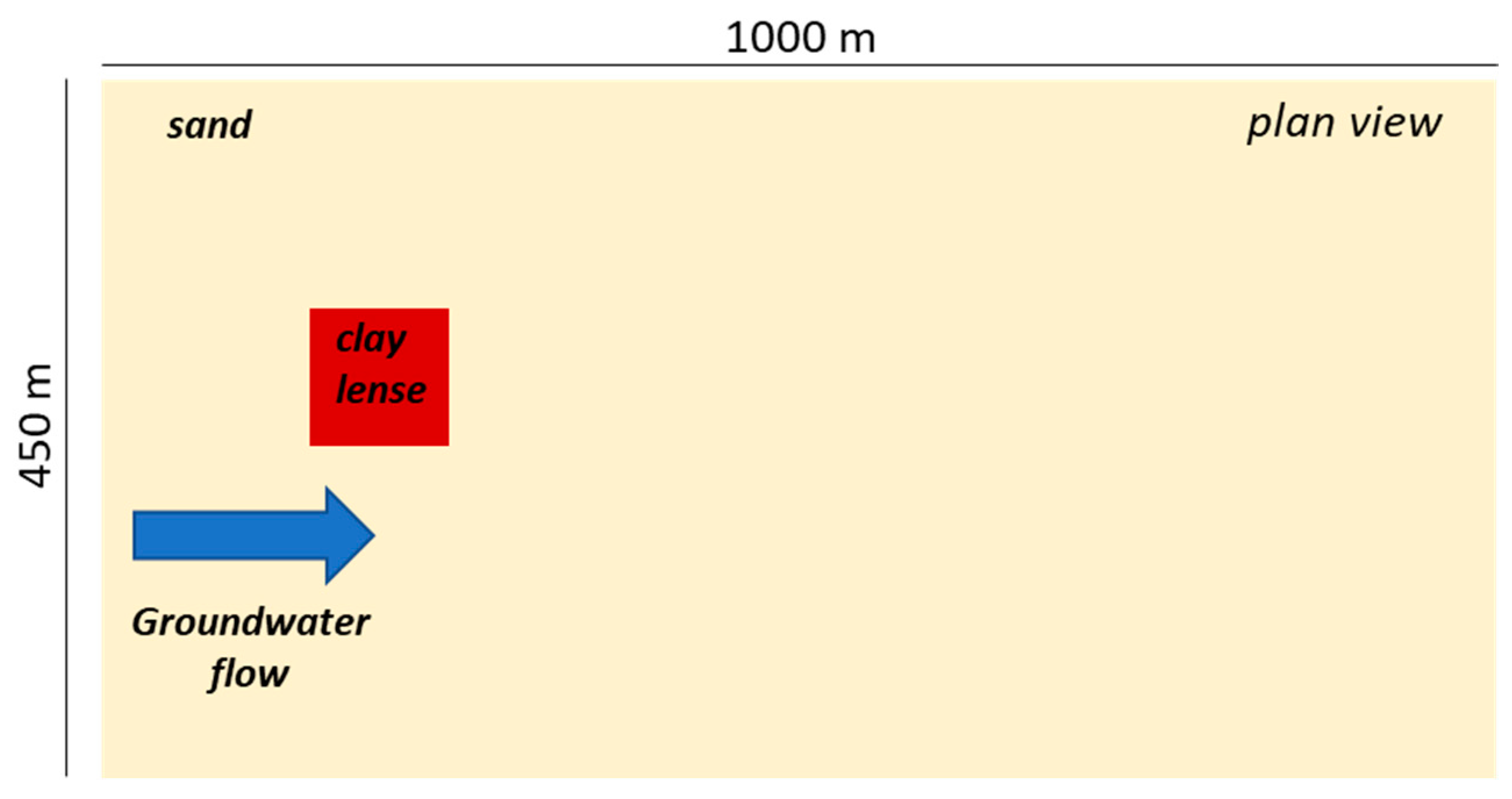
The second case study represents a synthetic case, specifically implemented to evaluate the clean-up time in the presence of low permeability (clay) layers. The simulated domain reproduces a rectangular aquifer portion 1 km long, 450 m wide, and 11 m thick. The aquifer material is mainly composed of sand, with the presence of a single square clay lense with an area of 100 × 100 m
2 and a thickness of 2.5 m, located 150 m downgradient of the model domain’s west boundary (
Figure 2).
The hydraulic head boundary conditions were implemented as constant heads conditions, of 11 and 9.6 m a.s.l. for the western and eastern boundaries, respectively. Such conditions impose a groundwater flow with a west–east direction and a hydraulic gradient of 0.14%.
In the aquifer, a Trichloroethylene (TCE) spill of 500 kg dispersed over a square area of 36 m2 was assumed to occur during a period of 5 years. TCE was chosen because it is a widespread contaminant and therefore could well represent many real situations; in any case, the choice of another compound does not affect the overall methodology.
The simulated scenarios follow:
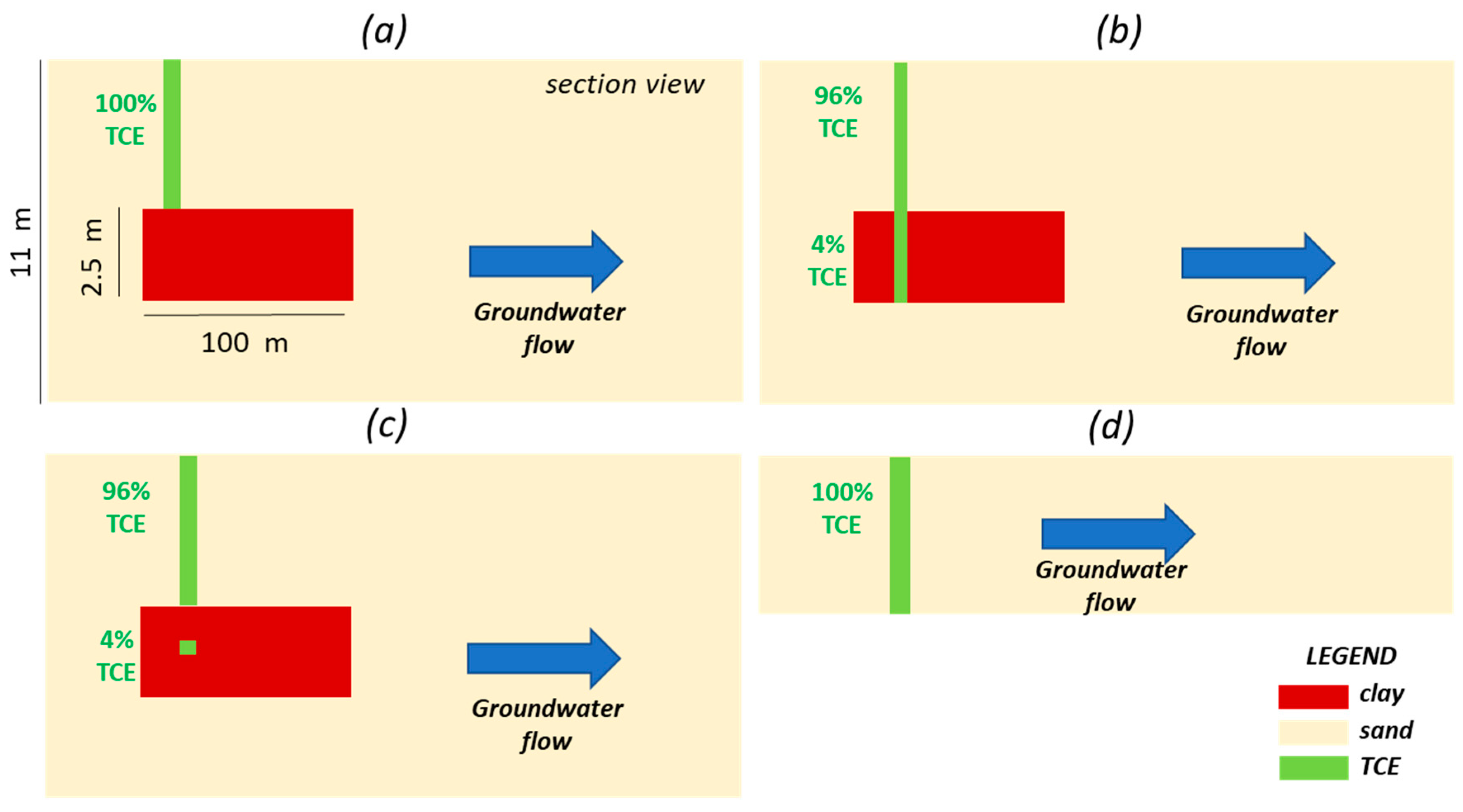
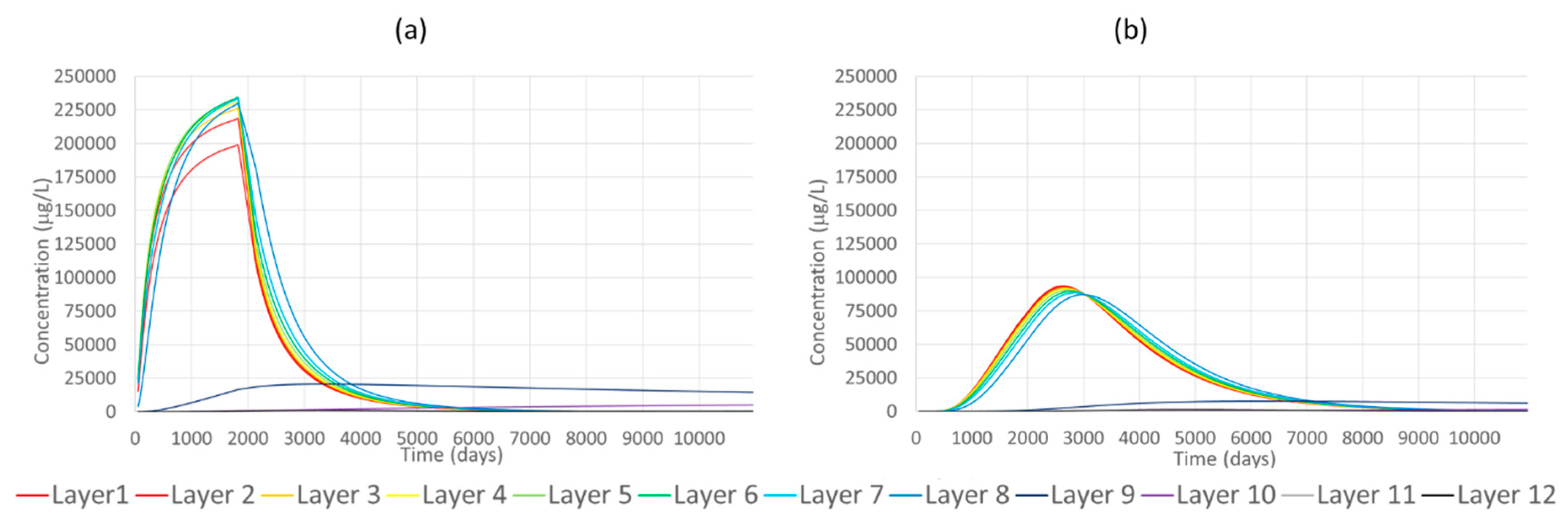
- (1)
Scenario A: the contaminant spreads vertically into the hydraulically transmissive material (sand) until it reaches the top of the clay lense; then it proceeds horizontally according to groundwater flow. The whole TCE mass is released in the transmissive zone (
Figure 3a).
- (2)
Scenario B: the contaminant spreads vertically into the sand up to the top of the clay lense, then it accumulates into the clay layer; 96% of the TCE mass remains in the transmissive layer while 4% migrates into the clay lense (
Figure 3b).
- (3)
Scenario C: 96% of the TCE mass is inside the sand aquifer, while 4% accumulates in a small central portion of the clay lense with thickness of 0.5 m (
Figure 3c).
- (4)
Scenario D: no clay lense is present and the aquifer is therefore homogeneous; the aquifer thickness is 4.5 m and the whole TCE mass is released into the sand (
Figure 3d).
The contamination source is assumed to be active for five years after which it is instantaneously removed. However, the concentrations in the aquifer downgradient of the source remain high, so two remediation solutions are hypothesized:
- (1)
Solution 1: monitored natural attenuation (i.e., no remediation system is activated), and the contamination evolution is monitored by means of a piezometer monitoring network.
- (2)
Solution 2: a P&T system with one pumping well located 140 m downgradient of the source and screened over the entire aquifer thickness is implemented together with monitoring piezometers. For scenarios A, B, and C, the pumping rate is 40 m3/day, while for scenario D is 7.2 m3/day.
The hydrogeological and physical-chemical properties of the aquifer material and the contaminant are shown in
Table 2.
3. Analytical and Numerical Approaches
Among all the analytical methods and numerical models available in the literature to evaluate the remediation time of a P&T system, the easiest to implement and most efficient analytical procedures were selected to assess the feasibility of a designed P&T. The theory behind the chosen approaches (batch flushing model, ADR model, and the square root model) is hereafter presented. Finally, the synthetic case implementation in a numerical model is discussed.
3.1. Batch Flushing Model
The batch flushing model is implicitly based on the number of pore volumes, and accounts only for advection and sorption processes, neglecting dispersion. The pore volume (PV) is the volume of groundwater within a contamination plume, which is defined as:
where b is the plume thickness (-), θ is the formation porosity (-), and A is the area of the plume (m
2). If the thickness is relatively uniform, then the following relationship applies:
where B is the average thickness of the plume (m).
The batch flushing model [
38,
39] is a useful approach for estimating the clean-up time in simple aquifer systems with chemicals for which interaction with the solid matrix can be represented by linear sorption. It simulates a situation in which clean water is circulated through a region that initially contains contaminated ground water; the approach assumes simple advective displacement of contaminated water, thus neglecting dispersive transport. It further assumes that the contaminant concentration in the influent water is always zero as the water enters the contaminated region, but it adjusts instantly to a concentration in equilibrium with the remaining sorbed contaminant mass after the water enters the contaminated region.
The replacement of water occurring due to the P&T system is simulated through a series of consecutive discrete flushing periods. During each flushing period, enough clean water is introduced, at a known rate, to fill the pore space in a given volume of aquifer. Soil and water concentrations at each flushing period i can be calculated by the following equations, assuming instantaneous linear equilibrium between solid and liquid phase concentrations:
where
is the soil total volatile organics concentration in (mg/kg) after i flushes, and C
w is the concentration of total volatile organics in the water in equilibrium with the soil (mg/L).
Once is evaluated as the ratio between and Kd, the value for can be entered into Equation (5) to calculate the soil concentration after the next flush. This is repeated until the soil and groundwater reach the desired concentrations.
Batch flushing described in [
38] is an explicit finite difference approximation of the solution to the governing differential equation. As this approximation is relatively difficult to use and is subject to numerical errors, [
7,
39] suggest using the exact solution to the governing differential equation, which is the following expression for the number of flushes (or pore volumes) required to reach the clean-up concentration C
f, starting from an initial contaminant concentration in groundwater of C
0, with R as the retardation factor:
From Equation (6), the relationship between the decrease in concentration as a function of the number of pore volume flushes (N
PV) is obtained:
The total groundwater volume (m
3) to be extracted (V
e) to reach a concentration in groundwater lower than the clean-up level is:
and since the duration of each flushing period (t) can be obtained dividing the contaminated volume PV by the discharge rate of the P&T system:
PV can be calculated as the product of the P&T system discharge rate (Q) and the flushing duration (t) and then substituting it into Equation (8). Hence, N
PV can be calculated as the ratio between V
e and Q·t, which can be entered into Equation (7) to obtain:
The total time required to reach remediation by a P&T system made up of n wells is then given by:
In case the P&T system is not yet active and/or the attenuation effect on the contamination due to the natural groundwater flow rate is to be assessed, the volume of water that naturally flows through a given section of the contaminated area can be calculated as:
where K
x is the hydraulic conductivity (m/s), A is the contaminated area given by the product of the width of the contamination plume and the saturated thickness of the contaminated aquifer, and “i” is the hydraulic gradient near the contaminated area.
The batch flushing model tends to underestimate clean-up time [
7] for several reasons: the assumption of chemical equilibrium between sorbed and dissolved contaminant mass; the assumption of linear sorption/desorption processes; the hypothesis that the concentration of the contaminant in the water used to flush the aquifer is less than or equal to the desired clean-up level, and that regardless of concentration, this level remains constant during the entire flushing process; the fact that it does not account for processes due to heterogeneities present in the domain; and the contamination source is assumed exhausted from the moment in which the estimation of the clean-up time starts.
3.2. Advection–Dispersion–Retardation Model
Another analytical model that accounts for advection, dispersion, and retardation processes but neglects matrix diffusion is the advection-dispersion-retardation (ADR) model, described in [
41]. The authors present an equation to simulate the flow of clean groundwater through a contaminated area and the resulting flushing of contamination within the volume of control, using a modified version from Ogata-Banks, in which longitudinal dispersivity equals 10% of the flow path length:
where C(t) is the contaminant concentration at time t (μg/L), C
0 is the highest concentration observed during the first two years of monitoring data (μg/L), and their ratio represents the normalized contaminant concentration. Knowing the normalized contaminant concentration and the retardation factor, the number of pore volumes to be extracted (N
PV) can be determined by solving Equation (13) iteratively. Multiplying this value for the pore volume (PV), the total amount of groundwater to be pumped is obtained. From the latter, based on the P&T system discharge, the time to reach site remediation is derived.
The ADR model can be applied at those sites where the governing transport processes do not imply the presence of diffusion. For this model, the same indications as for the batch flushing apply, with the exception that the ADR model also accounts for dispersive phenomena. The formulation of the ADR model presented by [
41] assumes that the contaminant is present in the dissolved and sorbed phase only, and that no other sources are present.
3.3. Square Root Model
The third analytical approach selected refers to the models known as the square root model (SRM) and Dandy-Sale model (DSM), which allow for the assessment of matrix diffusion effects and to understand whether remediation limits can be reached in a reasonable timeframe.
As a matter of fact, in complex hydrogeological sites, where the aquifer is heterogeneous and fine materials (clay or silt) are present, or NAPL contamination is revealed, the remediation time becomes longer because of matrix diffusion processes. In this case, the remediation timeframe can be evaluated by means of these models, both implemented in the Matrix Diffusion Toolkit. The Toolkit was developed on the basis of previous works (among many [
49]) by GSI Environmental Inc. in cooperation with the Colorado State University for ESTCP (Environmental Security Technology Certification Program) [
48]. The Toolkit is freely available software with a Microsoft Office Excel GUI and can perform analyses with both models by evaluating the effects of matrix diffusion in the source area, in the plume, and downgradient of a permeable reactive barrier.
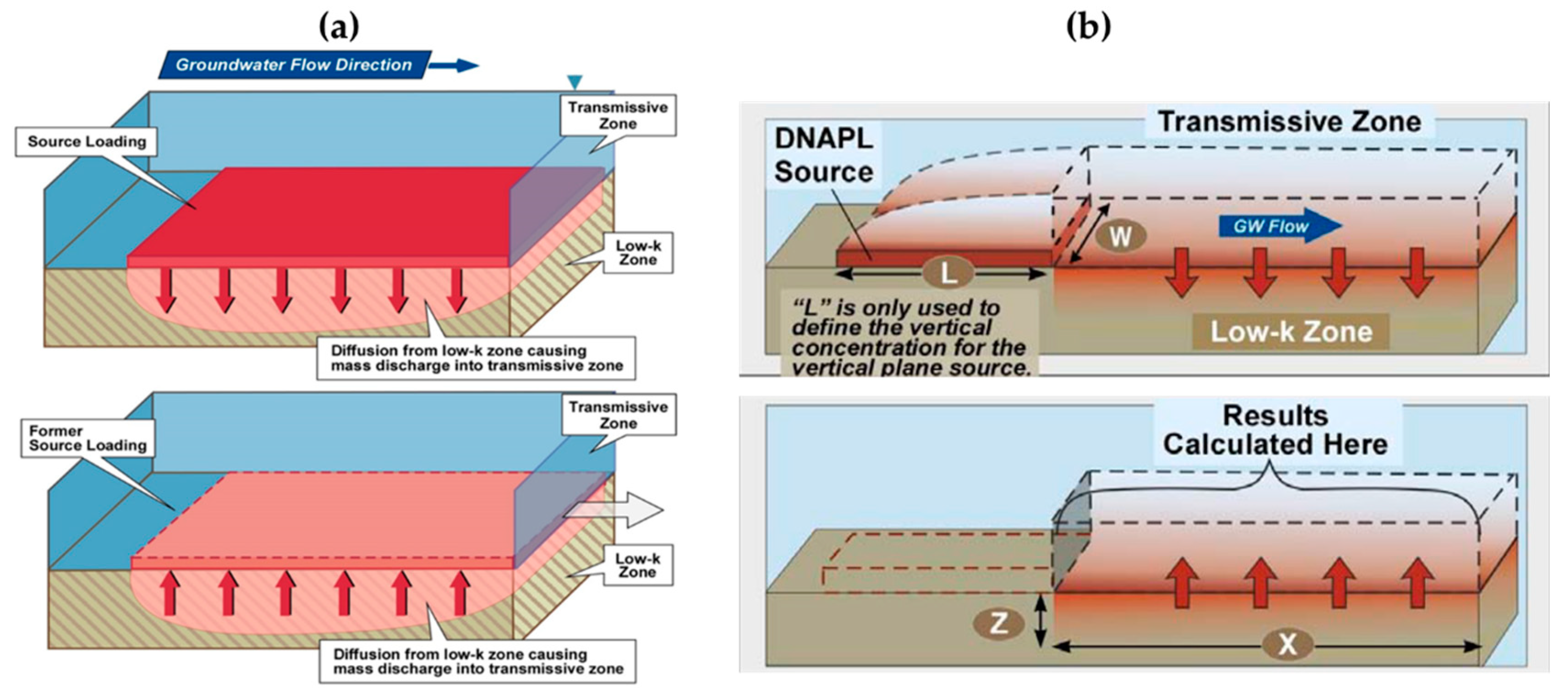
The Toolkit uses a simplified conceptual model of a two-layer aquifer system (a transmissive layer and a low permeability nontransmissive layer) where there are two different time periods: the “loading period”, where there is a constant concentration of contaminants in the transmissive zone that drives contaminants into the low permeability zone, and the “release period”, where the transmissive zone is assumed to have no concentration, and an upper-range estimate of release from the low permeability zone is generated. The low permeability zone is at least 1 m thick and there is no degradation in the low-k zone. The SRM assumes that the nontransmissive zone is “loaded” through a horizontal area placed exactly above it, as shown in
Figure 4a, while the DSM assumes that the source area is a vertical plane (parameter L) and assesses the effects of the diffusion only downgradient of this plane, as shown in
Figure 4b. Concentration results in the transmissive zone from both the SRM and DSM are based on estimates of mass discharge leaving the low permeability zone. Concentrations are calculated by assuming a 10-foot screened interval.
Since in this paper the SRM is used, the following considerations refer to this model only. The Toolkit provides an instantaneous mass discharge from the entire area (A) during the release period. This mass discharge from the entire low permeability zone is assumed to be transported instantaneously to the downgradient edge of the modeled area (there is no advection or travel time component of the SRM).
At any time t, the concentration of contaminants in the transmissive zone can be estimated using the equation:
where C(t) is the plume concentration in the transmissive zone at time t (μg/L), M
d the mass discharge from the low permeability layer into the transmissive layer (μg/s), v
D the Darcy velocity of the transmissive compartment (m/s), H the screened interval of the hypothetical well (m), and W the width of the modeled area (m).
Under the previous hypotheses, at any time t, the mass discharge into the low permeability layer underlying the pool can be estimated using the equation:
where t is the time after the source was introduced (year), t’ the time at which source was removed from the high-permeability compartment (year),
the porosity of low permeability zone (-), C
s the mean plume concentration above the low permeability compartment (μg/L), A the area of low permeability compartment beneath the plume (m
2), R the retardation factor for the low permeability compartment (-), and D
e the effective aqueous phase diffusion coefficient in the low permeability compartment (m
2/s) evaluated as the product of
(where p is the apparent tortuosity factor exponent) and D
0 (molecular diffusion coefficient in free water, m
2/s).
As seen, some of the input data are similar to those used for existing solute transport models, (e.g., Darcy groundwater velocity, size of the modeled area, information on when the source started) while other input data may appear particular (such as the tortuosity of the low permeability materials where matrix diffusion occurs); these are provided in
Table 1 and
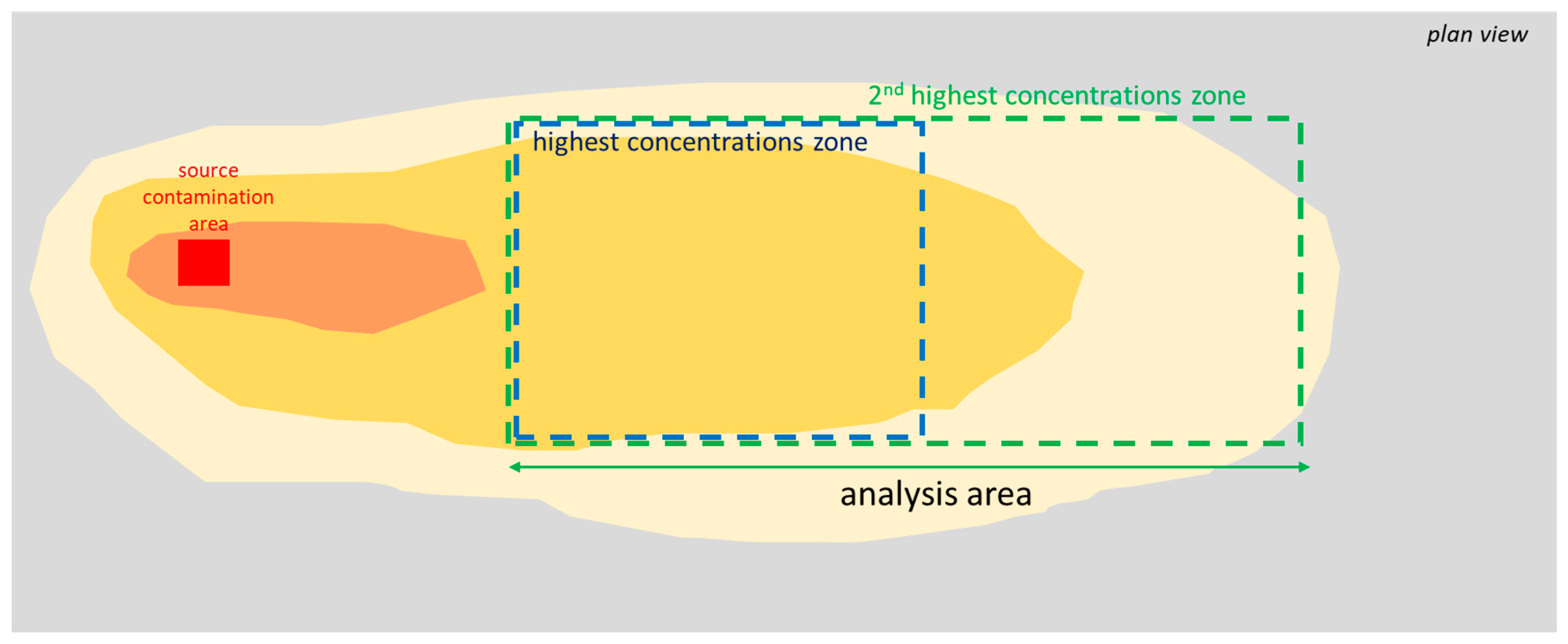
Table 2. Among the inputs, the mean concentration value at the interface between transmissive and nontransmissive zones is important, as well as the extension of the contaminated area. The length and width of the modeled area for the SRM can be entered directly or selected using a historical contour map, preferably one with the highest historical concentrations observed during the monitoring record (drawing a downgradient transect line perpendicular to groundwater flow and an upgradient transect line perpendicular to groundwater flow).
For the field and synthetic cases, the simulations were run performing a “plume analysis”, and the length and width of the polluted area were chosen as shown in
Figure 5. The blue box is usually drawn around the highest concentration contour downgradient of the source area, while the green box is usually drawn around the second highest concentration contour downgradient of the source area. The width of this green box is fixed on the basis of the transverse distance of two points referring to the same isocontour line. Because the model estimates the results on the right edge of the external rectangle, the length is defined on the basis of the position of the target point.
Both the loading concentration value in the modeled source area and the time when the contamination source started and stopped are crucial parameters to obtain good results. Since the contamination event often occurs much earlier than the installation of the monitoring wells, the assessment of the loading concentration value may be very difficult. In [
48], two approaches are suggested to evaluate the value: the first involves studying the history of the site and information about the processes (e.g., presence of Dense Not Aqueous Phase Liquids or other contaminants released); the second involves setting the maximum concentration measured over time as the load concentration value in the study area.
By means of the Toolkit, it is therefore possible to estimate both the concentration of contaminants at a monitoring point in the transmissive zone downgradient of the modeled area and the mean contaminant concentrations leaving the source area, as well as the concentration of contaminants at each point in the low permeability zone at different times. Moreover, the SRM allows for the evaluation of the mass discharge in the low permeability unit. Hence, in one monitoring point in the transmissive zone, it is possible to estimate the time to reach concentration values equal or lower than the remediation targets.
In the face of a relative ease of implementation and use, the SRM has some limitations related to the hydrogeological context or the type of contamination. For instance, the SRM evaluate the effects of only one contaminant at a time. Up until now the effect of matrix diffusion in a low transmissive zone has been studied for chlorinated solvents and Methyl Tertiary Butyl Ether (MTBE), although matrix diffusion processes can be valid for each dissolved contaminant, but the overall impact could be different [
48]. Moreover, additional interpretation and expertise is required to apply the model in fractured rocks [
48]. Finally, the system is assumed to be of the “on/off” type, with a “loading” period that is extended for a defined time and then instantly switches to a “release” period, when the concentrations in the transmissive unit, not resulting from back diffusion, are considered null.
3.4. Numerical Model
The flow and solute transport numerical model in the aquifer were implemented by means of the finite difference numerical code MODFLOW/MT3DMS, in order to replicate the four scenarios described in
Section 2.2. In the hydrogeology field, MODFLOW/MT3DMS are the most widely used programs to investigate environmental problems related to forecasting quantitative and qualitative impacts on groundwater resources. MODFLOW-2000 (version 2000, United States Geological Survey, Reston, VA, USA) [
40], developed in 1988 by the USGS (United States Geological Survey), is the most popular code for groundwater flow simulation in a three-dimensional porous medium. The partial differential equation that describes the three-dimensional transient groundwater flow in heterogeneous and anisotropic media, along the main directions (x, y, z), is written as:
where K
xx, K
yy, and K
zz are the hydraulic conductivities along the main directions (m/s), t the time (s), h the piezometric head (m), q
s the volumetric flow rate per unit volume of aquifer representing sources and sinks ((m
3/s)/m
3), and Ss the specific storage (m
−1).
MT3DMS (Model Transport in 3 Dimensional Multispecies) model is a modular three-dimensional multispecies transport model for simulation of advection, dispersion, and chemical reactions of contaminants in groundwater systems [
50], and it represents the evolution of MT3D. MT3DMS can be used to simulate concentration changes of miscible contaminants in groundwater considering advection, dispersion, diffusion, and some basic chemical reactions, with various types of boundary conditions and external sources or sinks. It can also accommodate very general spatial discretization schemes and transport boundary conditions and is designed for use with any block-centered finite difference flow model.
The partial differential equation describing the fate and transport of contaminants of species k in three-dimensional, transient groundwater flow systems, disregarding chemical reactions, can be written as follows [
50]:
where C
k is the dissolved mass concentration of species k (kg/m
3), D
ij the diffusion–dispersion matrix (m
2/s), C
s is the concentration of the sources or sinks (kg/m
3).
Several numerical models (
Table 3) were developed by implementing properties and hydraulic conditions of the four scenarios defined in
Section 2.2.
For each numerical model, the modeling domain was equal to the study area defined in
Section 2.2, the grid was discretized through 175 rows and 230 columns (
Figure 6), with square cell sizes ranging from 10 m in external area to 1 m in the central area where the clay lense was present. Twenty layers were implemented as vertical discretization in models named A, B, and C; the first 1.5 m thick and the subsequent ones 0.5 m thick (total thickness equal to 11 m); layers 8 to 20 were deleted (total thickness equal to 4.5 m) in model D. For each model, the first layer is partially saturated, unlike subsequent saturated layers.
Hydrogeological and physical properties assigned to the domain are described in
Table 2; sand properties were assigned to the transmissive zone cells (layers from 1 to 20), whereas clay lense properties were assigned to the nontransmissive zone cells (refined area in layers 8–12).
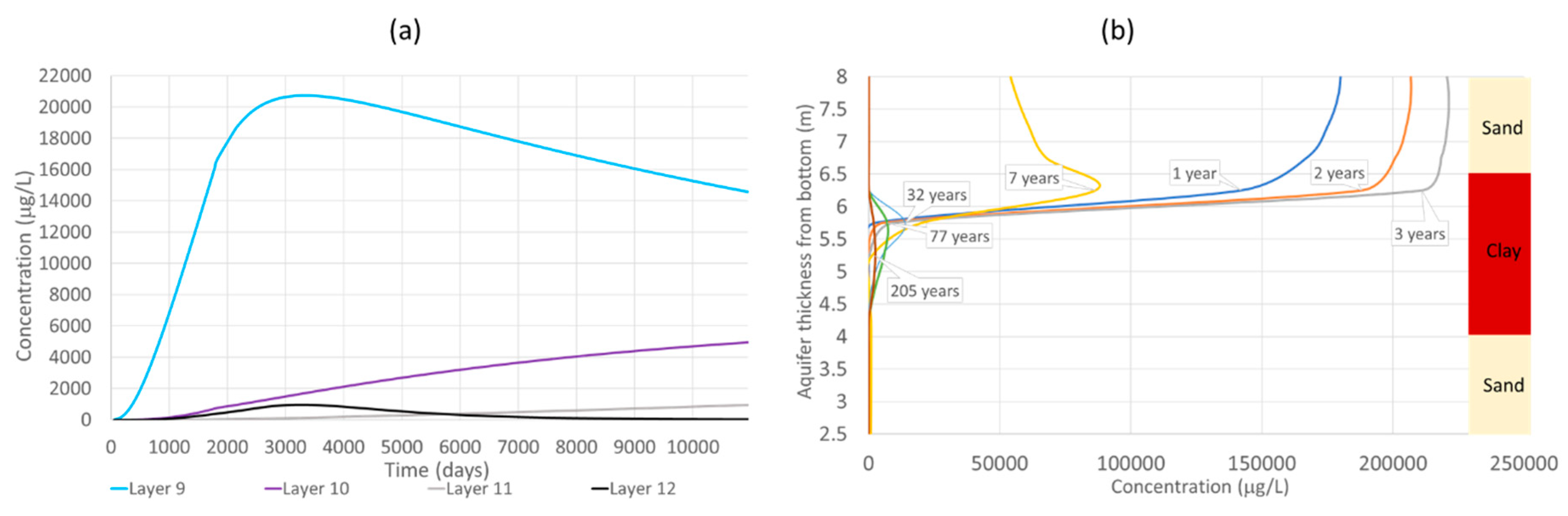
Initially, models A, B, C, and D were run in a transient regime 5 years long to reproduce the six “loading” phases of contamination in aquifer. Subsequently, numerical simulations of models A1, A2, B1, B2, C1, C2, D1, and D2 were run in a transient regime 200 years long to reproduce two different remediation scenarios; A1, B1, C1, and D1 simulated a remediation by natural attenuation (i.e., natural groundwater flow), whereas models A2, B2, C2, and D2 simulated a remediation by means of a P&T system.
For groundwater flow boundary conditions, two constant head boundary conditions (Dirichelet condition) were assigned at the west and east boundaries (values defined in
Section 2.2).
Internal conditions required some distinction according to the model developed:
- -
Model A: the internal specified mass flow condition was used defining a constant water flow with a specified concentration (Neumann condition) to reproduce the source of contamination; it was inserted in a specific area of the domain (36 m2) from layer 1 to 7. The concentration value (317.1 mg/L) was introduced into the aquifer as a TCE mass equal to 500 kg for 5 years, with a low flow rate (0.01 L/s, as not to influence the hydraulic head distribution). A1 and A2 models: the internal specified mass flow condition was no longer implemented. In the A1 model, no additional internal conditions were added, whereas in the A2 model, the Neumann condition (through “analytic element well”) was added, 140 m downgradient of the contamination source area, to reproduce the pumping operation of one well (flow rate equal to 40 m3/day).
- -
Model B: the same internal condition as model A was implemented at the same cells of model A, but from layer 1 to 12. A constant concentration value (304.4 mg/L to reproduce 480 kg TCE mass) in the transmissive zone and initial concentration value (3703.7 mg/L to reproduce 20 kg TCE) in the nontransmissive zone were assumed. B1 and B2 models: the internal specified mass flow condition was no longer implemented (i.e., primary source instantly removed). In B1, no additional internal conditions were added, whereas in B2 the same Neumann condition as in model A2 was implemented to simulate the pumping well.
- -
Model C: the same internal condition as model B to reproduce the contamination source (480 kg TCE mass); a constant concentration value (304.4 mg/L) was assigned at the same cells as in model A, from layer 1 to 7; another constant concentration value (18,518.5 mg/L) was implemented only in layer 10 on the same area (reproducing 20 kg TCE). C1 and C2 models: the internal specified mass flow condition was no longer implemented; in C1 no additional internal conditions were added, whereas in C2 the same Neumann condition as in A2 was implemented to simulate the pumping well.
- -
Model D: same Neumann condition as model A applied to simulate the contamination source. D1 and D2 models: the internal specified mass flow condition was deleted; in D1 no additional internal conditions were added, whereas in D2 the same the Neumann condition (through “analytic element well”) as in A2 was implemented to simulate the pumping well, but in this model the flow rate equaled 7.2 m3/day.
5. Conclusions
The P&T system is a very widespread remediation technology because of its simplicity and versatility. However, these systems have some limitations, which frequently do not allow for the achievement of remediation targets in reasonable times. Therefore, a preliminary methodology allows for an estimate of the remediation time of P&T systems and to understand if the planned strategy is feasible or an alternative methodology is needed, or if it is better to couple the P&T with a source control technology to enhance remediation. Indeed, often the hydrogeological setting (e.g., presence of areas with low permeability) or the type of contaminants (e.g., NAPL) lead to a prolongation of the remediation times of a P&T system.
In the present work, some easy to apply analytical approaches were used to evaluate the remediation time of a P&T system for a synthetic case study; the batch flushing (considering advection and sorption terms), ADR (considering advection sorption and dispersion terms), and SRM (also considering matrix diffusion) models were compared with a numerical solution. These analytical models were applied to a synthetic case to show how they are able to provide truthful results if applied in accordance with the hydrogeological model, without the need to implement a specific numerical model.
This study represents a first result showing that in the case of homogeneous and hydraulically transmissive domains, the use of the batch flushing and ADR models provide realistic evaluation of the remediation times due to the P&T system. In contrast, for cases where low permeability zones are present and matrix diffusion plays a key role, more complex models, such as SRM, need to be adopted.
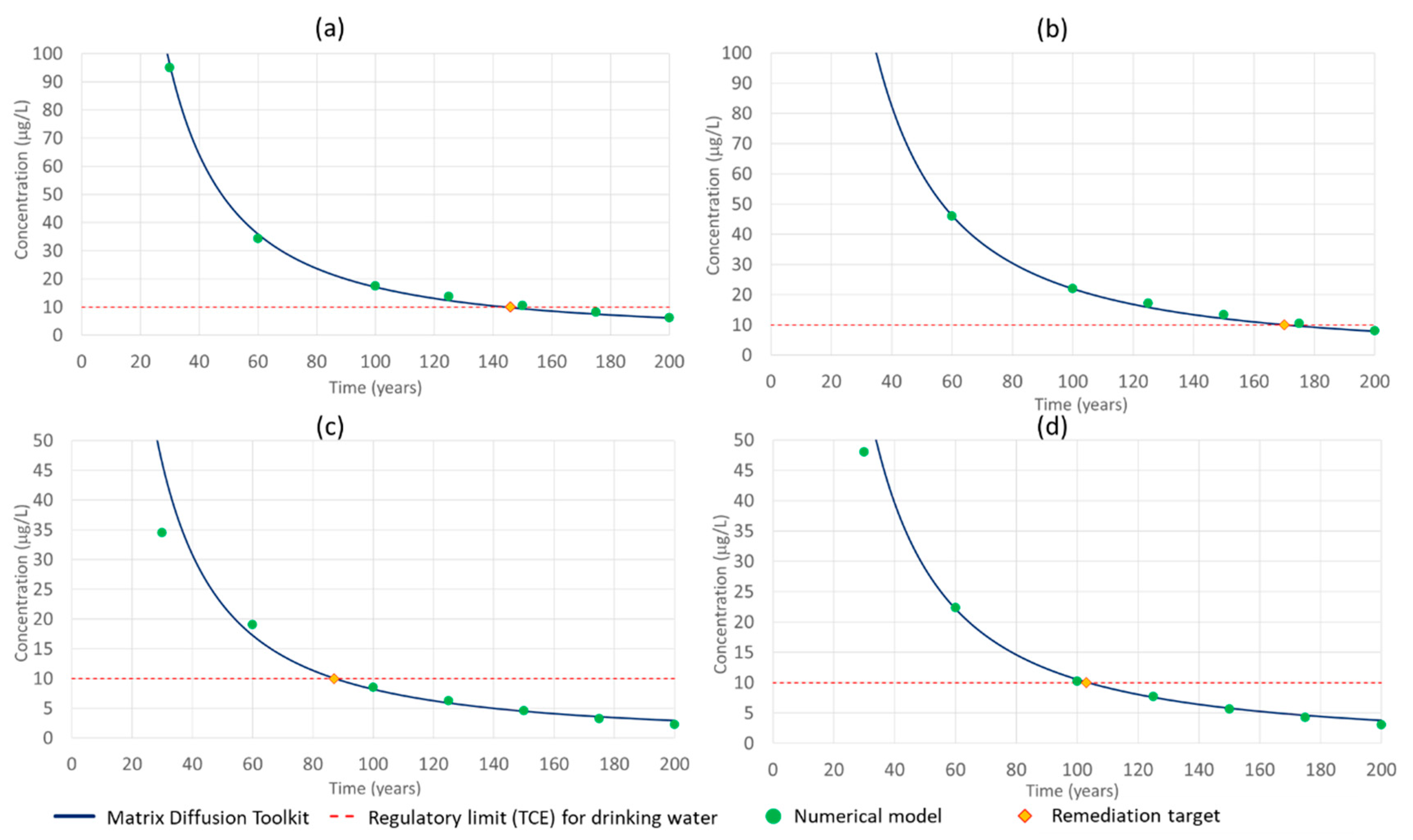
The analytical solutions were also applied at a field scale for 1,2-DCE contamination under natural attenuation and P&T conditions. Batch flushing and ADR model underestimated remediation times (less than 7 and 4 years, respectively) when compared to the results of actual monitoring data, whereas SRM provided remediation times (less than 30 years) that were more truthful. Moreover, for this case where a contamination event is ongoing, the installation of a P&T system would not cause any appreciable decrease in the remediation times. That means P&T can be a good solution for plume containment, but is expected to be unable to improve the clean-up time if not combined with other remediation techniques.
In the synthetic case, several numerical solute transport models were implemented in MODFLOW/MT3DMS in order to simulate the effects of natural groundwater flow and a P&T system, with and without the presence of hydrogeological heterogeneities (i.e., low permeability zones). The results of the numerical model, in terms of time to reach a target concentration value, were compared to those of the analytical solutions, thus assessing the reliability of the analytical methods. In particular, the influence of back diffusion, which is among the main reasons P&T systems often come out as ineffective and unsustainable over time, was carefully analyzed to understand whether the SRM (easier and less expensive and time consuming than a numerical model) could provide reasonable outcomes.
When the aquifer is homogeneous, the batch flushing model results were comparable to the numerical models: 38 vs. 39.5 years (natural groundwater flow) and 31.6 vs. 35 years (P&T remediation). When hydrogeological heterogeneities play an important role, this method fails to provide a reasonable estimate of the remediation time, while the SRM results are much more realistic compared to the numerical models: 170 vs. 178 years (natural groundwater flow) and 103 vs. 110 years (P&T remediation).
This study was necessary to assess the advantages or disadvantages of the different approaches. It should be seen as the first step to understand whether a specific analytical approach could be applied to a “higher level” (laboratory scale or field case). In the future, the SRM should be thoroughly compared with a real case where a P&T system is active, in order to better assess the real applicability of this method.
Concluding, when P&T is active, concentrations in groundwater decrease faster than with natural groundwater flow; despite this aspect, the presence of hydraulically nontransmissive layers did not allow for the attainment of concentration targets in a reasonable time. This result suggests that concentration values in the transmissive zone are mainly influenced by mass contaminant release from the low permeability layers because of back diffusion. This phenomenon cannot be simulated by means of the batch flushing or ADR models; therefore, if based on a correct definition of the initial parameters, SRM can be considered a valid and easy to implement an analytical approach to evaluate remediation times whenever a contaminant has sufficient time to penetrate into low permeability layers.