Three-Dimensional Unstructured Grid Finite-Volume Model for Coastal and Estuarine Circulation and Its Application
Abstract
1. Introduction
2. Governing Equations in GOM
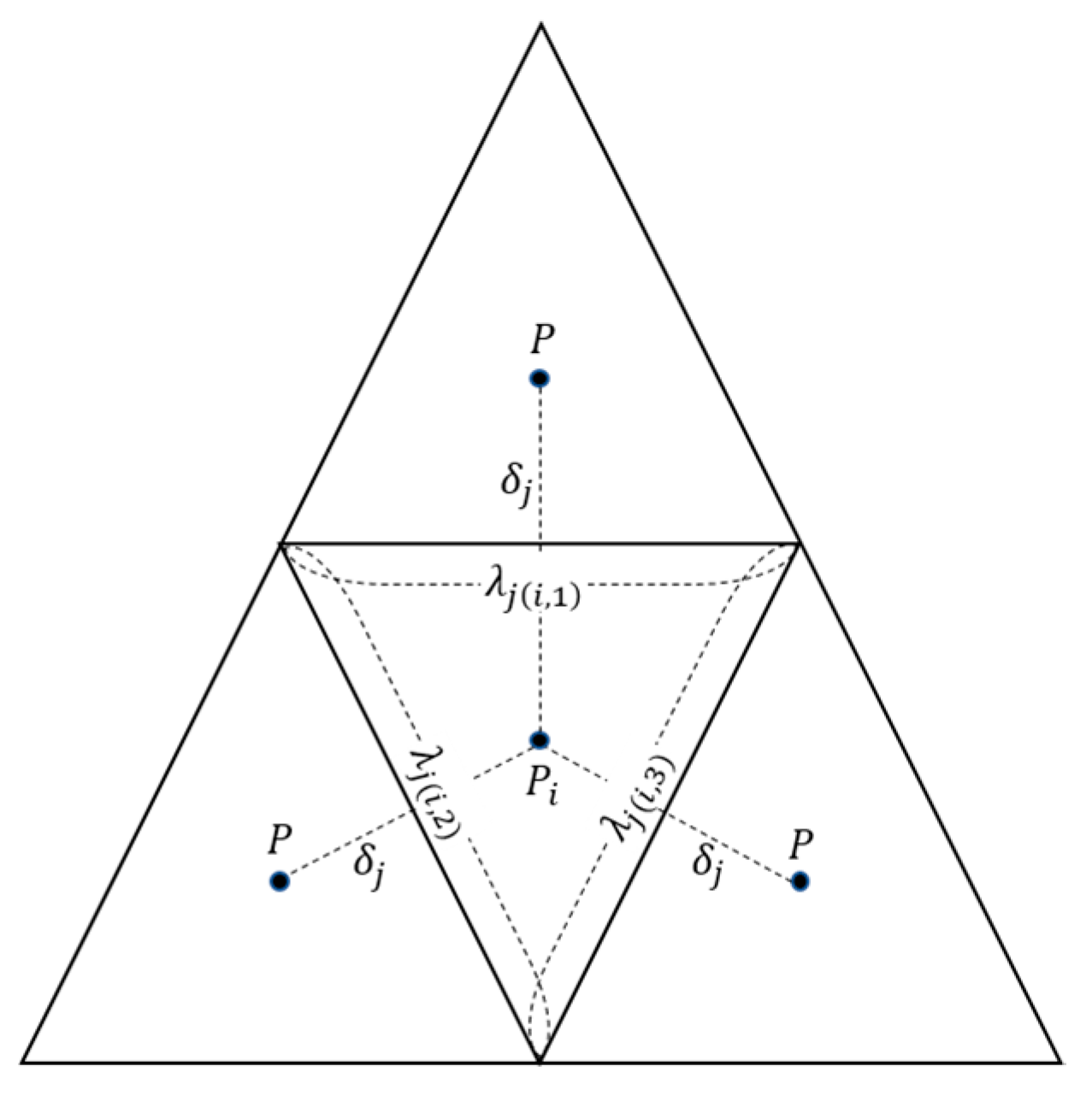
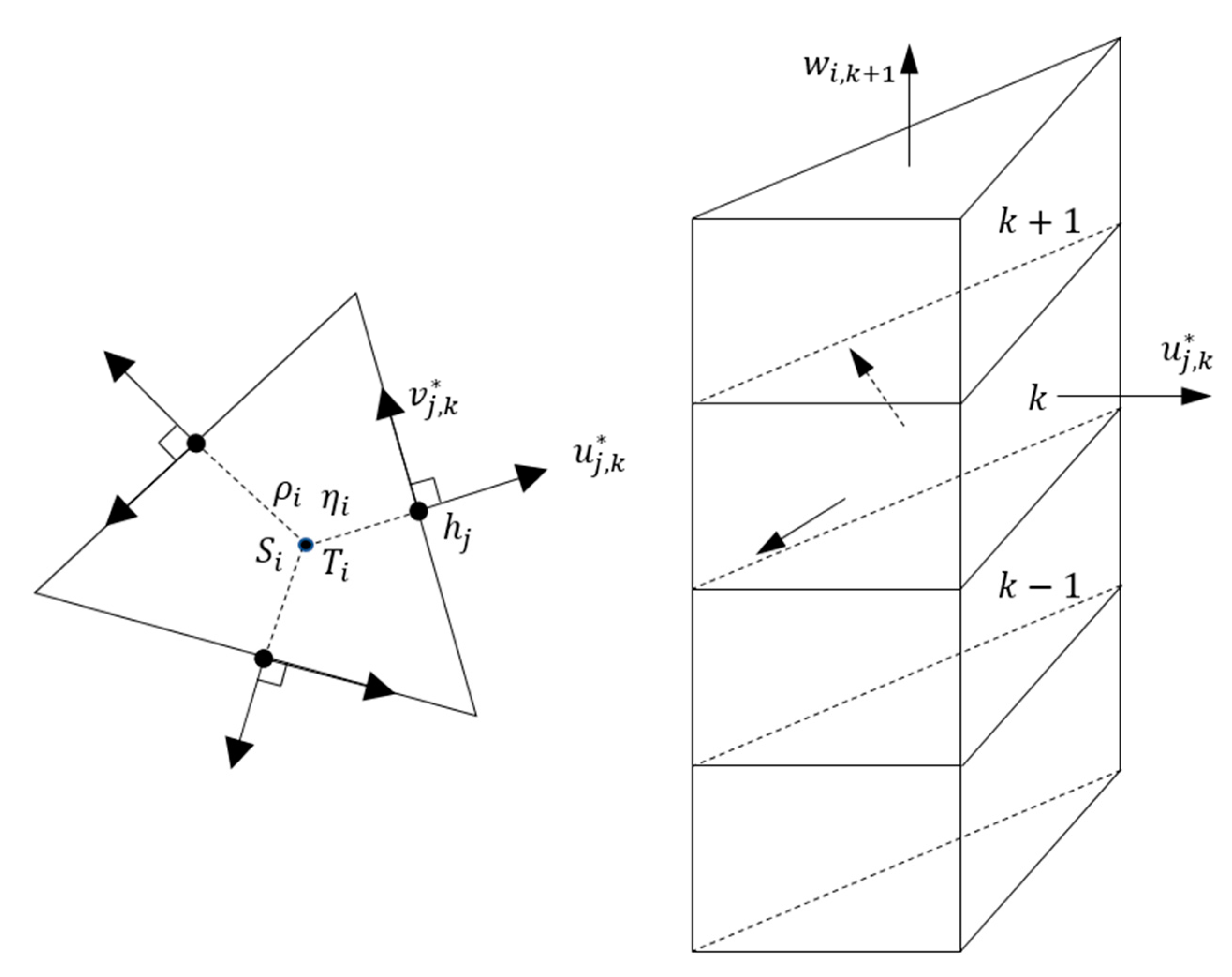
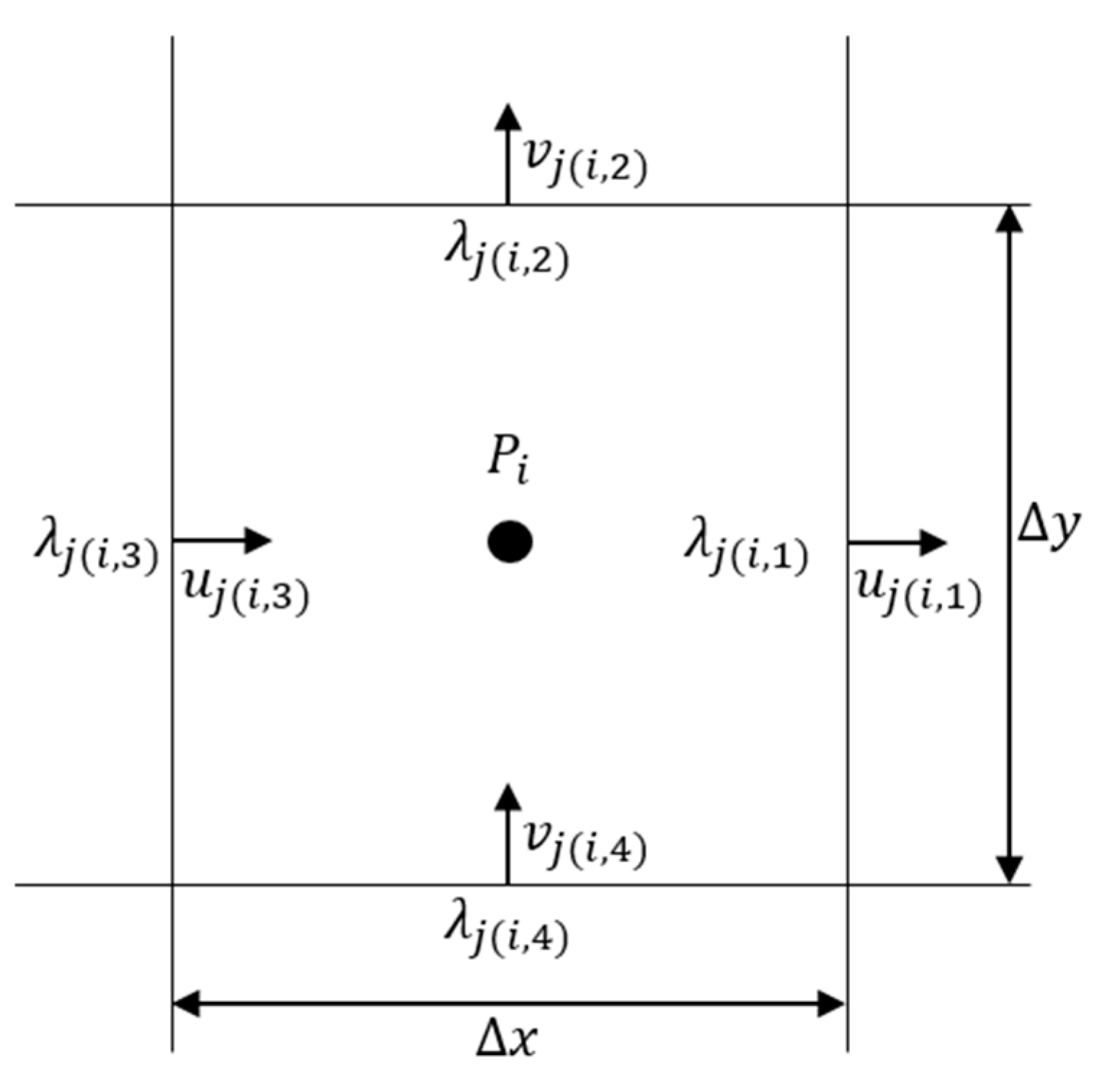
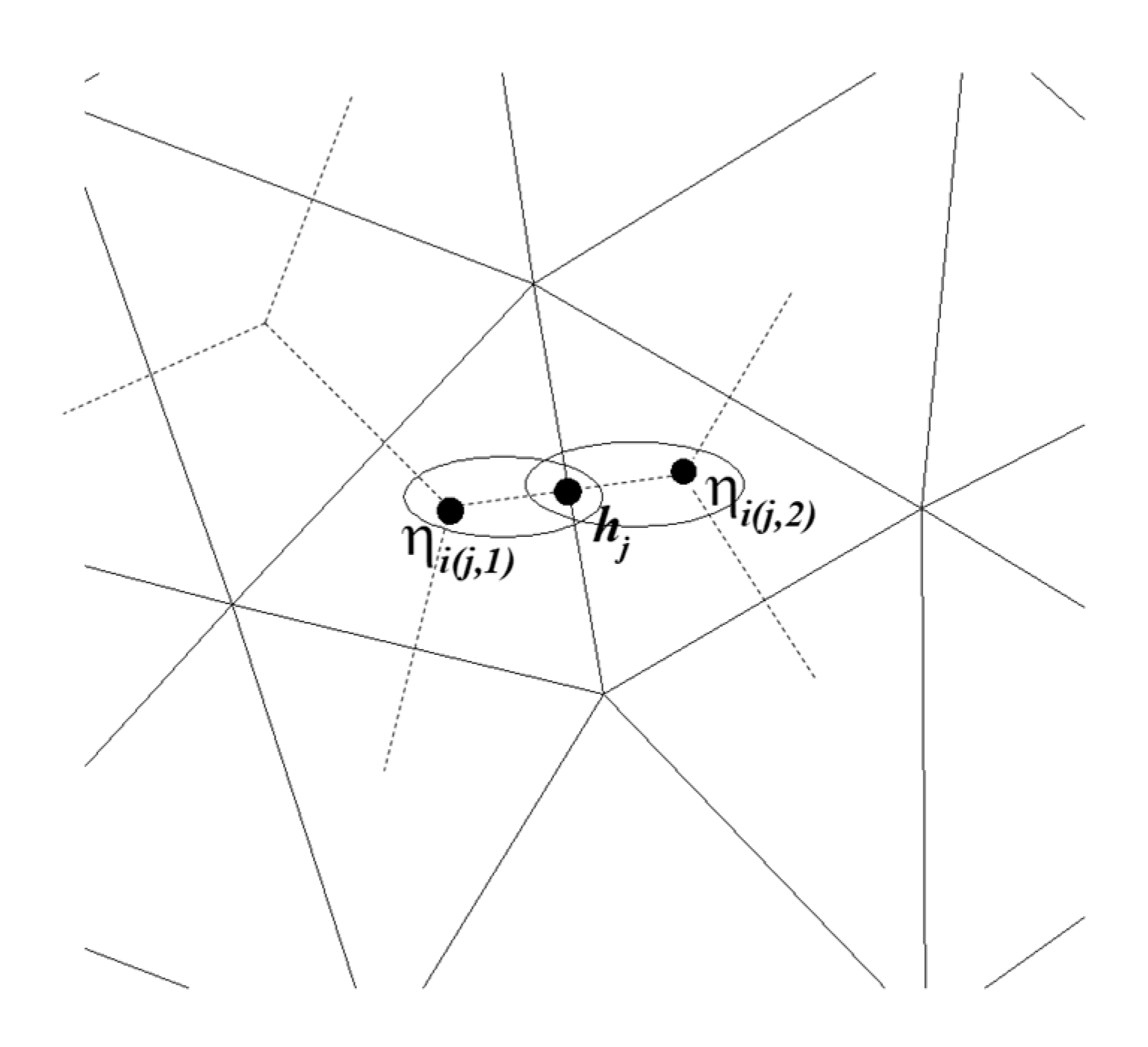
3. Unstructured Orthogonal Mesh and Index
4. Finite Volume and Difference Discretization
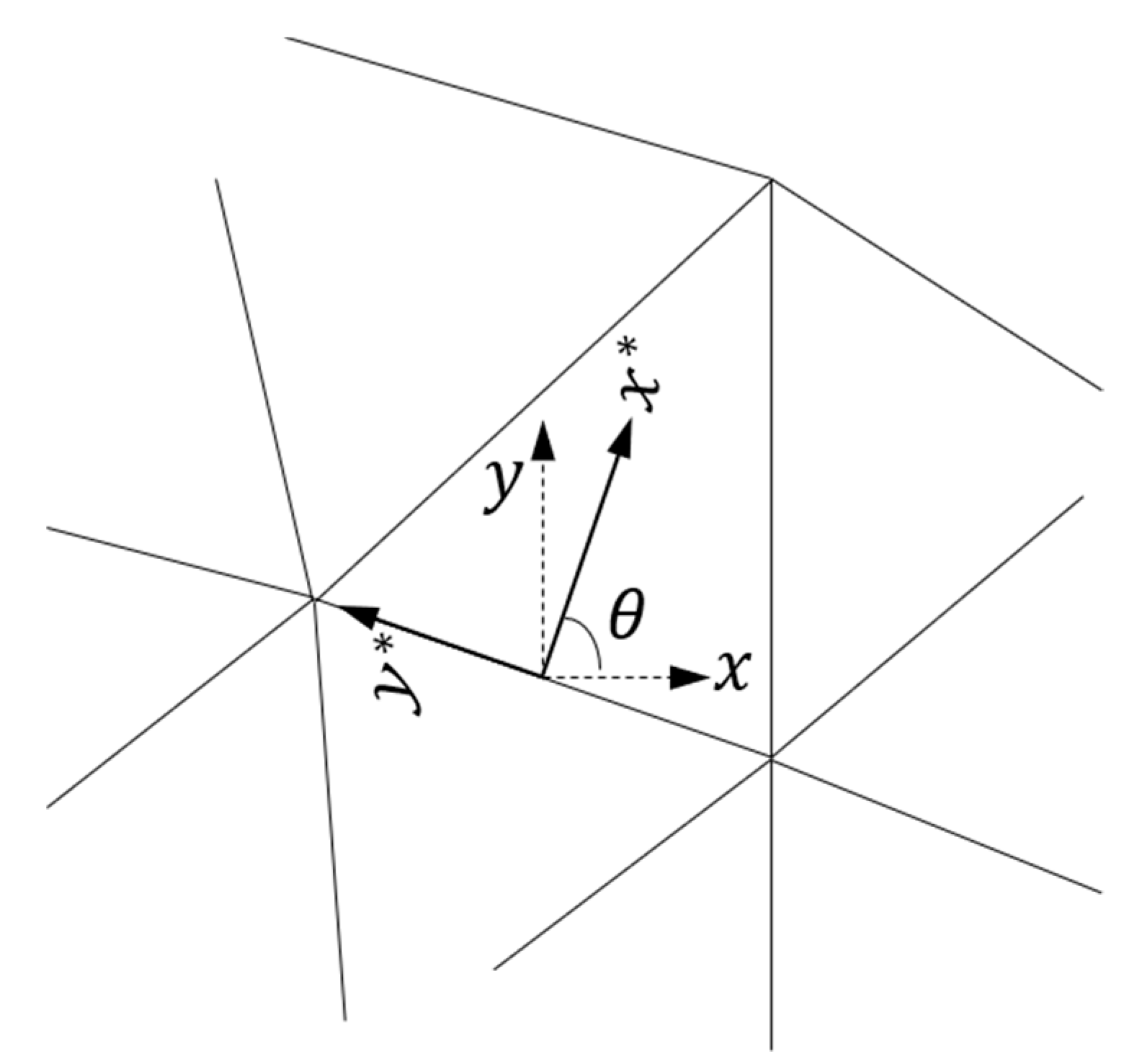
4.1. Momentum Equations in a New Coordinate
4.1.1. Barotropic Gradient and Vertical Mixing: (Semi-) Implicit Treatment
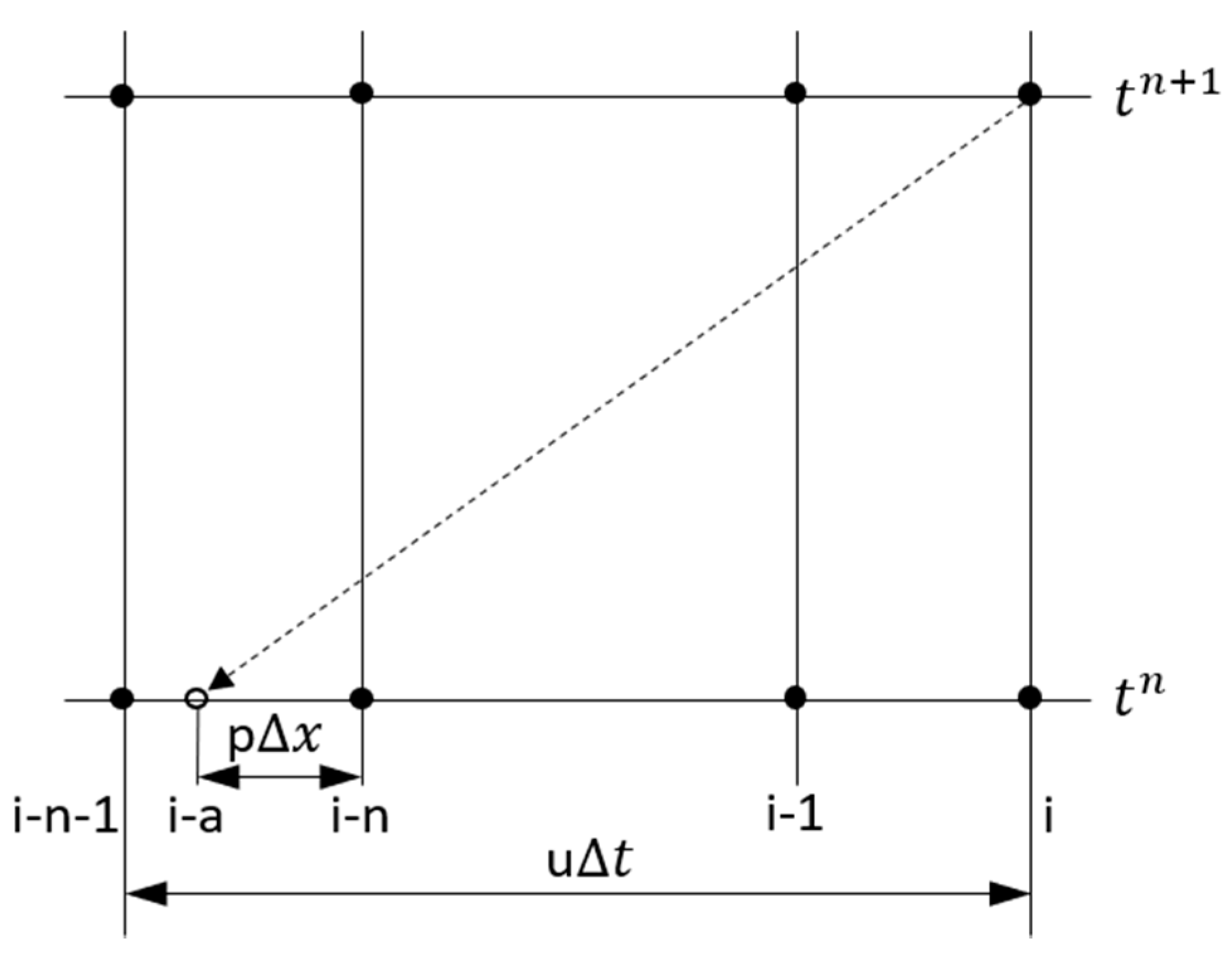
4.1.2. Nonlinear Advection: ELM
4.1.3. Coriolis: ELM
4.1.4. Horizontal Diffusion: The Finite Volume Cell-Centered Method
4.1.5. Atmospheric Pressure: Semi-Implicit Method
4.1.6. Baroclinic Gradient: Explicit
4.2. Boundary Treatment
4.2.1. Surface and Bottom Boundary Treatment for the Vertical Diffusion Term
4.2.2. Treatment of Open Boundary Conditions
4.3. Free Surface Equation
5. Solution Algorithm
5.1. Solution of Governing Equations
5.2. Treatment of Flooding and Drying
6. Model Verification with Analytical Solutions
6.1. Wind Setup
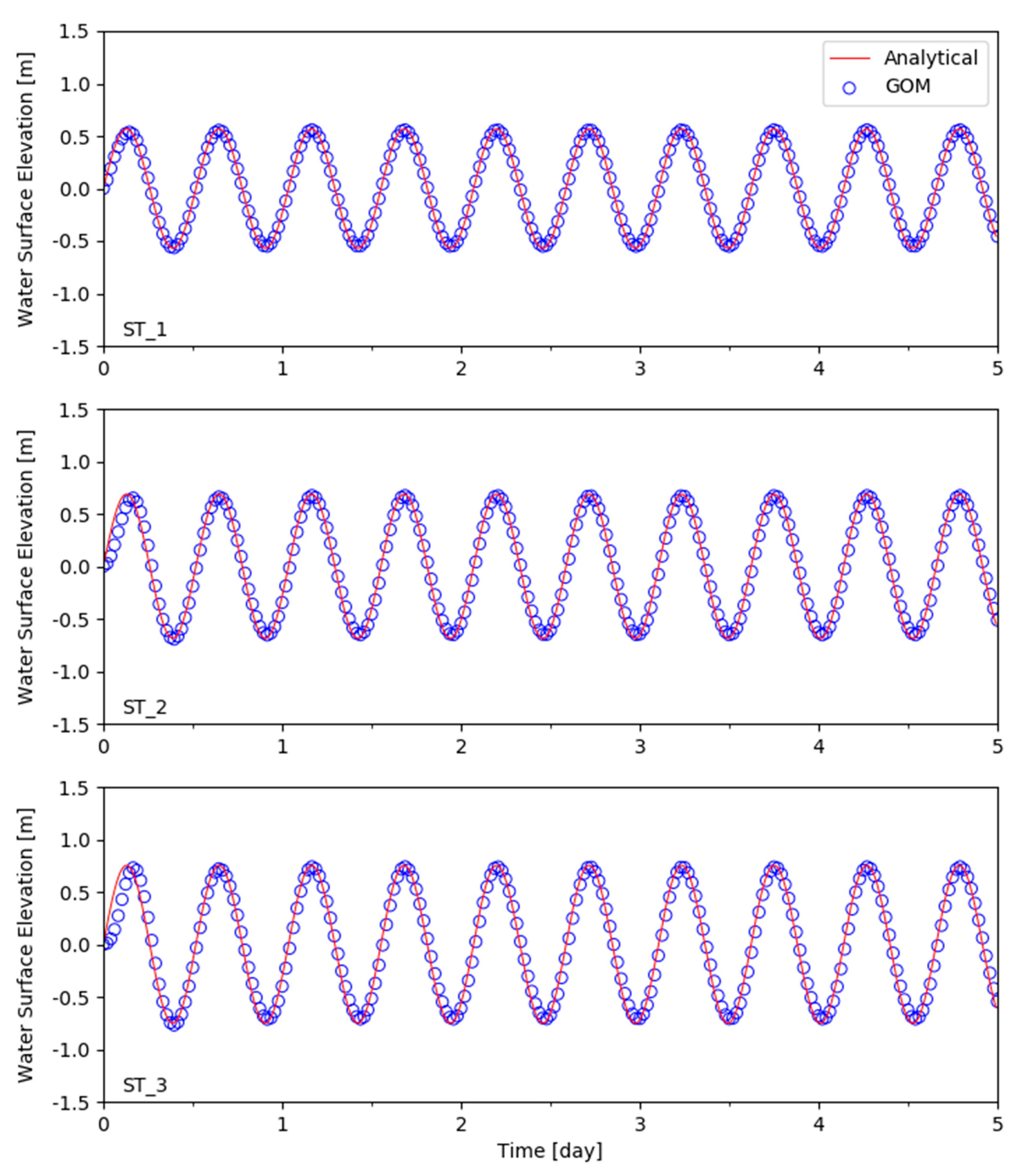
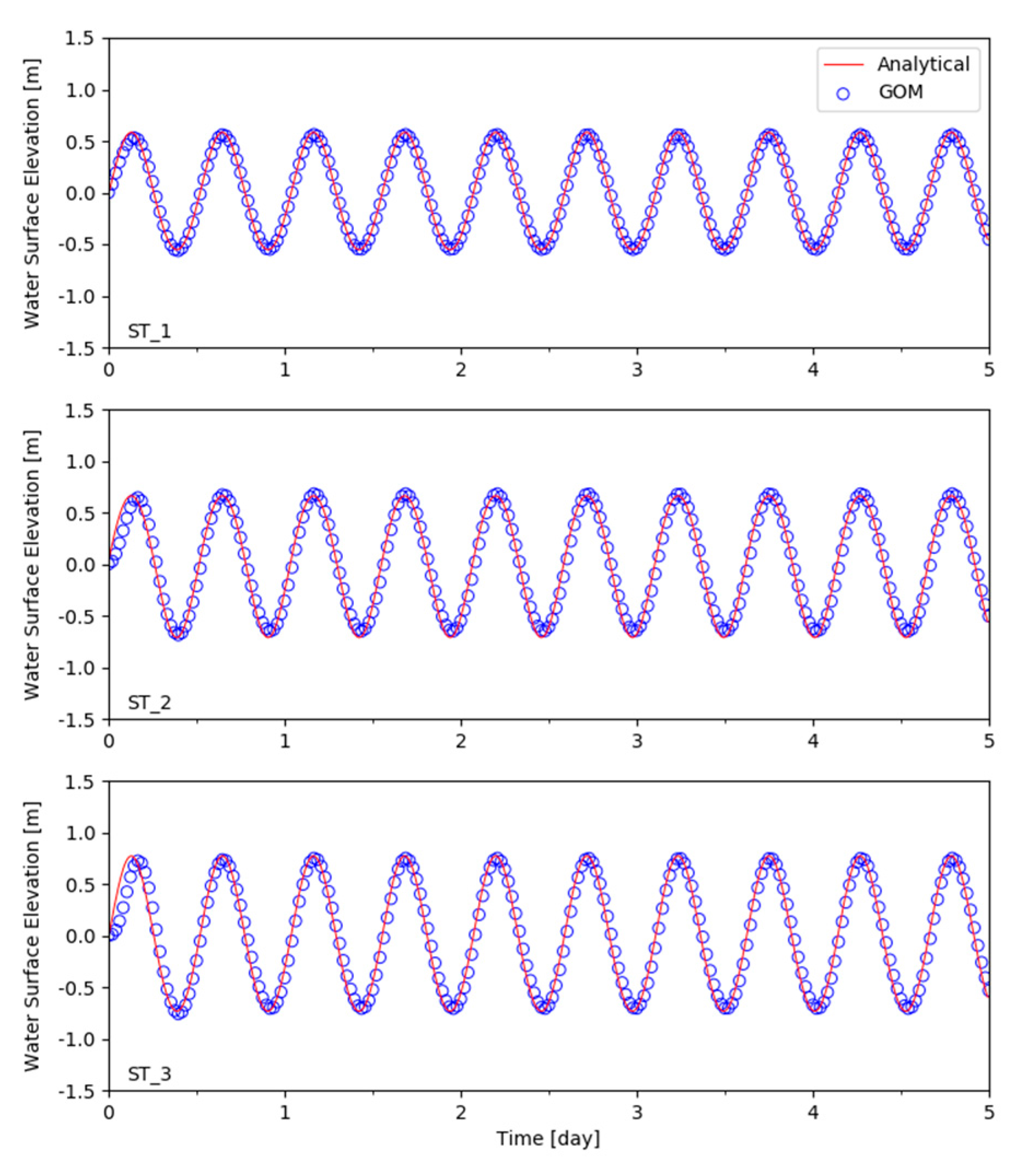
6.2. Tidal Propagation with Constant Depth
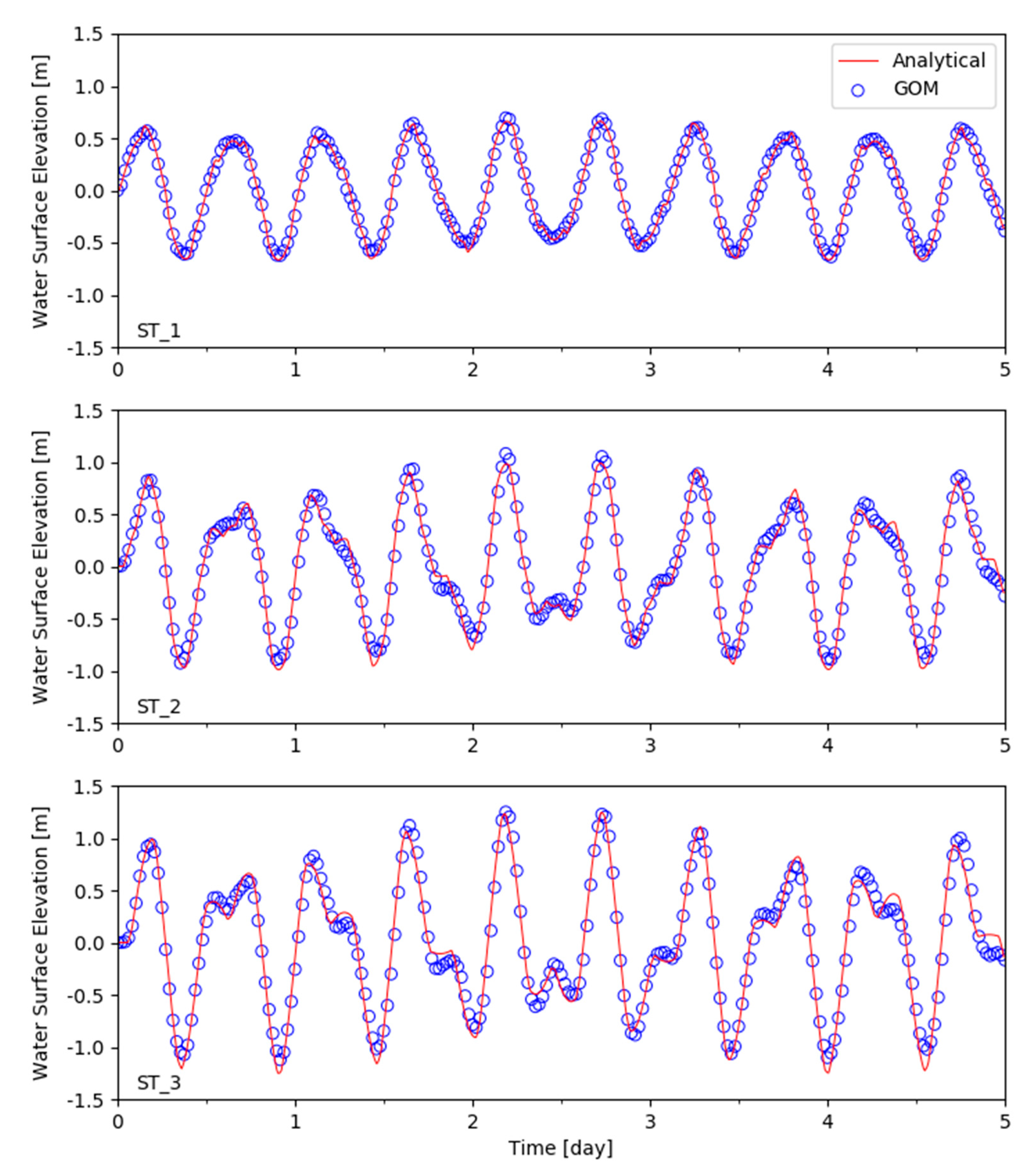
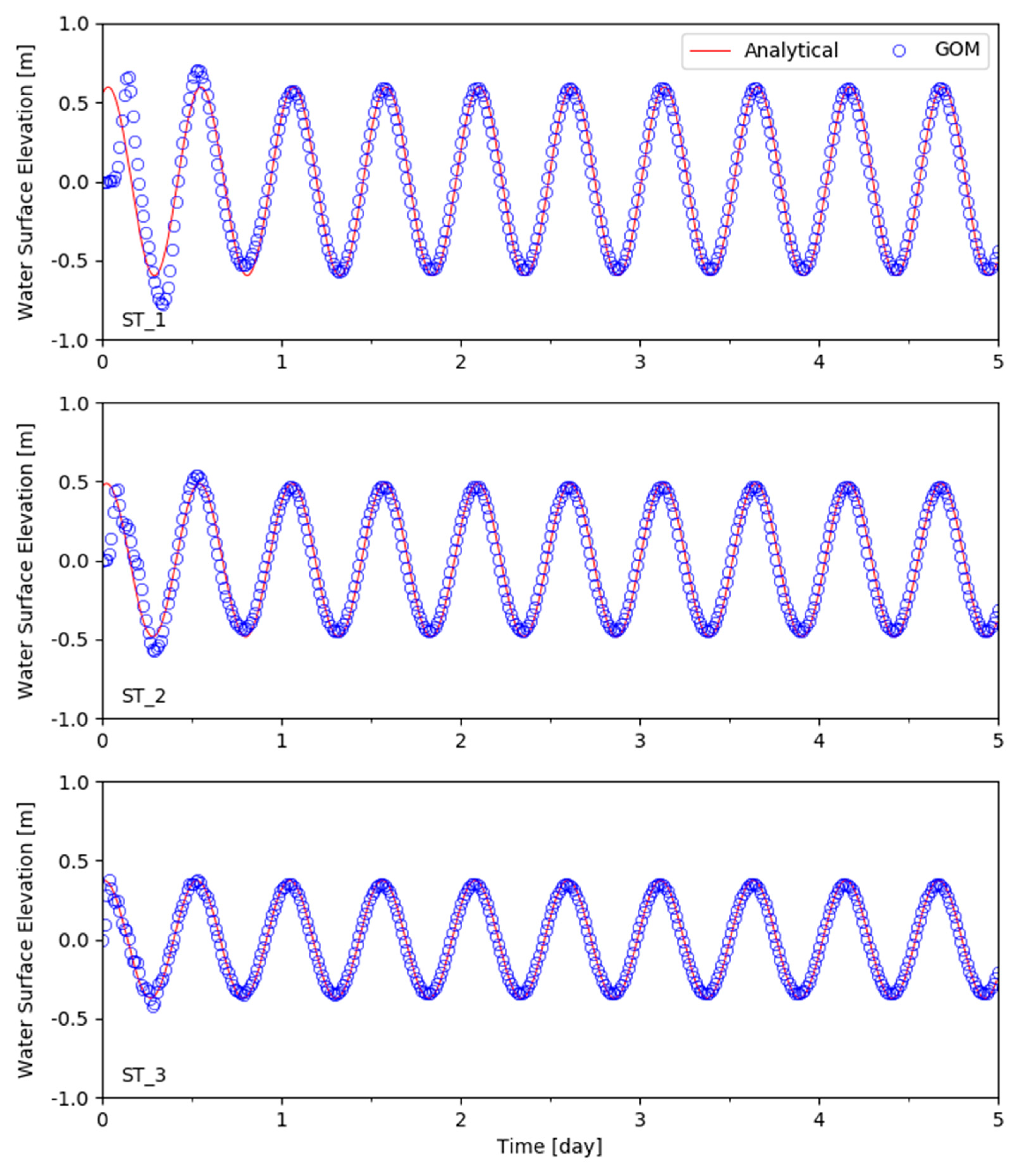
6.3. Tidal Propagation with Nonlinear Advection
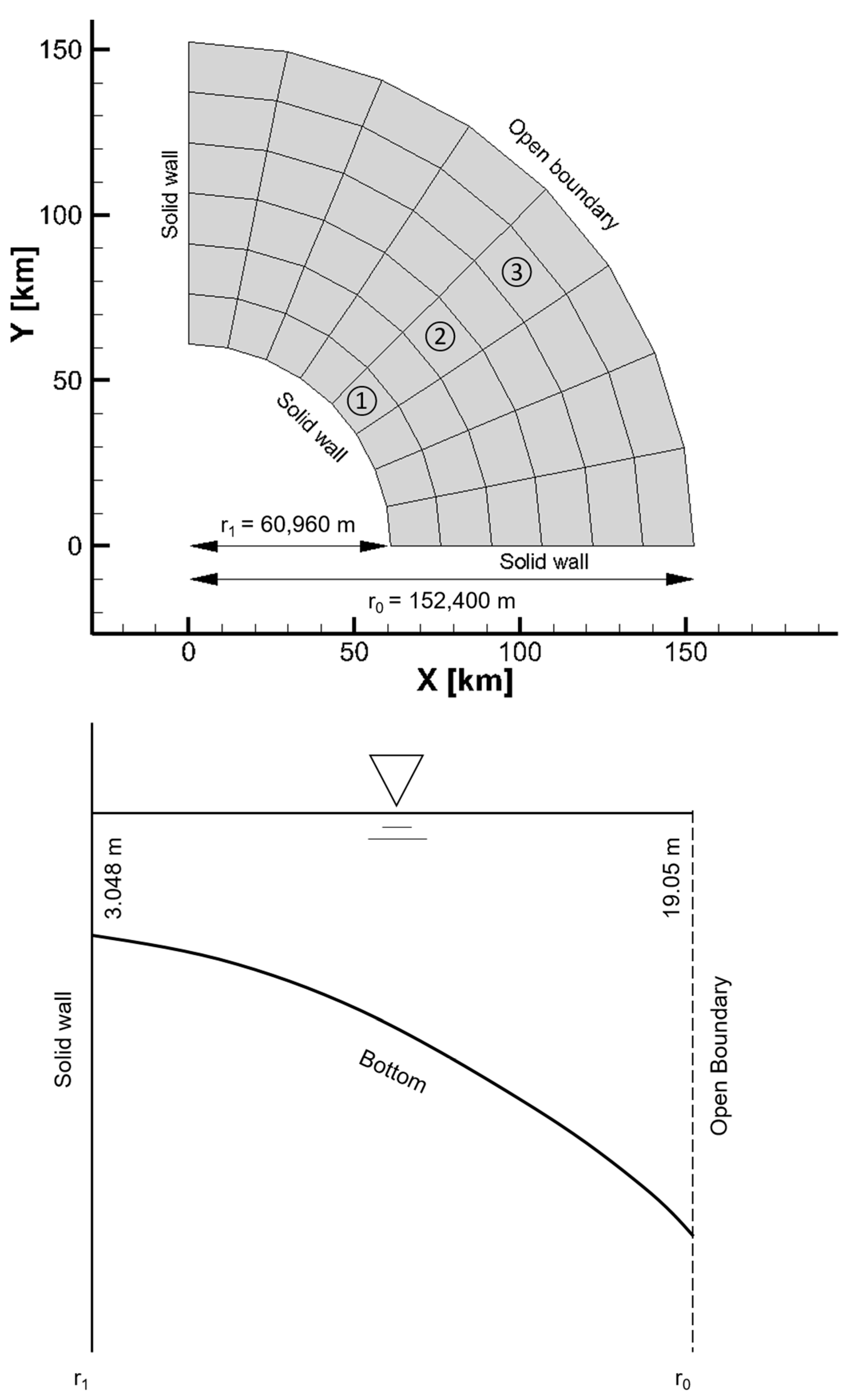
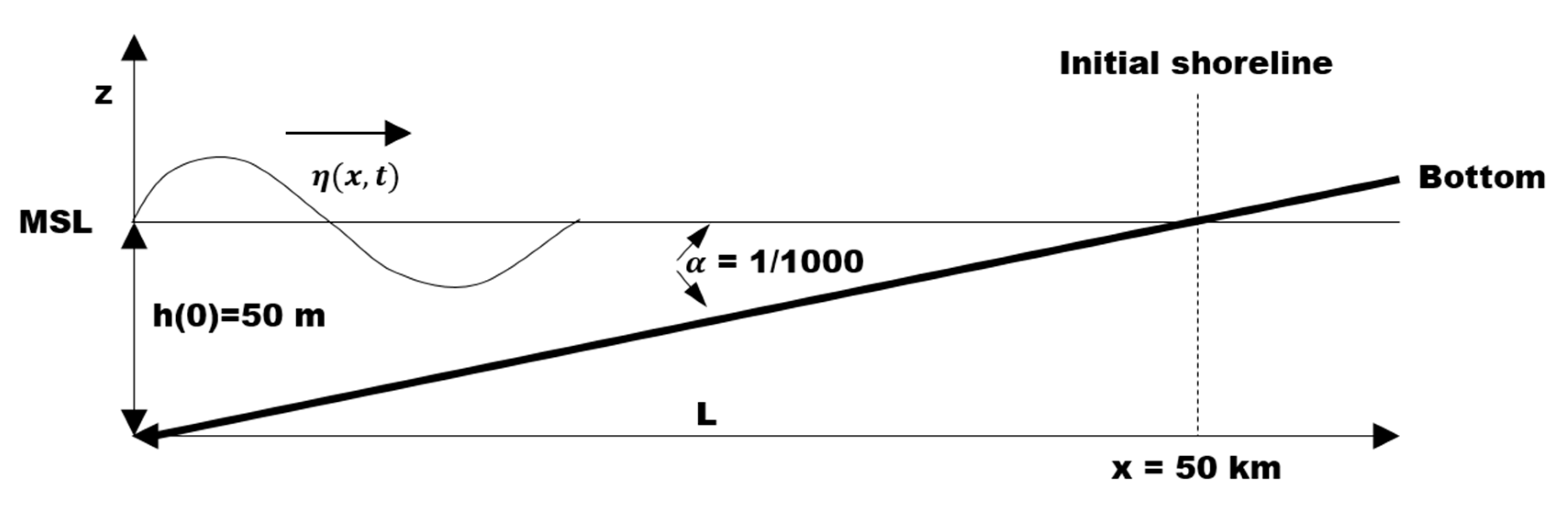
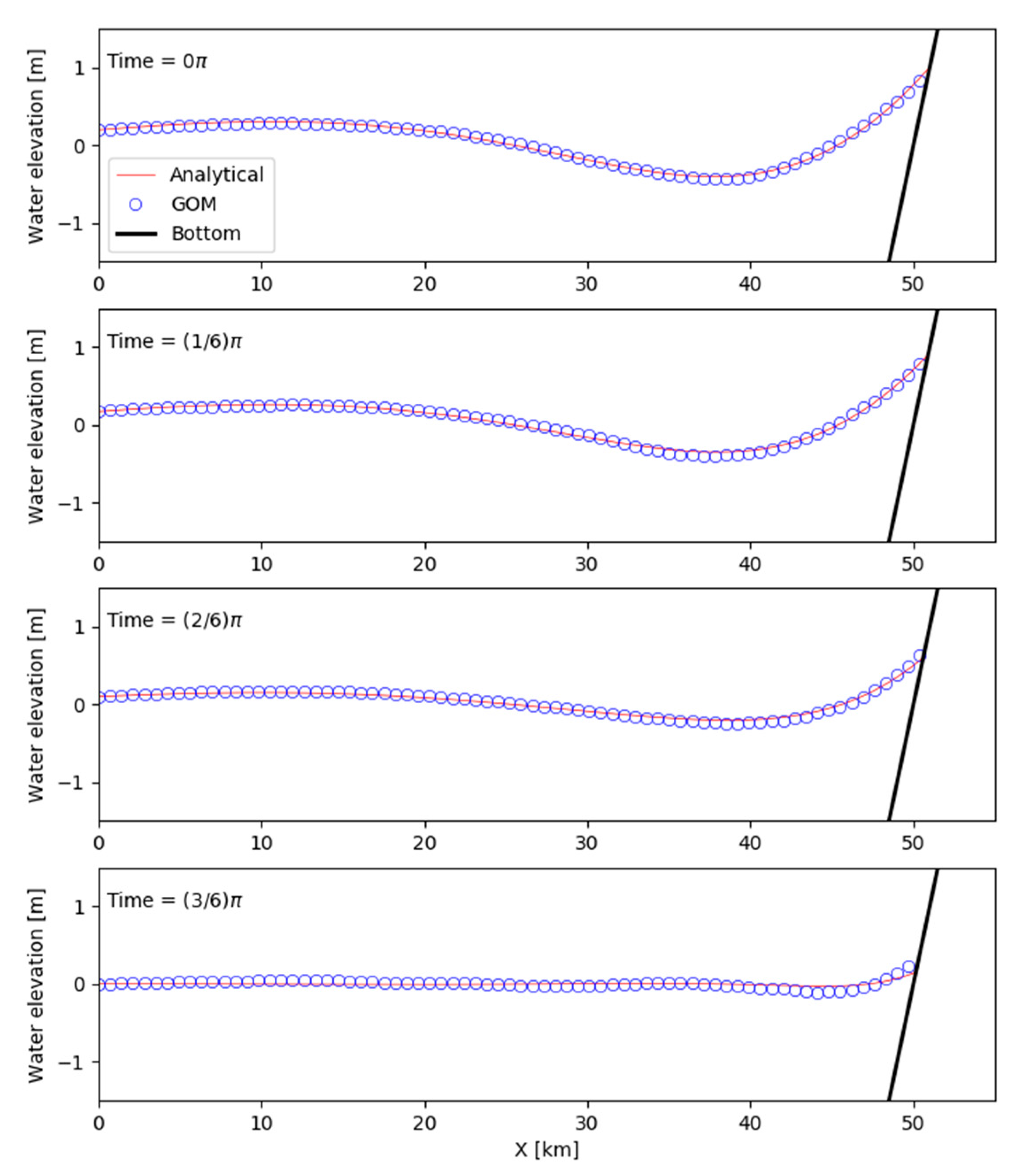
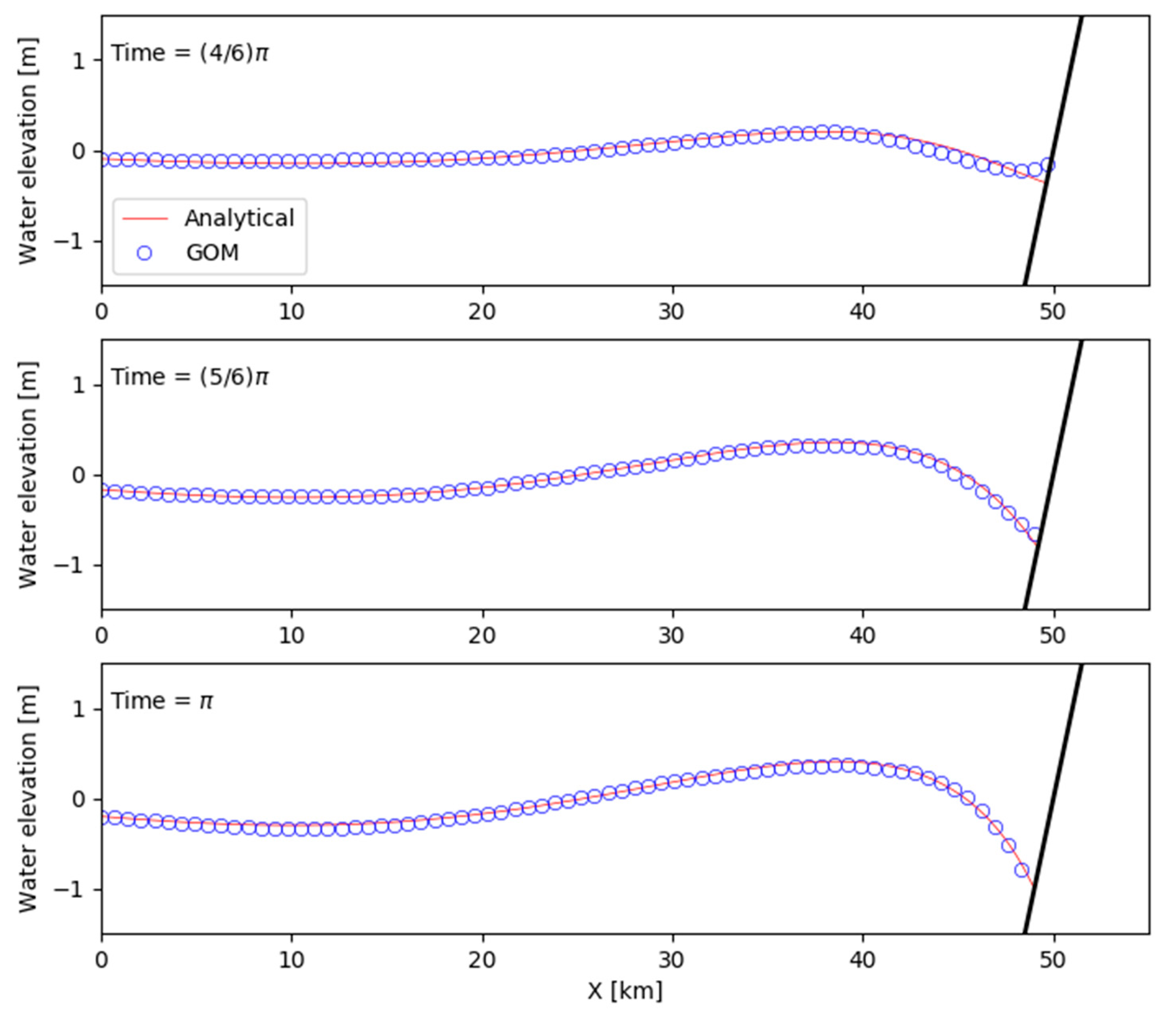
6.4. Quarter-Annular Harbor Test with a Sloping Bottom
6.5. Wetting and Drying Test on Tidal Flats
7. Model Application to the Texas Coast
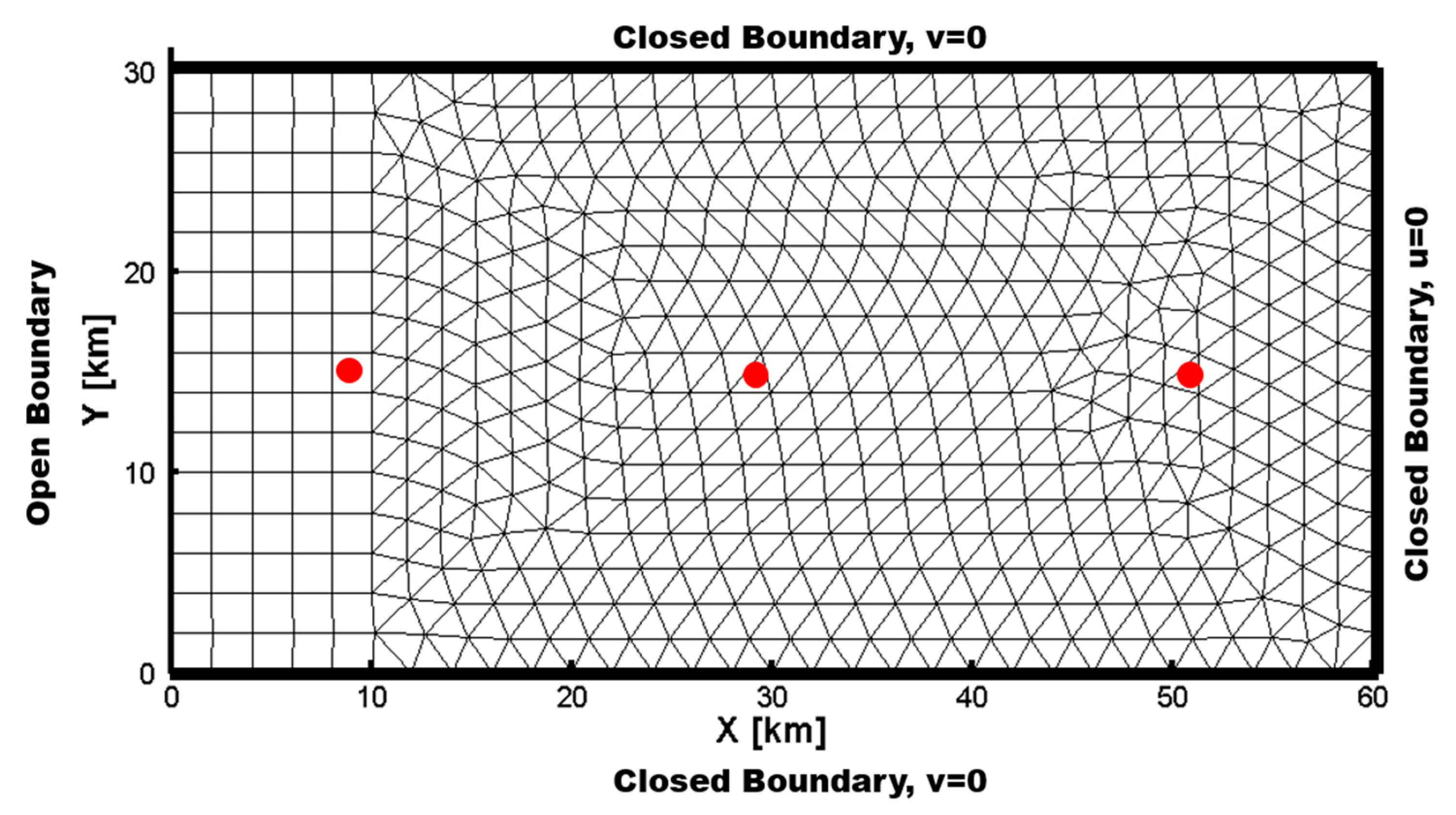
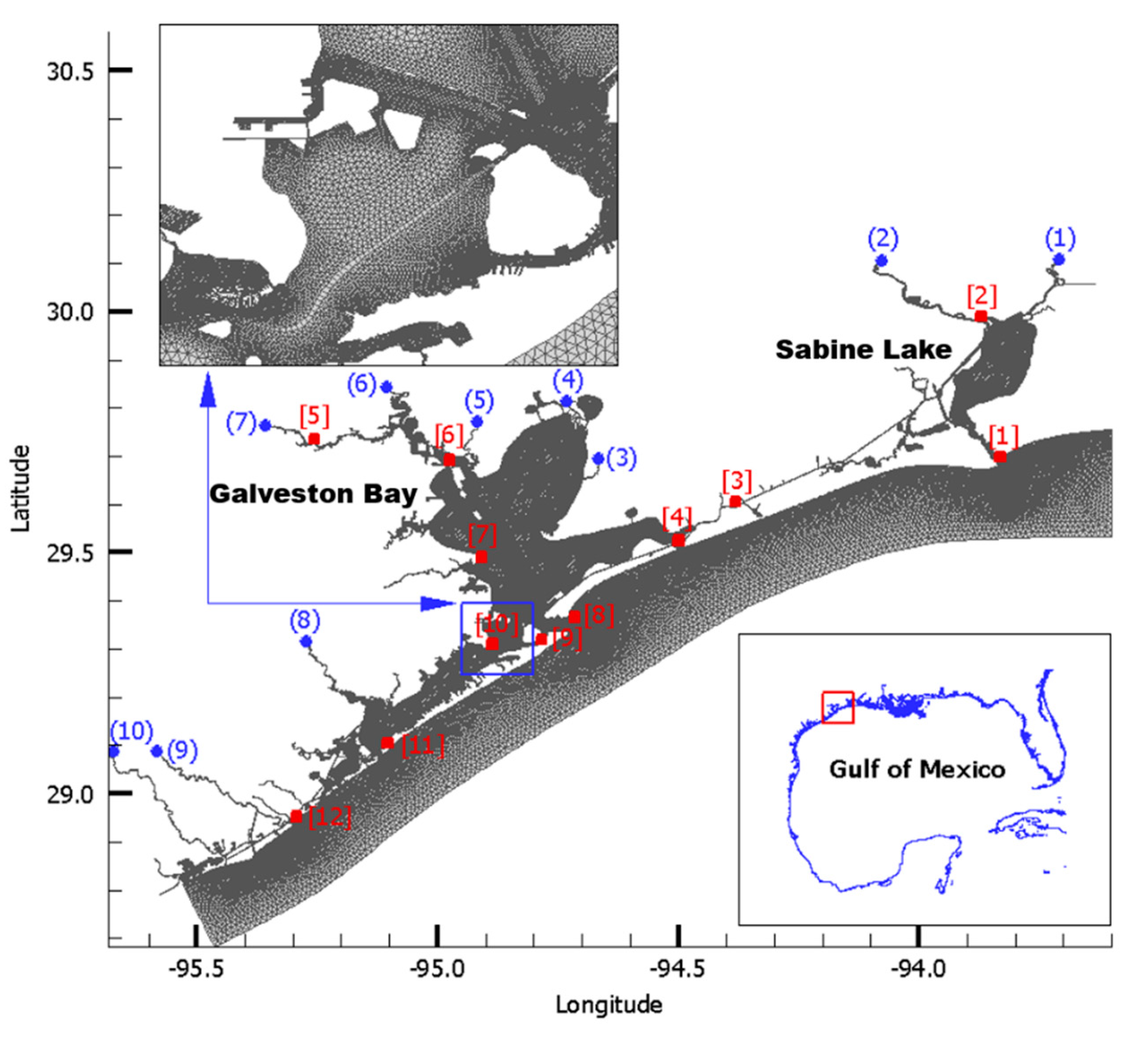
7.1. Model Domain and Grid Generation
7.2. Forcing Conditions and Model Setup
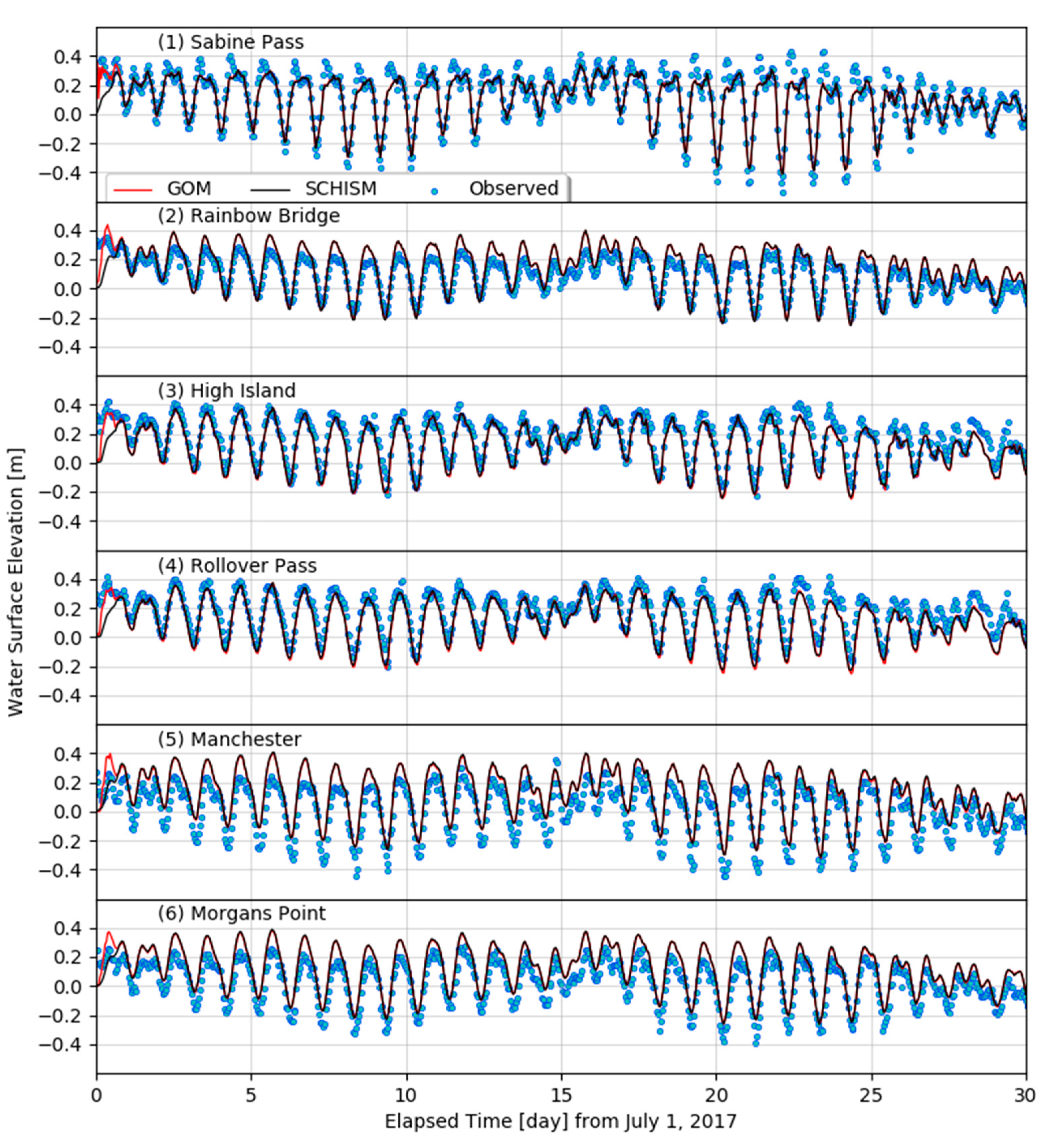
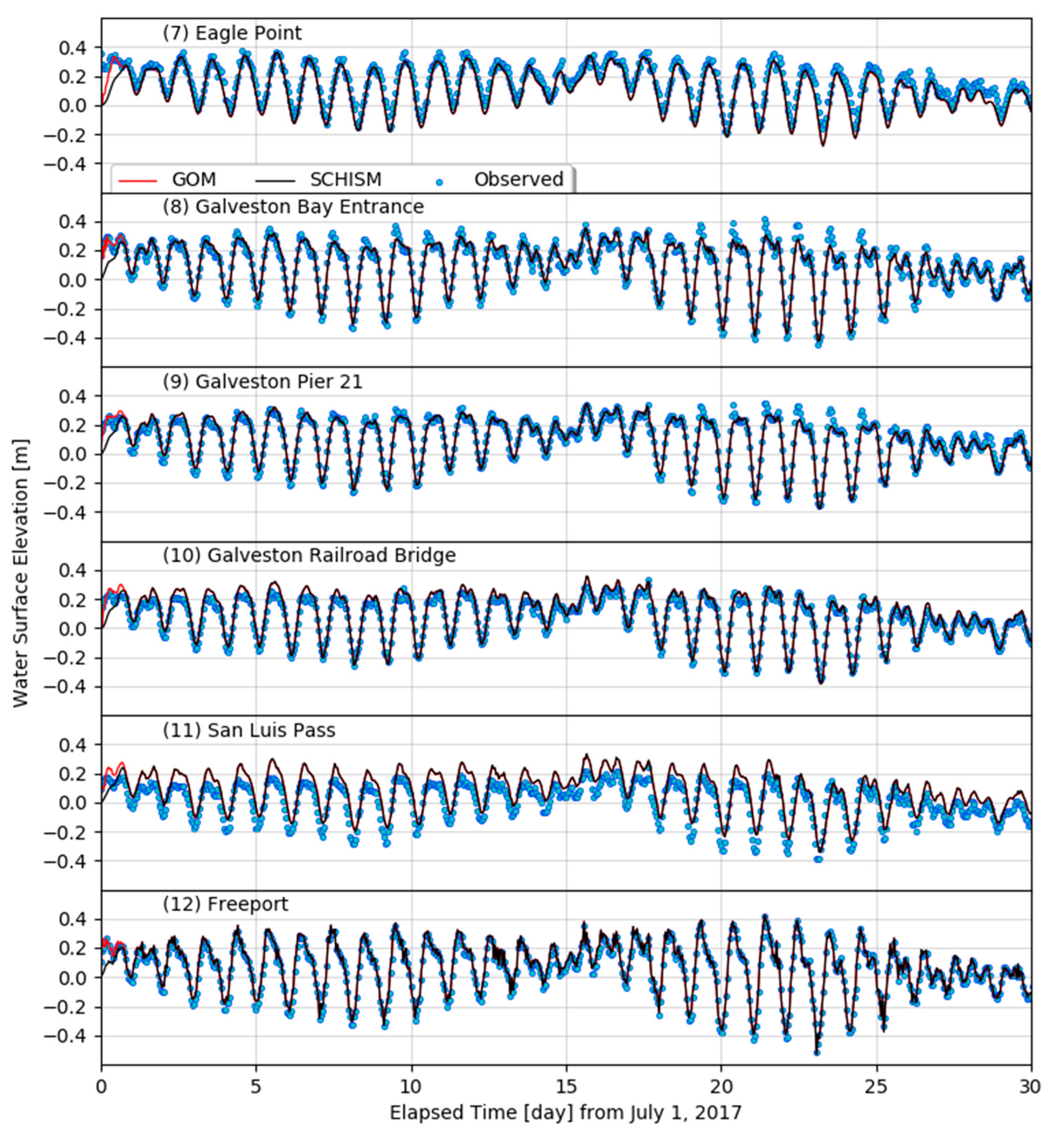
7.3. Model Validation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Casulli, V.; Walters, R.A. An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Fringer, O.; Gerritsen, M.; Street, R. An unstructured-grid, finite-volume, nonhydrostatic, parallel coastal ocean simulator. Ocean Model. 2006, 14, 139–173. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ateljevich, E.; Yu, H.-C.; Wu, C.H.; Yu, J.C.S. A new vertical coordinate system for a 3D unstructured-grid model. Ocean Model. 2015, 85, 16–31. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. Journal of Atmospheric and Oceanic Technology 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Lai, Z.; Chen, C.; Cowles, G.W.; Beardsley, R.C. A nonhydrostatic version of FVCOM: 1. Validation experiments. J. Geophys. Res. Space Phys. 2010, 115, C11. [Google Scholar] [CrossRef]
- Staniforth, A.; Côté, J. Semi-Lagrangian Integration Schemes for Atmospheric Models—A Review. Mon. Weather Rev. 1991, 119, 2206–2223. [Google Scholar] [CrossRef]
- MacWilliams, M.; Gross, E. Hydrodynamic Simulation of Circulation and Residence Time in Clifton Court Forebay. San Franc. Estuary Watershed Sci. 2013, 11. [Google Scholar] [CrossRef]
- MacWilliams, M.; Bever, A.J.; Gross, E.; Ketefian, G.; Kimmerer, W. Three-Dimensional Modeling of Hydrodynamics and Salinity in the San Francisco Estuary: An Evaluation of Model Accuracy, X2, and the Low-Salinity Zone. San Franc. Estuary Watershed Sci. 2015, 13. [Google Scholar] [CrossRef]
- MacWilliams, M.L.; Ateljevich, E.S.; Monismith, S.G.; Enright, C. An Overview of Multi-Dimensional Models of the Sacramento–San Joaquin Delta. San Franc. Estuary Watershed Sci. 2016, 14. [Google Scholar] [CrossRef]
- Fringer, O.B.; Dawson, C.; He, R.; Ralston, D.K.; Zhang, Y.J. The future of coastal and estuarine modeling: Findings from a workshop. Ocean Model. 2019, 143, 101458. [Google Scholar] [CrossRef]
- Cheng, R.T.; Casulli, V. Evaluation of the UnTRIM Model for 3-D Tidal Circulation. Estuar. Coast. Model. 2001, 628–642. [Google Scholar] [CrossRef]
- Leith, C.E. Atmospheric Predictability and Two-Dimensional Turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef]
- Cheng, R.T.; Casulli, V.; Milford, S.N. Eulerian-Lagrangian Solution of the Convection-Dispersion Equation in Natural Coordinates. Water Resour. Res. 1984, 20, 944–952. [Google Scholar] [CrossRef]
- Oliveira, A.; Baptista, A.M. On the role of tracking on Eulerian-Lagrangian solutions of the transport equation. Adv. Water Resour. 1998, 21, 539–554. [Google Scholar] [CrossRef]
- Lentine, M.; Grétarsson, J.T.; Fedkiw, R. An unconditionally stable fully conservative semi-Lagrangian method. J. Comput. Phys. 2011, 230, 2857–2879. [Google Scholar] [CrossRef]
- Garratt, J.R. Review of Drag Coefficients over Oceans and Continents. Mon. Weather Rev. 1977, 105, 915–929. [Google Scholar] [CrossRef]
- Smith, S.D. Wind Stress and Heat Flux over the Ocean in Gale Force Winds. J. Phys. Oceanogr. 1980, 10, 709–726. [Google Scholar] [CrossRef]
- Lynch, D.R.; Gray, W.G. Analytic Solutions for Computer Flow Model Testing. J. Hydraul. Div. 1978, 104, 1409–1428. [Google Scholar]
- Liu, Y. Two-Dimensional Finite-Difference Model for Moving Boundary Hydrodynamic Problems. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 1988. [Google Scholar]
- Lee, J. Three-Dimensional Unstructured Finite Difference and Volume Model for Barotropic Coastal and Estuarine Circulation and Application to Hurricane Ivan (2004) and Dennis (2005). Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2008. [Google Scholar]
- Lynch, D.R.; Officer, C.B. Analytic test cases for three-dimensional hydrodynamic models. Int. J. Numer. Methods Fluids 1985, 5, 529–543. [Google Scholar] [CrossRef]
- Luettich, R.A.; Muccino, J.C.; Foreman, M.G.G. Considerations in the Calculation of Vertical Velocity in Three-Dimensional Circulation Models. J. Atmos. Ocean. Technol. 2002, 19, 2063–2076. [Google Scholar] [CrossRef]
- Carrier, G.F.; Greenspan, H.P. Water waves of finite amplitude on a sloping beach. J. Fluid Mech. 1958, 4, 97–109. [Google Scholar] [CrossRef]
- Sobey, R.J. Wetting and drying in coastal flows. Coast. Eng. 2009, 56, 565–576. [Google Scholar] [CrossRef]
- Mungkasi, S.; Roberts, S.G. Approximations of the Carrier-Greenspan periodic solution to the shallow water wave equations for flows on a sloping beach. Int. J. Numer. Methods Fluids 2012, 69, 763–780. [Google Scholar] [CrossRef]
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Kim, C.-K.; Park, K. A modeling study of water and salt exchange for a micro-tidal, stratified northern Gulf of Mexico estuary. J. Mar. Syst. 2012, 96, 103–115. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Yun, S.-L.; Oh, H.-C. Development of a finite volume two-dimensional model and its application in a bay with two inlets: Mobile Bay, Alabama. Cont. Shelf Res. 2017, 146, 13–27. [Google Scholar] [CrossRef]
- Chen, C.; Huang, H.; Beardsley, R.C.; Liu, H.; Xu, Q.; Cowles, G. A finite volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models. J. Geophys. Res. Space Phys. 2007, 112, C03018. [Google Scholar] [CrossRef]
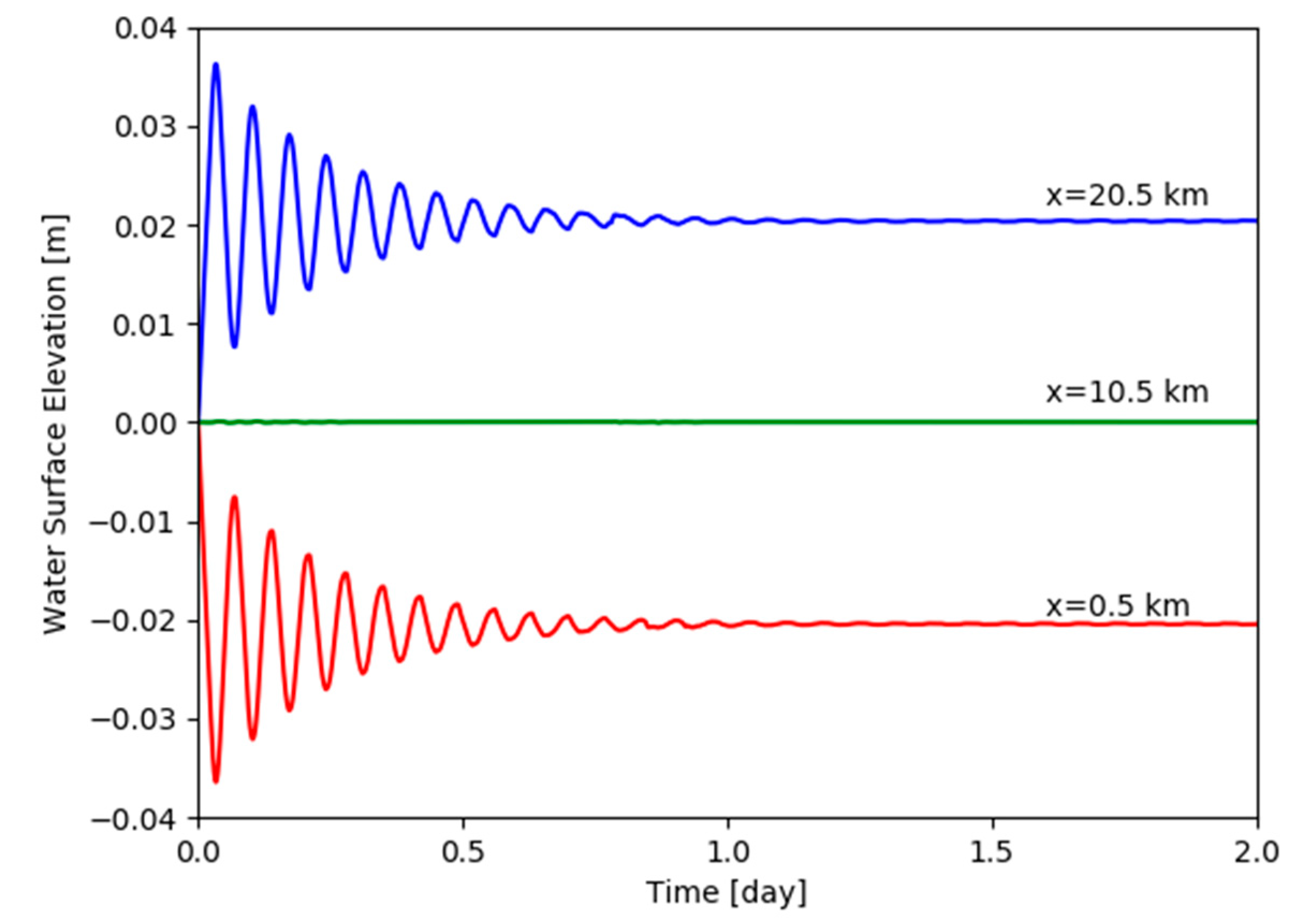
| 0.5 | −2.04 | −2.04 | −2.04 |
| 10.5 | 0 | 0 | 0 |
| 20.5 | 2.04 | 2.04 | 2.04 |
| # in Figure 17 | NOAA Station ID | Station Name | USGS Station ID | Station Name |
|---|---|---|---|---|
| 1 | 8770822 | Sabine Pass | 08030500 | Sabine River |
| 2 | 8770520 | Rainbow Bridge | 08041780 | Neches River |
| 3 | 8770808 | High Island | 08042558 | Double Bayou |
| 4 | 8770971 | Rollover Pass | 08067070 | Trinity River |
| 5 | 8770777 | Manchester | 08067500 | Cedar Bayou |
| 6 | 8770613 | Morgan’s Point | 08070200 | San Jacinto River |
| 7 | 8771013 | Eagle Point | 08074500 | Buffalo Bayou |
| 8 | 8771341 | Galveston Bay Entrance | 08078000 | Chocolate Bayou |
| 9 | 8771450 | Galveston Pier 21 | 08116650 | Brazos River |
| 10 | 8771486 | Galveston Railroad Br. | 08117705 | San Bernard River |
| 11 | 8771972 | San Luis Pass | - | - |
| 12 | 8772447 | Freeport | - | - |
| Tide Station | SCHISM | GOM | N | ||
|---|---|---|---|---|---|
| MAE (cm) | Skill | MAE (cm) | Skill | ||
| (1) Sabine Pass | 5.4 | 0.959 | 5.3 | 0.961 | 600 |
| (2) Rainbow Bridge | 5.5 | 0.945 | 5.5 | 0.945 | 600 |
| (3) High Island | 5.5 | 0.951 | 5.6 | 0.950 | 600 |
| (4) Rollover Pass | 6.4 | 0.934 | 6.5 | 0.931 | 600 |
| (5) Manchester | 10.8 | 0.897 | 10.5 | 0.901 | 600 |
| (6) Morgan’s Point | 9.1 | 0.909 | 8.8 | 0.912 | 600 |
| (7) Eagle Point | 5.0 | 0.957 | 5.1 | 0.955 | 600 |
| (8) Galveston Bay Entrance | 3.6 | 0.984 | 3.6 | 0.983 | 600 |
| (9) Galveston Pier 21 | 3.2 | 0.981 | 3.3 | 0.980 | 600 |
| (10) Galveston Railroad Br. | 3.2 | 0.984 | 3.2 | 0.983 | 600 |
| (11) San Luis Pass | 8.1 | 0.890 | 8.1 | 0.887 | 600 |
| (12) Freeport | 2.2 | 0.994 | 2.1 | 0.995 | 600 |
| Overall | 5.7 | 0.951 | 5.6 | 0.951 | 7200 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Lee, J.; Yun, S.-L.; Kim, S.-K. Three-Dimensional Unstructured Grid Finite-Volume Model for Coastal and Estuarine Circulation and Its Application. Water 2020, 12, 2752. https://doi.org/10.3390/w12102752
Lee J, Lee J, Yun S-L, Kim S-K. Three-Dimensional Unstructured Grid Finite-Volume Model for Coastal and Estuarine Circulation and Its Application. Water. 2020; 12(10):2752. https://doi.org/10.3390/w12102752
Chicago/Turabian StyleLee, Jun, Jungwoo Lee, Sang-Leen Yun, and Seog-Ku Kim. 2020. "Three-Dimensional Unstructured Grid Finite-Volume Model for Coastal and Estuarine Circulation and Its Application" Water 12, no. 10: 2752. https://doi.org/10.3390/w12102752
APA StyleLee, J., Lee, J., Yun, S.-L., & Kim, S.-K. (2020). Three-Dimensional Unstructured Grid Finite-Volume Model for Coastal and Estuarine Circulation and Its Application. Water, 12(10), 2752. https://doi.org/10.3390/w12102752






