Analytic Representation of the Optimal Flow for Gravity Irrigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Water Surface Flow
2.2. Water Flow in the Soil
2.3. Hydraulic Resistance Law
3. Results and Discussion
3.1. Numerical Relationship between the Optimal Flow and Length
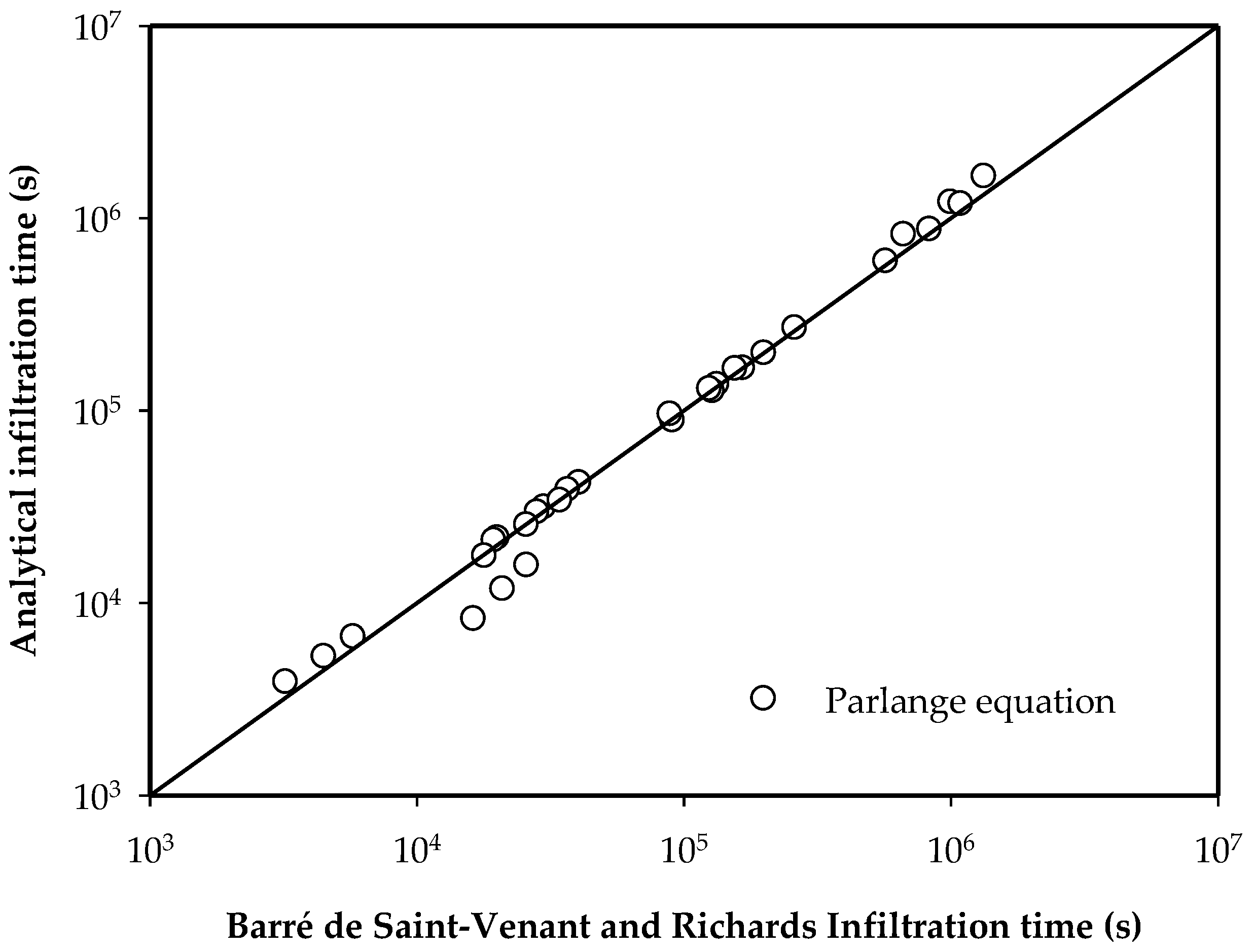
3.1.1. Optimal Flow in Border Irrigation
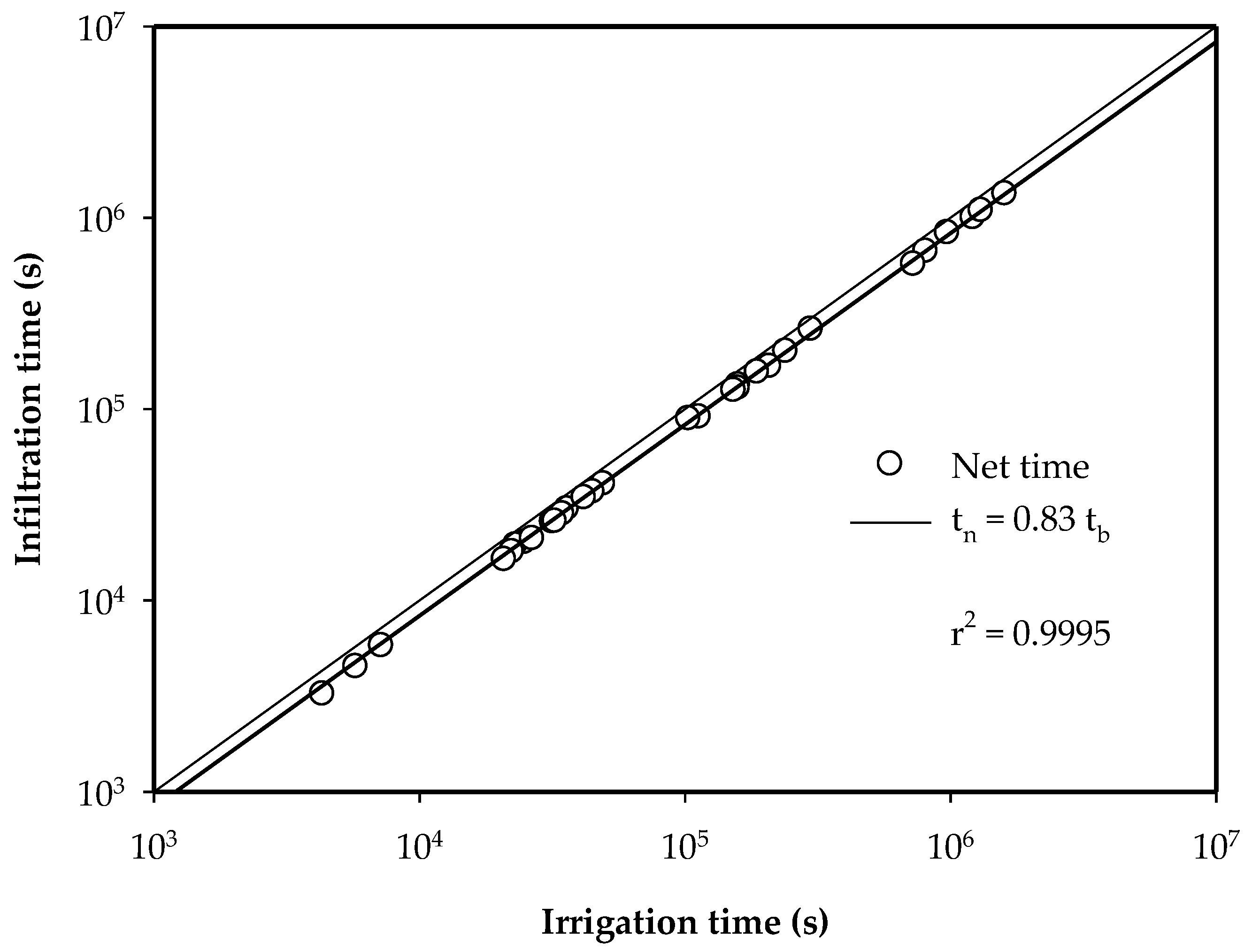
3.1.2. Irrigation Efficiencies
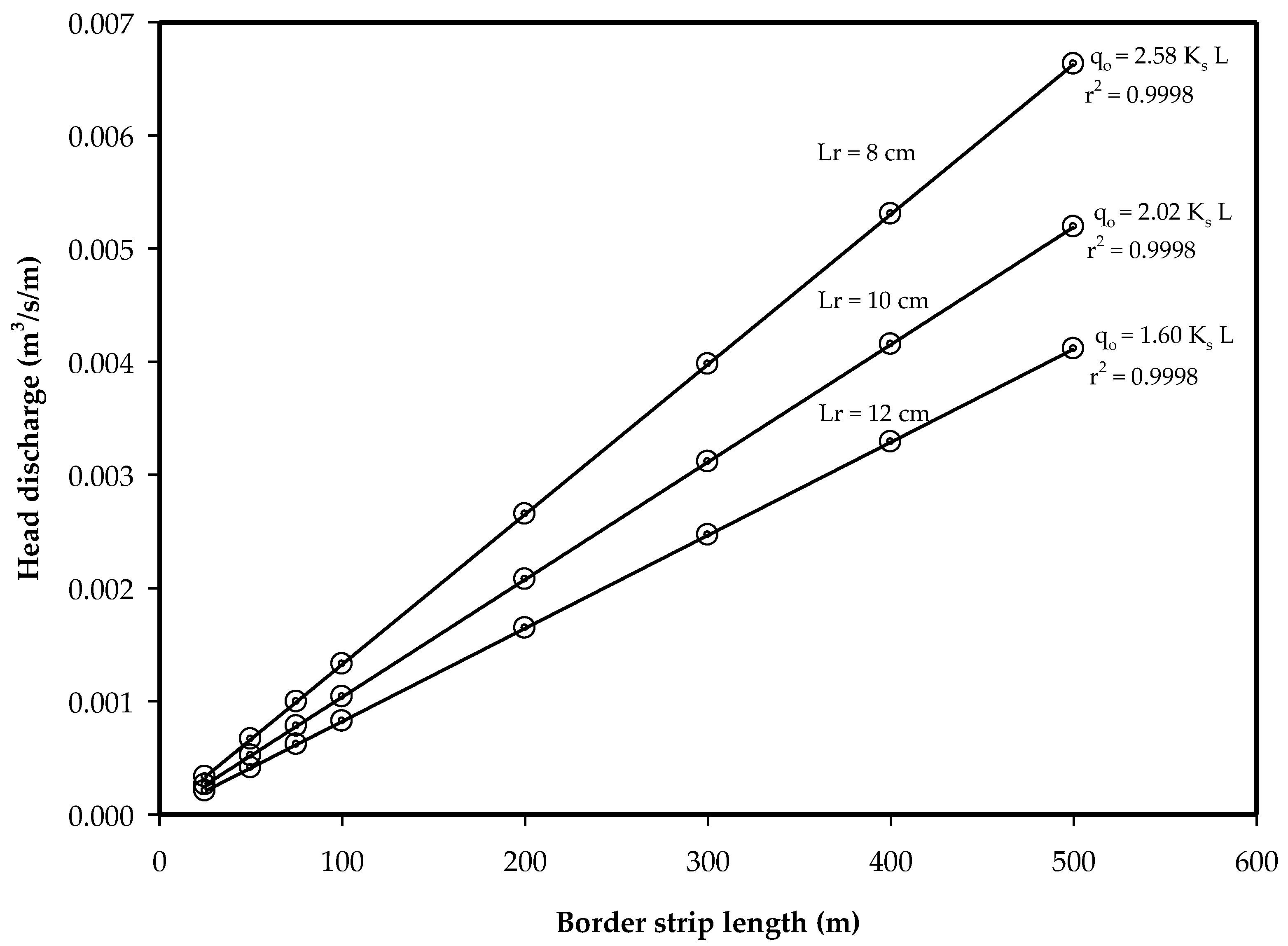
3.1.3. Optimal Flow-Length Relationship
3.1.4. Irrigation Design Table
3.2. Analytical Representation of the Relationship between the Optimal Flow and Length
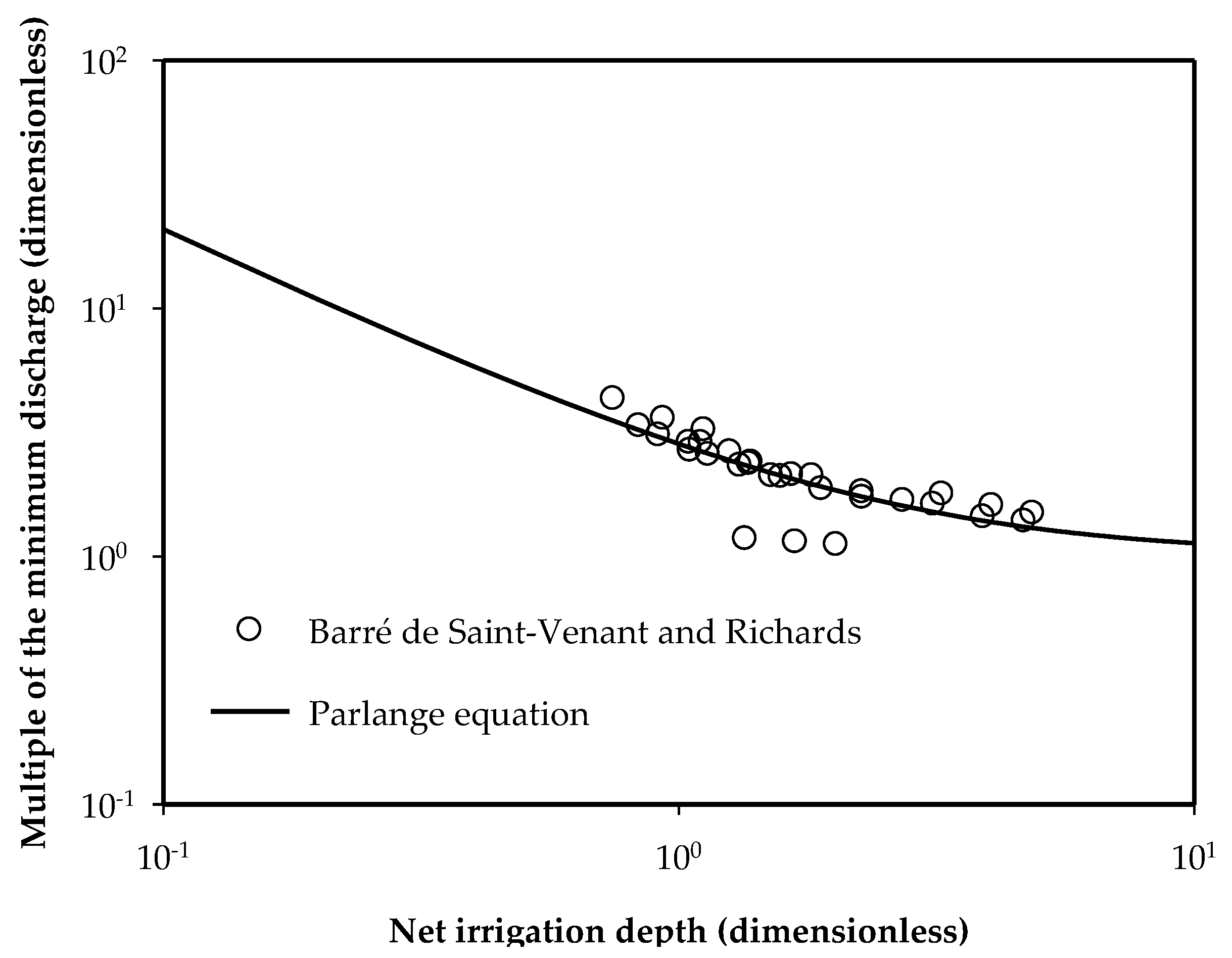
3.3. Application of the Analytical Formula in Furrow Irrigation Systems
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chávez, C.; Fuentes, C. Design and evaluation of surface irrigation systems applying an analytical formula in the irrigation district 085, La Begoña, Mexico. Agric. Water Manag. 2019, 221, 279–285. [Google Scholar] [CrossRef]
- Fuentes, C.; De León, B.; Saucedo, H.; Parlange, J.-Y.; Antonino, A.C.D. Saint-Venant and Richards equations system in surface irrigation: (1) Hydraulic resistance power law. Ing. Hidraul. Mexico 2004, 19, 65–75. [Google Scholar]
- Khanna, M.; Malano, H.M. Modelling of basin irrigation systems: A review. Agric. Water Manag. 2006, 83, 87–99. [Google Scholar] [CrossRef]
- Soroush, F.; Fenton, J.D.; Mostafazadeh-Fard, B.; Mousavui, S.F.; Abbasi, F. Simulation of furrow irrigation using the Slow-change/slow-flow equation. Agric. Water Manag. 2013, 116, 160–174. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Liaghat, A. Field Evaluation of Various Mathematical Models for Furrow and Border Irrigation Systems. Soil Water Res. 2011, 2, 91–101. [Google Scholar] [CrossRef]
- Furman, A.; Warrick, A.W.; Zerihun, D.; Sanchez, D.A. Modified Kostiakov infiltration function: Accounting for initial and boundary conditions. J. Irrig. Drain. Eng. 2006, 132, 587–597. [Google Scholar] [CrossRef]
- Parhi, P.K.; Mishra, S.K.; Singh, R. A modification to Kostiakov and modified Kostiakov infiltra-tion models. Water Resour. Manag. 2007, 21, 1973–1989. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, D.; Li, Y. A one-dimensional complete hydrodynamic model of border irrigation based on a hybrid numerical method. Irrig. Sci. 2011, 29, 93–102. [Google Scholar] [CrossRef]
- Strelkoff, T.; Katopodes, N. Border-irrigation hydraulics with zero inertia. J. Irrig. Drain. Div. ASCE 1977, 102, 325–342. [Google Scholar]
- Bautista, E.; Wallender, W.W. Hydrodynamic furrow irrigation model with especified space steps. J. Irrig. Drain. Eng. Div. ASCE 1992, 118, 450–465. [Google Scholar] [CrossRef]
- Sohrabi, B.; Behnia, A. Evaluation of Kostiakov´s infiltration equation in furrow irrigation design according to FAO Method. J. Agron. 2007, 6, 468–471. [Google Scholar]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Schlegel, J. Modern analysis of surface irrigation systems with WinSRFR. Agric. Water Manag. 2009, 96, 1146–1154. [Google Scholar] [CrossRef]
- Strelkoff, T.; Clemmens, A.J. Hydraulics of surface systems. In Design and Operation of Farm Irrigation Systems, 2nd ed.; Hoffman, G.J., Evans, R.G., Jensen, M.E., Martin, D.L., Elliot, R.L., Eds.; ASABE: St. Joseph, MO, USA, 2007; pp. 436–498. [Google Scholar]
- Gillies, M.H.; Smith, R.J. SISCO: Surface irrigation simulation, calibration and optimisation. Irrig. Sci. 2015, 33, 339–355. [Google Scholar] [CrossRef]
- Valipour, M. Comparison of surface irrigation simulation models: Full hydrodynamic, zero inertia, kinematic wave. J. Agric. Sci. 2012, 4, 68–74. [Google Scholar] [CrossRef]
- Mahdizadeh, K.M.; Gholami, S.M.A.; Valipour, M. Simulation of open- and closed-end border irrigation systems using SIRMOD. Arch. Agron. Soil Sci. 2015, 61, 929–941. [Google Scholar] [CrossRef]
- Salahou, M.K.; Jiao, X.; Lü, H. Border irrigation performance with distance-based cut-off. Agric. Water Manag. 2018, 201, 27–37. [Google Scholar] [CrossRef]
- Akbari, M.; Gheysari, M.; Mostafazadeh-Fard, B.; Shayannejad, M. Surface, irrigation simulation-optimization model based on meta-heuristic algorithms. Agric. Water Manag. 2018, 201, 46–57. [Google Scholar] [CrossRef]
- Lalehzari, R.; Nasab, S.B. Improved volume balance using upstream flow depth for advance time estimation. Agric. Water Manag. 2017, 186, 120–126. [Google Scholar] [CrossRef]
- Liu, K.H.; Jiao, X.Y.; Li, J.; An, Y.H.; Guo, W.H.; Salahou, M.K.; Sang, H. Performance of a zero-inertia model for irrigation with rapidly varied inflow discharges. Int. J. Agric. Biol. Eng. 2020, 13, 175–181. [Google Scholar]
- Moravejalahkami, B.; Mostafazadeh-Fard, B.; Heidarpour, M.; Abbasi, F. Research Paper: SW-Soil and Water Furrow infiltration and roughness prediction for different furrow inflow hydrographs using a zero-inertia model with a multilevel calibration approach. Biol. Eng. 2009, 103, 374–381. [Google Scholar]
- González, C.J.M.; Muñoz, H.B.; Acosta, H.R.; Mailhol, J.C. Kinematic wave model adapted to irrigation with closed-end furrows. Agrociencia 2006, 40, 731–740. [Google Scholar]
- Rendón, P.L.; Saucedo, H.; Fuentes, C. Diseño del Riego por Gravedad, 1st ed.; Fuentes, C., Rendón, L., Eds.; Universidad Autónoma de Querétaro: Santiago de Querétaro, Mexico, 2012; pp. 321–358. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Saucedo, H.; Fuentes, C.; Zavala, M. The Saint-Venant and Richards equation system in surface irrigation: (2) Numerical coupling for the advance phase in border irrigation. Ing. Hidraul. Mexico 2005, 20, 109–119. [Google Scholar]
- Saucedo, H.; Zavala, M.; Fuentes, C. Complete hydrodynamic model for border irrigation. Water Technol. Sci. 2011, 2, 23–38. [Google Scholar]
- Saucedo, H.; Zavala, M.; Fuentes, C.; Castanedo, V. Optimal flow model for plot irrigation. Water Technol. Sci. 2013, 4, 135–148. [Google Scholar]
- Castanedo, V.; Saucedo, H.; Fuentes, C. Comparison between a hydrodynamic full model and a hydrologic model in border irrigation. Agrociencia 2013, 47, 209–223. [Google Scholar]
- Schmitz, G.; Haverkamp, R.; Palacios, O. A coupled surface-subsurface modelor shallow water flow over initially dry-soil. In Proceedings of the 21st Congress (IAHR), Melbourne, Australia, 13–18 August 1985; Volume 1, pp. 23–30. [Google Scholar]
- Parlange, J.-Y.; Haverkamp, R.; Touma, J. Infiltration under ponded conditions. Part I. Optimal analytical solutions and comparisions with experimental observations. Soil Sci. 1985, 139, 305–311. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies in soil physics, I: The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Vázquez, F. Eficiencia de aplicación en el riego con surcos cerrados al existir dos pendientes. Ing. Investig. Tecnol. 2000, 3, 123–130. [Google Scholar]
- Darcy, H. Dètermination des lois d’ècoulement de l’eau à travers le sable. In Les Fontaines Publiques de la Ville de Dijon; Victor Dalmont: Paris, France, 1856; pp. 590–594. [Google Scholar]
- Fuentes, C.; Haverkamp, R.; Parlange, J.-Y. Parameter constraints on closed–form soil-water relationships. J. Hydrol. 1992, 134, 117–142. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Burdine, N.T. Relative permeability calculation from size distributions data. Trans. AIME 1953, 198, 171–199. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media. Hydrol. Pap. (Colo. State Univ.) 1964, 3, 27. [Google Scholar]
- Fuentes, C. Approche Fractale des Transferts Hydriques Dans les sols non Saturès. Ph.D. Thesis, Universidad Joseph Fourier de Grenoble, Francia, France, 1992; p. 267. [Google Scholar]
- Rendón, P.L.; Saucedo, H.; Fuentes, C. Gravity Irrigation Design. In Gravity Irrigation, 1st ed.; Fuentes, C., Rendón, L., Eds.; National Association of Irrigation Specialist: Mexico, Mexico, 2017; pp. 345–386. [Google Scholar]
- Lewis, M.R.; Milne, W.E. Analysis of border irrigation. Agric. Eng. 1938, 19, 267–272. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L. Estimating soil water retention from soil properties. Am. Soc. Civ. Eng. 1981, 108, 167–171. [Google Scholar]
- Bouwer, H. Rapid field measurement of air entry value and hydraulic conductivity of soil as significant parameters in flow system analysis. Water Resour. Res. 1964, 36, 411–424. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solutions. Soil Sci. 1957, 83, 345–357. [Google Scholar] [CrossRef]
- Parlange, J.-Y.; Braddock, R.D.; Lisle, I.; Smith, R.E. Three parameter infiltration equation. Soil Sci. 1982, 111, 170–174. [Google Scholar] [CrossRef]
- Talsma, T.; Parlange, J.-Y. One-dimensional vertical infiltration. Aust. J. Soil. Res. 1972, 10, 143–150. [Google Scholar] [CrossRef]
- Parlange, J.-Y. On solving the flow equation in unsaturated soils by optimization: Horizontal infiltration. Soil Sci. Soc. Am. Proc. 1975, 39, 415–418. [Google Scholar] [CrossRef]
- Fuentes, C. Teoría de la infiltración unidimensional: 2. La infiltración vertical. Agrociencia 1989, 78, 119–153. [Google Scholar]
| Soil Texture | θs (cm3/cm3) | λc (cm) | Ks (cm/h) | η | m | |ψd| (cm) |
|---|---|---|---|---|---|---|
| Clay | 0.525 | 140.26 | 0.010 | 61.10 | 0.0229 | 132.50 |
| Silty clay | 0.500 | 100.16 | 0.015 | 31.55 | 0.0440 | 94.70 |
| Silty-clay-loam | 0.500 | 60.12 | 0.070 | 15.34 | 0.0905 | 57.80 |
| Clay-loam | 0.475 | 36.00 | 0.150 | 19.30 | 0.0714 | 34.15 |
| Sandy clay | 0.425 | 25.72 | 0.200 | 41.50 | 0.0327 | 23.70 |
| Loam | 0.500 | 30.52 | 0.500 | 5.61 | 0.2477 | 30.70 |
| Silt | 0.475 | 20.04 | 0.700 | 13.93 | 0.0989 | 19.20 |
| Silty loam | 0.525 | 30.07 | 0.600 | 12.01 | 0.1165 | 29.35 |
| Sandy-clay-loam | 0.425 | 35.61 | 1.500 | 18.44 | 0.0736 | 33.35 |
| Sandy loam | 0.450 | 10.00 | 5.000 | 13.62 | 0.1004 | 9.52 |
| Soil Texture | θPMP (cm3/cm3) | θCC (cm3/cm3) | θ0 (cm3/cm3) |
|---|---|---|---|
| Clay | 0.350 | 0.450 | 0.400 |
| Silty clay | 0.275 | 0.425 | 0.350 |
| Silty clay-loam | 0.200 | 0.375 | 0.287 |
| Clay-loam | 0.190 | 0.340 | 0.265 |
| Sandy clay | 0.225 | 0.325 | 0.275 |
| Loam | 0.100 | 0.275 | 0.187 |
| Silt | 0.130 | 0.250 | 0.190 |
| Silt loam | 0.125 | 0.275 | 0.200 |
| Sandy-clay-loam | 0.150 | 0.250 | 0.200 |
| Sandy loam | 0.100 | 0.190 | 0.145 |
| Soil Texture | ℓn = 8 cm | ℓn = 10 cm | ℓn = 12 cm | |||
|---|---|---|---|---|---|---|
| qu (l/s/m2) | τb (h) | qu (l/s/m2) | τb (h) | qu (l/s/m2) | τb (h) | |
| Clay | 0.00012 | 224.1 | 0.00010 | 338.2 | 0.00009 | 445.0 |
| Silty clay | 0.00014 | 201.6 | 0.00012 | 270.5 | 0.00011 | 362.5 |
| Silty-clay-loam | 0.00060 | 44.1 | 0.00050 | 66.6 | 0.00046 | 82.9 |
| Clay-loam | 0.00088 | 31.4 | 0.00078 | 44.0 | 0.00072 | 57.8 |
| Sandy clay | 0.00090 | 28.7 | 0.00080 | 42.4 | 0.00077 | 52.0 |
| Loam | 0.00399 | 6.9 | 0.00333 | 10.0 | 0.00296 | 13.7 |
| Silt | 0.00411 | 6.4 | 0.00354 | 9.6 | 0.00326 | 12.5 |
| Silt-loam | 0.00446 | 6.2 | 0.00388 | 8.8 | 0.00349 | 11.6 |
| Sandy-Clay-loam | 0.00490 | 5.8 | 0.00476 | 7.4 | 0.00464 | 9.0 |
| Sandy-loam | 0.02476 | 1.2 | 0.02223 | 1.6 | 0.02073 | 2.0 |
| Soil Texture | S (cm/) | β | Soil Texture | S (cm/) | β |
|---|---|---|---|---|---|
| Clay | 0.583 | 0.820 | Loam | 2.958 | 0.584 |
| Silty clay | 0.655 | 0.800 | Silt | 2.761 | 0.744 |
| Silty-clay-loam | 1.296 | 0.750 | Silty loam | 3.338 | 0.721 |
| Clay loam | 1.469 | 0.773 | Sandy-clay-loam | 4.796 | 0.775 |
| Sandy clay | 1.223 | 0.820 | Sandy loam | 5.404 | 0.744 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuentes, C.; Chávez, C. Analytic Representation of the Optimal Flow for Gravity Irrigation. Water 2020, 12, 2710. https://doi.org/10.3390/w12102710
Fuentes C, Chávez C. Analytic Representation of the Optimal Flow for Gravity Irrigation. Water. 2020; 12(10):2710. https://doi.org/10.3390/w12102710
Chicago/Turabian StyleFuentes, Carlos, and Carlos Chávez. 2020. "Analytic Representation of the Optimal Flow for Gravity Irrigation" Water 12, no. 10: 2710. https://doi.org/10.3390/w12102710
APA StyleFuentes, C., & Chávez, C. (2020). Analytic Representation of the Optimal Flow for Gravity Irrigation. Water, 12(10), 2710. https://doi.org/10.3390/w12102710






