3.1. Case Study: Parambikulam–Aliyar Project (PAP)
We consider the Parambikulam–Aliyar Project (PAP) from India as this multi-reservoir system has been studied using AD-DP and FP methods in [
28,
49,
53], respectively. We provide only the minimum details that are interesting to know here about the system and to correspond with the numbering of reservoirs different here than in [
53]; detailed explanations of these reservoirs, their data and corresponding benefits and policies can be obtained from the above works. For the purpose of comparing results with those of four other methods reported in the literature, we use the same problem and objective functions, although that is not a restriction of the AD-RL method. In other words, any other highly non-linear or even discontinuous objective functions can easily be handled by the proposed model as RL is basically a simulation-based technique.
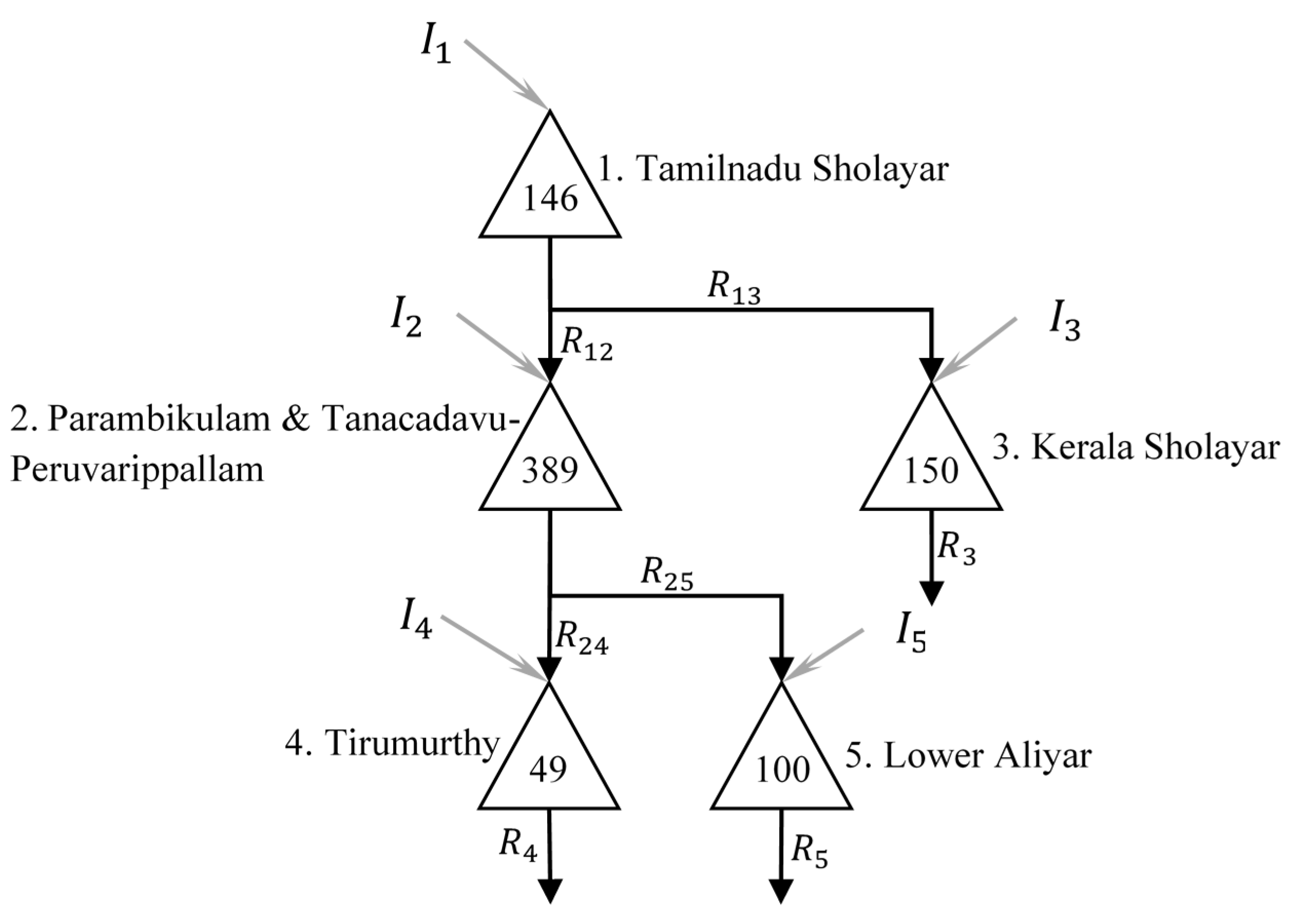
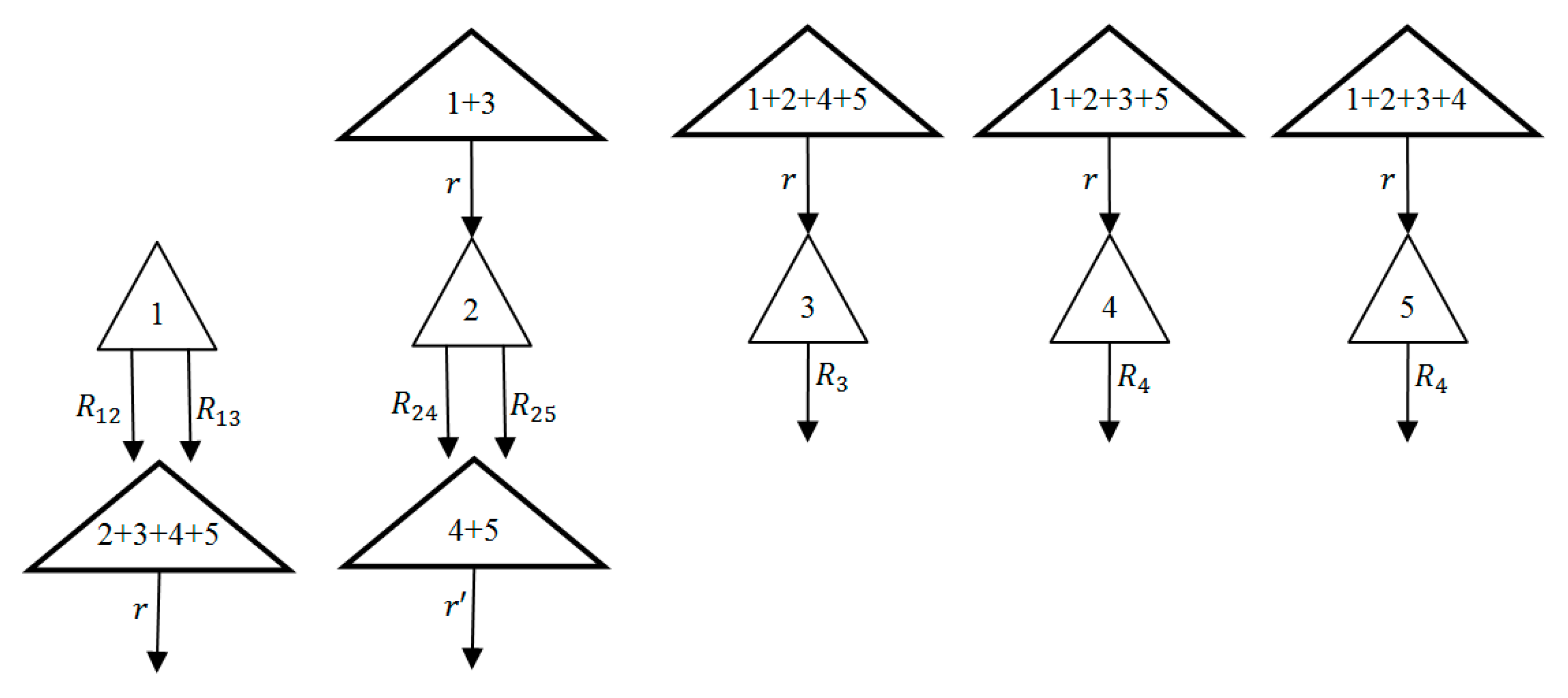
PAP, as studied, is presented in
Figure 3. The PAP system comprises of two series of reservoirs in which the left-side reservoirs are more important in terms of the volume of inflow and demands (i.e., the demands and inflows are remarkably high compared to other side). The number inside the triangle depicting each reservoir in
Figure 3 represent the live capacities, which can be considered as the maximum storage volume and the minimum (live) storage is zero. The subscript of inflow also represents the index of the reservoir and is used later for explanations.
The main purpose of this project is to conduct water from western slopes of Anamalai Mountains to irrigate the eastern arid area in two states (Tamilnadu and Kerala), and hydropower and fishing benefits are the secondary incomes of the project. Many operating constraints exist agreed upon in the inter-stage agreement between these two different states that should be taken into consideration for constructing any optimization model; the details are not provided here and are available in the original papers. The objective function is defined as;
where
is the benefit per unit release which is given in
Table 1 and is useful later to understand MAM-DP’s objective function. Note that the above simple linear objective function has been chosen to be exactly the same as the objective function used in the literature for other methods to which we compare our proposed model, and it is not a restriction.
It is worth noting that 20% loss should be considered for all releases flowing from the third reservoir (Paramabikulam reservoir) to the fourth reservoir (Tirumurthy) because of the long tunnel used for water flow between these reservoirs.
The lower release bounds are set to zero for all periods.
Table 2 also illustrates the upper bounds for all different connections in the PAP case study (i.e., the release from reservoir
to reservoir
). It is assumed that these bounds are the same for 12 months. The diagonal elements in this table indicate the total maximum releases for each of the five reservoirs.
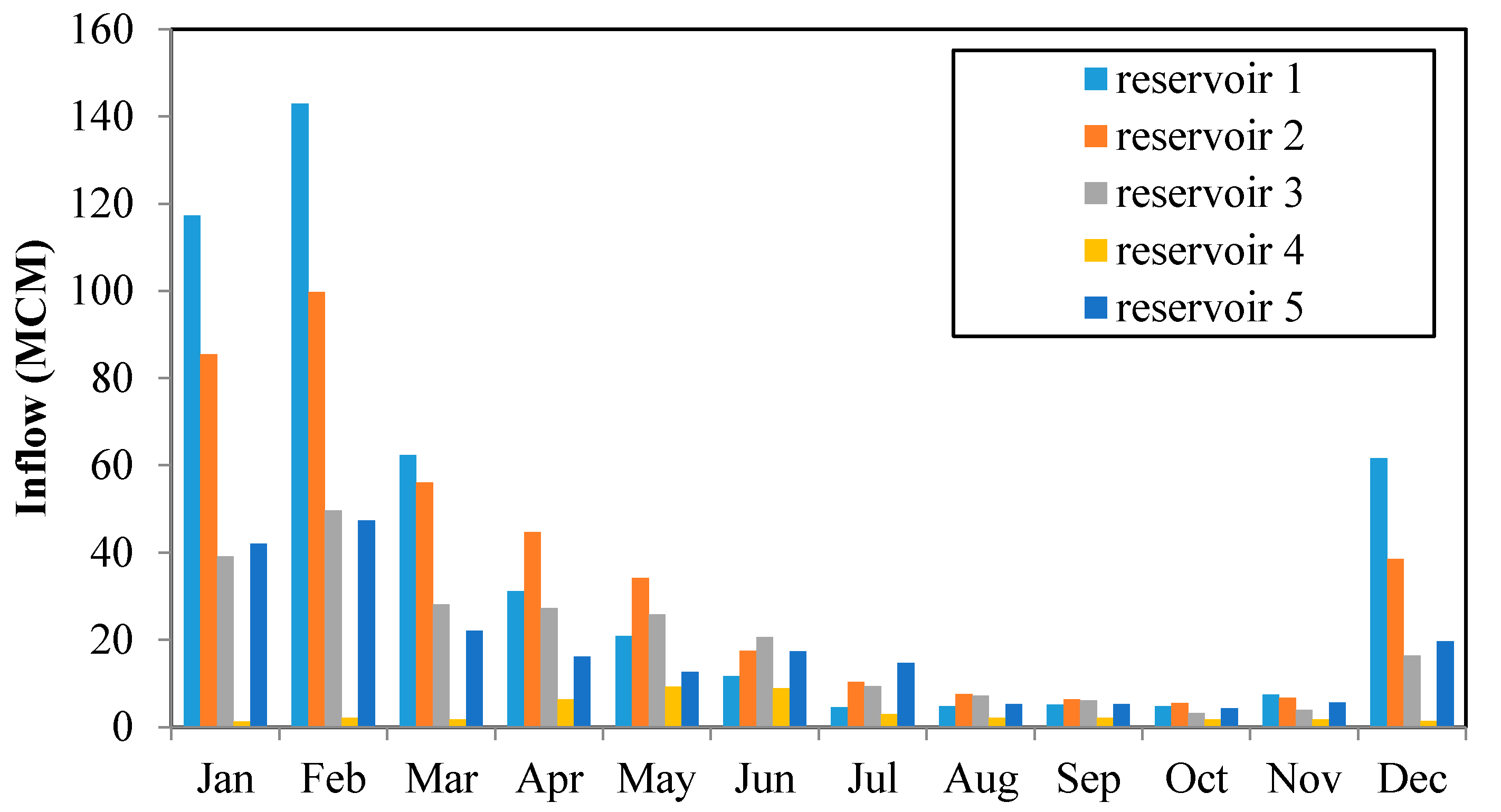
The hydrological data available on a monthly basis for the five reservoirs is in
Figure 4. The average monthly inflows to the first, second, third and fifth reservoirs are almost the same in which the rainy season starts from December to May. However, the main proportion of rainfall in the fourth reservoir occurs during the monsoon period (from May to September).
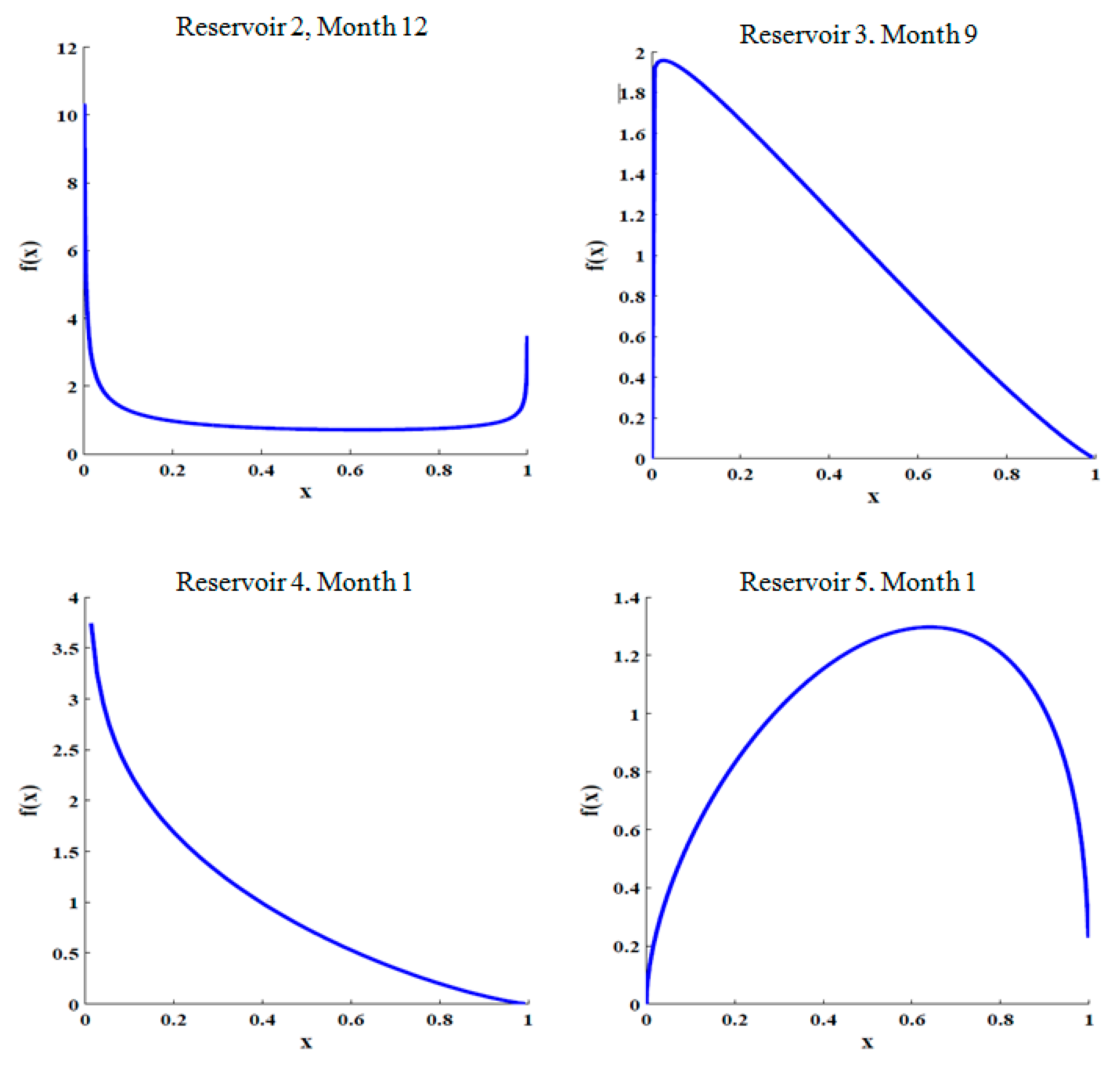
Given the available inflows for each month and the non-normal highly skewed nature of the inflows, the Kumaraswamy distribution was found to be the best fit and a few examples are shown in
Figure 5.
Furthermore, based on the nature of PAP case study, there are high correlations between the first reservoir (Tamilnadu Sholayar), the second reservoirs (Parambikalami and Tunacadavu-Peruvarippallam), the third reservoir (Lower Aliyar) and the fifth reservoir (Kerala Sholayar) in terms of natural inflows (
Table 3). The inflow to reservoir 4 is independent of other reservoirs’ inflows.
The PAP project is solved using three other different optimization methods, including the MAM-DP, AD-DP and FP techniques in order to verify the performance of the proposed AD-RL. Two different methods of aggregation/decomposition are used in MAM-DP and AD-DP which are explained in the following sub-sections.
3.5. AD-RL Method
To find a near-optimal policy by the Q-learning algorithm, a proper action-taking policy should be chosen. The discount factor (γ) for the learning step is 0.9 while the respective parameters including the learning factor (α) and ε (in ε-greedy policy) or τ (in Softmax policy) should be accurately set.
As previously mentioned, the main advantage of the Softmax policy is to explore more at the beginning of learning while increasing exploitation as learning continues. This behavior is controlled using the values of Q-factors while converging to the steady-state situation, that is, the action with a greater Q-factor should have a higher chance to be chosen in every interaction. However, while applying this policy, it is observed that the values of all Q-factors become almost close to each other as they converge to the steady-state situation. In other words, Softmax might end up with almost identical probabilities for admissible actions. Therefore, this action-taking policy may lead to a poor performance through converging to a far-optimal operating policy, which our numerical experiments accomplished herein confirmed this result too.
Despite the Softmax policy, in ε-greedy policy, the rate of exploration is constant over the learning process that may not guarantee reaching a near-optimal policy. To tackle this issue, the whole learning process can be implemented as episodic starting, with a big ε in the first episode and decrease the rate in the next episode. An episode comprises a predefined number of years that the learning (simulation) should be implemented. The initial state at the beginning of the learning in every episode can be randomly selected. It is worth mentioning that the value of ε in every episode is constant. To implement this way of learning in the PAP case study, we considered two different parameters: ε1 and ε2. The value of ε1 equals one in the first episode, so there will be no difference between all admissible actions in terms of probability of being selected. Parameter ε2 is the rate of exploration in the last episode, then the rate of exploration for other episodes is determined using a linear function of these two parameters.
The learning factor (
) is also an important parameter that should be precisely specified. There are different methods to set this parameter [
54]. It has been specified based on the number of updating for each action-state pair using the following equation:
where
is a smaller-than-one predefined parameter. The role of this parameter is to cope with the asynchronous error in the learning process [
54].
We use a robust ANN-based approach to tune the above-mentioned parameters. The respective input data for training the corresponding multilayer perceptron ANN is obtained using a combination of different values chosen for parameters
ε2 and
. To have a space-filling strategy, the values considered for each parameter should be uniformly distributed over its domain (for example
takes values of 0.1, 0.3, 0.5, 0.7 and 0.9). Given the sample values chosen for these parameters presented in
Table 4, there will be 25 different input data representing all possible combinations for these parameter values. AD-RL will be implemented then for each individual set of these input combinations 10 times. Given the operating policy for each implementation of Q-learning, one can run the respective simulation to obtain the expected value of the benefit. The expected value (
) and the semi variance (
) of all 10 expected values of benefit value obtained from the simulations are calculated using the following equations:
where
is the number of runs (10 in our experiments), and
and
are respectively the mean and semi variance values of objective function obtained by
ith run.
Recall that Q-learning is a simulation-based technique. Therefore, it could end up with different operating policies at the end of the learning process because of different sequences of synthetic data being generated over the learning phase. Obtaining more robust results for different runs of Q-learning (less variation of expected values at the end of simulation for different Q-learning implementations) is a good sign for the respective fine-tuned parameter values. To take the robustness of the results into account in ANN training task, one can use a function of the performance criterion ( in our experiments) as a desirable output.
To demonstrate how efficient the proposed tuning procedure is, one of the five reservoirs in the PAP case study (Tamilnadu Sholayar reservoir) is selected which can be considered a one-reservoir problem. Similar to what has been undertaken for training data, Q-learning is implemented for the test data set consisting of 100 data in our experiments, and the respective performance criterion is obtained for each test data. The outputs of the networks for these test data can be found using the trained network. The best outputs obtained from Q-learning and the trained networks are compared then to each other. If all or the most of these two different outputs are the same, we conclude that the training phase for tuning the parameters has been performed appropriately.
Table 5 demonstrates top- 3, 4, 5, 10, and 15 best sets of parameters in terms of the defined performance criterion (
). For instance, 3 out of 5 best sets of parameters based on the output of the trained network are among the 5 best sets of parameters based on the Q-learning approach.
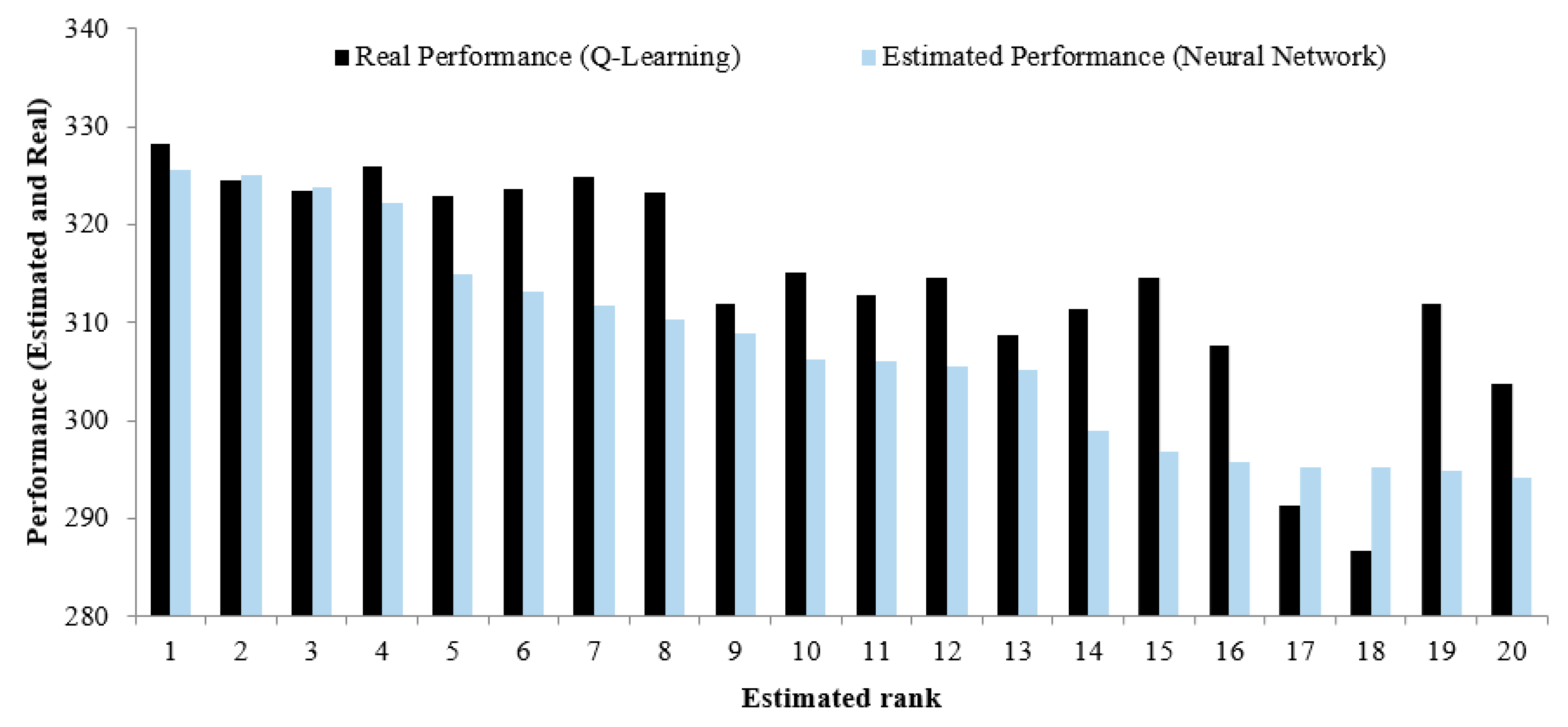
Figure 8 illustrates the comparisons between the performance obtained from the neural network for the top 20 sets of parameters and the respective ones based on Q-learning. It shows that the function trained maps the input data to desirable data appropriately. Such a training procedure can, therefore, be used in cases with a larger number of reservoirs.
Having the trained network using 25 examples given in
Table 5 for the five-reservoir case study (PAP project), one can select and sort a number of the best parameter sets using 100 test data (
Table 6). We used the first set of parameters to implement AD-RL.
The AD-RL algorithm was implemented 10 times, each with one hundred episodes for the learning process. Each episode comprises 1000 years.
Table 7 reports the average and the standard deviation of the annual benefit for all mentioned techniques applied in the PAP case study. It is worth noting that the average and standard deviation reported for the AD-RL method are their mean values obtained from running ten simulations. The AD-DP, MAM-DP, and AD-RL results are also determined by applying them to the same problem (PAP). Finally, the FP1 and FP2 results are from Mahootchi et al. [
53] where FP1 and FP2 correspond to different approximations for estimating releases from upstream reservoirs for the Kumaraswamy distributed inflows. See [
53] for details.
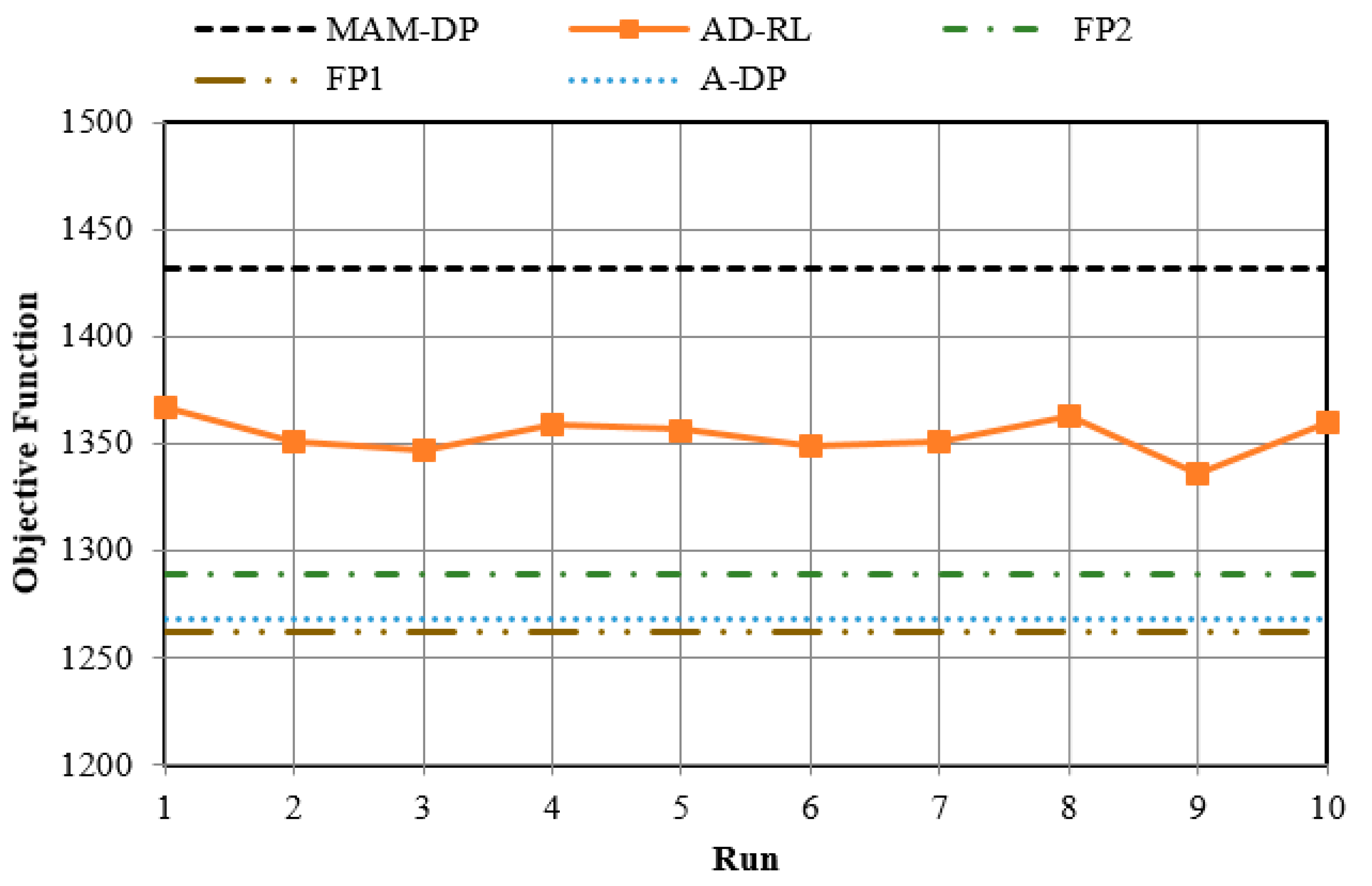
Figure 9 compares the average benefit for all 10 runs of Q-learning. This is a good verification showing how robust the Q-learning algorithm is. It also verifies that the derived-by-Q learning policy for all different 10 runs outperforms the policies derived by FP and AD-DP.