1. Introduction
Floods can have serious consequence in floodplains. Worldwide, many areas can become flooded or are at risk, and numerous people risk being displaced. Modeling the growth of a breach and the flow discharge hydrograph through the breach due to embankment failure are the first steps in mapping the resulting inundation in a floodplain and the potentially catastrophic floods generated by breaching of landslide dams [
1,
2]. Once a breach is formed, the embankment is separated into two banks, the ends of which are the two side slopes of the breach. During this process, the embankment failure is not complete because the flow discharge through the breach could still remove soil blocks and particles and enlarge the breach. Relatively large flow volumes result from the breach into a floodplain or downstream valley [
3,
4,
5]. Knowledge of breach widening mechanisms is important for defining the geometry, breach width and flow discharge of a breach.
Recent laboratory and field experiments have improved our knowledge of breach widening mechanisms of embankments [
6,
7,
8]. Because of the erosion at the foot of the embankment, an overhanging soil block (called headcut) was formed that eventually collapsed. The breach of embankments became wider as the episodic failure of the headcut [
9,
10]. It is the headcut migration of the breach side slope that contributes to the breach widening. The ability to predict the headcut migration is therefore a fundamental requirement for breach modeling and flood risk management.
Many investigations have been conducted to predict the breach widening process using physical based models [
3,
11,
12,
13]. Early models have considered breach widening as a continuous process by using the sediment transport capacity to calculate soil erosion. Next, the theory of river sediment transport was recognized as distinct from hydraulic erosion, which reflects the erodibility of soil during failure. In addition, the rate of erosion has widely been used to estimate losses in soil volume or the breach length with time. Recently, the headcut migration has been recognized as the contribution of the breach widening. The episodic failure of the headcut has replaced the continuous process with soil erosion as the breach widening mechanism. Two dimensional or three dimensional models have been developed to analyze the stability of the headcut [
14,
15]. However, it is difficult to implement the complex headcut migration models in breaching analysis. Therefore, a simple mathematical model of the headcut migration considering the embankment geometry, soil characteristics and discharge flow conditions will be studied in this paper.
The headcut migration is a function of the geometry of the headcut, geotechnical properties of the materials and hydraulic soil erosion at the toe of the side slope. Attempts have been made to predict the headcut migration. The experimental model was developed based on materials that are dependent and constant, water discharge and water head [
16,
17]. Zhao [
15] proposed a dynamic moment balance model to simulate the headcut migration. Bereta [
18] assumed the shear failure of the side slope stability analysis during breach widening. These models began to focus on the side slope stability analysis. However, understanding of the headcut migration is still unsatisfactory, because less attention was paid to the tensile failure of the side slope. Based on observations of the laboratory and field experiments, the headcut fails on the plane normal to the direction of tensile stress, which would suggest the tensile failure mode but the shear failure mode.
In this study, a headcut migration model was developed to predict the critical length of the headcut. This numerical model incorporated the classical tensile failure mode into the headcut migration. It considered the soil tensile strength and soil permeability into the headcut stability analysis for the first time. A simple equation was finally obtained to predict the critical length of the headcut migration. Then, the presented model was verified by the limit equilibrium method.
2. Headcut Migration
2.1. Tensile Failure Mode
As observed in the laboratory and field experiments, soil block failures more likely result from headcuts falling into the breach due to the evolution of the eroded notch [
8,
19,
20]. The formation of the eroded notch is a detachment process due to soil erosion. Based on the principles of soil erodibility, once the discharge flow shear stress exceeds the critical shear stress of the soil, the soil mass would be eroded [
21,
22,
23]. As the soil erosion develops, the eroded notch at the toe of the breach side slope enlarges (shown in
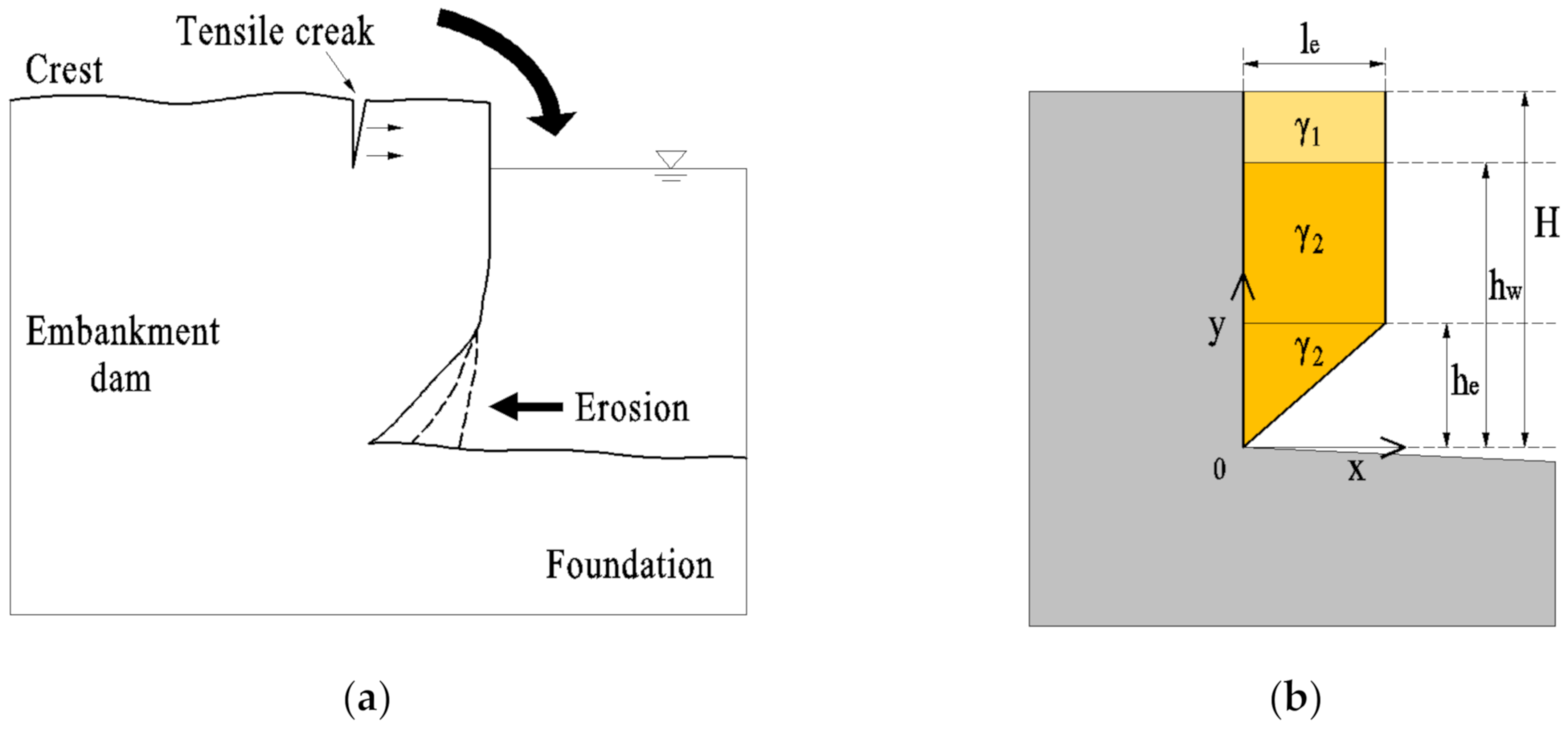
Figure 1a). As this eroded notch evolves, the soil block above it becomes a headcut that is fixed at the end of the breach side slope and is free at the other end of the breach. Removal of soil from the toe of the breach side slope effectively removes physical support for the upper part and results in headcut failure. These processes are shown in
Figure 1a, in which the dashed lines show the evolution of an eroded notch. As the eroded notch evolves, a crack is formed at the crest. Next, the crack expands along the breach side slope until the headcut fails. The headcut fails on the plane normal to the direction of tensile stress. This process is a typical mode of tensile failure [
23,
24,
25].
In the case of headcut migration during breach widening, the dimension of the headcut is more important in terms of the consequences of failure. This order of importance occurs because the generated amount of failure mass is generally removed over a short period of flow discharge and because the length of the headcut determines the width of the breach and the corresponding flow discharge.
2.2. Sketch of a Headcut
A 2D sketch of a simplified headcut cross-section is shown in
Figure 1b.
is the embankment height,
is the water head in breach,
is the erosion height, and
is the erosion length (equal to the length of the headcut). The soil mass of the headcut is divided into three different zones according to its specific weight (influenced by water conditions) and shapes. The first zone is rectangular, above the water surface, and has a specific weight of
. The second zone is the rectangular part of the headcut under the water surface with a specific weight of
. The third zone is the triangular portion of the headcut under the water surface with a specific weight of
. When simplifying the headcut geometry and dividing the soil zones, the following assumptions have been made:
- (1)
The crest level: The crest level near the generated headcut is assumed as horizontal with a uniform height, and the irregularities of the crest near the generated breach are not considered.
- (2)
The height of the headcut: It is calculated using the height of the embankment.
- (3)
Side slope of the headcut: Above the water surface, the side slope of a headcut is assumed vertical towards the breach.
- (4)
Three surfaces of the headcut are visible under the water surface: the right side, left side and under-side. The right side surface of the headcut is assumed as a vertical plane (a vertical line in this cross-section), and the under-side surface is assumed as a plane (a straight line in this cross-section).
- (5)
The water head near the headcut: The water level near the headcut is assumed to be equal to the average water level in the breach.
2.3. Tensile Failure Criterions
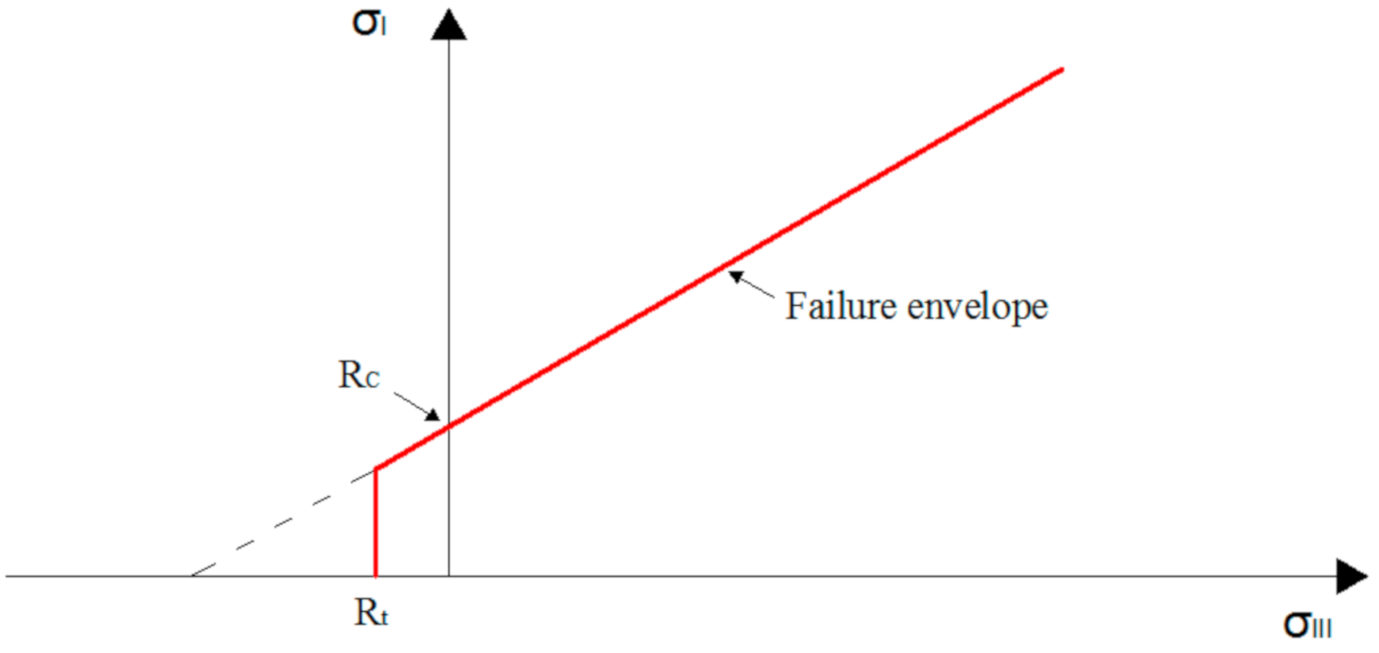
Tensile failure may occur when the maximum tensile stress (
) exceeds the soil tensile strength (
) (see Equation (1)).
One problem is to correctly predict
. As described above, the headcut fails on the plane normal to the direction of tensile stress. Therefore, the failure plane is perpendicular to
(see
Figure 2). A modified Mohr–Coulomb failure criterion was proposed to account for the transition from shear to tensile failure modes [
26]. As shown in
Figure 2, the failure envelope is composed of two straight lines. When
, the failure envelope is the same as the failure envelope of the Mohr–Coulomb failure criterion (see Equation (2)). When
, the perpendicular envelope presents the tensile failure of the material (see Equation (3)).
where
is the major principal stress.
is the minor principal stress.
is the internal friction angle.
is the soil cohesion.
can be expressed as
.
is the uniaxial compressive strength of the material and can be expressed as
[
27,
28,
29]. Thus,
and
can be estimated using soil properties. Therefore, only one parameter,
is used in this equation.
Predicting
of some soils is possible because some relationships between
and
are available. Generally, embankments are constructed of all types of geologic materials. Common orders of magnitude of the soil cohesion and internal friction angle are given in
Table 1. The orders of magnitude of soil properties are only based on engineering experience and can be used in primary evaluations.
The uniaxial compressive strength
can be roughly estimated by using the order of magnitude suggested in
Table 1. For example, in soil materials with a cohesion of 100 kPa and an internal friction angle of 10°, the calculated compressive strength is approximately 238 kPa. Based on the relationship
= 5 to 14, the corresponding tensile strengths range from 17 to 48.
3. Tensile Failure Calculations
As shown in
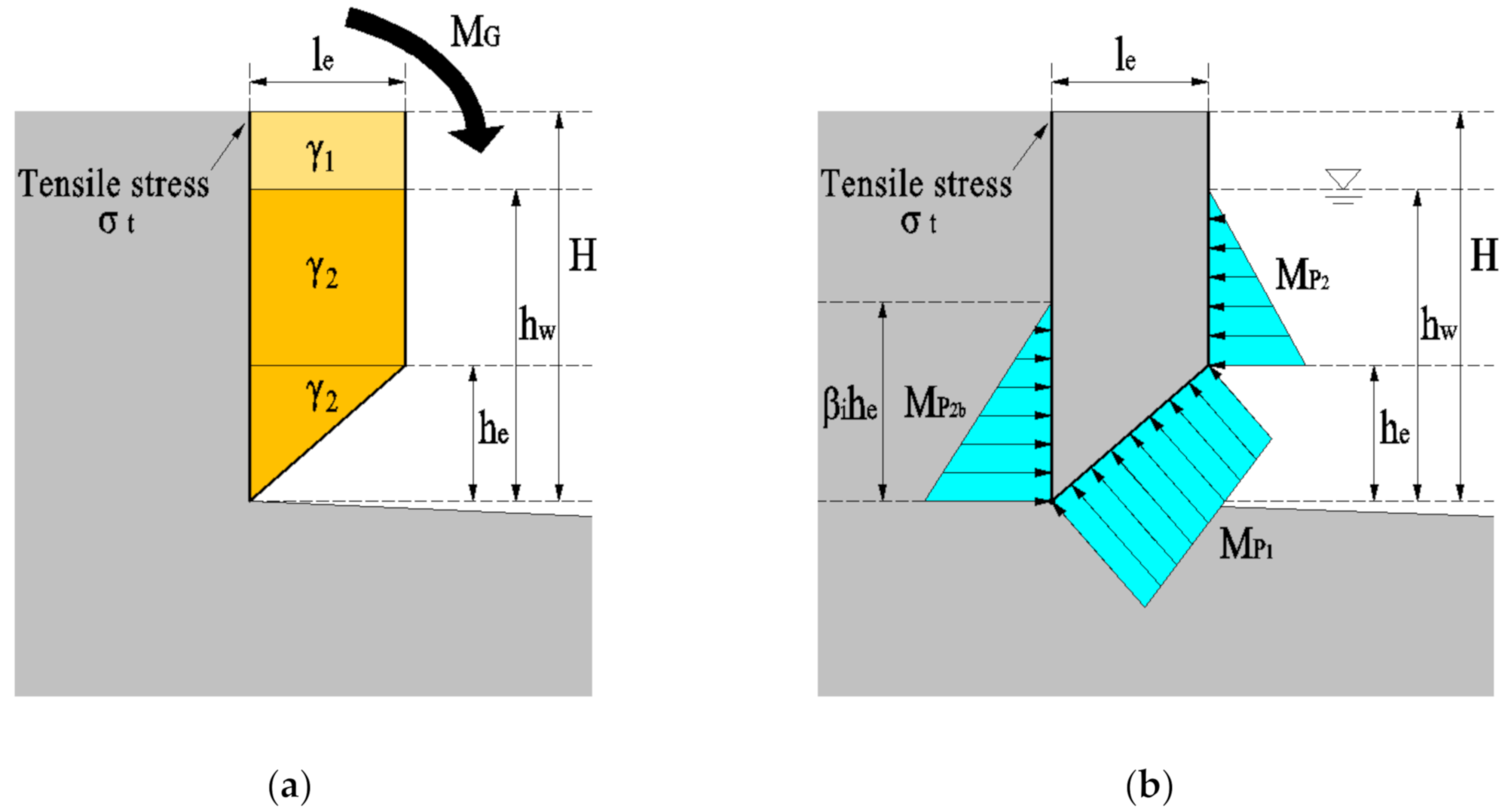
Figure 3, the normal stress on the fixed end section of the headcut consists of two portions: (1) the normal stress resulted from the bending moments, and (2) the normal stress resulted from the normal forces on the section. If distributions of the normal stress due to bending moments are assumed as linear, the distributions of the normal stress can be illustrated as shown in
Figure 3. The top part of the headcut is under tension and the lower part is under compression. The maximum tensile stress potentially occurs on the top of the headcut when assuming a linear stress distribution. This relationship can be written as Equation (4).
where
is the maximum tensile stress.
is the bending moment on the fixed end of the headcut per unit width and may be expressed as the sum of the moments of forces in Equation (5).
is the normal forces on the section. In addition,
is the distance from the neutral axis to the top of the headcut, and
is the moment of inertia of the lengthwise cross-section, which is assumed rectangular with a width of unit. Thus, the moment of inertia may be expressed as
. “-” means that the tensile stress of soil on the section is positive and the compressive stress is negative.
where
is the moment of dead weight.
is the moment of water pressure forces.
3.1. Moment of Dead Weight Per Unit Width
The moment of dead weight per unit width (
) is simply the dead weight multiplied by the distance from the horizontal centers of gravity to the origin (the fixed end of the headcut). Considering the three zones of the headcut (
Figure 4a), it may be expressed as:
3.2. Moments of Water Pressure Per Unit Width
The moments of water pressure per unit width (
) consists of three parts (
Figure 4b) as follows:
where
is the moment of the water pressure force applied on the under-side of the headcut (also called under pressure).
is the moment of water pressure force applied on the right side of the headcut (in the breach).
is the moment of water pressure force applied on the left side of the headcut (in the soil).
The water pressure stress applied on each of the borders can be expressed in each equation (see the coordinate system in
Figure 1b.
- (1)
The under water pressure stress
- (2)
The right side water pressure stress
- (3)
The left side water pressure stress
where
is the infiltration coefficient. For soils with low permeability (
), the pore pressure in the soil can be neglected. For soils with high permeability (
), pore pressure is present in the soil and should be considered as a contribution to the moment of forces on the fixed end of the headcut. In nature, no soil materials have zero or full permeability. Real soils have permeability between these extreme cases (
). Thus, a definition of parameter (
) is necessary when studying real cases.
3.2.1. Moment of the Under Water Pressure Force
The moment of the under water pressure force (
) per unit may be expressed as the integral of the differential under water pressure force multiplied by the distance from the central axis of the cross-section along the under surface of the headcut. When considering the unit width of the headcut, the central axis of the cross-section (rectangular) is the center of the left side of the headcut (0,
) (see
Figure 4b). The differential under water pressure force may be expressed as the under water pressure stress multiplied by the differential length of the under surface of the headcut,
:
where
is expressed by Equation (8).
is the differential under water pressure force. To simplify this calculation, it is divided into horizontal (
) and vertical (
) components (see Equation (12)). Thus, the moments of
and
generated by these two components can be written separately as shown in Equations (13) and (14).
where “−” means that the direction of moments is anticlockwise.
is the angle between the under water pressure force and the horizontal direction, and the differential length of the under surface of the headcut can be transformed as follows:
Thus, the moment of under water pressure force (
) is the summation of
and
. By integrating Equations (8), (11), (12) and (15),
may be expressed as follows:
3.2.2. The Moment of the Right Side Water Pressure Force
The moment of water pressure per unit width at the right side of the headcut (
) may be expressed as the integral of the water pressure force (
) multiplied by the distance from the origin (
, 0) along the right side surface of the headcut as follows:
where
is expressed by Equation (9) with a range of
. By integrating this equation,
can be obtained as follows:
3.2.3. The Moment of the Left Side Water Pressure
Pore pressure is present in the soil and should be considered as a contribution to the moment of forces on the fixed end of the headcut (see
Figure 4b). Thus, the moment of the left side water pressure force per unit width (
) may be expressed as follows:
where
is expressed by Equation (10) with a range of
. By integrating this equation,
can be obtained as follows:
By integrating Equations (16), (19) and (22) into equation (7), the equation of moments of water pressure per unit width (
) may be transformed as follows:
3.3. Bending Moment
The bending moment of the headcut per unit width (
) is found by integrating Equations (5), (6) and (23).
where
is a simplification parameter.
If the parameter
is defined as the ratio of the depth of erosion to the water head in the breach (see Equation (26)),
can be expressed as Equation (27).
3.4. Normal Forces
The normal forces on the section (
) may be expressed using Equation (28).
where
is the normal portion of the water pressure on the under surface of the headcut (the headcut notation is shown in
Figure 1b).
is the normal water pressure on the right side surface of the headcut, and
is the water pressure on the left side surface of the headcut. “−” in the equation means that the compressive force is positive and the tensile force is negative on the section.
3.4.1. Normal Force Due to Under Water Pressure
By integrating Equations (11) and (12), the normal portion of the water pressure on the under surface of the headcut (
) may be expressed as follows:
3.4.2. Normal Force Due to the Right Side Water Pressure
By integrating Equation (18) the normal water pressure on the right side surface of the headcut (
) may be expressed as follows:
3.4.3. Normal Force Due to the Left Side Water Pressure
By integrating Equation (21) the normal water pressure on the left side surface of the headcut (
) may be expressed as follows:
By integrating Equations (29)–(31) into Equation (28), the normal forces may be expressed using Equation (32).
3.5. Critical Length of the Headcut
A critical situation occurs when the maximum tensile stress (
) reaches the soil tensile strength (
) (see Equation (1)), and the headcut falls down to the breach and the side slope retreats. The critical length of the headcut (
) can be calculated by integrating Equations (24) and (32) into Equation (4). The maximum tensile stress (
) is replaced by the soil tensile strength (
), and the erosion length (
) is replaced by the critical length of the headcut (
).
4. Analytical Results and Discussions
The expressed critical length of the headcut due to tensile failure () was obtained. The constants were the height of the headcut () and the specific weights of the soil under and above the water surface ( and ). The variables included the water head in the breach (), the ratio of the depth of erosion to the water head in the breach (), the infiltration coefficient (), and the soil tensile strength ().
4.1. The Specific Soil Weight
The soil specific weight (
) was defined separately as
for the upper part and
for the lower part as follows:
where
is the specific gravity of the soil (non-dimensional).
is the degree of saturation (%).
is the void ratio of the volume of the pores to the volume of the soil. From this equation, the difference between
and
is due to saturation. For illustration purposes, a soil with the specific gravity of 2.6 and a void ratio of 80% was considered. If the soil saturation was assumed as 1 for the soil under the water surface and as 0.7 for the soil above the water surface, the specific weights were 18.5 kN/m
3 and 17.2 kN/m
3, respectively.
4.2. The Water Head in the Breach
The water head in the breach always varies with the discharge flow. Thus, the parameter
was defined to express the relative water head in the breach. The range of
is normally between 0 and 1 and can be larger than 1 for overtopping failure cases.
4.3. The Ratio of the Depth of Erosion to the Water Head
The ratio of the depth of erosion and the water head in the breach (
) was defined as Equation (26). It indicated the degree of soil erosion at the foot of the headcut. According to the literature review, the influence of the side slope on the distribution of the boundary shear stress in the rectangular open channel is concentrated in the lower region where the eroded depth is less than 0.65 times the breach height [
8,
31,
32]. Because the erosion at the foot of the headcut is controlled by the shear stress distribution, the value of
was assumed to be equal to 0.65.
4.4. Infiltration Coefficient
In real cases, the soil materials used in embankments vary widely, along with their permeabilities. As the erosion process evolves, the soil in the headcut gradually infiltrates and the water table in the soil varies. The water pressure stress along the right side of the headcut follows a linear distribution with a distance of from the foot of the headcut. The distributions of water pressure stress on the soil are based on the influences of the infiltration coefficient () as follows:
- (1)
If , the soil in the lower portion should be considered as dry;
- (2)
If , the soil in the lower portion should be considered as totally saturated;
- (3)
If , the soil in the lower portion should be considered as a situation that is between these two extreme situations.
4.5. Analytical Results
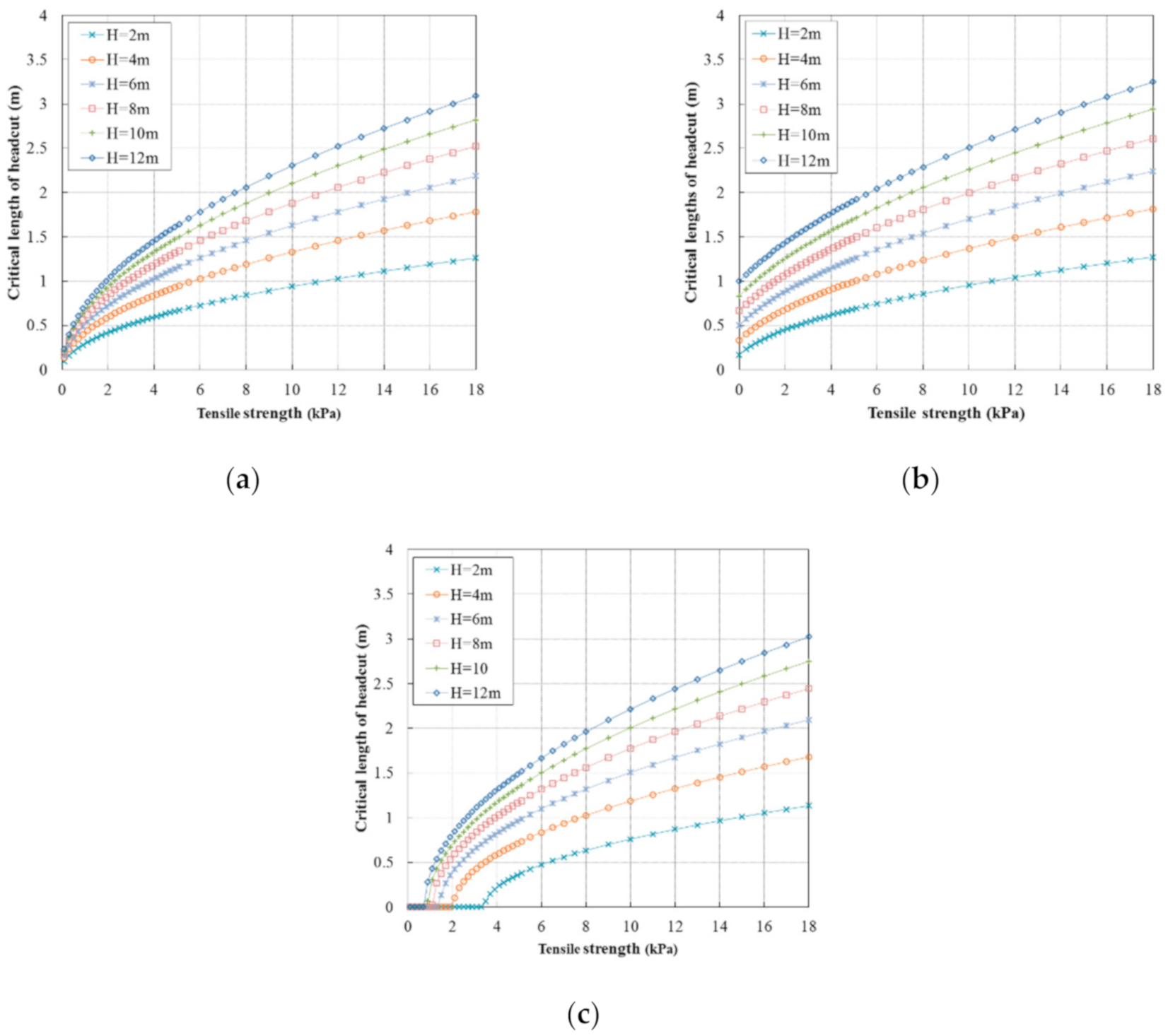
In order to extend the analysis of the critical length of the headcut to general situations, the embankment geometries and soil specific weights are discussed as follows. The range of the embankment height () was from 2 to 12 m, which is a common range for natural and man-made flood protected structures. A relative water depth () of 0.8 was chosen, which corresponded to the relative high water head in the breach. The ratio of the depth of erosion to the water head () equaled 0.65. As discussed in the last section, the specific weight of the saturated soil depends on the degree of saturation and the void ratio of a given soil. These parameters are not always available. Thus, the specific soil weight () and the specific saturated soil weight () were set as 18 kN/m3. The range of soil tensile strength () was considered to be from 0 to 18 kPa.
By applying the above parameters into the analytical Equation (33), interesting results were obtained. Three extreme situations were calculated: (1)
, soil of the embankment body with high permeability; (2)
, soil of the embankment body with moderate permeability; and (3)
, soil of the embankment body with no permeability. For each situation, the critical lengths of the headcut under different soil tensile strengths and for a range of embankment heights were obtained, as shown in
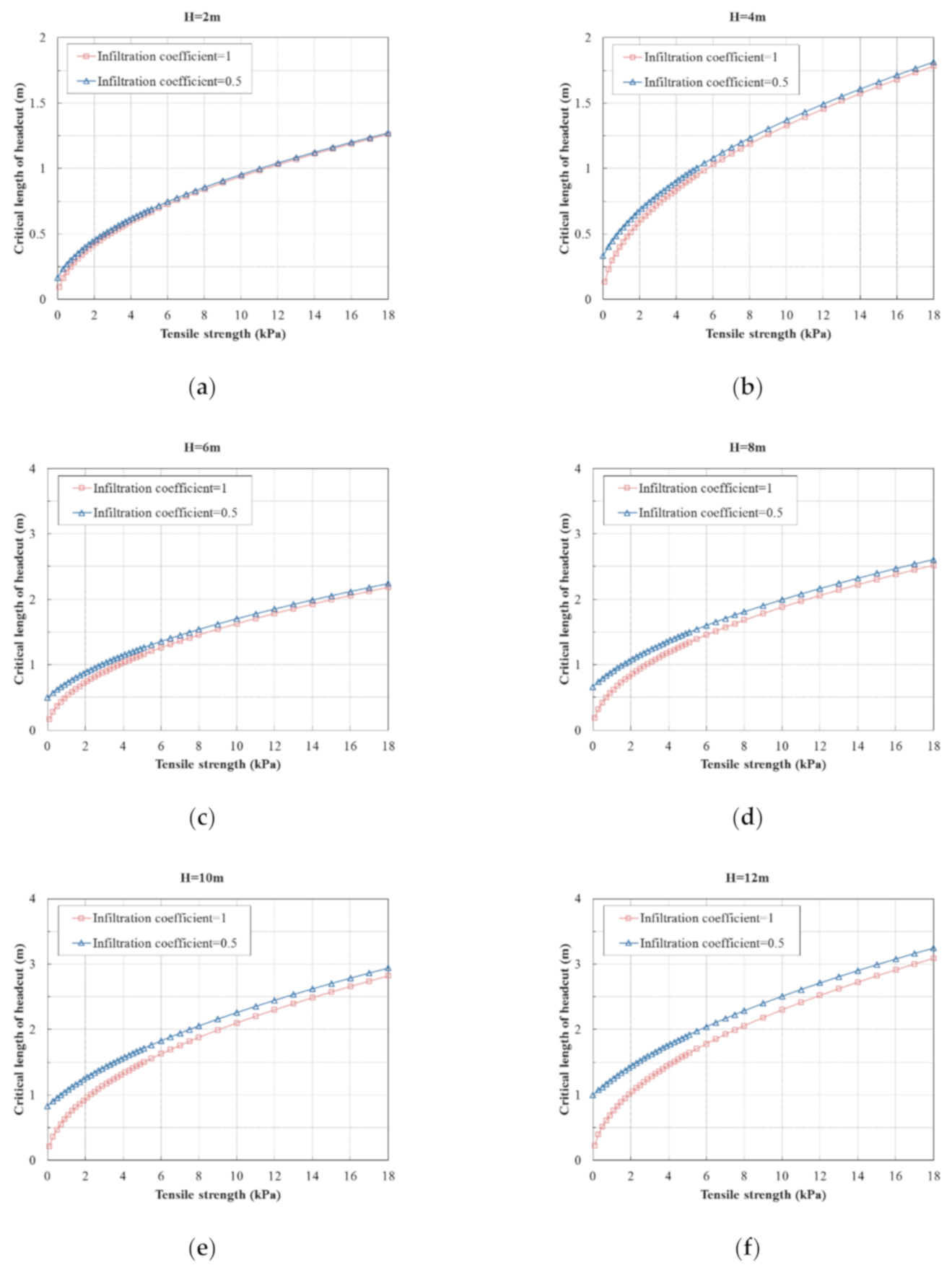
Figure 5a–c, respectively. In
Figure 5a, the critical lengths of the headcut are between 0.1 and 3.1 m. The maximum critical lengths of erosion were observed when the tensile strength of the soil reached the maximum value of 18 kPa. For all embankments of different heights, the critical lengths of the headcut increased as the soil tensile strength increased. In
Figure 5b, the critical lengths of the headcut are between 0 and 3.0 m. In
Figure 5c, the critical lengths of the headcut are between 0 and 3.0 m.
To understand how the distributions of the critical lengths of the headcuts were influenced by the soil infiltration coefficient (
), comparisons of the critical lengths of the headcuts under two soil permeability conditions were made (see
Figure 6a–f). The critical lengths of the headcuts obtained under two soil permeability situations (
and
) had the same magnitude. The critical lengths of the headcut obtained under the high soil permeability situation (
) was a little larger than that obtained under the moderate soil permeability situation (
), which was obvious when the embankment height was relatively low.
5. Verification of Headcut Migration by the Limit Equilibrium Method
A headcut migration model based on the soil tensile failure was presented. In order to verify the presented model, the limit equilibrium method (LEM) was chosen. The LEM is the most common approach for analyzing slope stability and can identify potential failure mechanisms and derive safety factors () for particular geotechnical situations. The LEM was an appropriate choice for assessing the stability of the headcut by considering the geometry, soil properties and groundwater conditions. Thus, the LEM was selected to verify the presented model by identifying the critical length of the headcut (). Slope/W is a well-known slope stability software for soil slopes and can be used to analyze the headcut stability problem using the LEM.
5.1. Model Created in Slope/W
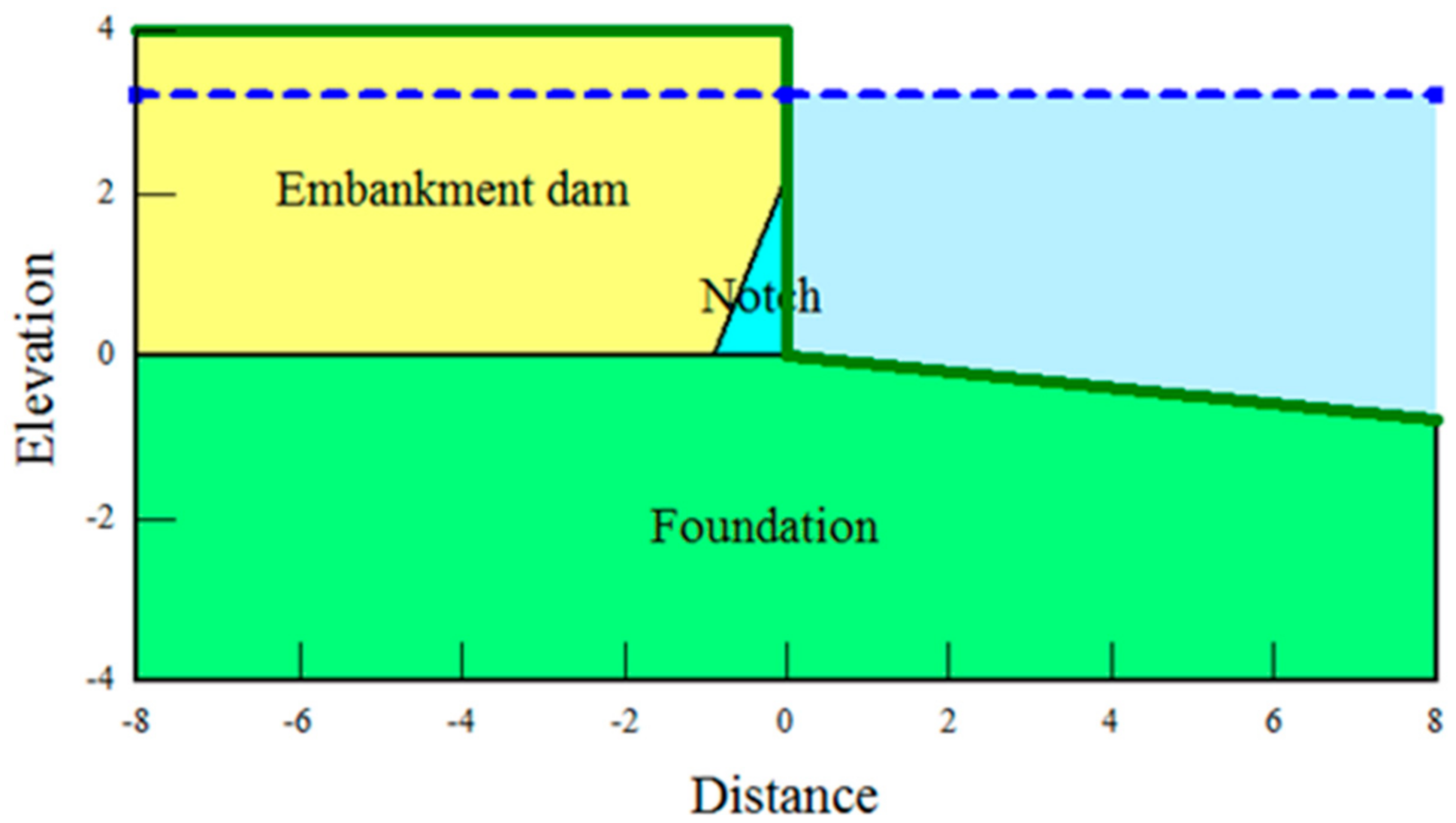
5.1.1. Definition of Geometry of Embankment and Eroded Notch
The definition and simplification of the geometry of an embankment, an eroded notch and a foundation are shown in
Figure 7. The embankment crest was assumed to remain at the same level near the breach. The embankment side slope surface above the water level was treated as vertical. A sharp triangle was defined as the eroded notch, which can be modified manually to simulate the continual lateral erosion process. The depth of the foundation was 4 m for each different embankment height. The relative water head (
) was set as 0.8. The ratio of erosion (
) was set as 0.65. The infiltration coefficient (
) was set as 1. Embankments with a small range of height (
) from 2 to 6 m were simulated.
5.1.2. Soil Properties Input
Three different material properties shall be given for the embankment side slope, the eroded notch and the foundation, respectively. To model the eroded notch at the foot of the headcut, the region of the eroded notch was treated specially with very low soil strength to transform the water pressure to the edge of the headcut under the surface.
Table 2 shows the parameters of the Hoek-Brown failure criterion that were used to represent the embankment soil strength. The Hoek-Brown model is a nonlinear shear strength model that accounts for the soil tensile strength. Considering the material of the embankments used here, it was important to use this failure criterion. The soil strength properties of the foundation and eroded notch are given in
Table 3.
5.1.3. Determination of the Critical Length of the Headcut
To simulate the erosion process, the lengths of the eroded notch were manually changed step by step. The increase in the length of the eroded notch during each step was determined by the safety factor (
). Thus, at the beginning of erosion, when the safety factor was still large, the increase in each step was set to a relatively larger value. When the safety factor decreased to less than 1, the increase was refined. The minimum increase in each step was set to 0.1 m. For each of the eroded notch geometries, the safety factors were calculated sequentially under the same hydraulic and geotechnical situations. Thus, a series of safety factors was obtained and recorded. The critical length of the eroded notch (equal to the critical length of the headcut (
), see
Section 2.2) corresponding to the safety factor of 1 (
) was obtained by an interpolation method.
5.1.4. Mathematical Model Verification
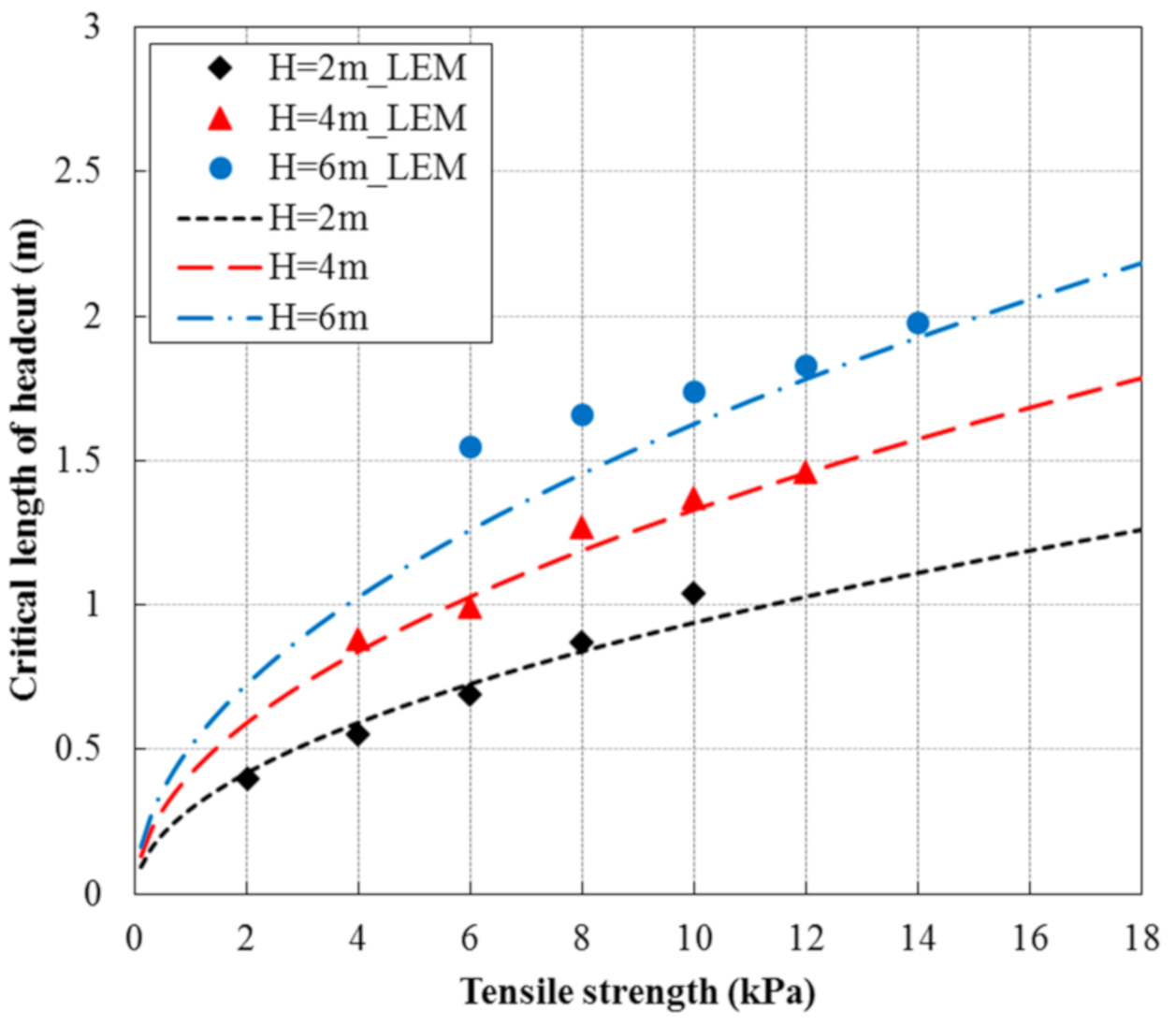
The method introduced above was used to determine the critical length of the headcut for each embankment dimension. As shown in
Figure 8, it is obvious that the simulated critical length varied as the soil tensile strength changed. Thus, the soil tensile strength was a significant index. Considering a 2 m tall embankment, the critical length varied from 0.5 to 1.1 m. Considering a tall embankment with a height of 6 m, the critical length of the headcut was between approximately 1.6 and 2.4 m.
5.2. Results and Discussions
Comparisons of the critical headcut lengths using the soil tensile strength based mathematical model and the simulated results obtained by the LEM are shown in
Figure 8. For a 2 m high embankment, simulated calculations were concentrated over a range of soil tensile strengths of 2 to 10 kPa. For the 4 and 6 m tall embankments, the simulated calculations were concentrated over a soil tensile strength range of 4 to 12 and 6 to 14 kPa, respectively. As shown in
Figure 8, the critical headcut lengths simulated by the LEM increased as the soil tensile strengths increased. The critical headcut lengths under different soil tensile strengths obtained by the LEM fit the present model well. The simulated results obtained by the LEM agreed reasonably well with the present model.
For the case H = 4 m, when the tensile strength was equal to 6 kPa, the simulated critical length of the headcut was smaller than the calculated result obtained by the present model, because of the accuracy of the manual changes of the lengths of the eroded notch during simulation. To simulate the erosion process, the lengths of the eroded notch were manually changed step by step. The minimum increase in each step was set to 0.1 m. For each of the eroded notch geometries, the safety factors () were calculated. Thus, a series of safety factors were obtained and recorded. The critical length of the eroded notch corresponding to the safety factor of 1 () was obtained by an interpolation method.
6. Comparisons with Tests
Due to lack of witness, it is difficult to compare the present model with real embankment breaching. From literature reviews, some field or laboratory tests were conducted to evaluate the widening of a breach:
(1) In the FP5 IMPACT project [
33,
34], a large-scale test of embankment breaching was performed. It was built with a height of 4.3 m embankment above the channel bottom, a width of 3 m at the crest and 15.04 m at the bottom. The properties of the embankment materials were obtained by testing with the soil density = 2341 kg/m
3, the angle of friction = 42° and the cohesion = 20 kN/m
2. The soil tensile strength can be estimated using the ratio
= 5–14; the soil tensile strength = 6–17 kN/m
2. The reservoir water level in the upstream was maintained at a relatively constant level of 4.1 m. However, as the test progressed, the reservoir water level dropped to 3.1 m. At the end of the test, there was almost no water in the reservoir. The averaged episodic failure width (headcut length) was 1.3 m when the reservoir water level was approximately 4.1 m, and 0.9 m when the reservoir water level was approximately 3.1 m.
(2) In the USDA-NRCS Test [
8,
35], the constructed embankment was 1.3 m in height with a 1.8 m crest width and 5.5 m section width. The reservoir water level in the upstream was maintained at a relatively constant level of 0.7 m. The properties of the embankment materials were obtained by testing with the dry unit weight of the soil = 17.6 kN/m
3, the water content = 12.7%, the compressive strength = 34 kPa and the plasticity index = 0%. The soil tensile strength can be estimated as 2–7 kN/m
2. The reservoir water level in the upstream was maintained at a relatively constant level. The averaged episodic failure width (headcut length) was 0.6 m.
Comparisons of the critical length of the headcut with experimental data and the present model are shown in
Table 4. Based on the estimated soil tensile strength of the two tests, the present model gives good predictions of the critical length of the headcut.
7. Conclusions
This study presents a headcut migration model of breach side slope for computing the critical length of the headcut during the breach widening. Removal of soil from the toe of the breach side slope effectively removes physical support for the upper part and results in headcut failure. As the eroded notch evolves, a crack is formed at the crest and then expands along the breach side slope until the headcut fails. The headcut fails on the plane normal to the direction of tensile stress. This process is a typical mode of tensile failure. Then, a numerical model of the headcut migration was established by integrating the effects of the soil tensile strength, soil permeability and embankment geotechnical characteristics. A simple analytical Equation (33) was finally obtained to predict the critical length of the headcut under different embankment scales, the soil tensile strength (based on embankment geologic materials) and the soil permeability. Analytical results show that the critical lengths of the headcuts obtained under two soil permeability situations have the same magnitude. The critical lengths of the headcut obtained under the high soil permeability situation is a little larger than that obtained under the moderate soil permeability situation, which is obvious when the embankment height is relative low. The present model was verified by using the limit equilibrium method for three typical embankment scales (2, 4 and 6 m high). The comparison indicates that the use of the present model appears to be a reasonable approach for modeling the critical length of the headcut. The present model could provide a simple method to predict the critical length of the headcut migration and easily be adopted to breach widening models of embankments and landslide dams.
More efforts are also needed to apply the present model to the breach widening process due to embankment failure. The breach width is determined by the distance between the two side slopes. The critical length of the headcut is calculated by the present model. If the excess shear equation is used to calculate the soil erosion rate on the corner of the headcut, the erosion time spent to reach a critical length of the eroded notch that generates the failure of the headcut can be obtained. Finally, the breach width at any time may be obtained.
Author Contributions
Writing—original draft preparation, Z.L.; writing—review and editing, T.L.; supervision, Y.D. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangxi Province (Project No. 2018ACB21017).
Acknowledgments
This work was supported by the Jiangxi Provincial Natural Science Foundation (Project Nos. 2018ACB21017). The financial support is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peng, M.; Zhang, L. Breaching parameters of landslide dams. Landslides 2012, 9, 13–31. [Google Scholar] [CrossRef]
- Shen, D.; Shi, Z.; Peng, M.; Zhang, L.; Jiang, M. Longevity analysis of landslide dams. Landslides 2020, 17, 1797–1821. [Google Scholar] [CrossRef]
- Feliciano Cestero, J.A.; Imran, J.; Chaudhry, M.H. Experimental investigation of the effects of soil properties on levee breach by overtopping. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Morris, M.; Hassan, M.; Kortenhaus, A.; Visser, P. Breach Processes: A State of the Art Review; Report No. T06-06-03; HR Wallingford: Oxfordshire, UK, 2009. [Google Scholar]
- Froehlich, D.C. Embankment dam breach parameters and their uncertainties. J. Hydraul. Eng. 2008, 134, 1708–1721. [Google Scholar] [CrossRef]
- Kakinuma, T.; Shimizu, Y. Large-scale experiment and numerical modeling of a riverine levee breach. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Ashraf, M.; Soliman, A.H.; El-Ghorab, E.; EI Zawahry, A. Assessment of embankment dams breaching using large scale physical modeling and statistical methods. Water Sci. 2018, 32, 362–379. [Google Scholar] [CrossRef]
- Hunt, S.L.; Hanson, G.J.; Cook, K.R.; Kadavy, K.C. Breach widening observations from earthen embankment tests. Trans. ASAE 2005, 48, 1115–1120. [Google Scholar] [CrossRef]
- Zhao, G. Breach Growth in Cohesive Embankments due to Overtopping; Delft Academic Press: Delft, The Netherlands, 2016. [Google Scholar]
- Wei, H.; Yu, M.; Wang, D.; Li, Y. Overtopping breaching of river levees constructed with cohesive sediments. Nat. Hazards Earth Syst. Sci. 2016, 16, 1541–1551. [Google Scholar] [CrossRef]
- Klijn, F.; Schweckendiek, T. Comprehensive Flood Risk Management; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Paquier, A. Testing a simplified breach model on Impact project test cases. In Proceeding of the 32nd Congress of IAHR, Venice, Italy, 1–6 July 2007. [Google Scholar]
- Fread, D.L.; Lewis, J.M. NWS FLDWAV model: The replacement of DAMBRK for dam-break flood prediction. In Proceedings of the 10th Annual ASDSO Conference, Kansas City, MO, USA, 26–29 September 1993. [Google Scholar]
- Wang, Z.; Bowles, D.S. Three-dimensional non-cohesive earthen dam breach model. Adv. Water Resour. 2006, 29, 1528–1545. [Google Scholar] [CrossRef]
- Zhao, G.; Visser, P.J.; Peeters, P.; Vrijling, J.K. Headcut migration prediction of the cohesive embankment breach. Eng. Geol. 2013, 164, 18–25. [Google Scholar] [CrossRef]
- Temple, D.M.; Hanson, G.J.; Neilsen, M.L.; Cook, K.R. Simplified breach analysis model for homogeneous embankments: Part I, Background and model components. In Proceedings of the 2005 US Society on Dams Annual Meeting and Conference, Salt Lake City, UT, USA, 6 June 2005; pp. 151–161. [Google Scholar]
- Hanson, G.J.; Cook, K.R. Determination of Material Rate Parameters for Headcut Migration of Compacted Earthen Materials. Available online: https://www.ars.usda.gov/research/publications/publication/?seqNo115=168159 (accessed on 3 July 2015).
- Bereta, G.; Hui, P.; Kai, H.; Guang, L.; Kefan, P.; Zhao, Y. Experimental Study of Cohesive Embankment Dam Breach Formation due to Overtopping. Period. Polytech. Civ. Eng. 2020, 64, 198–211. [Google Scholar] [CrossRef]
- Castedo, R.; Fernandez, M.; Trenhaile, A.S.; Paredes, C. Modeling cyclic recession of cohesive clay coasts: Effects of wave erosion and bluff stability. Mar. Geol. 2013, 335, 162–176. [Google Scholar] [CrossRef]
- Hayakawa, Y.S.; Matsukura, Y. Stability analysis of waterfall cliff face at Niagara Falls: An implication to erosional mechanism of waterfall. Eng. Geol. 2010, 116, 178–183. [Google Scholar] [CrossRef]
- Wan, C.; Fell, R. Investigation of rate of erosion of soils in embankment dams. J. Geotech. Geoenviron. Eng. 2004, 130, 373–380. [Google Scholar] [CrossRef]
- Hanson, G.; Simon, A. Erodibility of cohesive streambeds in the loess area of the midwestern USA. Hydrol. Processes 2001, 15, 23–38. [Google Scholar] [CrossRef]
- Castedo, R.; Murphy, W.; Lawrence, J.; Paredes, C. A new process–response coastal recession model of soft rock cliffs. Geomorphology 2012, 177, 128–143. [Google Scholar] [CrossRef]
- Kogure, T.; Aoki, H.; Maekado, A.; Hirose, T.; Matsukura, Y. Effect of the development of notches and tension cracks on instability of limestone coastal cliffs in the Ryukyus. Jpn. Geomorphology 2006, 80, 236–244. [Google Scholar] [CrossRef]
- Kogure, T.; Matsukura, Y. Critical notch depths for failure of coastal limestone cliffs: case study at Kuro-shima Island, Okinawa, Japan. Earth Surf. Process. Landf. 2010, 35, 1044–1056. [Google Scholar] [CrossRef]
- Paul, B. A modification of the Coulomb-Mohr theory of fracture. J. Appl. Mech. 1961, 28, 259–268. [Google Scholar] [CrossRef]
- Hoek, E. Estimating Mohr-Coulomb friction and cohesion values from the Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 1990, 27, 227–229. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek-Brown Failure Criterion–A 1988 Update. Available online: https://www.researchgate.net/profile/E_Brown/publication/247896456_The_Hoek-Brown_failure_criterion_-a_1988_update/links/54da95b00cf2ba88a68d4bd5.pdf (accessed on 30 April 2020).
- Meyer, J.P.; Labuz, J.F. Linear failure criteria with three principal stresses. Int. J. Rock Mech. Min. Sci. 2013, 60, 180–187. [Google Scholar] [CrossRef]
- Xiao, R. Soil Mechanics; Peking University Press: Beijing, China, 2006. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows. J. Hydraul. Eng. 1994, 120. [Google Scholar] [CrossRef]
- Zheng, Y.; Jin, Y. Boundary shear in rectangular ducts and channels. J. Hydraul. Eng. 1998, 124, 86–89. [Google Scholar] [CrossRef]
- Vaskinn, K.A.; Lovoll, A.; Hoeg, K. Physical Modeling of Breach Formation: Large Scale Field Tests. Available online: https://www.ars.usda.gov/research/publications/publication/?seqNo115=168160 (accessed on 3 December 2019).
- Bonelli, S. Erosion in Geomechanics Applied to Dams and Levees; ISTE: London, UK; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hanson, G.J.; Cook, K.R.; Britton, S.L. Evaluating erosion widening and headcut migration rates for embankment overtopping tests. Am. Soc. Agric. Biol. Eng. 2003. [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).