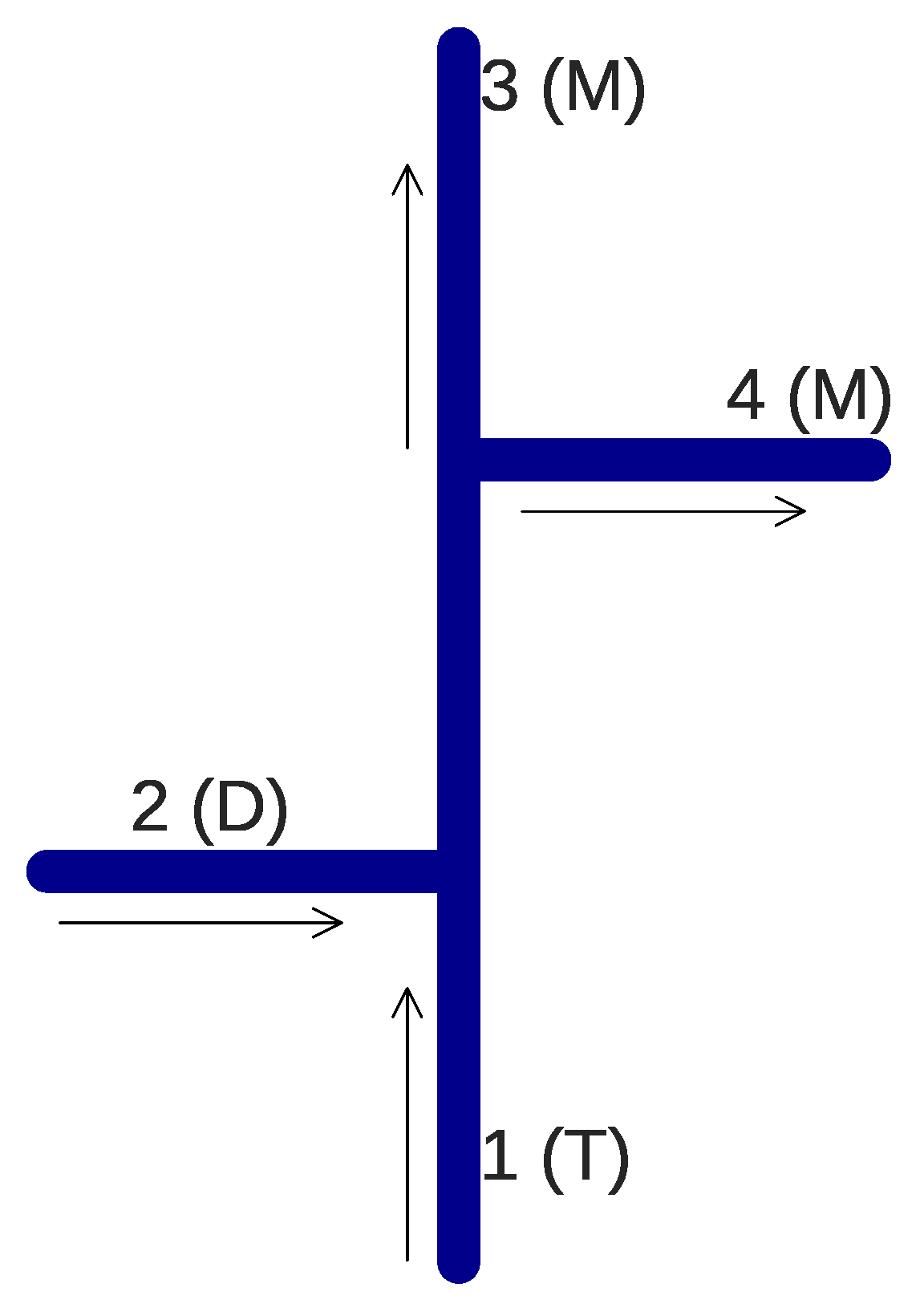
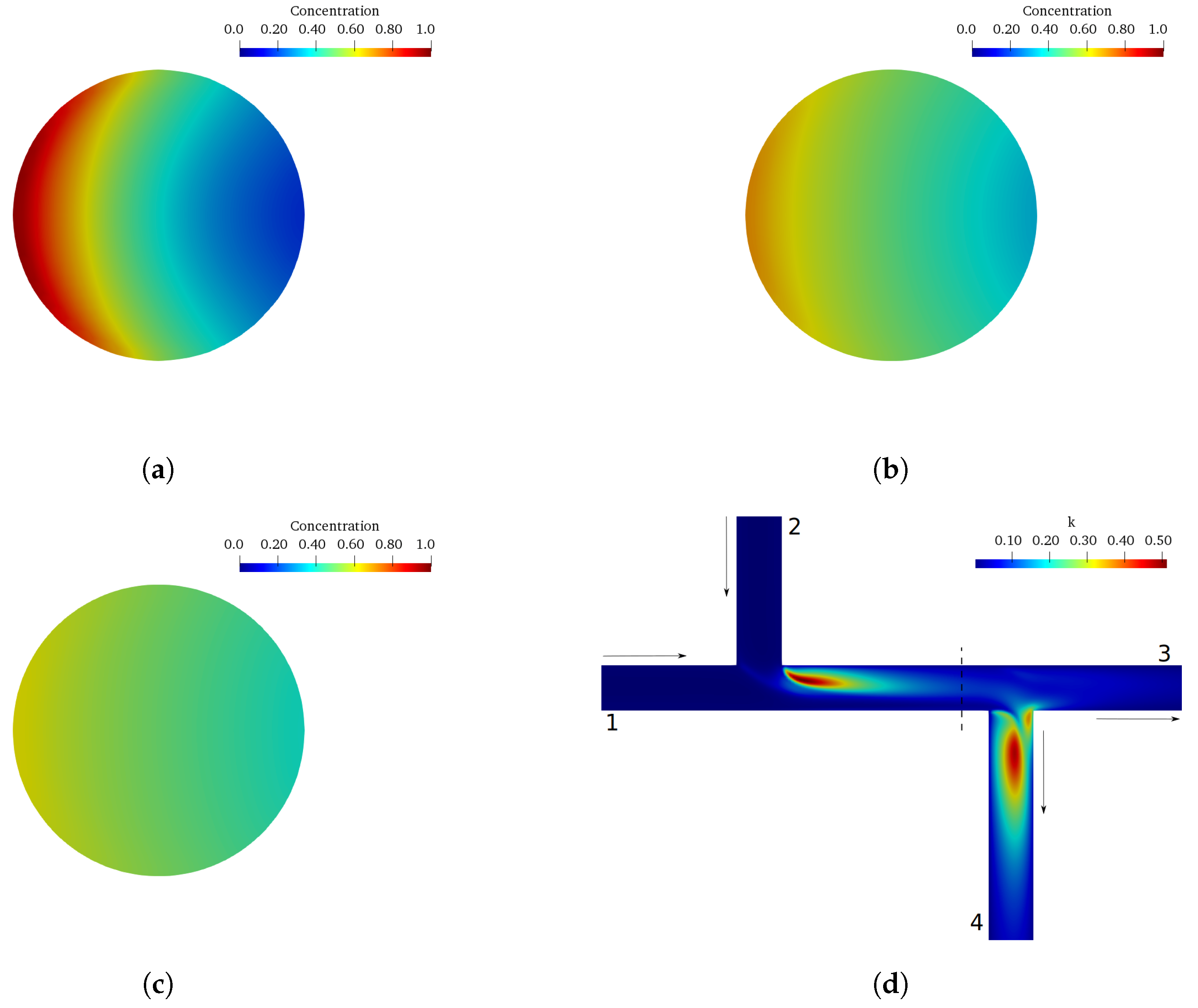
1. Introduction
The mixing of fluids in water distribution networks is a complex phenomenon that has been extensively subjected to research as it is relevant to several specific areas of application such as water distribution quality and safety [
1,
2,
3], pollution source detection systems (both large [
4,
5] and small networks [
6]), and optimal pollution sensor placement in a water distribution network [
7,
8,
9,
10]. The elements that form water distribution networks are pipes and junctions. When modeling mixing in a complex system, a correct mixing model must be applied to accurately describe the contaminant transport through the network due to the fact that a wrong solution could present a hazard to a great number of network users.
Usually, mixing in a pipe network is modeled as either complete mixing or bulk mixing. Complete mixing can be described as an even split of contamination at a network junction. Complete mixing models such as the one developed in the hydraulic analysis software EPANET are implemented by calculating the flow-weighted concentrations at the inlet pipes of a junction and then assuming an even split in the outlet pipes. The complete mixing model can be assumed correct only if there is a single outlet at a junction and if the distance between two junctions is great enough. For certain distances [
11,
12], it does not describe the physical process of mixing correctly.
Bulk mixing is an idealized mixing in which the flow between two inlet pipes is not interacting and the diffusive behavior between the inlet pipe streams is ignored (the streams are only touching at an interface). To model the bulk mixing, the flow momentum in the inlet pipes is calculated, and it determines how the concentration splits between the outlets. The inlet pipe with the higher momentum will dominate in concentration transfer into the outlet pipe, which follows the same direction as the inlet pipe. The inlet pipe with lower flow momentum will only transfer the concentration into its neighboring outlet pipe. This kind of mixing behavior is usually specific to cross junctions. The bulk mixing model is implemented in the software EPANET-BAM [
13] (which can be considered as an extension of EPANET). If the expected mixing behavior is neither complete nor bulk, an experimentally-calibrated mixing model parameter can be used, by which type of mixing is defined.
In research by McKenna et al. [
14], it is shown that, for a cross junction (which is a special case of a double-Tee junction in which the distance between converging and diverging pipes is equal to zero), a strong deviation from complete mixing occurs when the Reynolds number at each inlet and outlet pipe is equal. On the other hand, stronger turbulence can also create a considerable unpredictability of mixing in cross junctions [
15]. The mixing that occurs at two sequential Tee junctions is especially complex due to increased chaotic eddying of flow, which in turn increases the diffusion between the streams. It is proved in several studies [
12,
16,
17] that the length between double-Tee junctions is important since it determines the behavior of mixing of fluids or rather the transport of contaminant into each diverging pipe. In addition, variation of flows at both inlet and outlet pipes causes the mixing behavior to vary [
11,
12]. Another property of a pipe system that can cause an incomplete mixing behavior are uneven pipe diameters, where a large difference between pipe diameters can produce a more complete mixing [
18]. The orientation of pipes for a double-Tee junction also affects the mixing behavior, and it is shown that mixing for a case when the pipes are at a opposite side compared to the case where they are at the same side, behaves differently [
11,
12] (assuming planar configuration). It is also shown that transitional and laminar flows in pipes exhibit a specific mixing behavior [
19].
Instead of an experimental approach to studying mixing behavior in double-Tee junctions, computational fluid dynamics (CFD) can also be used. A species transport model coupled with RANS turbulence models yields good results [
12,
16] that can be used to further enhance simpler 1D mixing models (such as EPANET-BAM). Additionally, a high fidelity LES turbulence model can also be used to study mixing with more detail [
20]. The problem with CFD simulations and the contaminant transport model is that they need to be calibrated as they are dependant on the turbulent Schmidt number, the value of which is very much case-specific [
21,
22] and has been differently reported in several studies regarding CFD analysis of mixing in double-Tee junctions [
12,
23,
24]. Furthermore, CFD simulations are computationally expensive and producing results for a range of combinations of mixing scenarios (varying inlet and outlet flow, distance between junctions, and even pipe diameters) is quite impractical. Alternatively, mixing behavior can be predicted by use of data analysis (i.e., interpolation on a fixed previously produced dataset), as was done in a previous study [
25] where Kriging and Delaunay triangulation were combined to describe mixing for different Reynolds numbers.
Recently, machine learning (ML) algorithms used in hydrology and hydraulics include Artificial Neural Networks (ANN) and variations [
26,
27], Random Forest [
28], and Support Vector Machine [
29]. ML has been previously successfully implemented in pipe flow systems. A selection of ML algorithms such as Random Forest, Bagging Algorithm, and Regression Tree were used to predict various characteristics of a wastewater pipe system and it was found that Regression Trees are most successful [
30]. Several ML algorithms were also used to predict pressure gradients, liquid holdup, and flow pattern identification of multiphase flow on a pipe segment (where data were generated by CFD) and, for some of the characteristics, the Gradient Boosting algorithm and Support Vector Machine yielded best results [
31]. Deep learning (i.e., ANN) was successfully applied to produce the best valve scheduling scenario in the case of pipe network contamination instead of searching for a contamination source [
32]. Similarly, Support Vector Regression (SVR) was used to detect anomalies in a pipe network system [
33] and a modified ANN approach was used for pipe network management [
34].
A ML approach can be also used to evaluate the mixing behavior based on previously obtained data (either by experiment or by CFD). In this study, two ML algorithms—SVR and ANN—were tested in predicting mixing behavior for a combination of different inlet and outlet pipe flow ratios and different distances between double-Tee junctions, on one pipe configuration. Training data were generated by 3D CFD that was calibrated on an experiment presented in a previous study [
12]. A supercomputer was used for CFD modeling due to its high computational demand and need to generate as many data as possible for better ML training.
4. Summary and Conclusions
In this paper, a new methodology for double-Tee junctions mixing modeling is presented based on an experiment from the previous literature. A CFD model was calibrated with the experimental data to serve both as a computational efficiency benchmark and a data-generator for a ML approach for the presented double-Tee junction mixing phenomena assessment problem.
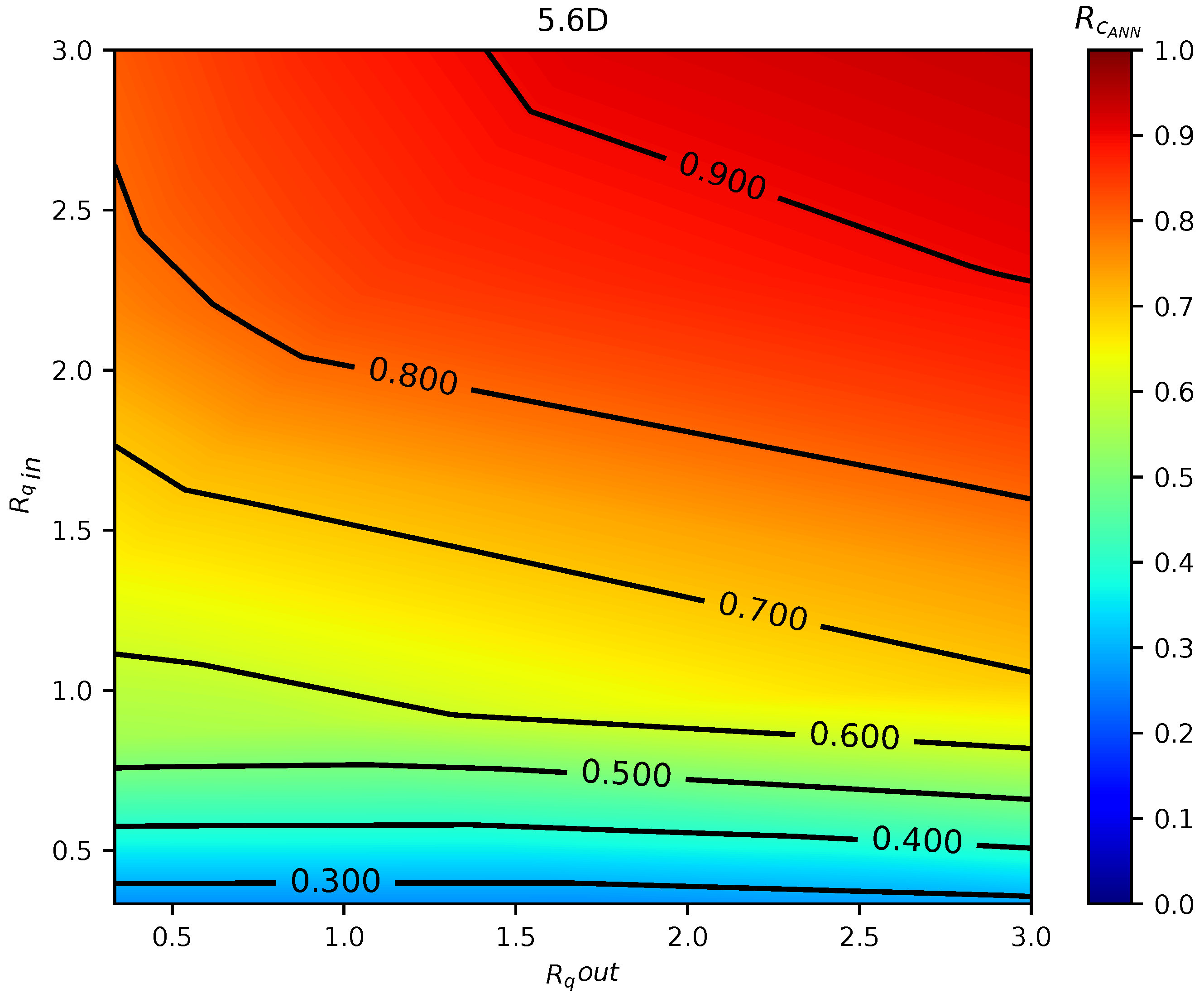
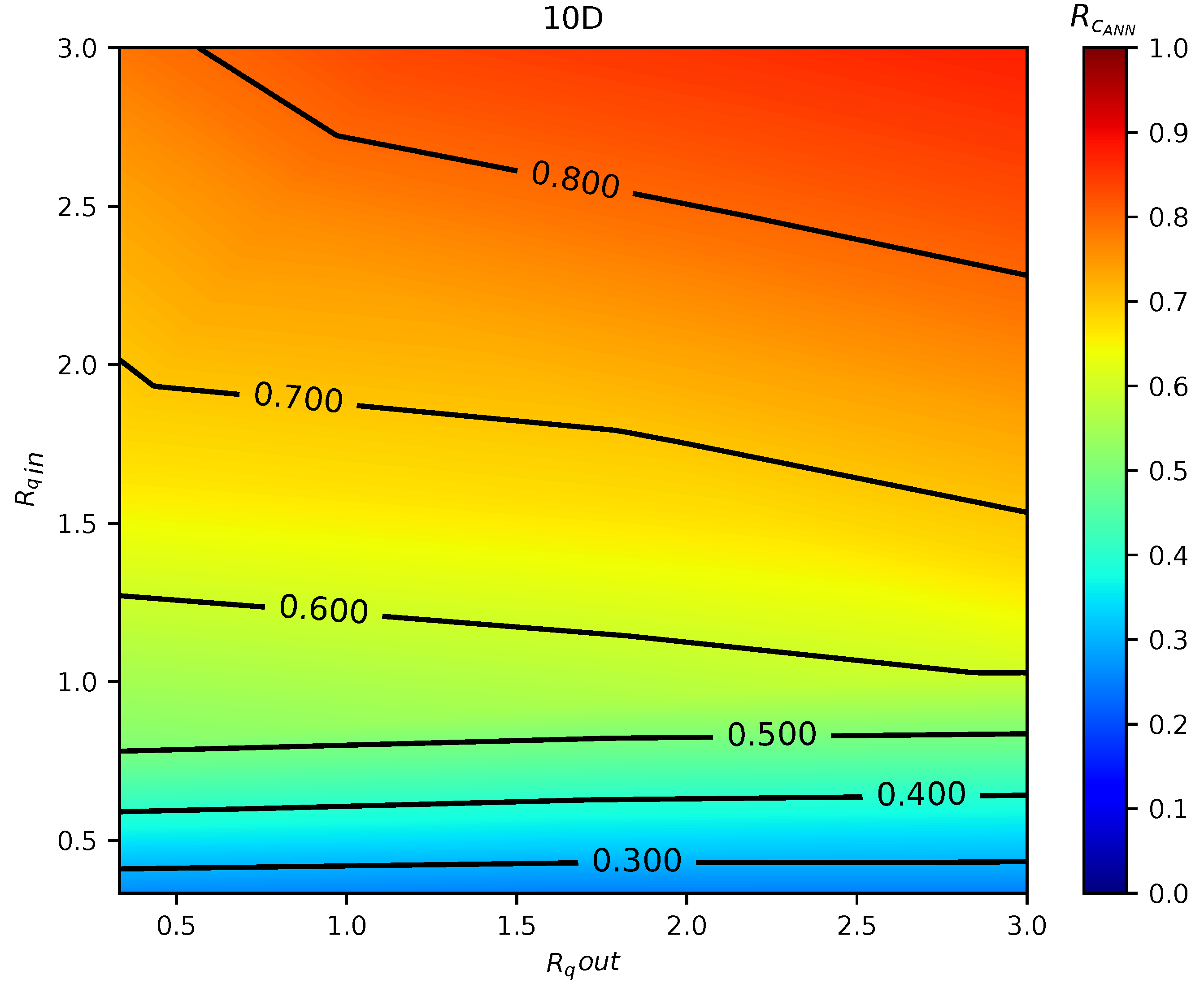
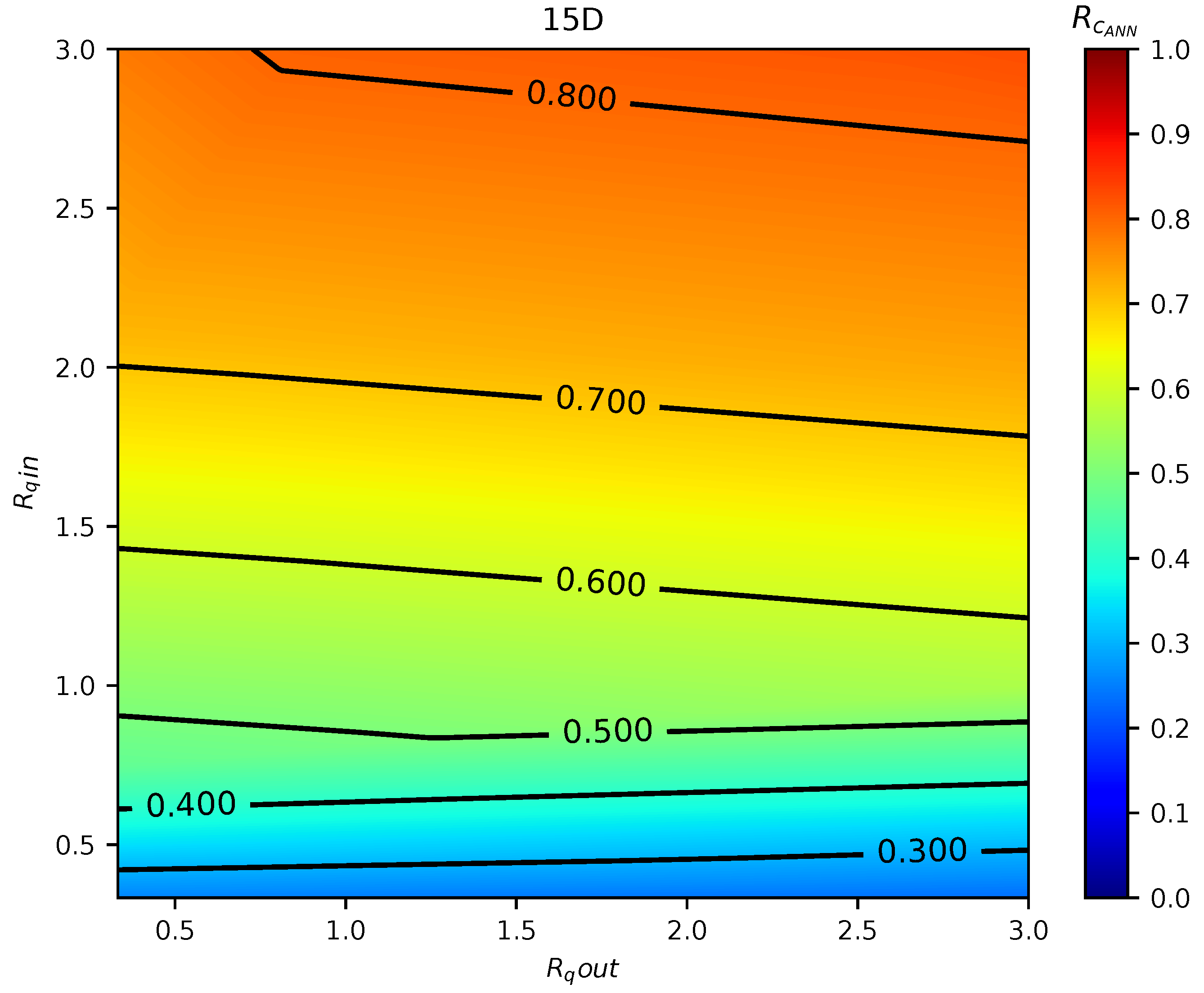
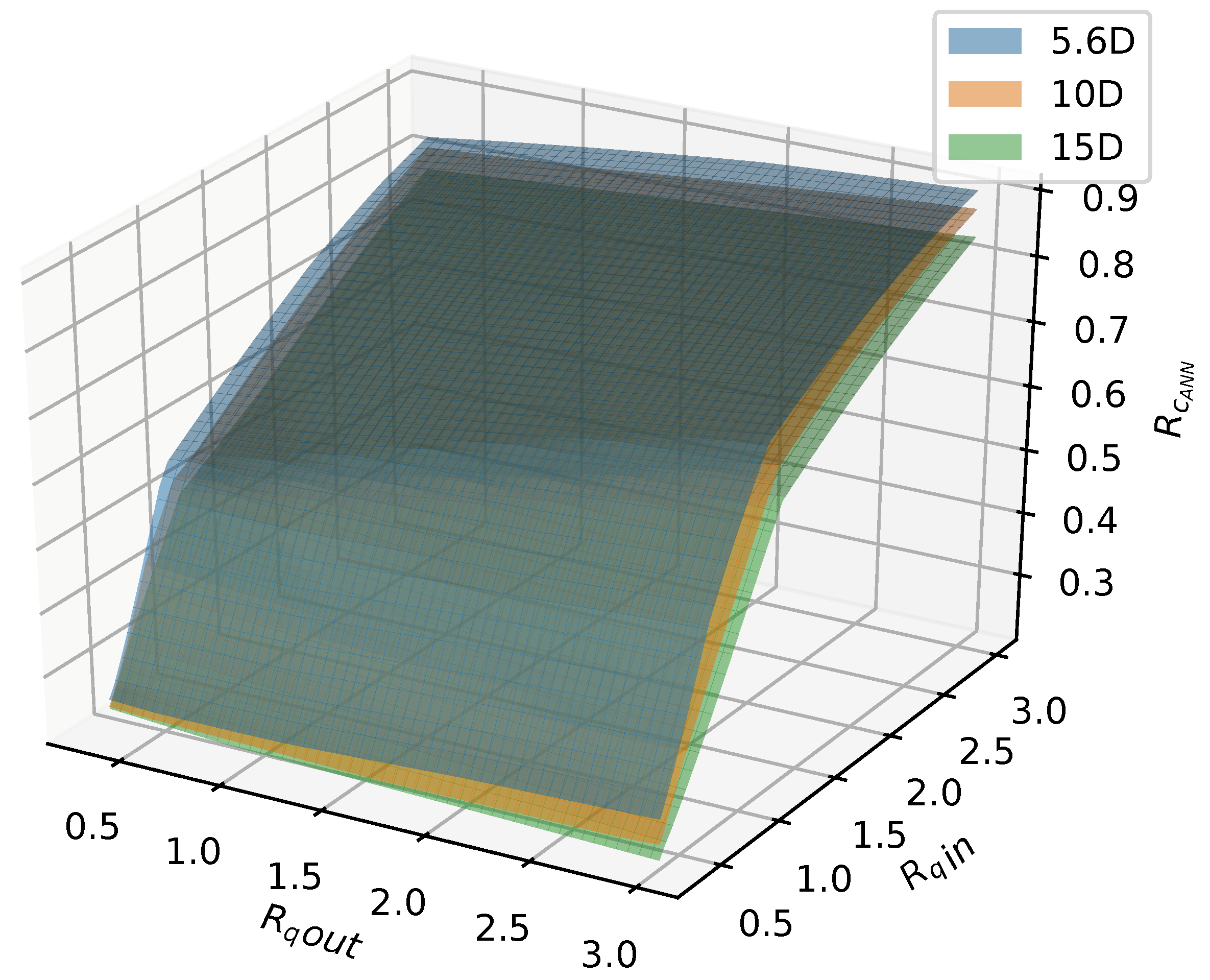
In total, 75 simulations were done by the calibrated CFD RANS k- turbulence model and the data were used to train two different ML models. The input variables were defined as the inlet pipe flow ratio, the outlet pipe flow ratio, and distance between the double-Tee junction, while the output was the outlet branch pipe to main inlet pipe conductivity ratio, which is a relevant variable that describes the mixing behavior in a double-Tee junction.
The two tested ML algorithms were Support Vector Regression and Artificial Neural Network (specifically Feedforward Multilayer Perceptron), and, of the two, ANN outperformed SVR in accuracy. Empirical results obtained with the ANN model used show good approximation in predicting the mixing behavior for different distances between double-Tee junctions and inlet/outlet pipe flow ratios.
Besides the accuracy of ANN, it was determined that the computational efficiency of the ANN model is much greater than that of the CFD model, which makes it a great tool for modeling this kind of phenomena. Since many previous studies produced experimental data for a great number of different combinations (which include different Reynolds numbers ranges in pipes, varied pipe diameters, distances between double-Tees, pipe configuration, etc.), a further study could be done to create an ANN that takes into account all of these variables and produces all the relevant parameters to accurately model mixing. With its computational efficiency, a fast model such as ANN could be directly incorporated into complex water network supply pipe network models (such as EPANET and similar), which would greatly improve their accuracy and in turn make them a more powerful tool for predicting water network pollution dispersion and similar hazardous phenomena.