Multi-Objective Optimization for Selecting and Siting the Cost-Effective BMPs by Coupling Revised GWLF Model and NSGAII Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Sources
2.2. The Watershed Model
- NtrStorei,t represents the amount of nutrient load in reach i at day t;
- UpNtri,t represents the amount of nutrient load from upstream in reach i at day t;
- LandNtri,t represents the amount of nutrient load from local land area in reach i at day t;
- PntNtri,t represents the amount of nutrient load from a point source in reach i at day t;
- NtrOuti,t represents the amount of nutrient load to an outflow before attenuation in reach i at day t;
- NtrOuti,t’ represents the amount of nutrient load to an outflow after attenuation in reach i at day t;
- θi represent the nutrient attenuation exponent in reach i; and
- TravelTimei,t represents the flow travel time in reach i at day t.
2.3. BMPs and Costs
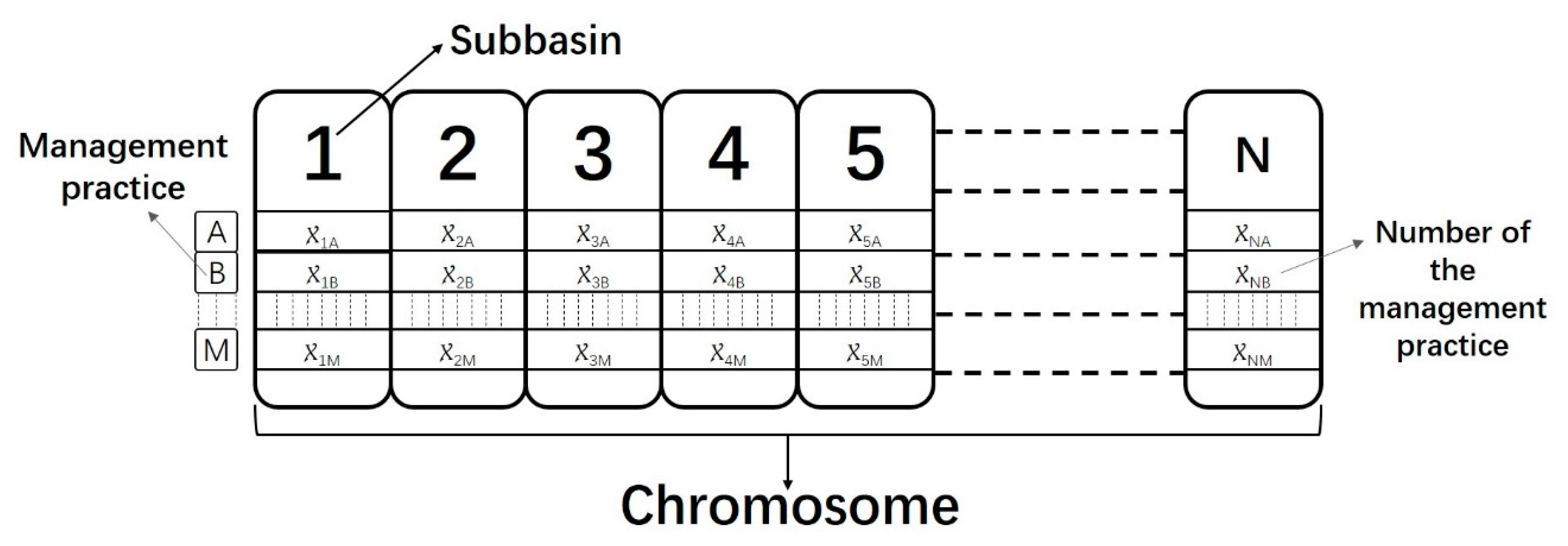
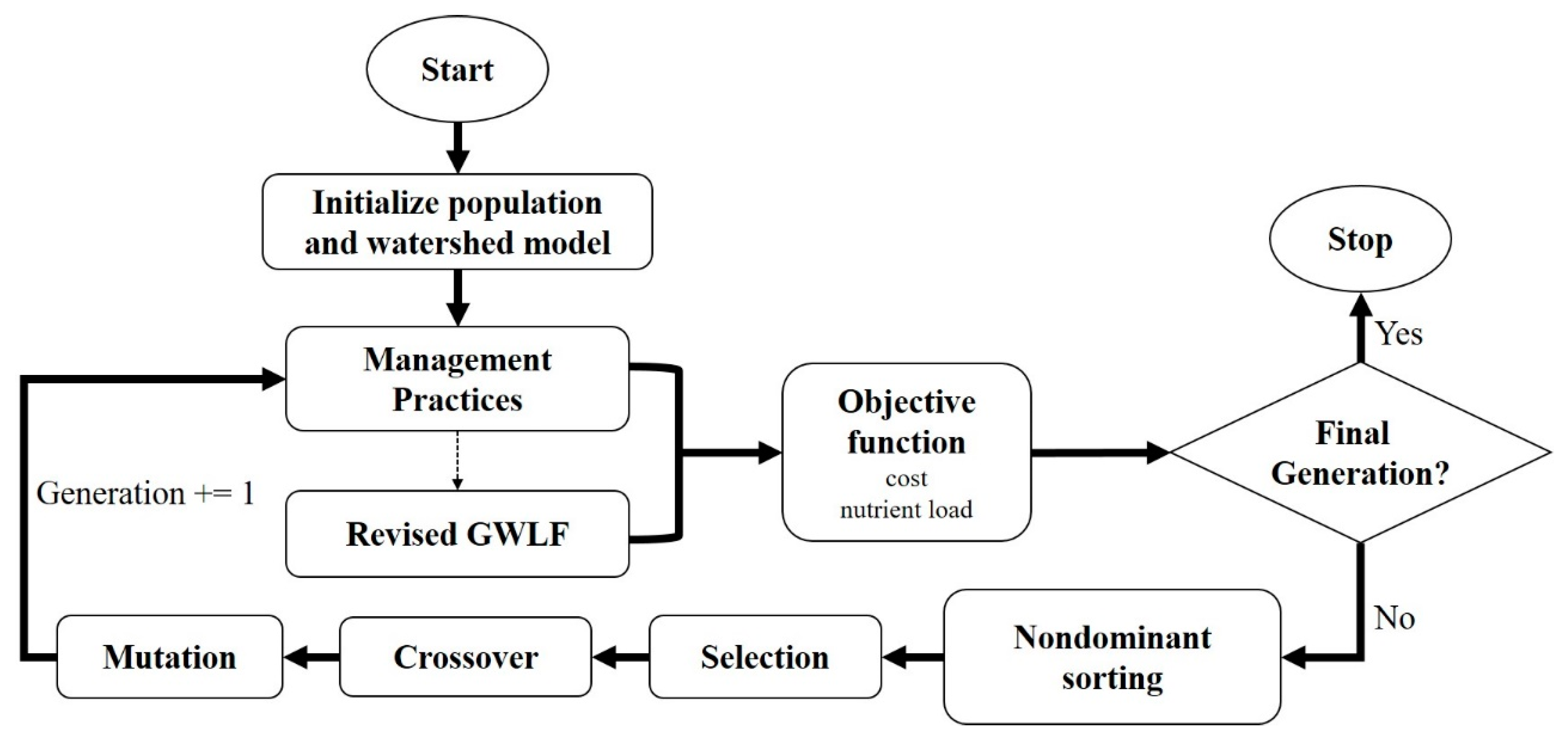
2.4. Multi-Objective Functions and NSGAII Optimization Processes
- (1)
- Initialize the population and read the watershed model input data. Then, simulate the baseline scenario.
- (2)
- For the two objective functions, obtain the pollutant load of the basin model and the net cost of each management measure combination.
- (3)
- Through a series of processes, including non-dominated sorting, calculation of crowded distance, selection, crossover, and mutation, NSGAII obtains the Pareto-optimal result set of the current generation.
- (4)
- Repeat the second process, determine whether it is the last generation, and then perform the third process.
3. Results and Discussion
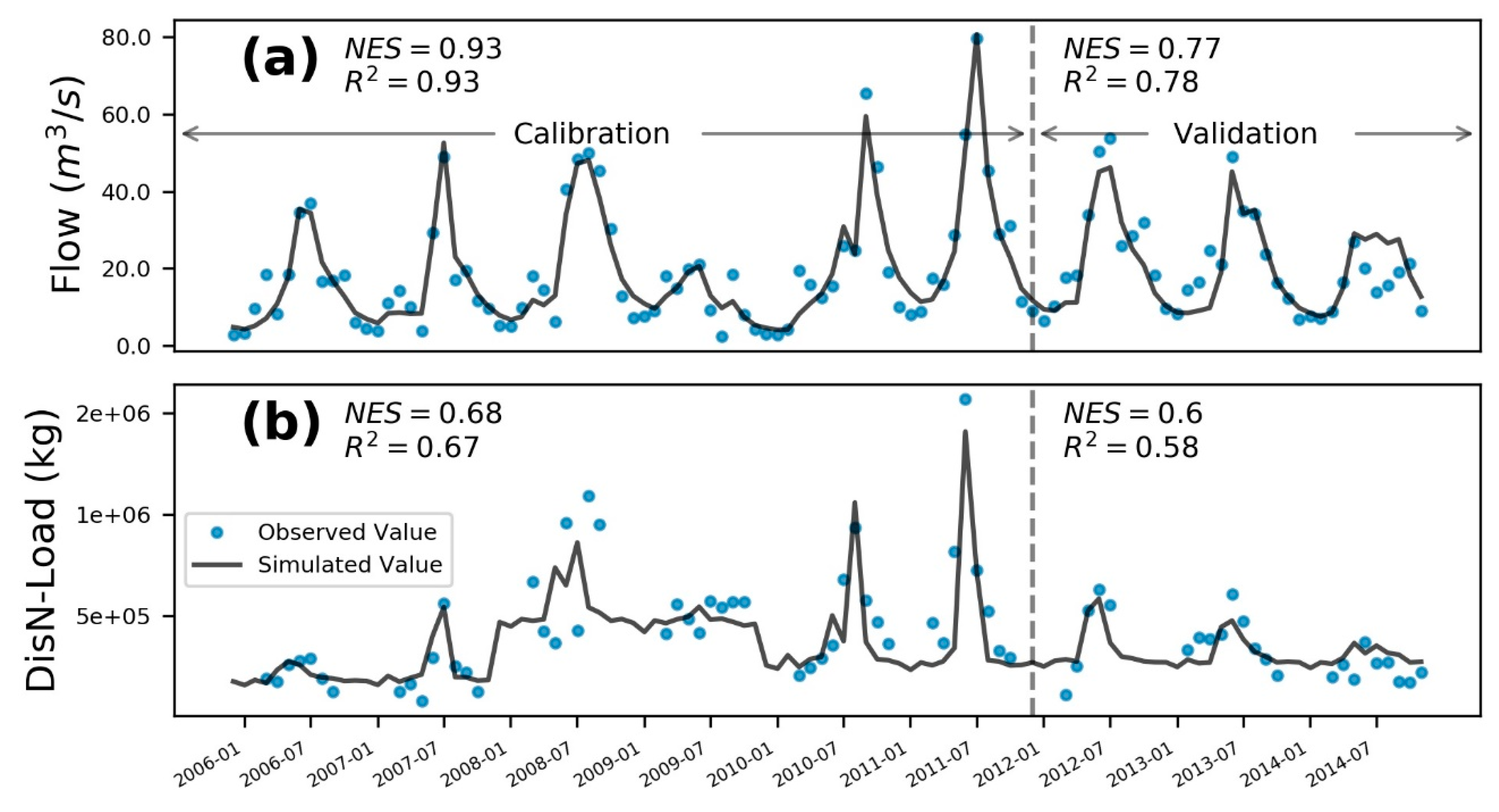
3.1. RGWLF Model Calibration and Validation
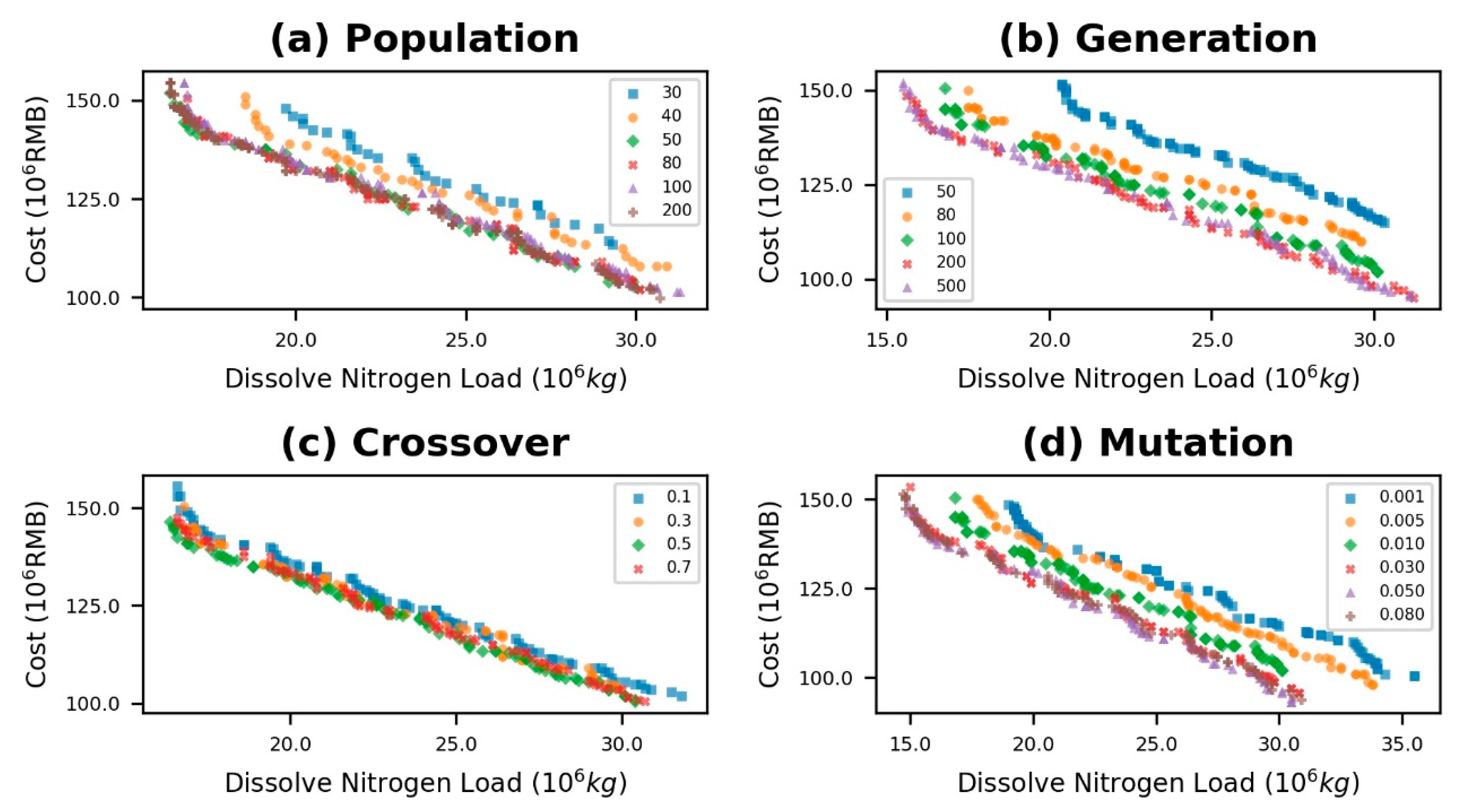
3.2. Sensitivity Analysis of NSGAII Operational Parameters
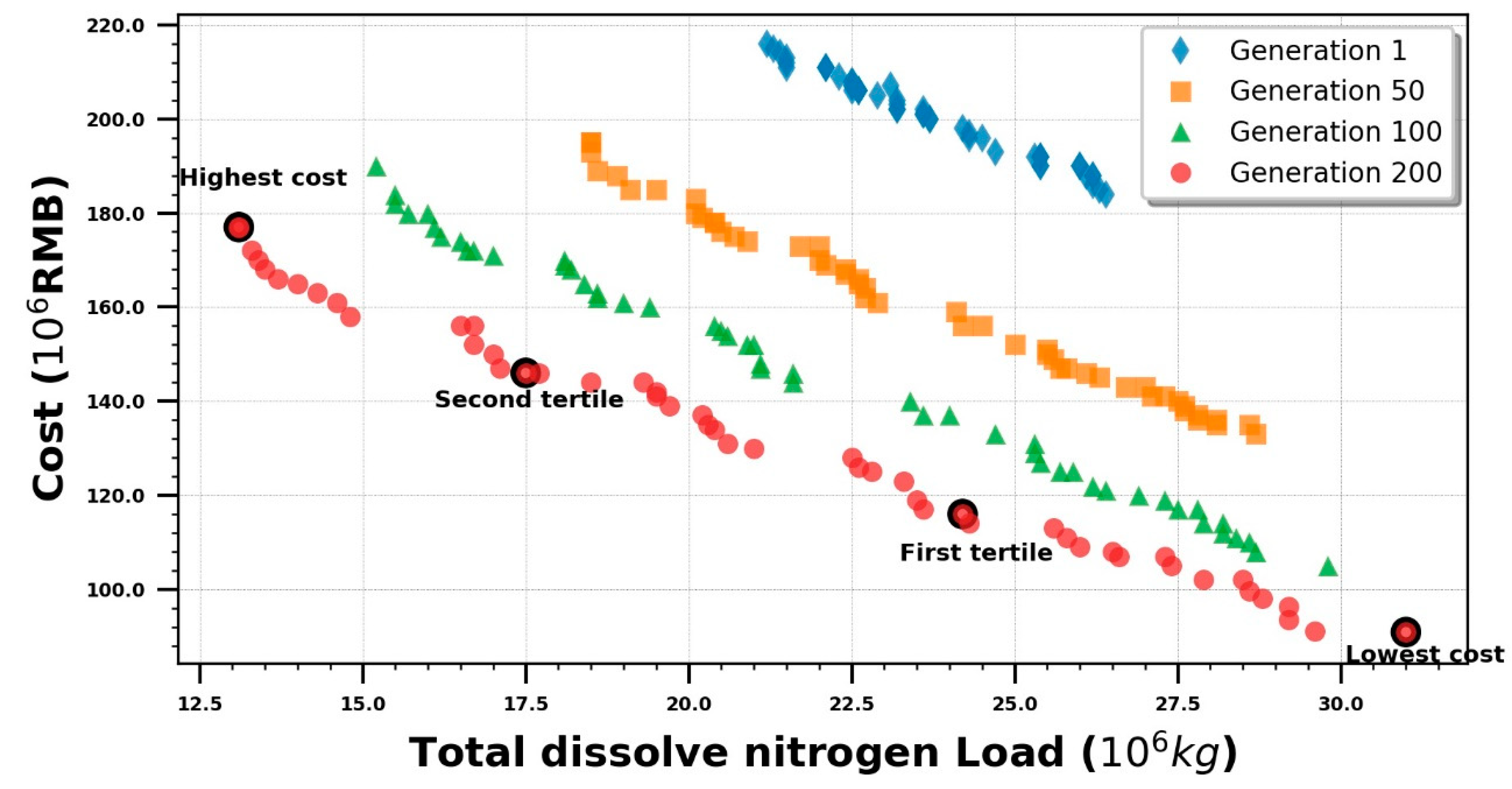
3.3. Optimization Result and Cost-Effectiveness Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gleick, P.H. Global freshwater resources: Soft-path solutions for the 21st century. Science 2003, 302, 1524–1528. [Google Scholar] [CrossRef]
- Fleifle, A.; Saavedra, O.; Yoshimura, C.; Elzeir, M.; Tawfik, A. Optimization of integrated water quality management for agricultural efficiency and environmental conservation. Environ. Sci. Pollut. Res. 2014, 21, 8095–8111. [Google Scholar] [CrossRef]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of applications. Trans. ASAE 2004, 47, 789–803. [Google Scholar] [CrossRef]
- Hering, D.; Borja, A.; Carstensen, J.; Carvalho, L.; Elliott, M.; Feld, C.K.; Heiskanen, A.-S.; Johnson, R.K.; Moe, J.; Pont, D.; et al. The European Water Framework Directive at the age of 10: A critical review of the achievements with recommendations for the future. Sci. Total Environ. 2010, 408, 4007–4019. [Google Scholar] [CrossRef]
- Qu, J.; Fan, M. The current state of water quality and technology development for water pollution control in China. Crit. Rev. Environ. Sci. Technol. 2010, 40, 519–560. [Google Scholar] [CrossRef]
- Xie, H.; Chen, L.; Shen, Z. Assessment of agricultural best management practices using models: Current issues and future perspectives. Water 2015, 7, 1088–1108. [Google Scholar] [CrossRef]
- Balana, B.B.; Vinten, A.; Slee, B. A review on cost-effectiveness analysis of agri-environmental measures related to the EU WFD: Key issues, methods, and applications. Ecol. Econ. 2011, 70, 1021–1031. [Google Scholar] [CrossRef]
- Guo, H.; Hu, Q.; Jiang, T. Annual and seasonal streamflow responses to climate and land-cover changes in the Poyang Lake basin, China. J. Hydrol. 2008, 355, 106–122. [Google Scholar] [CrossRef]
- Hundecha, Y.; Bardossy, A. Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model. J. Hydrol. 2004, 292, 281–295. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective genetic algorithms: Problem difficulties and construction of test problems. Evol. Comput. 1999, 7, 205–230. [Google Scholar] [CrossRef] [PubMed]
- Kaini, P.; Artita, K.; Nicklow, J.W. Optimizing structural best management practices using SWAT and genetic algorithm to improve water quality goals. Water Resour. Manag. 2012, 26, 1827–1845. [Google Scholar] [CrossRef]
- Qi, H.; Altinakar, M.S.; Vieira, D.A.N.; Alidaee, B. Application of Tabu search algorithm with a coupled AnnAGNPS-CCHE1D model to optimize agricultural land use. J. Am. Water Resour. Assoc. 2008, 44, 866–878. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Decision support for watershed management using evolutionary algorithms. J. Water Resour. Plan. Manag. 2005, 131, 35–44. [Google Scholar] [CrossRef]
- Qiu, J.; Shen, Z.; Huang, M.; Zhang, X. Exploring effective best management practices in the Miyun reservoir watershed, China. Ecol. Eng. 2018, 123, 30–42. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Maringanti, C.; Chaubey, I.; Arabi, M.; Engel, B. Application of a multi-objective optimization method to provide least cost alternatives for NPS pollution control. Environ. Manag. 2011, 48, 448–461. [Google Scholar] [CrossRef]
- Maringanti, C.; Chaubey, I.; Popp, J. Development of a multiobjective optimization tool for the selection and placement of best management practices for nonpoint source pollution control. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ahmadi, M.; Arabi, M.; Hoag, D.L.; Engel, B.A. A mixed discrete-continuous variable multiobjective genetic algorithm for targeted implementation of nonpoint source pollution control practices. Water Resour. Res. 2013, 49, 8344–8356. [Google Scholar] [CrossRef]
- Geng, R.; Yin, P.; Sharpley, A.N. A coupled model system to optimize the best management practices for nonpoint source pollution control. J. Clean. Prod. 2019, 220, 581–592. [Google Scholar] [CrossRef]
- Wellen, C.; Kamran-Disfani, A.-R.; Arhonditsis, G.B. Evaluation of the current state of distributed watershed nutrient water quality modeling. Environ. Sci. Technol. 2015, 49, 3278–3290. [Google Scholar] [CrossRef]
- Arabi, M.; Govindaraju, R.S.; Hantush, M.M. Cost-effective allocation of watershed management practices using a genetic algorithm. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Qi, H.; Altinakar, M.S. Vegetation buffer strips design using an optimization approach for non-point source pollutant control of an agricultural watershed. Water Resour. Manag. 2011, 25, 565–578. [Google Scholar] [CrossRef]
- Qi, Z.; Kang, G.; Chu, C.; Qiu, Y.; Xu, Z.; Wang, Y. Comparison of SWAT and GWLF model simulation performance in humid south and semi-arid north of China. Water 2017, 9, 567. [Google Scholar] [CrossRef]
- Qi, Z.; Kang, G.; Shen, M.; Wang, Y.; Chu, C. The improvement in GWLF model simulation performance in watershed hydrology by changing the transport framework. Water Resour. Manag. 2019, 33, 923–937. [Google Scholar] [CrossRef]
- Haith, D.A.; Shoemaker, L.L. Generalized watershed loading functions for stream flow nutrients. JAWRA J. Am. Water Resour. Assoc. 1987, 23, 471–478. [Google Scholar] [CrossRef]
- Schwarz, G.; Hoos, A.B.; Alexander, R.; Smith, R. The SPARROW surface water-quality model—Theory, application and user documentation. In U.S. Geological Survey Techniques and Methods; Series number 6-B3; U.S. Geological Survey: Reston, VA, USA, 2006; 248p. [Google Scholar]
- Shi, H.; Wang, L. Treatment of the corn starch wastewater by UASB-SBR process. Shanxi Archit. 2003, 29, 71–72. (In Chinese) [Google Scholar]
- Yu, H. UASB-SBR Technical Processing Starch Wastewater. Master’s Thesis, Changan University, Xi’an, China, 2007. (In Chinese). [Google Scholar]
- Liu, J.; Zheng, X.; Gao, C.; Chen, L. Study on area, operating and construction costs of urban wastewater treatment plants. Chin. J. Environ. Eng. 2010, 4, 2522–2526. (In Chinese) [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Beven, K.; Smith, P.; Freer, J. Comment on “Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology” by Pietro Mantovan and Ezio Todini. J. Hydrol. 2007, 338, 315–318. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hamby, D. A comparison of sensitivity analysis techniques. Health Phys. 1995, 68, 195–204. [Google Scholar] [CrossRef] [PubMed]
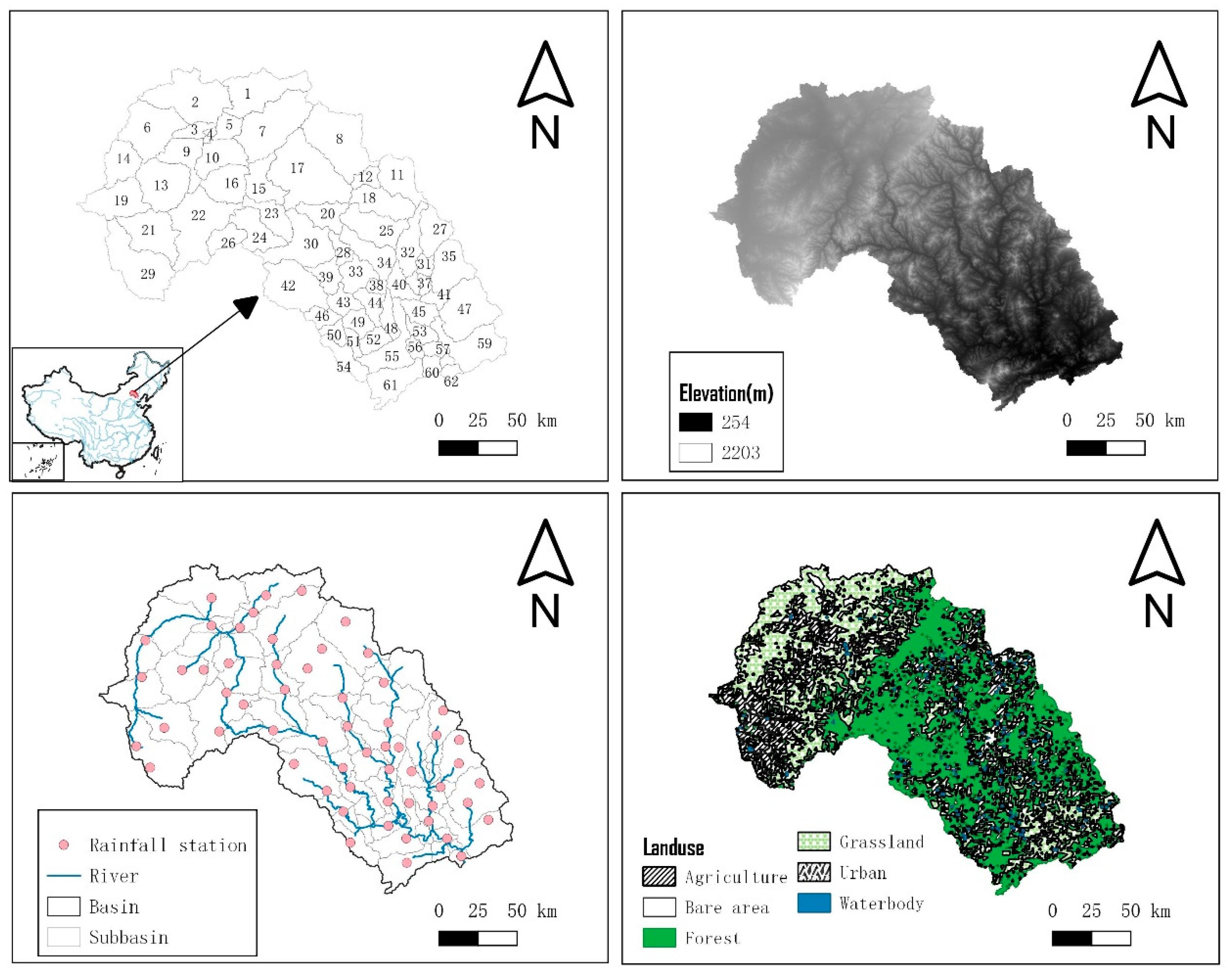

| Data Type | Data Description | Source | Time |
|---|---|---|---|
| Weather | Rainfall stations with the daily precipitation; | Annual Hydrological Report P.R. China | 2005–2014 |
| Temperature stations with the daily average temperature | China Meteorological Data Service Center (http://cdc.cma.gov.cn/en) | 2005–2014 | |
| DEM | Digital elevation model (30 m × 30 m) | Geospatial Data Cloud (http://www.gscloud.cn/) | 2009 |
| Land-use | Shapefile | Institute of Geographic Sciences and Natural Resources Research, CAS | 2010 |
| Hydrology | Streamflow/Monthly | Annual Hydrological Report P.R. China | 2006–2014 |
| Water Quality | Dissolved Nitrogen/Monthly | Chinese Academy of Environmental Planning | 2006–2014 |
| Point source | Annual discharge | Chinese Academy of Environmental Planning | 2005–2014 |
| Practice | Type | Sub-Basin | Cost |
|---|---|---|---|
| Wastewater treatment 1 | 0%, 10%, 20%, 30%, 40%, 50% | 8, 9, 34, 53–55 | 1.42 yuan/m3 |
| Converting farmland to forest | 0%, 10%, 20%, 30% | All | 5250 yuan/ha |
| Filter strips | 0, 5, 10, 20, 30 m | All | 2.83 yuan/m2 |
| Parameters Name | Initial | Range | Calibration |
|---|---|---|---|
| Recession coefficient | 0.008 | [0, 0.015] | 0.00782 |
| Seepage coefficient | 0.01 | [0, 0.02] | 0.00671 |
| Recession threshold | 10 | [0, 20] | 17.784 |
| Seepage threshold | 10 | [0, 20] | 6.497 |
| Leakage coefficient | 0.06 | [0, 0.08] | 0.0436 |
| CN2 1 | - | [−0.15, 0.15] | −0.0418 |
| Agriculture | 75 | - | - |
| Forest | 35 | - | - |
| Grass | 45 | - | - |
| Urban | 95 | - | - |
| Dissolved nitrogen Concentration (mg/L) | - | - | - |
| Agriculture | 4.0 | [2.0, 6.0] | 4.66 |
| Forest | 0.2 | [0.1, 0.3] | 0.12 |
| Grass | 2.0 | [1.0, 3.0] | 1.76 |
| During fertilizer (mg/L) Agriculture | 10.0 | [7.0, 15.0] | 12.47 |
| Underground dissolved nitrogen concentration | 0.1 | [0.01, 0.5] | 0.24 |
| Dissolved nitrogen attenuation exponent | 0.0004 | [0.0, 0.0008] | 0.000233 |
| Order | Population Size | Generations | Crossover Probability | Mutation Probability |
|---|---|---|---|---|
| 1 | 30 | 50 | 0.1 | 0.001 |
| 2 | 40 | 80 | 0.3 | 0.005 |
| 3 | 50 | 100 | 0.5 | 0.01 |
| 4 | 80 | 200 | 0.7 | 0.03 |
| 5 | 100 | 500 | - | 0.05 |
| 6 | 200 | - | - | 0.08 |
| default | 80 | 100 | 0.5 | 0.01 |
| optimal | 50 | 200 | 0.5 | 0.03 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Kang, G.; Wu, X.; Sun, Y.; Wang, Y. Multi-Objective Optimization for Selecting and Siting the Cost-Effective BMPs by Coupling Revised GWLF Model and NSGAII Algorithm. Water 2020, 12, 235. https://doi.org/10.3390/w12010235
Qi Z, Kang G, Wu X, Sun Y, Wang Y. Multi-Objective Optimization for Selecting and Siting the Cost-Effective BMPs by Coupling Revised GWLF Model and NSGAII Algorithm. Water. 2020; 12(1):235. https://doi.org/10.3390/w12010235
Chicago/Turabian StyleQi, Zuoda, Gelin Kang, Xiaojin Wu, Yuting Sun, and Yuqiu Wang. 2020. "Multi-Objective Optimization for Selecting and Siting the Cost-Effective BMPs by Coupling Revised GWLF Model and NSGAII Algorithm" Water 12, no. 1: 235. https://doi.org/10.3390/w12010235
APA StyleQi, Z., Kang, G., Wu, X., Sun, Y., & Wang, Y. (2020). Multi-Objective Optimization for Selecting and Siting the Cost-Effective BMPs by Coupling Revised GWLF Model and NSGAII Algorithm. Water, 12(1), 235. https://doi.org/10.3390/w12010235




