1. Introduction
The Chinese water crisis is getting more and more serious. China is one of the 13 water-scarce countries in the world, with per capita water consumption accounting for only 25% of the world’s per capita water consumption [
1]. In 2017, the Chinese effective utilization coefficient for farmland irrigation water was only 0.542, which is far below the global level of 0.7–0.8. The total agricultural water consumption in Heilongjiang Province was 31.644 billion cubic meters, accounting for 89.6% of the province’s total water consumption [
2]. The paddy field in Heilongjiang Province is vast, and the irrigation water consumption of farmland is huge. Due to the aging and imperfection of farmland water conservancy projects, a large proportion of water resources is wasted. Groundwater resources in some areas are overexploited. To tackle the problem of inefficient agricultural water consumption, Central Document No. 1 has reformed many agricultural areas. One of the areas of comprehensive agricultural reform is water price, with the goal being to adjust the price of agricultural water and promote water conservation. Again, the rational allocation of water rights is a fundamental aspect of the comprehensive reform of agricultural water prices, and will also play a role in effective water saving [
3].
The comprehensive reform of agricultural water price measures is intended to raise the price of water, which is an effective method to guarantee national food and water security. Therefore, it is very important to formulate a reasonable agricultural water price system [
4,
5,
6,
7]. Dono proposed two methods for the application of agricultural water pricing. The first method, based on the metered use of water by farms, is known as the volumetric pricing method; the second is an area-based pricing method, whereby fees are charged per hectare according to the estimated average water use for each crop [
8]. Poor measurement facilities in agricultural irrigation districts lead to poor applicability of traditional water rights allocation methods. Färe used the directional output distance function to derive estimates of production inefficiency, shadow prices for polluting outputs, and the associated pollution costs [
9]. Shadow prices reflect the scarcity of resources and the demands for final products in the social economy, but cannot reflect economic changes and changes in demand. Shadow prices could increase the water elasticity demands and production output framework [
10,
11]. In summary, multiple factors need to be considered in establishing a reasonable agricultural water price system. Differentiated water pricing methods can reflect changes in the social economy and make agricultural water prices more reasonable [
12,
13,
14,
15,
16].
A number of uncertain optimization methods can be introduced to help water managers face the challenges of uncertainties and their interactions [
17,
18,
19,
20,
21,
22,
23]. When irrigation meets the water demand, it will produce benefits; and when the demand is not satisfied, losses will occur. Therefore, one type of stochastic programming (SP), named two-stage stochastic programming (TSP), can be used to handle uncertainties expressed as probabilistic distributions. TSP provides an effective link between policies and economic penalties, and has advantages in terms of reflecting the complexities of system uncertainties as well as analyzing policy scenarios when preregulated targets are violated [
24]. On the one hand, there are no accurate data; on the other hand, the dynamic changes of influencing factors cannot be predicted. This makes it impossible to deal with ambiguity in the water resources system. Zeng developed a two-stage credibility-constrained programming with a Hurwicz criterion (TCP-CH) approach for water resources management and planning under uncertainty. It can also check for system failure risk based on different risk preferences of decision makers [
25]. Incorporation of interval-parameter programming (IPP) within a two-stage stochastic programming (TSP) framework can reflect not only the uncertainties expressed as probability distributions but also interval numbers. Moreover, it can provide an effective link between conflicting economic benefits and the associated penalties handed out for the violation of the predefined policies [
26,
27,
28,
29,
30]. Previously, a number of researchers have incorporated quadratic programming (QP), inexact credibility-constrained programming (ICP), and fuzzy programming (FP) into a framework for water resources management. For example, Zeng et al. (2015) developed a mixed inexact‒quadratic fuzzy water resources management model (IQT-WMMF) for floodplains, incorporating techniques of credibility-constrained programming (CP), two-stage programming (TP), interval-parameter programming (IPP), and QP within a general framework of limited data availability [
31]. Unfortunately, few studies have previously focused on the IPP, FP, and TSP methods of sustainable WMF planning within a two-stage context.
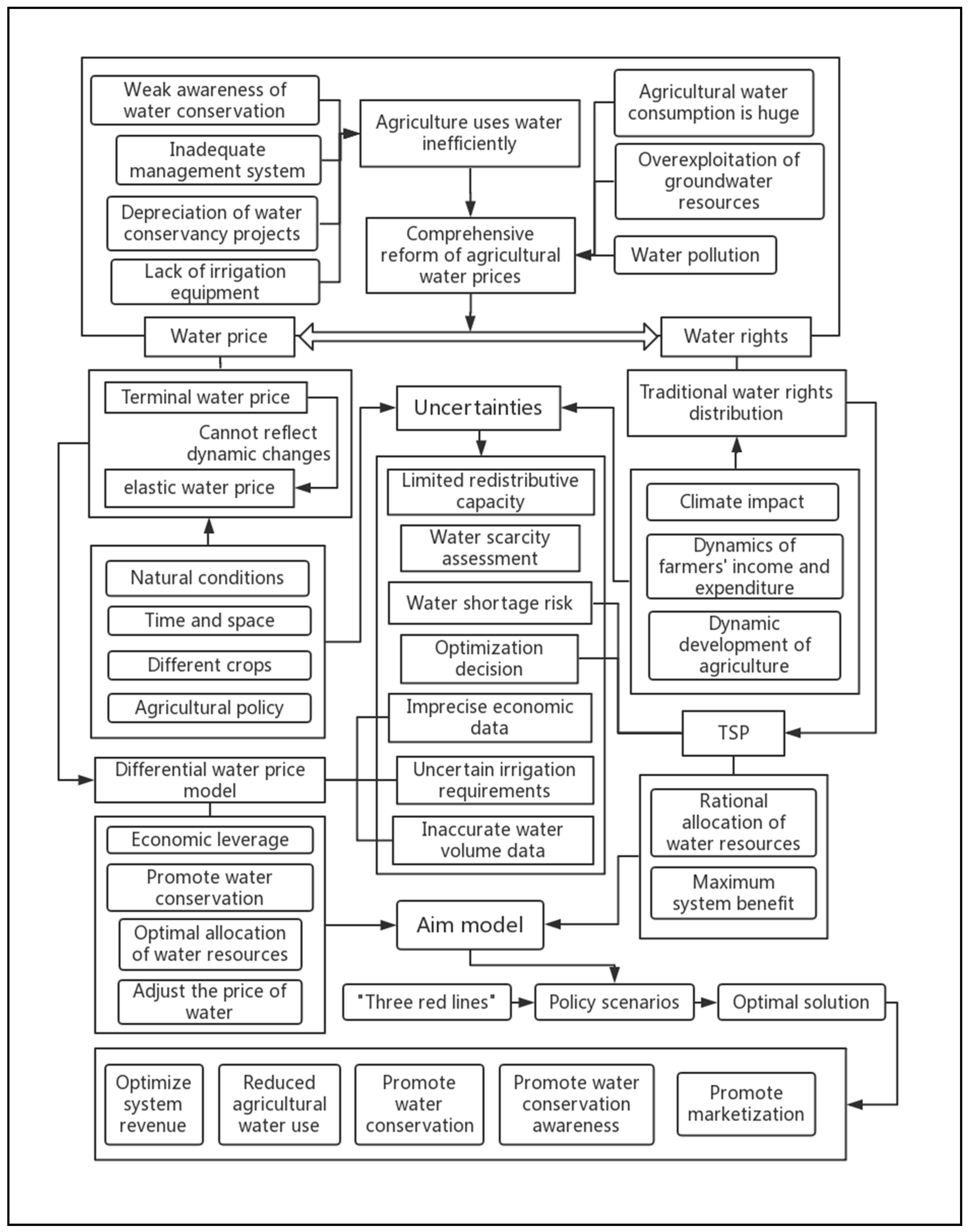
Therefore, the objective of this study is to develop an agricultural interval two-stage fuzzy differential water price model (ITS-DWPM) for initial water rights allocation. The developed ITS-DWPM method is an integrated optimization technique for tackling multiple uncertainties expressed as discrete intervals, nonlinearity, and fuzzy sets. The method is applied to a real case study of initial water rights allocation in Hulin City, China. Keeping in mind the uncertain irrigation needs when considering water prices and water demand, the method can improve the practicality and pertinence of the two stages. At the same time, we carried out a policy analysis of the irrigation water utilization coefficient in the initial water rights allocation. At the same time, the impact of the changes on the initial water rights allocation is quantified. Finally, we couple the results of the two analyses to support irrigation district managers in initial water rights allocation planning and policy adjustment. The method can provide scientific guidance for the initial water rights allocation of each agricultural irrigation district in the region.
2. Methodology
Figure 1 presents the framework of ITS-DWPM application in Hulin City. This method can lead to the achievement of the water consumption target when there is uncertain water demand for irrigation, and can also improve the practicability and pertinence of the two stages. Meanwhile, the effect of the utilization coefficient of irrigation water on initial water rights allocation was considered and a risk analysis was carried out by combining uncertainty and the water weight allocation system. Finally, coupled with the results of the two analyses, the results can support irrigation district managers in carrying out initial water rights allocation planning and policy adjustment.
Due to the loss of irrigation and water conservancy projects, a lack of irrigation district management system, a lack of matching terminal metering equipment in irrigation areas, and the low price of agricultural irrigation water, the efficiency of agricultural water use in Hulin is low. Therefore, the wasting of agricultural water can be reduced by optimizing the initial allocation of water rights in this area. Some factors considered include climate, the dynamic development of agriculture, and farmers’ income and expenditure; however, the redistribution capacity is limited by the scarcity of water resources, and the fluctuation of water prices and other factors cannot be reflected. This paper optimizes the allocation of water resources through the adjustment of economic leverage, and formulates matching empirical decisions. Due to temporal and spatial differences in water provision and demand, the initial water rights allocation designs will vary under different policy requirements and allocation targets. If the initial water rights allocation aims preregulated by decision makers is too high, the actual water consumption will not be met; a shortage would thus be generated. Correspondingly, the demand must be curtailed with reduced production activities, resulting in a decreased net system benefit (i.e., a penalty due to shortfalls). In addition, if the aims as preregulated by the decision makers are too low, a surplus may be generated (i.e., a wastly due to surpls). We must constantly adjust the allocation of water rights to formulate reasonable agricultural water prices, ultimately finding the optimal allocation of initial water rights for agricultural irrigation in the area, maximizing the system revenue, reducing agricultural water consumption, and promoting agricultural water users ‘awareness of water saving measures. The goal of comprehensive reform of agricultural water prices should be taken into account.
In a practical problem of initial water rights allocation, uncertainties may be expressed as random variables, which result in the relevant decisions being made under varying probability levels. Such a problem can be formulated as a two-stage stochastic programming (TSP) model [
32]. However, in an initial water rights allocation system, the impacts on differential water price of uncertain benefits and penalty data may cause relevant objective function nonlinearity. Interval programming can deal with the nonlinearities in the objective function and reflect uncertainty, expressed as interval values. Therefore, by introducing ITS into the TSP model, an inexact two-stage programming (ITSP) model can be expressed as follows:
Subject to
where
F is the system benefits and
is the vector of first-stage decision variables. Since water demand (i.e., the first-stage decision variables) is often confirmed by decision makers according to previous empirical values, it would be altered by random events in actual water resources situations in planning periods, leading to first-stage benefits
.
is the recourse at the second stage in response to events (e.g., present water shortages), which leads to the expected value of the second-stage penalties
.
is each water rights value;
is the expected price of each water right (which varies with the distributable water rights);
is the real price of each water right (current agricultural water price);
is the total water rights that agriculture can distribute; and
is the total water available for agriculture.
Water demand and the water price model were initialized by James and Lee:
where
Q is the actual water consumption in irrigated areas;
K is constant;
is the actual price of water; and
E1 is the coefficient of elasticity of water price. Mao (2005) took into account the influence of rainfall and evaporation in the rice growing season and built an agricultural water demand and water price model [
12]:
where
Pmax is the maximum price that farmers can afford to pay for water;
R is the average annual evaporation during the growing season;
Z is the average annual rainfall during the growing season;
E2 is the coefficient of elasticity of evaporation; and
E3 is the coefficient of elasticity of rainfall. The theory is to add the regulation of water price into the initial allocation of water rights, so as to affect the distribution of water rights among various agricultural irrigation areas and at the same time ensure the maximization of system income, and finally to achieve a more optimal distribution of initial agricultural water rights [
30,
31,
32]. Expected water price will change as the demand for water changes, so replace the expected water price with the changed water price.
subject to
Then, an interval linear programming (ILP) solution is proposed for solving the interval two-stage programming (ITS) model. The objective function is not only a net profit, but also a ‘punishment’. In the above planning, it is difficult to determine whether should correspond to , and should correspond to (decision will generate large economic benefits, but brings with it a lot of risk; corresponds to a small economic benefit, but also small risk). Since each irrigation area has a fallow irrigation area every year, when decision appears, excess water can irrigate these fields. Therefore, corresponds to , and should correspond to .
Solving steps:
subject to
- (2)
This corresponds to :
Solve for this linear program to find , and . is given and yi is substituted.
(3) This corresponds to
:
subject to
Determine the optimal solution and the optimal value:
For the water allocation problem corresponding to the initial model, the optimal allocation quantity can be determined:
3. Case Study
Hulin City is located in the eastern part of Heilongjiang Province, at the southern foot of the Wanda Mountains and on the left bank of the Wusuli River. The geographical coordinates are 45°23′ to 46°36′ N and 132°11′ to 133°56′ E. The northwest of Hulin is bordered by Baolong County with Laolongbei and Jiangjun Ridge of the Wandashan tributary; the northeast is bordered by Qiliqin River and Raohe County; the west is bordered by Bailong Ridge and Mishan City, geographical location as shown in
Figure 2.
For a long time, Heilongjiang Province has been a major agricultural province, but inadequate irrigation systems have led to farmers’ use of irrigation water not being standardized. For example, local managers in some areas have not been able to collect water charges for a long time; farmers have directly pumped river water or pumped wells to extract groundwater without passing through management stations. Disordered irrigation often results in a lack of timely access to water in downstream irrigation areas. The exclusive crop in the study area was rice, and mostly surface water such as reservoirs and rivers was used for irrigation. In areas without surface runoff, groundwater is used for irrigation.
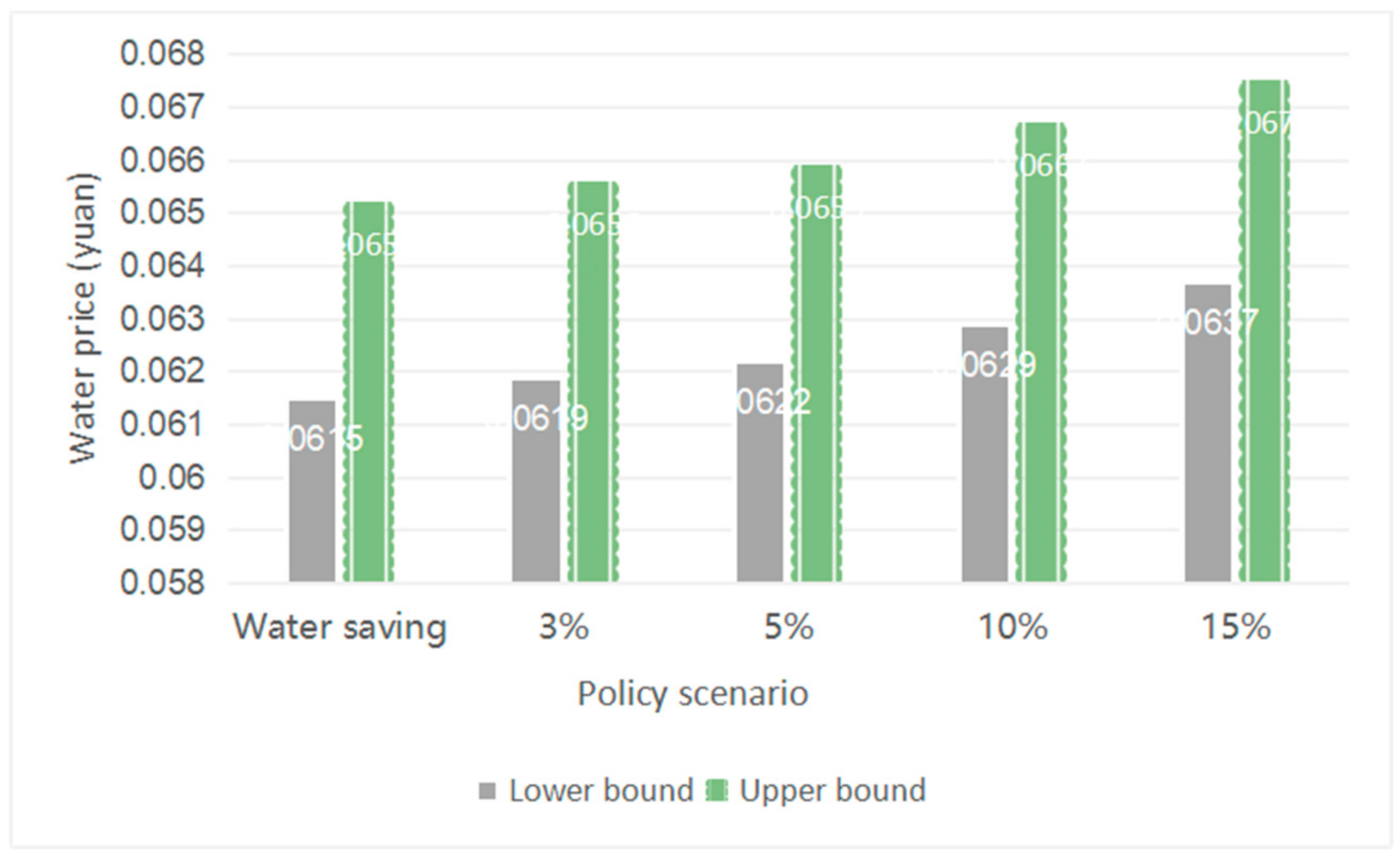
The price of the production of water in the Hulin area is 3.7 yuan/m3: the price of domestic water is 2.6 yuan/m3, while the price of agricultural water is only 0.062 yuan/m3. The agricultural water price is too low, resulting in farmers’ poor awareness of the necessity of saving water.
In order to establish a benign operating mechanism for agricultural water-saving and farmland water conservancy projects, in January 2016, the General Office of the State Council issued its “Opinions on Promoting Comprehensive Reforms of Agricultural Water Prices” to promote comprehensive reforms of agricultural water prices across the country.
The lack of water resources in Hulin City is an important factor restricting its social and economic development. The total amount of water available for agriculture in Hulin City is reduced, and the proportion of agricultural water consumption is high. Agricultural irrigation water is inexpensive and farmland water conservancy projects have seriously declined, causing this area to be a major source of agriculture water waste. Therefore, we should accelerate the comprehensive reform of agricultural water prices and improve the efficiency of agricultural water use. Raising the price of agricultural water will strengthen farmers’ awareness of water conservation so that they can take measures to improve the efficiency of agricultural water use.
Lining main canals and branch canals is the most important measure to save water in agricultural irrigated areas. The irrigation water utilization coefficient has a logarithmic relationship with the lining rate of the canal. With the gradual increase in the lining rate, the irrigation water utilization coefficient increases less and less, so the result shows a trend of decreasing marginal efficiency. By studying the influence of channel lining on irrigation water utilization coefficient, the relationship between channel lining rate and canal water utilization coefficient was developed [
33]. The Hulin City field water utilization coefficient is 0.824, The lining rate of the canal is the independent variable, and the irrigation water utilization coefficient is the dependent variable. The quantitative relationship can be expressed as follows:
where
η is the utilization coefficient of irrigation water and
λ is the channel lining rate.
According to the engineering matching rate, controlled area, regional water resource conditions, and water-saving capacity, the net water quota of each irrigated area in the city can be controlled at 0.65 m3/m2. By 2020, the effective utilization coefficient of irrigation water will be raised to more than 0.55 (No. 1 document of the CPC Central Committee in 2011). By 2030, the effective utilization coefficient of irrigation water for farmland will be increased to more than 0.6, according to the National Comprehensive Plan for Water Resources.
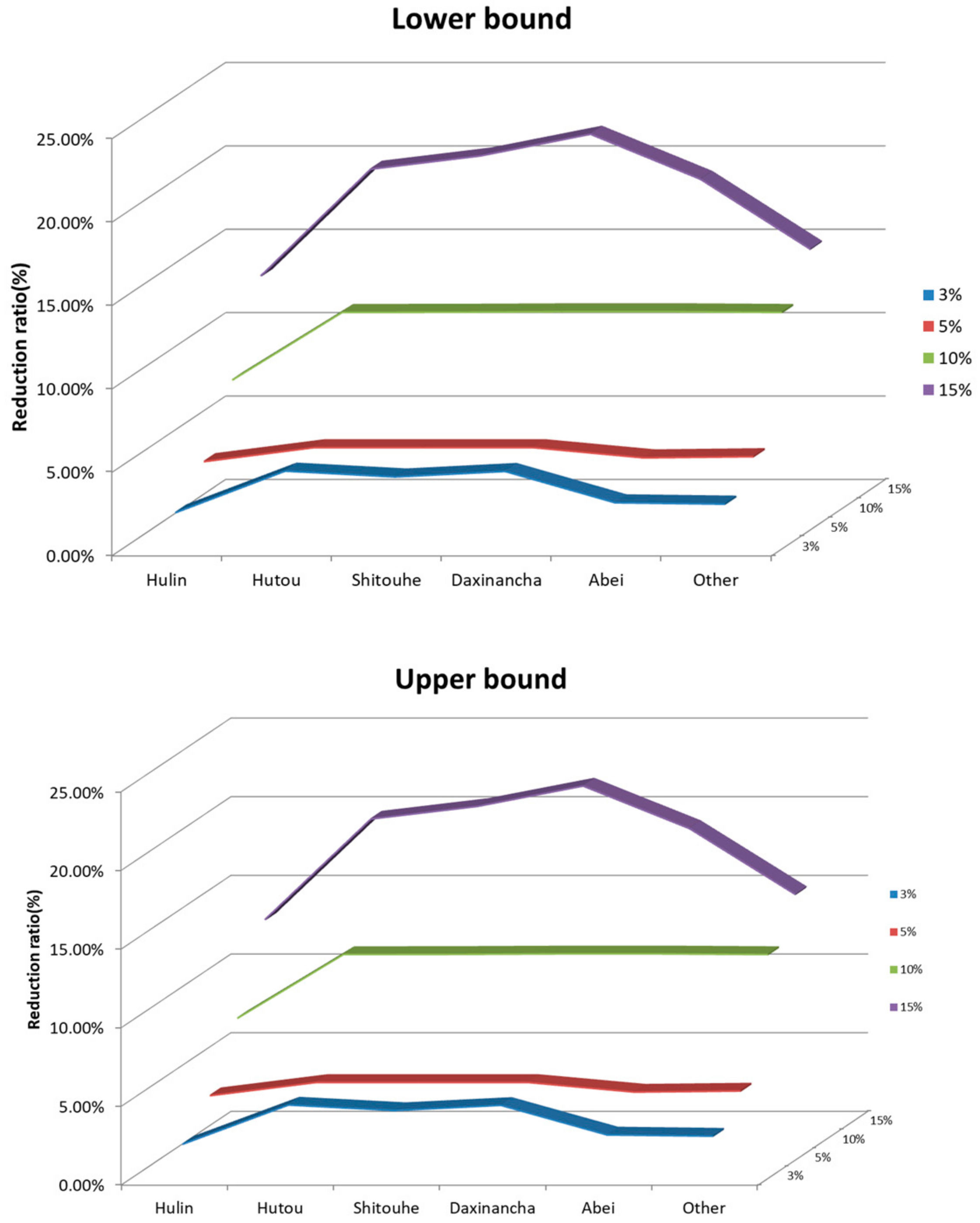
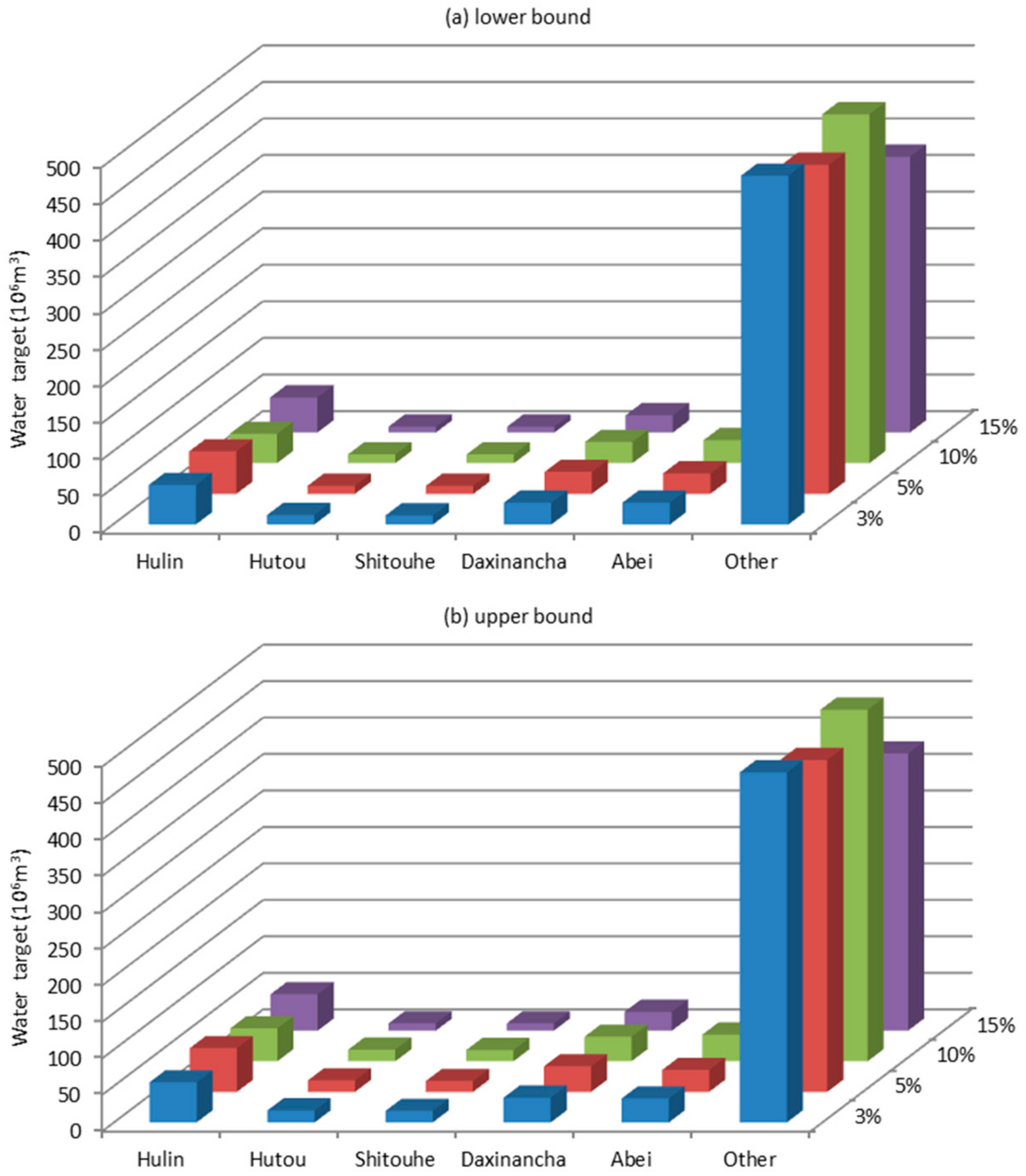
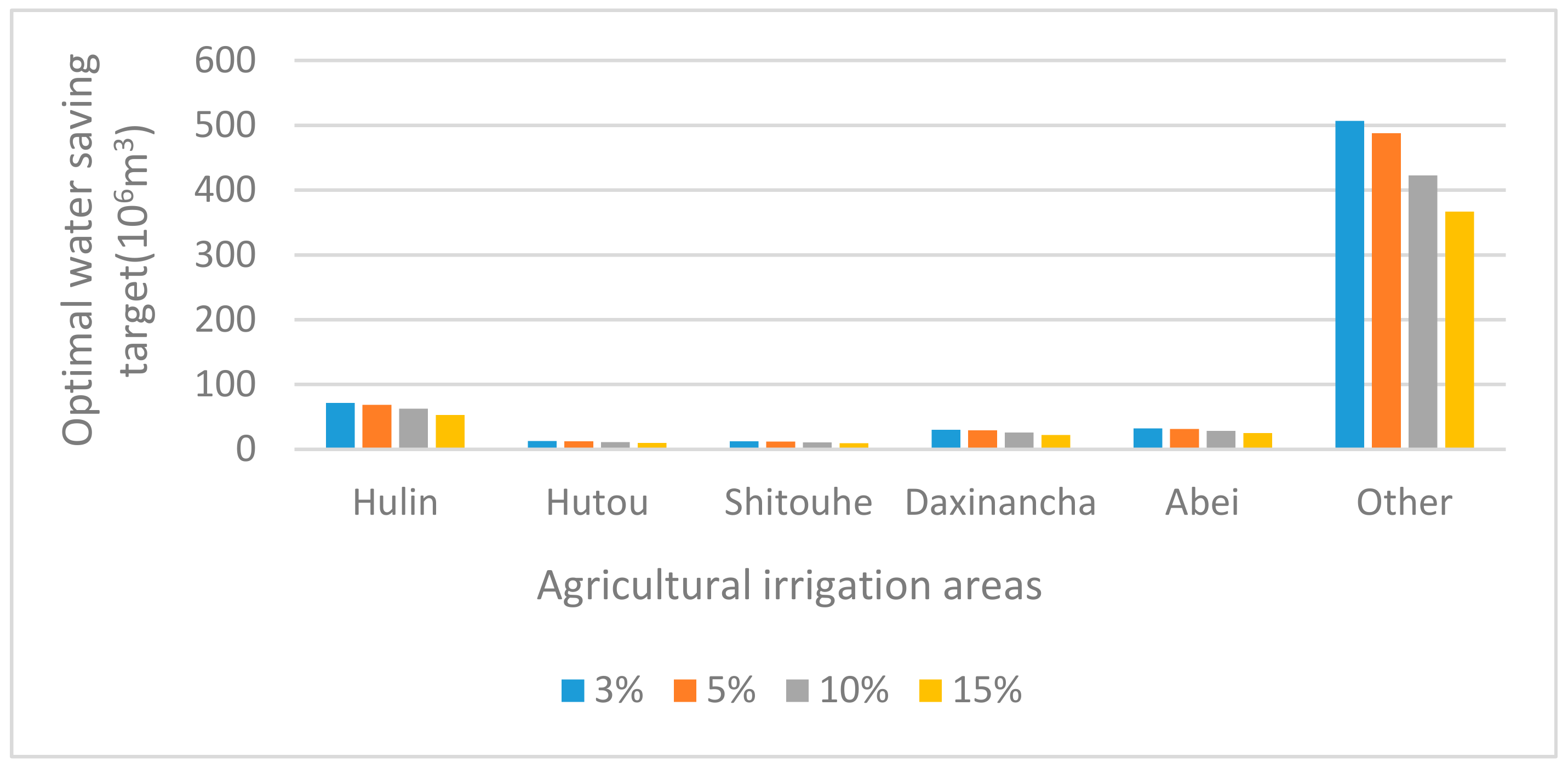
The proposed ITS-DWPM method is considered to be applicable for tackling such a problem. Thus, we set up the following water-saving efficiency policy scenarios:
subject to
where
is the benefit of each water conservation right;
is the anticipated water conservation rights.;
is the cost savings for each water right;
is the number of water rights after optimized allocation in the second stage;
is the expected water price;
is the water-saving reward;
is the expected rate of lining of agricultural irrigation channels; and
is the real rate of lining of agricultural irrigation channels.
- (1)
Agricultural water distribution
According to the above analysis of the overall ideas and basic conditions for agricultural water use rights, it is clear that agricultural water distribution and paddy field irrigation area are two key factors. The area of irrigation of the paddy field determines the proportion of water allocated to each irrigation district. Taking the total water control of “three red lines” in Hulin City as the target, after deducting the domestic water, ecological water, nonagricultural production water, and reserved water, the remaining water will be used for agricultural water distribution in Hulin City. It is calculated as follows:
where
is the total agricultural water distribution;
is Hulin City’s 2017 “Three Red Lines” total water control indicators;
is the life water distribution;
is the ecological water distribution;
is the industry water distribution; and
is the reserved water distribution.
The total water control indicators of the “three red lines” in Hulin City are 397 × 106 m3 of surface water and 365 × 106 m3 of groundwater, totaling 762 × 106 m3. According to the accounting of agricultural water distribution in Hulin City, the amount of water that can be distributed in agriculture is 713 × 106 m3, of which the surface water is 377 × 106 m3, and the groundwater is 336 × 106 m3.
- (2)
Agricultural water rights allocation
According to the Heilongjiang Provincial Farmland Water Conservancy Management Station’s 2015 Heilongjiang Paddy Field Development Report, compiled by the Heilongjiang Provincial Farmland Water Management Center, we adjusted the effective area of large-scale irrigation according to the data provided by the Hulin City Irrigation District Management Station. The amount of water that can be allocated for agriculture is calculated based on the accounting results, as shown in
Table 1 for the expected water rights threshold.
From
Table 2, the distribution of agricultural water use in Hulin City and the actual verification, the amount of water allocated to large-scale irrigation districts in Hulin City is 171.85 × 10
6 m
3. According to the data provided by the Hulin City Irrigation District Management Station, there are five large-scale irrigation districts in the county, and the current water price of agricultural products in Hulin City is 0.062 yuan/m
3.
- (3)
Economic data
In 2016, the total GDP of Hulin City was 13,186.78 × 10
6 yuan, of which the primary, secondary, and tertiary industries’ added value were 7983.92 × 10
6 yuan, 1709.73 × 10
6 yuan, and 3493.13 × 10
6 yuan, respectively. In 2016, the total population of Hulin City reached 281,114, including 195,342 urban residents and 85,772 rural residents. In 2016, the per capita disposable income of urban residents in Hulin reached 23,067 yuan, and the per capita disposable income of rural residents reached 16,462 yuan [
35,
36].
Table 3 shows the unit water rights gains and losses under different policy scenarios.
Hulin has a temperate continental monsoon climate and is in a mild and humid climate zone in the Sanjiang Plain. Cold and snowy in winter; summers are short, warm, and rainy; windy in spring; autumns are rainy and cool. The annual average temperature is 3.5 °C, with the coldest temperatures in January. The monthly average temperature in January is −18.3 °C, while the extreme minimum temperature recorded was −36.1 °C. The weather is hottest in July, with a monthly average temperature of 21.6 °C and an extreme maximum temperature of 35.2 °C. The annual average rainfall amount is 566 mm, the precipitation in the growing season (May to September) can account for 80–90% of the total amount in a year, and the regional humidification coefficient is 0.7. Hulin City is located in Heilongjiang Province, and the rainfall is mostly in the growing season, which is 85% of the year. The annual evaporation is basically only in the growing season.
5. Conclusions
In this study, an inexact two-stage initial water rights allocation (ITS) model has been developed that combines the approaches of two-stage stochastic programming (TSP) and interval-parameter programming (IPP). Meanwhile, it can resolve imprecise economic data and non-linear in DWPM. The main research contents and policy recommendations are as follows:
- (1)
Main research contents
This study considers the uncertainty and complexity in the water resources planning system to ensure the maximum return of the system while considering the dynamic changes of various factors. Taking the market influence and economic leverage adjustment as the preconditions, with total agricultural water control and efficiency as the goals, we constructed an initial water rights optimization allocation model that incorporated the changes in differentiated water prices. Continuous optimization of empirical decision-making by a two-stage planning method, based on the actual water-saving target of the agricultural irrigation district in Hulin City, led to an initial water rights allocation model (ITS-WRIDM) based on differential water prices for water-saving adjustment in various agricultural irrigation districts in Hulin City. The developed model reflects dynamic water price changes and real-time changes in agricultural policies, as well as the multiple uncertainties in the process of establishing and solving the optimization model, which makes the initial water rights allocation in the agricultural irrigation district more reasonable.
- (2)
Policy recommendations
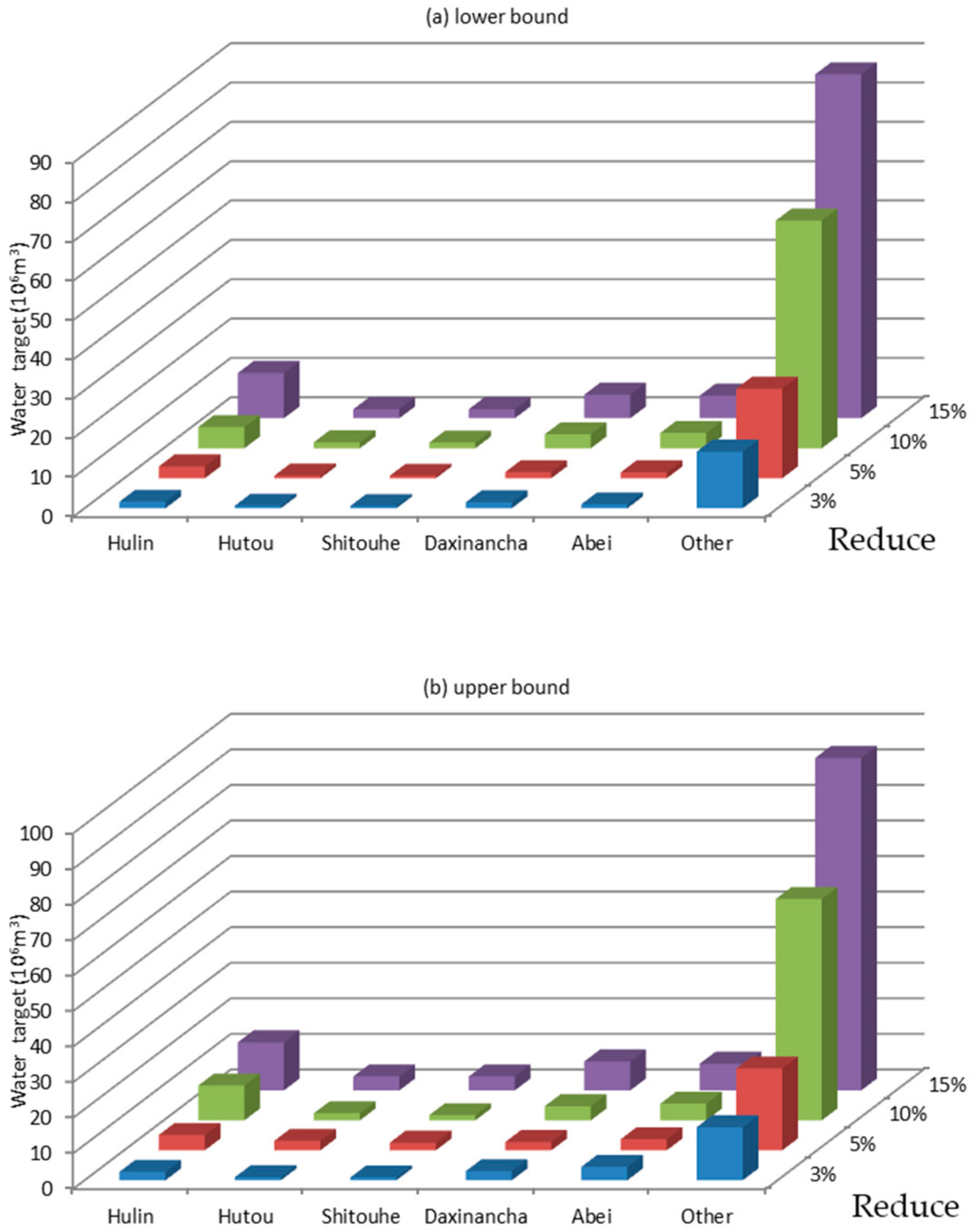
(a) When the total amount of agricultural water is carefully controlled and users’ water-saving awareness is encouraged, the water rights reduction of each irrigation area can reach 20%, which is an extreme value; continued reduction will have a great impact on agricultural production and the social economy. (b) When agricultural water efficiency is controlled, the agricultural irrigation water utilization coefficient will eventually reach a certain extreme value. At this time, increasing investment will cause economic waste. In 2020, the irrigation water utilization coefficient of each agricultural irrigation area in Hulin City should reach 0.55. Hutou needs to increase its agricultural irrigation channels by at least 4.49%, Shitouhe by at least 4.03%, and Daxinancha by at least 4.49%. (c) The imperfection of the current agricultural water-saving reward mechanism will lead to a significant reduction in water-saving enthusiasm in each irrigation district. Water-saving rewards can be set up according to the amount of water saving. The higher the water-saving amount, the higher the unit’s water-saving reward; however, the reward threshold should not be set too high if it is to be an efficient water-saving and compensation mechanism. The government can formulate the corresponding compensation measures according to the actual water-saving benefit of the irrigation district and the actual local economic level. (d) While the government strengthens macro-control, it should also consider the laws of the market economy, promotes the optimal allocation of water resources, and improves the efficiency of water resources utilization. The implementation of the agricultural water rights confirmation system must not only follow a reasonable initial water rights optimization allocation system, but also a reasonable water intake system and irrigation system.