A 2D Real-Time Flood Forecast Framework Based on a Hybrid Historical and Synthetic Runoff Database
Abstract
1. Introduction
2. Methods
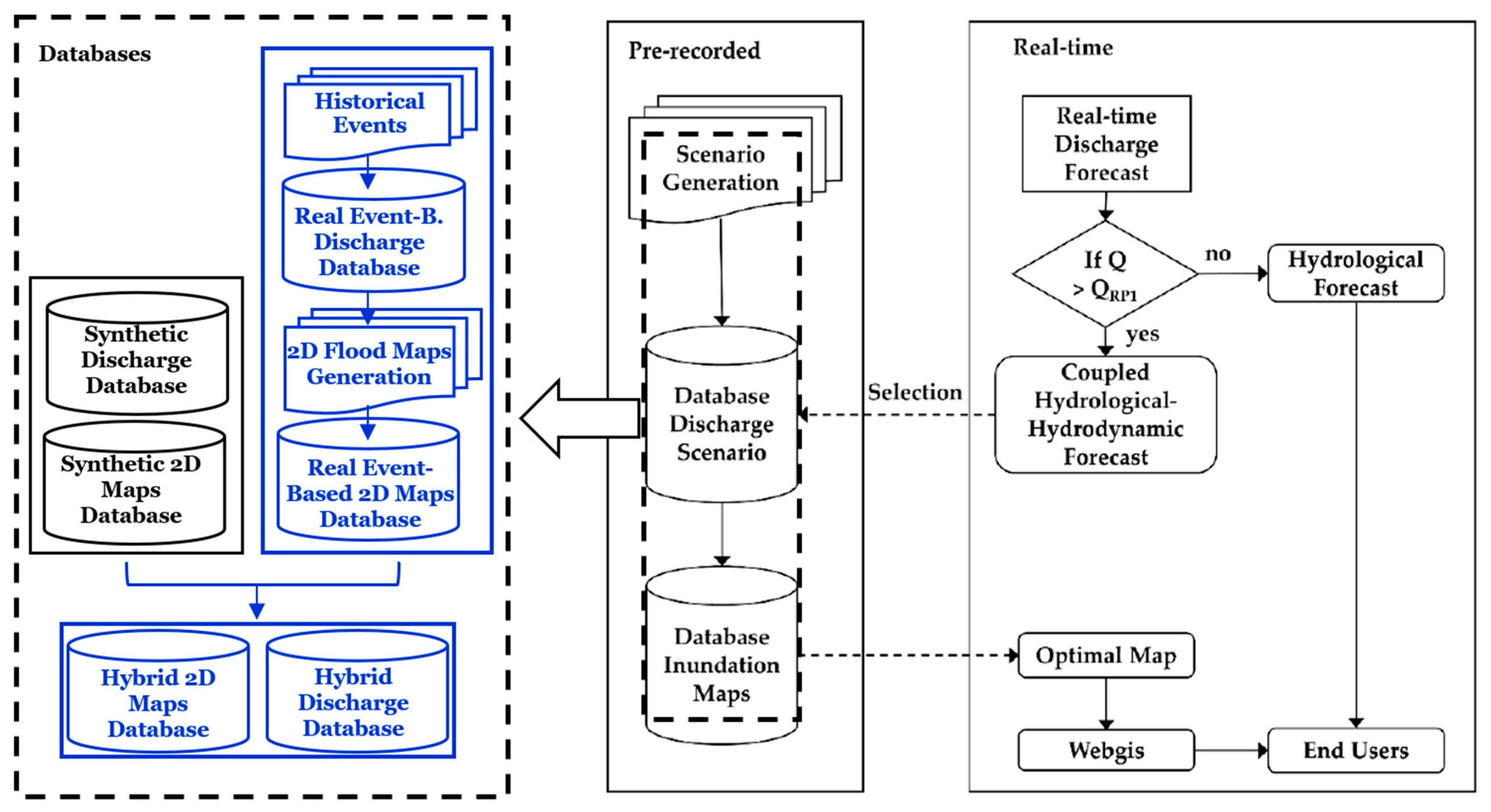
2.1. Framework for Real-Time Flood Forecast
2.2. Evaluation Metrics
2.3. Offline Runoff Databases
2.3.1. Real Event-Based Database (REBD)
2.3.2. Synthetic Database (SD)
2.3.3. Hybrid Database (HD)
2.4. Hydrodynamical Model
2.4.1. Main Equations
2.4.2. Model and Boundary Conditions
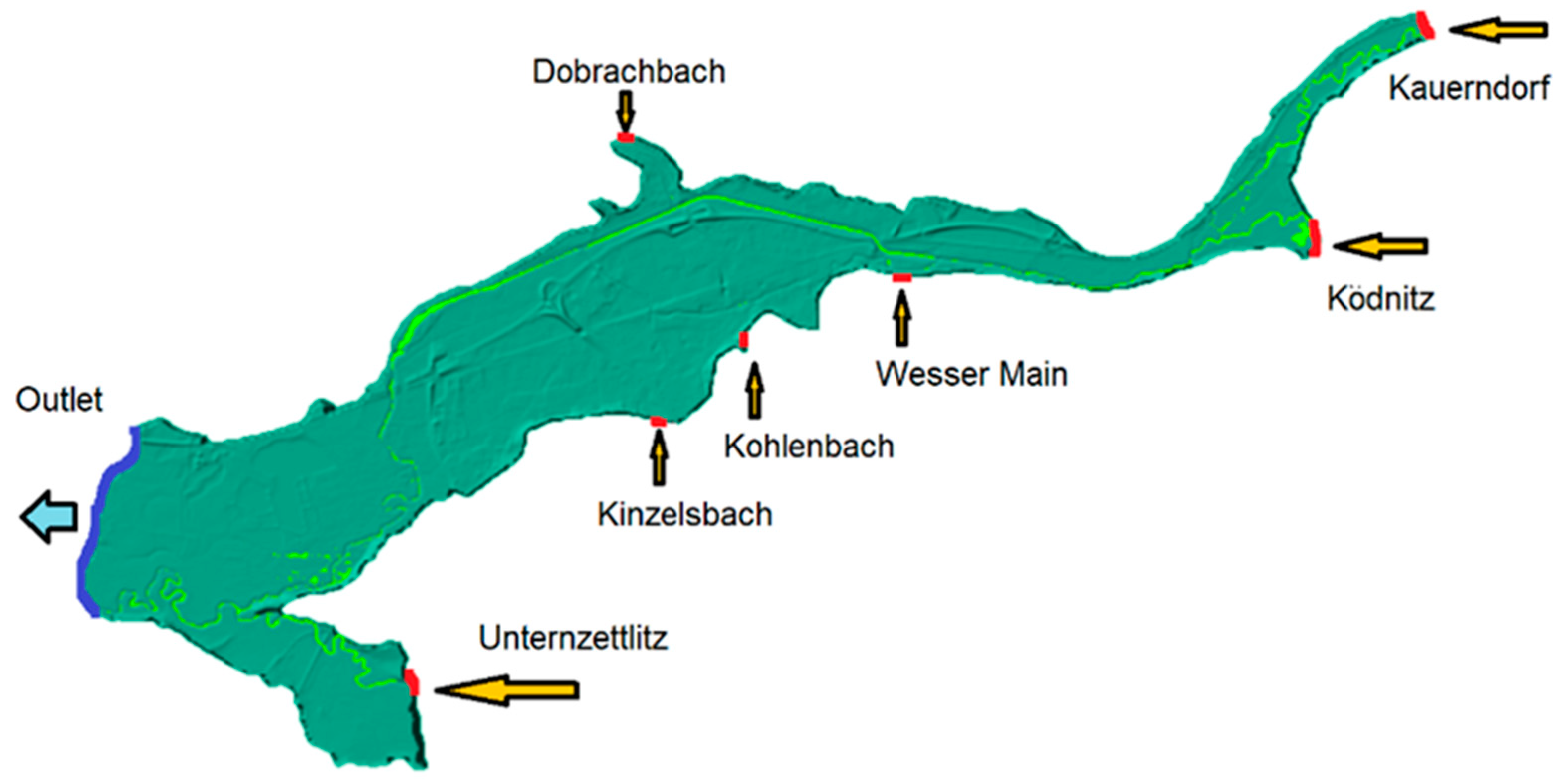
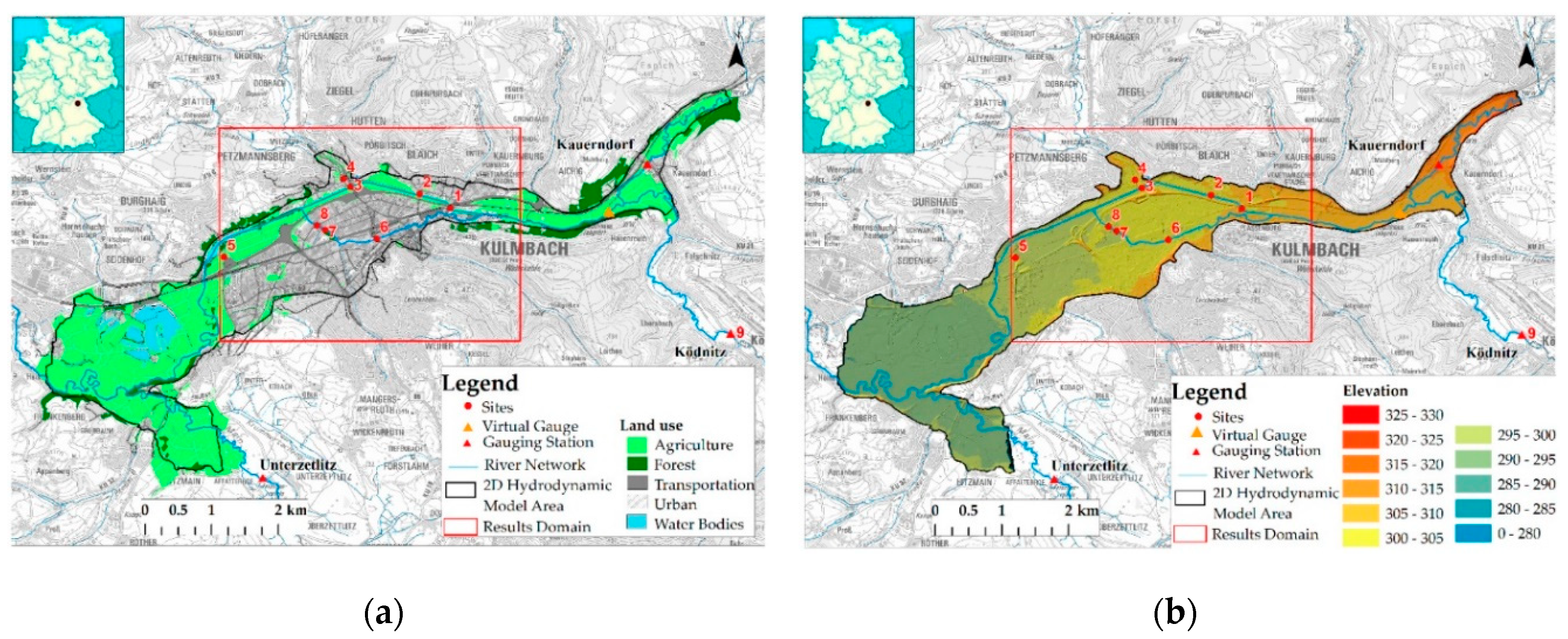
3. Study Area and Data
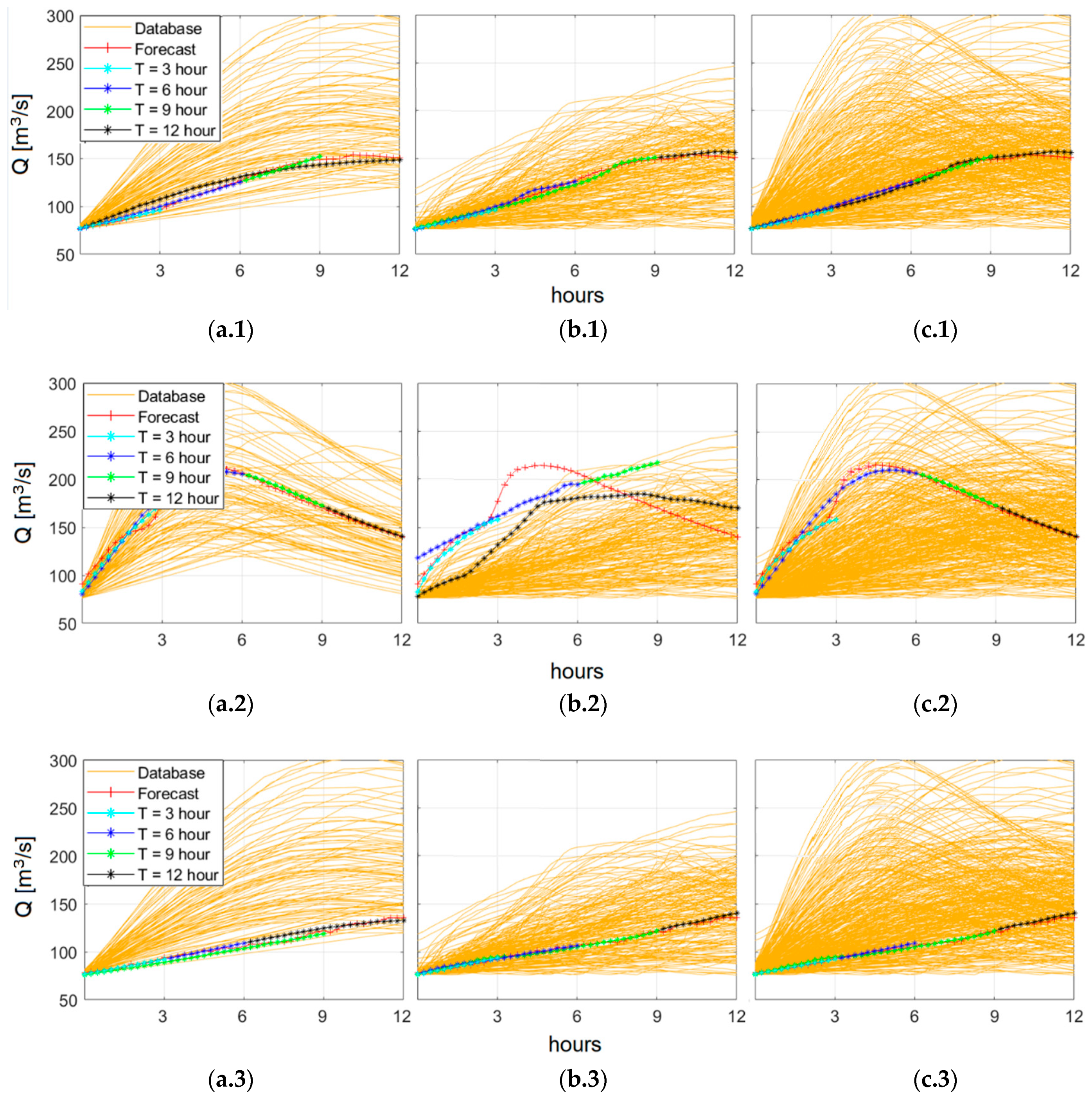
4. Application of the FloodEvac Framework
5. Results and Discussion
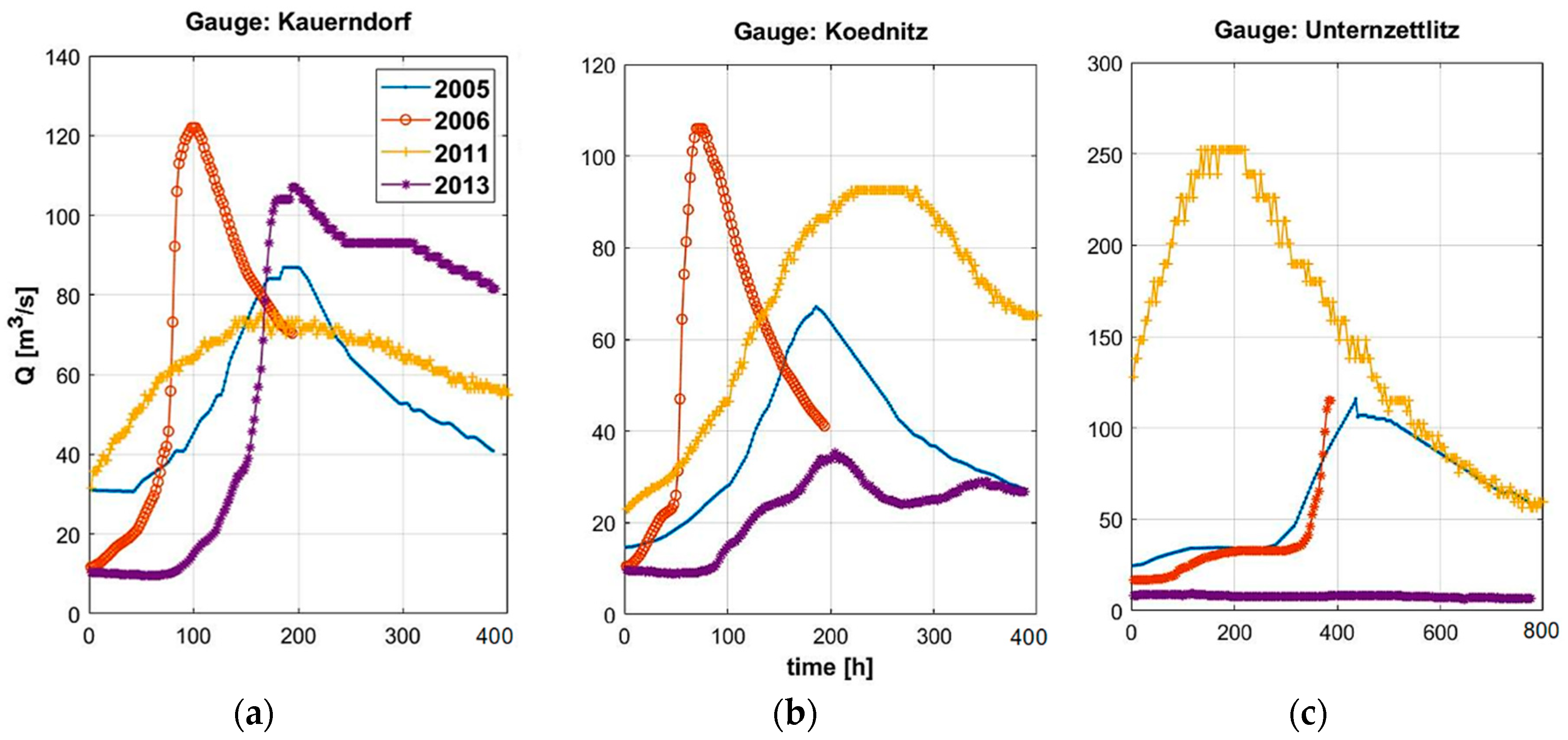
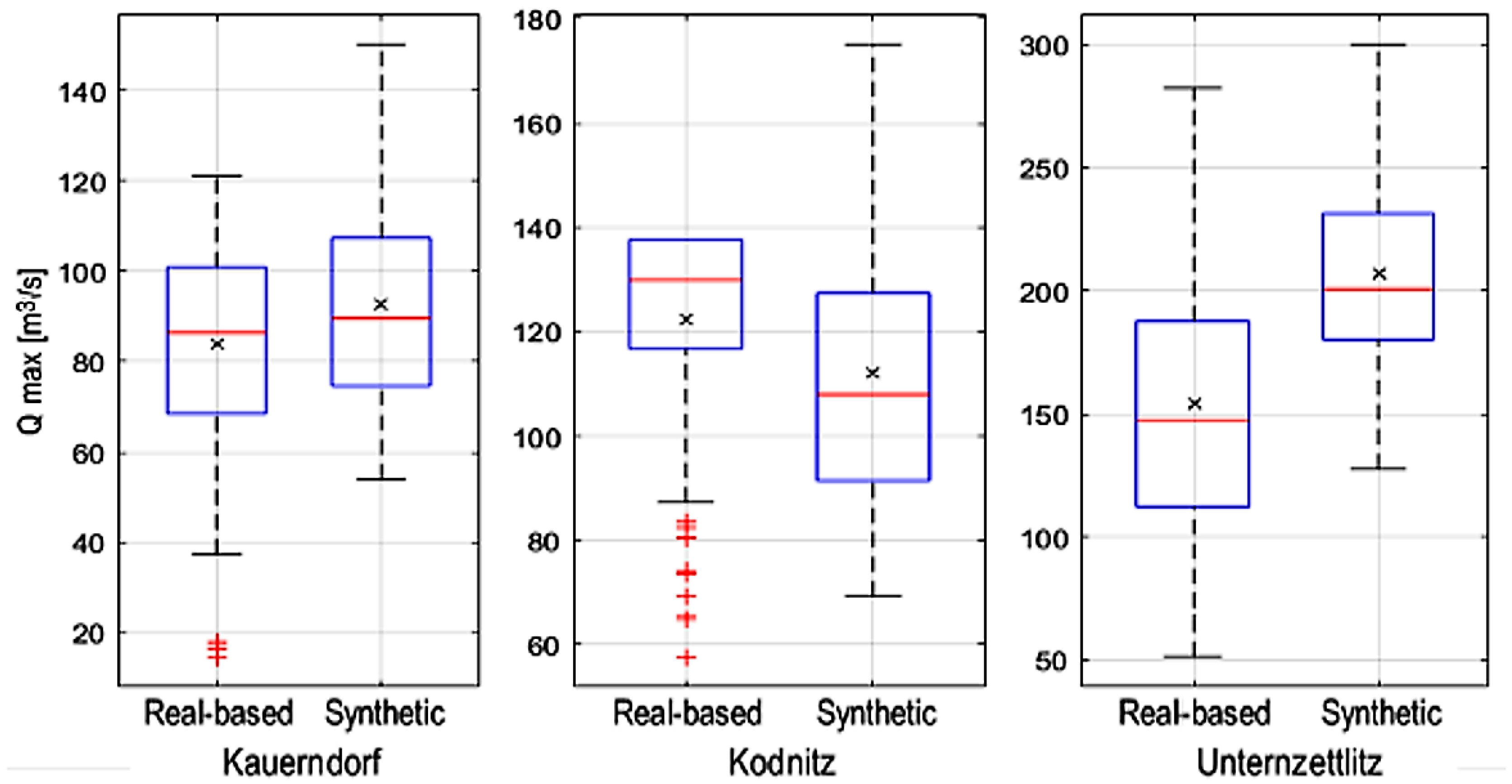
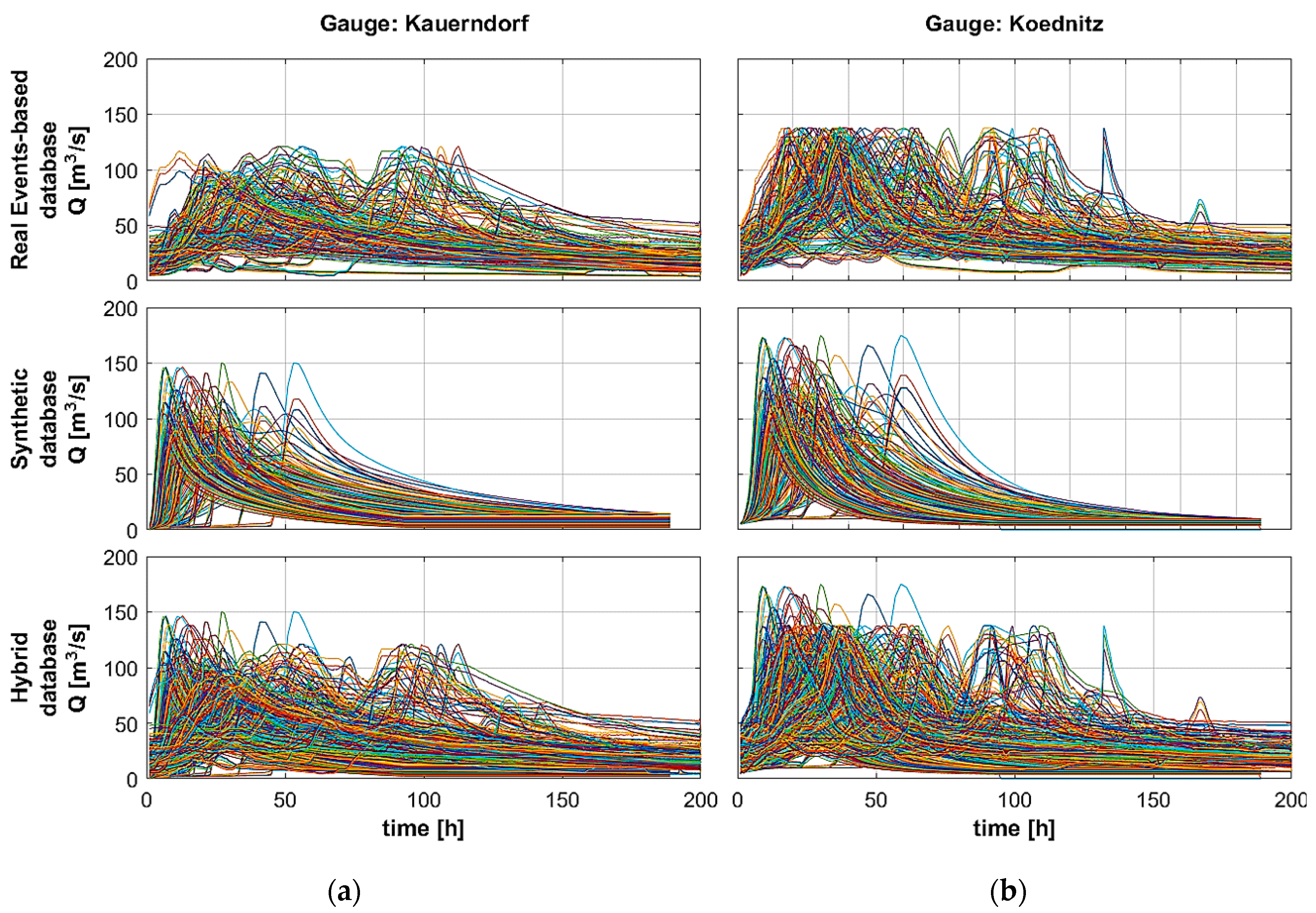
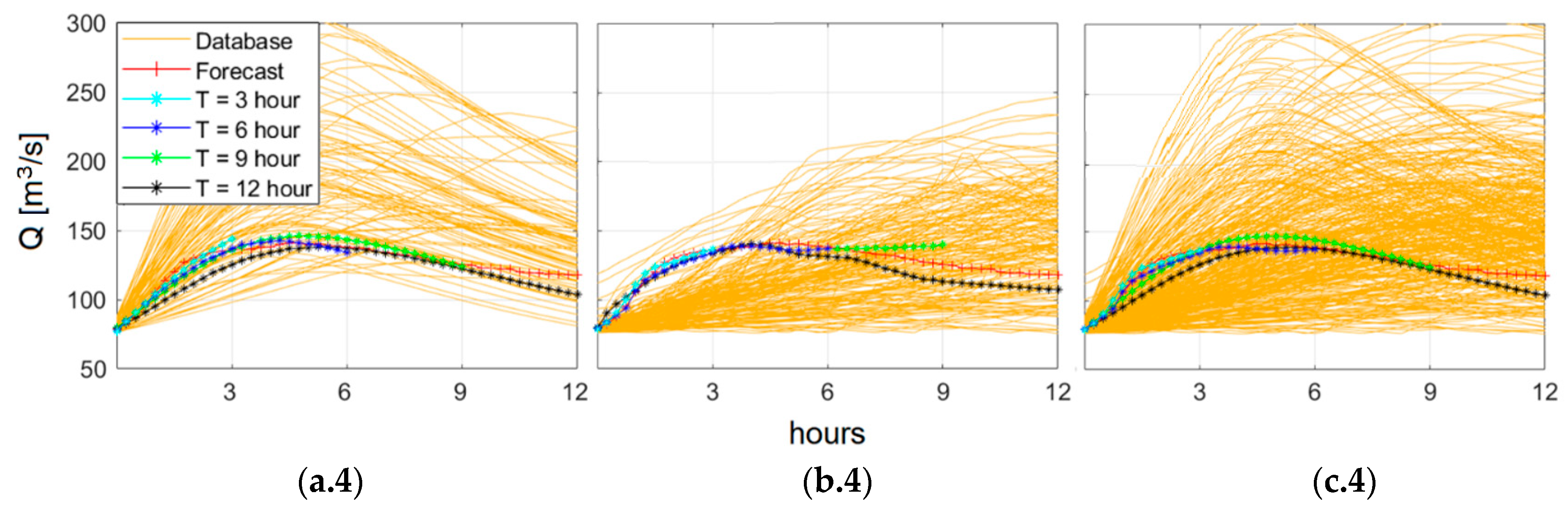
5.1. Databases
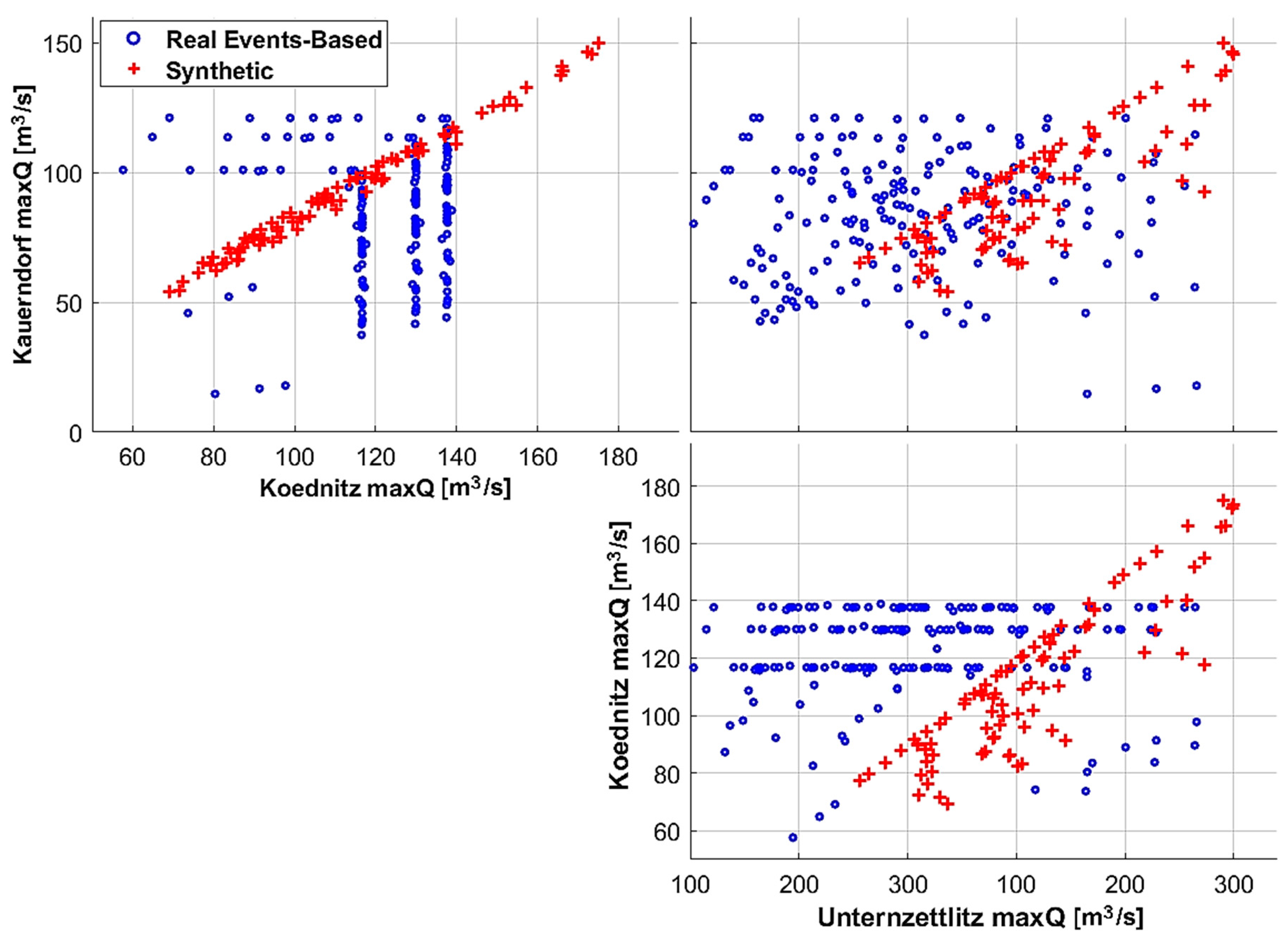
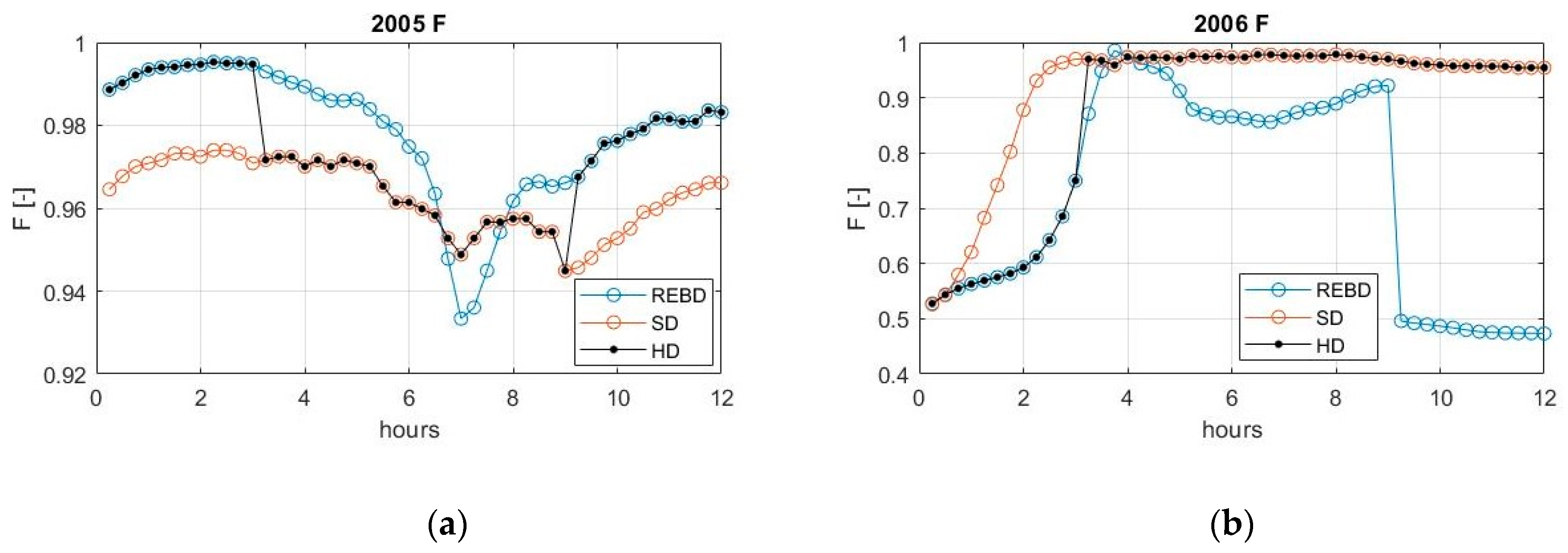
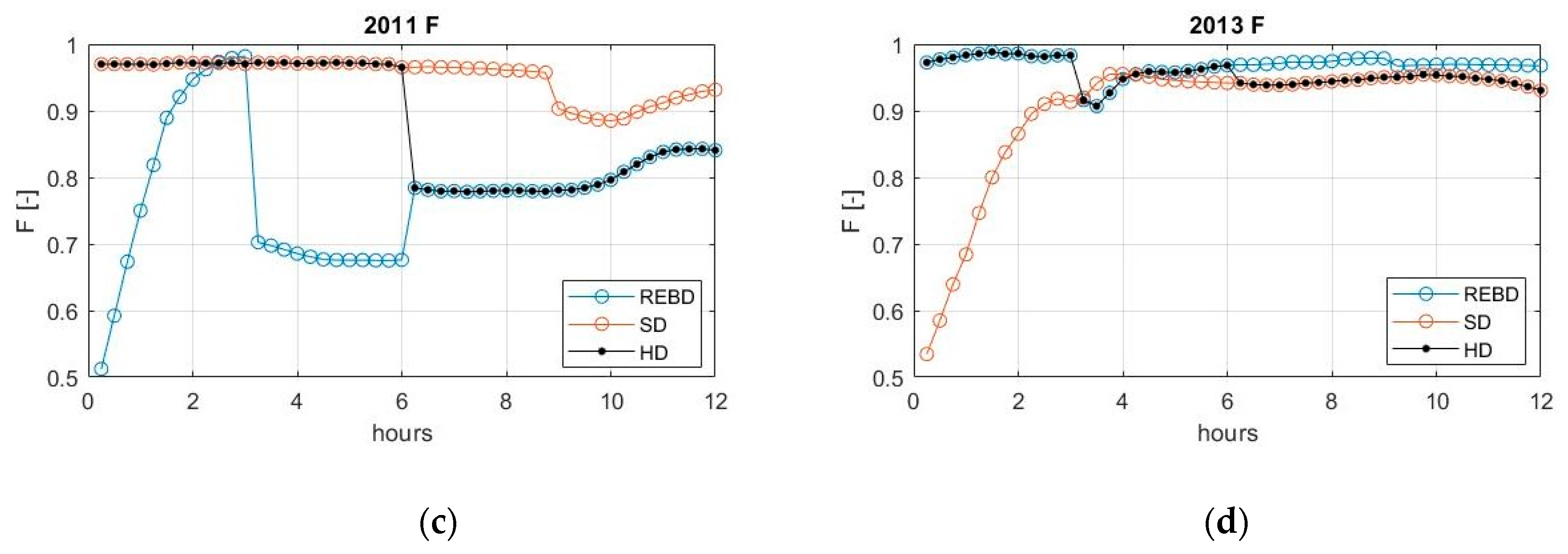
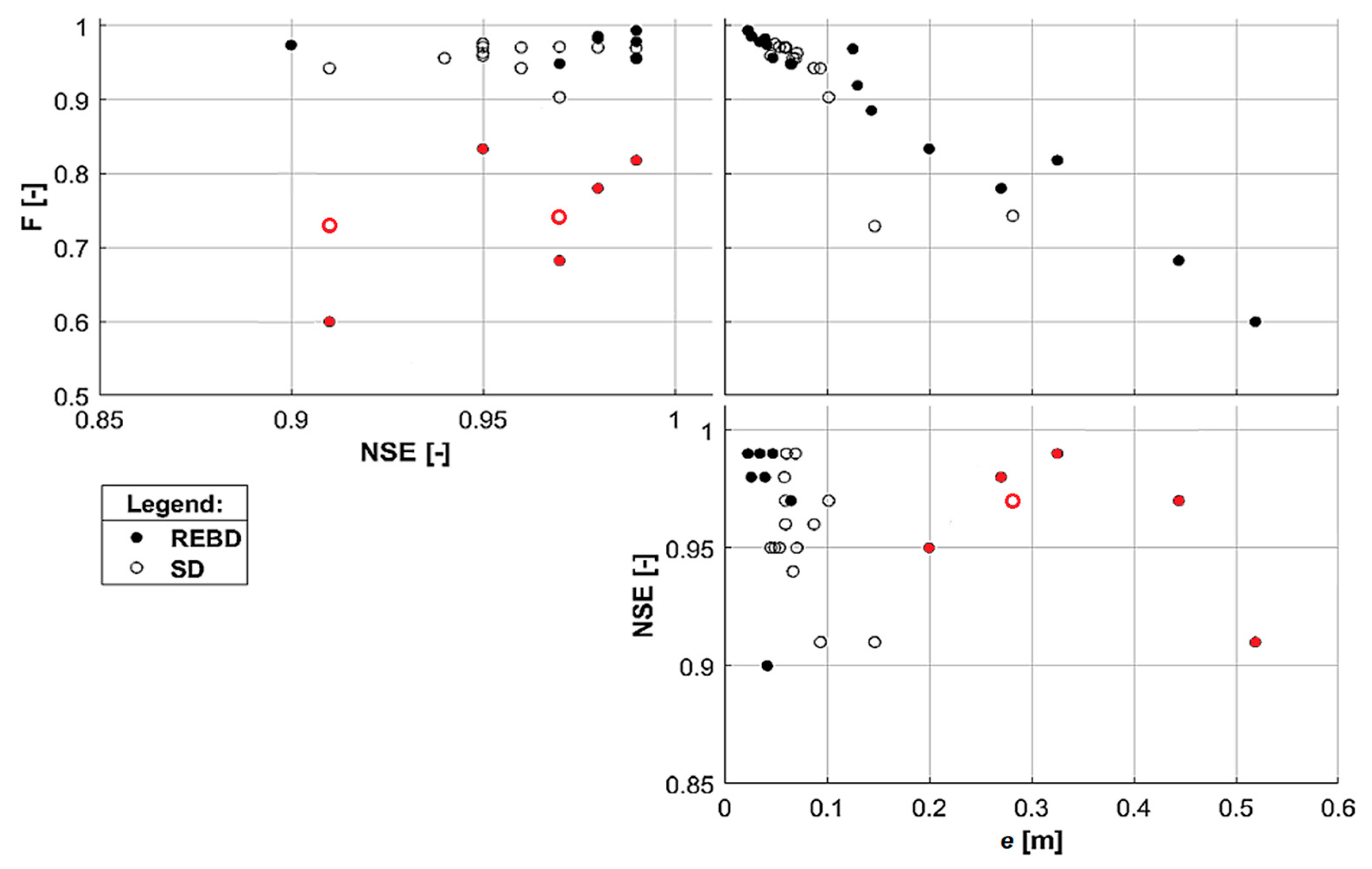
5.2. Database Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kundzewicz, Z.W.; Lugeri, N.; Dankers, R.; Hirabayashi, Y.; Döll, P.; Pińskwar, I.; Dysarz, T.; Hochrainer, S.; Matczak, P. Assessing river flood risk and adaptation in Europe-review of projections for the future. Mitig. Adapt. Strateg. Glob. Chang. 2010, 15, 641–656. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Feyen, L.; Forzieri, G. Global warming increases the frequency of river floods in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2247–2260. [Google Scholar] [CrossRef]
- Vojinovic, Z.; van Teeffelen, J. An integrated stormwater management approach for small islands in tropical climates. Urban Water J. 2007, 4, 211–231. [Google Scholar] [CrossRef]
- Price, R.K.; Vojinovic, Z. Urban flood disaster management. Urban Water J. 2008, 5, 259–276. [Google Scholar] [CrossRef]
- Bhola, P.; Leandro, J.; Disse, M. Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models. Geosciences 2018, 8, 346. [Google Scholar] [CrossRef]
- UNISDR. Stormwater Management Handbook. Int. J. Eng. Technol. 2014, 2, 44. [Google Scholar]
- Bhatt, C.M.; Rao, G.S.; Diwakar, P.G.; Dadhwal, V.K. Development of flood inundation extent libraries over a range of potential flood levels: A practical framework for quick flood response. Geomat. Nat. Hazards Risk 2017, 8, 384–401. [Google Scholar] [CrossRef]
- Kim, G.; Barros, A.P. Quantitative flood forecasting using multisensor data and neural networks. J. Hydrol. 2001, 246, 45–62. [Google Scholar] [CrossRef]
- Campolo, M.; Soldati, A.; Andreussi, P. Artificial neural network approach to flood forecasting in the River Arno. Hydrol. Sci. J. 2003, 48, 381–398. [Google Scholar] [CrossRef]
- Pedersen, L.; Jensen, N.E.; Madsen, H. Calibration of Local Area Weather Radar-Identifying significant factors affecting the calibration. Atmos. Res. 2010, 97, 129–143. [Google Scholar] [CrossRef]
- Molina, L.S.T.; Harmsen, E.W.; Cruz-Pol, S. Flood alert system using rainfall forecast data in Western Puerto Rico. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 574–577. [Google Scholar]
- Acosta-Coll, M. Low-Cost Weather Radars For Precipitation Detection And Development Of Air Operations In Colombia. Rev. Colomb. Tecnol. Adv. 2013, 2–22, 1692–7257. [Google Scholar]
- Bhola, P.K.; Nair, B.B.; Leandro, J.; Rao, S.N.; Disse, M. Flood inundation forecasts using validation data generated with the assistance of computer vision. J. Hydroinformatics 2019, 21, 240–256. [Google Scholar] [CrossRef]
- Acosta-Coll, M.; Ballester-Merelo, F.; Martinez-Peiró, M.; de la Hoz-Franco, E. Real-time early warning system design for pluvial flash floods—A review. Sensors (Switzerland) 2018, 18, 2255. [Google Scholar] [CrossRef]
- Cama-Pinto, A.; Acosta-Coll, M.; Piñeres-Espitia, G.; Caicedo-Ortiz, J.; Zamora-Musa, R.; Sepulveda-Ojeda, J. Diseño de una red de sensores inalámbricos para la monitorización de inundaciones repentinas en la ciudad de Barranquilla, Colombia. Ingeniare. Rev. Chil. Ing. 2016, 24, 581–599. [Google Scholar] [CrossRef]
- Ramírez-Cerpa, E.; Acosta-Coll, M.; Vélez-Zapata, J. Análisis de condiciones climatológicas de precipitaciones de corto plazo en zonas urbanas: Caso de estudio Barranquilla, Colombia. Idesia (Arica) 2017, 35, 87–94. [Google Scholar] [CrossRef]
- Hénonin, J. Urban flood real-time forecasting and modelling: A state-of-the-art review. In Proceedings of the DHI Conference, Kastrup, Denmark, 6–7 September 2010; p. 21. [Google Scholar]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling-a state of the art. J. Hydroinformatics 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Raymond, M.; Peyron, N.; Bahl, M.; Martin, A.; Alfonsi, F. ESPADA: Un outil innovant pour la gestion en temps réel des crues urbaines. In Proceedings of the 6th Novatech 2007—Sustainable Techniques and Strategies in Urban Water Management, Lyon, France, 25–28 June 2007. [Google Scholar]
- Dottori, F.; Kalas, M.; Salamon, P.; Bianchi, A.; Alfieri, L.; Feyen, L. An operational procedure for rapid flood risk assessment in Europe. Nat. Hazards Earth Syst. Sci. 2017, 17, 1111–1126. [Google Scholar] [CrossRef]
- Leandro, J.; Konnerth, I.; Bhola, P.; Amin, K.; Köck, F.; Disse, M. Floodevac Interface zur Hochwassersimulation mit Integrierten Unsicherheitsabschätzungen; Tag der Hydrologie–Forum für Hydrologie und Wasserbewirtschaftung: Trier, Germany, 2017; pp. 185–192. [Google Scholar]
- Bhola, P.; Leandro, J.; Konnerth, I.; Amin, K.; Disse, M. Dynamic Flood Inundation Forecast for the City of Kulmbach Using Offline Two-Dimensional Hydrodynamic Models. In Proceedings of the HIC 2018 13th International Conference on Hydrodynamics, Wuxi, China, 20 September 2018; Volume 3, pp. 258–265. [Google Scholar]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Quirogaa, V.M.; Kurea, S.; Udoa, K.; Manoa, A. Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5. Ribagua 2016, 3, 25–33. [Google Scholar] [CrossRef]
- Leandro, J.; Djordjević, S.; Chen, A.S.; Savić, D.A.; Stanić, M. Calibration of a 1D/1D urban flood model using 1D/2D model results in the absence of field data. Water Sci. Technol. 2011, 64, 1016–1024. [Google Scholar] [CrossRef] [PubMed]
- Bavarian Environmental Agency. GKD Bayern. Available online: https://www.gkd.bayern.de/en/9 (accessed on 10 April 2019).
- HEC-RAS River Analysis System—Hydraulic Reference Manual, Version 5.0; USACE: Davis, CA, USA, 2016.
- Leandro, J.; Chen, A.S.; Schumann, A. Accepted Manuscript A 2D Parallel Diffusive Wave Model for floodplain inundation with variable time step (P-DWave) A 2D Parallel Diffusive Wave Model for floodplain inundation with variable time step (P-DWave) 1. J. Hydrol. 2014, 517, 38–39. [Google Scholar] [CrossRef]
- Bhola, P.K.; Leandro, J.; Disse, M. Reducing uncertainties in flood inundation outputs of a two-dimensional hydrodynamic model by constraining roughness. Nat. Hazards Earth Syst. Sci. 2019, 19, 1445–1457. [Google Scholar] [CrossRef]
| Surface | Manning’s n (s/m1/3) |
|---|---|
| Water bodies | 0.022 |
| Crops and fields | 0.043 |
| Forests | 0.189 |
| Main roads | 0.014 |
| Urban area | 0.074 |
| Event | Interval (h) | REBD | SD | HD | |||
|---|---|---|---|---|---|---|---|
| Ev. Index | NSE/Wr2 (-) | Ev. Index | NSE/Wr2 (-) | Ev. Index | NSE/Wr2 (-) | ||
| 2005 | 3 | 180 | 0.99 | 9 | 0.98 | 180_R | 0.99 |
| 6 | 73 | 0.98 | 6 | 0.99 | 6_S | 0.99 | |
| 9 | 14 | 0.99 | 6 | 0.99 | 6_S | 0.99 | |
| 12 | 14 | 0.99 | 67 | 0.94 | 14_R | 0.99 | |
| 2006 | 3 | 51 | 0.91 | 135 | 0.91 | 51_R | 0.91 |
| 6 | 87 | 0.70 | 173 | 0.95 | 173_S | 0.95 | |
| 9 | 87 | 0.54 | 173 | 0.95 | 173_S | 0.95 | |
| 12 | 157 | 0.05 | 173 | 0.95 | 173_S | 0.95 | |
| 2011 | 3 | 83 | 0.95 | 10 | 0.96 | 10_S | 0.96 |
| 6 | 76 | 0.97 | 10 | 0.97 | 10_S | 0.97 | |
| 9 | 172 | 0.98 | 14 | 0.95 | 172_R | 0.98 | |
| 12 | 172 | 0.99 | 10 | 0.97 | 172_R | 0.99 | |
| 2013 | 3 | 41 | 0.98 | 115 | 0.97 | 41_R | 0.98 |
| 6 | 141 | 0.97 | 150 | 0.96 | 141_R | 0.97 | |
| 9 | 141 | 0.90 | 120 | 0.91 | 120_S | 0.91 | |
| 12 | 49 | 0.69 | 95 | 0.87 * | 95_S | 0.87 * | |
| F and e | 2005 | 2006 | 2011 | 2013 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| REBD | SD | HD | REBD | SD | HD | REBD | SD | HD | REBD | SD | HD | ||
| F (-) | 3 h | 0.99 | 0.97 | 0.99 | 0.60 | 0.77 | 0.60 | 0.83 | 0.97 | 0.97 | 0.98 | 0.78 | 0.98 |
| 6 h | 0.99 | 0.97 | 0.97 | 0.92 | 0.97 | 0.97 | 0.68 | 0.97 | 0.97 | 0.95 | 0.95 | 0.95 | |
| 9 h | 0.96 | 0.95 | 0.95 | 0.89 | 0.98 | 0.98 | 0.78 | 0.96 | 0.78 | 0.97 | 0.94 | 0.94 | |
| 12 h | 0.98 | 0.96 | 0.98 | 0.48 | 0.96 | 0.96 | 0.82 | 0.91 | 0.82 | 0.97 | 0.95 | 0.95 | |
| e (m) | 3 h | 0.02 | 0.06 | 0.02 | 0.52 | 0.13 | 0.52 | 0.20 | 0.06 | 0.06 | 0.04 | 0.26 | 0.04 |
| 6 h | 0.03 | 0.06 | 0.06 | 0.13 | 0.05 | 0.05 | 0.44 | 0.06 | 0.06 | 0.06 | 0.08 | 0.06 | |
| 9 h | 0.05 | 0.07 | 0.07 | 0.14 | 0.05 | 0.05 | 0.27 | 0.07 | 0.27 | 0.04 | 0.09 | 0.09 | |
| 12 h | 0.03 | 0.06 | 0.03 | 0.55 | 0.05 | 0.05 | 0.33 | 0.10 | 0.33 | 0.13 | 0.06 | 0.06 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crotti, G.; Leandro, J.; Bhola, P.K. A 2D Real-Time Flood Forecast Framework Based on a Hybrid Historical and Synthetic Runoff Database. Water 2020, 12, 114. https://doi.org/10.3390/w12010114
Crotti G, Leandro J, Bhola PK. A 2D Real-Time Flood Forecast Framework Based on a Hybrid Historical and Synthetic Runoff Database. Water. 2020; 12(1):114. https://doi.org/10.3390/w12010114
Chicago/Turabian StyleCrotti, Giampaolo, Jorge Leandro, and Punit Kumar Bhola. 2020. "A 2D Real-Time Flood Forecast Framework Based on a Hybrid Historical and Synthetic Runoff Database" Water 12, no. 1: 114. https://doi.org/10.3390/w12010114
APA StyleCrotti, G., Leandro, J., & Bhola, P. K. (2020). A 2D Real-Time Flood Forecast Framework Based on a Hybrid Historical and Synthetic Runoff Database. Water, 12(1), 114. https://doi.org/10.3390/w12010114





