Abstract
In this study, Random SubSpace-based classification and regression tree (RSCART) was introduced for landslide susceptibility modeling, and CART model and logistic regression (LR) model were used as benchmark models. 263 landslide locations in the study area were randomly divided into two parts (70/30) for training and validation of models. 14 landslide influencing factors were selected, such as slope angle, elevation, aspect, sediment transport index (STI), topographical wetness index (TWI), stream power index (SPI), profile curvature, plan curvature, distance to rivers, distance to road, soil, normalized difference vegetation index (NDVI), land use, and lithology. Finally, the hybrid RSCART model and two benchmark models were applied for landslide susceptibility modeling and the receiver operating characteristic curve method is used to evaluate the performance of the model. The susceptibility is quantitatively compared based on each pixel to reveal the system spatial pattern between susceptibility maps. At the same time, area under ROC curve (AUC) and landslide density analysis were used to estimate the prediction ability of landslide susceptibility map. The results showed that the RSCART model is the optimal model with the highest AUC values of 0.852 and 0.827, followed by LR and CART models. The results also illustrate that the hybrid model generally improves the prediction ability of a single landslide susceptibility model.
1. Introduction
Landslides are large-scale movements of rocks, mud, and gravel from the top to the bottom of the mountain [1]. According to statistics, five percent of the world’s natural disasters were landslides from 1994 to 2013 [2]. Landslides pose serious risks to human life, environment, resources, and property. Therefore, for the sake of decreasing the hazards caused by landslides, landslide susceptibility evaluation is becoming a common topic.
Landslide susceptibility refers to the probability of landslide occurring in an area on account of local geological environmental factors [3,4]. Geographic information system (GIS) has been diffusely applied for evaluating landslide susceptibility in recent decades, and many methods have been proposed. These methods mainly include deterministic methods, traditional statistical methods, and machine learning technologies [4,5].
In deterministic models, the stability of the slope is in the form of a calculated safety factor, which is suitable for small watersheds [6,7]. Statistical models, such as evidential belief function (EBF) [8,9], weights of evidence [10,11,12], frequency ratio [13,14,15,16,17], logistic regression [18,19,20,21], linear multivariate regression, multivariate adaptive regression spline [22,23,24], and statistical index [25,26] have been widely used. However, these traditional statistical methods do not provide satisfactory evaluation of the correlation between landslide influencing factors [4,27].
Therefore, machine learning technologies have drawn extensive attention, and many kinds of machine learning methods have been developed and used, such as classification and regression trees [28,29], adaptive neuro-fuzzy inference systems [30,31], fuzzy logic [32,33], alternating decision trees [34,35,36], support vector machine [37,38,39], artificial neural networks [40,41], and random forest [4,42,43,44,45]. In particular, hybrid models are increasingly used, such as the rotation forest-based decision trees [46,47], frequency ratio-based ANFIS model [48], bagging-based reduced error pruning trees [49], and multiboost-based support vector machines [50].
Spatial prediction of landslide is not only the first important step, but also one of the most difficult tasks [31,51]. Many modeling methods have been used in the construction of landslide susceptibility maps in the past, but the accuracy of these models has not been accepted by all researchers [52]. Youssef et al. used CART model to study landslide susceptibility in Wadi Tayyah Basin. The result of post-cart model is not optimal [53]. However, when Felicísimo et al. studied the landslide susceptibility, CART shows a high predictive ability [54]. Hong et al. studied the landslide susceptibility in Wuning area of China after modeling the hybrid model of free subspace and support vector machine. The mixed model RSSVM model also achieved optimal performance (AUC = 0.857) [55]. Therefore, the hybrid models are often considered to be more precise to single models [55].
The Loess Plateau is one of the most vulnerable regions in China. The special geological environment of the area has led to the development of environmental geological problems. Zichang County is in the hinterland of the Loess Plateau. Due to the large area coverage of the Quaternary loess, various geological problems induced by geological processes became more apparent. Therefore, the main purpose of this study is to apply and analyze the hybrid integration method of Random Subspace (RS) and CART, namely RSCART, in landslide susceptibility assessment for the Zichang County. Also, the EBF model was used to evaluate the correlation between landslides and influencing factors, and the single CART model and well known LR model were selected as benchmark models. Finally, the ROC curve and AUC values were used for comparing the performance of models.
2. Description of the Study Area
The study area selected for this study is Zichang County in Shaanxi Province, China (Figure 1). The length of the County is 72 km from east to west, 55.7 km from north to south, and the total area is 2450 km2. It is in east longitude 109°11′22″~110°01′22″ E, latitude 36°30′59″~37°30′00″ N. The altitude ranges from 933 m to 1574 m above sea level. Topographically, the slope less than 10° accounts for about 10.44% of the total area, the slope of 10–20° is about 26.09%, 20–30° is about 35.14%, 30–40° is about 23.9%, and 40–50° is about 4.41%. The slope greater than 50° is only 0.02%. From the perspective of geomorphology, Zichang County belongs to the Loess Plateau gully region in northern Shaanxi Province. The complex geomorphology types in the area were formed after the loess was eroded and cut by the Xiuyan River, the Luanhe River, and other tributaries. The loess from the Middle Pleistocene to the Late Pleistocene formed a lot of valleys and river systems after the Loess Plateau uplift. The penetration of the Yellow River led to the formation of many loess ridges, loess hills, and gullies in the area. According to the landform genesis, the area is divided into loess landforms and river landforms.
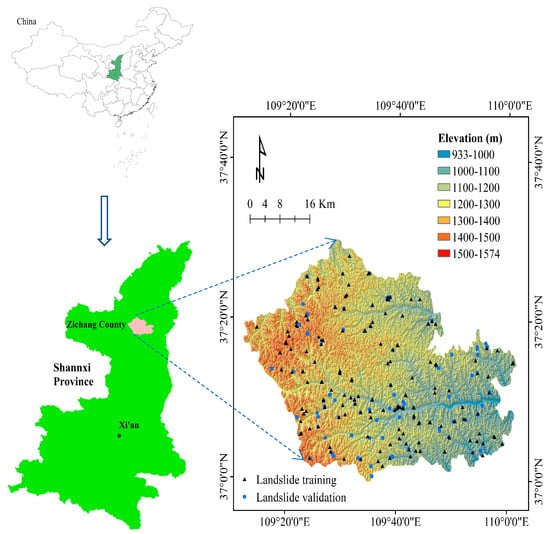
Figure 1.
Study area.
3. Methodology
The methodology of this study is shown in Figure 2. There are mainly four steps in the current study: (1) data preparation including preparation of a landslide inventory map and landslide conditioning factors, (2) multicollinearity analysis and consideration of the correlation between landslide locations and conditioning factors, (3) three models are used for landslide susceptibility model (RSCART,CART,LR), and (4) validation of landslide susceptibility maps produced by the ROC curve.
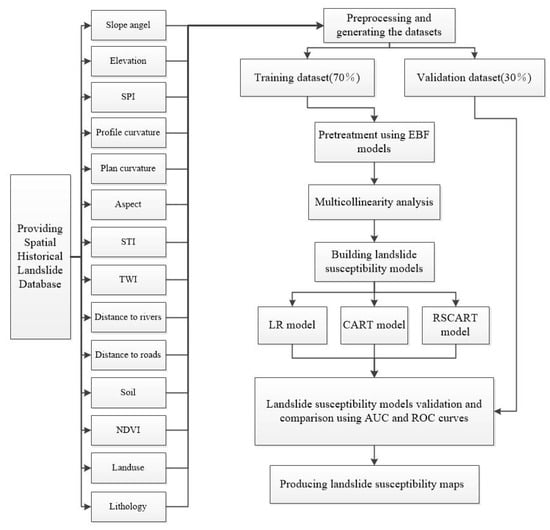
Figure 2.
Flowchart of the study.
3.1. Data Preparation
The landslides inventory includes the location of past and recent landslides [56]. It also allows people to understand the type and timing of landslides [57]. This study constructed a landslide inventory including 263 landslide locations by consulting aerial photos and collecting historical landslide events, of which most of the landslides were slides (201), the others included 62 falls [58]. According to an analysis in the GIS environment, the largest landslide was more than 1 × 107 m3, and the smallest landslide was nearly 120 m3. Rainfall and human engineering activities, such as urban and rural construction, road engineering construction and water conservancy engineering, are the main triggering factors of landslides. To establish and verify the landslide model, the landslides were randomly divided into two parts: (1) 70% were used to construct the training dataset; (2) the remaining 30% were used to generate validation dataset.
Based on literature review and data availability [42,56,59,60], 14 landslide influencing factors were used in this study. Slope angle, elevation, aspect, sediment transport index (STI), topographical wetness index (TWI), stream power index (SPI), profile curvature, plan curvature, distance to rivers, distance to roads, soil, NDVI, land use, and lithology were considered.
Slope angle, elevation and slope aspect are often used in landslide susceptibility mapping [61,62,63,64,65]. In this study, slope angles were divided into six classes: <10°, 10–20°, 20–30°, 30–40°, 40–50°, >50° (Figure 3a, Table 1). The elevation of the study area was reclassified into seven categories with an interval of 100 m, such as <1000 m, 1000–1100 m, 1100–1200 m, 1200–1300 m, 1300–1400 m, 1400–1500 m, and >1500 m (Figure 3b, Table 1). Slope aspect was divided into nine types as follows: flat, north, northeast, east, southeast, south, southwest, west, and northwest (Figure 3c, Table 1).
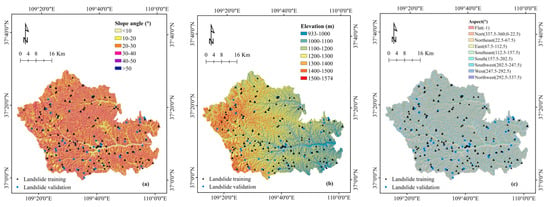
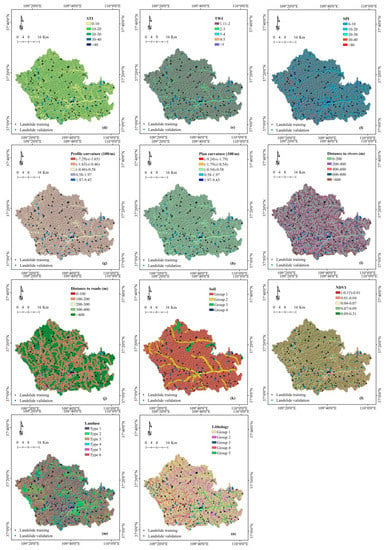
Figure 3.
Thematic maps of the study area.

Table 1.
Correlation between landslides and influencing factors using EBF model.
STI reflects the erosion force of surface water flow on the ground [66]. It can be expressed by Equation (1) [67,68]:
where α is the specific watershed area, and β is the slope. In this study, STI values were classified into five classes, such as <10, 10–20, 20–30, 30–40, and >40 (Figure 3d, Table 1).
TWI affects slope material by affecting soil moisture and groundwater flow. It can be represented by Equation (2) as follows [68]:
where α is the area drained per unit contour length at a point, and β is the slope. In the study area, the TWI was also divided into five categories: 1–2, 2–3, 3–4, 4–5, and >5 (Figure 3e, Table 1).
The SPI is an important hydrologic factor, which shows the process of potential flow erosion [68]. It can be represented by Equation (3) as follows [68]:
where α is the specific watershed area, and β is the slope. In the study area, the SPI was also divided into five categories: 1–2, 2–3, 3–4, 4–5 and >5 (Figure 3f, Table 1).
Profile curvature and plane curvature are important topographic factors. Profile curvature is defined as the curvature at any point is perpendicular to the slope [69]. Profile curvature is divided into five types: (−7.92)–(−1.65), (−1.65)–(−0.46), (−0.46)–0.58, 0.58–1.97, 1.97–9.45 (Figure 2g, Table 1). Plan curvature is described as the curvature of the contour formed by the intersection with the plane [70]. Plan curvature was divided into five categories: (−9.24)–(−1.79), (−1.79)–(−0.54), (−0.46)–0.38, 0.38–1.44, 1.44–7.56 (Figure 3h, Table 1).
The distance to rivers and distance to roads are important factors in landslide susceptibility modeling [71,72]. The river causes the bedrock to produce enough topographic change through erosion. This process makes the slope more prone to block failure [73]. Distance to rivers was divided into five classes with an interval of 200 m (Figure 3i, Table 1). The natural conditions of the slope were destroyed during the construction of transportation facilities, and oil and gas development, and other human engineering activities [74]. In the present study, distance to roads was grouped into five buffing zones using an interval of 100 m (Figure 3j, Table 1).
With the increase of soil depth, the runoff velocity decreases. The unstable nature of shallow is more likely to lead to landslides [75]. There are four types of soil, such as: cultivated loessal soils, alluvial soils, red clay soils and water (Figure 3k, Table 1).
NDVI can quantitatively estimate vegetation growth and biomass by measuring surface reflectance [76]. The NDVI value is calculated based on the following formula:
where IR is the infrared band, and R is the red band. The NDVI value was reclassified into five categories: −0.15–0.11, 0.01–0.04, 0.04–0.07, 0.07–0.09, 0.09–0.31 (Figure 3l, Table 1).
Land use is affected by environmental changes and plays an important role in slope stability. In this paper, land use is divided into six categories, including farmland, forestland, grasslands, water bodies, residential areas and others (Figure 3m, Table 1).
Lithological units greatly influence the landslide occurrence [77]. The lithologic units were divided into five groups (Figure 3n, Table 1): the first group is quaternary (loess, silt), the second group is tertiary (mudstone, conglomerate), the third group is cretaceous (arkose), the fourth group is Jurassic (shale, sandstone, mudstone, conglomerate), and the fifth group is Triassic (mudstone, sandstone, conglomerate).
Finally, all the 14 landslide influencing factors were converted to the same resolution of 30 m × 30 m.
3.2. Evidential Belief Function (EBF)
The EBF is an evidence algorithm which is a mathematical method based on bivariate statistics [78]. The EBF is a flexible model, because it not only accepts uncertainty but also absorbs the belief of many sources. The EBF model is made up of four mathematical functions: the degree of belief (Bel), the degree of disbelief (Dis), the degree of uncertainty (Unc), and the degree of plausibility (Pls). 0 to 1 is the range of these functions [79]. This study uses Bel values to represent the correlation between landslides and factors, and Bel values can be represented by the following expression:
where Beli is the extent of belief of ith influencing factor.
3.3. Classification and Regression Tree (CART)
The CART is an effective method because it has attested to be a technique for dealing with difficult classification problems [80]. CART is a decision tree proposed by Breiman [81]. The data is processed in a recursive form by the CART model [82]. In this process, the value of internal node features is “yes” and “no”. Categorical and continuous dependent variables (regression) are predicted by classification and regression trees.
If the dependent variable is a category scale, CART will generate a classification tree, and if the dependent variable is a continuous data, CART will generate a regression tree [83]. The classification tree using CART can be constructed in four main steps: (1) building tree, (2) stopping tree building, (3) pruning tree, and (4) selecting optimal tree [84]. The information that needs to be processed is represented by CART in an intuitive way, and the metrics between the predictive variables do not affect the model results [53].
CART has many advantages as a classifier that it is not only a method suitable for numeric data types, but also generates an invariant for the transformation of independent variables. In addition, CART does not have to pick a variable first [85].
3.4. Random Subspace (RS)
The RS was proposed by Ho in 1998, which is defined as a classical integration algorithm [86]. The RS can establish the training subset, which is randomly selected from the original training set [87,88,89,90,91,92]. Also, the RS can modify the training data set in the feature space. RS is also a very effective integration algorithm because it can solve the data sets with redundant features and over-fitting problems. The RS enables the training data to maintain the highest accuracy. However, it cannot be ignored is that the growth of training data increases the complicacy of accuracy [93].
The main goal of RS is to collect the feature set of the high-dimensional feature space into the low-dimensional subspace, and then construct a classifier to classify the class based on the subspace. The final result is obtained by the majority voting rule [94]. More specifically, let the n-dimensional vector Xin be the n features (landslide influencing factors) of the training sample Xi. In RS, randomly select r < n features from the n-dimensional data set of the original space X to obtain the random subspace of r dimension. The modified training data set Xe contains the r-dimensional training object . Finally, the classifier is constructed in the RS Xe and the majority voting rule is adopted, as follows [91]:
where is a decision of the classifier, is the Kronecker symbol, Ca(x) are the generated classifiers (a = 1,2, …, A) [91].
3.5. Logistic Regression (LR)
Logistic regression can analyze a series of problems whose results are affected by one or more factors. The factors influencing the results are called independent variables, which can be continuous, discrete, or a combination of the two types. Logistic regression coefficients can figure out the influence of independent variables on landslide occurrence [95,96]. LR is defined as the follows:
where A is the linear combination, β0 is the intercept, β1, β2, …βn are the coefficients of logistic regression, and Y1, Y2, …Yn are the independent variables [97]. Using Equation (3), the landslide probability P is expressed as:
4. Results
4.1. Correlation Analysis of Influencing Factors
In the present study, Bel value was used to represent the correlation between landslide and various landslide influencing factors. The results (Table 1) showed that Bel value in the south is the highest (0.181), followed by Bel value in the southwest (0.165), and Bel value in the southeast (0.151). At an altitude of more than 1500 m (0.305) greater regional influence landslide occurred right. The results indicate that slopes between 40–50 have a greater impact on the occurrence of landslides (Bel = 0.309). In terms of plan curvature, Bel value is the highest for the class of 1.44–7.56 (0.279). In terms of profile curvature, the class of 0.58–1.97 has the highest value (0.288), so it has a greater impact on the landslide occurrence. TWI value between 2 and 3 has the highest Bel value, which is 0.388. Areas within 200 m to rivers are more prone to landslides (Bel = 0.590) because rivers provide wetter soil for landslides. Similarly, areas within 100 m to the road networks have a greater impact on landslides occurrence (Bel = 0.313). This is because the soil near the road becomes more loosely structured during human activity. For the NDVI, the area between 0.07 and 0.09 has a higher impact on landslide occurrence. Residential areas have higher impact on landslide events (Bel = 0.385). In terms of lithology, Bel value of the fourth group is 0.31, indicating that Jurassic rocks were more sensitive to landslide occurrences. The area covered by red clay has a greater impact on landslide occurrence (Bel = 0.614). The highest Bel values of SPI and STI are 0.234 and 0.219, respectively, and the corresponding ranges are 20–30 and 30–40, respectively. The regions within these ranges have a greater impact on the landslide occurrence.
The multicollinearity test of landslide influencing factors is very important in landslide susceptibility mapping. The two most widely used indices in multicollinearity analysis are tolerance and variance inflation factors (VIF). If the tolerance value is <0.1 or the VIF value is >10, it indicates that there is serious multicollinearity among landslide influencing factors [98,99,100]. Tolerance and VIF values of 14 landslide influencing factors show that the distance to the river has the smallest tolerance value of 0.715 (>0.1), and the largest VIF value is 1.399 (<10) (Table 2). Therefore, there is no multicollinearity among the 14 landslide influencing factors.

Table 2.
Multicollinearity analysis.
At the same time, this study also evaluated the importance of 14 landslide influencing factors using the 10-fold cross-validation correlation attribute evaluation method (CAE) in Weka software [101]. The evaluation results are sorted in descending order according to the average merit (Table 3). The results show that all factors have a positive effect on the landslide and can be further analyzed. The distance to rivers has the highest average merit among all influencing factors (AM = 0.378), followed by slope angle(AM = 0.213), lithology (AM = 0.181), distance to roads (AM = 0.173), and elevation (AM = 0.172), TWI (AM = 0.171), SPI (AM = 0.154), aspect (AM = 0.143), soil (AM = 0.143), profile curvature (AM = 0.138), NDVI (AM = 0.103), land use (AM = 0.098), plan curvature (0.042) and STI (0.04).

Table 3.
Selection of conditioning factors.
4.2. Application of Hybrid and Benchmark Model
RS integration can not only use random subspace to construct and aggregate the basic classifier, but also make the basic classifier easier to train than in the smaller subspaces. Therefore, the performance of the base classifier in the RS may be better than the original feature space, and the feature-to-instance ratio is significantly improved. The RSCART model is constructed by using Weka software [102] through optimization and classification steps. In the optimization step, RS is trained to obtain the sub-data set, which is randomly divided by the original data set. The training data set is divided by the iterative method. In the classification step, combined with the CART algorithm, the optimal training data set obtained in the previous step is used for spatial prediction of landslide [28]. In the process of RSCART model construction, the optimal number of iterations was 28, the optimal number of execution slots was 1. Finally, the landslide susceptibility map is developed by using the RSCART model and reclassified into five classes using the natural break method [103,104]. The very high class occupies a very small area of 9.27%. The moderate, very low, low, and high areas are accounting for 30.56%, 13.31%, 27.22% and 19.63%, respectively (Figure 4a and Figure 5).
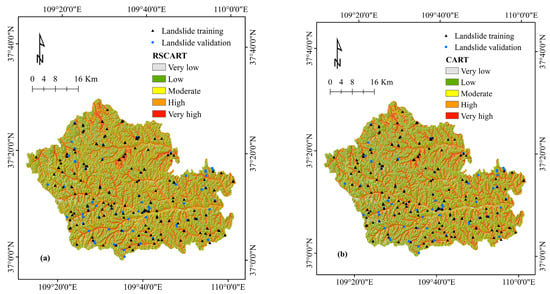
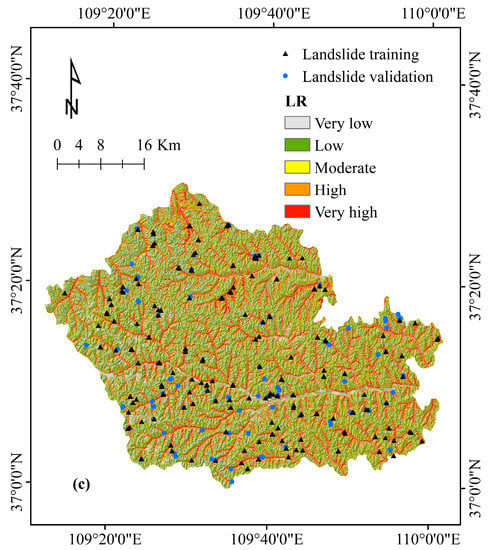
Figure 4.
Landslide susceptibility maps: (a) RSCART model; (b) CART model; (c) LR model.
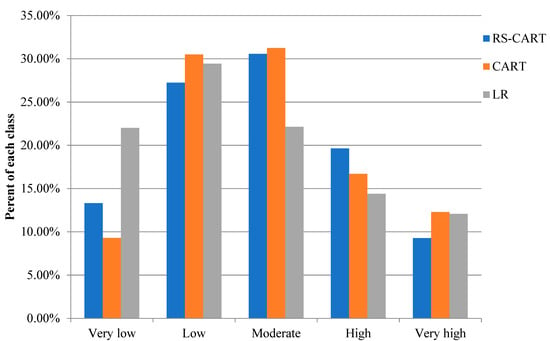
Figure 5.
Percentages of landslide susceptibility classes.
According to Equation (8), logistic regression coefficients of all landslide influencing factors are positive (Table 4), which indicate that all influencing factors are positively correlated with the landslide occurrence. Finally, the landslide susceptibility map was divided into five categories according to the natural break method. It can be seen that the area percentage with low susceptibility is the largest (29.42%), followed by moderate, very low and high (22.13%, 22%, and 14.38%, respectively). The area proportion of very high is the smallest (12.06%) (Figure 4c and Figure 5)

Table 4.
Coefficients of LR model.
4.3. Validation and Comparison of Models
The landslide susceptibility map should have the ability to verify with existing landslide data and predict future landslides [105]. Therefore, in this study, the ROC curve and the AUC are used to assess the prediction capability of models [106,107,108]. The best models tend to have the highest AUC among the models studied [4,109]. ROC curves and AUC values of the training dataset of the three models are shown in Figure 6. The RSCART model has the highest AUC value (0.852), followed by LR model (0.797) and CART model (0.793). The ROC curves and AUC values of the validation dataset are shown in Figure 7. The prediction accuracy of RSCART model (AUC = 0.827) is higher than that of the LR model (AUC = 0.758) and CART model (AUC = 0.749). Therefore, the comparison of AUC values indicates that the RSCART model is the best of the three models. In addition, the landslide susceptibility map can be verified by calculating the landslide density. LD is defined as the ratio of the percentage of landslide points in each susceptibility classification to the percentage in each susceptibility classification [110]. The landslide density calculation results of the three models are shown in Table 5. RSCART model, CART model, and LR model had the highest values in the very high category, which were 4.264, 3.156 and 3.845, respectively. Then, high (1.743, 2.004, 1.692), moderate (0.634, 0.670, 0825), low (0.223, 0.212, 0.310) and very low (0.057, 0.041, 0.086).
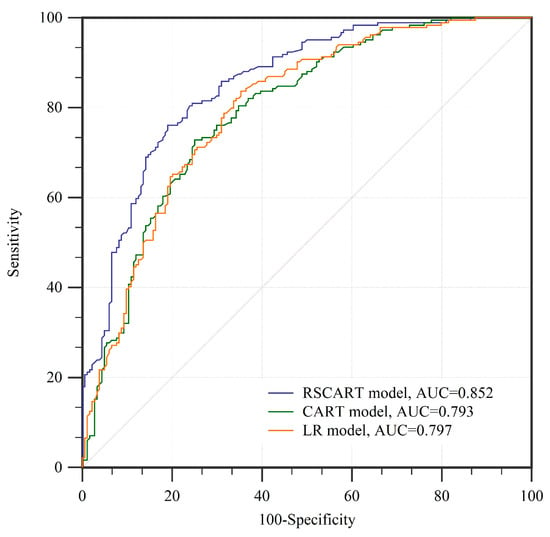
Figure 6.
ROC curves using training dataset.
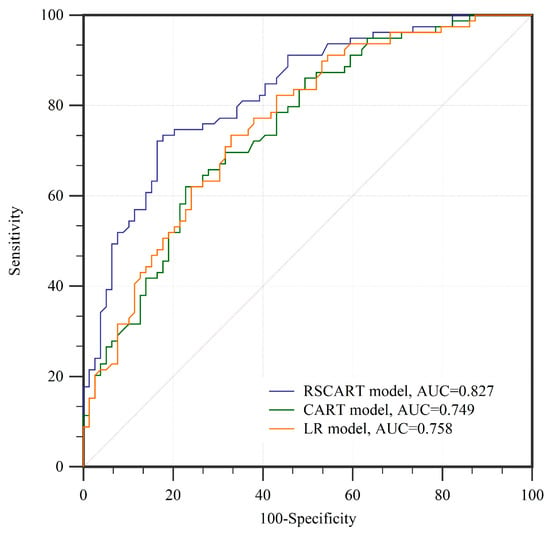
Figure 7.
ROC curves using validation dataset.

Table 5.
Landslide density analysis on landslide susceptibility maps.
4.4. Comparison of Landslide Susceptibility Maps
This study also quantitatively compares the susceptibility values on each pixel to reveal the systematic spatial pattern of the differences between susceptibility maps, following the methodology proposed by [111]. The RSCART model was selected as the benchmark because it has a higher AUC value than the other two models. The susceptibility map of the baseline model is used in a GIS system to pair with the remaining models and subtract their values to define their differences (Figure 8). The values of the comparison map are divided into three levels: “underestimation”, “approximation” and “overestimation”. The values of both comparison maps are broken at −0.2 and 0.2. The percentage of each grade in the total area is shown in Table 6. At the same time, to explore the key factors influencing the susceptibility difference, overestimation and underestimation statistics were performed for each category of each impact factor (Table 7 and Table 8). For each class, we calculate “A” as a percentage of the total area of each class. “B” is the ratio of the underestimated (overestimated) pixels found in this class to the total underestimated (overestimated) pixels, “B–A”, as the difference ratio between the two maps, can be used to identify key class of underestimation (overestimation) anomaly clustering. According to the “B–A” value defined for each class, the class with the highest degree of imbalance was identified (Table 8). To be able to clearly illustrate the relationship between the most imbalanced classification and the underestimated or overestimated area, the visual inspection is required. Underestimations of “RSCART-LR” driven by slope angle (40°–50°) (Figure 9a), overestimations of “RSCART-LR” driven by slope angle (<10°) (Figure 10a), Underestimations of “RSCART-CART” driven by distance to rivers (0–200 m) (Figure 9d) and overestimations of “RSCART-LR” driven by slope angle (<10°) (Figure 10d). As shown in Figure 9a, almost all the underestimated pixels are in the classification with slope of 40–50, and the percentage is 98.55%. In Figure 10a, 99.35% of the overestimation pixels are in the slope of 0°–10°. In Figure 9d, all underestimation pixels are clustered in a distance to rivers of 0–200 m. In Figure 10d, 76.87% of the overestimation pixels are in the classification with a slope less than 10°.
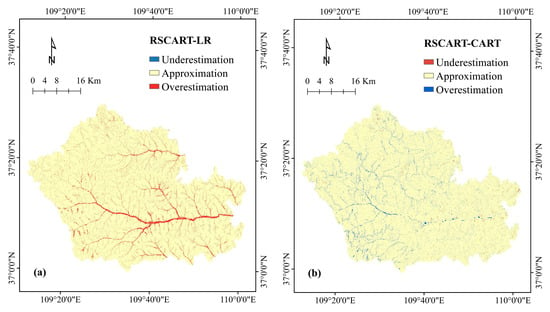
Figure 8.
Comparison maps: (a) RSCART-LR; (b) RSCART-CART.

Table 6.
Classification of comparison maps.

Table 7.
Statistics on underestimation pixels and overestimation pixels of RSCART-LR.

Table 8.
Statistics on underestimation pixels and overestimation pixels of RSCART-CART.
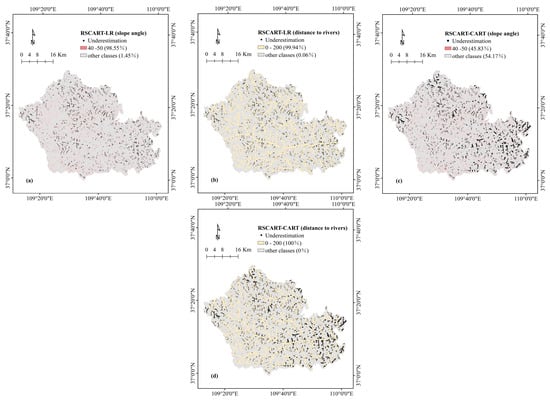
Figure 9.
Spatial location of underestimations, in relationship with the imbalanced classes.
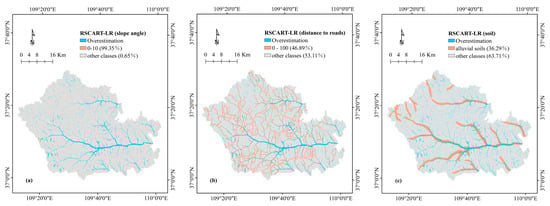
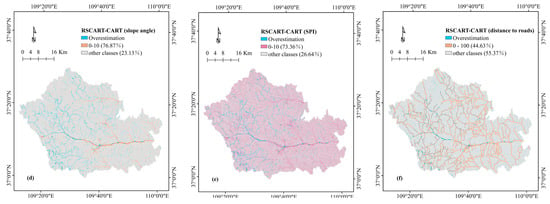
Figure 10.
Spatial location of overestimations, in relationship with the imbalanced classes.
5. Discussion
The selection of landslide influencing factors will affect the quality of landslide susceptibility analysis [112,113]. In this study, 14 landslide influencing factors were selected. The EBF model is used to analyze the correlation between the subclasses of landslide influencing factors and landslide, and to reclassify the landslide influence factors. Then, through the multicollinearity analysis, it was found that there was no multicollinearity among all landslide influencing factors (Table 2), and all factors contributed to the model. Finally, the results of the CAE model’s importance analysis and Bel values were used to analyze the various landslide influencing factors. According to the results of the importance analysis, the distance to rivers (AM = 0.378) is the most important landslide influencing factor in the study area. The results of the Bel value are similar to those found in previous studies, with a higher probability of landslides near the river area [114]. Different geomorphic parts of the river cause different external forces and stress distributions on the slope, so the failure modes of the slope are also different. The distance to roads (AM = 0.173, Bel = 0.313) has similar results. The closer we get to the road, the higher the probability of a landslide [115]. This is easy to understand because road construction can destabilize the slope by breaking the support of the slope foot [116]. As for the slope (AM = 0.213), the possibility of landslides will increase with the increase of the slope, because the gravity load and stress of the material forming the slope will increase [117]. It can be seen from the Bel value that landslides are most likely to occur in areas with a slope of 40–50. Different types of lithology (AM = 0.181) will result in different slope strengths [118]. According to the Bel value, it can be seen that shale, sandstone, mudstone, and conglomerate have a certain effect on the occurrence of landslides. Elevation (AM = 0.172) has always been a key factor in landslide susceptibility mapping [119,120]. The weathering and shear strength of rocks at different elevations are also different [119,120]. According to the Bel value, it can be concluded that the possibility of landslides of 1500 m–1574 m in the study area is higher. Therefore, it can be judged that landslides are more likely to occur in higher research areas. TWI (AM = 0.171) and SPI (AM = 0.154) are usually indispensable constraints in landslide susceptibility modeling [110,121,122]. Aspect (AM = 0.143, Bel = 0.181) in the south are more likely to cause landslides. This may be due to the more intense solar radiation when the slope is facing south, which may result in different weathering degree. Previous studies have shown that the susceptibility of different types of soil (AM = 0.143) to landslides is also different [101]. According to the Bel value, red clay is the key factor leading to landslides in the study area. The shear strength of red clay soils during rainwater infiltration is reduced, making slopes more prone to landslides [123]. Profile curvature (AM = 0.138) can affect the stress distribution of the slope, and the variations in curvature may be useful to identify depletion and accumulation zones [124]. NDVI (AM = 0.103) is an important influencing factor for landslides. Many studies have shown that plants play an active role in the occurrence of landslides because their root systems can increase soil strength and reduce water infiltration [125,126,127]. In addition, for those factors whose AM value is less than 1, many scholars have studied their relationship with the occurrence of landslides, and these factors should not be ignored when mapping landslide susceptibility [128,129,130].
From the results we can observe that the number of overestimation and underestimation is limited (the highest proportion is 0.057). However, it has a great influence on the value of AUC. This is because overestimation and underestimation are not randomly distributed, but there are some spatial patterns [111]. From Figure 2 we can see that the overestimations of the two comparisons have some similarities in spatial distribution. From Table 9 we can find that in the two comparisons, the overestimation has almost the same class of imbalance factors. Slopes less than 10 are classified as the most unbalanced class. From Figure 10, we can find that the classification with a slope of less than 10 has a high degree of overlap with the spatial distribution of the river. Areas with a slope of less than 10 are all closer to the river. For the “RSCART-LR” comparison map, Alluvial soils is also an unbalanced class. In Figure 10c, we can find that the spatial distribution of alluvial soil also overlaps with the river. This is because alluvial soil develops. The classification with the distance to the road less than 100 is also the overestimated imbalanced class of the two comparison maps (Figure 10b,f), and it has a high spatial overlap with the overestimated pixels. The class with a slope of 40–50 is the most unbalanced class in the “RSCART-LR” comparison, which contains 98.55% of the underestimated pixels (Figure 9a). At the same time, “RSCART-LR” was also significantly affected by the distance to the river less than 200 (“B-A” = 71.3%) (Figure 9b). In the comparison of “RSCART-CART”, the classification with the river distance less than 200 included all the underestimated pixels (Figure 9d) and was also driven by the slope classification of 40–50 (“B-A” = 41.42%). From Figure 9, we can see that the overlap of the spatial distribution of the underestimated pixels with a distance from the river less than 200 is extremely high. The remaining imbalance classes do not significantly dominate the underestimated spatial distribution. In summary, the integrated model RSCART can better use the landform information related to the river and the information closer to the road than the other two models. However, it is easy to ignore the influence of the river itself and the high slope on the susceptibility to landslides.

Table 9.
Most imbalanced classes driving the spatial distribution of underestimations and overestimation.
Some studies have proved that LR model is an excellent model for landslide susceptibility research. Polykretis and Chalkias shows that the performance of LR model is better than that of weight of evidence and artificial neural networks in landslide susceptibility mapping in drainage basin of Selinous River [131]. Oh et al. conclude that the LR model has the highest prediction and training accuracy compared with EBF and support vector machine (SVM) in the region surrounding Yongin, South Korea [132]. According to the results of Luc Yen district by Pham et al., the performance of CART model is better than that of LR model [28]. The results also show that the performance of CART model is lower than that of LR model. In addition, some studies have shown that RS is an excellent ensemble algorithm. Hong et al. indicate that the integrated model RSSVM has the optimal performance [55]. In this study, training (goodness of fit) and validation (prediction accuracy) data sets were used to compare the proposed integration model with the benchmark model. The goodness of fit results of the landslide model show that RSCART (AUC = 0.852) is superior to CART (AUC = 0.793) and LR (AUC = 0.797). The validation results show that RSCART model has better prediction accuracy than CART (AUC = 0.749) and LR (AUC = 0.758) models. The RSCART model has the advantages of RS integration and CART classifier. When integrated with the RS model, the performance of the CART model, whose performance is lower than the benchmark LR model, is improved significantly. This is because RS integration constructs the benchmark model by using the random subspace, and the performance of the base classifier in the random subspace is optimized. Therefore, the RSCART model based on machine learning hybrid method is more effective than the single basic model. In addition, the landslide susceptibility figure can be verified by calculating the landslide density (Table 5). In general, higher LD values are associated with higher landslide susceptibility levels. As can be seen from the result of LD, the results of the three models are consistent. The LD value of the very high type is the highest, followed by high, moderate, low, and very low. Therefore, the three base maps of landslide susceptibility are reliable, and the optimal model RSCART also has the highest LD value. Therefore, the model used in this study to generate the landslide susceptibility map has reference significance for the study area. In addition, the selection of factors and the construction of models are also of reference values for similar studies.
6. Conclusions
In this study, the combined CART with RS and two benchmark models (LR and CART) were used to draw three landslide susceptibility maps for Zichang County. The correlation between influencing factors and landslide was evaluated using multicollinearity analysis and EBF method. The AUC value was used to test the performance of the three models. The validating results show that the RSCART model has the highest performance, followed by the LR model and CART model. Finally, this paper also uses a method to quantitatively compare the susceptibility values of each pixel to reveal the systematic spatial pattern of the differences between susceptibility maps. In conclusion, the landslide susceptibility maps compiled in this study are useful for land use and decision-making in landslide-prone areas. In addition, this study also proves the superiority of hybrid model in landslide susceptibility modeling.
Author Contributions
Y.L. and W.C. contributed equally to the work. Y.L. and W.C. collected field data and conducted the landslide susceptibility mapping and analysis. Y.L. and W.C. wrote and revised the manuscript. All the authors discussed the results and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No. 41807192), Natural Science Basic Research Program of Shaanxi (Program No. 2019JLM-7, ProgramNo. 2019JQ-094), China Postdoctoral Science Foundation (Grant No. 2018T111084, 2017M613168), and Project funded by Shaanxi Province Postdoctoral Science Foundation (Grant No. 2017BSHYDZZ07).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cruden, D.M. A simple definition of a landslide. Bull. Eng. Geol. Environ. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Centre for Research on Epidemiology of Disasters, Université catholique de. The Human Cost of Natural Disasters 2015: A Global Perspective; Centre for Research on Epidemiology of Disasters, Université catholique de: Brussels, Belgium, 2015. [Google Scholar]
- Van Westen, C.; Van Asch, T.W.; Soeters, R. Landslide hazard and risk zonation—why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the gis-based data mining techniques of best-first decision tree, random forest, and naïve bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Canli, E.; Mergili, M.; Thiebes, B.; Glade, T. Probabilistic landslide ensemble prediction systems: Lessons to be learned from hydrology. Nat. Hazards Earth Syst. Sci. 2018, 18, 2183–2202. [Google Scholar] [CrossRef]
- Cervi, F.; Berti, M.; Borgatti, L.; Ronchetti, F.; Manenti, F.; Corsini, A. Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: A case study in the northern apennines (reggio emilia province, italy). Landslides 2010, 7, 433–444. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, Ø.B. Regional prediction of landslide hazard using probability analysis of intense rainfall in the hoa binh province, vietnam. Nat. Hazards 2013, 66, 707–730. [Google Scholar]
- Pradhan, B.; Abokharima, M.H.; Jebur, M.N.; Tehrany, M.S. Land subsidence susceptibility mapping at kinta valley (malaysia) using the evidential belief function model in gis. Nat. Hazards 2014, 73, 1019–1042. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- Hong, H.; Naghibi, S.A.; Dashtpagerdi, M.M.; Pourghasemi, H.R.; Chen, W. A comparative assessment between linear and quadratic discriminant analyses (lda-qda) with frequency ratio and weights-of-evidence models for forest fire susceptibility mapping in china. Arab. J. Geosci. 2017, 10, 167. [Google Scholar] [CrossRef]
- Wang, L.-J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J.; Woo, I. The effect of spatial resolution on the accuracy of landslide susceptibility mapping: A case study in boun, korea. Geosci. J. 2004, 8, 51. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Probabilistic landslide hazards and risk mapping on penang island, malaysia. J. Earth Syst. Sci. 2006, 115, 661–672. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. Gis-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping. Environ. Geol. 2008, 54, 311–324. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Rajamanickam, V.; Kumaravel, P.; Saranathan, E. Landslide susceptibility analysis using probabilistic likelihood ratio model—a geospatial-based study. Arab. J. Geosci. 2013, 6, 429–440. [Google Scholar] [CrossRef]
- Chen, W.; Fan, L.; Li, C.; Pham, B.T. Spatial prediction of landslides using hybrid integration of artificial intelligence algorithms with frequency ratio and index of entropy in nanzheng county, china. Appl. Sci. 2020, 10, 29. [Google Scholar] [CrossRef]
- Lee, S.; Song, K.-Y.; Oh, H.-J.; Choi, J. Detection of landslides using web-based aerial photographs and landslide susceptibility mapping using geospatial analysis. Int. J. Remote Sens. 2012, 33, 4937–4966. [Google Scholar] [CrossRef]
- Demir, G.; Aytekin, M.; Akgün, A.; Ikizler, S.B.; Tatar, O. A comparison of landslide susceptibility mapping of the eastern part of the north anatolian fault zone (turkey) by likelihood-frequency ratio and analytic hierarchy process methods. Nat. Hazards 2013, 65, 1481–1506. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in gis and their comparison at mugling–narayanghat road section in nepal himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Ozdemir, A.; Altural, T. A comparative study of frequency ratio, weights of evidence and logistic regression methods for landslide susceptibility mapping: Sultan mountains, sw turkey. J. Asian Earth Sci. 2013, 64, 180–197. [Google Scholar] [CrossRef]
- Bui, D.T.; Hoang, N.-D.; Samui, P. Spatial pattern analysis and prediction of forest fire using new machine learning approach of multivariate adaptive regression splines and differential flower pollination optimization: A case study at lao cai province (viet nam). J. Environ. Manag. 2019, 237, 476–487. [Google Scholar]
- Chu, L.; Wang, L.-J.; Jiang, J.; Liu, X.; Sawada, K.; Zhang, J. Comparison of landslide susceptibility maps using random forest and multivariate adaptive regression spline models in combination with catchment map units. Geosci. J. 2019, 23, 341–355. [Google Scholar] [CrossRef]
- Conoscenti, C.; Agnesi, V.; Cama, M.; Caraballo-Arias, N.A.; Rotigliano, E. Assessment of gully erosion susceptibility using multivariate adaptive regression splines and accounting for terrain connectivity. Land Degrad. Dev. 2018, 29, 724–736. [Google Scholar] [CrossRef]
- Shafapour Tehrany, M.; Kumar, L.; Neamah Jebur, M.; Shabani, F. Evaluating the application of the statistical index method in flood susceptibility mapping and its comparison with frequency ratio and logistic regression methods. Geomat. Nat. Hazards Risk 2019, 10, 79–101. [Google Scholar] [CrossRef]
- Nicu, I.C. Application of analytic hierarchy process, frequency ratio, and statistical index to landslide susceptibility: An approach to endangered cultural heritage. Environ. Earth Sci. 2018, 77, 79. [Google Scholar] [CrossRef]
- Tien Bui, D.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. Gis-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with adaboost, bagging, and multiboost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1–22. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on random subspace and classification and regression trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Tien Bui, D.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of gis-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (anfis) with genetic algorithm (ga), differential evolution (de), and particle swarm optimization (pso) for landslide spatial modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Loupasakis, C.; Nikolakopoulos, K.; Angelitsa, V.; Ilia, I. Developing a landslide susceptibility map based on remote sensing, fuzzy logic and expert knowledge of the island of lefkada, greece. Environ. Earth Sci. 2018, 77, 363. [Google Scholar] [CrossRef]
- Sahana, M.; Sajjad, H. Evaluating effectiveness of frequency ratio, fuzzy logic and logistic regression models in assessing landslide susceptibility: A case from rudraprayag district, india. J. Mt. Sci. 2017, 14, 2150–2167. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. Gis-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, naïve-bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the yihuang area (china) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (china) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Zhang, T.-Y.; Han, L.; Zhang, H.; Zhao, Y.-H.; Li, X.-A.; Zhao, L. Gis-based landslide susceptibility mapping using hybrid integration approaches of fractal dimension with index of entropy and support vector machine. J. Mt. Sci. 2019, 16, 1275–1288. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of gis-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of ambon, indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Ngadisih; Bhandary, N.P.; Yatabe, R.; Dahal, R.K. Logistic Regression and Artificial Neural Network Models for Mapping of Regional-Scale Landslide Susceptibility in Volcanic Mountains of West Java (Indonesia). AIP Conf. Proc. 2016. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.X. Gis-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Tofani, V.; Segoni, S.; Catani, F.; Casagli, N. A tool for classification and regression using random forest methodology: Applications to landslide susceptibility mapping and soil thickness modeling. Environ. Model. Assess. 2017, 22, 201–214. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. Prioritization of landslide conditioning factors and its spatial modeling in shangnan county, china using gis-based data mining algorithms. Bull. Eng. Geol. Environ. 2018, 77, 611–629. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Tran, H.T.; Le, T.M.; Van Phong, T.; Khoi, D.K.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modelling using rotation forest ensemble and different base classifiers. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, china. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Pradhan, B.; Panahi, M. Landslide susceptibility assessment using a novel hybrid model of statistical bivariate methods (fr and woe) and adaptive neuro-fuzzy inference system (anfis) at southern zagros mountains in iran. Environ. Earth Sci. 2017, 76, 237. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using reduced error pruning trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the multiboost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning. Eng. Geol. 2008, 102, 99–111. [Google Scholar] [CrossRef]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, turkey. Landslides 2012, 9, 93–106. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at wadi tayyah basin, asir region, saudi arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the wuning area (china). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Mandal, S.; Mandal, K. Bivariate statistical index for landslide susceptibility mapping in the rorachu river basin of eastern sikkim himalaya, india. Spat. Inf. Res. 2018, 26, 59–75. [Google Scholar] [CrossRef]
- Pradhan, A.; Kim, Y. Evaluation of a combined spatial multi-criteria evaluation model and deterministic model for landslide susceptibility mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Varnes, D.J. Slope movement types and processes. In: Schuster RL, Krizek RJ (eds) Landslides, analysis and control, Transportation research board, National Academy of Sciences, Washington, DC. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y.; et al. Landslide spatial modelling using novel bivariate statistical based naïve bayes, rbf classifier, and rbf network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive bayes and rbfnetwork models for the long county area (china). Bull. Eng. Geol. Environ. 2019, 78, 247–266. [Google Scholar] [CrossRef]
- Yalcin, A. Gis-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in ardesen (turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Duman, T.Y.; Durmaz, S. Landslide susceptibility mapping for a part of tectonic kelkit valley (eastern black sea region of turkey). Geomorphology 2008, 94, 401–418. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using gis. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Galli, M.; Ardizzone, F.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Comparing landslide inventory maps. Geomorphology 2008, 94, 268–289. [Google Scholar] [CrossRef]
- Yalcin, A.; Bulut, F. Landslide susceptibility mapping using gis and digital photogrammetric techniques: A case study from ardesen (ne-turkey). Nat. Hazards 2007, 41, 201–226. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.; Rezaeian, J.; Sattarian, A. Gis-based frequency ratio and index of entropy models for landslide susceptibility assessment in the caspian forest, northern iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Physical basis of the length-slope factor in the universal soil loss equation 1. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Yilmaz, C.; Topal, T.; Süzen, M.L. Gis-based landslide susceptibility mapping using bivariate statistical analysis in devrek (zonguldak-turkey). Environ. Earth Sci. 2012, 65, 2161–2178. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (ahp) to landslide susceptibility mapping at haraz watershed, iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Nourani, V.; Pradhan, B.; Ghaffari, H.; Sharifi, S.S. Landslide susceptibility mapping at zonouz plain, iran using genetic programming and comparison with frequency ratio, logistic regression, and artificial neural network models. Nat. Hazards 2014, 71, 523–547. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, J.; Qi, X.; Ding, J. Landslides induced by the wenchuan earthquake and the subsequent strong rainfall event: A case study in the beichuan area of china. Eng. Geol. 2011, 122, 22–33. [Google Scholar] [CrossRef]
- Korup, O.; Clague, J.J.; Hermanns, R.L.; Hewitt, K.; Strom, A.L.; Weidinger, J.T. Giant landslides, topography, and erosion. Earth Planet. Sci. Lett. 2007, 261, 578–589. [Google Scholar] [CrossRef]
- Guo, C.; Qin, Y.; Ma, D.; Xia, Y.; Chen, Y.; Si, Q.; Lu, L. Ionic composition, geological signature and environmental impacts of coalbed methane produced water in china. Energy Sources Part A Recovery Util. Environ. Effects 2019. [Google Scholar] [CrossRef]
- Sharma, L.; Patel, N.; Debnath, P.; Ghose, M. Assessing landslide vulnerability from soil characteristics—a gis-based analysis. Arab. J. Geosci. 2012, 5, 789–796. [Google Scholar] [CrossRef]
- Hall, F.G.; Townshend, J.R.; Engman, E.T. Status of remote sensing algorithms for estimation of land surface state parameters. Remote Sens. Environ. 1995, 51, 138–156. [Google Scholar] [CrossRef]
- Restrepo, C.; Vitousek, P.; Neville, P. Landslides significantly alter land cover and the distribution of biomass: An example from the ninole ridges of hawai’i. Plant Ecol. 2003, 166, 131–143. [Google Scholar] [CrossRef]
- Shafer, G. A mathematical theory of evidence. Technometrics 1976, 20, 242. [Google Scholar]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- Lee, T.-S.; Chiu, C.-C.; Chou, Y.-C.; Lu, C.-J. Mining the customer credit using classification and regression tree and multivariate adaptive regression splines. Comput. Stat. Data Anal. 2006, 50, 1113–1130. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Subarkah, P.; Ikhsan, A.N.; Setyanto, A. In The effect of the number of attributes on the selection of study program using classification and regression trees algorithms. In Proceedings of the 3rd International Conference on Information Technology, Information System and Electrical Engineering (ICITISEE 2018), Yogyokarata, Indonesia, 15–22 October 2018; pp. 1–5. [Google Scholar]
- Pham, B.T.; Bui, D.T.; Prakash, I. Application of Classification and Regression Trees for Spatial Prediction of Rainfall-Induced Shallow Landslides in the Uttarakhand Area (India) Using Gis. In Climate Change, Extreme Events and Disaster Risk Reduction; Springer: Cham, Switzerland, 2018; pp. 159–170. [Google Scholar]
- Timofeev, R. Classification and Regression Trees (Cart) Theory and Applications; Humboldt University: Berlin, Germany, 2004. [Google Scholar]
- Barandiaran, I. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1–22. [Google Scholar]
- Kotsiantis, S. Combining bagging, boosting, rotation forest and random subspace methods. Artif. Intell. Rev. 2011, 35, 223–240. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Plumpton, C.O. In Choosing parameters for random subspace ensembles for fmri classification. In Proceedings of the International Workshop on Multiple Classifier Systems, Cairo, Egypt, 7–9 April 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 54–63. [Google Scholar]
- Mielniczuk, J.; Teisseyre, P. Using random subspace method for prediction and variable importance assessment in linear regression. Comput. Stat. Data Anal. 2014, 71, 725–742. [Google Scholar] [CrossRef]
- Bertoni, A.; Folgieri, R.; Valentini, G. Bio-molecular cancer prediction with random subspace ensembles of support vector machines. Neurocomputing 2005, 63, 535–539. [Google Scholar] [CrossRef]
- Skurichina, M.; Duin, R.P. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B.B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]
- Chandra, S.; Maheshkar, S. Verification of static signature pattern based on random subspace, rep tree and bagging. Multimed. Tools Appl. 2017, 76, 19139–19171. [Google Scholar] [CrossRef]
- Xia, J.; Dalla Mura, M.; Chanussot, J.; Du, P.; He, X. Random subspace ensembles for hyperspectral image classification with extended morphological attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4768–4786. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of gis-based logistic regression for landslide susceptibility mapping in the kakuda-yahiko mountains, central japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Shahabi, H.; Shirzadi, A.; Khosravi, K.; Chai, H.; Zhang, S.; Zhang, L.; Ma, J.; Chen, Y.; et al. Spatial prediction of landslide susceptibility by combining evidential belief function, logistic regression and logistic model tree. Geocarto Int. 2019, 34, 1177–1201. [Google Scholar] [CrossRef]
- Bui, D.T.; Lofman, O.; Revhaug, I.; Dick, O. Landslide susceptibility analysis in the hoa binh province of vietnam using statistical index and logistic regression. Nat. Hazards 2011, 59, 1413. [Google Scholar] [CrossRef]
- O’Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Chen, W.; Tsangaratos, P.; Ilia, I.; Duan, Z.; Chen, X. Groundwater spring potential mapping using population-based evolutionary algorithms and data mining methods. Sci. Total Environ. 2019, 684, 31–49. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Frank, E.; Hall, A.M.; Witten, H.I. The Weka Workbench. Online Appendix for "Data Mining: Practical Machine Learning Tools and Techniques", 4th ed.; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Chen, W.; Pradhan, B.; Li, S.; Shahabi, H.; Rizeei, H.M.; Hou, E.; Wang, S. Novel hybrid integration approach of bagging-based fisher’s linear discriminant function for groundwater potential analysis. Nat. Resour. Res. 2019, 28, 1239–1258. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C.; et al. Gis-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide susceptibility modeling based on gis and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S.; et al. Spat. Predict. Landslide Susceptibility Using Gis-Based Data Min. Tech. Anfis Whale Optim. Algorithm (Woa) Grey Wolf Optim. (Gwo). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Khosravi, K.; Pourghasemi, H.R.; Rezaie, F.; Parvinnezhad, D. Spatial prediction of groundwater potentiality using anfis ensembled with teaching-learning-based and biogeography-based optimization. J. Hydrol. 2019, 572, 435–448. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Gis-based evaluation of landslide susceptibility models using certainty factors and functional trees-based ensemble techniques. Appl. Sci. 2020, 10, 16. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling flood susceptibility using data-driven approaches of naïve bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M. Rotation forest fuzzy rule-based classifier ensemble for spatial prediction of landslides using gis. Nat. Hazards 2016, 83, 97–127. [Google Scholar] [CrossRef]
- Xiao, T.; Segoni, S.; Chen, L.; Yin, K.; Casagli, N. A step beyond landslide susceptibility maps: A simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 2019, 1–14. [Google Scholar] [CrossRef]
- Irigaray, C.; Fernández, T.; El Hamdouni, R.; Chacón, J. Evaluation and validation of landslide-susceptibility maps obtained by a gis matrix method: Examples from the betic cordillera (southern spain). Nat. Hazards 2007, 41, 61–79. [Google Scholar] [CrossRef]
- Romer, C.; Ferentinou, M. Shallow landslide susceptibility assessment in a semiarid environment—A quaternary catchment of kwazulu-natal, south africa. Eng. Geol. 2016, 201, 29–44. [Google Scholar] [CrossRef]
- Pandey, V.K.; Sharma, M.C. Probabilistic landslide susceptibility mapping along tipri to ghuttu highway corridor, garhwal himalaya (india). Remote Sens. Appl. Soc. Environ. 2017, 8, 1–11. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from longju in the three gorges reservoir area, china. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (wi) and adaptive neuro-fuzzy inference system (anfis) model at alborz mountains (iran). Environ. Earth Sci. 2016, 75, 553. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (swara) technique and adaptive neuro-fuzzy inference system (anfis) for regional landslide hazard assessment in iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Gassner, C.; Petschko, H.; Bell, R.; Glade, T. In Effect of lithological data of different scales on modelling landslide susceptibility maps. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 11262. [Google Scholar]
- Wu, Y.; Li, W.; Liu, P.; Bai, H.; Wang, Q.; He, J.; Liu, Y.; Sun, S. Application of analytic hierarchy process model for landslide susceptibility mapping in the gangu county, gansu province, china. Environ. Earth Sci. 2016, 75, 422. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Chen, W.; Xu, C. In Comparing the performance of a logistic regression and a random forest model in landslide susceptibility assessments. The case of Wuyaun Area, China. In Proceedings of the Workshop on World Landslide Forum; Ljubljana, Slovenia, 29 May–2 June 2017, Springer: Cham, Switzerland, 2017; pp. 1043–1050. [Google Scholar]
- Hue, T.; Duong, T.; Toan, D.; Nghinh, L.; Minh, V.; Pho, N.; Xuan, P.; Hoan, L.; Huyen, N.; Pha, P. Investigation and Assessment of the Types of Geological Hazard in the Territory of Vietnam and Recommendation of Remedial Measures. Phase II: A Study of the Northern Mountainous Province; Vietnam Academy of Science and Technology, Institute of Geological Sciences: Hanoi, Vietnam, 2004. [Google Scholar]
- Conforti, M.; Pascale, S.; Pepe, M.; Sdao, F.; Sole, A. Denudation processes and landforms map of the camastra river catchment (basilicata–south italy). J. Maps 2013, 9, 444–455. [Google Scholar] [CrossRef]
- Chen, Y.; Li, B.; Xu, Y.; Zhao, Y.; Xu, J. Field study on the soil water characteristics of shallow layers on red clay slopes and its application in stability analysis. Arab. J. Sci. Eng. 2019, 44, 5107–5116. [Google Scholar] [CrossRef]
- Pascale, S.; Parisi, S.; Mancini, A.; Schiattarella, M.; Conforti, M.; Sole, A.; Murgante, B.; Sdao, F. In Landslide susceptibility mapping using artificial neural network in the urban area of senise and san costantino albanese (basilicata, southern italy). In Proceedings of the International Conference on Computational Science and Its Applications, Ho Chi Minh City, Vietnam, 24–27 June 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 473–488. [Google Scholar]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Plant-soil reinforcement response under different soil hydrological regimes. Geoderma 2017, 285, 141–150. [Google Scholar] [CrossRef]
- Ordak, M.; Wesolowski, M.; Radecka, I.; Muszynska, E.; Bujalska-Zazdrozny, M. Seasonal variations of mercury levels in selected medicinal plants originating from poland. Biol. Trace Elem. Res. 2016, 173, 514–524. [Google Scholar] [CrossRef]
- Zhang, C.-B.; Chen, L.-H.; Jiang, J. Why fine tree roots are stronger than thicker roots: The role of cellulose and lignin in relation to slope stability. Geomorphology 2014, 206, 196–202. [Google Scholar] [CrossRef]
- He, Q.; Xu, Z.; Li, S.; Li, R.; Zhang, S.; Wang, N.; Pham, B.T.; Chen, W. Novel entropy and rotation forest-based credal decision tree classifier for landslide susceptibility modeling. Entropy 2019, 21, 106. [Google Scholar] [CrossRef]
- Yilmaz, I. A case study from koyulhisar (sivas-turkey) for landslide susceptibility mapping by artificial neural networks. Bull. Eng. Geol. Environ. 2009, 68, 297–306. [Google Scholar] [CrossRef]
- Truong, X.; Mitamura, M.; Kono, Y.; Raghavan, V.; Yonezawa, G.; Do, T.; Tien Bui, D.; Lee, S. Enhancing prediction performance of landslide susceptibility model using hybrid machine learning approach of bagging ensemble and logistic model tree. Appl. Sci. 2018, 8, 1046. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C. Comparison and evaluation of landslide susceptibility maps obtained from weight of evidence, logistic regression, and artificial neural network models. Nat. Hazards 2018, 93, 249–274. [Google Scholar] [CrossRef]
- Oh, H.-J.; Kadavi, P.R.; Lee, C.-W.; Lee, S. Evaluation of landslide susceptibility mapping by evidential belief function, logistic regression and support vector machine models. Geomat. Nat. Hazards Risk 2018, 9, 1053–1070. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).