Landslide Susceptibility Evaluation Using Hybrid Integration of Evidential Belief Function and Machine Learning Techniques
Abstract
1. Introduction
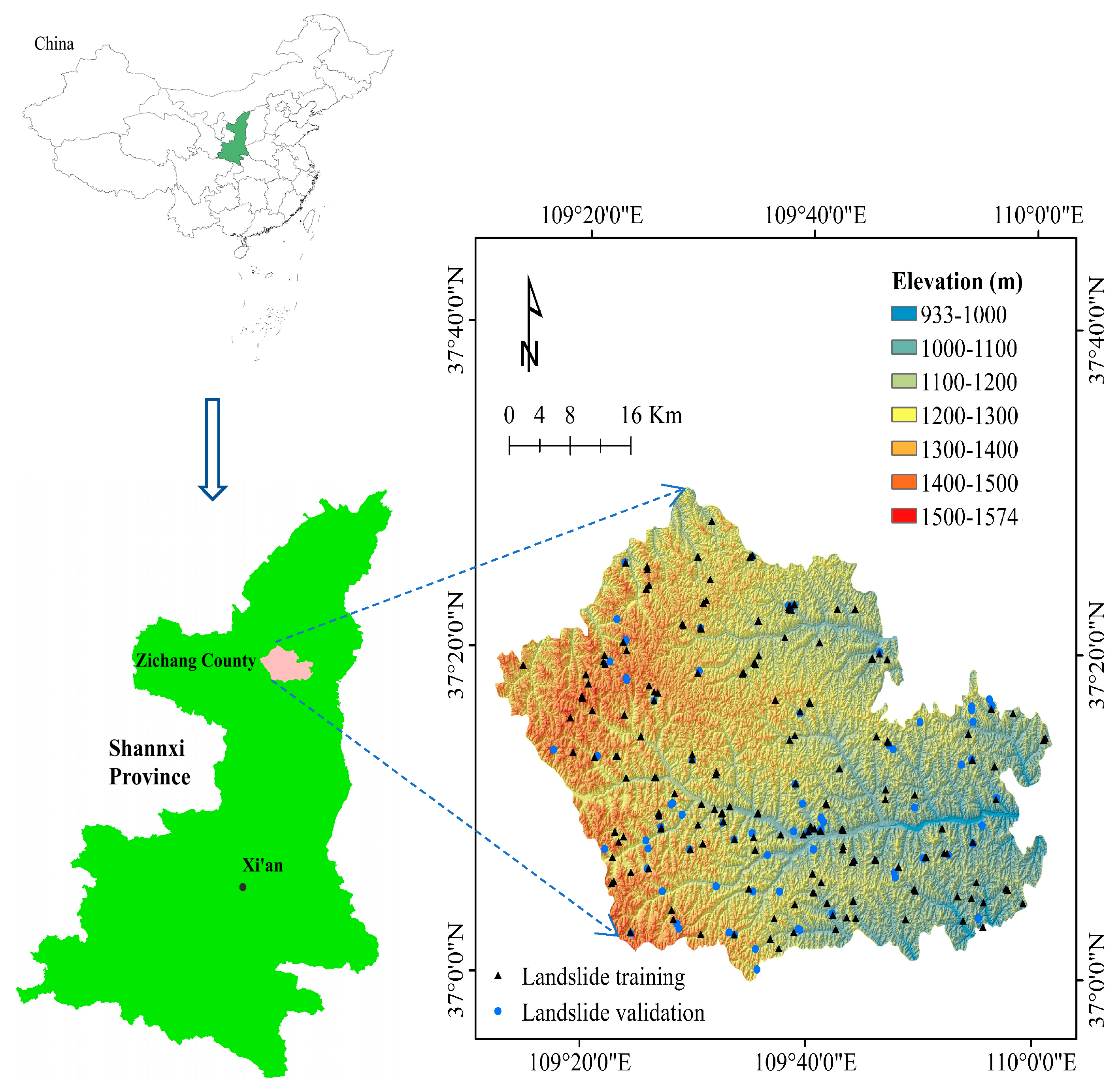
2. Description of the Study Area
3. Methodology
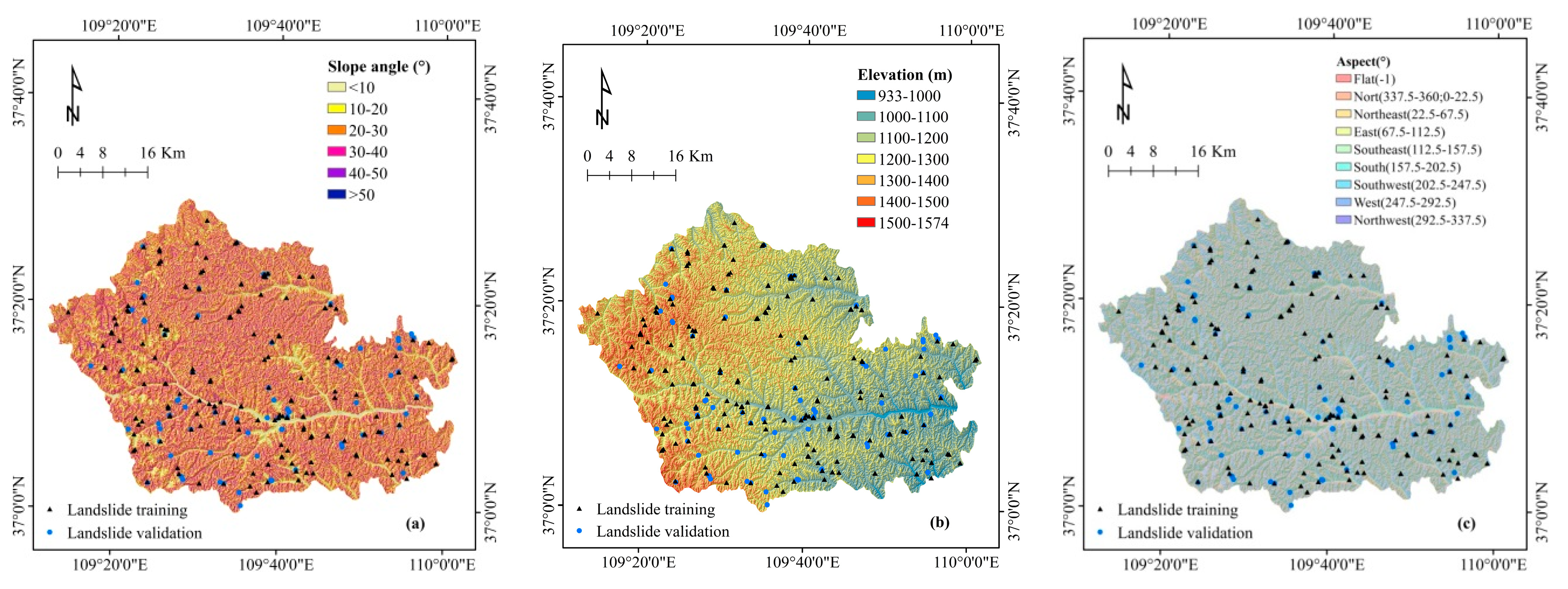
3.1. Data Preparation
3.2. Evidential Belief Function (EBF)
3.3. Classification and Regression Tree (CART)
3.4. Random Subspace (RS)
3.5. Logistic Regression (LR)
4. Results
4.1. Correlation Analysis of Influencing Factors
4.2. Application of Hybrid and Benchmark Model
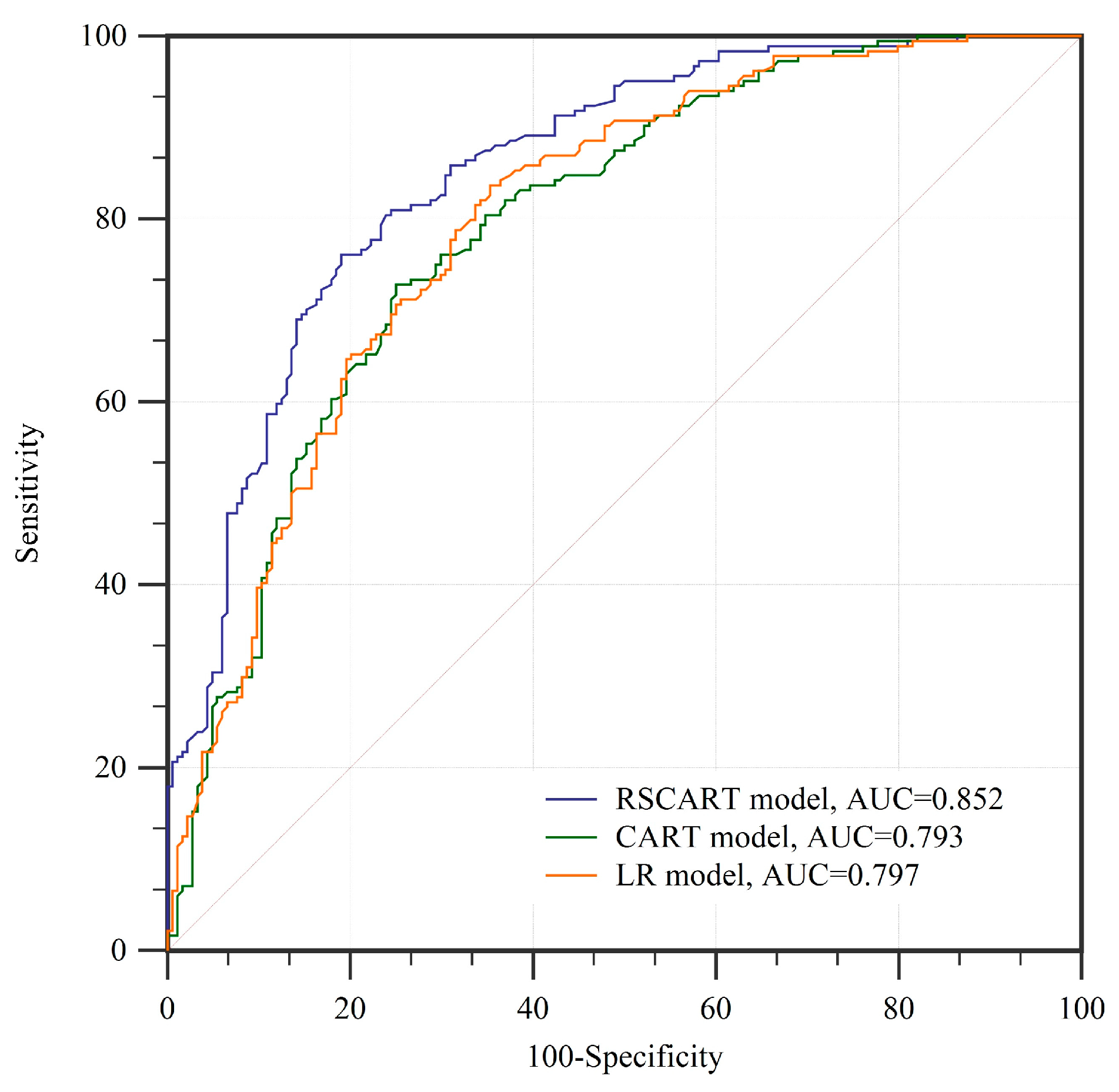
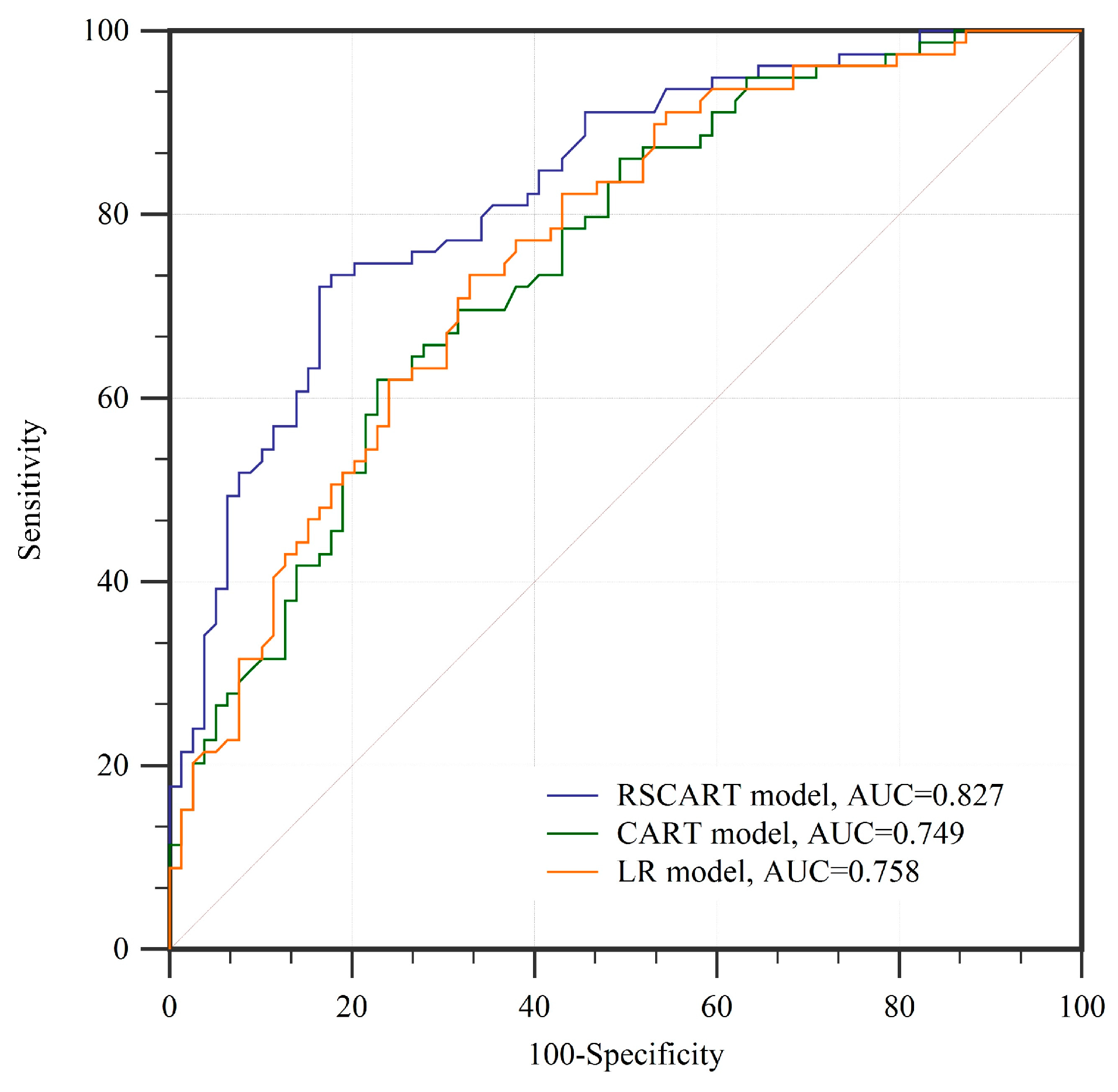
4.3. Validation and Comparison of Models
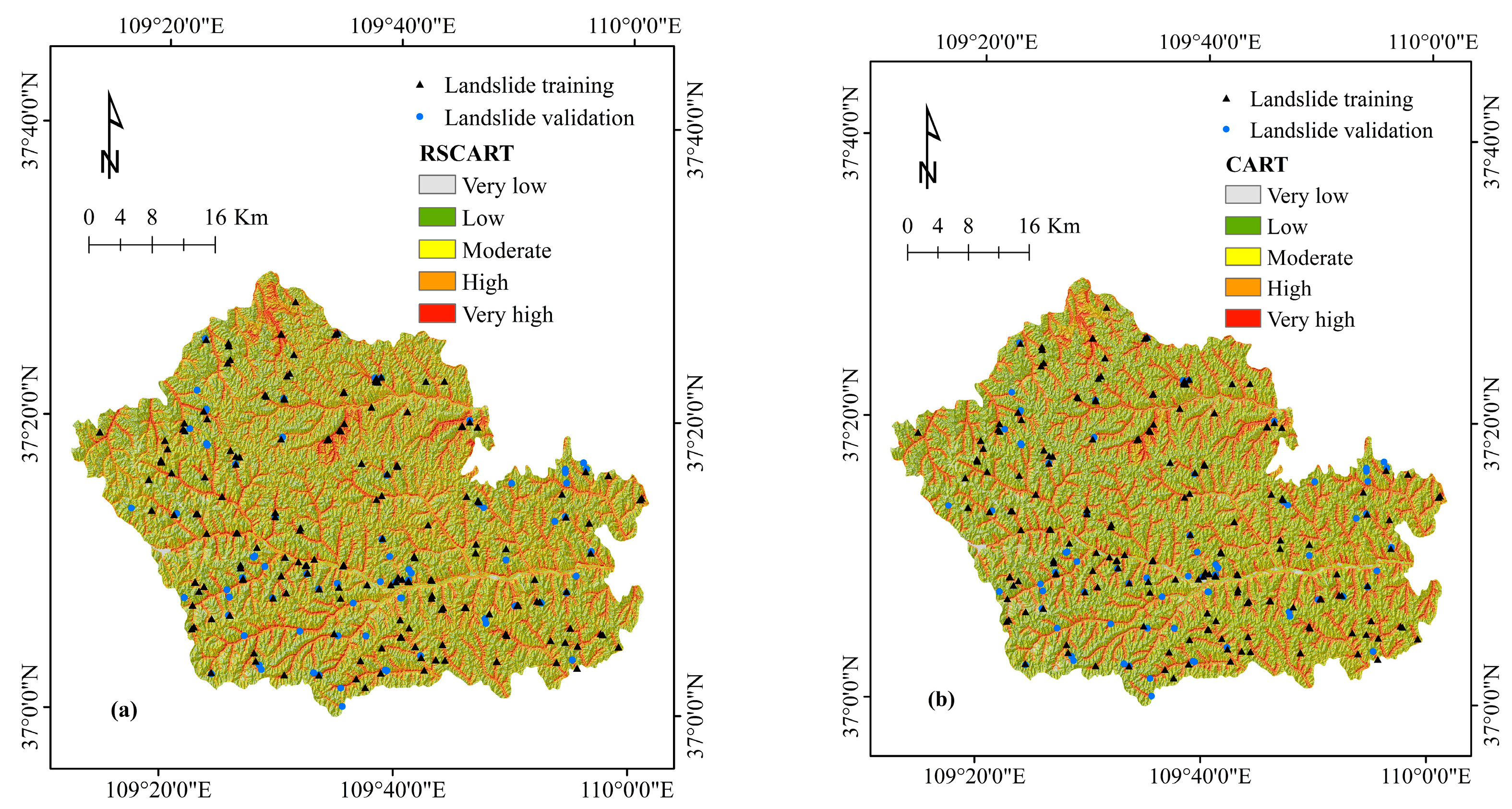
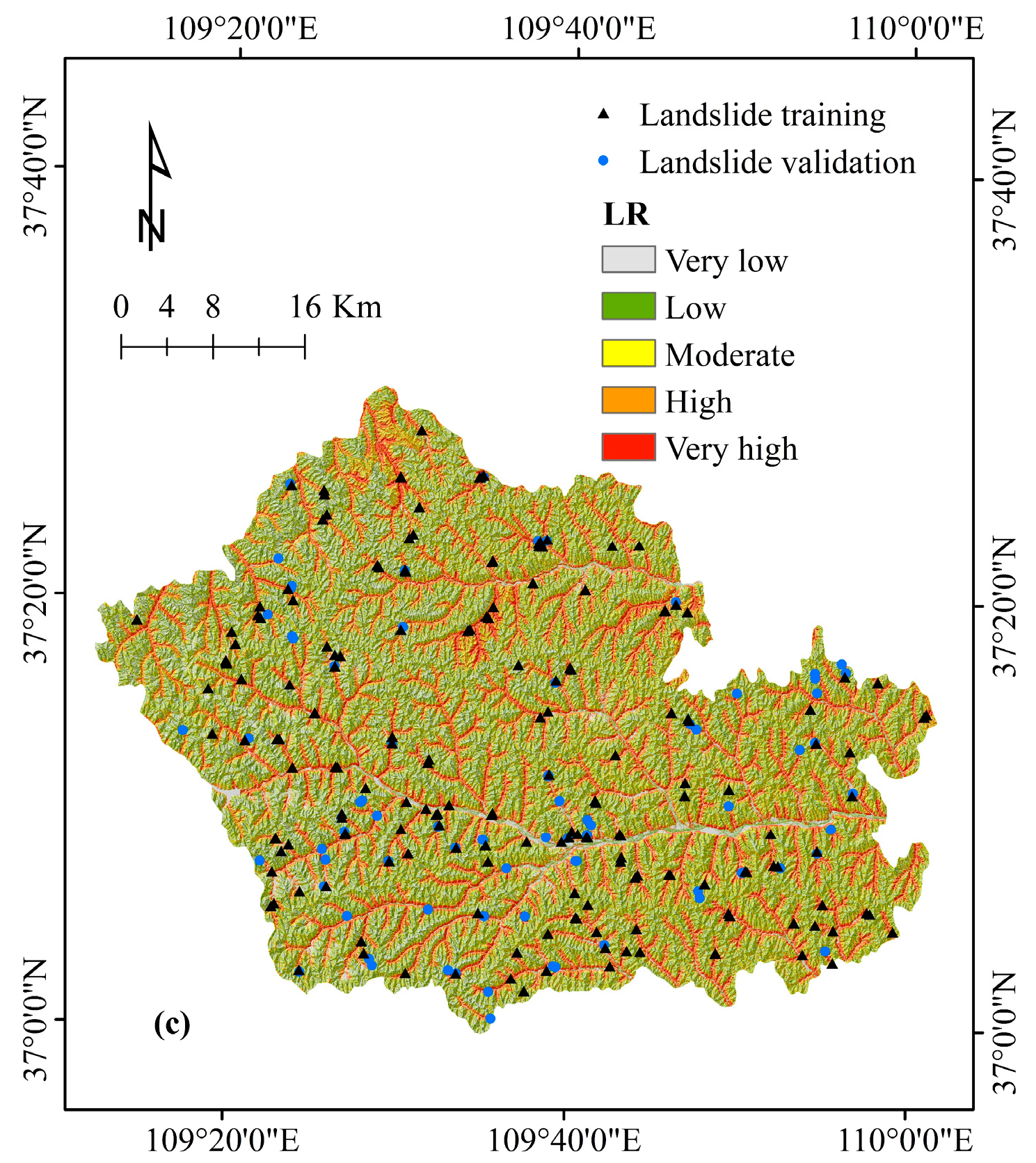
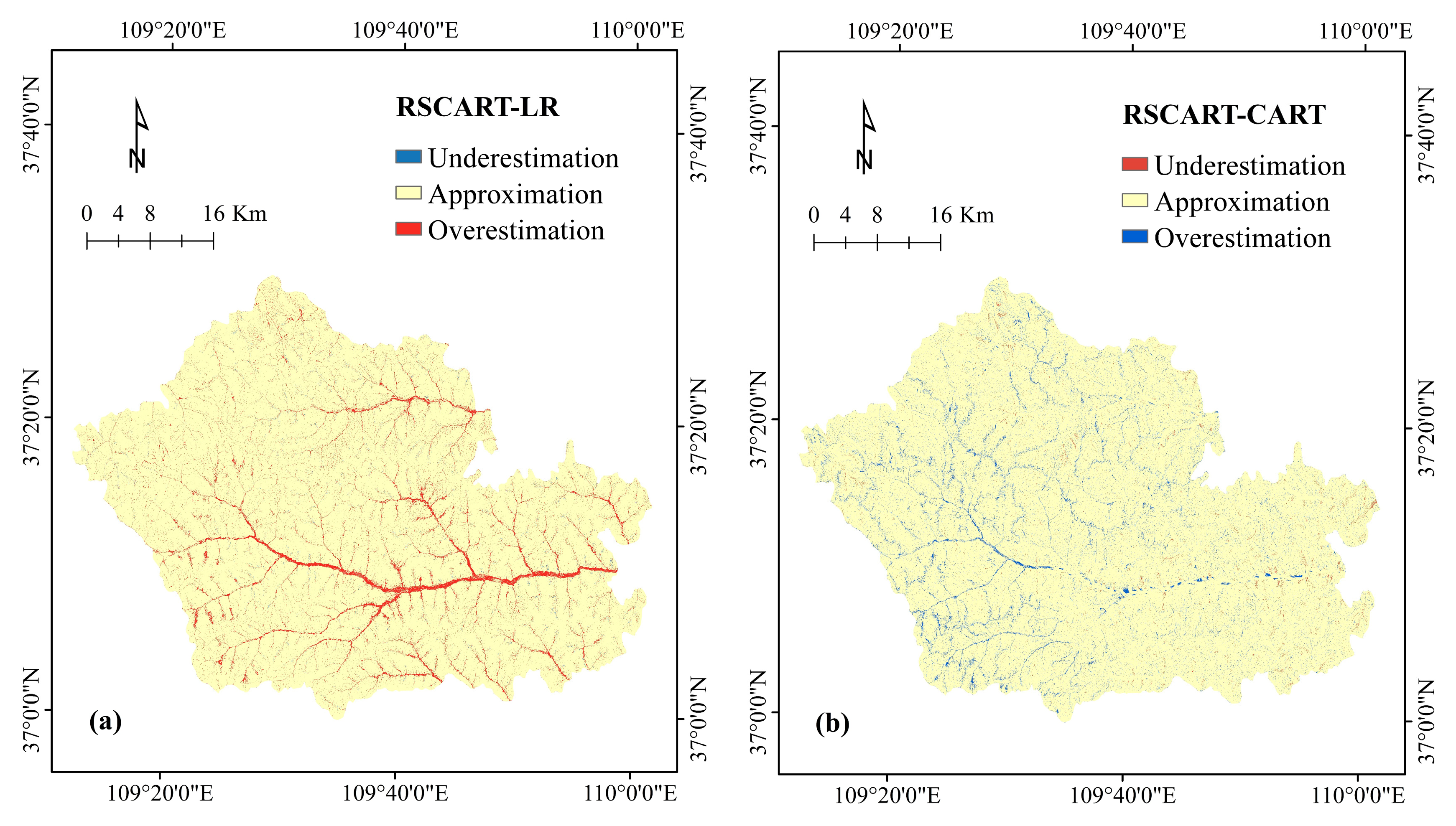
4.4. Comparison of Landslide Susceptibility Maps
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cruden, D.M. A simple definition of a landslide. Bull. Eng. Geol. Environ. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Centre for Research on Epidemiology of Disasters, Université catholique de. The Human Cost of Natural Disasters 2015: A Global Perspective; Centre for Research on Epidemiology of Disasters, Université catholique de: Brussels, Belgium, 2015. [Google Scholar]
- Van Westen, C.; Van Asch, T.W.; Soeters, R. Landslide hazard and risk zonation—why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the gis-based data mining techniques of best-first decision tree, random forest, and naïve bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Canli, E.; Mergili, M.; Thiebes, B.; Glade, T. Probabilistic landslide ensemble prediction systems: Lessons to be learned from hydrology. Nat. Hazards Earth Syst. Sci. 2018, 18, 2183–2202. [Google Scholar] [CrossRef]
- Cervi, F.; Berti, M.; Borgatti, L.; Ronchetti, F.; Manenti, F.; Corsini, A. Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: A case study in the northern apennines (reggio emilia province, italy). Landslides 2010, 7, 433–444. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, Ø.B. Regional prediction of landslide hazard using probability analysis of intense rainfall in the hoa binh province, vietnam. Nat. Hazards 2013, 66, 707–730. [Google Scholar]
- Pradhan, B.; Abokharima, M.H.; Jebur, M.N.; Tehrany, M.S. Land subsidence susceptibility mapping at kinta valley (malaysia) using the evidential belief function model in gis. Nat. Hazards 2014, 73, 1019–1042. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- Hong, H.; Naghibi, S.A.; Dashtpagerdi, M.M.; Pourghasemi, H.R.; Chen, W. A comparative assessment between linear and quadratic discriminant analyses (lda-qda) with frequency ratio and weights-of-evidence models for forest fire susceptibility mapping in china. Arab. J. Geosci. 2017, 10, 167. [Google Scholar] [CrossRef]
- Wang, L.-J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J.; Woo, I. The effect of spatial resolution on the accuracy of landslide susceptibility mapping: A case study in boun, korea. Geosci. J. 2004, 8, 51. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Probabilistic landslide hazards and risk mapping on penang island, malaysia. J. Earth Syst. Sci. 2006, 115, 661–672. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. Gis-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping. Environ. Geol. 2008, 54, 311–324. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Rajamanickam, V.; Kumaravel, P.; Saranathan, E. Landslide susceptibility analysis using probabilistic likelihood ratio model—a geospatial-based study. Arab. J. Geosci. 2013, 6, 429–440. [Google Scholar] [CrossRef]
- Chen, W.; Fan, L.; Li, C.; Pham, B.T. Spatial prediction of landslides using hybrid integration of artificial intelligence algorithms with frequency ratio and index of entropy in nanzheng county, china. Appl. Sci. 2020, 10, 29. [Google Scholar] [CrossRef]
- Lee, S.; Song, K.-Y.; Oh, H.-J.; Choi, J. Detection of landslides using web-based aerial photographs and landslide susceptibility mapping using geospatial analysis. Int. J. Remote Sens. 2012, 33, 4937–4966. [Google Scholar] [CrossRef]
- Demir, G.; Aytekin, M.; Akgün, A.; Ikizler, S.B.; Tatar, O. A comparison of landslide susceptibility mapping of the eastern part of the north anatolian fault zone (turkey) by likelihood-frequency ratio and analytic hierarchy process methods. Nat. Hazards 2013, 65, 1481–1506. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in gis and their comparison at mugling–narayanghat road section in nepal himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Ozdemir, A.; Altural, T. A comparative study of frequency ratio, weights of evidence and logistic regression methods for landslide susceptibility mapping: Sultan mountains, sw turkey. J. Asian Earth Sci. 2013, 64, 180–197. [Google Scholar] [CrossRef]
- Bui, D.T.; Hoang, N.-D.; Samui, P. Spatial pattern analysis and prediction of forest fire using new machine learning approach of multivariate adaptive regression splines and differential flower pollination optimization: A case study at lao cai province (viet nam). J. Environ. Manag. 2019, 237, 476–487. [Google Scholar]
- Chu, L.; Wang, L.-J.; Jiang, J.; Liu, X.; Sawada, K.; Zhang, J. Comparison of landslide susceptibility maps using random forest and multivariate adaptive regression spline models in combination with catchment map units. Geosci. J. 2019, 23, 341–355. [Google Scholar] [CrossRef]
- Conoscenti, C.; Agnesi, V.; Cama, M.; Caraballo-Arias, N.A.; Rotigliano, E. Assessment of gully erosion susceptibility using multivariate adaptive regression splines and accounting for terrain connectivity. Land Degrad. Dev. 2018, 29, 724–736. [Google Scholar] [CrossRef]
- Shafapour Tehrany, M.; Kumar, L.; Neamah Jebur, M.; Shabani, F. Evaluating the application of the statistical index method in flood susceptibility mapping and its comparison with frequency ratio and logistic regression methods. Geomat. Nat. Hazards Risk 2019, 10, 79–101. [Google Scholar] [CrossRef]
- Nicu, I.C. Application of analytic hierarchy process, frequency ratio, and statistical index to landslide susceptibility: An approach to endangered cultural heritage. Environ. Earth Sci. 2018, 77, 79. [Google Scholar] [CrossRef]
- Tien Bui, D.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. Gis-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with adaboost, bagging, and multiboost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1–22. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on random subspace and classification and regression trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Tien Bui, D.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of gis-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (anfis) with genetic algorithm (ga), differential evolution (de), and particle swarm optimization (pso) for landslide spatial modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Loupasakis, C.; Nikolakopoulos, K.; Angelitsa, V.; Ilia, I. Developing a landslide susceptibility map based on remote sensing, fuzzy logic and expert knowledge of the island of lefkada, greece. Environ. Earth Sci. 2018, 77, 363. [Google Scholar] [CrossRef]
- Sahana, M.; Sajjad, H. Evaluating effectiveness of frequency ratio, fuzzy logic and logistic regression models in assessing landslide susceptibility: A case from rudraprayag district, india. J. Mt. Sci. 2017, 14, 2150–2167. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. Gis-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, naïve-bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the yihuang area (china) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (china) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Zhang, T.-Y.; Han, L.; Zhang, H.; Zhao, Y.-H.; Li, X.-A.; Zhao, L. Gis-based landslide susceptibility mapping using hybrid integration approaches of fractal dimension with index of entropy and support vector machine. J. Mt. Sci. 2019, 16, 1275–1288. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of gis-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of ambon, indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Ngadisih; Bhandary, N.P.; Yatabe, R.; Dahal, R.K. Logistic Regression and Artificial Neural Network Models for Mapping of Regional-Scale Landslide Susceptibility in Volcanic Mountains of West Java (Indonesia). AIP Conf. Proc. 2016. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.X. Gis-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Tofani, V.; Segoni, S.; Catani, F.; Casagli, N. A tool for classification and regression using random forest methodology: Applications to landslide susceptibility mapping and soil thickness modeling. Environ. Model. Assess. 2017, 22, 201–214. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. Prioritization of landslide conditioning factors and its spatial modeling in shangnan county, china using gis-based data mining algorithms. Bull. Eng. Geol. Environ. 2018, 77, 611–629. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Tran, H.T.; Le, T.M.; Van Phong, T.; Khoi, D.K.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modelling using rotation forest ensemble and different base classifiers. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, china. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Pradhan, B.; Panahi, M. Landslide susceptibility assessment using a novel hybrid model of statistical bivariate methods (fr and woe) and adaptive neuro-fuzzy inference system (anfis) at southern zagros mountains in iran. Environ. Earth Sci. 2017, 76, 237. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using reduced error pruning trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the multiboost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning. Eng. Geol. 2008, 102, 99–111. [Google Scholar] [CrossRef]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, turkey. Landslides 2012, 9, 93–106. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at wadi tayyah basin, asir region, saudi arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the wuning area (china). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Mandal, S.; Mandal, K. Bivariate statistical index for landslide susceptibility mapping in the rorachu river basin of eastern sikkim himalaya, india. Spat. Inf. Res. 2018, 26, 59–75. [Google Scholar] [CrossRef]
- Pradhan, A.; Kim, Y. Evaluation of a combined spatial multi-criteria evaluation model and deterministic model for landslide susceptibility mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Varnes, D.J. Slope movement types and processes. In: Schuster RL, Krizek RJ (eds) Landslides, analysis and control, Transportation research board, National Academy of Sciences, Washington, DC. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y.; et al. Landslide spatial modelling using novel bivariate statistical based naïve bayes, rbf classifier, and rbf network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive bayes and rbfnetwork models for the long county area (china). Bull. Eng. Geol. Environ. 2019, 78, 247–266. [Google Scholar] [CrossRef]
- Yalcin, A. Gis-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in ardesen (turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Duman, T.Y.; Durmaz, S. Landslide susceptibility mapping for a part of tectonic kelkit valley (eastern black sea region of turkey). Geomorphology 2008, 94, 401–418. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using gis. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Galli, M.; Ardizzone, F.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Comparing landslide inventory maps. Geomorphology 2008, 94, 268–289. [Google Scholar] [CrossRef]
- Yalcin, A.; Bulut, F. Landslide susceptibility mapping using gis and digital photogrammetric techniques: A case study from ardesen (ne-turkey). Nat. Hazards 2007, 41, 201–226. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.; Rezaeian, J.; Sattarian, A. Gis-based frequency ratio and index of entropy models for landslide susceptibility assessment in the caspian forest, northern iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Physical basis of the length-slope factor in the universal soil loss equation 1. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Yilmaz, C.; Topal, T.; Süzen, M.L. Gis-based landslide susceptibility mapping using bivariate statistical analysis in devrek (zonguldak-turkey). Environ. Earth Sci. 2012, 65, 2161–2178. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (ahp) to landslide susceptibility mapping at haraz watershed, iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Nourani, V.; Pradhan, B.; Ghaffari, H.; Sharifi, S.S. Landslide susceptibility mapping at zonouz plain, iran using genetic programming and comparison with frequency ratio, logistic regression, and artificial neural network models. Nat. Hazards 2014, 71, 523–547. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, J.; Qi, X.; Ding, J. Landslides induced by the wenchuan earthquake and the subsequent strong rainfall event: A case study in the beichuan area of china. Eng. Geol. 2011, 122, 22–33. [Google Scholar] [CrossRef]
- Korup, O.; Clague, J.J.; Hermanns, R.L.; Hewitt, K.; Strom, A.L.; Weidinger, J.T. Giant landslides, topography, and erosion. Earth Planet. Sci. Lett. 2007, 261, 578–589. [Google Scholar] [CrossRef]
- Guo, C.; Qin, Y.; Ma, D.; Xia, Y.; Chen, Y.; Si, Q.; Lu, L. Ionic composition, geological signature and environmental impacts of coalbed methane produced water in china. Energy Sources Part A Recovery Util. Environ. Effects 2019. [Google Scholar] [CrossRef]
- Sharma, L.; Patel, N.; Debnath, P.; Ghose, M. Assessing landslide vulnerability from soil characteristics—a gis-based analysis. Arab. J. Geosci. 2012, 5, 789–796. [Google Scholar] [CrossRef]
- Hall, F.G.; Townshend, J.R.; Engman, E.T. Status of remote sensing algorithms for estimation of land surface state parameters. Remote Sens. Environ. 1995, 51, 138–156. [Google Scholar] [CrossRef]
- Restrepo, C.; Vitousek, P.; Neville, P. Landslides significantly alter land cover and the distribution of biomass: An example from the ninole ridges of hawai’i. Plant Ecol. 2003, 166, 131–143. [Google Scholar] [CrossRef]
- Shafer, G. A mathematical theory of evidence. Technometrics 1976, 20, 242. [Google Scholar]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- Lee, T.-S.; Chiu, C.-C.; Chou, Y.-C.; Lu, C.-J. Mining the customer credit using classification and regression tree and multivariate adaptive regression splines. Comput. Stat. Data Anal. 2006, 50, 1113–1130. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Subarkah, P.; Ikhsan, A.N.; Setyanto, A. In The effect of the number of attributes on the selection of study program using classification and regression trees algorithms. In Proceedings of the 3rd International Conference on Information Technology, Information System and Electrical Engineering (ICITISEE 2018), Yogyokarata, Indonesia, 15–22 October 2018; pp. 1–5. [Google Scholar]
- Pham, B.T.; Bui, D.T.; Prakash, I. Application of Classification and Regression Trees for Spatial Prediction of Rainfall-Induced Shallow Landslides in the Uttarakhand Area (India) Using Gis. In Climate Change, Extreme Events and Disaster Risk Reduction; Springer: Cham, Switzerland, 2018; pp. 159–170. [Google Scholar]
- Timofeev, R. Classification and Regression Trees (Cart) Theory and Applications; Humboldt University: Berlin, Germany, 2004. [Google Scholar]
- Barandiaran, I. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1–22. [Google Scholar]
- Kotsiantis, S. Combining bagging, boosting, rotation forest and random subspace methods. Artif. Intell. Rev. 2011, 35, 223–240. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Plumpton, C.O. In Choosing parameters for random subspace ensembles for fmri classification. In Proceedings of the International Workshop on Multiple Classifier Systems, Cairo, Egypt, 7–9 April 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 54–63. [Google Scholar]
- Mielniczuk, J.; Teisseyre, P. Using random subspace method for prediction and variable importance assessment in linear regression. Comput. Stat. Data Anal. 2014, 71, 725–742. [Google Scholar] [CrossRef]
- Bertoni, A.; Folgieri, R.; Valentini, G. Bio-molecular cancer prediction with random subspace ensembles of support vector machines. Neurocomputing 2005, 63, 535–539. [Google Scholar] [CrossRef]
- Skurichina, M.; Duin, R.P. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B.B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]
- Chandra, S.; Maheshkar, S. Verification of static signature pattern based on random subspace, rep tree and bagging. Multimed. Tools Appl. 2017, 76, 19139–19171. [Google Scholar] [CrossRef]
- Xia, J.; Dalla Mura, M.; Chanussot, J.; Du, P.; He, X. Random subspace ensembles for hyperspectral image classification with extended morphological attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4768–4786. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of gis-based logistic regression for landslide susceptibility mapping in the kakuda-yahiko mountains, central japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Shahabi, H.; Shirzadi, A.; Khosravi, K.; Chai, H.; Zhang, S.; Zhang, L.; Ma, J.; Chen, Y.; et al. Spatial prediction of landslide susceptibility by combining evidential belief function, logistic regression and logistic model tree. Geocarto Int. 2019, 34, 1177–1201. [Google Scholar] [CrossRef]
- Bui, D.T.; Lofman, O.; Revhaug, I.; Dick, O. Landslide susceptibility analysis in the hoa binh province of vietnam using statistical index and logistic regression. Nat. Hazards 2011, 59, 1413. [Google Scholar] [CrossRef]
- O’Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Chen, W.; Tsangaratos, P.; Ilia, I.; Duan, Z.; Chen, X. Groundwater spring potential mapping using population-based evolutionary algorithms and data mining methods. Sci. Total Environ. 2019, 684, 31–49. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Frank, E.; Hall, A.M.; Witten, H.I. The Weka Workbench. Online Appendix for "Data Mining: Practical Machine Learning Tools and Techniques", 4th ed.; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Chen, W.; Pradhan, B.; Li, S.; Shahabi, H.; Rizeei, H.M.; Hou, E.; Wang, S. Novel hybrid integration approach of bagging-based fisher’s linear discriminant function for groundwater potential analysis. Nat. Resour. Res. 2019, 28, 1239–1258. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C.; et al. Gis-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide susceptibility modeling based on gis and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S.; et al. Spat. Predict. Landslide Susceptibility Using Gis-Based Data Min. Tech. Anfis Whale Optim. Algorithm (Woa) Grey Wolf Optim. (Gwo). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Khosravi, K.; Pourghasemi, H.R.; Rezaie, F.; Parvinnezhad, D. Spatial prediction of groundwater potentiality using anfis ensembled with teaching-learning-based and biogeography-based optimization. J. Hydrol. 2019, 572, 435–448. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Gis-based evaluation of landslide susceptibility models using certainty factors and functional trees-based ensemble techniques. Appl. Sci. 2020, 10, 16. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling flood susceptibility using data-driven approaches of naïve bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M. Rotation forest fuzzy rule-based classifier ensemble for spatial prediction of landslides using gis. Nat. Hazards 2016, 83, 97–127. [Google Scholar] [CrossRef]
- Xiao, T.; Segoni, S.; Chen, L.; Yin, K.; Casagli, N. A step beyond landslide susceptibility maps: A simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 2019, 1–14. [Google Scholar] [CrossRef]
- Irigaray, C.; Fernández, T.; El Hamdouni, R.; Chacón, J. Evaluation and validation of landslide-susceptibility maps obtained by a gis matrix method: Examples from the betic cordillera (southern spain). Nat. Hazards 2007, 41, 61–79. [Google Scholar] [CrossRef]
- Romer, C.; Ferentinou, M. Shallow landslide susceptibility assessment in a semiarid environment—A quaternary catchment of kwazulu-natal, south africa. Eng. Geol. 2016, 201, 29–44. [Google Scholar] [CrossRef]
- Pandey, V.K.; Sharma, M.C. Probabilistic landslide susceptibility mapping along tipri to ghuttu highway corridor, garhwal himalaya (india). Remote Sens. Appl. Soc. Environ. 2017, 8, 1–11. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from longju in the three gorges reservoir area, china. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (wi) and adaptive neuro-fuzzy inference system (anfis) model at alborz mountains (iran). Environ. Earth Sci. 2016, 75, 553. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (swara) technique and adaptive neuro-fuzzy inference system (anfis) for regional landslide hazard assessment in iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Gassner, C.; Petschko, H.; Bell, R.; Glade, T. In Effect of lithological data of different scales on modelling landslide susceptibility maps. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 11262. [Google Scholar]
- Wu, Y.; Li, W.; Liu, P.; Bai, H.; Wang, Q.; He, J.; Liu, Y.; Sun, S. Application of analytic hierarchy process model for landslide susceptibility mapping in the gangu county, gansu province, china. Environ. Earth Sci. 2016, 75, 422. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Chen, W.; Xu, C. In Comparing the performance of a logistic regression and a random forest model in landslide susceptibility assessments. The case of Wuyaun Area, China. In Proceedings of the Workshop on World Landslide Forum; Ljubljana, Slovenia, 29 May–2 June 2017, Springer: Cham, Switzerland, 2017; pp. 1043–1050. [Google Scholar]
- Hue, T.; Duong, T.; Toan, D.; Nghinh, L.; Minh, V.; Pho, N.; Xuan, P.; Hoan, L.; Huyen, N.; Pha, P. Investigation and Assessment of the Types of Geological Hazard in the Territory of Vietnam and Recommendation of Remedial Measures. Phase II: A Study of the Northern Mountainous Province; Vietnam Academy of Science and Technology, Institute of Geological Sciences: Hanoi, Vietnam, 2004. [Google Scholar]
- Conforti, M.; Pascale, S.; Pepe, M.; Sdao, F.; Sole, A. Denudation processes and landforms map of the camastra river catchment (basilicata–south italy). J. Maps 2013, 9, 444–455. [Google Scholar] [CrossRef]
- Chen, Y.; Li, B.; Xu, Y.; Zhao, Y.; Xu, J. Field study on the soil water characteristics of shallow layers on red clay slopes and its application in stability analysis. Arab. J. Sci. Eng. 2019, 44, 5107–5116. [Google Scholar] [CrossRef]
- Pascale, S.; Parisi, S.; Mancini, A.; Schiattarella, M.; Conforti, M.; Sole, A.; Murgante, B.; Sdao, F. In Landslide susceptibility mapping using artificial neural network in the urban area of senise and san costantino albanese (basilicata, southern italy). In Proceedings of the International Conference on Computational Science and Its Applications, Ho Chi Minh City, Vietnam, 24–27 June 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 473–488. [Google Scholar]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Plant-soil reinforcement response under different soil hydrological regimes. Geoderma 2017, 285, 141–150. [Google Scholar] [CrossRef]
- Ordak, M.; Wesolowski, M.; Radecka, I.; Muszynska, E.; Bujalska-Zazdrozny, M. Seasonal variations of mercury levels in selected medicinal plants originating from poland. Biol. Trace Elem. Res. 2016, 173, 514–524. [Google Scholar] [CrossRef]
- Zhang, C.-B.; Chen, L.-H.; Jiang, J. Why fine tree roots are stronger than thicker roots: The role of cellulose and lignin in relation to slope stability. Geomorphology 2014, 206, 196–202. [Google Scholar] [CrossRef]
- He, Q.; Xu, Z.; Li, S.; Li, R.; Zhang, S.; Wang, N.; Pham, B.T.; Chen, W. Novel entropy and rotation forest-based credal decision tree classifier for landslide susceptibility modeling. Entropy 2019, 21, 106. [Google Scholar] [CrossRef]
- Yilmaz, I. A case study from koyulhisar (sivas-turkey) for landslide susceptibility mapping by artificial neural networks. Bull. Eng. Geol. Environ. 2009, 68, 297–306. [Google Scholar] [CrossRef]
- Truong, X.; Mitamura, M.; Kono, Y.; Raghavan, V.; Yonezawa, G.; Do, T.; Tien Bui, D.; Lee, S. Enhancing prediction performance of landslide susceptibility model using hybrid machine learning approach of bagging ensemble and logistic model tree. Appl. Sci. 2018, 8, 1046. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C. Comparison and evaluation of landslide susceptibility maps obtained from weight of evidence, logistic regression, and artificial neural network models. Nat. Hazards 2018, 93, 249–274. [Google Scholar] [CrossRef]
- Oh, H.-J.; Kadavi, P.R.; Lee, C.-W.; Lee, S. Evaluation of landslide susceptibility mapping by evidential belief function, logistic regression and support vector machine models. Geomat. Nat. Hazards Risk 2018, 9, 1053–1070. [Google Scholar] [CrossRef]


| Factors | Class | No. of Pixels | No. of Landslide | Bel |
|---|---|---|---|---|
| Slope angle | <10 | 278,839 | 0 | 0.000 |
| 10–20 | 696,966 | 56 | 0.244 | |
| 20–30 | 938,802 | 68 | 0.220 | |
| 30–40 | 638,483 | 48 | 0.228 | |
| 40–50 | 117,745 | 12 | 0.309 | |
| >50 | 527 | 0 | 0.000 | |
| Elevation (m) | 933–1000 | 30,442 | 4 | 0.197 |
| 1000–1100 | 357,423 | 41 | 0.172 | |
| 1100–1200 | 753,794 | 61 | 0.121 | |
| 1200–1300 | 829,706 | 54 | 0.098 | |
| 1300–1400 | 546,264 | 17 | 0.047 | |
| 1400–1500 | 148,806 | 6 | 0.060 | |
| 1500–1574 | 4927 | 1 | 0.305 | |
| Aspect | F (−1) | 1237 | 0 | 0.000 |
| N (0–22.5; 337.5–360) | 247,049 | 14 | 0.103 | |
| NE (22.5–67.5) | 351,476 | 12 | 0.062 | |
| E (67.5–112.5) | 436,578 | 32 | 0.133 | |
| SE (112.5–157.5) | 300,883 | 25 | 0.151 | |
| S (157.5–202.5) | 270,755 | 27 | 0.181 | |
| SW (202.5–247.5) | 341,265 | 31 | 0.165 | |
| W (247.5–292.5) | 412,506 | 33 | 0.145 | |
| NW (292.5–337.5) | 309,613 | 10 | 0.059 | |
| STI | (0–10) | 1,289,473 | 81 | 0.147 |
| (10–20) | 827,143 | 62 | 0.176 | |
| (20–30) | 299,541 | 28 | 0.219 | |
| (30–40) | 112,670 | 6 | 0.125 | |
| >40 | 142,535 | 7 | 0.115 | |
| TWI | (1.11–2) | 1,504,887 | 102 | 0.319 |
| (2–3) | 885,873 | 73 | 0.388 | |
| (3–4) | 196,513 | 7 | 0.168 | |
| (4–5) | 75,716 | 2 | 0.124 | |
| >5 | 8373 | 0 | 0.000 | |
| SPI | (0–10) | 867,208 | 37 | 0.113 |
| (10–20) | 526,106 | 46 | 0.232 | |
| (20–30) | 362,454 | 32 | 0.234 | |
| (30–40) | 218,983 | 19 | 0.230 | |
| >40 | 696,611 | 50 | 0.190 | |
| Profile curvature | (−7.29)–(−1.65) | 215,910 | 13 | 0.182 |
| (−1.65)–(−0.46) | 643,747 | 29 | 0.136 | |
| (−0.46)–(0.58) | 1,050,656 | 77 | 0.222 | |
| (0.58)–(1.97) | 567,015 | 54 | 0.288 | |
| (1.97)–(9.45) | 194,034 | 11 | 0.172 | |
| Plan curvature | (−9.24)–(−1.79) | 143,702 | 5 | 0.106 |
| (−1.79)–(−0.54) | 480,381 | 29 | 0.185 | |
| (−0.54)-0.38 | 1,124,169 | 83 | 0.226 | |
| 0.38–1.44 | 703,523 | 47 | 0.204 | |
| 1.44–7.56 | 219,587 | 20 | 0.279 | |
| Distance to rivers (m) | 0–200 | 765,053 | 127 | 0.590 |
| 200–400 | 678,212 | 27 | 0.141 | |
| 400–600 | 597,921 | 17 | 0.101 | |
| 600–800 | 417,041 | 6 | 0.051 | |
| >800 | 213,135 | 7 | 0.117 | |
| Distance to roads (m) | 0–100 | 406,132 | 51 | 0.313 |
| 100–200 | 304,978 | 32 | 0.262 | |
| 200–300 | 303,291 | 22 | 0.181 | |
| 300–400 | 238,548 | 12 | 0.126 | |
| >400 | 1,418,413 | 67 | 0.118 | |
| Soil | Cultivated loessal soils | 2,288,420 | 141 | 0.158 |
| Alluvial soils | 316,038 | 28 | 0.228 | |
| Red clay soils | 62,809 | 15 | 0.614 | |
| Water | 4095 | 0 | 0.000 | |
| NDVI | (−0.15–0.01) | 372,914 | 26 | 0.207 |
| (0.01–0.04) | 452,559 | 21 | 0.138 | |
| (0.04–0.07) | 599,799 | 31 | 0.154 | |
| (0.07–0.09) | 733,152 | 65 | 0.264 | |
| (0.09–0.31) | 512,938 | 41 | 0.238 | |
| Land use | Farmland | 987,416 | 47 | 0.142 |
| Forestland | 505,630 | 37 | 0.219 | |
| Grassland | 1,167,441 | 99 | 0.254 | |
| Water bodies | 2665 | 0 | 0.000 | |
| Residential areas | 7769 | 1 | 0.385 | |
| Others | 441 | 0 | 0.000 | |
| Lithology | Group 1 | 2,008,004 | 111 | 0.133 |
| Group 2 | 330,841 | 40 | 0.292 | |
| Group 3 | 25,061 | 1 | 0.096 | |
| Group 4 | 178,708 | 23 | 0.310 | |
| Group 5 | 128,748 | 9 | 0.169 |
| Factors | Collinearity Statistics | ||
|---|---|---|---|
| Tolerance | VIF | ||
| Slope angle | 0.873 | 1.145 | |
| Elevation | 0.878 | 1.139 | |
| Aspect | 0.865 | 1.156 | |
| STI | 0.881 | 1.135 | |
| TWI | 0.830 | 1.205 | |
| SPI | 0.848 | 1.180 | |
| Profile curvature | 0.821 | 1.219 | |
| Plan curvature | 0.926 | 1.080 | |
| Distance to rivers | 0.715 | 1.399 | |
| Distance to roads | 0.869 | 1.150 | |
| Soil | 0.954 | 1.048 | |
| NDVI | 0.830 | 1.205 | |
| Land use | 0.954 | 1.048 | |
| Lithology | 0.830 | 1.205 | |
| Landslide Conditioning Factor | Average Merit (AM) | Standard Deviation (SD) |
|---|---|---|
| Distance to rivers | 0.378 | ±0.015 |
| Slope angle | 0.213 | ± 0.008 |
| Lithology | 0.181 | ± 0.012 |
| Distance to roads | 0.173 | ±0.014 |
| Elevation | 0.172 | ± 0.016 |
| TWI | 0.171 | ± 0.014 |
| SPI | 0.154 | ± 0.015 |
| Aspect | 0.143 | ± 0.012 |
| Soil | 0.143 | ± 0.013 |
| Profile curvature | 0.138 | ± 0.019 |
| NDVI | 0.103 | ± 0.024 |
| Land use | 0.098 | ± 0.013 |
| Plan curvature | 0.042 | ± 0.012 |
| STI | 0.04 | ± 0.015 |
| Landslide Influencing Factor | Coefficients |
|---|---|
| Slope angle | 10.866 |
| Elevation | 5.226 |
| Aspect | 6.428 |
| STI | 0.708 |
| TWI | 4.833 |
| SPI | 5.437 |
| Profile curvature | 4.139 |
| Plan curvature | 1.150 |
| Distance to rivers | 2.855 |
| Distance to roads | 1.645 |
| Soil | 2.285 |
| NDVI | 2.390 |
| Land use | 1.137 |
| Lithology | 1.449 |
| Intercept | −10.521 |
| Class | RSCART Model | CART Model | LR Model | |||
|---|---|---|---|---|---|---|
| % Landslides | LD | % Landslides | LD | % Landslides | LD | |
| Very Low | 0.760 | 0.057 | 0.004 | 0.041 | 0.019 | 0.086 |
| Low | 6.084 | 0.223 | 0.065 | 0.212 | 0.091 | 0.310 |
| Moderate | 19.392 | 0.634 | 0.209 | 0.670 | 0.183 | 0.825 |
| High | 34.221 | 1.743 | 0.335 | 2.004 | 0.243 | 1.692 |
| Very High | 39.544 | 4.264 | 0.388 | 3.156 | 0.464 | 3.845 |
| Comparison | Value | Classification | Percentage | |
|---|---|---|---|---|
| RSCART-LR | −0.27–0.386 | Underestimation | −0.27–(−0.2) | 0.003 |
| Approximation | −0.2–0.2 | 0.940 | ||
| Overestimation | 0.2–0.386 | 0.057 | ||
| RSCART-CART | −0.31–0.42 | Underestimation | −0.31–(−0.2) | 0.008 |
| Approximation | −0.2–0.2 | 0.948 | ||
| Overestimation | 0.2–0.42 | 0.044 | ||
| Factors | Class | A (%) | Underestimation RSCART-LRB (%) | B-A (%) | Overestimation RSCART-LRB (%) | B-A (%) |
|---|---|---|---|---|---|---|
| Slope angle | <10 | 10.44 | 0.00 | −10.44 | 99.35 | 88.91 |
| 10–20 | 26.09 | 1.44 | −24.65 | 0.00 | −26.09 | |
| 20–30 | 35.14 | 0.00 | −35.14 | 0.38 | −34.76 | |
| 30–40 | 23.90 | 0.01 | −23.89 | 0.05 | −23.85 | |
| 40–50 | 4.41 | 98.55 | 94.14 | 0.00 | −4.41 | |
| >50 | 0.02 | 0.00 | −0.02 | 0.22 | 0.20 | |
| Elevation (m) | 933–1000 | 1.14 | 1.69 | 0.55 | 8.45 | 7.31 |
| 1000–1100 | 13.38 | 23.76 | 10.38 | 33.85 | 20.47 | |
| 1100–1200 | 28.22 | 32.57 | 4.35 | 27.21 | −1.01 | |
| 1200–1300 | 31.06 | 39.37 | 8.31 | 19.09 | −11.97 | |
| 1300–1400 | 20.45 | 2.45 | −18.00 | 8.33 | −12.12 | |
| 1400–1500 | 5.57 | 0.11 | −5.46 | 2.70 | −2.87 | |
| 1500–1574 | 0.18 | 0.05 | −0.14 | 0.39 | 0.20 | |
| Aspect | F | 0.05 | 0.00 | −0.05 | 0.00 | −0.05 |
| N | 9.25 | 7.52 | −1.73 | 10.07 | 0.82 | |
| NE | 13.16 | 11.01 | −2.15 | 8.06 | −5.09 | |
| E | 16.34 | 22.56 | 6.22 | 13.25 | −3.09 | |
| SE | 11.26 | 7.45 | −3.82 | 14.65 | 3.39 | |
| S | 10.14 | 6.03 | −4.10 | 19.69 | 9.55 | |
| SW | 12.77 | 9.48 | −3.29 | 15.88 | 3.10 | |
| W | 15.44 | 20.99 | 5.55 | 12.62 | −2.83 | |
| NW | 11.59 | 14.96 | 3.37 | 5.78 | −5.81 | |
| STI | (0–10) | 48.27 | 0.77 | −47.50 | 85.09 | 36.82 |
| (10–20) | 30.96 | 59.22 | 28.25 | 7.74 | −23.22 | |
| (20–30) | 11.21 | 33.37 | 22.16 | 3.64 | −7.57 | |
| (30–40) | 4.22 | 5.23 | 1.01 | 1.80 | −2.42 | |
| >40 | 5.34 | 1.41 | −3.92 | 1.73 | −3.61 | |
| TWI | (1.11–2) | 56.33 | 93.66 | 37.33 | 0.41 | −55.93 |
| (2–3) | 33.16 | 6.34 | −26.82 | 61.88 | 28.72 | |
| (3–4) | 7.36 | 0.00 | −7.36 | 21.60 | 14.24 | |
| (4–5) | 2.83 | 0.00 | −2.83 | 14.79 | 11.96 | |
| >5 | 0.31 | 0.00 | −0.31 | 1.32 | 1.01 | |
| SPI | (0–10) | 32.46 | 0.01 | −32.45 | 61.60 | 29.13 |
| (10–20) | 19.69 | 22.99 | 3.29 | 9.28 | −10.41 | |
| (20–30) | 13.57 | 0.65 | −12.92 | 4.81 | −8.76 | |
| (30–40) | 8.20 | 39.35 | 31.15 | 3.14 | −5.06 | |
| >40 | 26.08 | 37.01 | 10.93 | 21.17 | −4.91 | |
| Profile curvature | (−7.29)–(−1.65) | 8.08 | 22.85 | 14.77 | 2.80 | −5.28 |
| (−1.65)–(−0.46) | 24.10 | 11.86 | −12.24 | 10.60 | −13.50 | |
| (−0.46)–(0.58) | 39.33 | 22.82 | −16.51 | 57.65 | 18.32 | |
| (0.58)–(1.97) | 21.23 | 29.05 | 7.82 | 25.00 | 3.78 | |
| (1.97)–(9.45) | 7.26 | 13.42 | 6.16 | 3.94 | −3.33 | |
| Plan curvature | (−9.24)−(–1.79) | 5.38 | 1.33 | −4.05 | 3.75 | −1.63 |
| (−1.79)–(−0.54) | 17.98 | 18.25 | 0.26 | 12.85 | −5.13 | |
| (−0.54)−0.38 | 42.08 | 40.14 | −1.94 | 62.01 | 19.93 | |
| 0.38–1.44 | 26.34 | 22.84 | −3.49 | 17.30 | −9.03 | |
| 1.44–7.56 | 8.22 | 17.44 | 9.22 | 4.09 | −4.13 | |
| Distance to rivers (m) | 0–200 | 28.64 | 99.94 | 71.30 | 73.01 | 44.37 |
| 200–400 | 25.39 | 0.01 | −25.38 | 11.65 | −13.74 | |
| 400–600 | 22.38 | 0.00 | −22.38 | 7.16 | −15.22 | |
| 600–800 | 15.61 | 0.00 | −15.61 | 4.90 | −10.72 | |
| >800 | 7.98 | 0.05 | −7.93 | 3.28 | −4.69 | |
| Distance to roads (m) | 0–100 | 15.20 | 0.98 | −14.23 | 46.89 | 31.69 |
| 100–200 | 11.42 | 3.96 | −7.46 | 15.81 | 4.40 | |
| 200–300 | 11.35 | 7.14 | −4.21 | 8.45 | −2.91 | |
| 300–400 | 8.93 | 9.43 | 0.50 | 4.36 | −4.57 | |
| >400 | 53.10 | 78.49 | 25.39 | 24.49 | −28.61 | |
| Soil | Cultivated loessal soils | 85.66 | 87.94 | 2.28 | 59.88 | −25.79 |
| Alluvial soils | 11.83 | 11.31 | −0.52 | 36.29 | 24.46 | |
| Red clay soils | 2.35 | 0.71 | −1.64 | 3.61 | 1.26 | |
| Water | 0.15 | 0.04 | −0.12 | 0.22 | 0.07 | |
| NDVI | (−0.15–0.01) | 13.96 | 22.88 | 8.92 | 11.12 | −2.84 |
| (0.01–0.04) | 16.94 | 12.85 | −4.09 | 12.55 | −4.39 | |
| (0.04–0.07) | 22.45 | 15.18 | −7.28 | 26.68 | 4.23 | |
| (0.07–0.09) | 27.44 | 32.28 | 4.83 | 35.72 | 8.28 | |
| (0.09–0.31) | 19.20 | 16.82 | −2.38 | 13.94 | −5.27 | |
| Land use | Farmland | 36.96 | 16.63 | −20.34 | 35.67 | −1.29 |
| Forestland | 18.93 | 19.87 | 0.94 | 16.81 | −2.12 | |
| Grassland | 43.70 | 63.37 | 19.67 | 44.74 | 1.04 | |
| Water bodies | 0.10 | 0.09 | −0.01 | 0.36 | 0.26 | |
| Residential areas | 0.29 | 0.05 | −0.24 | 2.36 | 2.07 | |
| Others | 0.02 | 0.00 | −0.02 | 0.05 | 0.04 | |
| Lithology | Group 1 | 75.17 | 68.36 | −6.81 | 42.36 | −32.81 |
| Group 2 | 12.38 | 17.25 | 4.86 | 16.10 | 3.72 | |
| Group 3 | 0.94 | 4.90 | 3.96 | 0.80 | −0.14 | |
| Group 4 | 6.69 | 3.19 | −3.50 | 16.22 | 9.53 | |
| Group 5 | 4.82 | 6.30 | 1.48 | 24.52 | 19.70 |
| Factors | Class | A (%) | Underestimation RSCART-CART B (%) | B-A (%) | Overestimation RSCART-CART B (%) | B-A (%) |
|---|---|---|---|---|---|---|
| Slope angle | <10 | 10.44 | 0.00 | −10.44 | 76.87 | 66.43 |
| 10–20 | 26.09 | 34.83 | 8.74 | 6.94 | −19.15 | |
| 20–30 | 35.14 | 11.04 | −24.11 | 14.28 | −20.87 | |
| 30–40 | 23.90 | 8.30 | −15.60 | 1.63 | −22.27 | |
| 40–50 | 4.41 | 45.83 | 41.42 | 0.00 | −4.41 | |
| >50 | 0.02 | 0.00 | −0.02 | 0.29 | 0.27 | |
| Elevation (m) | 933–1000 | 1.14 | 5.45 | 4.31 | 1.26 | 0.12 |
| 1000–1100 | 13.38 | 42.21 | 28.83 | 9.86 | −3.52 | |
| 1100–1200 | 28.22 | 22.95 | −5.27 | 23.76 | −4.45 | |
| 1200–1300 | 31.06 | 24.88 | −6.18 | 26.64 | −4.42 | |
| 1300–1400 | 20.45 | 4.37 | −16.08 | 27.01 | 6.56 | |
| 1400–1500 | 5.57 | 0.15 | −5.42 | 10.78 | 5.21 | |
| 1500–1574 | 0.18 | 0.00 | −0.18 | 0.68 | 0.50 | |
| Aspect | F | 0.05 | 0.00 | −0.05 | 0.00 | −0.04 |
| N | 9.25 | 8.15 | −1.10 | 8.63 | −0.62 | |
| NE | 13.16 | 4.51 | −8.65 | 12.34 | −0.82 | |
| E | 16.34 | 13.65 | −2.69 | 14.35 | −1.99 | |
| SE | 11.26 | 10.49 | −0.78 | 14.01 | 2.75 | |
| S | 10.14 | 15.24 | 5.11 | 14.73 | 4.60 | |
| SW | 12.77 | 14.38 | 1.60 | 14.09 | 1.32 | |
| W | 15.44 | 27.72 | 12.28 | 13.04 | −2.40 | |
| NW | 11.59 | 5.86 | −5.73 | 8.80 | −2.79 | |
| STI | (0–10) | 48.27 | 26.71 | −21.56 | 86.04 | 37.77 |
| (10–20) | 30.96 | 46.44 | 15.48 | 6.85 | −24.11 | |
| (20–30) | 11.21 | 17.54 | 6.33 | 3.42 | −7.79 | |
| (30–40) | 4.22 | 6.27 | 2.05 | 1.50 | −2.71 | |
| >40 | 5.34 | 3.04 | −2.29 | 2.18 | −3.15 | |
| TWI | (1.11–2) | 56.33 | 49.57 | −6.77 | 20.92 | −35.41 |
| (2–3) | 33.16 | 49.94 | 16.78 | 56.19 | 23.02 | |
| (3–4) | 7.36 | 0.46 | −6.90 | 12.35 | 4.99 | |
| (4–5) | 2.83 | 0.04 | −2.80 | 8.99 | 6.16 | |
| >5 | 0.31 | 0.00 | −0.31 | 1.55 | 1.24 | |
| SPI | (0–10) | 32.46 | 2.30 | −30.16 | 73.36 | 40.90 |
| (10–20) | 19.69 | 28.85 | 9.15 | 5.97 | −13.73 | |
| (20–30) | 13.57 | 13.85 | 0.28 | 2.93 | −10.64 | |
| (30–40) | 8.20 | 25.32 | 17.12 | 1.78 | −6.41 | |
| >40 | 26.08 | 29.68 | 3.61 | 15.96 | −10.12 | |
| Profile curvature | (−7.29)–(−1.65) | 8.08 | 8.85 | 0.76 | 7.63 | −0.46 |
| (−1.65)–(−0.46) | 24.10 | 4.55 | −19.55 | 32.30 | 8.20 | |
| (−0.46)–(0.58) | 39.33 | 24.42 | −14.91 | 41.48 | 2.15 | |
| (0.58)–(1.97) | 21.23 | 53.71 | 32.48 | 14.45 | −6.78 | |
| (1.97)–(9.45) | 7.26 | 8.47 | 1.21 | 4.14 | −3.12 | |
| Plancurvature | (−9.24)–(−1.79) | 5.38 | 4.15 | −1.23 | 3.26 | −2.12 |
| (−1.79)–(−0.54) | 17.98 | 21.91 | 3.93 | 11.23 | −6.75 | |
| (−0.54)–0.38 | 42.08 | 50.18 | 8.10 | 43.99 | 1.91 | |
| 0.38–1.44 | 26.34 | 18.79 | −7.54 | 31.82 | 5.48 | |
| 1.44–7.56 | 8.22 | 4.96 | −3.26 | 9.70 | 1.48 | |
| Distance to rivers (m) | 0–200 | 28.64 | 100.00 | 71.36 | 19.01 | −9.63 |
| 200–400 | 25.39 | 0.00 | −25.39 | 26.60 | 1.21 | |
| 400–600 | 22.38 | 0.00 | −22.38 | 21.30 | −1.08 | |
| 600–800 | 15.61 | 0.00 | −15.61 | 23.98 | 8.37 | |
| >800 | 7.98 | 0.00 | −7.98 | 9.11 | 1.13 | |
| Distance to roads (m) | 0–100 | 15.20 | 0.14 | −15.06 | 44.63 | 29.43 |
| 100–200 | 11.42 | 1.11 | −10.31 | 13.67 | 2.26 | |
| 200–300 | 11.35 | 6.50 | −4.85 | 8.83 | −2.52 | |
| 300–400 | 8.93 | 10.64 | 1.71 | 5.58 | −3.35 | |
| >400 | 53.10 | 81.61 | 28.52 | 27.29 | −25.81 | |
| Soil | Cultivated loessal soils | 85.66 | 75.02 | −10.64 | 82.11 | −3.56 |
| Alluvial soils | 11.83 | 14.70 | 2.87 | 14.95 | 3.12 | |
| Red clay soils | 2.35 | 10.27 | 7.92 | 2.61 | 0.26 | |
| Water | 0.15 | 0.00 | −0.15 | 0.32 | 0.17 | |
| NDVI | (−0.15–0.01) | 13.96 | 14.62 | 0.66 | 8.82 | −5.14 |
| (0.01–0.04) | 16.94 | 30.21 | 13.27 | 6.53 | −10.41 | |
| (0.04–0.07) | 22.45 | 34.02 | 11.57 | 14.70 | −7.75 | |
| (0.07–0.09) | 27.44 | 12.11 | −15.33 | 43.89 | 16.44 | |
| (0.09–0.31) | 19.20 | 9.04 | −10.16 | 26.05 | 6.85 | |
| Land use | Farmland | 36.96 | 33.24 | −3.72 | 41.50 | 4.53 |
| Forestland | 18.93 | 21.84 | 2.91 | 15.58 | −3.34 | |
| Grassland | 43.70 | 44.23 | 0.53 | 41.66 | −2.04 | |
| Water bodies | 0.10 | 0.60 | 0.50 | 0.10 | 0.00 | |
| Residential areas | 0.29 | 0.08 | −0.21 | 1.13 | 0.84 | |
| Others | 0.02 | 0.00 | −0.02 | 0.03 | 0.01 | |
| Lithology | Group 1 | 75.17 | 78.27 | 3.11 | 66.03 | −9.13 |
| Group 2 | 12.38 | 3.55 | −8.83 | 15.56 | 3.17 | |
| Group 3 | 0.94 | 5.21 | 4.27 | 0.26 | −0.68 | |
| Group 4 | 6.69 | 0.38 | −6.31 | 15.20 | 8.51 | |
| Group 5 | 4.82 | 12.58 | 7.76 | 2.95 | −1.87 |
| Comparison Maps | Imbalanced Classes | |
|---|---|---|
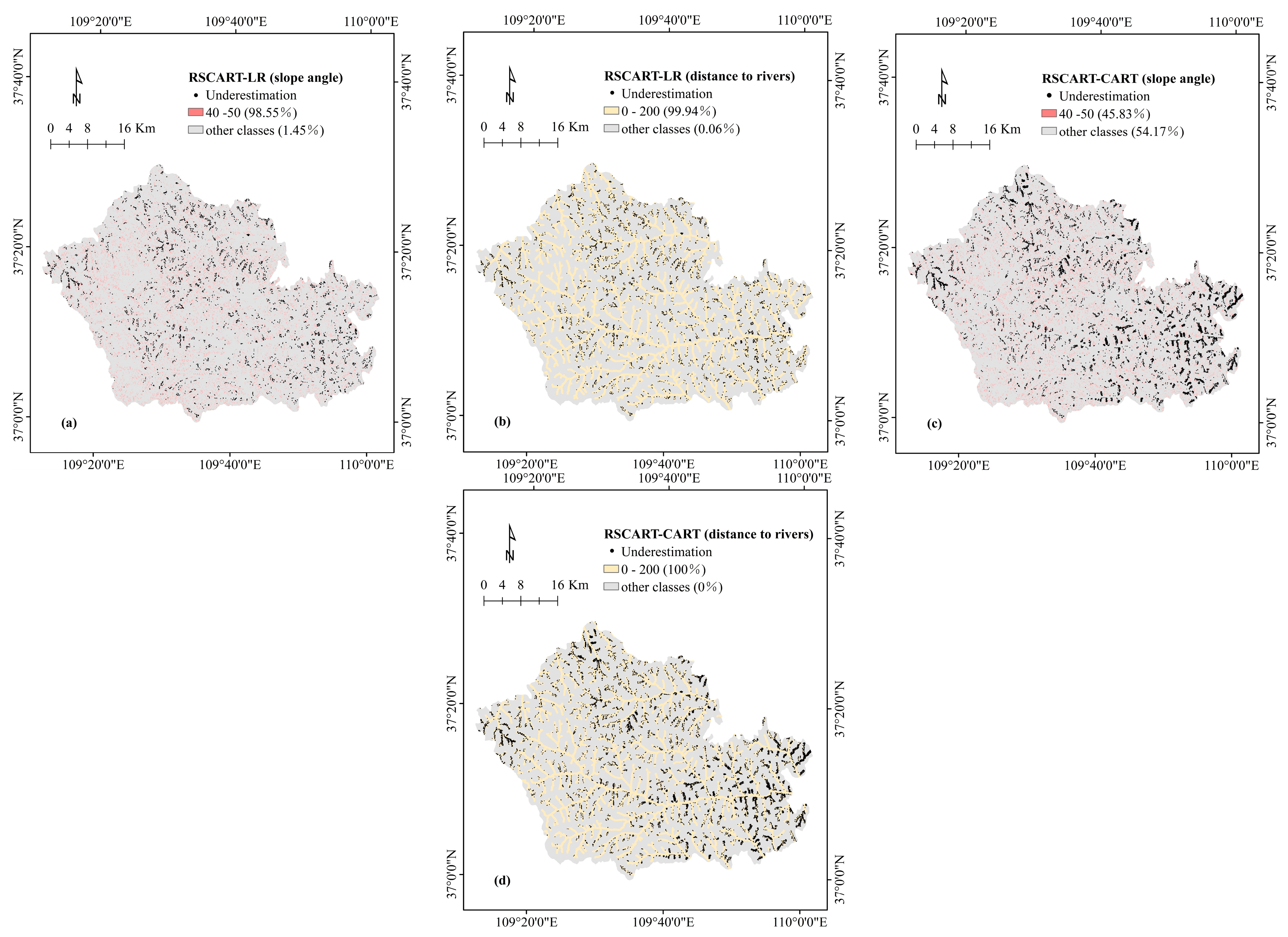
| Underestimation | RSCART-LR | slope, 40–50; STI, 10–20; TWI,1.11–2; SPI, 30–40; distance to rivers, 0–200; distance to roads, >400 |
| RSCART-CART | slope, 40–50; elevation, 1000–1100; profile, 0.58–1.97; distance to rivers, 0–200; distance to roads, >400 | |
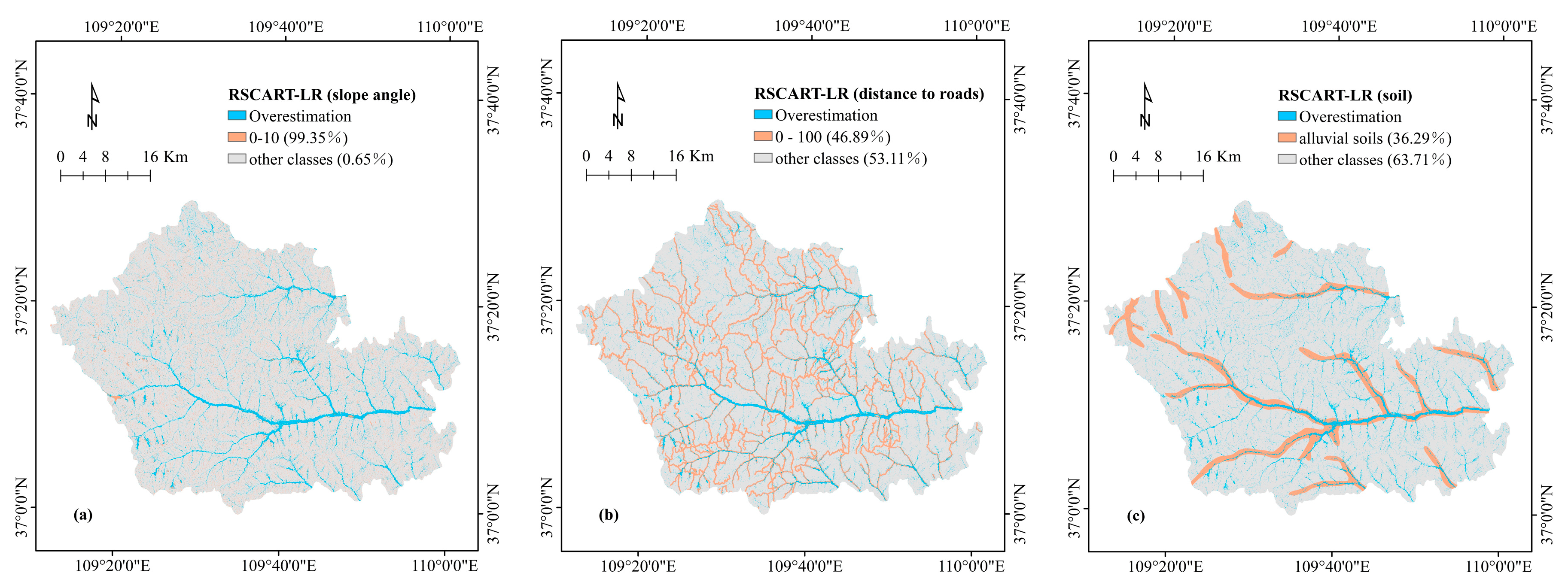
| Overestimation | RSCART-LR | slope, <10; STI, 0–10; TWI, 2–3; SPI, 0–10; distance to roads, 0–100; soil, group2; |
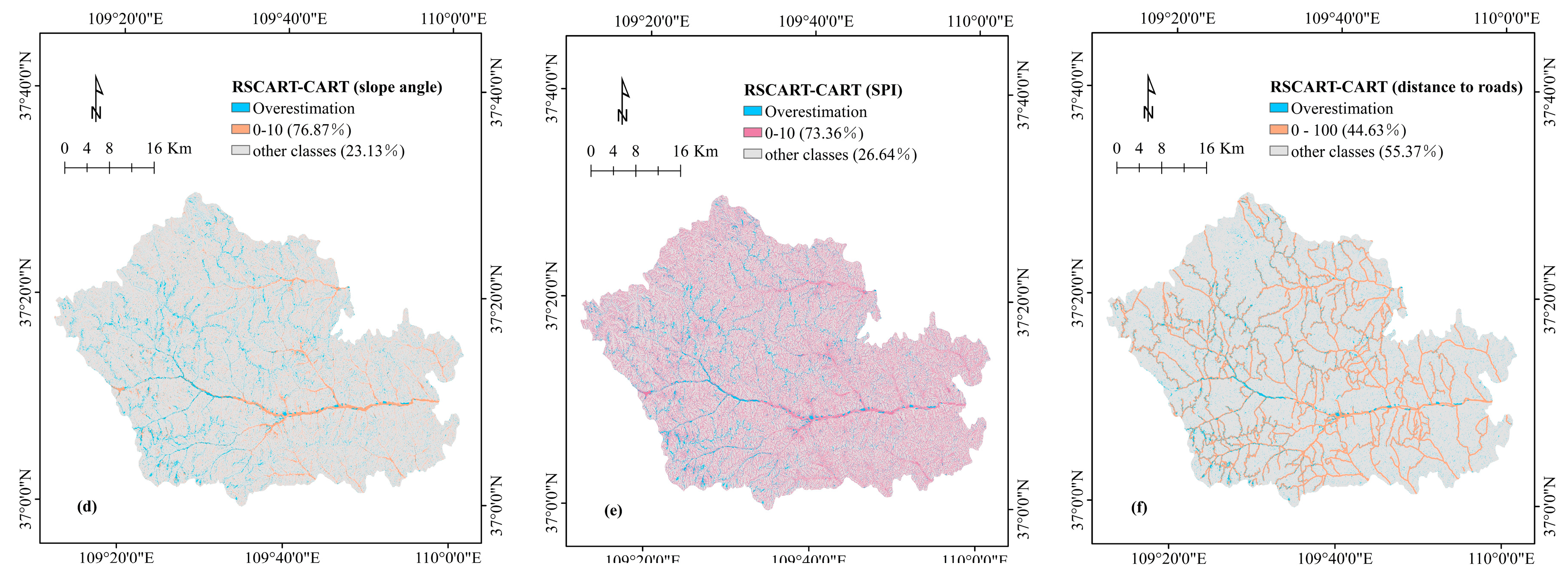
| RSCART-CART | slope, <10; STI, 0–10; SPI, 0–10; distance to roads, 0–100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Chen, W. Landslide Susceptibility Evaluation Using Hybrid Integration of Evidential Belief Function and Machine Learning Techniques. Water 2020, 12, 113. https://doi.org/10.3390/w12010113
Li Y, Chen W. Landslide Susceptibility Evaluation Using Hybrid Integration of Evidential Belief Function and Machine Learning Techniques. Water. 2020; 12(1):113. https://doi.org/10.3390/w12010113
Chicago/Turabian StyleLi, Yang, and Wei Chen. 2020. "Landslide Susceptibility Evaluation Using Hybrid Integration of Evidential Belief Function and Machine Learning Techniques" Water 12, no. 1: 113. https://doi.org/10.3390/w12010113
APA StyleLi, Y., & Chen, W. (2020). Landslide Susceptibility Evaluation Using Hybrid Integration of Evidential Belief Function and Machine Learning Techniques. Water, 12(1), 113. https://doi.org/10.3390/w12010113






