Support Vector Regression Integrated with Fruit Fly Optimization Algorithm for River Flow Forecasting in Lake Urmia Basin
Abstract
1. Introduction
2. Study Area
3. Techniques Applied in Modeling
3.1. M5 Model Tree
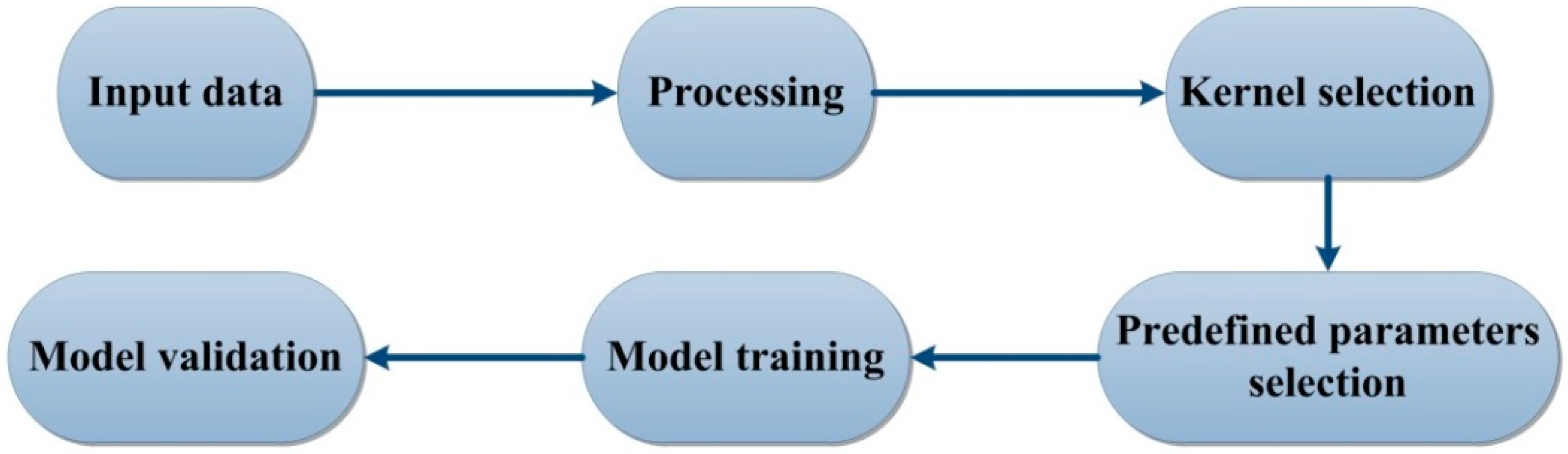
3.2. Support Vector Regression (SVR)
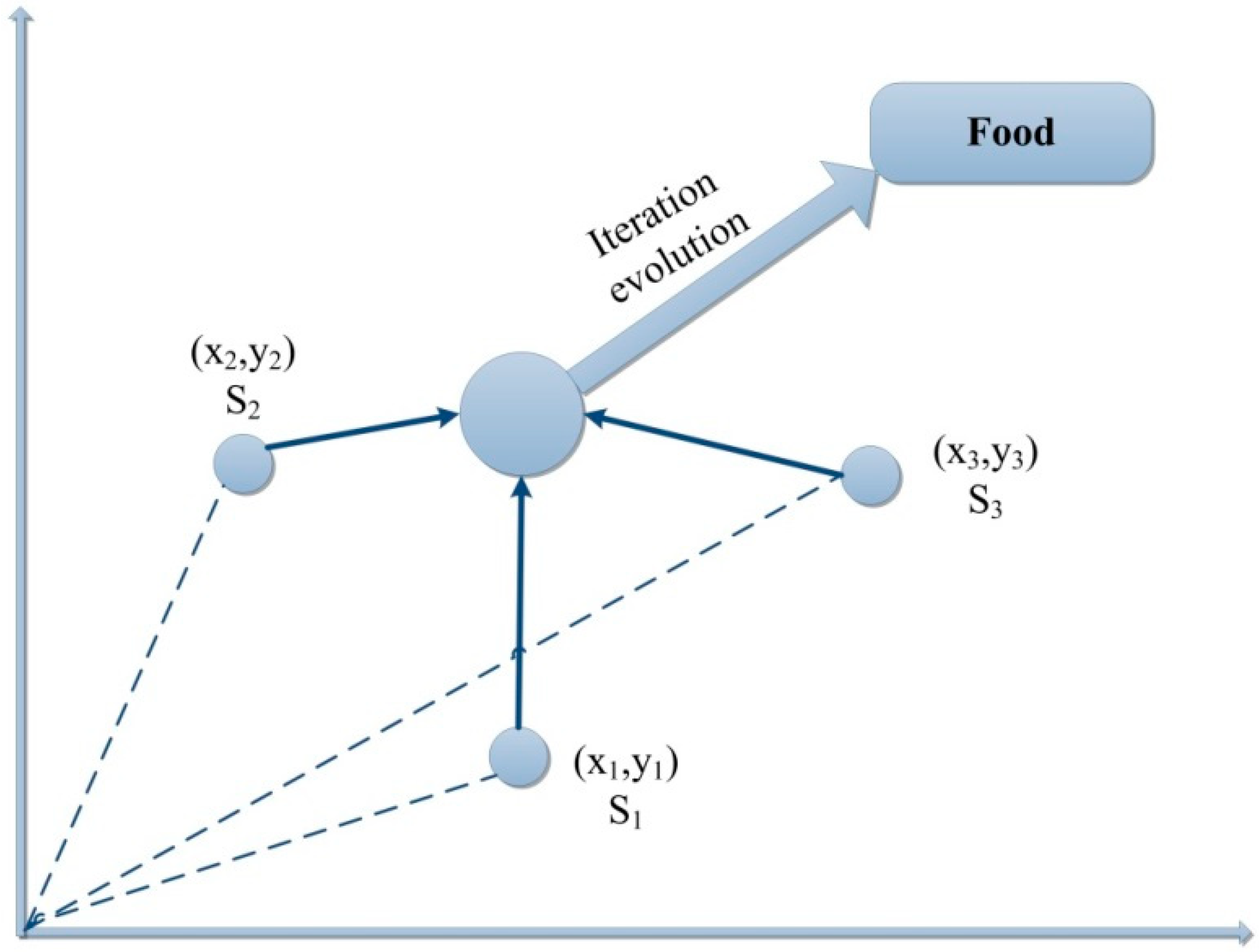
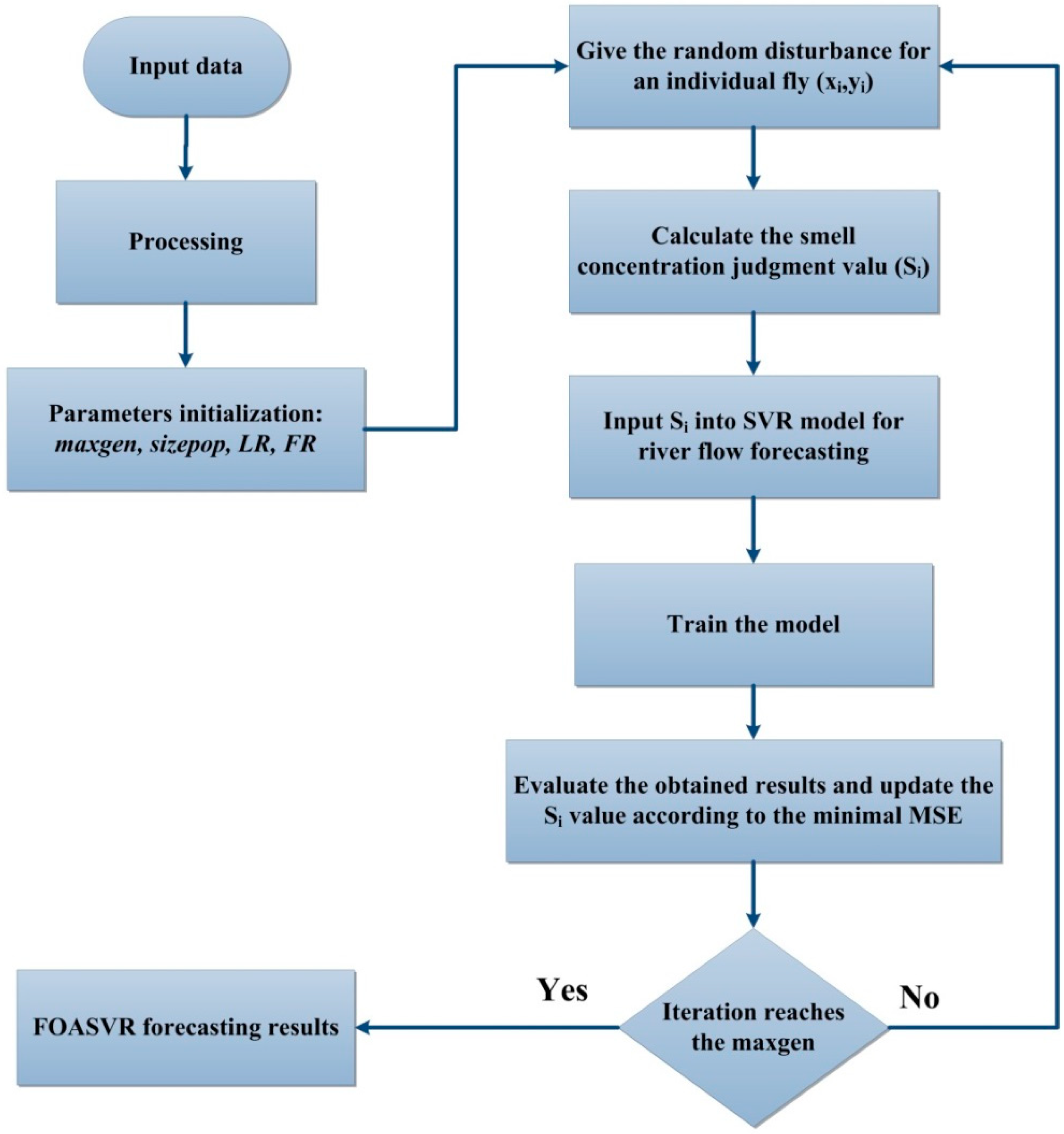
3.3. Fruit fly Optimization Algorithm (FOA)
4. Evaluation Parameters
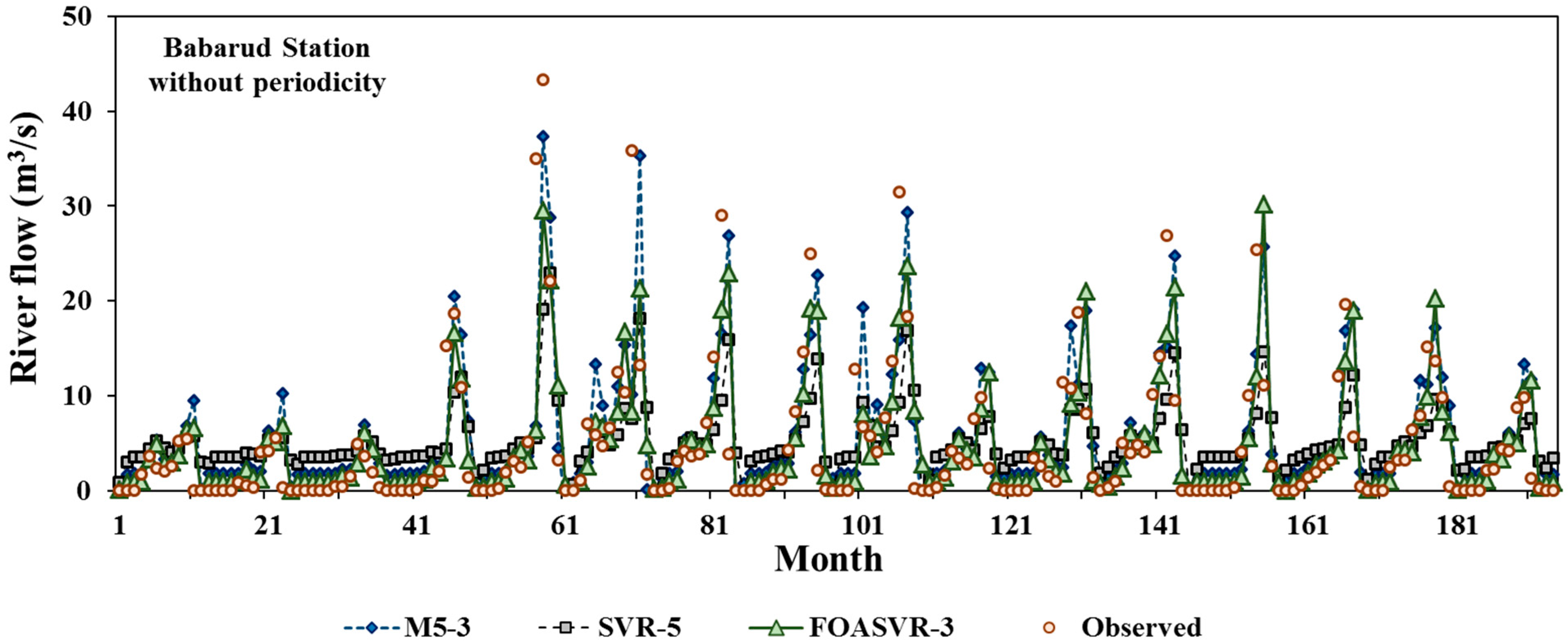
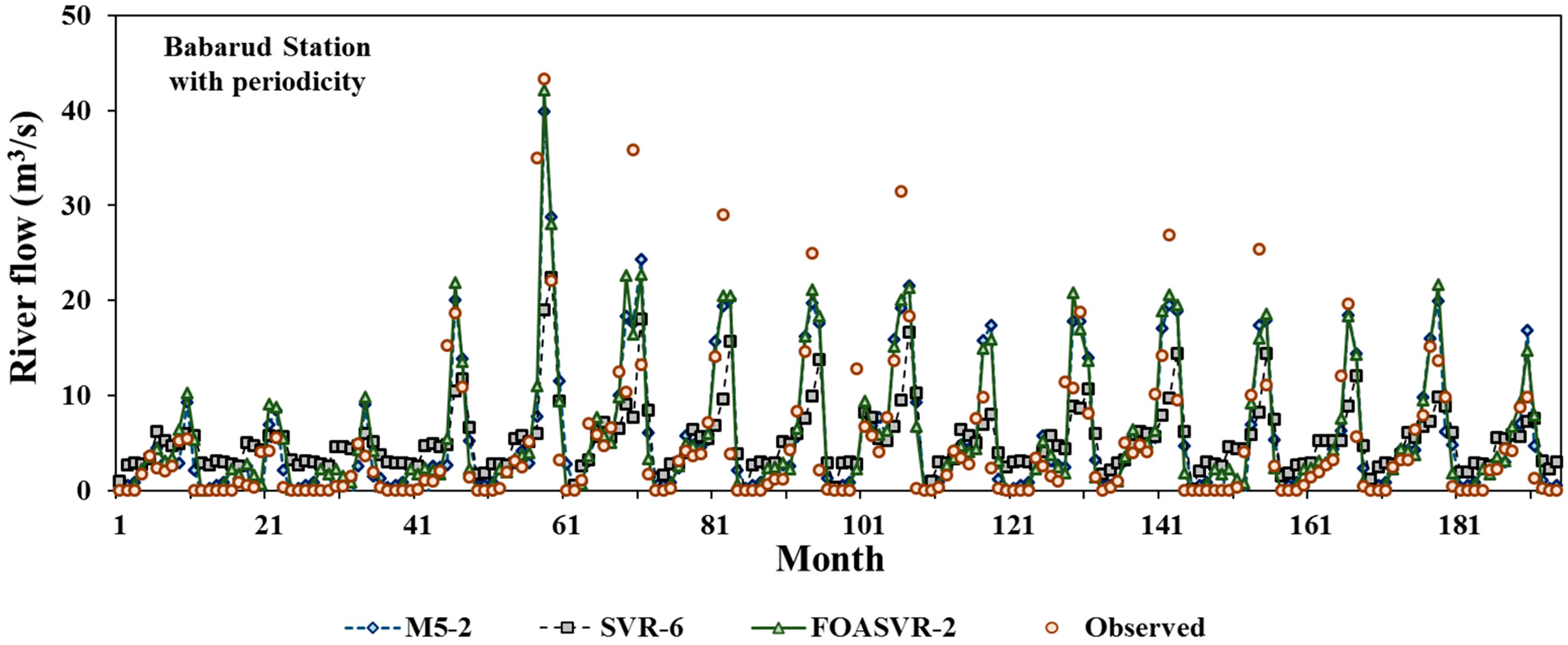
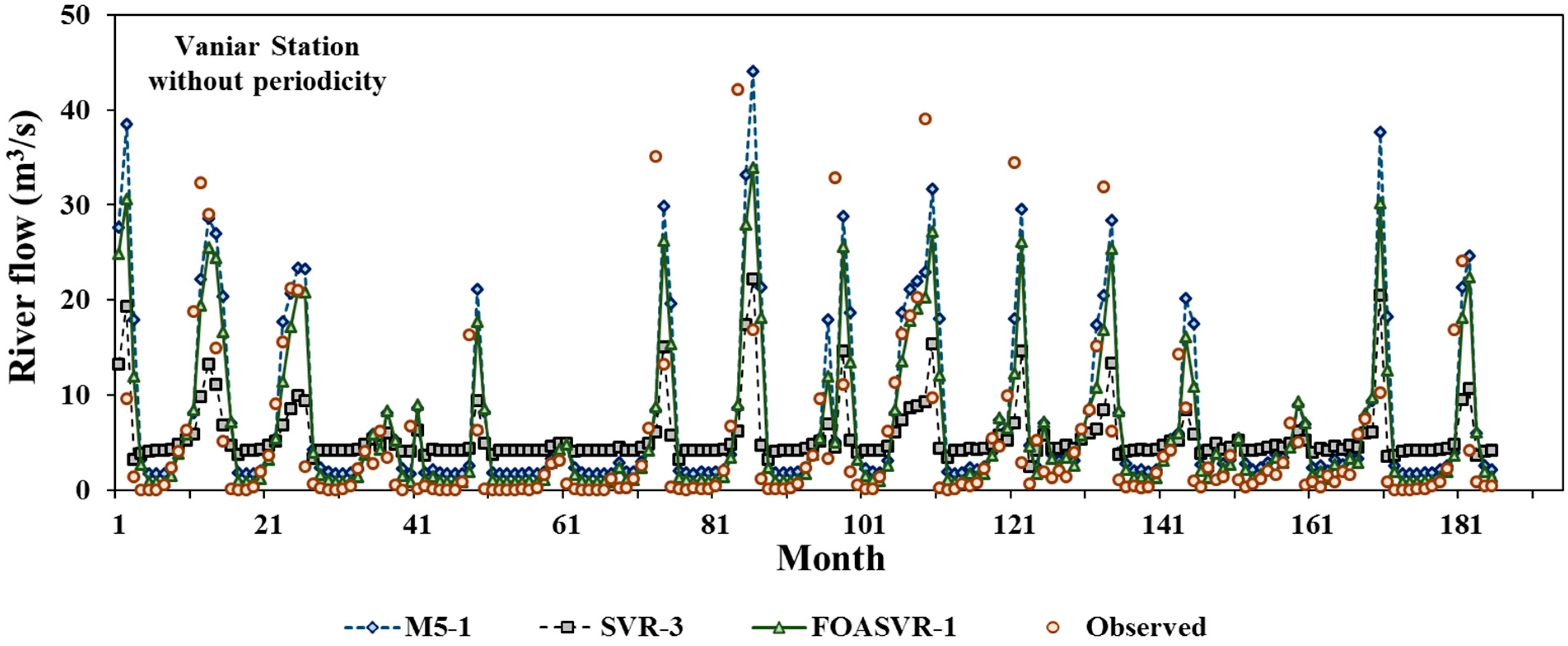
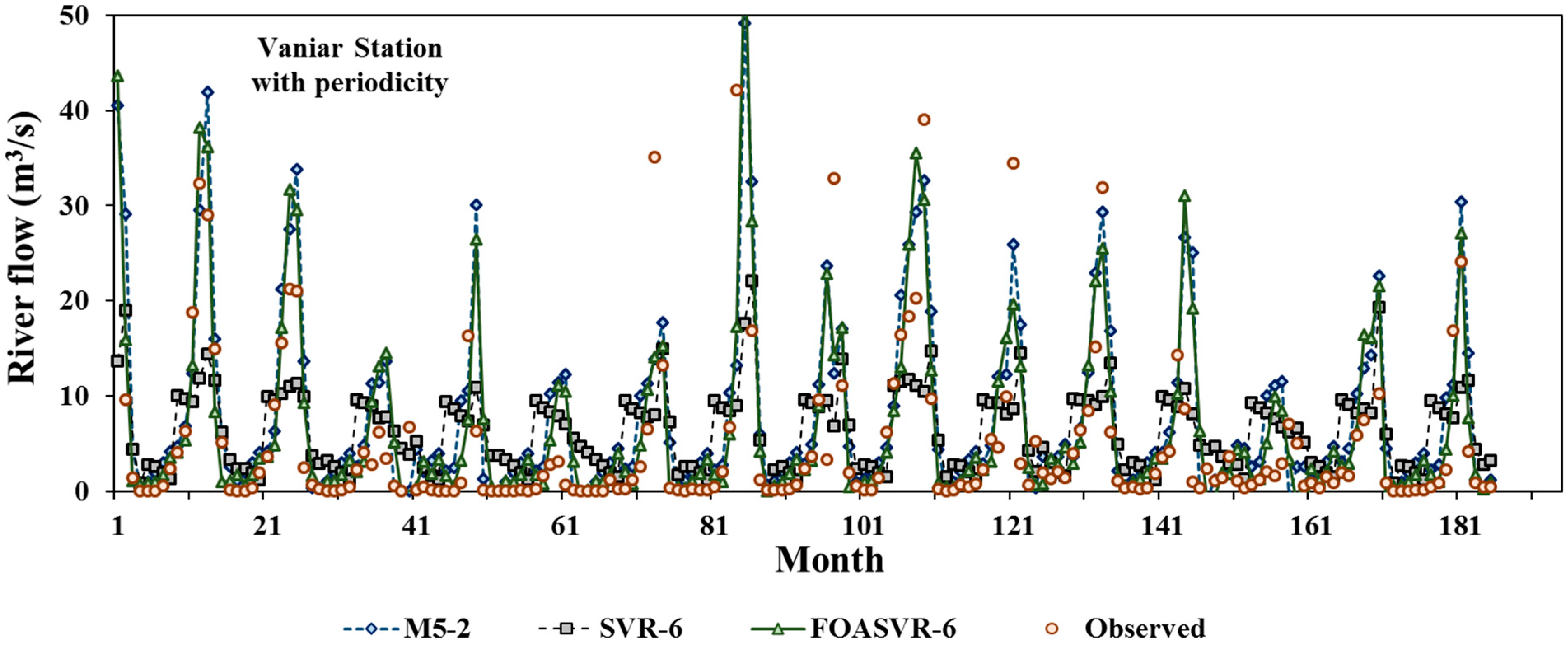
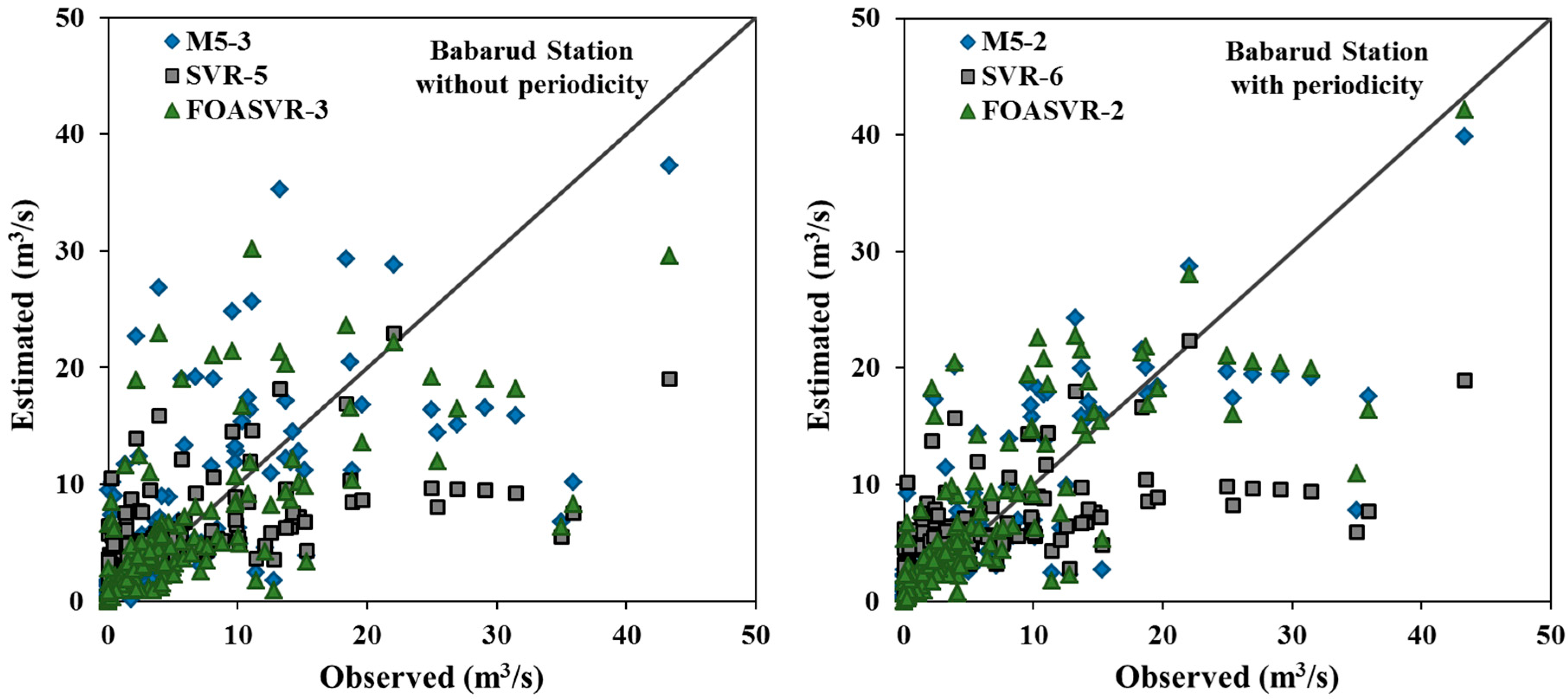
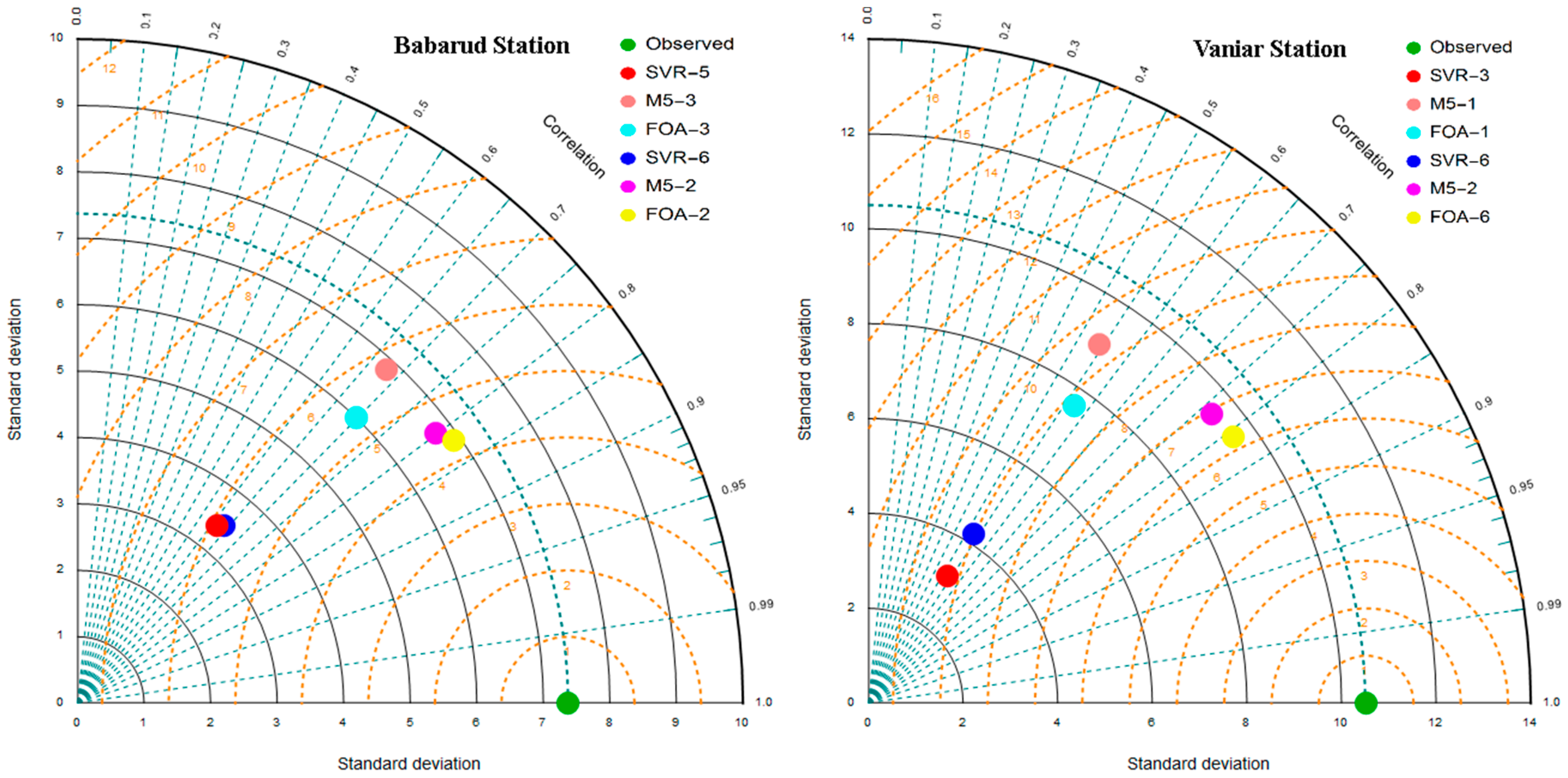
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Onyari, E.; Ilunga, F. Application of MLP neural network and M5P model tree in predicting streamflow: A case study of Luvuvhu catchment, South Africa. In Proceedings of the International Conference on Information and Multimedia Technology (ICMT), Hong Kong, China, 28–30 December 2010; pp. 156–160. [Google Scholar]
- Harrigan, S.; Prudhomme, C.; Parry, S.; Smith, K.; Tanguy, M. Benchmarking ensemble streamflow prediction skill in the UK. Hydrol. Earth Syst. Sci. 2018, 22, 2023–2039. [Google Scholar] [CrossRef]
- Muhammad, A.; Stadnyk, T.; Unduche, F.; Coulibaly, P. Multi-model approaches for improving seasonal ensemble streamflow prediction scheme with various statistical post-processing techniques in the Canadian Prairie region. Water 2018, 10, 1604. [Google Scholar] [CrossRef]
- Bou-Fakhreddine, B.; Mougharbel, I.; Faye, A.; Chakra, S.A.; Pollet, Y. Daily river flow prediction based on Two-Phase Constructive Fuzzy Systems Modeling: A case of hydrological–meteorological measurements asymmetry. J. Hydrol. 2018, 558, 255–265. [Google Scholar] [CrossRef]
- Baydaroğlu, Ö.; Koçak, K.; Duran, K. River flow prediction using hybrid models of support vector regression with the wavelet transform, singular spectrum analysis and chaotic approach. Meteorol. Atmos. Phys. 2018, 130, 349–359. [Google Scholar] [CrossRef]
- Fernando, A.K.; Shamseldin, A.Y.; Abrahart, B.J. River Flow Forecasting Using Gene Expression Programming Models. In Proceedings of the 10th International Conference on Hydroinformatics HIC 2012, Hamburg, Germany, 14–18 July 2012. [Google Scholar]
- Rehana, S. River Water Temperature Modelling Under Climate Change Using Support Vector Regression. In Hydrology in a Changing World; Springer: Cham, Switzerland, 2019; pp. 171–183. [Google Scholar]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2018, 569, 387–408. [Google Scholar] [CrossRef]
- Azad, A.; Farzin, S.; Kashi, H.; Sanikhani, H.; Karami, H.; Kisi, O. Prediction of river flow using hybrid neuro-fuzzy models. Arab. J. Geosci. 2018, 11, 718. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An Ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Qasem, S.N.; Samadianfard, S.; Nahand, H.S.; Mosavi, A.; Shamshirband, S.; Chau, K.W. Estimating Daily Dew Point Temperature Using Machine Learning Algorithms. Water 2019, 11, 582. [Google Scholar] [CrossRef]
- Tongal, H.; Booij, M.J. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Darwen, P.J. Bayesian model averaging for river flow prediction. Appl. Intell. 2019, 49, 103–111. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D.P. Neural networks and M5 model trees in modeling water level–discharge relationship. Neurocomputing 2005, 63, 381–396. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D.P. Machine learning in sedimentation modeling. Neural Netw. 2006, 19, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.S.; See, L. Rainfall-Runoff Modeling Using Data-Driven and Statistical Methods; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2006. [Google Scholar]
- Siek, M.; Solomatine, D.P. Tree-like machine learning models in hydrologic forecasting: Optimality and expert knowledge. Geophys. Res. Abstr. 2007, 9, 2–5. [Google Scholar]
- Stravs, L.; Brilly, M. Development of a low flow forecasting model using the M5 machine learning method. Hydrol. Sci. 2007, 52, 466–477. [Google Scholar] [CrossRef]
- Samadianfard, S.; Nazemi, A.H.; Sadraddini, A.A. M5 model tree and gene expression programming based modeling of sandy soil water movement under surface drip irrigation. Agric. Sci. Dev. 2014, 3, 178–190. [Google Scholar]
- Samadianfard, S.; Sattari, M.T.; Kisi, O.; Kazemi, H. Determining flow friction factor in irrigation pipes using data mining and artificial intelligence approaches. Appl. Artif. Intell. 2014, 28, 793–813. [Google Scholar] [CrossRef]
- Esmaeilzadeh, B.; Sattari, M.T.; Samadianfard, S. Performance evaluation of ANNs and an M5 model tree in Sattarkhan Reservoir inflow prediction. ISH J. Hydraul. Eng. 2017, 23, 283–292. [Google Scholar] [CrossRef]
- Londhe, S.N.; Dixit, P.R. Forecasting Stream Flow Using Model Trees. Int. J. Earth Sci. Eng. 2011, 4, 282–285. [Google Scholar]
- Sattari, M.T.; Pal, M.; Apaydin, H.; Ozturk, F. M5 Model Tree Application in Daily River Flow Forecasting in Sohu Stream, Turkey. Water Resour. 2013, 40, 233–242. [Google Scholar] [CrossRef]
- Liong, S.Y.; Sivapragasam, C. Flood stage forecasting with support vector machines. J. AWRA 2002, 38, 173–186. [Google Scholar] [CrossRef]
- Yu, X.Y.; Liong, S.Y.; Babovic, V. EC-SVM approach for realtime hydrologic forecasting. J. Hydroinf. 2004, 6, 209–233. [Google Scholar] [CrossRef]
- Kalteh, A.M. Monthly river flow forecasting using artificial neural network and support vector regression models coupled with wavelet transform. Comput. Geosci. 2013, 54, 1–8. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. River stage prediction based on a distributed support vector regression. J. Hydrol. 2008, 358, 96–111. [Google Scholar] [CrossRef]
- Londhe, S.; Gavraskar, S.S. Forecasting One Day Ahead Stream Flow Using Support Vector Regression. Aquat. Procedia 2015, 4, 900–907. [Google Scholar] [CrossRef]
- Cao, G.; Wu, L. Support vector regression with fruit fly optimization algorithm for seasonal electricity consumption forecasting. Energy 2016, 115, 734–745. [Google Scholar] [CrossRef]
- Lijuan, W.; Guohua, C. Seasonal SVR with FOA algorithm for single-step and multi-step ahead forecasting in monthly inbound tourist flow. Knowl.-Based Syst. 2016, 110, 157–166. [Google Scholar] [CrossRef]
- Kurup, P.U.; Dudani, N.K. Neural networks for profiling stress history of clays from PCPT data. J. Geotech. Geoenviron. Eng. 2014, 128, 569–579. [Google Scholar] [CrossRef]
- Pal, M. M5 model tree for land cover classification. Int. J. Remote Sens. 2006, 27, 825–831. [Google Scholar] [CrossRef]
- Samadianfard, S.; Delirhasannia, R.; Kisi, O.; Agirre-Basurko, E. Comparative analysis of ozone level prediction models using gene expression programming and multiple linear regression. Geofizika 2013, 30, 43–74. [Google Scholar]
- Deo, R.C.; Ghorbani, M.A.; Samadianfard, S.; Maraseni, T.; Bilgili, M.; Biazar, M. Multi-layer perceptron hybrid model integrated with the firefly optimizer algorithm for windspeed prediction of target site using a limited set of neighboring reference station data. Renew. Energy 2018, 116, 309–323. [Google Scholar] [CrossRef]
- Samadianfard, S.; Asadi, E.; Jarhan, S.; Kazemi, H.; Kheshtgar, S.; Kisi, O.; Sajjadi, S.; Abdul Manaf, A. Wavelet neural networks and gene expression programming models to predict short-term soil temperature at different depths. Soil Tillage Res. 2018, 175, 37–50. [Google Scholar] [CrossRef]
- Available online: https://earth.google.com/web/@32.205151,53.07029487,2852.42968574a,2667368.97567809d,35y,0.11753984h,16.72644158t,-0r (accessed on 21 February 2019).
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations; Morgan Kaufmann: San Francisco, CA, USA, 2005. [Google Scholar]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the Fifth Australian Joint Conf. on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; Adams, A., Sterling, L., Eds.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Gunn, S.R. Support Vector Machines for Classification and Regression, Technical Report; University of Southampton: Southampton, UK, 1998. [Google Scholar]
- Cimen, M. Estimation of daily suspended sediments using support vector machines. Hydrol. Sci. J. 2008, 53, 656–666. [Google Scholar] [CrossRef]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Wu, C.-H.; Tzeng, G.-H.; Lin, R.-H. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
- Pan, W.-T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. Training v-support vector classifiers: Theory and algorithms. Neural Comput. 2001, 13, 2119–2147. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Model Selection and Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]


| Station | Data Set | Xmean (m3/s) | Xmax (m3/s) | Xmin (m3/s) | Sx (m3/s) | Csx (m3/s) | r1 | r2 | r3 |
|---|---|---|---|---|---|---|---|---|---|
| Babarud | Training data | 8.75 | 66.50 | 0.00 | 9.63 | 2.05 | 0.70 | 0.25 | −0.07 |
| Testing data | 4.71 | 43.27 | 0.00 | 7.37 | 2.54 | 0.59 | 0.14 | −0.12 | |
| Entire data | 7.74 | 66.50 | 0.00 | 9.28 | 2.13 | 0.69 | 0.25 | −0.05 | |
| Vaniar | Training data | 14.28 | 178.29 | 0.00 | 21.35 | 2.94 | 0.62 | 0.15 | −0.11 |
| Testing data | 5.66 | 65.30 | 0.00 | 10.50 | 3.02 | 0.50 | 0.11 | −0.05 | |
| Entire data | 12.13 | 178.29 | 0.00 | 19.58 | 3.19 | 0.63 | 0.18 | −0.07 |
| Model | Input Parameters | Output Parameters |
|---|---|---|
| 1 | Qt−1 | Qt |
| 2 | Qt−1, π | Qt |
| 3 | Qt−1, Qt−2 | Qt |
| 4 | Qt−1, Qt−2, π | Qt |
| 5 | Qt−1, Qt−2, Qt−3 | Qt |
| 6 | Qt−1, Qt−2, Qt−3, π | Qt |
| Model Input | Model | Statistical Parameters | |||
|---|---|---|---|---|---|
| RMSE (m3/s) | MAE (m3/s) | R | BIC | ||
| Qt−1 | SVR-1 | 6.10 | 4.10 | 0.59 | 706.88 |
| M5-1 | 5.94 | 3.62 | 0.61 | 696.57 | |
| FOASVR-1 | 5.74 | 3.29 | 0.63 | 683.28 | |
| Qt−1, π | SVR-2 | 5.97 | 3.88 | 0.61 | 703.79 |
| M5-2 | 4.54 | 2.73 | 0.80 | 597.55 | |
| FOASVR-2 | 4.36 | 2.40 | 0.82 | 581.85 | |
| Qt−1, Qt−2 | SVR-3 | 5.98 | 4.04 | 0.62 | 704.44 |
| M5-3 | 5.79 | 3.49 | 0.68 | 691.92 | |
| FOASVR-3 | 5.33 | 2.90 | 0.70 | 659.80 | |
| Qt−1, Qt−2, π | SVR-4 | 5.85 | 3.83 | 0.64 | 701.18 |
| M5-4 | 4.55 | 2.83 | 0.80 | 603.67 | |
| FOASVR-4 | 4.50 | 2.67 | 0.80 | 599.39 | |
| Qt−1, Qt−2, Qt−3 | SVR-5 | 5.91 | 3.90 | 0.62 | 705.14 |
| M5-5 | 5.79 | 3.50 | 0.68 | 697.18 | |
| FOASVR-5 | 5.69 | 3.20 | 0.67 | 690.42 | |
| Qt−1, Qt−2, Qt−3, π | SVR-6 | 5.82 | 3.77 | 0.64 | 704.46 |
| M5-6 | 4.54 | 2.84 | 0.80 | 608.09 | |
| FOASVR-6 | 4.58 | 2.67 | 0.79 | 611.49 | |
| Model Input | Model | Statistical Parameters | |||
|---|---|---|---|---|---|
| RMSE (m3/s) | MAE (m3/s) | R | BIC | ||
| Qt−1 | SVR-1 | 9.33 | 5.60 | 0.50 | 831.52 |
| M5-1 | 9.57 | 5.44 | 0.54 | 840.91 | |
| FOASVR-1 | 8.78 | 4.77 | 0.57 | 809.04 | |
| Qt−1, π | SVR-2 | 9.04 | 5.31 | 0.52 | 825.05 |
| M5-2 | 7.19 | 4.46 | 0.77 | 740.34 | |
| FOASVR-2 | 6.58 | 3.86 | 0.79 | 707.53 | |
| Qt−1, Qt−2 | SVR-3 | 9.21 | 5.57 | 0.53 | 831.95 |
| M5-3 | 9.80 | 5.46 | 0.59 | 854.92 | |
| FOASVR-3 | 8.88 | 4.97 | 0.55 | 818.45 | |
| Qt−1, Qt−2, π | SVR-4 | 8.96 | 5.33 | 0.54 | 826.99 |
| M5-4 | 7.58 | 4.64 | 0.76 | 765.10 | |
| FOASVR-4 | 6.48 | 3.75 | 0.80 | 707.09 | |
| Qt−1, Qt−2, Qt−3 | SVR-5 | 9.22 | 5.73 | 0.52 | 837.57 |
| M5-5 | 9.79 | 5.55 | 0.60 | 859.76 | |
| FOASVR-5 | 8.99 | 5.53 | 0.55 | 828.22 | |
| Qt−1, Qt−2, Qt−3, π | SVR-6 | 9.01 | 5.53 | 0.53 | 834.27 |
| M5-6 | 7.61 | 4.62 | 0.75 | 771.78 | |
| FOASVR-6 | 6.33 | 3.71 | 0.81 | 703.64 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samadianfard, S.; Jarhan, S.; Salwana, E.; Mosavi, A.; Shamshirband, S.; Akib, S. Support Vector Regression Integrated with Fruit Fly Optimization Algorithm for River Flow Forecasting in Lake Urmia Basin. Water 2019, 11, 1934. https://doi.org/10.3390/w11091934
Samadianfard S, Jarhan S, Salwana E, Mosavi A, Shamshirband S, Akib S. Support Vector Regression Integrated with Fruit Fly Optimization Algorithm for River Flow Forecasting in Lake Urmia Basin. Water. 2019; 11(9):1934. https://doi.org/10.3390/w11091934
Chicago/Turabian StyleSamadianfard, Saeed, Salar Jarhan, Ely Salwana, Amir Mosavi, Shahaboddin Shamshirband, and Shatirah Akib. 2019. "Support Vector Regression Integrated with Fruit Fly Optimization Algorithm for River Flow Forecasting in Lake Urmia Basin" Water 11, no. 9: 1934. https://doi.org/10.3390/w11091934
APA StyleSamadianfard, S., Jarhan, S., Salwana, E., Mosavi, A., Shamshirband, S., & Akib, S. (2019). Support Vector Regression Integrated with Fruit Fly Optimization Algorithm for River Flow Forecasting in Lake Urmia Basin. Water, 11(9), 1934. https://doi.org/10.3390/w11091934





