Implementation of a Full Momentum Conservative Approach in Modelling Flow Through Tidal Structures
Abstract
1. Introduction
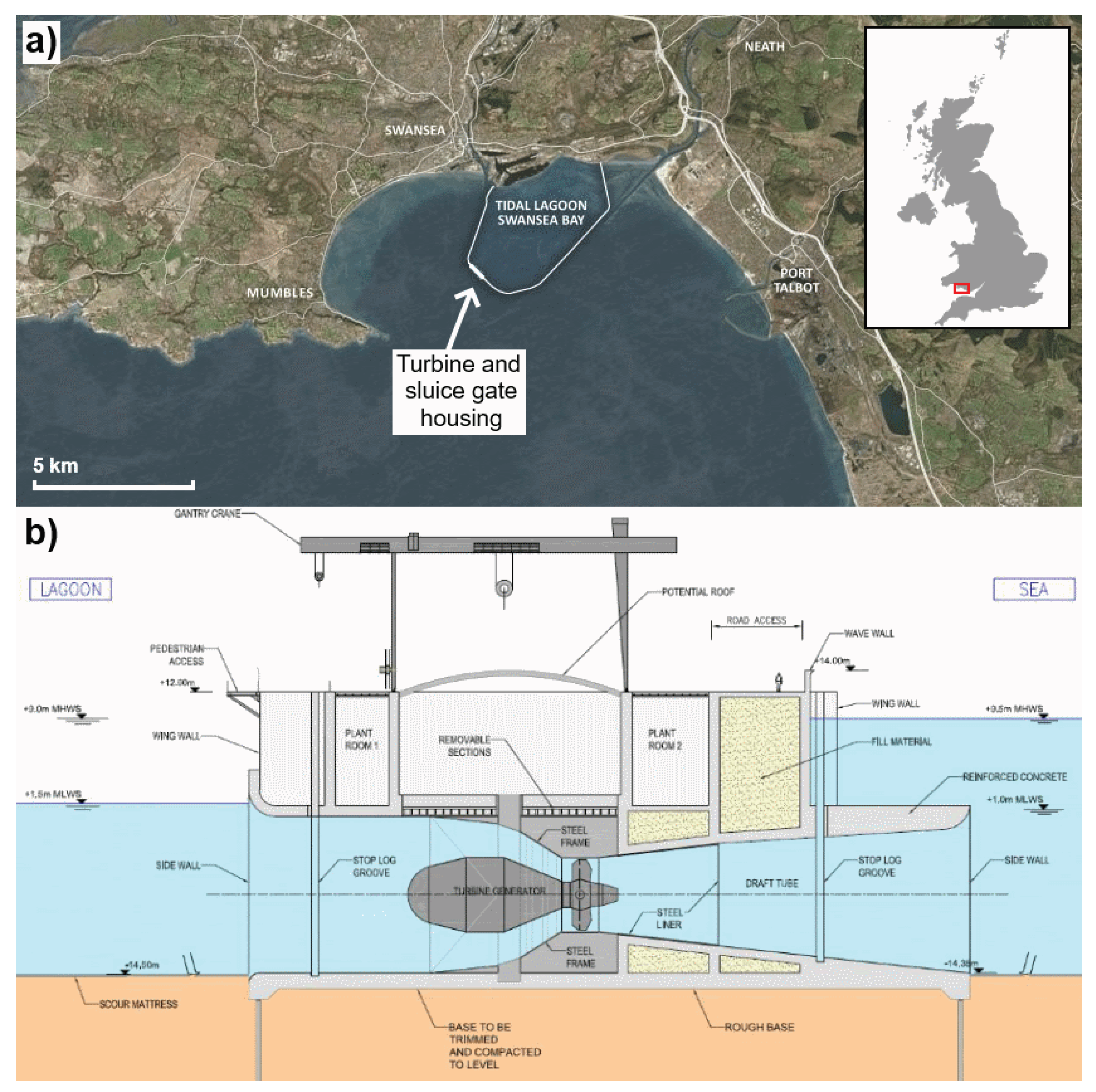
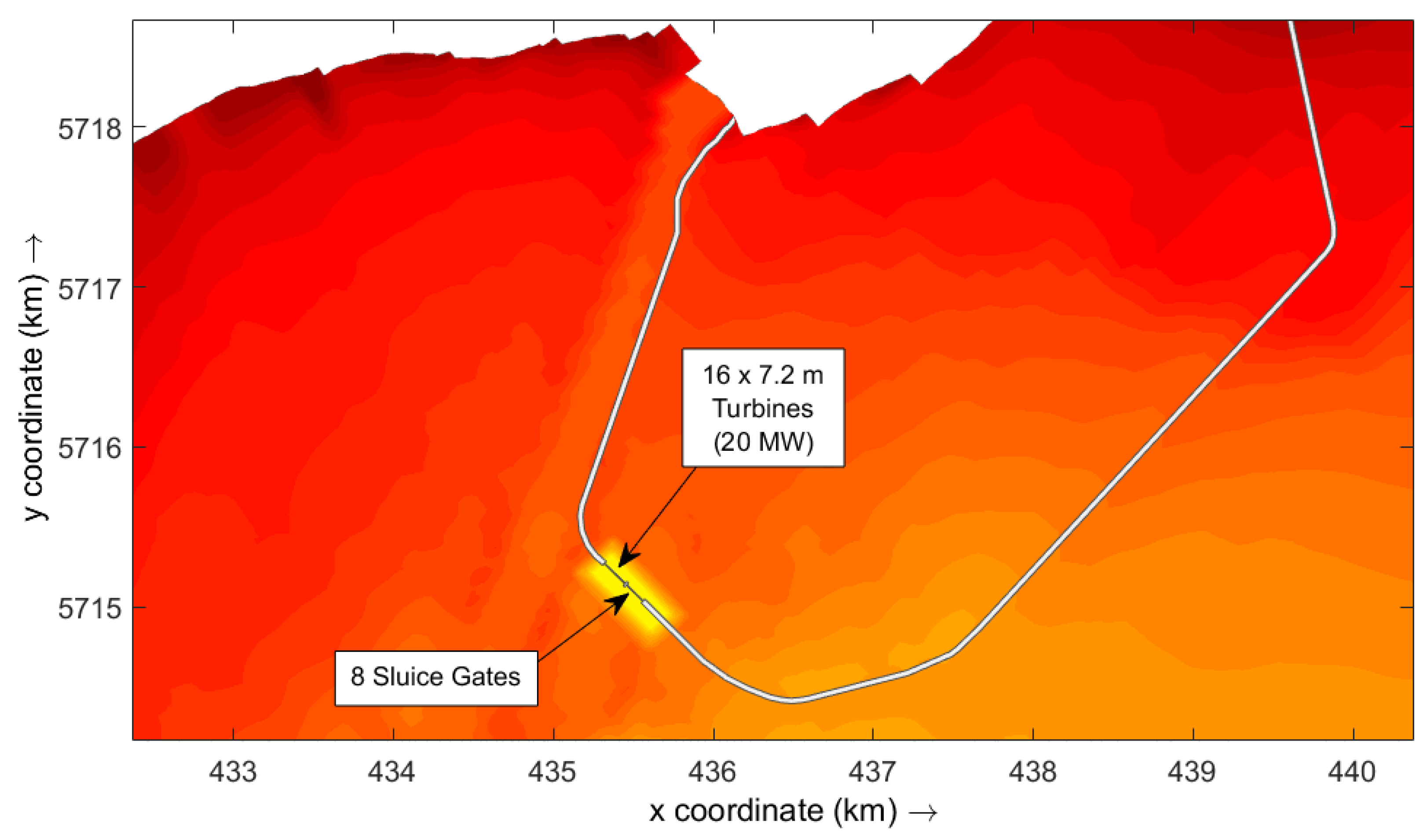
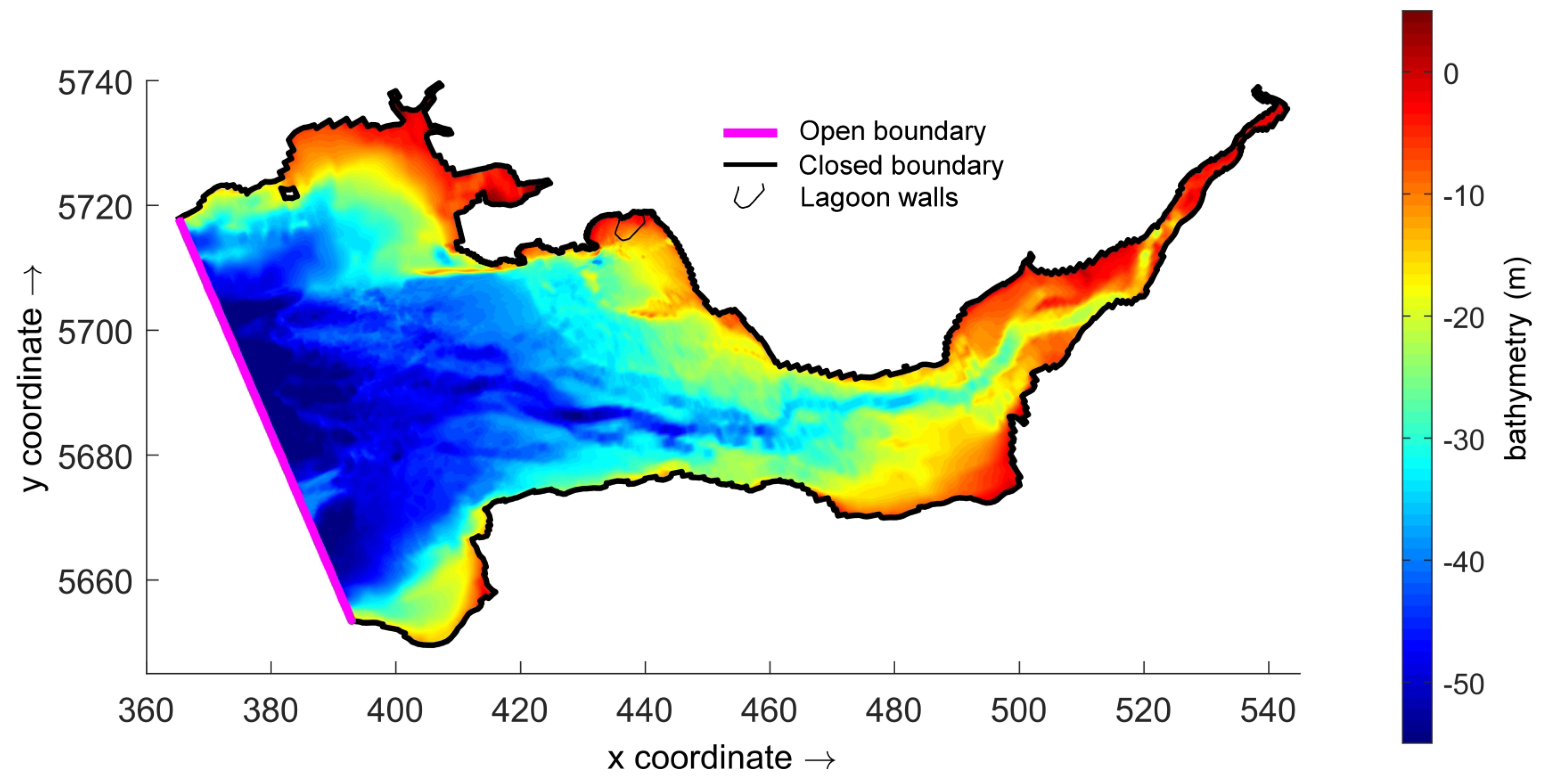
2. Swansea Bay Tidal Lagoon
3. Methodology
3.1. Delft3D and Governing Equations
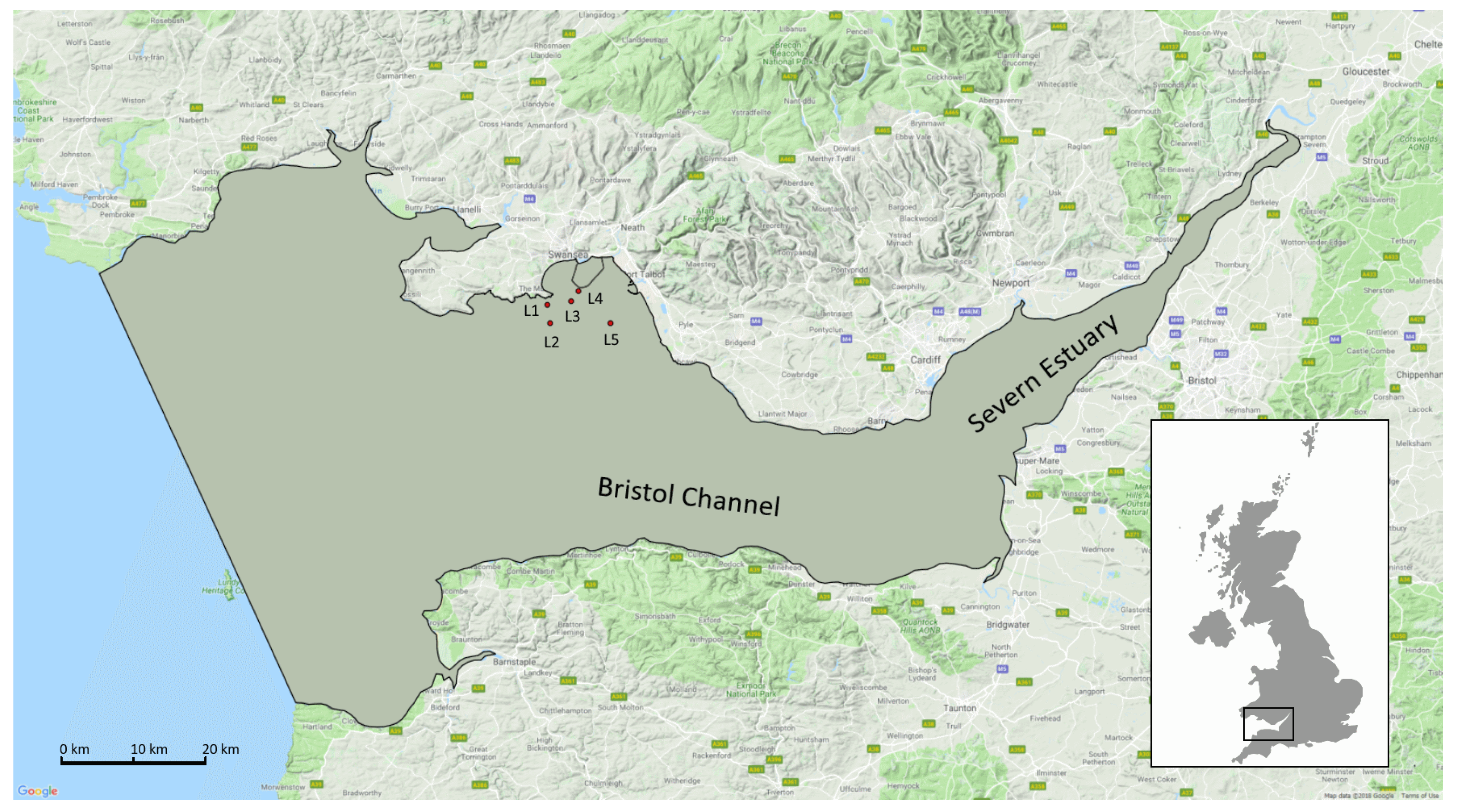
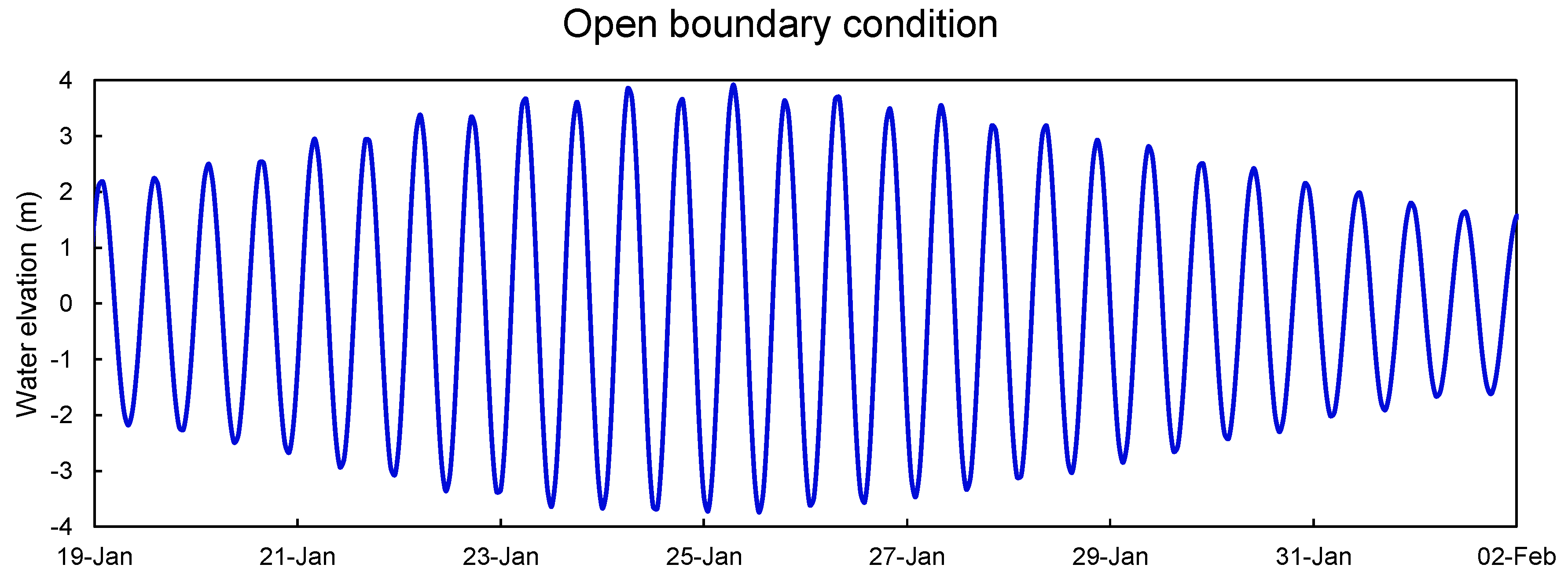
3.2. Setup of Hydrodynamic Model
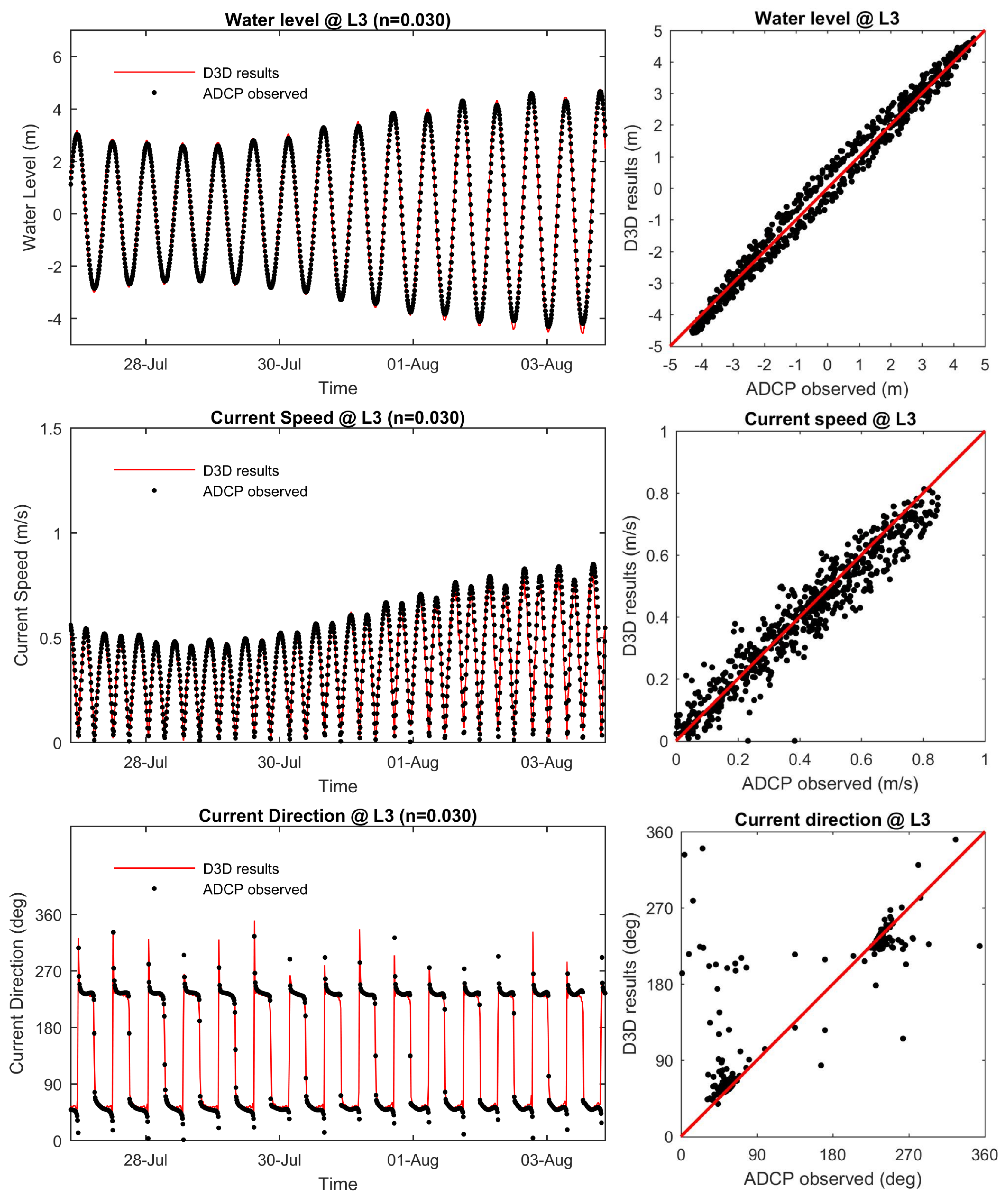
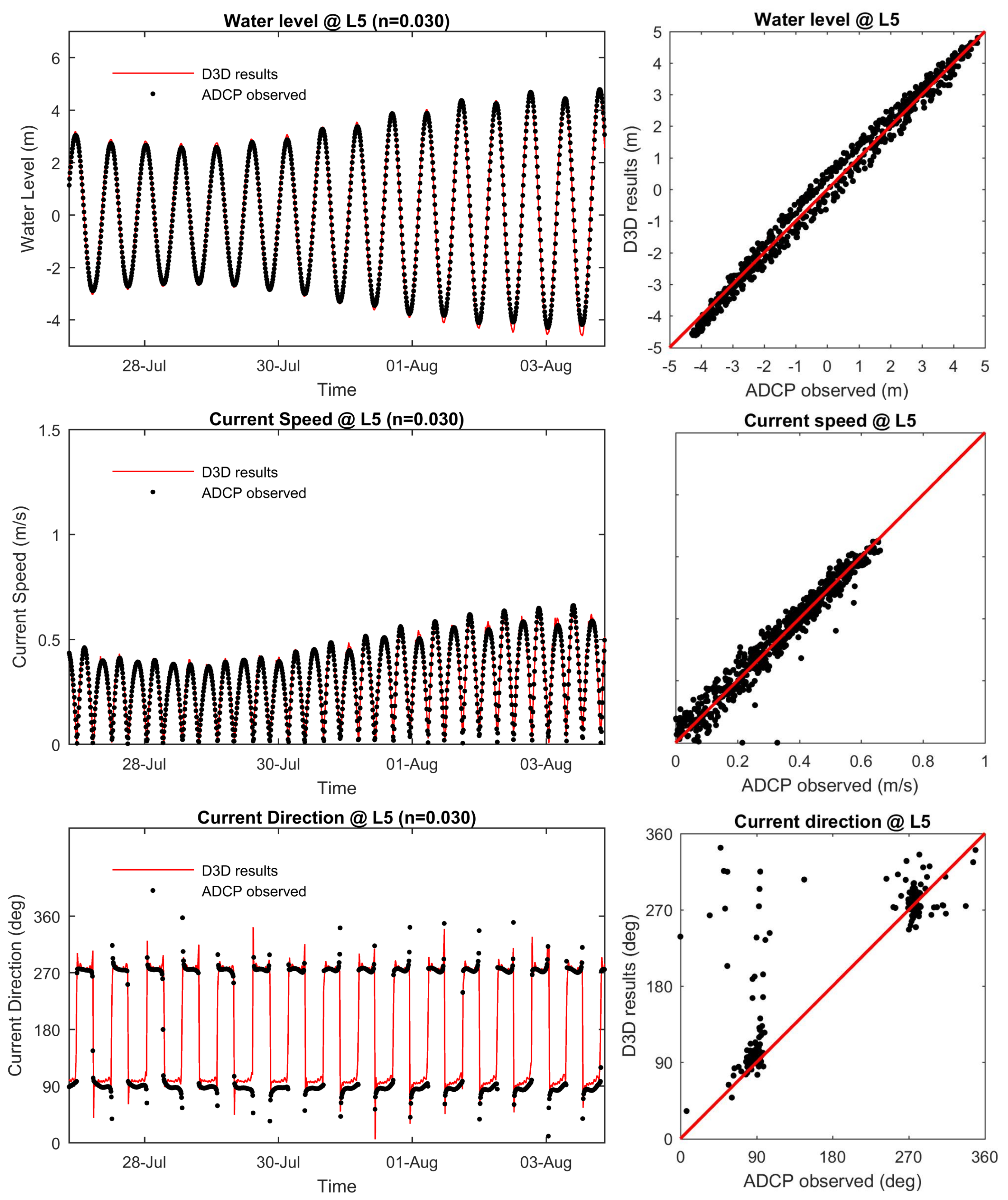
3.3. Model Validation
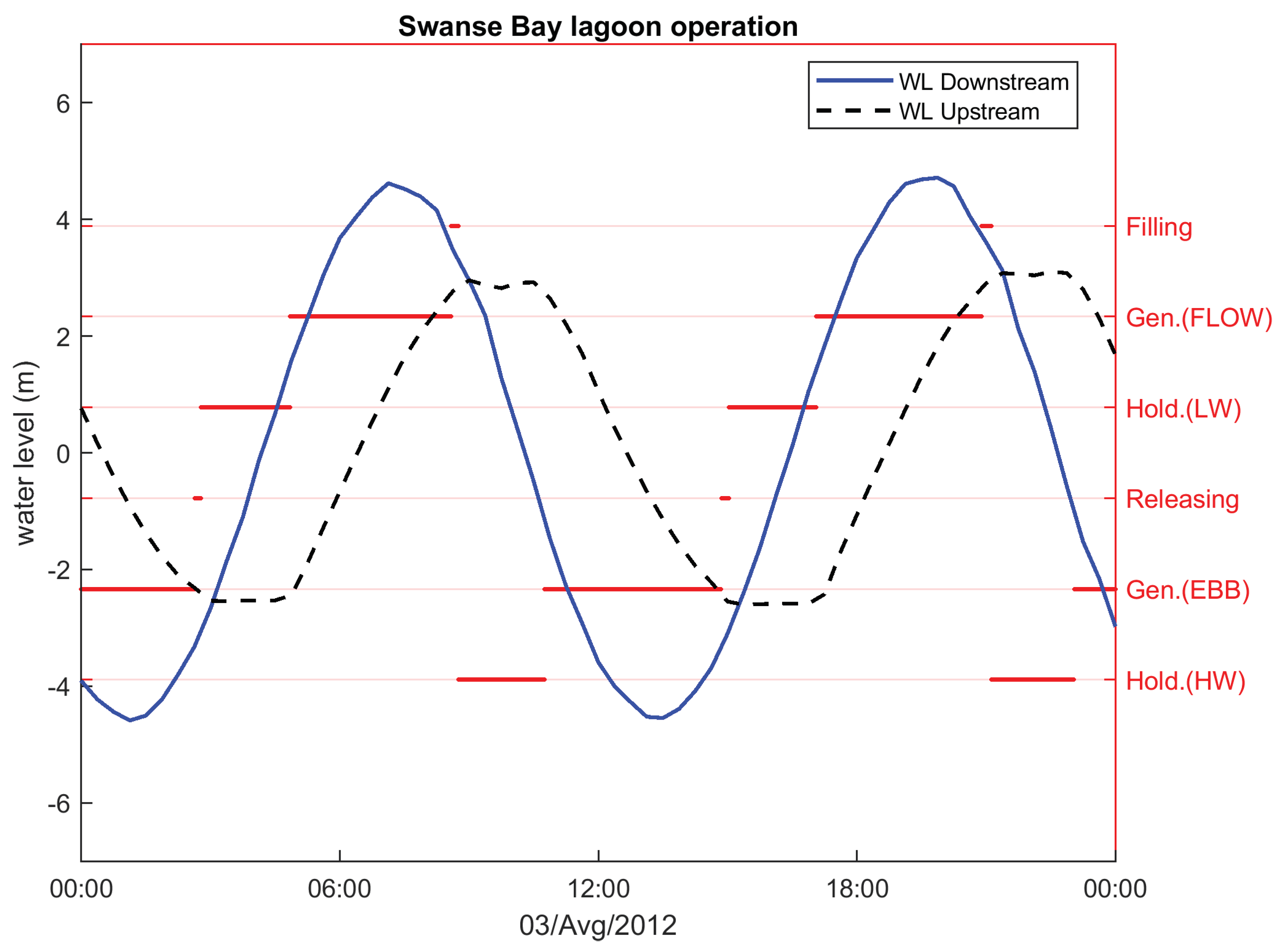
3.4. Tidal Lagoon Modelling
3.5. Momentum Conservation
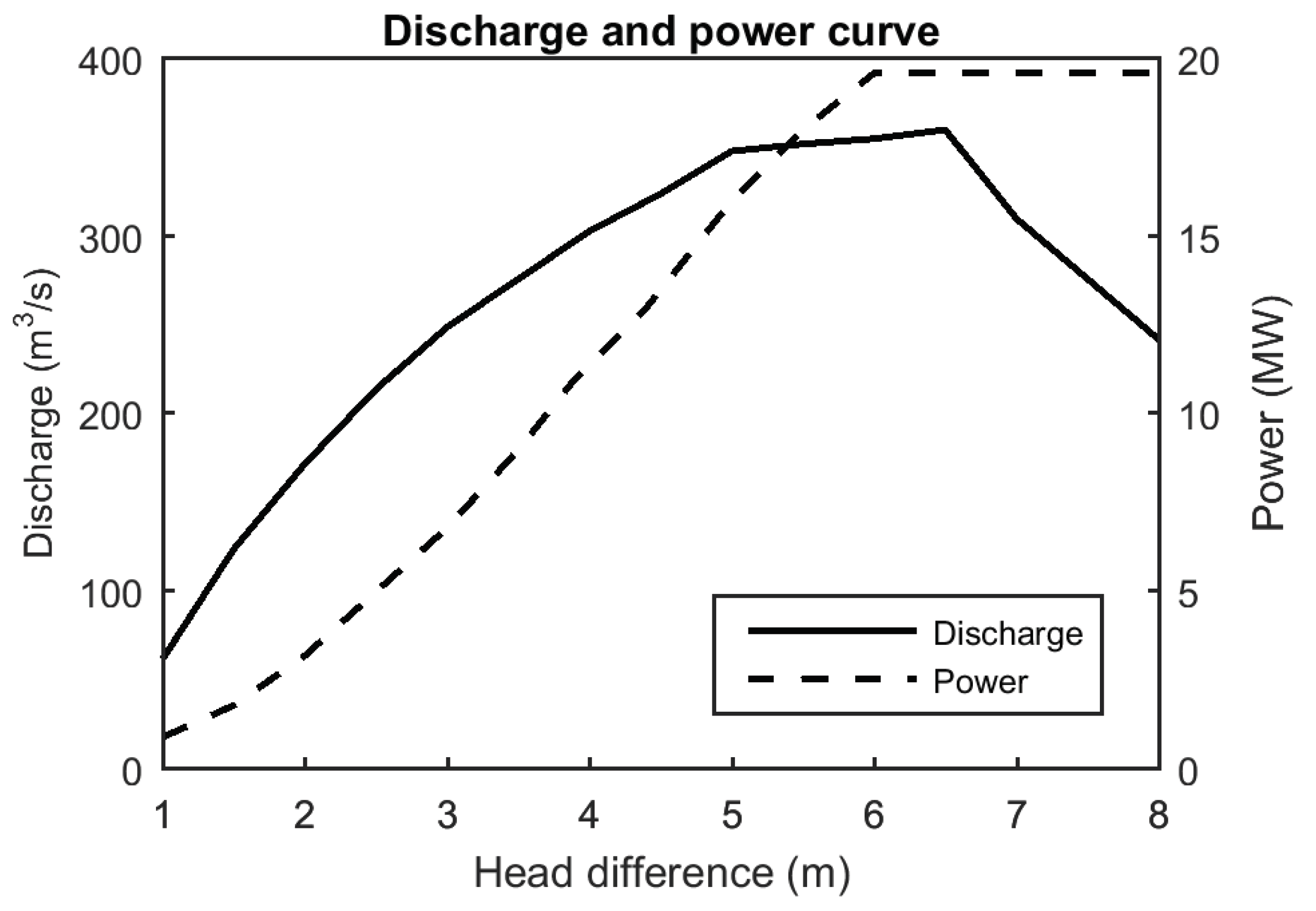
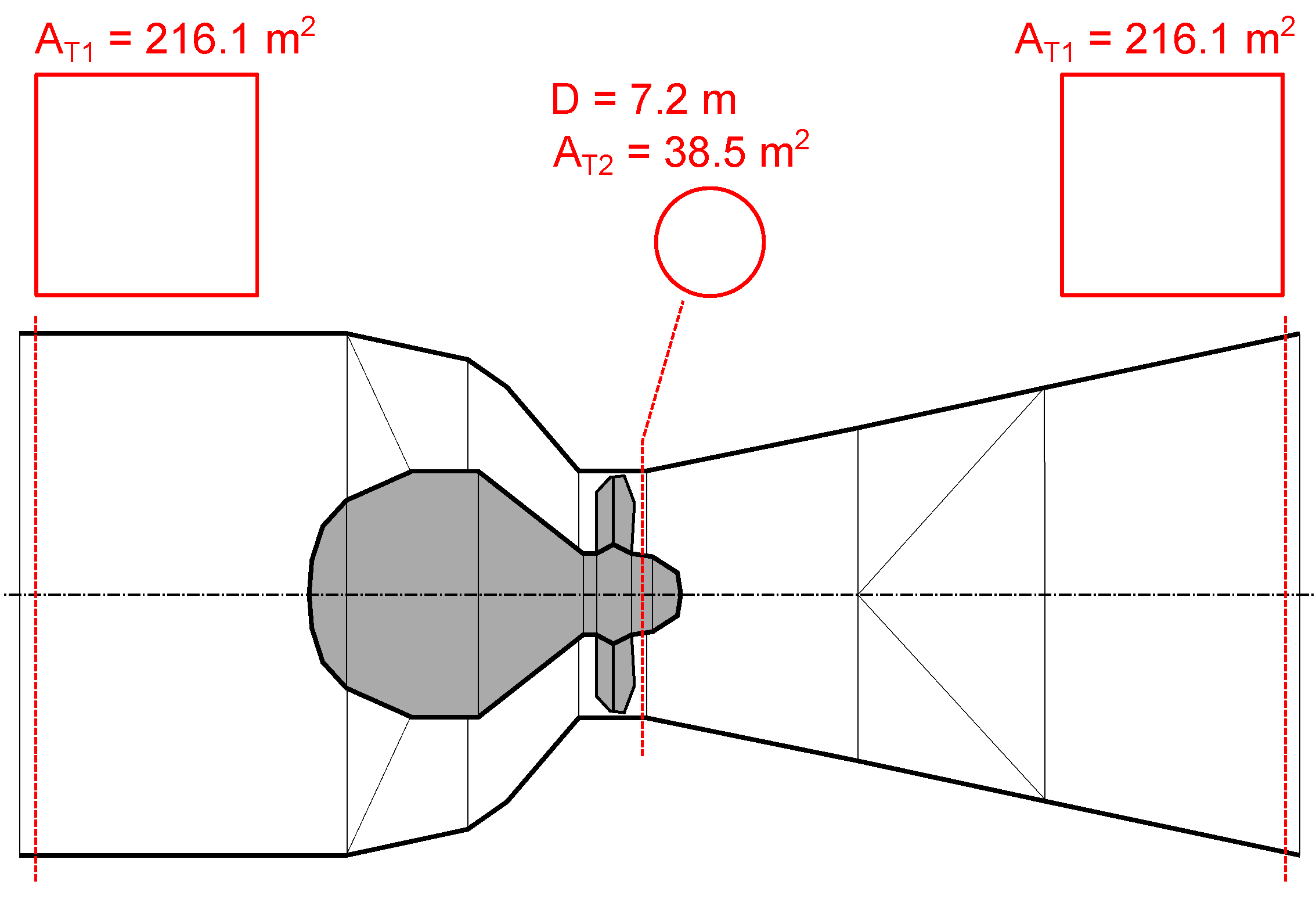
3.6. Representation of Turbine Discharge
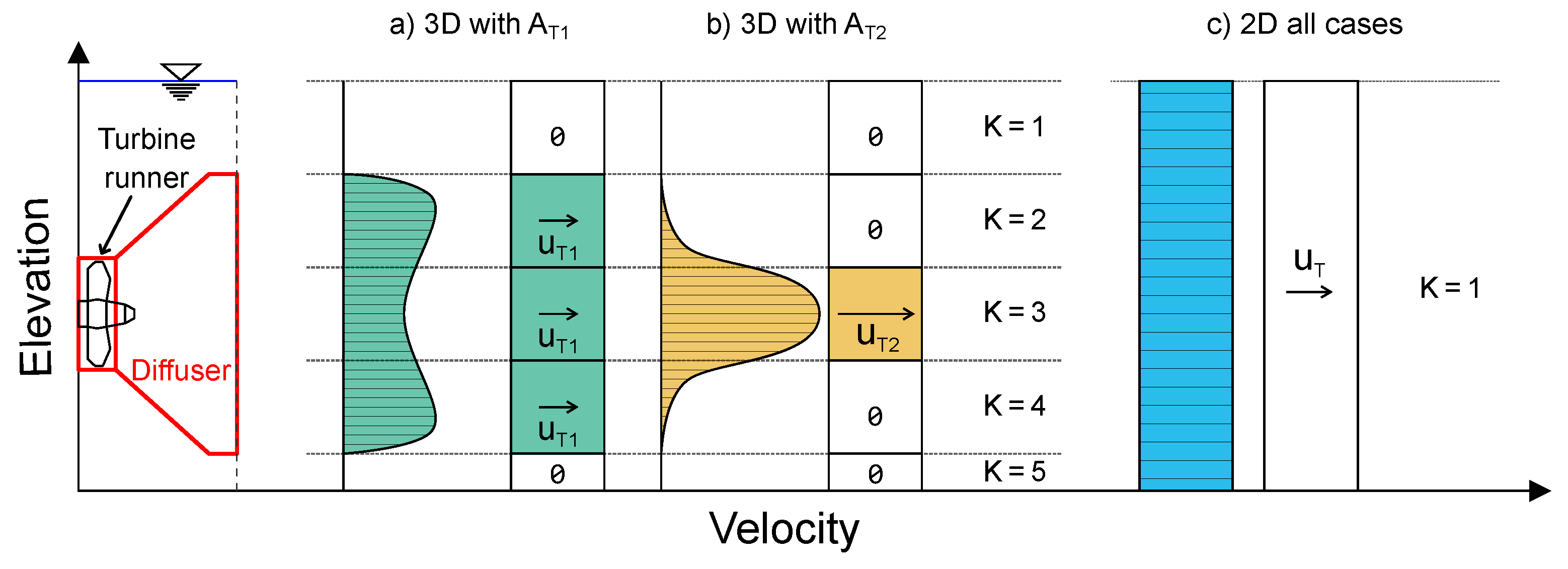
3.6.1. Realistic Velocity Distribution
3.6.2. Simplified Velocity Distribution
4. Results
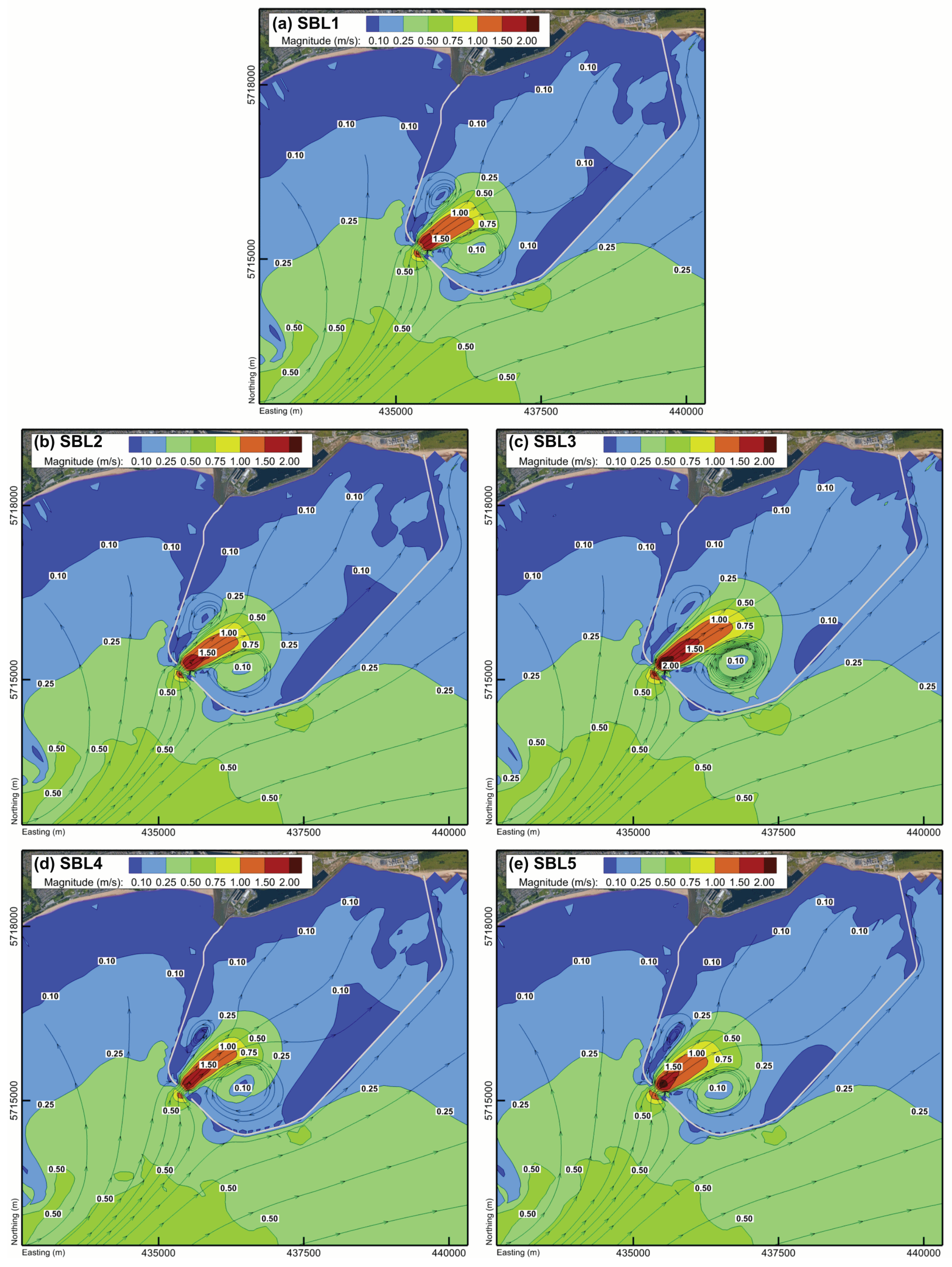
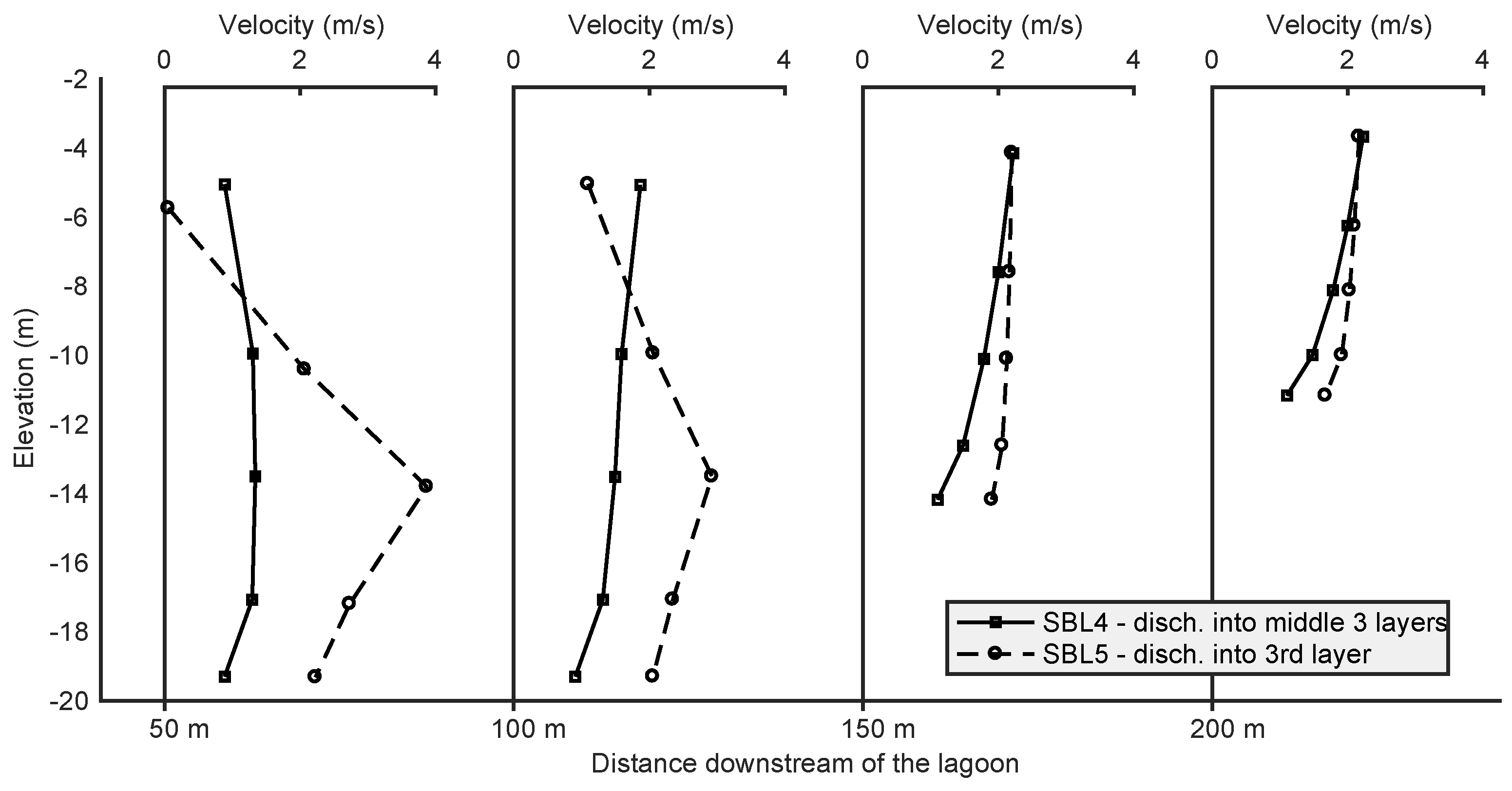
4.1. Velocity Field
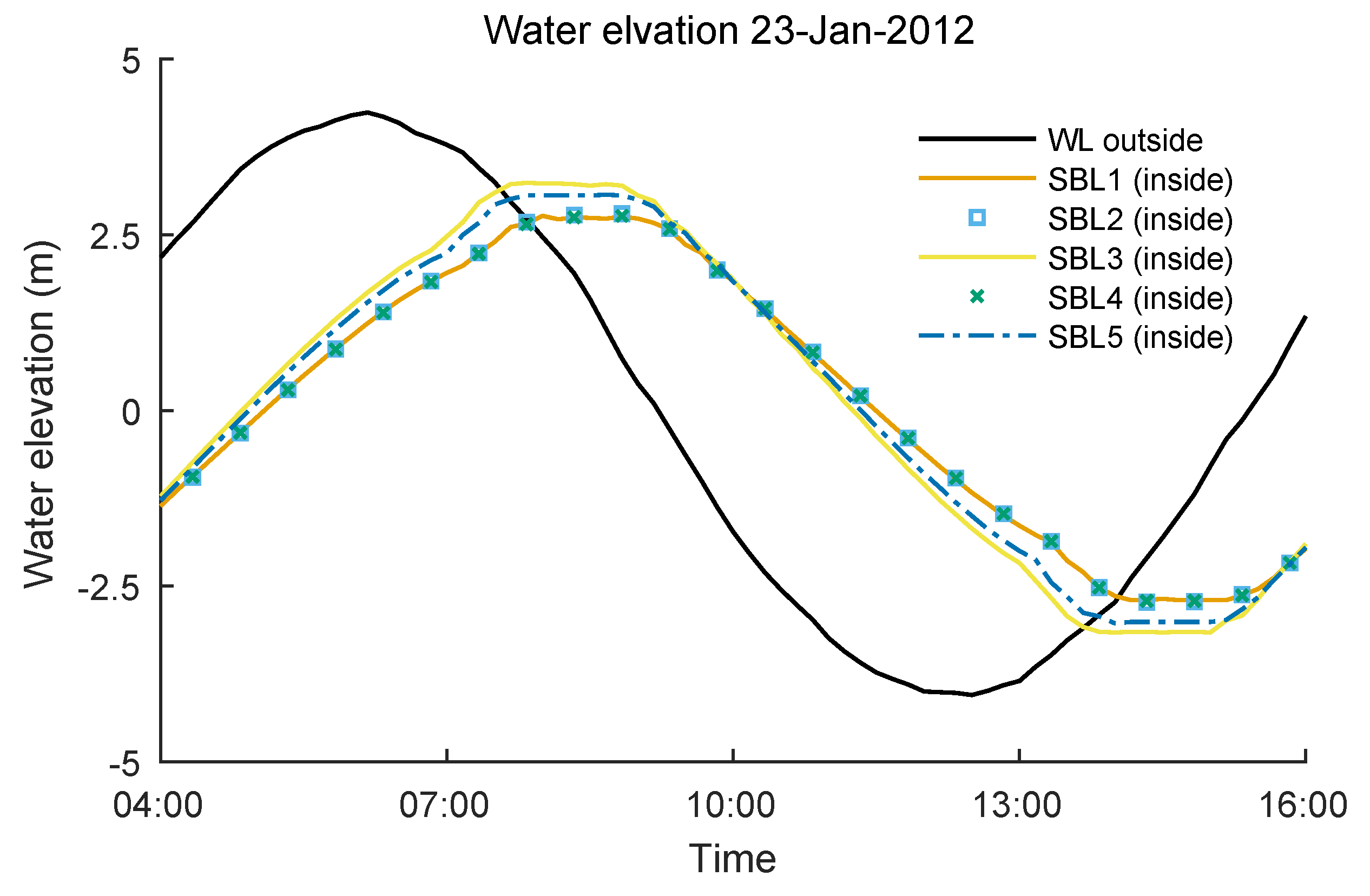
4.2. Water Levels
4.3. Power Output
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TRS | Tidal range structures |
| CFD | Computational fluid dynamics |
| RANS | Reynolds-averaged Navier–Stokes equations |
| DCO | Development consent order |
| ADI | Alternating direction implicit method |
| CD | Chart datum |
| MSL | Mean sea level |
| ADCP | Acoustic Doppler current profiler |
| NSE | Nash-Sutcliffe model efficiency |
References
- Bray, S.; Ahmadian, R.; Falconer, R.A. Impact of representation of hydraulic structures in modelling a Severn barrage. Comput. Geosci. 2016, 89, 96–106. [Google Scholar] [CrossRef]
- Angeloudis, A.; Falconer, R.A.; Bray, S.; Ahmadian, R. Representation and operation of tidal energy impoundments in a coastal hydrodynamic model. Renew. Energy 2016, 99, 1103–1115. [Google Scholar] [CrossRef]
- DUKES. Digest of UK Energy Statistics (DUKES): Renewable sources of energy. arXiv 2017, arXiv:1103.5922v2. [Google Scholar] [CrossRef]
- Charlier, R.H. Forty candles for the Rance River TPP tides provide renewable and sustainable power generation. Renew. Sustain. Energy Rev. 2007, 11, 2032–2057. [Google Scholar] [CrossRef]
- Waters, S.; Aggidis, G.A. Tidal range technologies and state of the art in review. Renew. Sustain. Energy Rev. 2016, 59, 514–529. [Google Scholar] [CrossRef]
- Department of Energy and Climate Change (DECC). Severn Tidal Power—Feasibility Study: Conclusions and Summary Report Ref: 10D/808. 2010. Available online: https://www.gov.uk/government/publications/ 1-severn-tidal-power-feasibility-study-conclusions-and-summary-report (accessed on 28 March 2016).
- Uncles, R.J. Physical properties and processes in the Bristol Channel and Severn Estuary. Mar. Pollut. Bull. 2010, 61, 5–20. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Falconer, R.A.; Lin, B. Hydrodynamic impact of a tidal barrage in the Severn Estuary, UK. Renew. Energy 2010, 35, 1455–1468. [Google Scholar] [CrossRef]
- Xia, J.; Falconer, R.A.; Lin, B.; Tan, G. Estimation of future coastal flood risk in the Severn Estuary due to a barrage. J. Flood Risk Manag. 2011, 4, 247–259. [Google Scholar] [CrossRef]
- Kadiri, M.; Ahmadian, R.; Bockelmann-Evans, B.N.; Rauen, W.; Falconer, R.A. A review of the potential water quality impacts of tidal renewable energy systems. Renew. Sustain. Energy Rev. 2012, 16, 329–341. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.A.; Lin, B. Hydro-environmental modeling of proposed Severn barrage, UK. Energy 2010, 163, 107–117. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.A.; Bockelmann-Evans, B. Comparison of hydro–environmental impacts for ebb-only and two-way generation for a Severn Barrage. Comput. Geosci. 2014, 71, 11–19. [Google Scholar] [CrossRef]
- Angeloudis, A.; Falconer, R.A. Sensitivity of tidal lagoon and barrage hydrodynamic impacts and energy outputs to operational characteristics. Renew. Energy 2017, 114, 337–351. [Google Scholar] [CrossRef]
- Ahmadian, R.; Xue, J.; Falconer, R.A.; Hanousek, N. Optimisation of Tidal Range Schemes. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1–6. [Google Scholar]
- Xue, J.; Ahmadian, R.; Falconer, R. Optimising the Operation of Tidal Range Schemes. Energies 2019, 12, 2870. [Google Scholar] [CrossRef]
- Angeloudis, A.; Ahmadian, R.; Falconer, R.A.; Bockelmann-Evans, B.N. Numerical model simulations for optimisation of tidal lagoon schemes. Appl. Energy 2016, 165, 522–536. [Google Scholar] [CrossRef]
- Xia, J.; Falconer, R.A.; Lin, B. Impact of different tidal renewable energy projects on the hydrodynamic processes in the Severn Estuary, UK. Ocean Model. 2010, 32, 86–104. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Borthwick, A.G.; Houlsby, G.T. The Open Boundary Problem in Tidal Basin Modelling with Energy Extraction. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011; pp. 1–7. [Google Scholar]
- Bourban, S.E.; Couch, S.J.; Baldock, A.; Cheeseman, S. Coastal shelf model of northern European waters to inform tidal power industry decisions: SMARTtide. Underw. Technol. 2014, 32, 15–26. [Google Scholar] [CrossRef]
- Aggidis, G.A.; Benzon, D.S. Operational optimisation of a tidal barrage across the Mersey estuary using 0-D modelling. Ocean Eng. 2013, 66, 69–81. [Google Scholar] [CrossRef]
- Neill, S.P.; Angeloudis, A.; Robins, P.E.; Walkington, I.; Ward, S.L.; Masters, I.; Lewis, M.J.; Piano, M.; Avdis, A.; Piggott, M.D.; et al. Tidal range energy resource and optimization—Past perspectives and future challenges. Renew. Energy 2018, 127, 763–778. [Google Scholar] [CrossRef]
- Jeffcoate, P.; Stansby, P.K.; Apsley, D. Flow Due to Multiple Jets Downstream of a Barrage: Experiments, 3D Computational Fluid Dynamics, and Depth-Averaged Modeling. J. Hydraul. Eng. 2013, 139, 754–762. [Google Scholar] [CrossRef]
- Jeffcoate, P.; Stansby, P.K.; Apsley, D. Flow and bed-shear magnification downstream of a barrage with swirl generated in ducts by stators and rotors. J. Hydraul. Eng. 2017, 143, 1–8. [Google Scholar] [CrossRef]
- Wilhelm, S.; Balarac, G.; Métais, O.; Ségoufin, C. Head losses prediction and analysis in a bulb turbine draft tube under different operating conditions using unsteady simulations. In Proceedings of the 28th AHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016; pp. 839–848. [Google Scholar] [CrossRef]
- Ahmadian, R.; Morris, C.; Falconer, R.A. Hydro-environmental modelling of off-shore and coastally attached impoundments of The North Wales coast. In Proceedings of the 1st European IAHR Congress, Edinburgh, UK, 4–6 May 2010. [Google Scholar]
- Bae, Y.H.; Kim, K.O.; Choi, B.H. Lake Sihwa tidal power plant project. Ocean Eng. 2010, 37, 454–463. [Google Scholar] [CrossRef]
- Waters, S.; Aggidis, G.A. A world first: Swansea Bay tidal lagoon in review. Renew. Sustain. Energy Rev. 2016, 56, 916–921. [Google Scholar] [CrossRef]
- Hendry, C. The role of tidal lagoons. arXiv 2016, arXiv:astro-ph/0504232v1. [Google Scholar]
- Tidal Lagoon Plc. Swansea Bay—Tidal Lagoon. Available online: http://www.tidallagoonpower.com/projects/swansea-bay/ (accessed on 22 September 2018).
- Tidal Lagoon Plc. Key Statistics—Tidal Lagoon. Available online: http://www.tidallagoonpower.com/projects/swansea-bay/key-statistics/ (accessed on 19 April 2017).
- Petley, S.; Aggidis, G.A. Swansea Bay tidal lagoon annual energy estimation. Ocean Eng. 2016, 111, 348–357. [Google Scholar] [CrossRef]
- Deltares. Delft3D-FLOW User Manual Hydro-Morphodynamics, version 3.15; Deltares: Delft, The Netherlands, 2014. [Google Scholar]
- Falconer, R.A.; Xia, J.; Lin, B.; Ahmadian, R. The Severn Barrage and other tidal energy options: Hydrodynamic and power output modeling. Sci. China Ser. E Technol. Sci. 2009, 52, 3413–3424. [Google Scholar] [CrossRef]
- Uncles, R.J. Hydrodynamics of the Bristol Channel. Mar. Pollut. Bull. 1984, 15, 47–53. [Google Scholar] [CrossRef]
- The National Oceanography Centre. Continental Shelf Model (CS3 and CS3-3D). Available online: https://www.noc.ac.uk/ (accessed on 18 August 2017).
- The University of Edinburgh. Digimap(R). Available online: https://digimap.edina.ac.uk/ (accessed on 1 September 2016).
- Seazone. 1 Arcsecond Gridded Bathymetry [ASC Geospatial Data]. Available online: http://www.seazone.com/ (accessed on 24 April 2013).
- Xia, J.; Falconer, R.A.; Lin, B. Impact of different operating modes for a Severn Barrage on the tidal power and flood inundation in the Severn Estuary, UK. Appl. Energy 2010, 87, 2374–2391. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, S.; Falconer, R.A. Effects of open boundary location on the far-field hydrodynamics of a Severn Barrage. Ocean Model. 2014, 73, 19–29. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I-a Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Baker, A. Tidal power. IEE Proc. A Phys. Sci. Meas. Instrum. Manag. Educ. Rev. 1987, 134, 392. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Draper, S.; Nishino, T. Tidal power generation—A review of hydrodynamic modelling. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 755–771. [Google Scholar] [CrossRef]
- Brammer, J.; Falconer, R.A.; Ellis, C.; Ahmadian, R. Physical and numerical modelling of the Severn Barrage. Sci. China Technol. Sci. 2014, 57, 1471–1481. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.A.; Bockelmann-Evans, B.N. Far-field modelling of the hydro–environmental impact of tidal stream turbines. Renew. Energy 2012, 38, 107–116. [Google Scholar] [CrossRef]
- Ramos, V.; Carballo, R.; Álvarez, M.; Sánchez, M.; Iglesias, G. Assessment of the impacts of tidal stream energy through high-resolution numerical modeling. Energy 2013, 61, 541–554. [Google Scholar] [CrossRef]
- Lin, J.; Jian, S.; Liu, L.; Chen, Y.; Lin, B. Refined representation of turbines using a 3D SWE model for predicting distributions of velocity deficit and tidal energy density. Int. J. Energy Res. 2015, 39, 1828–1842. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Gubin, M.F. Draft Tubes of Hydro-Electric Stations; Published for the Bureau of Reclamation, U.S. Dept. of the Interior and National Science Foundation; Amerind Pub. Co.: Washington, DC, USA, 1973; p. 246. [Google Scholar]
- Angeloudis, A.; Kramer, S.C.; Avdis, A.; Piggott, M.D. Optimising tidal range power plant operation. Appl. Energy 2018, 212, 680–690. [Google Scholar] [CrossRef]
| Location | Water Elevation | Velocity Magnitude | Current Direction |
|---|---|---|---|
| L1 | 0.982 | 0.776 | 0.840 |
| L2 | 0.987 | 0.953 | 0.922 |
| L3 | 0.984 | 0.928 | 0.874 |
| L4 | 0.985 | 0.898 | 0.791 |
| L5 | 0.988 | 0.967 | 0.878 |
| Dimension | 2D | 3D | |||
|---|---|---|---|---|---|
| Simulation Run | SBL1 | SBL2 | SBL3 | SBL4 | SBL5 |
| Momentum conservation | No | Yes | Yes | Yes | Yes |
| Velocity distribution | - | Realistic | Simplified | Realistic | Simplified |
(m2) | - | 216.1 | 38.5 | 216.1 | 38.5 |
| Ebb | Flood | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | Layer | (m/s) | (m/s) | (m3/s) | (m) | (m/s) | (m/s) | (m3/s) | (m) |
| SBL1 | K = 0 | 1.37 | - | 4408 | 3.49 | 1.32 | - | 4336 | 3.47 |
| ine SBL2 | K = 0 | 1.48 | - | 4411 | 3.50 | 1.41 | - | 4377 | 3.48 |
| ine SBL3 | K = 0 | 2.05 | - | 5364 | 4.60 | 1.97 | - | 5192 | 4.48 |
| ine | K = 1 | 1.06 | 0.99 | ||||||
| K = 2 | 1.50 | 1.20 | |||||||
| SBL4 | K = 3 | 1.47 | 1.40 | 4381 | 3.47 | 1.40 | 1.27 | 4348 | 3.44 |
| K = 4 | 1.23 | 1.09 | |||||||
| K = 5 | 0.93 | 0.62 | |||||||
| ine | K = 1 | 0.88 | 1.05 | ||||||
| K = 2 | 1.89 | 1.95 | |||||||
| SBL5 | K = 3 | 1.76 | 2.75 | 4973 | 4.13 | 1.84 | 2.77 | 4954 | 4.17 |
| K = 4 | 2.18 | 2.19 | |||||||
| K = 5 | 1.90 | 1.90 | |||||||
| Scenario | Max out (m) | % from SBL1 | Max in (m) | % from SBL1 | Min out (m) | % from SBL1 | Min in (m) | % from SBL1 |
|---|---|---|---|---|---|---|---|---|
| SBL1 | 4.24 | - | 2.80 | - | −4.05 | - | −2.72 | - |
| SBL2 | 4.24 | 0.0% | 2.83 | 1.1% | −4.05 | 0.0% | −2.72 | −0.8% |
| SBL3 | 4.25 | 0.1% | 3.24 | 16.0% | −4.05 | 0.1% | −2.72 | −16.8% |
| SBL4 | 4.22 | −0.6% | 2.80 | 0.2% | −4.04 | 0.1% | −2.72 | −0.4% |
| SBL5 | 4.22 | −0.5% | 3.09 | 10.6% | −4.05 | −0.2% | −2.72 | −11.6% |
| Scenario | Annual Energy (GWh) | % from SBL1 |
|---|---|---|
| SBL1 | 578.39 | - |
| SBL2 | 584.98 | 1.1% |
| SBL3 | 515.36 | −10.9% |
| SBL4 | 578.63 | 0.0% |
| SBL5 | 532.85 | −7.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čož, N.; Ahmadian, R.; Falconer, R.A. Implementation of a Full Momentum Conservative Approach in Modelling Flow Through Tidal Structures. Water 2019, 11, 1917. https://doi.org/10.3390/w11091917
Čož N, Ahmadian R, Falconer RA. Implementation of a Full Momentum Conservative Approach in Modelling Flow Through Tidal Structures. Water. 2019; 11(9):1917. https://doi.org/10.3390/w11091917
Chicago/Turabian StyleČož, Nejc, Reza Ahmadian, and Roger A. Falconer. 2019. "Implementation of a Full Momentum Conservative Approach in Modelling Flow Through Tidal Structures" Water 11, no. 9: 1917. https://doi.org/10.3390/w11091917
APA StyleČož, N., Ahmadian, R., & Falconer, R. A. (2019). Implementation of a Full Momentum Conservative Approach in Modelling Flow Through Tidal Structures. Water, 11(9), 1917. https://doi.org/10.3390/w11091917







