Estimation of Unsaturated Hydraulic Conductivity of Granular Soils from Particle Size Parameters
Abstract
1. Introduction
2. Estimation of Saturated Hydraulic Conductivity
2.1. Estimation Equations Based on Grain Size Parameters
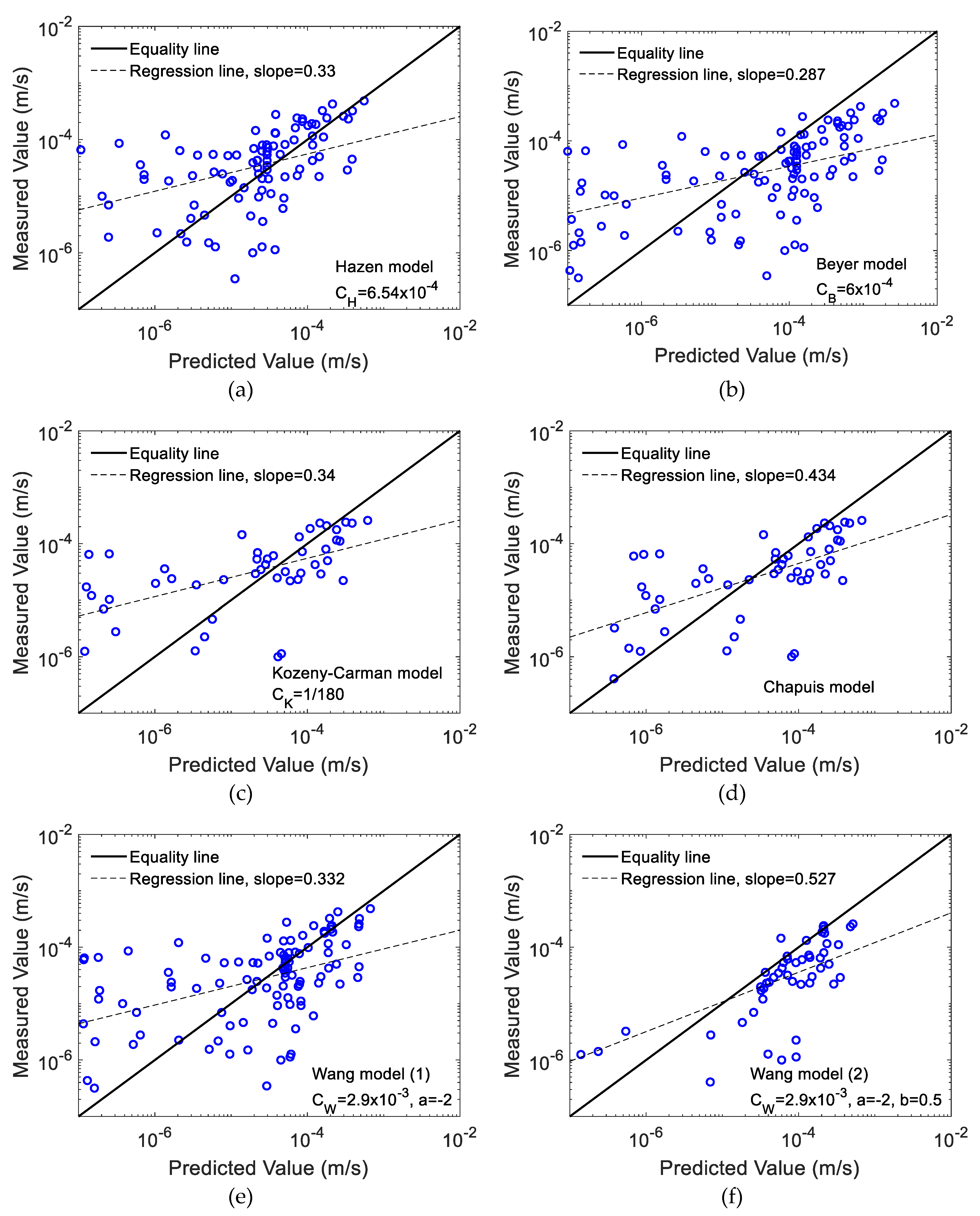
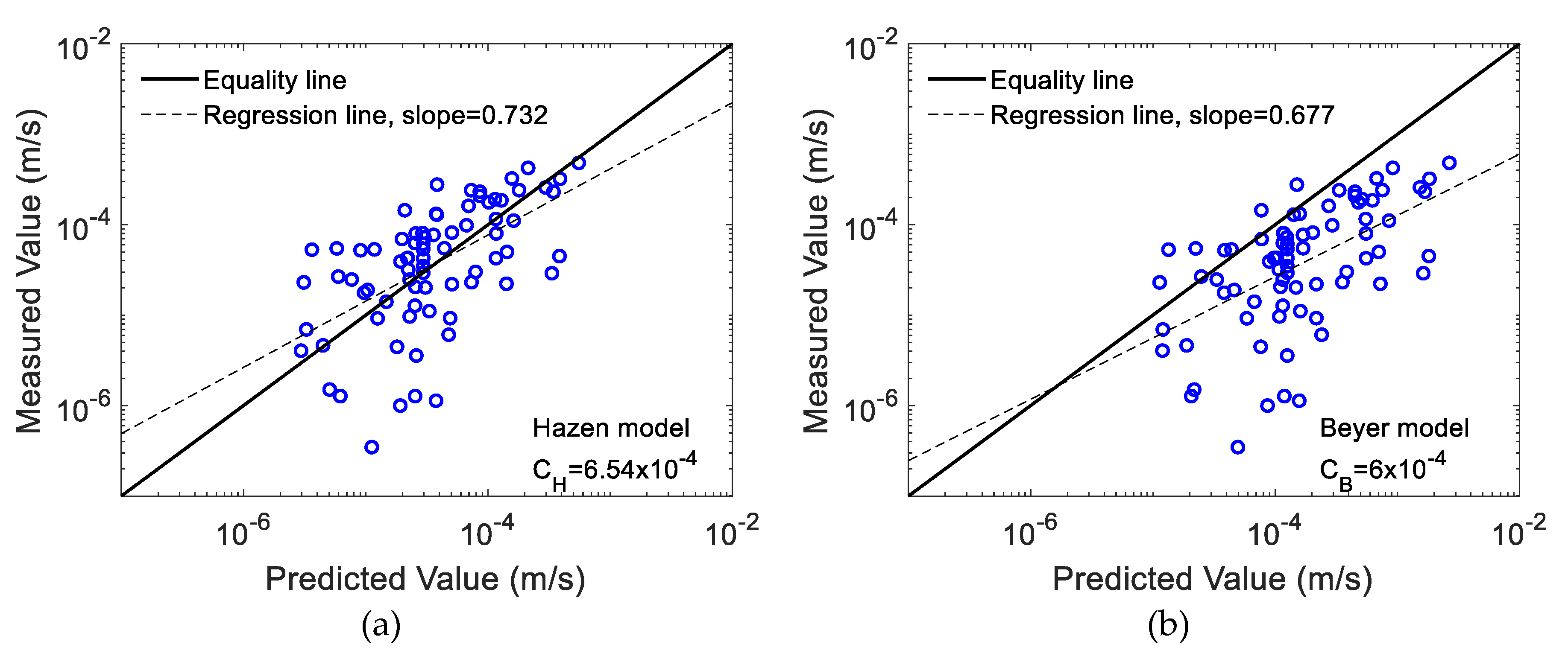
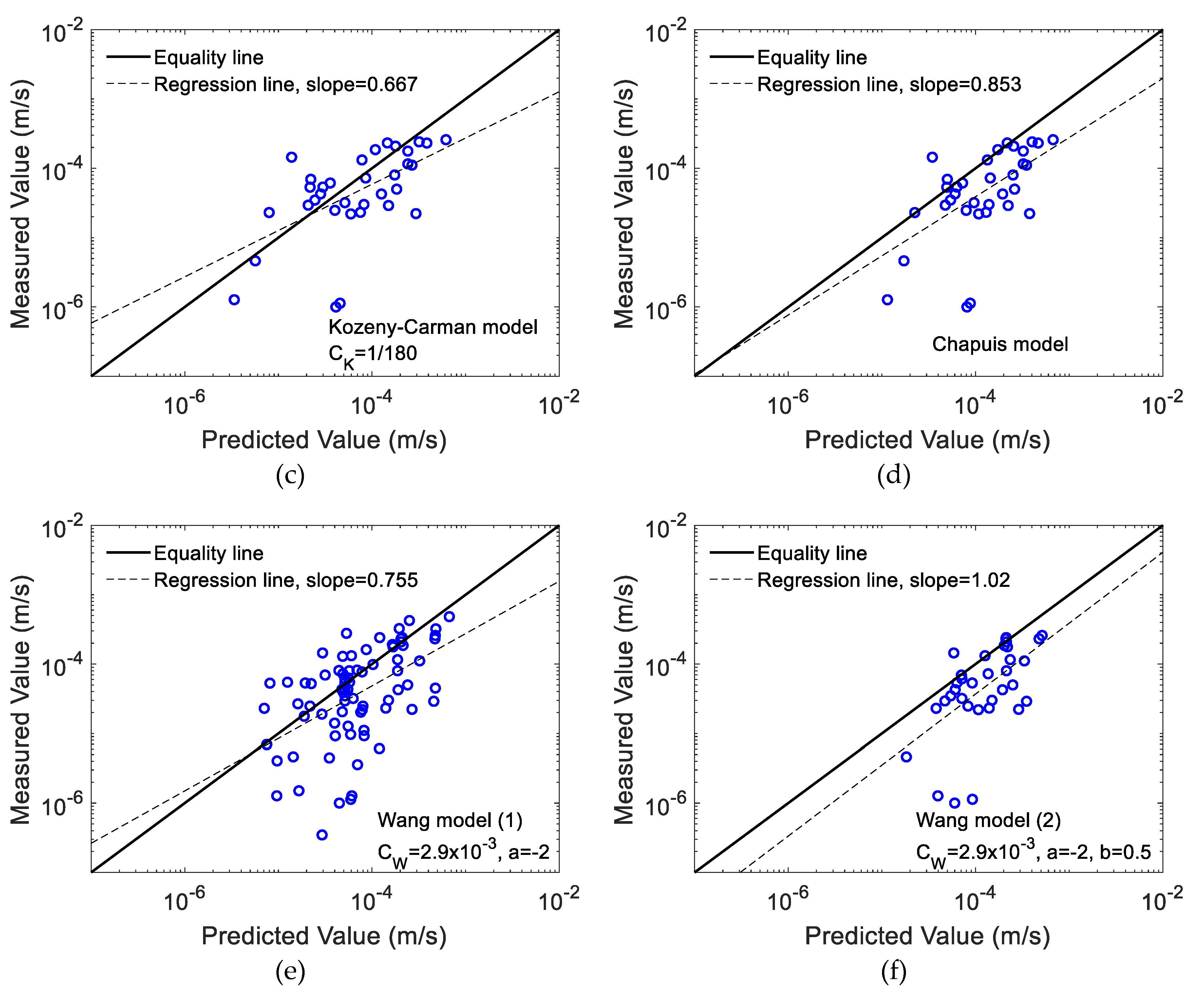
2.2. Applicability and Validity of the Estimation Equation
3. Prediction of Unsaturated Relative Permeability
3.1. Van Genuchten’s Closed-Form Equation
3.2. Prediction of Van Genuchten’s Parameters from Particle Size Distribution
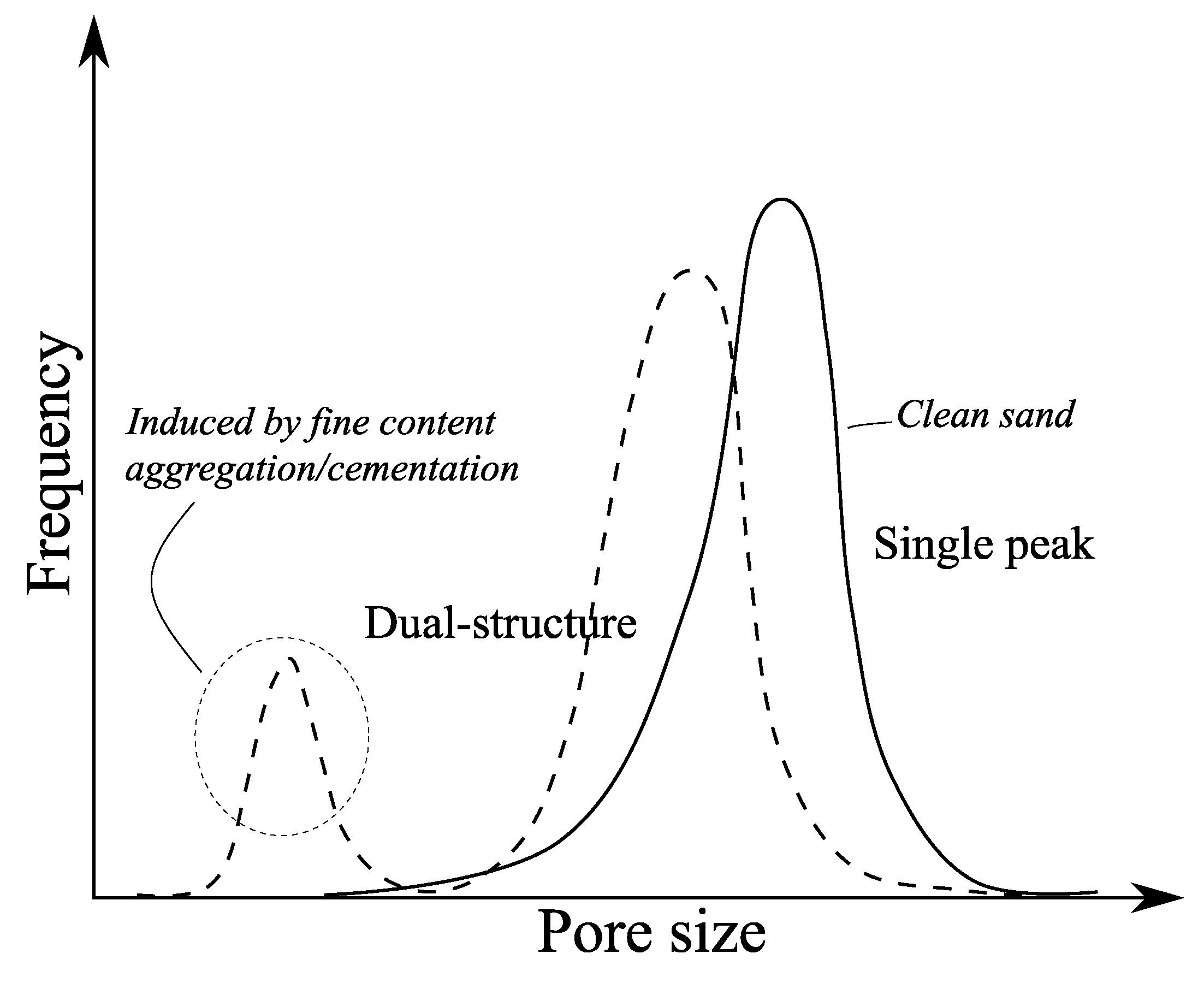
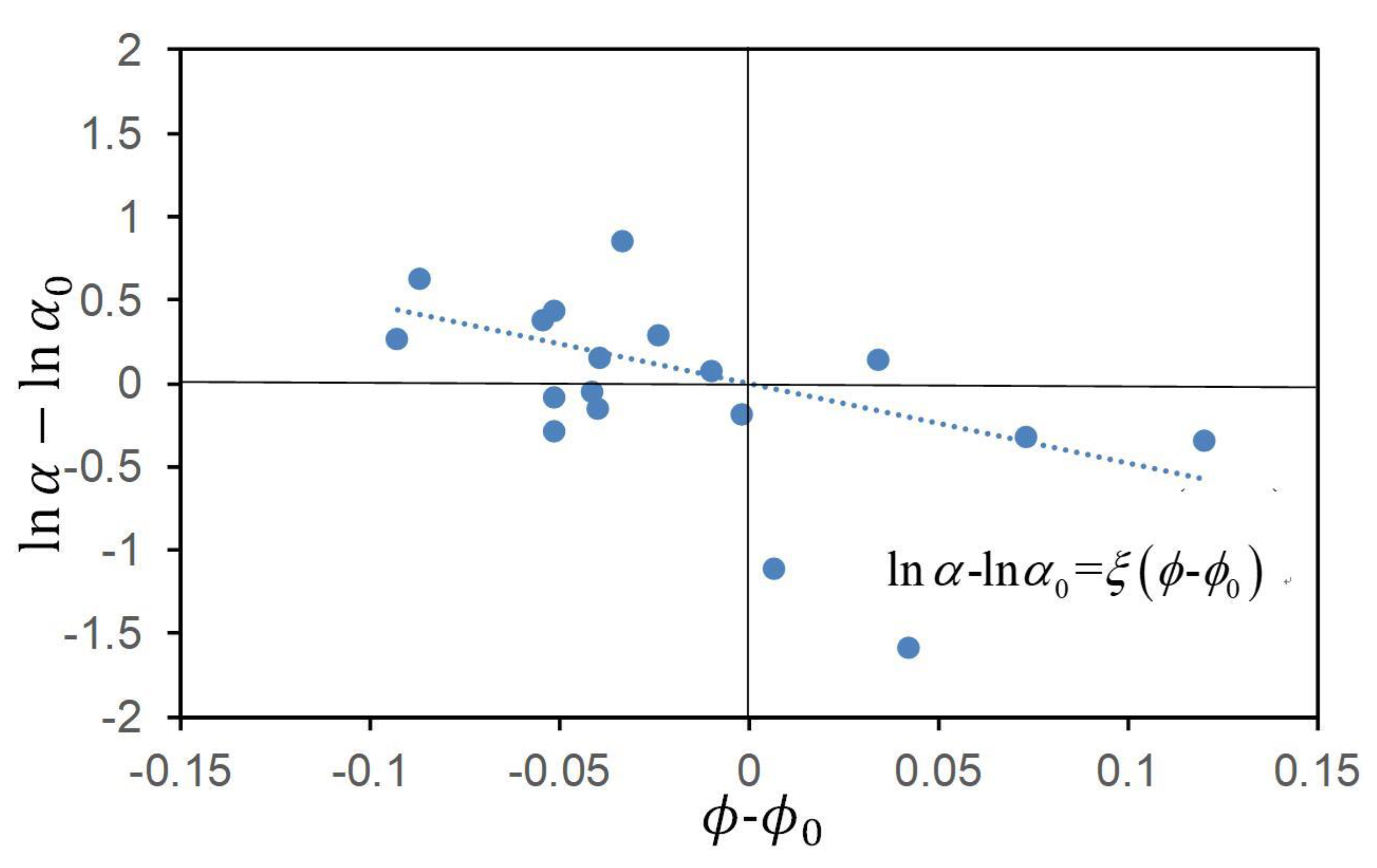
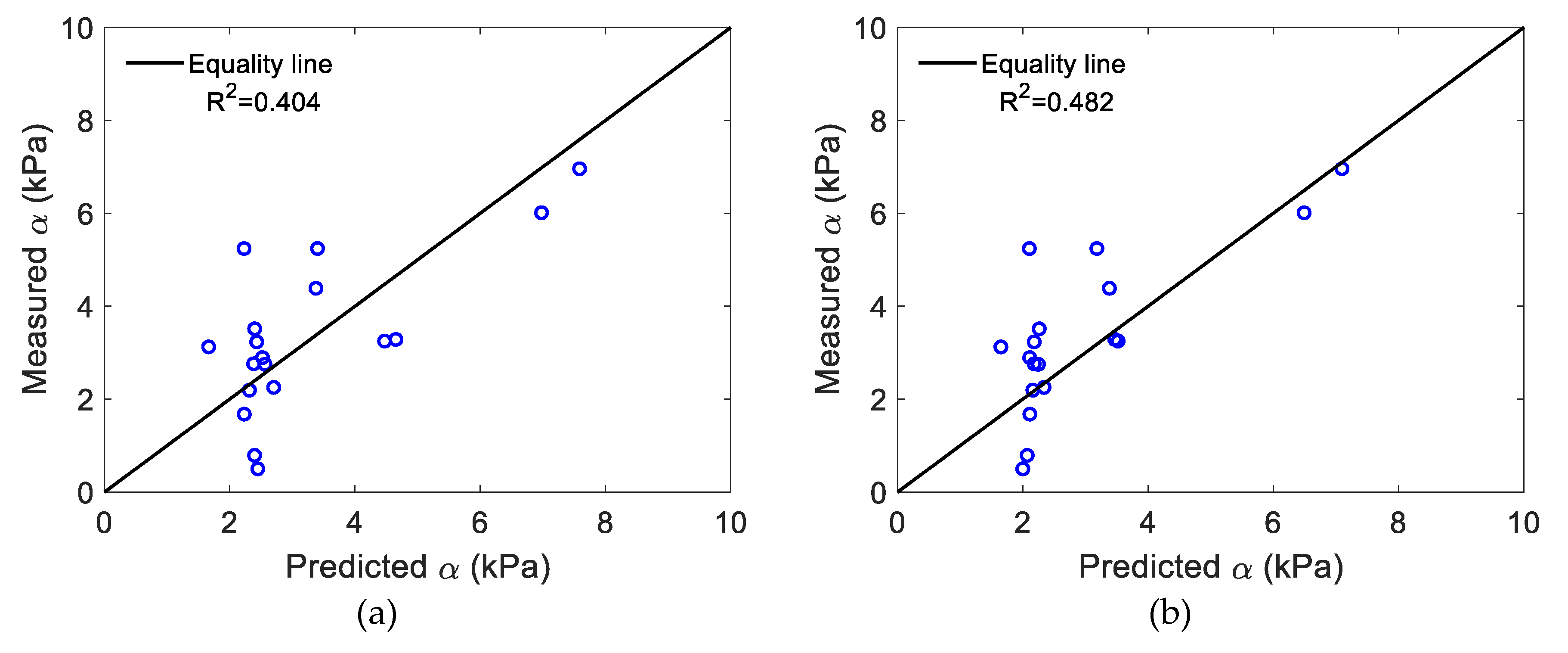
3.3. Effect of Porosity Variation on the Air Entry Value
4. Verification of the Estimation Model
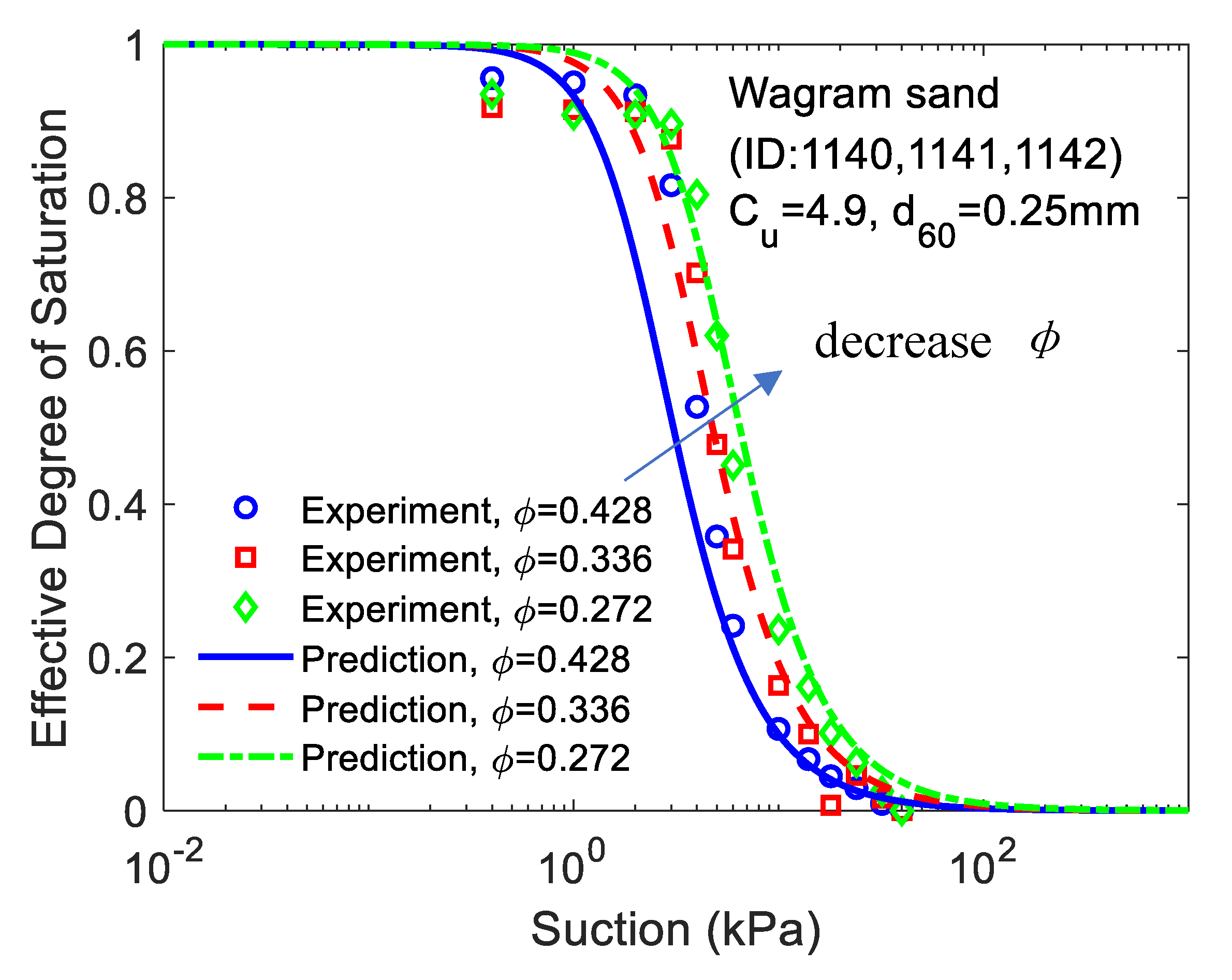
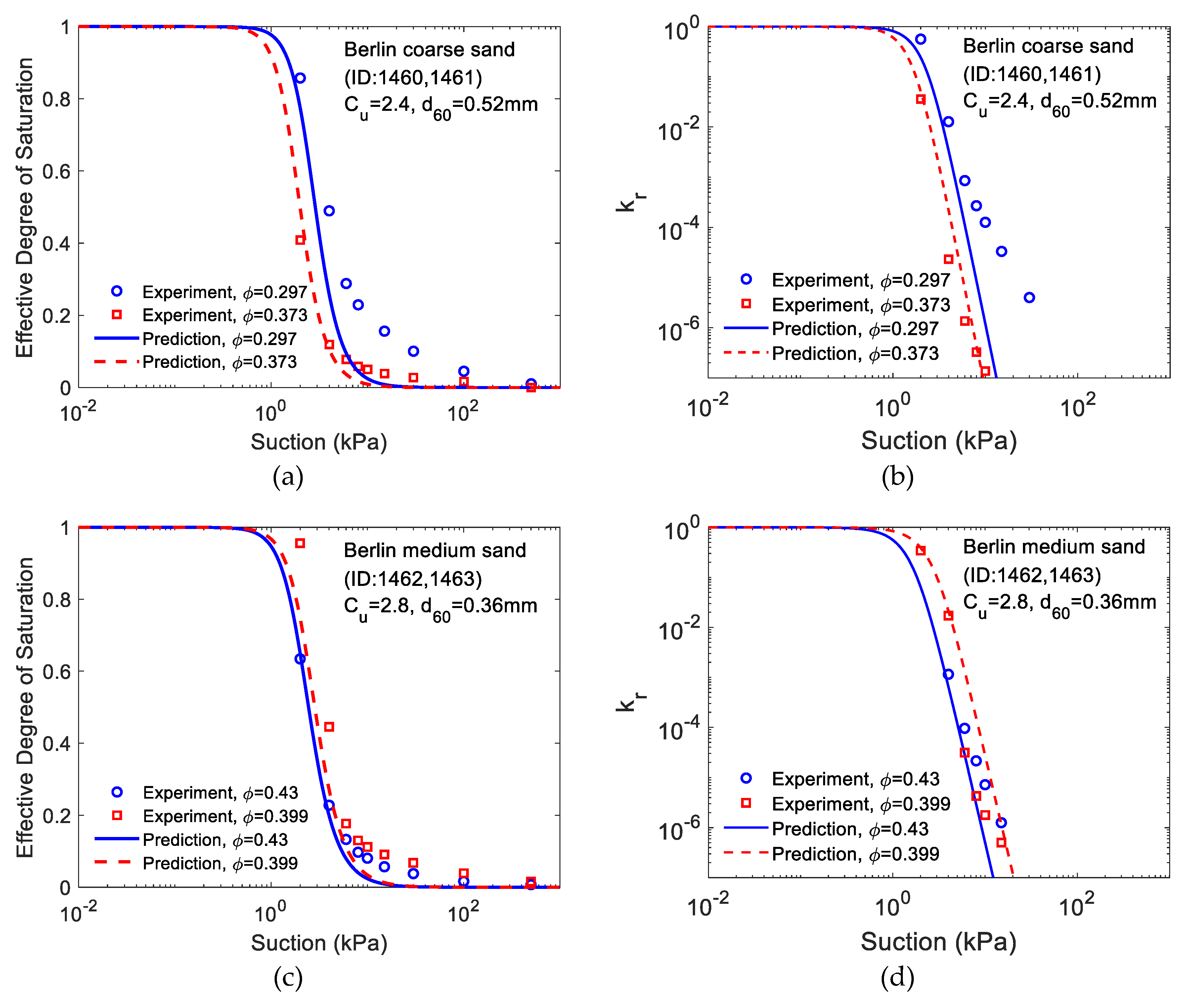
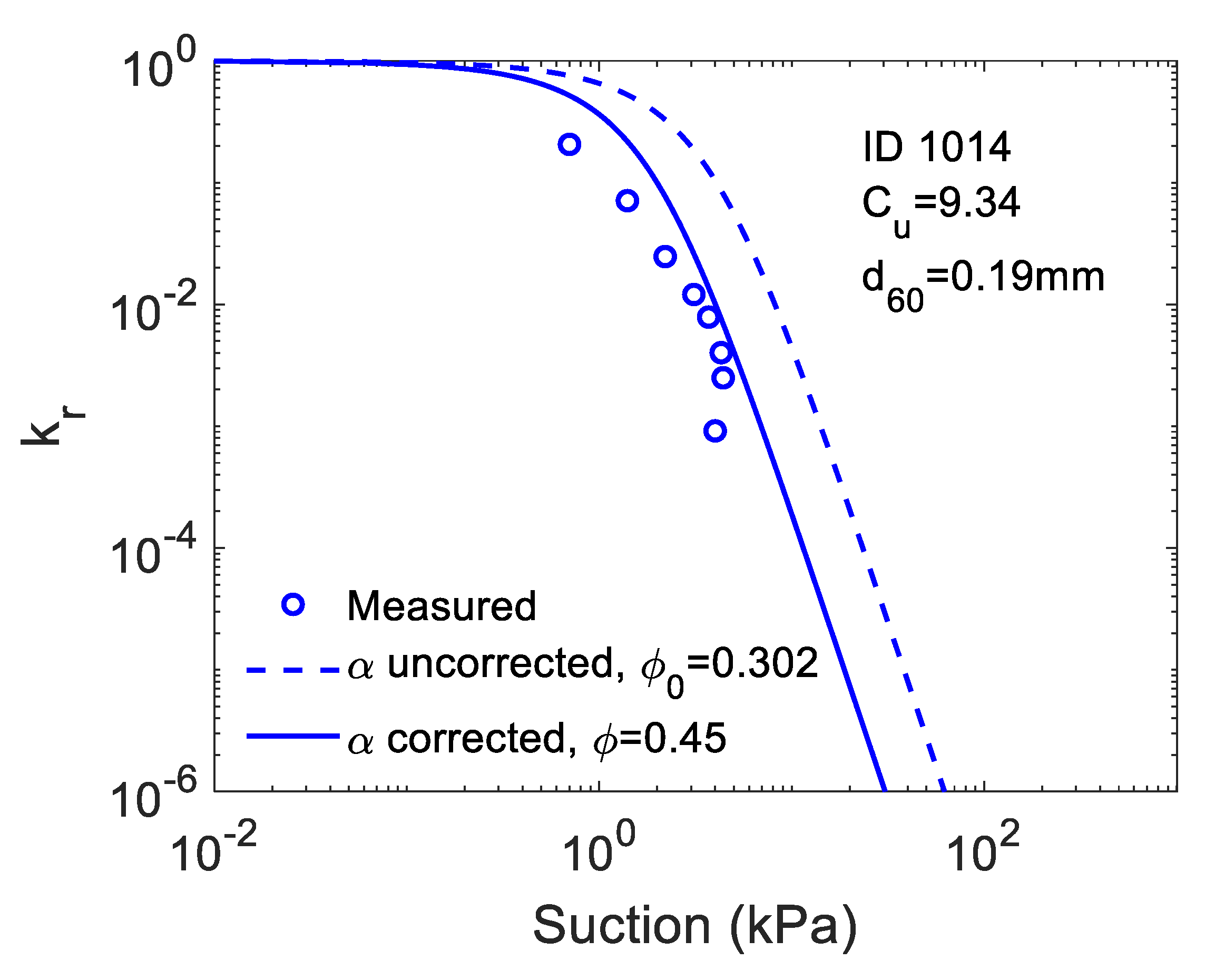
4.1. The Effect of Porosity on Predictions of Water Retention Curve (WRC) and Relative Permeability
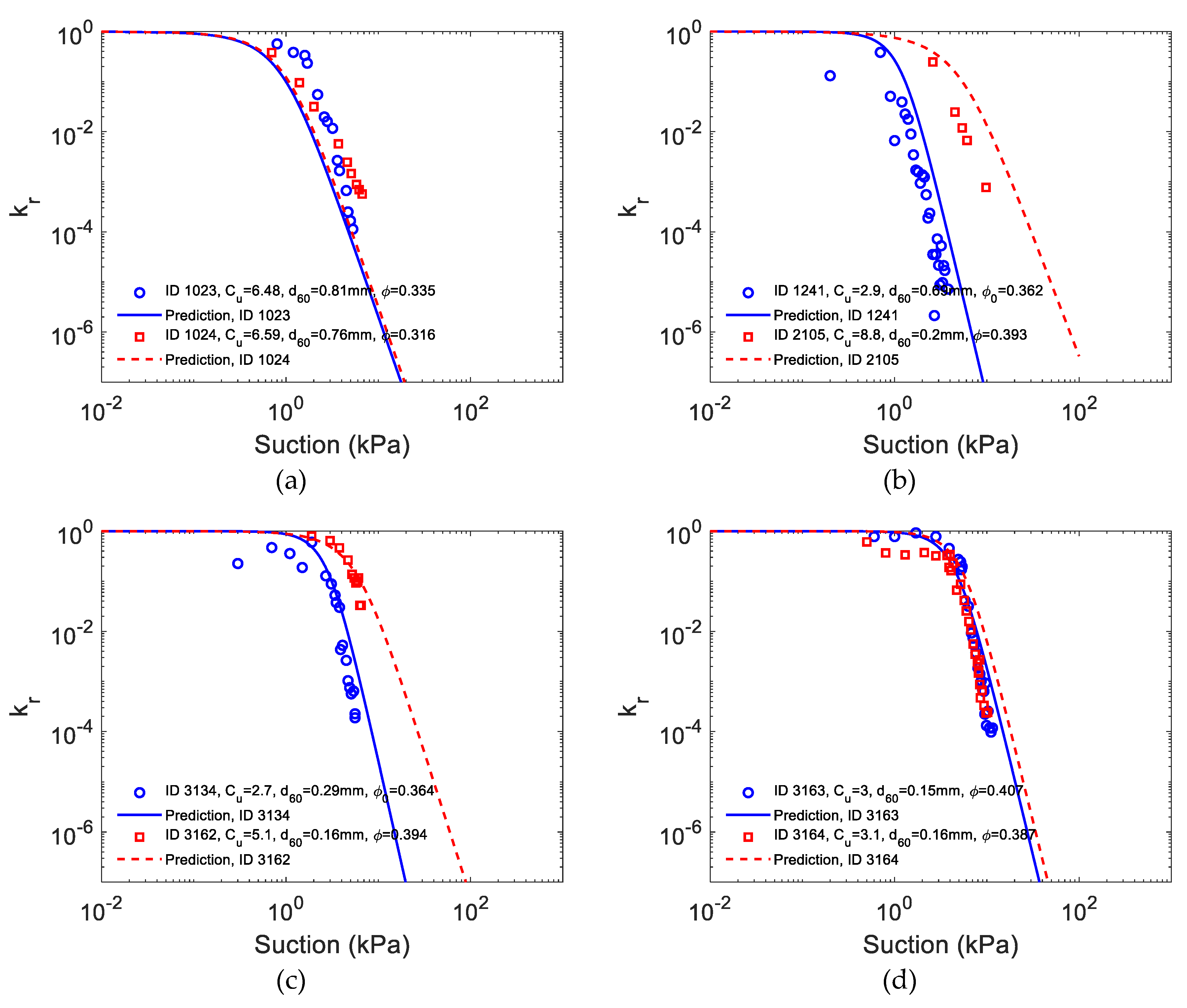
4.2. Verification on a Set of Field Test Data by Instantaneous Profile Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gardner, W.R. Calculation of Capillary Conductivity from Pressure Plate Outflow Data. Soil Sci. Soc. Am. Proc. 1956, 20, 317–320. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Hazen, A. Some Physical Properties of Sands and Gravels with Reference to Their Use Infiltration; Report to the Massachusetts State Board of Health: Boston, MA, USA, 1892; pp. 539–556. [Google Scholar]
- Beyer, W. Zur Bestimmung der Wasserdurchlassigkeit von Kieson und Sanduen aus der Kornverteilung. Wasserwirtsch. Wassertech. 1964, 14, 165–169. [Google Scholar]
- Kozeny, J. Das Wasser im Boden. Grundwasserbewegung. In Hydraul: Ihre Grundlagen und Praktische Anwendung; Springer: Berlin/Heidelberg, Germany, 1953; pp. 380–445. [Google Scholar]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of sand and gravel using effective diameter and void ratio. Can. Geotech. J. 2004, 41, 787–795. [Google Scholar] [CrossRef]
- Wang, J.-P.; François, B.; Lambert, P. Equations for hydraulic conductivity estimation from particle size distribution: A dimensional analysis. Water Resour. Res. 2017, 53, 8127–8134. [Google Scholar] [CrossRef]
- Scheinost, A.C.; Sinowski, W.; Auerswald, K. Regionalization of soil water retention curves in a highly variable soilscape, I. Developing a new pedotransfer function. Geoderma 1997, 78, 129–143. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Using neural networks to predict soil water retention and soil hydraulic conductivity. Soil Tillage Res. 1998, 47, 37–42. [Google Scholar] [CrossRef]
- Chiu, C.F.; Yan, W.M.; Yuen, K.-V. Estimation of water retention curve of granular soils from particle-size distribution—A Bayesian probabilistic approach. Can. Geotech. J. 2012, 49, 1024–1035. [Google Scholar] [CrossRef]
- Wang, J.-P.; Hu, N.; François, B.; Lambert, P. Estimating water retention curves and strength properties of unsaturated sandy soils from basic soil gradation parameters. Water Resour. Res. 2017, 53, 6069–6088. [Google Scholar] [CrossRef]
- Harleman, D.; Mehlhorn, P.; Rumer, R. Dispersion-permeability correlation in porous media. J. Hydraul. Div. 1963, 89, 67–85. [Google Scholar]
- Carman, P. Fluid flow through granular beds. Trans. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases Through Porous Media; Butterworth Scientific Publications: London, UK, 1956. [Google Scholar]
- Kozeny, J. Über kapillare leitung des wassers im boden: (aufstieg, versickerung und anwendung auf die bewässerung). Hölder Pichler Tempsky 1927, 136, 271–306. [Google Scholar]
- Vukovic, M.; Soro, A. Determination of Hydraulic Conductivity of Porous Media from Grain-Size Composition; Water Resources Publications: Littleton, CO, USA, 1992. [Google Scholar]
- Rosas, J.; Lopez, O.; Missimer, T.M.; Coulibaly, K.M.; Dehwah, A.H.A.; Sesler, K.; Lujan, L.R.; Mantilla, D. Determination of Hydraulic Conductivity from Grain-Size Distribution for Different Depositional Environments. Groundwater 2014, 52, 399–413. [Google Scholar] [CrossRef] [PubMed]
- Leij, F.J.; Alves, W.J.; van Genuchten, M.T.; Williams, J.R. The UNSODA Unsaturated Soil Hydraulic Database: User’s Manual; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Ada, OK, USA, 1996.
- Du, Y.-J.; Jiang, N.-J.; Liu, S.-Y.; Jin, F.; Singh, D.N.; Puppala, A.J. Engineering properties and microstructural characteristics of cement-stabilized zinc-contaminated kaolin. Can. Geotech. J. 2014, 51, 289–302. [Google Scholar] [CrossRef]
- Oualmakran, M.; Mercatoris, B.C.N.; François, B. Pore-size distribution of a compacted silty soil after compaction, saturation, and loading. Can. Geotech. J. 2016, 53, 1902–1909. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Hu, R.; Chen, Y.-F.; Liu, H.-H.; Zhou, C.-B. A water retention curve and unsaturated hydraulic conductivity model for deformable soils: Consideration of the change in pore-size distribution. Géotechnique 2013, 63, 1389–1405. [Google Scholar] [CrossRef]
- Zhou, W.-H.; Yuen, K.-V.; Tan, F. Estimation of soil–water characteristic curve and relative permeability for granular soils with different initial dry densities. Eng. Geol. 2014, 179, 1–9. [Google Scholar] [CrossRef]
- Wang, J.-P.; Lambert, P.; De Kock, T.; Cnudde, V.; François, B. Investigation of the effect of specific interfacial area on strength of unsaturated granular materials by X-ray tomography. Acta Geotech. 2019, 1–15. [Google Scholar] [CrossRef]
- Watson, K.K. An instantaneous profile method for determining the hydraulic conductivity of unsaturated porous materials. Water Resour. Res. 1966, 2, 709–715. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.M.; Fredlund, D.G. Wetting front advancing column test for measuring unsaturated hydraulic conductivity. Can. Geotech. J. 2009, 46, 1431–1445. [Google Scholar] [CrossRef]

| Sample ID * | (mm) | (mm) | (mm) | ϕ | Fitted Parameters | Goodness of Fitting | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| SSE | RMSE | R2 | ||||||||
| 1011 | 0.00946 | 0.10699 | 0.15511 | 19.743 | 0.43 | 0.43 | 2.75 | 0.016 | 0.047 | 0.989 |
| 1014 | 0.02078 | 0.11454 | 0.16293 | 9.350 | 0.45 | 0.94 | 2.66 | 0.007 | 0.027 | 0.995 |
| 1461 | 0.21825 | 0.30949 | 0.43887 | 2.395 | 0.37 | 9.47 | 3.70 | 0.050 | 0.085 | 0.933 |
| 1462 | 0.12691 | 0.23000 | 0.30867 | 2.818 | 0.43 | 5.70 | 3.43 | 0.037 | 0.068 | 0.955 |
| 1463 | 0.12733 | 0.23915 | 0.31552 | 2.846 | 0.40 | 6.21 | 3.65 | 0.025 | 0.056 | 0.970 |
| 1464 | 0.10089 | 0.14356 | 0.20548 | 2.552 | 0.37 | 6.15 | 3.13 | 0.049 | 0.078 | 0.950 |
| 1465 | 0.02491 | 0.07375 | 0.10463 | 5.000 | 0.38 | 2.08 | 1.88 | 0.005 | 0.025 | 0.996 |
| 1466 | 0.05631 | 0.07855 | 0.09897 | 2.034 | 0.41 | 5.44 | 4.56 | 0.009 | 0.034 | 0.993 |
| 1467 | 0.02932 | 0.20852 | 0.31649 | 13.299 | 0.31 | 2.13 | 1.58 | 0.011 | 0.037 | 0.989 |
| 3330 | 0.04041 | 0.20388 | 0.28925 | 8.526 | 0.42 | 1.62 | 1.65 | 0.024 | 0.069 | 0.971 |
| 3331 | 0.11858 | 0.22780 | 0.29709 | 2.861 | 0.44 | 4.53 | 2.58 | 0.026 | 0.072 | 0.975 |
| 3332 | 0.20284 | 0.25656 | 0.32451 | 1.799 | 0.43 | 7.78 | 3.48 | 0.014 | 0.054 | 0.987 |
| 3340 | 0.12617 | 0.18315 | 0.26612 | 2.549 | 0.46 | 3.95 | 2.26 | 0.086 | 0.055 | 0.973 |
| 4523 | 0.12133 | 0.16532 | 0.21988 | 2.106 | 0.41 | 8.83 | 7.04 | 0.072 | 0.081 | 0.969 |
| 4650 | 0.07221 | 0.23130 | 0.31953 | 5.201 | 0.38 | 2.20 | 2.01 | 0.032 | 0.037 | 0.992 |
| 4651 | 0.08383 | 0.22687 | 0.32525 | 4.646 | 0.38 | 1.95 | 2.01 | 0.029 | 0.036 | 0.992 |
| 4660 | 0.06469 | 0.21709 | 0.30134 | 5.488 | 0.46 | 0.45 | 1.48 | 0.036 | 0.039 | 0.986 |
| 4661 | 0.07221 | 0.22944 | 0.31132 | 5.022 | 0.43 | 0.79 | 1.74 | 0.015 | 0.026 | 0.995 |
| Soil Type * | Sample ID ** | (mm) | (mm) | (mm) | ϕ | Fitted Parameters | Goodness of Fitting | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SSE | RMSE | R2 | |||||||||
| Wagram sand | 1140 | 0.051 | 0.147 | 0.25 | 4.9 | 0.428 | 3.752 | 3.657 | 0.011 | 0.031 | 0.995 |
| 1141 | 0.336 | 4.318 | 3.340 | 0.024 | 0.044 | 0.989 | |||||
| 1142 | 0.272 | 4.889 | 2.881 | 0.023 | 0.043 | 0.989 | |||||
| Berlin coarse sand | 1460 | 0.217 | 0.308 | 0.522 | 2.4 | 0.297 | 5.510 | 8.236 | 3.950 | 0.703 | 0.444 |
| 1461 | 0.373 | 3.123 | 3.702 | 0.050 | 0.085 | 0.933 | |||||
| Berlin medium sand | 1462 | 0.127 | 0.235 | 0.360 | 2.8 | 0.43 | 3.233 | 3.424 | 0.037 | 0.068 | 0.955 |
| 1463 | 0.399 | 3.514 | 3.654 | 0.025 | 0.056 | 0.970 | |||||
| Sample ID | (mm) | (mm) | (mm) | (mm) | (mm) | |
|---|---|---|---|---|---|---|
| 1014 | 0.021 | 0.115 | 0.163 | 0.194 | 0.469 | 9.35 |
| 1023 | 0.125 | 0.555 | 0.713 | 0.808 | 1.473 | 6.48 |
| 1024 | 0.115 | 0.515 | 0.665 | 0.755 | 1.347 | 6.59 |
| 1241 | 0.237 | 0.415 | 0.598 | 0.689 | 1.252 | 2.90 |
| 2105 | 0.022 | 0.106 | 0.161 | 0.198 | 0.430 | 8.83 |
| 3134 | 0.107 | 0.163 | 0.250 | 0.289 | 0.444 | 2.70 |
| 3162 | 0.031 | 0.085 | 0.132 | 0.160 | 0.358 | 5.11 |
| 3163 | 0.051 | 0.087 | 0.129 | 0.154 | 0.289 | 2.99 |
| 3164 | 0.052 | 0.091 | 0.135 | 0.161 | 0.338 | 3.09 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-P.; Zhuang, P.-Z.; Luan, J.-Y.; Liu, T.-H.; Tan, Y.-R.; Zhang, J. Estimation of Unsaturated Hydraulic Conductivity of Granular Soils from Particle Size Parameters. Water 2019, 11, 1826. https://doi.org/10.3390/w11091826
Wang J-P, Zhuang P-Z, Luan J-Y, Liu T-H, Tan Y-R, Zhang J. Estimation of Unsaturated Hydraulic Conductivity of Granular Soils from Particle Size Parameters. Water. 2019; 11(9):1826. https://doi.org/10.3390/w11091826
Chicago/Turabian StyleWang, Ji-Peng, Pei-Zhi Zhuang, Ji-Yuan Luan, Tai-Heng Liu, Yi-Ran Tan, and Jiong Zhang. 2019. "Estimation of Unsaturated Hydraulic Conductivity of Granular Soils from Particle Size Parameters" Water 11, no. 9: 1826. https://doi.org/10.3390/w11091826
APA StyleWang, J.-P., Zhuang, P.-Z., Luan, J.-Y., Liu, T.-H., Tan, Y.-R., & Zhang, J. (2019). Estimation of Unsaturated Hydraulic Conductivity of Granular Soils from Particle Size Parameters. Water, 11(9), 1826. https://doi.org/10.3390/w11091826






