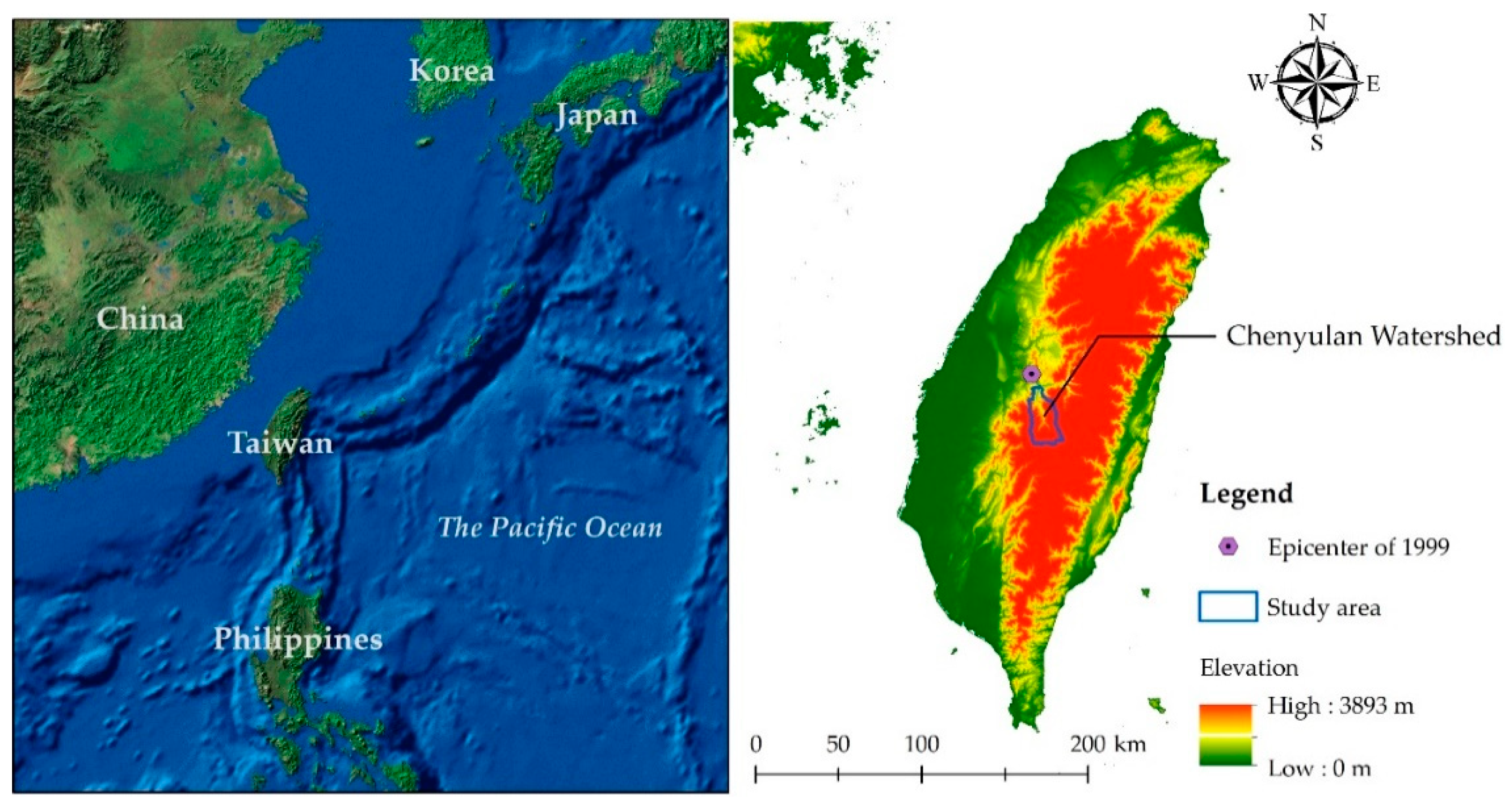
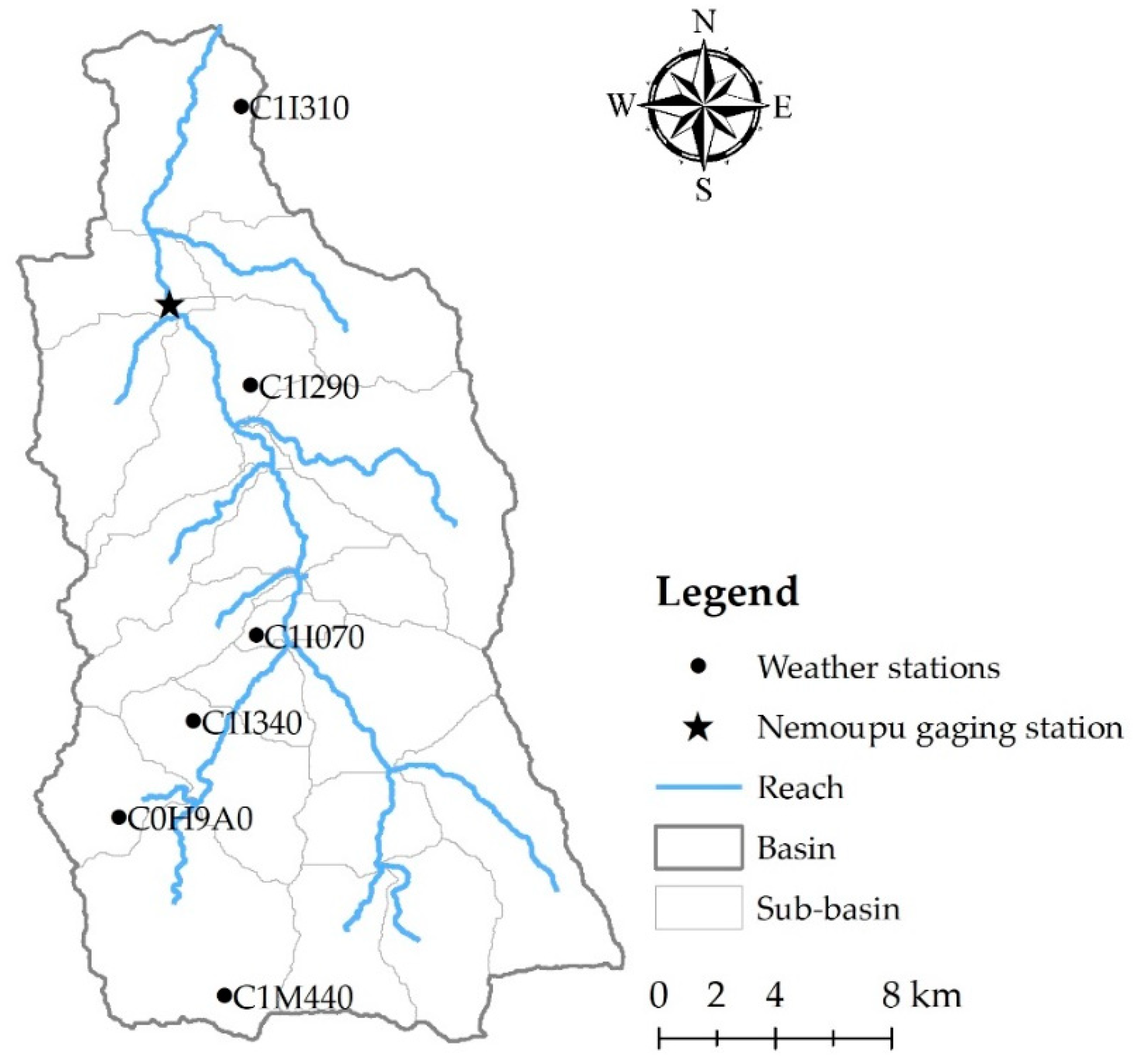
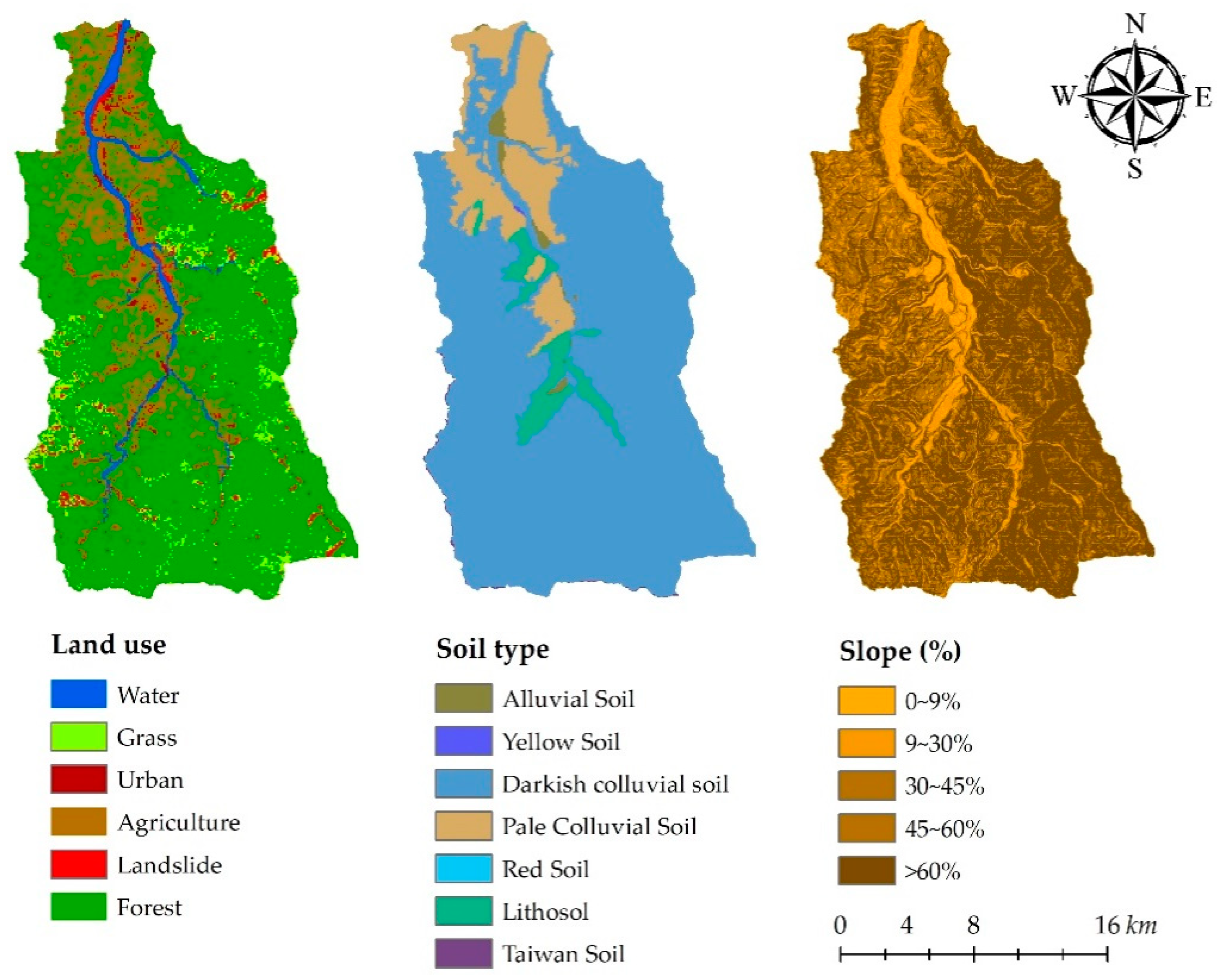
1. Introduction
The amount and occurrence time of sediment export from the watersheds are mainly caused by different types of soil erosion, such as channel bed and bank erosion, overland surface erosion, and glacier erosion [
1]. As soil erosion causes shear stress by rainfall, surface runoff brings most sediment yields from the overland eroded soil and then is usually transported to the downstream [
2]. Moreover, extreme natural disturbances (i.e., typhoons, earthquakes, landslides, and floods) also play as the trigger for abnormal sediment yields in some regions [
3], and further change the characteristics of sediment yields and sediment transports in watersheds [
4]. Many studies have indicated that climate change has caused higher rainfall intensity and annual precipitation, leading to increases in sediment yields and soil erosion rates [
5].
In order to comprehensively quantify the impacts of rainfall, soil erodibility, land use cover, topography, and support practice to sediment yields, the universal soil loss equation (USLE) [
6] and the modified universal soil loss equation (MUSLE) [
7] have been developed. These two empirical equations have been used to estimate the soil loss in watersheds worldwide [
8]. Some other physically-based erosion models were developed in the past decades, such as those used in ANSWERS (Areal Nonpoint Source Watershed Environmental Response Simulation) [
9], EPIC (Environmental Policy Integrated Climate) model [
10], WEPP (Water Erosion Prediction Project) [
11], and EUROSEM (European Soil Erosion Model) [
12]. The main difference between MUSLE and USLE is that USLE uses rainfall as an indicator of erosive energy, while MULSE uses the amount of runoff to simulate erosion and sediment yield. Sadeghi et al. [
8] reviewed 49 papers of MUSLE application worldwide, and presented that most of MUSLE studies were to estimate the sediment yield on a storm basis (73.91%), monthly basis (2.17%), and annual basis (17.39%), while other applications of MUSLE (6.53%) were studied in soil erosion in storm-wise scale, pollutant estimation, and return periods of annual sediment yield. Therefore, MUSLE can better simulate the sediment yields during single storms with a low level of estimation error [
13]. Since USLE and MUSLE were developed based on experiment watersheds in the U.S., [
8] indicated that MUSLE would have huge errors without the calibration but can present reliable results for sediment yield on a storm basis after calibration, especially when it is applied under appropriate conditions (i.e., rangeland watersheds, similar climatic conditions as the USA) similar to where the original model was developed.
The process of erosion is usually described in three stages, which are detachment, transport and deposition; and four main types, which are sheet, rill, gully and in-stream erosion [
14]. Sheet erosion and rill erosion are often classified as overland flow erosion caused by raindrop or overland flow [
2,
15]. Both types of erosions are usually considered together in erosion modelling. Gully erosion is the removal of soil along the channels of concentrated flow and is controlled by the thresholds related to slope and catchment area [
2]. In-stream erosion involves the direct removal of sediment from stream beds and stream banks, especially during high flow periods huge amount of sediment transported through the stream network originates from the stream channel [
14]. Erosion/sediment transport models can be categorized into three types: empirical model, conceptual model, and physics-based model [
14]. The empirical models, the simplest ones, are based on the statistical observations of experiment areas in response to the characteristics of sediment transport [
16], while conceptual models usually represent the catchment as a series of internal storages with parameters values determined through calibration against observed data [
17]. Physics-based models integrate some fundamental physical equations, such as the equations of conservation of mass and momentum for flow, and those equations for sediment [
14]. Compared to physics-based models and more complex conceptual models, which usually lack of sufficient spatially distributed input data, empirical and conceptual models are suggested to be combined for presenting the event responsiveness and sensitivity to climate variability [
14].
The soil and water assessment Tool (SWAT) is a semi-distributed hydrological watershed model, which can simulate water balance, plant growth, and transport of sediment, nutrients, heavy metals and pesticides. The SWAT model has been used worldwide for simulating the impact of climate change and land use change on streamflow, sediment and nutrients exports, and best management practices (BMPs) on watershed responses in different countries [
18,
19,
20]. Generally, the SWAT model performed well for simulating streamflow, sediment and nutrient exports at various spatio-temporal scales. MUSLE plays an important role of the simulation of continuous sediment loads [
21]. Sediment transport is often called total sediment load, which is the sum of bed load and suspended load. The sediment transport is generally modeled through the sediment flow caused by overland flow and the channel erosion [
22]. Some studies indicated unsatisfactory sediment simulation of the SWAT model. Addis et al. [
23] used the SWAT model to simulate discharge and sediment transport at a small mountainous catchment in Ethiopian plateau, and showed that SWAT performed well for discharge but overestimated daily sediment transport with NSE = 0.07 and −1.76 for calibration and validation, respectively, mainly due to insufficient observed data and the heavy rainfall during simulation period. Bressiani et al. [
24] indicated that the SWAT model was suitable for sediment simulation in most areas in Brazil and suggested the change in transmission of sediment should be reflected in the current SWAT version.
As the sediment transport and sediment concentration can affect the nutrient and turbidity in water, the estimation of sediment transport or sediment concentration need to be more reasonable. Arnold et al. [
25] advised that SWAT users need to calibrate the discharge and sediment transport or concentration sequentially before simulating the nutrients. However, extreme rainfalls in Taiwan result in serious debris flows and landslides, making it more difficult to simulate the sediment transport in the river. As the runoff and sediment hazards in Taiwan are increasing, Lee et al. [
26] indicated that the runoff and sediment yield would increase with the storm events and become more frequently occurred, especially in the small mountainous catchments. Chiu et al. [
27] simulated the sediment yield in the Shihmen reservoir in Taiwan, and revealed that natural distributions (i.e., typhoon, storm, and earthquake) have become an important potential source of sediment yield. Therefore, Chang et al. [
28] suggested that landslide should be considered in the model to simulate more accurate and reasonable sediment exports. In order to more accurately simulate the sediment transport and sediment yields in a small mountainous watershed in Taiwan, we aim to: (1) integrate Taiwan universal soil loss equation (TUSLE) and the landslide area-volume estimation equation into the SWAT model (version 664) as SWAT-Twn model; (2) examine five sediment transport methods in the SWAT model; (3) provide the calibration and validation experience of sediment transport simulation for the SWAT users.
3. Results
In this study, we compared three SWAT models, which are the official SWAT 2016 (version 664), SWAT-TUSLE and SWAT-Twn. The SWAT-TUSLE was modified with TUSLE which calculates C factor based on NDVI and L factors based on the slope. The SWAT-Twn was the integration of SWAT-TUSLE and landslide volume equation. Since we did not modify the streamflow-related equations in SWAT, the streamflow simulations are the same for all these three models. We first calibrated the official SWAT 2016 model for daily streamflow and compared the performance of sediment load simulations from SWAT 2016, SWAT-TUSLE, and SWAT-Twn.
3.1. Model Calibration and Validation for Streamflow
The observed streamflow from 2004 to 2015 was used for model calibration and validation. The streamflow-related parameters for calibration were referred to the previous study [
30]. The parameters include curve number (CN2), plant uptake compensation factor (EPCO), surface runoff lag time (SURLAG), baseflow alpha factor (ALPHA_BF), effective hydraulic conductivity in main channel alluvium (CH_K2), and Manning’s “
n” value for the main channel (CH_N2). In addition, we included Manning’s “
n” value for the tributary channel (CH_N1) and effective hydraulic conductivity in tributary channel alluvium (CH_K1) as they are also sensitive in this study. In order to differentiate the characteristics of the parameters in various land use, slope, and soil, some parameters (i.e., CN2, ALPHA_BF, CH_K1, CH_K2, CH_N1, CH_N2, CH_K1) were individually calibrated for specific land use, slop and soil.
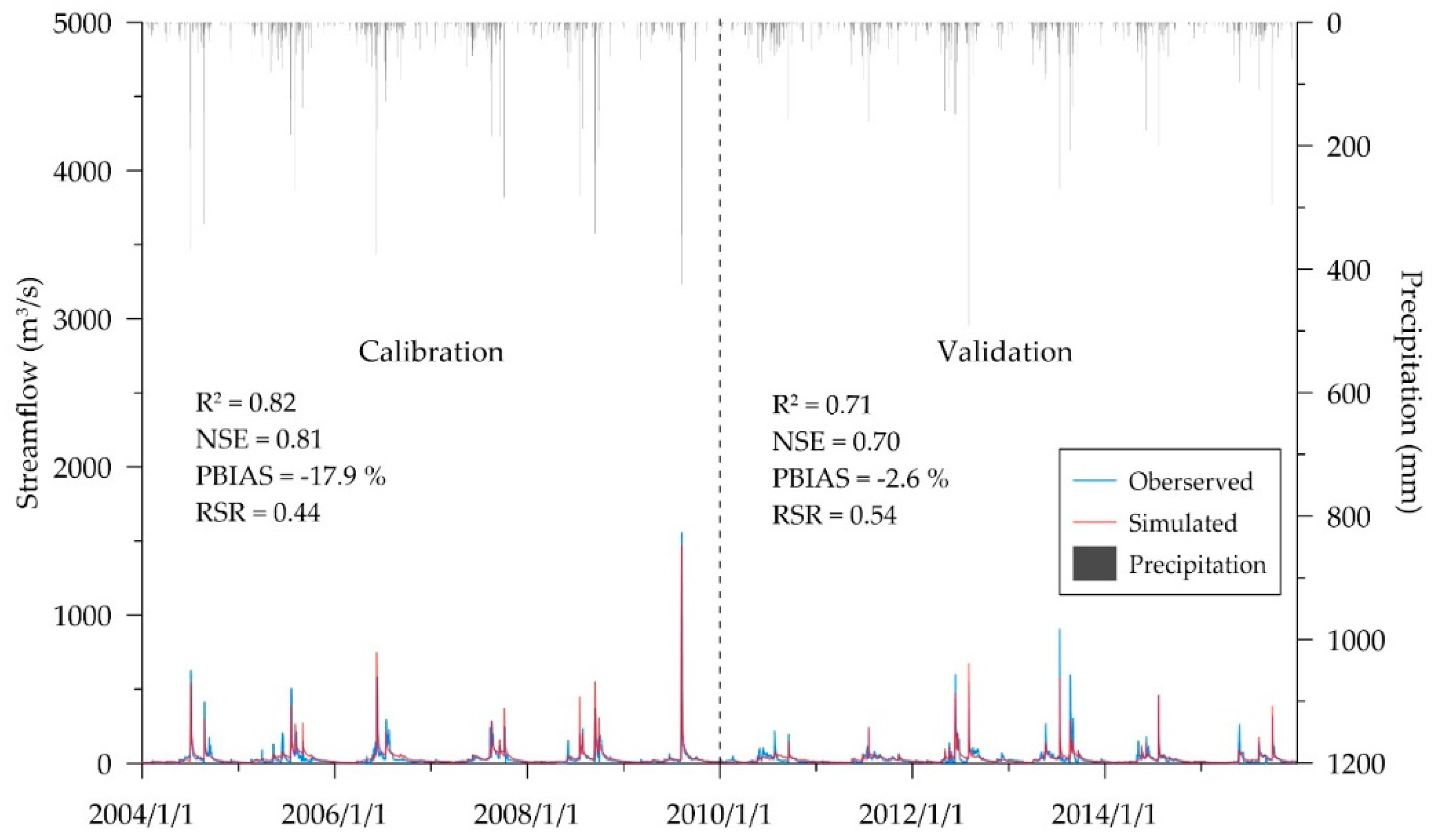
Table 5 shows the calibrated ranges and fitted parameter values for daily streamflow simulation. The model did satisfactory and good performance for the calibration and validation, respectively (
Figure 7), indicating the fitted streamflow parameters in model could well reflect the runoff characteristics of the Chenyulan watershed.
3.2. Comparison of SWAT 2016 and Modified SWAT Models
After calibrating the daily streamflow, we compared the uncalibrated simulated sediment yields from SWAT 2016, SWAT-TUSLE, and SWAT-Twn to quantify the impacts of using TUSLE and landslide volume equation on sediment yields at HRU and watershed levels (
Table 6 and
Table 7). It should be noted that we only used the sediment yield data during the streamflow calibration period because the fitted parameter values during validation period are different than those during calibration period. However, the range of parameter values are the same for both calibration and validation periods, and the simulation results can reflect the model uncertainty. Thus, we used the simulated sediment yield data during the calibration period (2004–2009) with calibrated fitted streamflow-related parameters and default sediment-related parameters to demonstrate the difference driven by different models.
The major differences between SWAT 2016 and the two other modified SWAT (SWAT-TUSLE and SWAT-Twn) are the LS factor, which has more influence in steep slope areas (slope > 9%), and the C factor, which was calculated by NDVI resulting various C factor values for different land uses. There were 77.12% and 80.29% of urban and agricultural lands located in areas with steeper slope (slope > 9%). Therefore, with unchanged C factor for urban, sediment yield from urban had decreased by approximate 60% due to the modified LS factors in TUSLE (
Table 6). However, sediment yields from agricultural lands did not change significantly by modified SWAT models. It was because the C factor calculated by NDVI is doubled than the SWAT default value (
Table 3), compensating the decrease in sediment yields by modified LS factor in TUSLE. Besides urban and agricultural lands, significant changes in sediment yields from forest, grassland and landslide were found. Although LS factors could influence the sediment yields, the C factor of forest and grassland which were changed from 0.001–0.003 to 0.2, played an important role in increases in sediment yields.
In the SWAT-Twn model, the landslide volume estimation is activated when the daily precipitation reaches over 350 mm. It should be noted that landslide volume estimation is only applied to the landslide area, not other land uses. It is obvious that sediment yields from landslide area increased significantly when the landslide volume estimation was activated in SWAT-Twn. Moreover, since forest is the main land use occupying 74.46% of the watershed and the NDVI-calculated C factor of forest is greater than SWAT default C factor, the annual sediment yields from the watershed were increased by 59.9% and 65.7% by SWAT-TUSLE and SWAT-Twn, respectively (
Table 7). The increase of 5.8% of sediment yield by SWAT-Twn was due to landslide volume estimation at the landslide areas. It shows that landslide volume estimation should be considered as the major contribution to sediment yields.
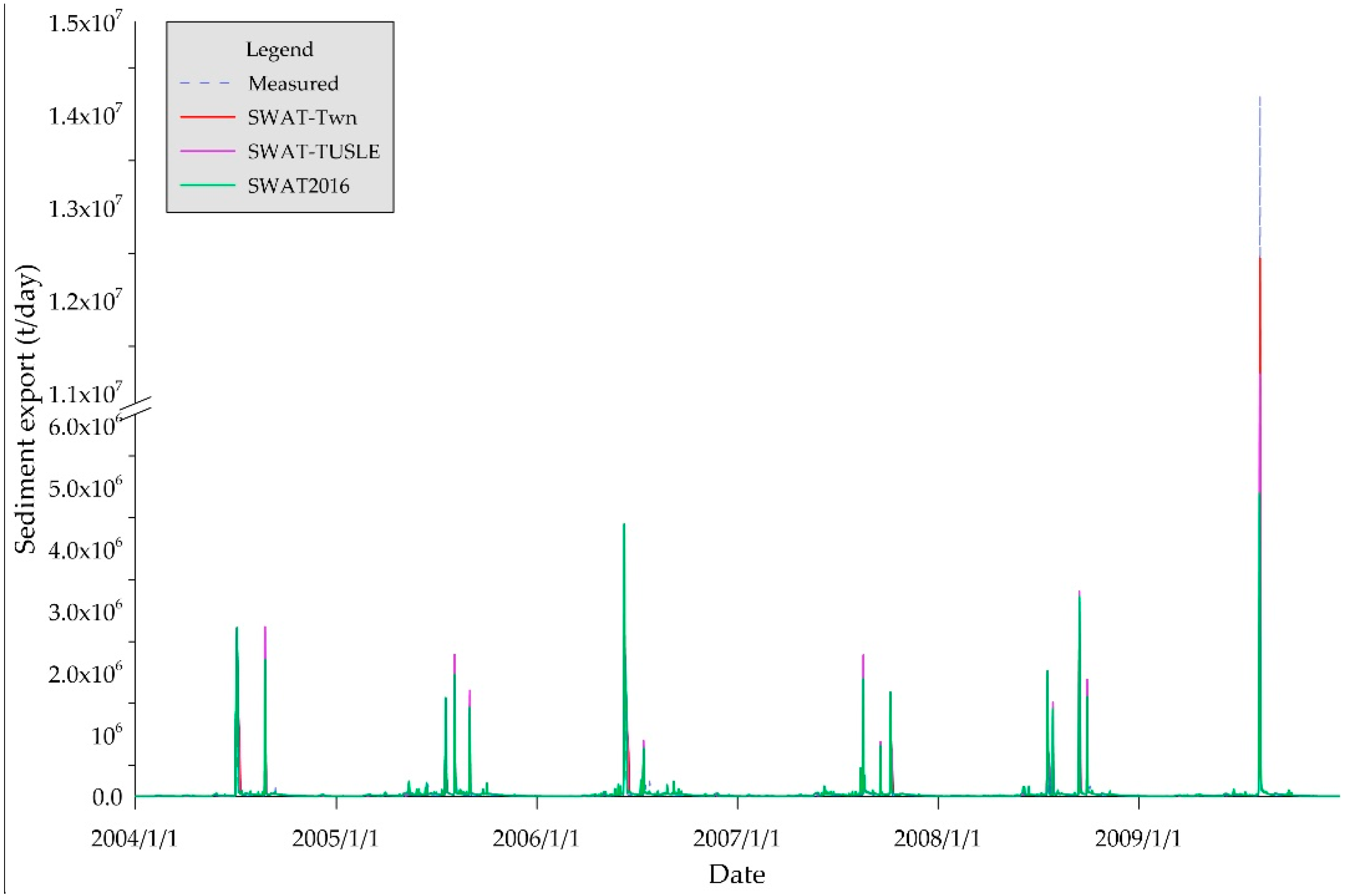
Before calibrating the sediment, these models overestimated the daily sediment load in terms of great positive PBIAS values (
Figure 8). However, SWAT-TUSLE and SWAT-Twn performed better than SWAT 2016 in terms of greater R
2, NSE and smaller RSR, especially the SWAT-Twn performance had better statistical criteria values (R
2 = 0.74, NSE = 0.66, RSR = 0.58). Therefore, we used SWAT-Twn for further sediment calibration and validation.
3.3. Model Calibration and Validation for Sediment
The SWAT-Twn model was calibrated and validated for sediment loads with five different sediment transport methods (i.e., EQN0–4). The calibration (2004–2009) and validation (2010–2015) periods for sediment loads were the same as those for streamflow. First, the sensitivity analyses for sediment parameters for different sediment transport methods were examined (
Table 8). A total of eight sediment-related parameters were identified as sensitive parameters. Four of these parameters (i.e., SPCON, SPEXP, PRF_BSN, ADJ_PKR) are estimated on basin level (*.bsn), meaning that the parameter values are fixed for the entire watershed; while the rest of parameters (i.e., CH_COV1, CH_BNK_D50, CH_BED_D50) are estimated on reach level (*.rch), which could be varied by spatial and slope conditions.
The linear parameter (SPCON), exponent parameter (SPEXP) and peak rate adjustment factor (PRF_BSN) are only activated for the simplified Bagnold equation (EQN0 and EQN1). The peak rate adjustment factor (ADJ_PKR) was found to be sensitive to EQN0, EQN3 and EQN4. In order to identify the difference in the reach-level parameters, we separated the watershed by slope of 60% as almost half (49.58%) of the Chenyulan watershed is at a slope greater than 60%.
The channel bank vegetation coefficient for shear stress (CH_COV1) at the sub-basins with mean slope greater than 60% was sensitive for EQN2, EQN3 and EQN4, indicating that the vegetation at steeper slope areas would have great influence on sediment load compared to that at flatter slope areas. The median particle diameter of channel bank (CH_BNK_D50) at steeper slope areas was only sensitive for EQN4, while the median particle diameter of channel bed (CH_BED_D50) were sensitive for EQN1, EQN2, and EQN3. It shows that the median particle diameter of channel bank or bed should be measured for increasing the accuracy of sediment simulation with EQN1-4. Although both EQN0 and EQN1 are simplified Bagnold stream power equations, the EQN0 (default in SWAT 2005 version) does not keep track of sediment pools in various particle sizes, while the EQN1 (additional stream power equation in SWAT 2016) has been incorporated with physics-based approach for channel erosion. Moreover, the simulation of channel erosion with EQN0 is not partitioned between stream bank and stream bed. Thus, both CH_BNK_D50 and CH_BED_D50 are not sensitive for EQN0, while the EQN1 was sensitive with bed erosion (CH_BED_D50).
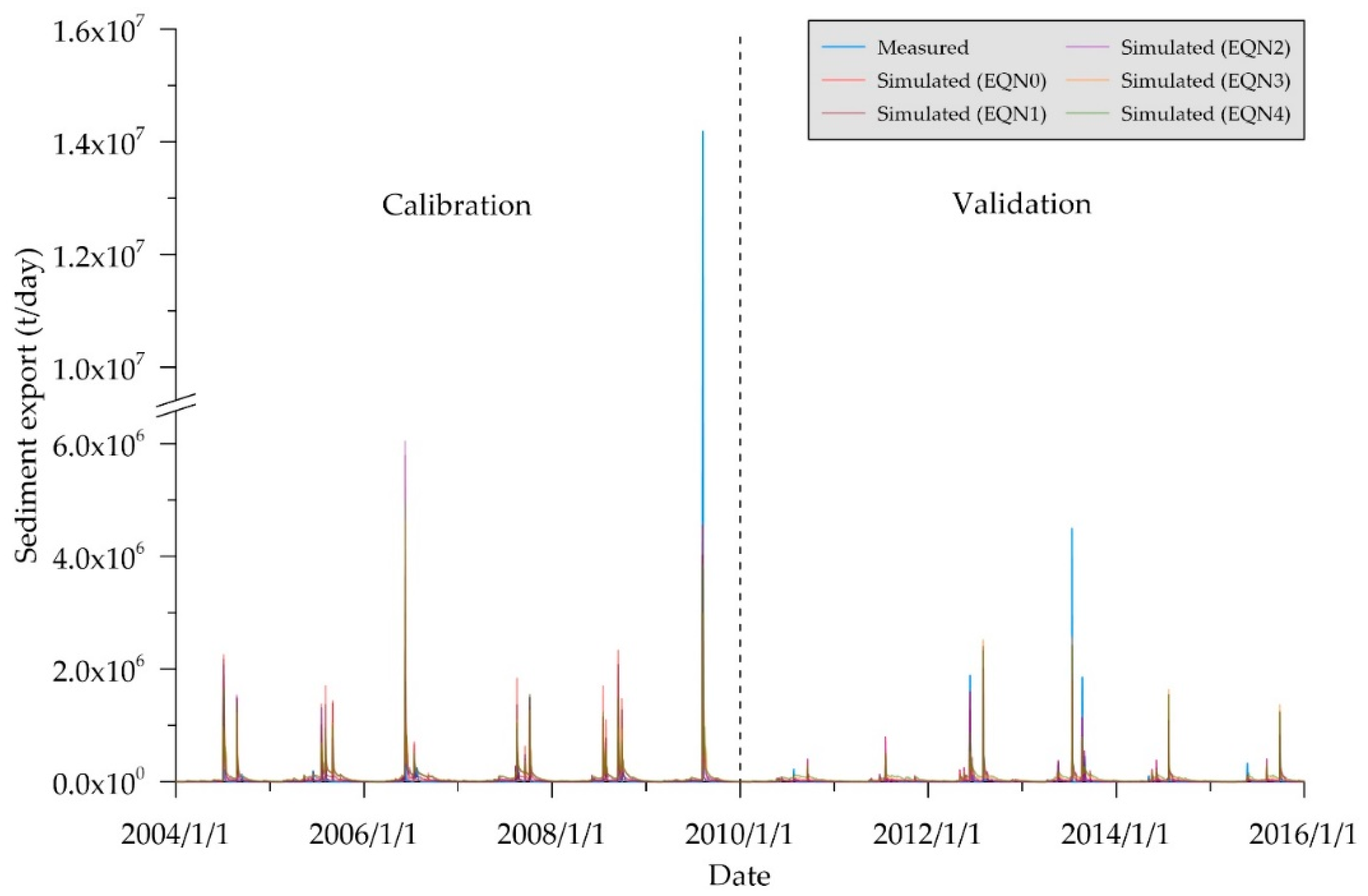
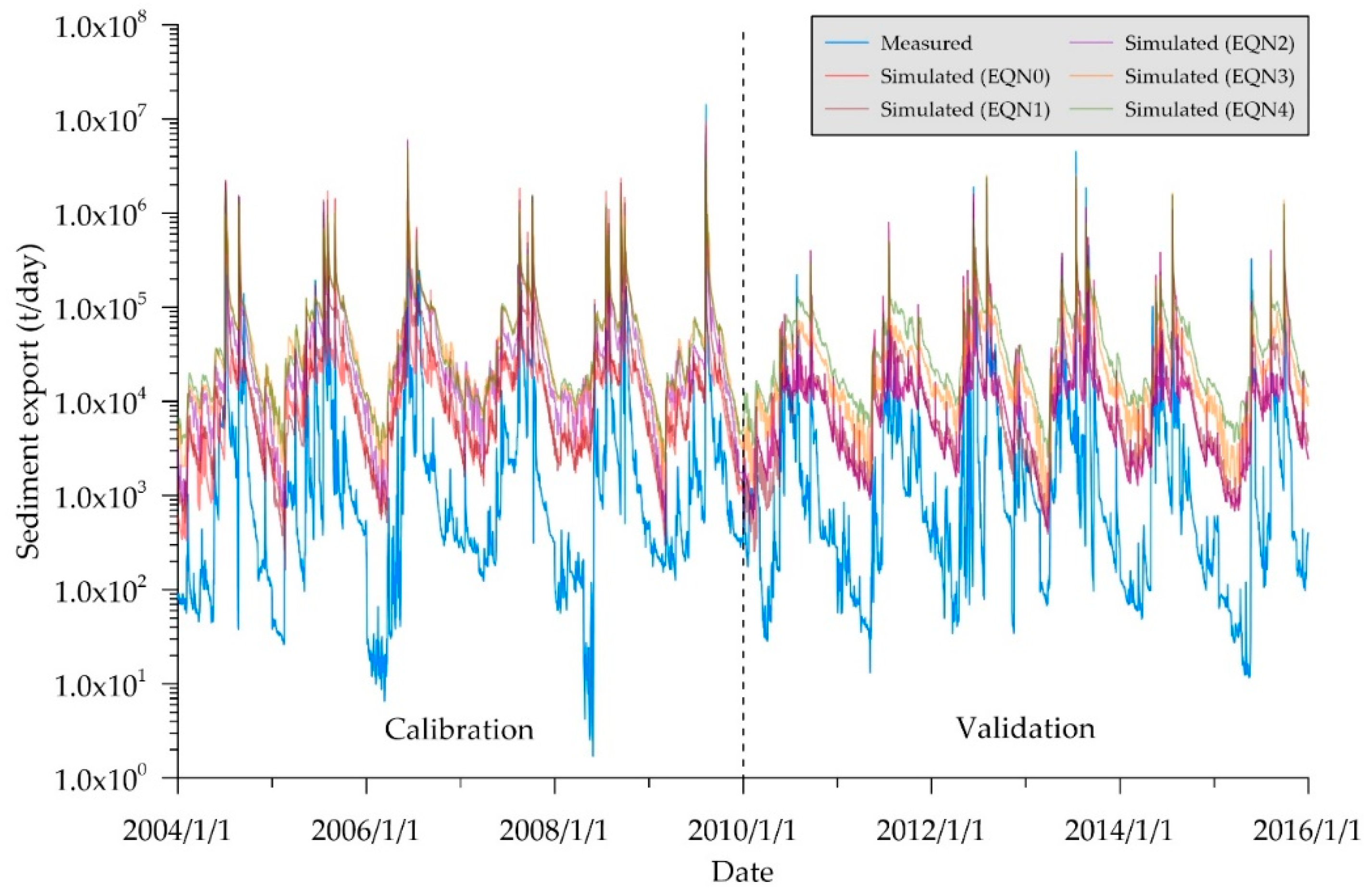
After identifying the sensitive parameters for those five sediment transport methods, the SWAT-Twn was calibrated and validated separately with each sediment transport method (
Table 9 and
Figure 9). Generally, the simulation results by EQN0 and EQN1 were better than those by other sediment transport methods, in terms of R
2 and NSE greater than 0.5. It indicates that Bagnold equation is more suitable for the Chenyulan watershed. Moreover, the SWAT-Twn with EQN2, EQN3 or EQN4 was found to underestimate for peak flows and overestimate for low flows (
Figure 9). Thus, the overestimated low flows at the most flow period resulted in great negative PBIAS values.
5. Conclusions
The Chenyulan watershed has suffered from serious landslide and debris flow induced by heavy rainfall and typhoons. In this study, we integrated the TUSLE and landslide volume estimation into the SWAT model as SWAT-Twn. By evaluating the simulated sediment yields from different land uses, the importance of topographic (LS) factor and NDVI-calculated weighted C factor were identified and landslide volume estimation should be taken into concern. The examination of five different sediment transport methods revealed some important issues. First, the level of sensitivity of sediment-related parameters is different for those sediment transport methods, and parameters (i.e., CH_COV1, CH_BNK_D50, CH_BED_D50) that are estimated on each level, are suggested to be calibrated by spatial and slope conditions. Second, it is more accurate to investigate the channel vegetation (CH_COV1) and measure the particle sizes of channel bank and bed sediment (CH_BNK_D50 and CH_BED_D50). The calibrated parameter values by SWAT-CUP for different sediment transport methods may be misleading. Third, the particle size distribution assumed by SWAT is suggested to be an option that can be edited by users. Furthermore, the calculation of fall velocity is suggested to not be only limited for median particle size as it would be biased for channels of wide range of particle sizes. Last but not the least, like the streamflow simulation in SWAT and SWAT-CUP, an option for the user to compare and plot the sediment simulation in logarithmic scale would provide more insights into sediment calibration. In sum, the SWAT-Twn model performed better than SWAT 2016 and SWAT-TUSLE, as TUSLE calculated less sediment at steep area, resulting reasonable sediment export simulation at low flow condition and landslide volume estimation reflected the real situation. Additional improvements in SWAT and SWAT-CUP need to be made to better predict the sediment yields and loads at mountainous watersheds.