1. Introduction
Water scarcity is a growing challenge in the arid and semiarid regions of the world [
1,
2,
3,
4]. In these regions, the use of wastewater for irrigation and other purposes has become a common and often unregulated practice, and groundwater quality assessments are seldom carried out [
5,
6]. In Latin America, it is estimated that 70% of the raw wastewater used in irrigation reaches an underlying aquifer [
7,
8]. The pollutants impacting the aquifer and the vadose zone with this practice include excess salts and heavy metals [
1]. In its movement from the unsaturated zone to the saturated zone, groundwater quality changes due to various processes, including carbonate dissolution, ion exchange, and silicate weathering [
9]. Unfortunately, few studies have focused on groundwater quality changes in both quality and spatial extent related to the irrigation use of wastewater [
3,
4,
10].
The Mezquital Valley is a semiarid region in Central Mexico that utilizes about 1500 million m
3 per year of wastewater effluent from Mexico City for irrigation purposes [
11]. The study region is composed of 5647.88 ha of the 90,000 ha that compose the entire Mezquital Valley [
12]. The wastewater recharge rate in the study area is approximately 25 m
3/s, and corresponds to 13.3 times the natural recharge rate in the Mezquital Valley [
12]. The accelerated recharge rate facilitates the transport of persistent pollutants to the unconfined aquifer, and results in a deleterious impact on groundwater quality [
13]. Previous studies have reported the pollution of groundwater related to high levels of NO
3− [
14], as well as TDS (total dissolved solids) and Na
+ above the maximum allowable limits [
15]. Additionally, arsenic (As) and lead (Pb) were also reported exceeding the maximum permissible limits (MPL) for drinking water [
6,
13,
16].
In the study region, the available studies have focused on the impact of wastewater on heavy metal contamination on soil and crops, and the effect on soil properties and plant growth. However, groundwater classification and spatial quality characterization, with the purpose of identifying the most vulnerable regions to assist groundwater policy makers make informed decisions, has not been addressed.
However, it is a challenge to evaluate the complex, highly dimensional groundwater hydrogeochemical datasets. Multivariate statistical approaches, such as principal component analysis (PCA) and K-means clustering are robust tools for groundwater resources management [
17,
18,
19,
20,
21]. They have been successfully used to define and understand the hydrogeochemical processes that dominate groundwater quality and identify pollution sources [
22,
23].
PCA explains the variance of large datasets of correlated variables, and converts them into a reduced set of uncorrelated variables known as their principal component (PC) [
24,
25]. K-means clustering is a powerful technique for discovery internal relationships and different characteristics of objects [
26]. The K-means clustering algorithm partitions a set of objects into groups, where similar objects belong to unique clusters [
17,
22,
24]. A water quality index (WQI) is also an efficient tool for identifying water quality and its suitability for a particular use [
17,
24,
27]. Moreover, Piper and Stiff diagrams and ion relation scatter diagrams are standard methods to study geochemical data and analyze water–rock interactions, respectively [
28,
29].
In this study, K-means clustering, and PCA were used to identify the relevant hydrogeochemical processes that define groundwater quality. WQI was used to assess groundwater quality for drinking purposes and its spatial variations in a wastewater irrigation district in the Mezquital Valley, México.
2. Study Area
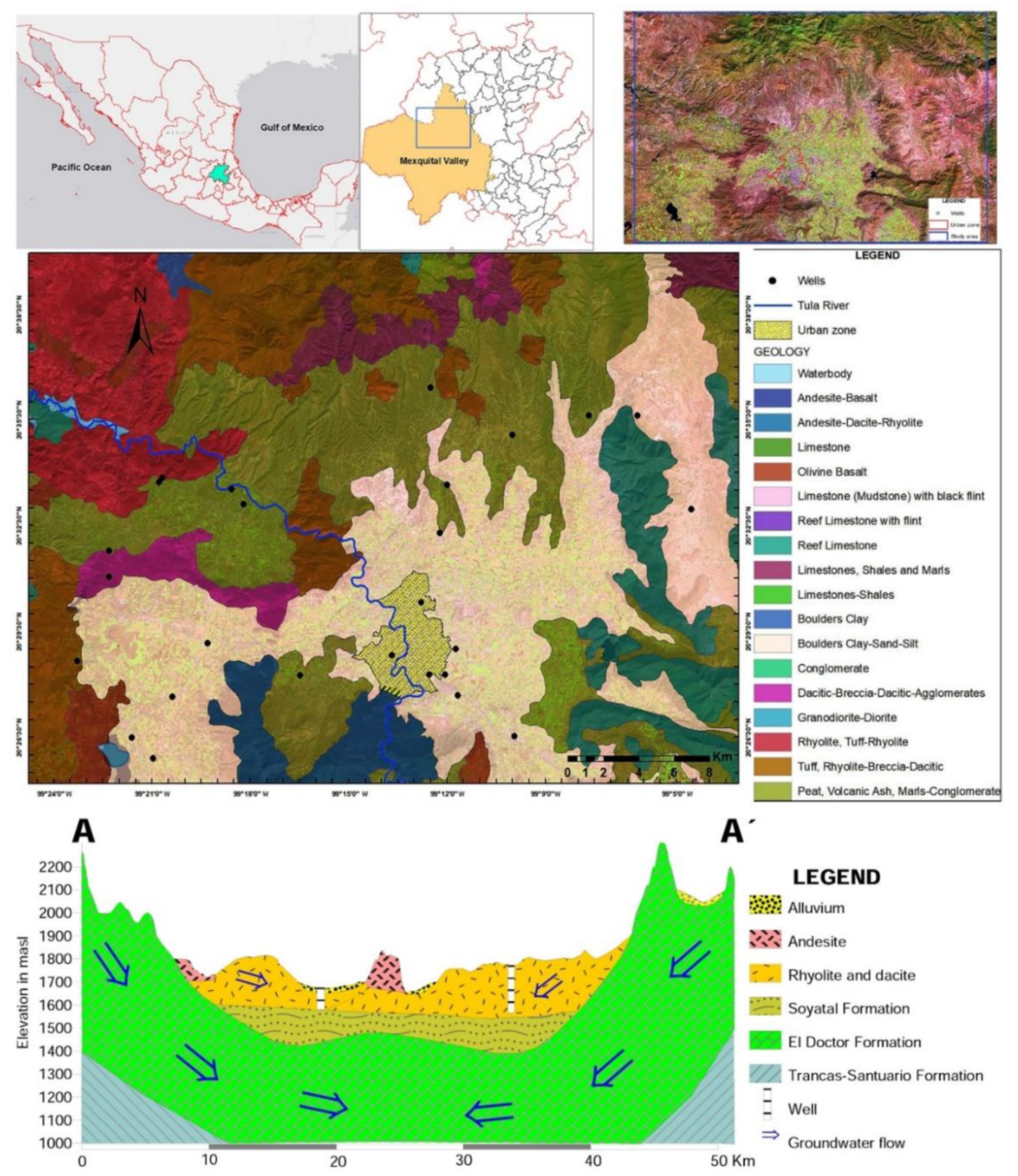
The study area is on the northern end of the Mezquital Valley (
Figure 1). It has an area of approximately 2200 km
2. According to [
13], there are three dominant soil types in the region: (1) Phaeozems, (2) Leptosols, and (3) Vertisols. The climate is semiarid, with a mean annual temperature of 18 °C [
12,
13,
30]. Rainfall amounts range from 300 to 500 mm/year, while potential evapotranspiration (around of 2100 mm/year) exceeds the mean annual precipitation [
12,
13,
30,
31].
2.1. Geologic Setting
The geology of the Mezquital region includes volcanic rocks and a minor amount of sedimentary rocks. The El Doctor, Mexcala, and Soyatal formations belong to the Upper Cretaceous, and are mostly composed of limestone, sandstone, and shale respectively (
Figure 1). In addition, a sequence of interbedded shale, sand, and siltstone predominate in the Mexcala Formation [
31,
32].
Tertiary deposits are comprised primarily of detrital continental and volcanic rocks corresponding to the Medium Pliocene [
32]. The Pachuca group composition varies from basaltic to rhyolitic rock. The thickest sequence of rocks is known as Pachuca mountain range. The Don Guinyó Formation encloses volcanic tuff and breaches, as well as compacted ignimbrites made up of dacitic and rhyolitic rock. The Zumate Formation includes a sequence of andesitic and dacitic rocks, with interbedded lava and lahar deposits. The Taximay Formation is comprised of lacustrine deposits composed of clay, with a thickness greater than 50 m. It is located across a hydrographic ridge between the Mezquital and Zumpango Valley. The San Juan group is composed of a succession of lava spills, with a few interbedded layers of tuff, breach, and volcanic agglomerates with thicknesses less than 400 m. The Tarango Formation is made up of interbedded layers of gravel, sand, silt, and clay.
The quaternary deposits are enclosed by lava spills and cineritic cones, in addition to alluvial and fluvial sediments. They are composed of sands, clays, and gravels covering the valley’s surface [
31,
32].
2.2. Hydrogeologic Setting
The aquifer underlies the Tula River watershed (
Figure 1), and its recharge sources are irrigation and precipitation. It has a groundwater flow direction going from south to north [
30,
32]. Previous studies describe the aquifer as unconfined to semi-confined, heterogeneous, and anisotropic, and it is composed of an upper and a lower portion. The upper aquifer consists of porous formations of fluvial origin composed of interbedded granular alluvial material, volcanic rocks, and pyroclastic sediments with thicknesses of up to 400 m [
31]. The lower (semi-confined) aquifer is made up of volcanic rocks, with interbedded lava of the Tarango formation [
32].
The aquifer transmissivity ranges from 0.06 × 10
−3 to 6.47 × 10
−3 m
2/s, while the hydraulic conductivity ranges between 4 × 10
−7 and 1.2 × 10
−3 m/s. The static water level depth ranges from 20 to 100 m, increasing from the central zone toward aquifer limits [
31].
3. Material and Methods
3.1. Sample Collection
A total of 31 groundwater samples were collected from wells at urban settlements within the study area during the rainy season, in a sampling period from 15 July to 20 July 2014 (
Figure 1). Two samples per location were collected into 500 mL polyethylene bottles. The first sample at each location was used for cation analysis, and preserved with 2 mL of HNO
3. The second sample was used for anion analysis, with no acid added [
33].
3.2. Analytical Methods
All samples were analyzed according to the standards set by the American Public Health Association [
33]. The pH, electric conductivity (EC), and total dissolved solids (TDS) were measured in situ by using a Hanna (HI9828, Hanna, USA) multi-parameter. Concentrations of major cations, such as calcium (Ca
2+), magnesium (Mg
2+), sodium (Na
+), and potassium (K
+), were analyzed using a Flame Photometer. Concentrations of bicarbonate (HCO
3−), carbonate (CO
32−), chloride Cl
−, and total hardness (TH) as CaCO
3 were determined by the acid titration method, while anions nitrate NO
3− and sulfate SO
42− were analyzed using an ultraviolet spectrophotometer. The sodium adsorption ratio (
SAR) was defined by Richards (1954) in the United States Department of Agriculture (USDA) Handbook 60. The
SAR was calculated by Equation (1):
where
SAR is a non-dimensional number, and concentrations of Na
+ (
Na), Ca
2+ (
Ca), and Mg
2+ (
Mg) are expressed in mEq/L.
Results of the chemical analyses were tested by the percent charge balance error (%
CBE). According to [
34], this is defined as
where
is the absolute value of the ionic valence, and
and
are the molality of the cationic and anionic species, respectively. In this study, the charge balance error of all samples was between −2.81% and 3%. These results are in agreement with previous studies for the statistical treatment of datasets [
35,
36].
3.3. Water Quality Index (WQI)
Water quality indexes are used to identify the suitability of groundwater quality for drinking purposes [
37]. WQI is the most useful method to measure water quality [
38]. The WQI was developed by Bascaron [
39], as shown in Equation (3). It is defined as an algorithm that determines the qualitative state of the water [
40]. The WQI represents a single value that numerically summarizes multiple water parameters [
24]. The WQI can be calculated either by deductive or inductive methods [
41]. In this study, the WQI was computed to assess the suitability of groundwater for drinking standards, according to the Mexican Official Norm [
42] and the World Health Organization [
43]. The WQI is expressed by Equation (3):
where
is the total number of parameters,
is the percentage value assigned to the parameter (
i) according to the concentrations,
is the relative weight assigned to each parameter, and
is a subjective constant taken from the values in
Table 1.
The WQI is calculated in four steps. In the first step, each of the 13 physicochemical parameters considered (temperature, Ca
2+, Mg
2+, Na
+, K
+, TH (CaCO
3), HCO
3−, pH, EC, TDS, SO
42−, Cl
−, and NO
3−) is assigned a relative weight (
) on a scale of 1 to 4. The highest weight of 4 is designated to parameters with critical health effects that have concentrations above the permissible limits established by the WHO [
43]. The second step is to calculate the relative weight using Equation (4):
where
is the relative weight and
is the weight of each parameter. In the third step, a percentage value
is assigned to each parameter after normalization.
Table 2 shows the different parameters used in the calculation of the WQI, as well as their relative weights and the normalization factors. These values were adopted from previous studies [
44,
45,
46,
47,
48], which are based on the World Health Organization [
43] and the Mexican Official Norm [
42].
In the fourth-step, the WQI is calculated (Equation (3)). For each sample considered, the sum of the weighted parameters is computed and multiplied by the constant
, which characterizes water aesthetics and odor (
Table 1). The WQI values ranges between 0 and 100, where 0 indicates “extremely polluted” water quality and 100 indicates “excellent” water quality. Different scales have been used by different authors [
41,
45,
46,
48,
49,
50,
51,
52,
53]. In this study, the calculated WQI values were defined according to the quality scale proposed by [
49], shown in
Table 3. The WQI was mapped to evaluate spatial variability in the study zone.
3.4. Multivariate Statistical Analysis
Multivariate analysis was carried out by K-means clustering analysis and principal component analysis (PCA). Statistical analysis, including descriptive statistics, a correlations matrix, PCA, and cluster analysis were performed using RStudio software V. 1.0.153 (Copyright RStudio Inc., Boston, MA, USA).
3.4.1. Data Preprocessing
The optimal results of statistical multivariate methods such as PCA require an univariate and multivariate normal distribution [
54,
55,
56,
57,
58,
59,
60], as well as homogeneity of variances (homoscedasticity) [
61,
62]. The univariate and multivariate normality condition was verified by Shapiro–Wilk’s tests [
63] and Royston’s test [
64], respectively. The empirical distributions of most variables deviated from a normal distribution, except for pH. A non-normal distribution was observed on the dataset based on Royston’s test. A logarithmic transformation (natural logarithm) was applied to the original set of variables to achieve a normal-like distribution. In this regard, it is recommended to start with this type of univariate transformation before applying the multivariate transformation methods [
65]. Feature scaling on the database was made through standardization (or
Z-score normalization) to approach the optimal conditions of the multivariate analysis. Standardization reduces the difference in variances in variables, and prevents dissimilarity measures like the Euclidian distance obtained from being severely affected. Each variable was standardized to their corresponding
Z scores [
66], which are calculated by Equation (5):
where
Zi is the standardized
Z score,
Xi is the value of each variable, and
mean and
S are the mean value and the standard deviation of each variable, respectively. The adjustment of the transformed variables to the normal log distribution was evaluated favorably using the Kolmogorov–Smirnov (K–S) test [
22,
67]. A matrix of 14 hydrogeochemical variables and 31 observations was analyzed. The choice of Spearman’s rank correlation was due to the non-normal distribution of the water quality parameters [
22,
68]. This test is more robust for variables moving away from the normal distribution, and deviations are minimized for correlations between the variables [
69].
To test the data accuracy and suitability for PCA, Kaiser–Meyer–Olkin (KMO) and Bartlett’s sphericity statistics were carried out. KMO is a measure of sampling validity, and indicates the proportion of the variance, which might be sourced by unknown factors [
22,
58]. KMO values larger than 0.9 indicate high validity for applying PCA, between 0.5 and 0.9 indicates sufficient validity, and KMO values less than 0.5 are considered not valid [
70]. In this study, a KMO (valid) value of 0.78 was obtained. Bartlett’s test of sphericity validates that the analyzed variables are correlated adequately. In this study, the significance level was less than 0.05, showing significant relationships among variables.
3.4.2. K-Means Clustering Analysis
K-means clustering uses criteria to segment the data based on intrinsic characteristics, proximity, or degree of similarity [
71,
72,
73,
74]. Similarly, the purpose of K-means clustering is to achieve both high (internal) homogeneity within a cluster and (external) heterogeneity among different clusters [
72].
The principal objective of the K-means clustering algorithm is to partition an unlabeled dataset into
K clusters (groups or categories), represented by centroids [
72]. According to [
75], in each repetition, instances allocated to the closest clusters founded on the Euclidean distance between instances and centroids (Equation (6)):
where
is the distance,
is the point in the space representing a given object,
is cluster q,
is known as the
jth attribute of the
pth instance,
as the
jth attribute of the
qth cluster, and
D is known as the total number of attributes. Each cluster centroid is updated through averaging all of the instances belonging to that group. For optimization purposes, the K-means algorithm attempts to minimize the sum of squared error by using Equation (7):
where
is the number of clusters
;
;
represents an instance set
;
and is a
dimensional vector, and
is known as the
kth cluster centroid.
In K-means clustering, an important parameter that needs to be defined is the number of clusters. There are more than 30 indices that have been published for identifying the optimal number of clusters. To determine the optimal number of clusters in a dataset, the R package NbClust [
76] was used. These provided 24 indexes for identifying the optimal number of clusters. Eight of these indexes suggested that wells are grouped in two clusters (See
Supplementary Materials, Table S1). The K-means algorithm was run using R’s K-means function in stats [
77]. On this function, the number of clusters (
k = 2) is specified, and the algorithm randomly selects each
k-center. The resulting outputs are highly sensitive to the initial random assignments of the centers; therefore, multiple random initializations (25, 50, 75, and 100) were tested with the argument “nstart”. The “set.seed” function is used to have some reproducibility of the results of the initial
k-center assignments. This process allows us to evaluate the results of the K-means algorithm for each set of initial random results, by means of a practical visual evaluation and through geographic information system (GIS).
3.4.3. Principal Component Analysis (PCA)
The primary purpose of PCA is to explain the variance within the dataset while reducing the dimensionality of the data structure. PCA was carried out to transform the original correlated variables into a smaller set of uncorrelated variables called the principal components (PCs) [
22,
67,
73,
78]. PCs are the uncorrelated variables calculated by multiplying correlated variables with the eigenvector, and are expressed as loadings. The loadings show the contribution of a given variable to each of the extracted PCs [
73].
According to [
79], the principal component (PC) is expressed by the following equation:
where
is known as the component score,
is the component loading,
is the estimated value of the variable,
is the component number,
is the sample number, and
is the total number of variables.
4. Results and Discussion
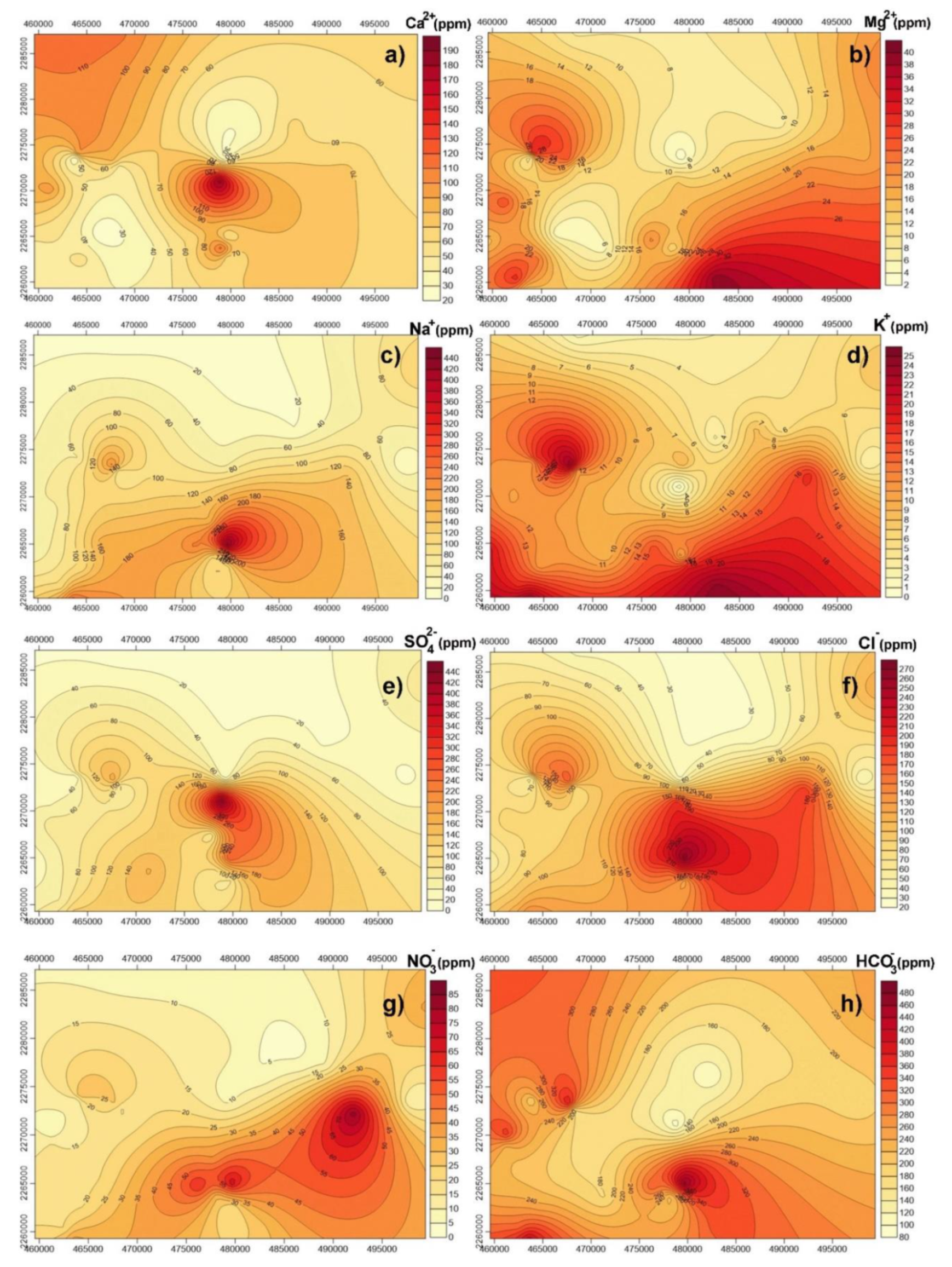
4.1. Ionic Dominance
Maximum, minimum, and mean values of the chemical composition of groundwater are shown in the
Supplementary Material (Supplementary Materials Table S2). Major cations were analyzed, and the abundance of ions was in the order of Na
+ > Ca
2+ > Mg
2+ > K
+. Na
+ was in exceedance (440.95 mg/L) of the MPL (200 mg/L) [
42,
43]. High Na
+ levels can be due to the use of untreated wastewater for irrigation. In previous studies, researchers reported high Na
+ levels in wastewater, and were attributed to long-term irrigation practices with untreated wastewater. Calcium concentrations ranged from 21.64 to 188.78 mg/L. Magnesium concentrations ranged from 2.79 to 39.37 mg/L. K
+ concentrations ranged from 0.12 to 24.48 mg/L. Anions showed dominance in the following order: Cl
− > HCO
3− > SO
42− > CO
32−. The high concentration of HCO
3− can be explained by carbonate dissolution. Elevated concentrations of SO
42−, which are higher than the MPL (250 mg/L), can be due to mineral dissolution and the use of wastewater for irrigation. The Cl
− concentration in sewage is high, so its use as irrigation water results in a significant increase in the concentrations of Cl
− in the groundwater (
Table S2). Nitrate showed a range of concentration between 5.7 and 83.29 mg/L. The highest NO
3− levels can be attributed to the use of fertilizers and irrigation with untreated wastewater.
4.2. Hydrochemical Facies
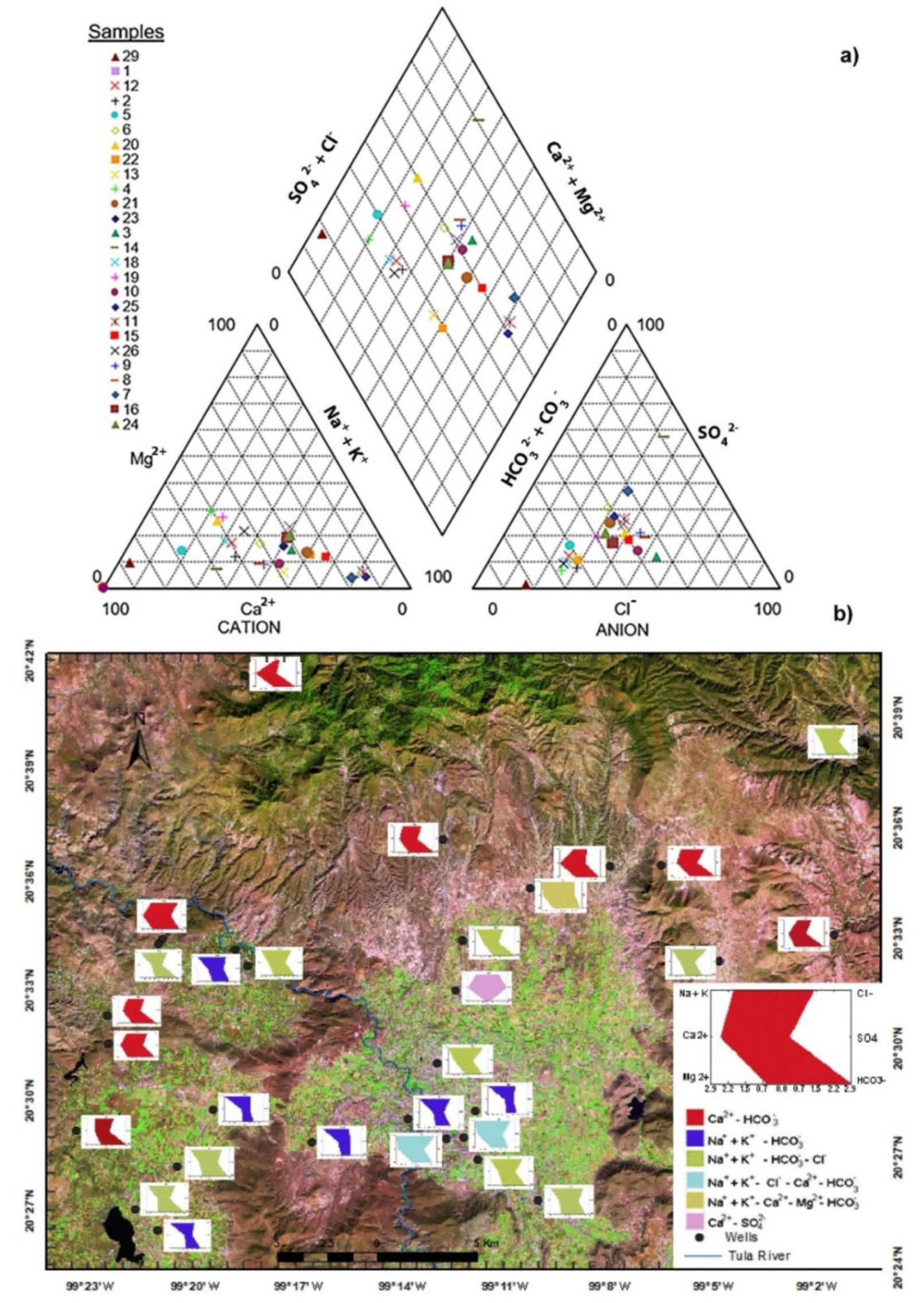
Hydrochemical facies are employed for delineating the chemical composition of groundwater. In order to identify hydrochemical types and delineate the spatial variation of dominant ions, the Piper diagram [
80] and Stiff diagram [
81] were elaborated (
Figure 2). The trilinear diagram (
Figure 2) indicates that the dominant cations (Na
+ and Ca
2+) and anions (Cl
− and HCO
3−) play a decisive role in defining water type. Three distinct hydrogeochemical facies were identified in the study zone. The Na
+–Cl
− type of water predominates among three facies with 37.9%, and the Ca
2+–HCO
3− type is the second dominant water type with 27.6%. The mixed Ca
2+–Na
+–Mg
2+–HCO
3−–Cl
− (34.5%) water type is also present.
Stiff diagram analysis was used to assess the spatial incidence of the major ions and water type distribution. It observed that Na
+ + K
+–Cl
− type water is located within the central and southern parts of urban and agricultural zones, as well as close to the Tula River, other natural flow streams, and irrigation canals (
Figure 2). This suggests that Na
+, K
+, and Cl
− predominance has increased by continuous irrigation with wastewater. The Ca
2+–HCO
3− dominated water is present on the northern portion of the study area, in the surroundings mountains (
Figure 2), indicating that fresh water recharge is taking place. Mixed Ca
2+–Na
+–Mg
2+–HCO
3−–Cl
− water type is found in the central and southern areas, in settlements, urban and agricultural zones, natural flow streams, and irrigation canals (
Figure 2). This suggests that the mixed nature of water is affected by multiple factors, such as wastewater irrigation, carbonate dissolution, and cation exchange processes.
4.3. Application of the Water Quality Index and the Quality of Water for Drinking Purposes
Water quality indexes (WQIs) were computed for the samples using the concentrations of Ca
2+, Mg
2+, Na
+, K
+, TH (CaCO
3), HCO
3−, pH, EC, TDS, SO
42−, Cl
−, and NO
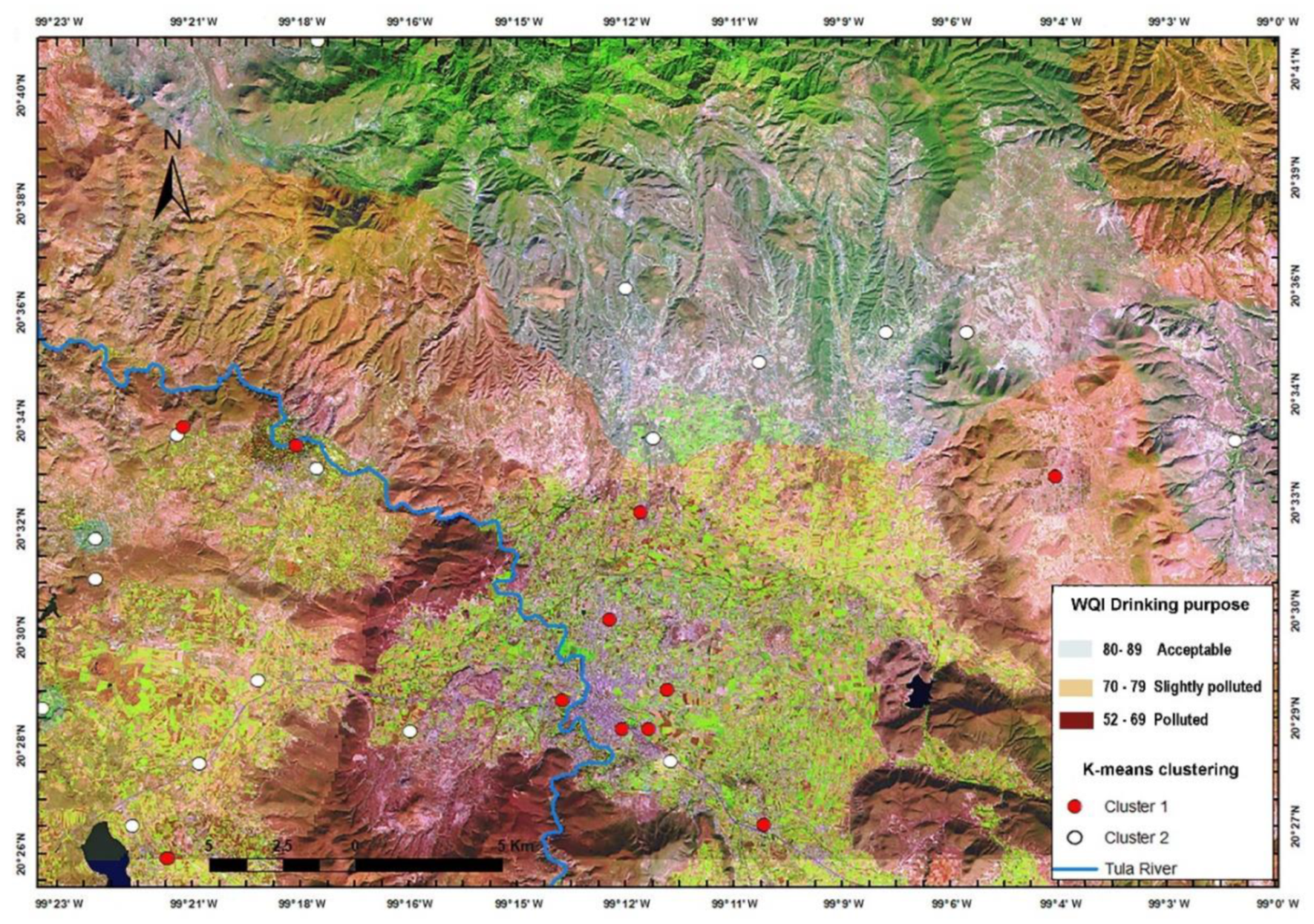
3−. WQI values range from 52 to 87, as shown in
Figure 3. According to the water quality index classification (
Table 3), 41.4% of the samples were polluted, 20.7% were slightly polluted, and 37.9% were acceptable for drinking purposes. The percentages indicate that groundwater treatment is warranted before use for drinking water purposes (
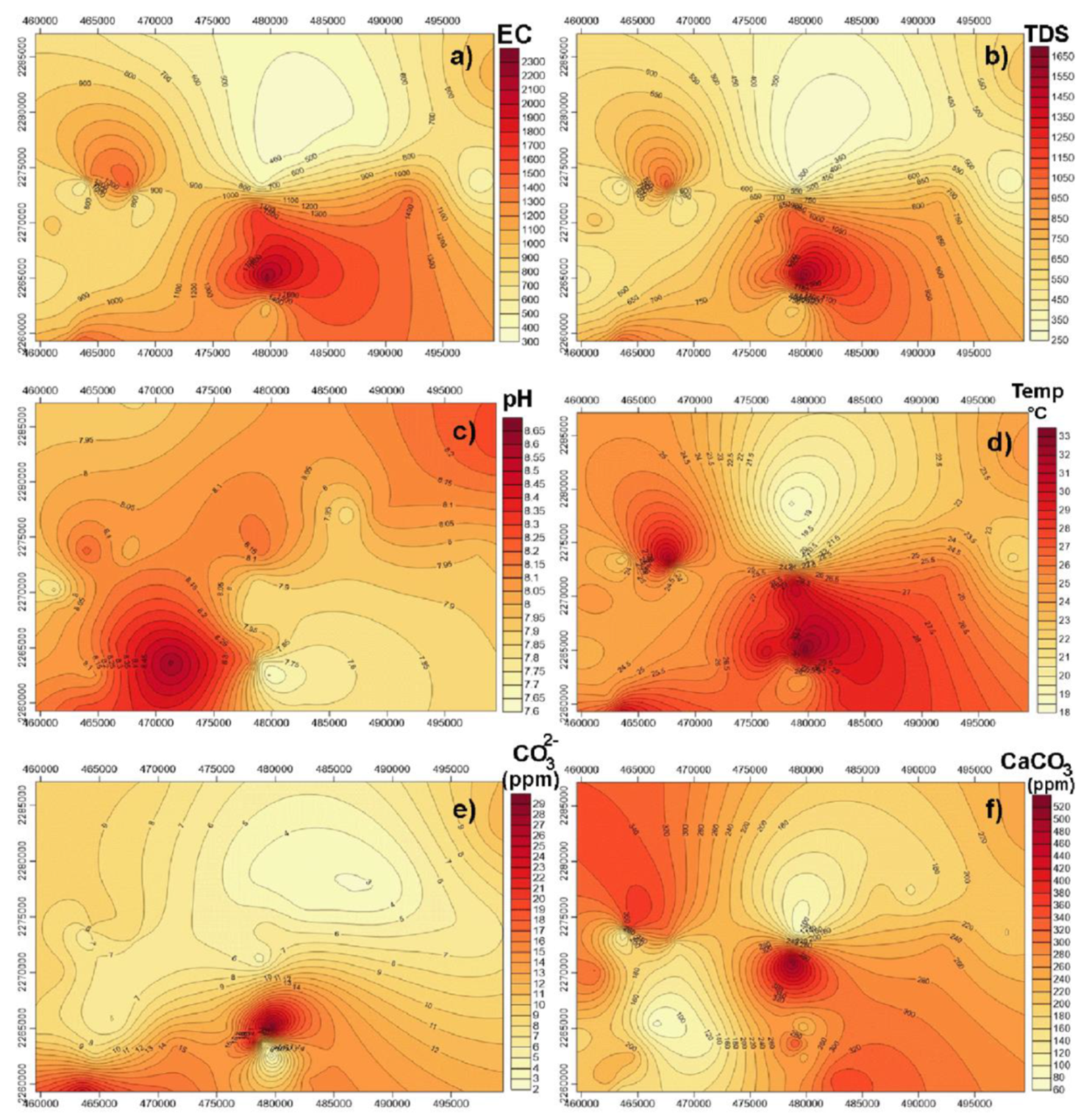
Table 3). The spatial distribution of the WQI indicates that groundwater unsuitable for human consumption is found in urban areas, wastewater irrigated zones, and the surroundings of the Tula River. On the other hand, high-quality groundwater is found in recharge zones, rural settlements, and seasonal agricultural fields.
Low-range WQIs for groundwater (WQI > 70) are attributed to exceedances of EC, TDS, Cl
−, Na
+, K
+, NO
3−, pH, and TH (CaCO
3) (
Supplementary Materials, Tables S2 and S3). This can be linked primarily to infiltration and recharge of untreated industrial-domestic wastewater and fertilizers, and also hydro-geochemical interactions. Similar studies have reported that lower quality groundwater is due primarily to high concentrations of Na
+, TH (CaCO
3), TDS, and EC sourced from the infiltration of untreated wastewater [
1,
4].
4.4. Correlation Among Variables
The Spearman’s rank correlation (
r) was computed to measure and establish the interrelationship between two variables. The correlation matrix of 16 selected parameters is presented in
Table 4. In this study, an
r value greater than 0.7 indicates a high correlation, and an
r value in the range of
r > 0.5 or ≤0.7 indicates a moderate correlation.
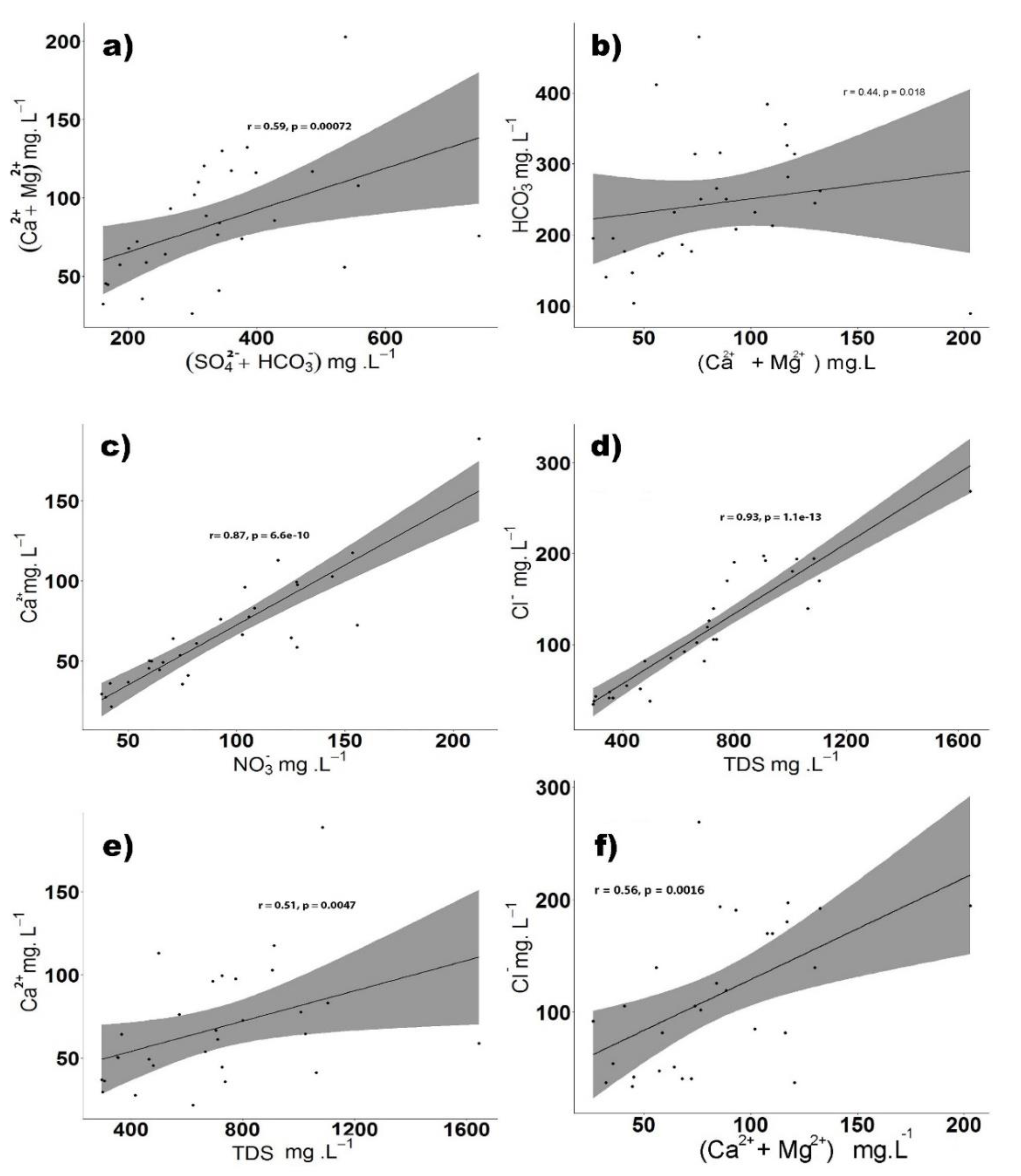
Ca
2+ and Na
+ have the highest correlation coefficient (0.966). This suggests that cation exchange processes are occurring, where a Ca
2+ ion is taken as the exchanger by a release of Na
+ ions [
9,
10,
35]. Moreover, Ca
2+ showed a positive correlation (
Figure 4a,b) with CO
32− (0.785) and HCO
3− (0.772), indicating the dissolution and precipitation of calcite [
9,
74,
82,
83,
84,
85].
A high positive correlation between Ca
2+ and NO
3− (0.87) suggests that the source of nitrate and calcium is the same (
Figure 4c), and could be attributed to nitrate from agricultural fertilizers leaching to the aquifer [
86]. Additional processes, such as nitrification, may increase the dissolution of carbonate minerals [
87,
88].
Mg
2+ and SAR showed a high positive correlation (0.913), indicating a cation exchange process. When there are high concentrations of Na
+ in irrigation water, Na
+ ions are absorbed by clay particles, exchanging Mg
2+ ions [
1,
89] (
Supplementary Materials, Figure S1). The high positive association between Na
+ and total hardness (0.708) reveals the strong influence of Na
+ ion on the increase in TH (CaCO
3), through the dissolution of bicarbonates [
26] and cation exchange [
23,
69] (
Figure 4b).
High positive correlations of 0.860 and 0.783 were obtained by K
+ with SO
42− and TH, respectively. This indicates that potassium ions may originate naturally from the dissolution and weathering of K-feldspars and carbonate rocks, as well as from two anthropogenic sources: (1) agricultural fertilizers and (2) wastewater infiltration and recharge [
1,
24,
36,
90].
High correlations between pH and K
+ and SO
42− (0.952 and 0.818, respectively) were obtained. This could be due to the recharge of potassium and sulfate salts from the weathering process of rocks and the continuous usage of wastewater for irrigation [
1,
36,
74]. The pH showed a positive correlation with TDS (0.622) and EC (0.627). This suggests that pH is defined primarily by the leaching of salts sourced from long-term usage of sewage for irrigation, which circulates the water within the aquifer. Wastewater is mostly alkaline, with significant variations of EC and TDS [
1,
35,
88]. High salinity levels are caused by dissolution of minerals and soluble salts, such as Cl
−, Ca
2+, Mg
2+, and Na
+ [
1,
10]. These results establish the significant contribution of the ions to the mineralization and salinization processes (
Figure 4d–f). A moderate positive correlation (0.514) between pH and temperature could indicate more intensive water–rock interaction and the infiltration of warm wastewater [
91,
92]. A high positive correlation (0.939) between pH and WQI suggests that pH is a good indicator of groundwater quality in regions with significant anthropogenic influence.
4.5. Cluster Analysis
Cluster analysis by the partition K-means method was used to identify similarity groups among the sampling sites. The results of spatial cluster analysis for the 31 water samples is shown in
Figure 3. Two distinct groups were identified with distinct water quality characteristics. Cluster 1 includes 38% of the total samples, and 62% of the water samples were classified in cluster 2. Cluster 1 shows characteristics of high salinity by wastewater recharge and agricultural pollution. Groundwaters of cluster 1 were defined by elevated concentrations of EC, TDS, Na
+, SO
42−, Cl
−, K
+, and NO
3− (
Table 5). Cluster 2 is characterized by mineralization processes from rock–water interaction, such as the dissolution of carbonates (calcite and dolomite). Cluster 2 groundwater is characterized by high concentrations of TH (CaCO
3), Ca
2+, K
+, and pH, as well as high temperature (
Table 5)
EC and TDS in cluster 1 were found to have higher concentrations (mean = 1552.55 and mean = 1003.49, respectively) than in cluster 2 (mean = 733.11 and mean = 513.92, respectively) as shown in
Table 5. High EC and TDS can be attributed to infiltration and recharge with wastewater. There is evidence that long-term irrigation practices with wastewater increase EC and TDS in groundwater [
1,
10]. The concentrations of Na
+, Cl
−, SO
42−, K
+, and NO
3− in cluster 1 are higher on average than those in cluster 2, and may be associated with wastewaters. Na
+ and Cl
− concentrations in wastewater are very high, and irrigation, infiltration, and recharge increase their presence in groundwater [
88,
93]. Studies reported by the WHO have demonstrated that agriculture is the primary source of NO
3− released to the groundwater [
43]. A significant increase in the concentrations of SO
42− and K
+ are linked with agricultural fertilizers and sewage effluents [
27,
36,
90]. The water wells classified in cluster 1 are located in urban areas, wastewater irrigated zones, and the nearby Tula River. Meanwhile, water samples from wells and streams classified in cluster 2 are located in the vicinity of urban settlements and temporary agricultural fields (
Figure 3).
4.6. Principal Component Analysis (PCA)
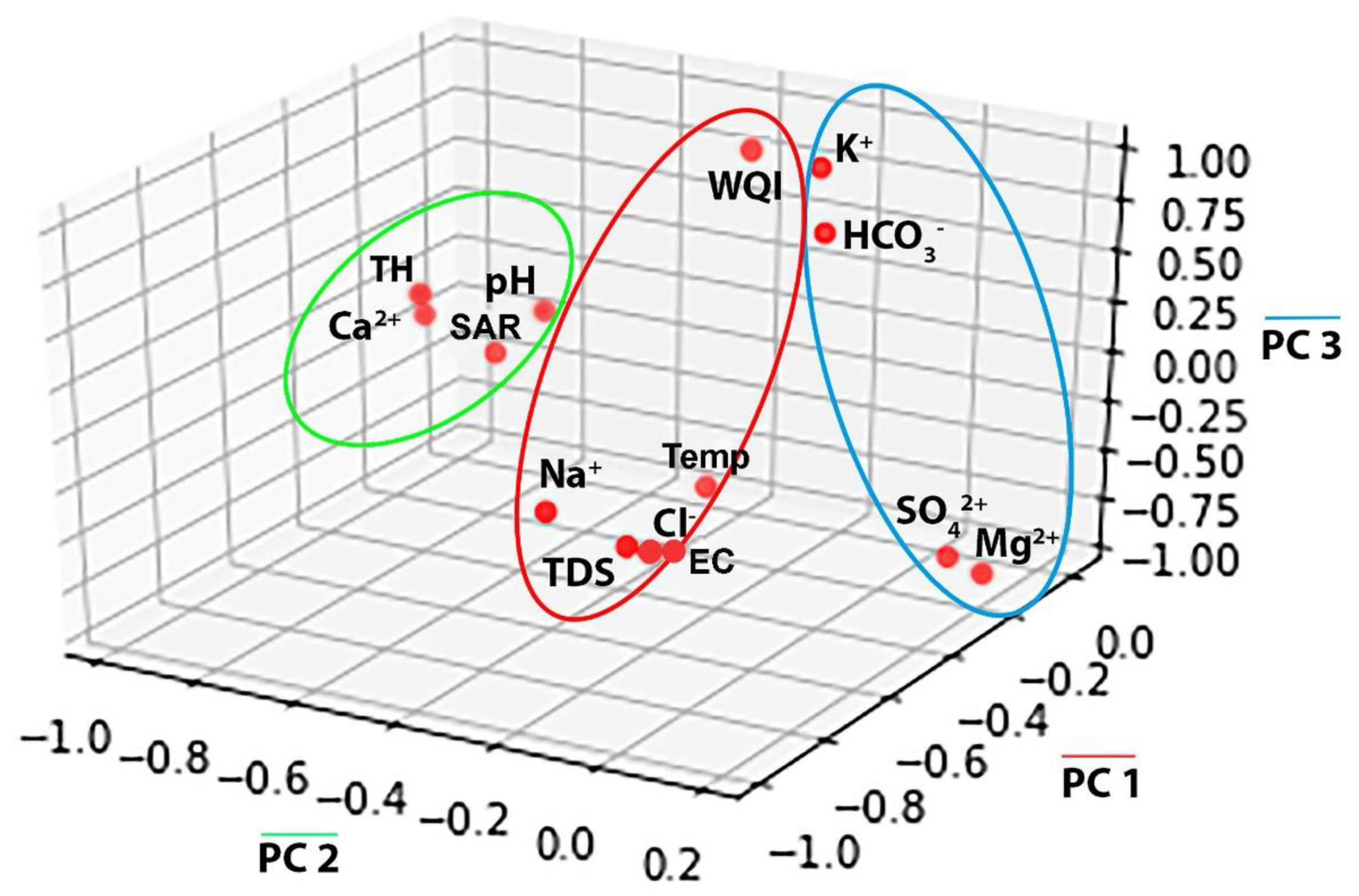
PCA was performed on a groundwater dataset consisting of 31 observations and 14 physicochemical parameters. Three main PCs were extracted with an eigenvalue greater than 1, accounting for 85.1% of the total variance in the groundwater quality dataset (
Table 6 and
Figure 5).
The first component (PC1) explains 56.31% of the total variance. PC1 has a robust negative loading of −0.87 to −0.988 on TDS, EC, temperature, Cl
−, and Na
+, and a robust positive loading of 0.96 on WQI. PC1 indicates that the occurrence of salinization processes in the aquifer is associated with anthropogenic activity. Inverse correlation between WQI and TDS, EC, Cl
−, and Na
+ indicates that the water quality is characterized by changes in salinity. An increase in the WQI results in a decrease in the concentrations of Cl
−, Na
+, EC, TDS, and pH, as shown in
Figure 6c,f and
Figure 7a–c. High salt (TDS, EC, Cl
−, and Na
+) concentrations are caused by irrigation with wastewater practices occurring for over a century [
12,
15]. Similar studies in other countries have reported the impacts of wastewater irrigation on groundwater quality [
1,
4,
10].
The second component (PC2) describes 18.53% of the variability of the data. PC2 has a robust positive loading of 0.981 and 0.963 for Ca
2+ and TH (CaCO
3), respectively. PC2 has negative correlations of −0.831 and −0.76 for pH and SAR, respectively. PC2 describes changes in water quality by the increase in hardness. An inverse correlation between TH (CaCO
3), Ca
2+, and pH reveals that the significant contribution of hardness is linked to the dissolution of salts coming from infiltrated wastewater, in addition to carbonate dissolution and evaporation. Similar studies of the wastewater irrigation show similar findings [
1,
4]. The spatial distribution showed an increase in hardness in wastewater irrigated lands and the surroundings of the Tula River, as shown in
Figure 1 and
Figure 7f.
The third component (PC3) explains 10.26% of the total variance. PC3 has strong positive loadings of 0.951, 0.926, and 0.705 for K
+, Mg
2+, and HCO
3−, respectively. PC3 has a negative loading of −0.876 for SO
42−. PC3 explains the groundwater pollution by sulfate, potassium, and magnesium concentrations sourced from rock–water interactions, as well as wastewater infiltration and recharge. The inverse correlation between SO
42− and K
+, Mg
2+, and HCO
3− indicates that the principal source of sulfate is associated with agricultural fertilizers [
36,
90] and industrial and domestic wastewater, as well as their effluents [
24,
27]. The concentrations of SO
42− were significantly higher in agricultural zones (
Figure 1 and
Figure 6e). In other areas, sulfate concentrations decreased while concentrations of K
+ and Mg
2+ increased, as shown in
Figure 6b,d,h. This reveals that the significant contribution of magnesium and potassium is due to the interactions with the underlying basaltic rock [
17,
94], and by the dissolution and weathering of silicate minerals, such as potassium, feldspar minerals, and clays [
9,
24,
95].
5. Conclusions
The results obtained from statistical analysis and Piper and Stiff diagrams indicate that cation predominance in groundwater is in the following order: Na+ > Ca2+ > Mg2+ > K+. In addition, the predominance of anions is HCO3− > SO42− > Cl− > CO32−. The prevailing hydrochemical types of groundwater disclosed by the Piper and Stiff diagrams was found to be Na+–Cl− (37.9%), Ca2+–HCO3− (27.6%), and Ca2+–Na+–Mg2+–HCO3−–Cl− (34.5%). The Na+–Cl− groundwater type can be attributed to wastewater irrigation, local hydrogeological conditions, and shallow groundwater evaporation; this groundwater type is found on the central and southern portions of the study area, characterized by urban and agricultural zones near the Tula River, as well as other natural flow streams and irrigation canals. The Ca2+–Na+–Mg2+–HCO3−–Cl− groundwater type suggests the mixing of native groundwater and infiltrated wastewater; this groundwater type is found on the central and southern portions of the study area, characterized by rural and urban settlements, as well as agricultural land with natural flow streams and irrigation canals. The Ca2+–HCO3− type indicates that natural recharge is occurring on the northern, mountainous part of the study area.
K-means clustering and PCA were successfully applied to assess the groundwater quality and identify hydrogeochemical processes. Three components defined in the PCA are responsible for 85.1% of the total variance in the hydrochemical dataset, and were found to be dominated by three processes: salinization, mineralization, and groundwater contamination. Salinization processes are controlled by high Cl− and Na+ concentrations and high EC and TDS, attributed to wastewater irrigation and mineralization processes. Mineralization process are dominated by Ca2+, TH (CaCO3), pH, and SAR, and are related to the dissolution of salts in infiltrated wastewater, as well as carbonate dissolution and evaporation. Groundwater contamination is defined by high levels of sulfate, potassium, and magnesium concentrations sourced from rock–water interaction, as well as wastewater irrigation, infiltration, and recharge.
The K-means algorithm identified two distinct groundwater classes. The first class (cluster 1), characterized by low quality (WQI < 70), warrants significant water treatment prior to human consumption. This class of water was found in urban areas, wastewater irrigated zones, and the surroundings of the Tula River. This type of water is characterized by high concentrations of TDS, Cl−, and Na+, as well as high EC from long-term irrigation practices with wastewater and mineralization. Significant SO42−, K+, and NO3− concentrations were linked to agricultural pollution by wastewater irrigation and agricultural fertilizers. The second class (cluster 2) is characterized by higher quality (WQI between 70 and 89), and is suitable for drinking purposes after some water treatment. This type of water was found in groundwater recharge zones, rural settlements, and seasonal agricultural fields. Cluster 2 groundwater is associated with mineralization processes sourced by rock–water interaction, such as the dissolution of carbonates. Waters of cluster 2 were associated with high concentrations of TH (CaCO3), Ca2+, HCO3−, and K+, as well as high pH and temperature. Na+ plus the K+–Cl− type of water was related to cluster 1, while the Ca2+–HCO3− type of water was associated with cluster 2. The results indicate good agreement between the results from the Piper and Stiff diagrams and K-means clustering.
A suite of multivariate statistics coupled with geo-spatial analysis proved useful for the identification of hydrogeochemical processes in the evolution of groundwater. The methodology used in this study will be useful for local water resource managers for developing strategies to mitigate and prevent groundwater contamination.
Supplementary Materials
The following are available online at
https://www.mdpi.com/2073-4441/11/8/1702/s1, Figure S1: Spatial distribution map of the sodium adsorption ratio (SAR) in the study zone, Table S1: Number of clusters suggested by each index, Table S2: Basic statistics of analyzed hydrochemical parameters in the study area, Table S3: Correlation of groundwater quality with World Health Organization (WHO) and Mexican Official Standards for drinking purposes.
Author Contributions
Conceptualization, A.E.M.C.; methodology, J.A.R.L. and D.A.M.C.; formal analysis, A.E.M.C. and D.A.M.C.; resources, J.A.R.L.; writing—original draft preparation, A.E.M.C.; writing—review and editing, J.T.V. and J.D.L.B.; visualization, J.T.V., J.D.L.B., and J.M.R.
Funding
This research received no external funding.
Acknowledgments
The authors thank the Instituto Potosino de Investigación Científica y Tecnológica, A. C. (IPICYT) and the Consejo Nacional de Ciencia y Tecnología (CONACYT).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chandran, S.; Karmegam, M.; Kumar, V.; Dhanasekarapandian, M. Evaluation of groundwater quality in an untreated wastewater irrigated region and mapping—A case study of Avaniyapuram sewage farm, Madurai. Arab. J. Geosci. 2017, 10, 159. [Google Scholar] [CrossRef]
- Elgallal, M.; Fletcher, L.; Evans, B. Assessment of potential risks associated with chemicals in wastewater used for irrigation in arid and semiarid zones: A review. Agric. Water Manag. 2016, 177, 419–431. [Google Scholar] [CrossRef]
- Jampani, M.; Huelsmann, S.; Liedl, R.; Sonkamble, S.; Ahmed, S.; Amerasinghe, P. Spatio-temporal distribution and chemical characterization of groundwater quality of a wastewater irrigated system: A case study. Sci. Total Environ. 2018, 636, 1089–1098. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Wang, L.; Wang, S.; Tian, R.; Xue, C.; Feng, W.; Li, Y. Spatiotemporal variation of groundwater quality in an arid area experiencing long-term paper wastewater irrigation, Northwest China. Environ. Earth Sci. 2017, 76, 460. [Google Scholar] [CrossRef]
- Drechsel, P.; Evans, A.E.V. Wastewater use in irrigated agriculture. Irrig. Drain. Syst. 2010, 24, 1–3. [Google Scholar] [CrossRef]
- Guédron, S.; Duwig, C.; Prado, B.L.; Point, D.; Flores, M.G.; Siebe, C. (Methyl) Mercury, arsenic, and lead contamination of the world’s largest wastewater irrigation system: The Mezquital Valley (Hidalgo State—Mexico). Water Air Soil Pollut. 2014, 225, 1–19. [Google Scholar] [CrossRef]
- Fabro, A.Y.R.; Ávila, J.G.P.; Alberich, M.V.E.; Sansores, S.A.C.; Camargo-Valero, M.A. Spatial distribution of nitrate health risk associated with groundwater use as drinking water in Merida, Mexico. Appl. Geogr. 2015, 65, 49–57. [Google Scholar] [CrossRef]
- World Bank. Integrated Urban Water Management Lessons and Recommendations from Regional Experiences in Latin America, Central Asia, and Africa; World Bank: Washington, DC, USA, 2012; p. 30. [Google Scholar]
- Sajil Kumar, P.J.; James, E.J. Identification of hydrogeochemical processes in the Coimbatore district, Tamil Nadu, India. Hydrol. Sci. J. 2016, 61, 719–731. [Google Scholar] [CrossRef]
- Li, P.; Wu, J.; Qian, H.; Zhang, Y.; Yang, N.; Jing, L.; Yu, P. Hydrogeochemical characterization of groundwater in and around a wastewater irrigated forest in the southeastern edge of the Tengger desert, Northwest China. Expo. Health 2016, 8, 331–348. [Google Scholar] [CrossRef]
- Cuellar Carrasco, E.; Ortega Esccobar, M.; Ramírez Ayala, C.; Sánchez Bernal, E.I. Evaluación de la relación de adsorción de sodio de las aguas de la red hidrográfica del valle del mezquital, hidalgo. Rev. Mex. Cienc. Agríc. 2015, 6, 977–989. [Google Scholar]
- Hernández-Espriú, A.; Arango-Galván, C.; Reyes-Pimentel, A.; Martínez-Santos, P.; Pita de la Paz, C.; Macías-Medrano, S.; Arias-Paz, A.; Breña-Naranjo, J. Water supply source evaluation in unmanaged aquifer recharge zones: The Mezquital Valley (Mexico) case study. Water 2017, 9, 4. [Google Scholar] [CrossRef]
- Lesser, L.E.; Mora, A.; Moreau, C.; Mahlknecht, J.; Hernández-Antonio, A.; Ramírez, A.I.; Barrios-Piña, H. Survey of 218 organic contaminants in groundwater derived from the world’s largest untreated wastewater irrigation system: Mezquital Valley, Mexico. Chemosphere 2018, 198, 510–521. [Google Scholar] [CrossRef] [PubMed]
- Gallegos, E.; Warren, A.; Robles, E.; Campoy, E.; Calderon, A.; Sainz, M.G.; Bonilla, P.; Escolero, O. The effects of wastewater irrigation on groundwater quality in Mexico. Water Sci. Technol. 1999, 40, 45–52. [Google Scholar] [CrossRef]
- Rubio-Franchini, I.; López-Hernández, M.; Ramos-Espinosa, M.G.; Rico-Martínez, R. Bioaccumulation of metals arsenic, cadmium, and lead in zooplankton and fishes from the Tula river watershed, Mexico. Water Air Soil Pollut. 2015, 227, 5. [Google Scholar] [CrossRef]
- Lesser-Carrillo, L.E.; Lesser-Illades, J.M.; Arellano-Islas, S.; González-Posadas, D. Balance hídrico y calidad del agua subterránea en el acuífero del valle del mezquital, México central. Rev. Mex. Cienc. Geol. 2011, 28, 323–336. [Google Scholar]
- Islam, A.T.; Shen, S.; Haque, M.A.; Bodrud-Doza, M.; Maw, K.; Habib, M.A. Assessing groundwater quality and its sustainability in Joypurhat district of Bangladesh using GIS and multivariate statistical approaches. Environ. Dev. Sustain. 2017, 20, 1935–1959. [Google Scholar] [CrossRef]
- Okiongbo, K.S.; Douglas, R.K. Evaluation of major factors influencing the geochemistry of groundwater using graphical and multivariate statistical methods in Yenagoa city, southern Nigeria. Appl. Water Sci. 2015, 5, 27–37. [Google Scholar] [CrossRef]
- M’nassri, S.; Dridi, L.; Schäfer, G.; Hachicha, M.; Majdoub, R. Groundwater salinity in a semi-arid region of central-eastern Tunisia: Insights from multivariate statistical techniques and geostatistical modelling. Environ. Earth Sci. 2019, 78, 288. [Google Scholar] [CrossRef]
- Jalali, M.; Karami, S.; Fatehi Marj, A. On the problem of the spatial distribution delineation of the groundwater quality indicators via multivariate statistical and geostatistical approaches. Environ. Monit. Assess. 2019, 191, 323. [Google Scholar] [CrossRef]
- Gulgundi, M.S.; Shetty, A. Groundwater quality assessment of urban Bengaluru using multivariate statistical techniques. Appl. Water Sci. 2018, 8, 43. [Google Scholar] [CrossRef]
- Muangthong, S.; Shrestha, S. Assessment of surface water quality using multivariate statistical techniques: Case study of the Nampong river and Songkhram river, Thailand. Environ. Monit. Assess. 2015, 187, 548. [Google Scholar] [CrossRef] [PubMed]
- Qin, R.; Wu, Y.; Xu, Z.; Xie, D.; Zhang, C. Assessing the impact of natural and anthropogenic activities on groundwater quality in coastal alluvial aquifers of the lower Liaohe river plain, NE China. Appl. Geochem. 2013, 31, 142–158. [Google Scholar] [CrossRef]
- Howladar, M.F.; Al Numanbakth, M.A.; Faruque, M.O. An application of water quality index (WQI) and multivariate statistics to evaluate the water quality around Maddhapara Granite Mining Industrial Area, Dinajpur, Bangladesh. Environ. Syst. Res. 2017, 6, 13. [Google Scholar] [CrossRef]
- Villegas, P.; Paredes, V.; Betancur, T.; Ribeiro, L. Assessing the hydrochemistry of the Urabá aquifer, Colombia by principal component analysis. J. Geochem. Explor. 2013, 134, 120–129. [Google Scholar] [CrossRef]
- Peng, K.; Li, X.; Wang, Z. Hydrochemical characteristics of groundwater movement and evolution in the Xinli deposit of the Sanshandao gold mine using FCM and PCA methods. Environ. Earth Sci. 2015, 73, 7873–7888. [Google Scholar] [CrossRef]
- Boateng, T.K.; Opoku, F.; Acquaah, S.O.; Akoto, O. Groundwater quality assessment using statistical approach and water quality index in Ejisu-Juaben Municipality, Ghana. Environ. Earth Sci. 2016, 75, 489. [Google Scholar] [CrossRef]
- Li, Z.; Wang, G.; Wang, X.; Wan, L.; Shi, Z.; Wanke, H.; Uugulu, S.; Uahengo, C.I. Groundwater quality and associated hydrogeochemical processes in Northwest Namibia. J. Geochem. Explor. 2018, 186, 202–214. [Google Scholar] [CrossRef]
- Yidana, S.M.; Banoeng-Yakubo, B.; Akabzaa, T.M. Analysis of groundwater quality using multivariate and spatial analyses in the Keta basin, Ghana. J. Afr. Earth Sci. 2010, 58, 220–234. [Google Scholar] [CrossRef]
- Ramírez, C.V.C. Sistemas de riego en ixmiquilpan, tetepango y tula, siglos xvii-xix. Relac. Estudios Hist. Soc. 2013, 34, 147–185. [Google Scholar]
- CONAGUA. Actualización de la Disponibilidad Media Anual de Agua en el Acuífero de Ixmiquilpan (1312), Estado de Hidalgo; CONAGUA: Mexico City, Mexico, 2013. [Google Scholar]
- Del Arenal, C.R. Estudio hidrogeoquímico de la porción centro-oriental del valle del mezquital, hidalgo. Rev. Mex. Cienc. Geol. 1985, 6, 86–97. [Google Scholar]
- APHA. Standard Methods for the Examination of Water and Wastewater; American Public Health, Association (APHA); American Water Works Association (AWWA); Water Pollution Control Federation (WPCF): New York, NY, USA, 1998. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Upper Saddle River, NJ, USA, 1979; p. 604. [Google Scholar]
- Li, P.; Wu, J.; Qian, H. Hydrochemical appraisal of groundwater quality for drinking and irrigation purposes and the major influencing factors: A case study in and around Hua county, China. Arab. J. Geosci. 2015, 9, 15. [Google Scholar] [CrossRef]
- Zghibi, A.; Merzougui, A.; Zouhri, L.; Tarhouni, J. Understanding groundwater chemistry using multivariate statistics techniques to the study of contamination in the Korba unconfined aquifer system of cap-bon (North-East of Tunisia). J. Afr. Earth Sci. 2014, 89, 1–15. [Google Scholar] [CrossRef]
- Sethy, S.N.; Syed, T.H.; Kumar, A. Evaluation of groundwater quality in parts of the southern Gangetic plain using water quality indices. Environ. Earth Sci. 2017, 76, 116. [Google Scholar] [CrossRef]
- Akter, T.; Jhohura, F.T.; Akter, F.; Chowdhury, T.R.; Mistry, S.K.; Dey, D.; Barua, M.K.; Islam, M.A.; Rahman, M. Water quality index for measuring drinking water quality in rural Bangladesh: A cross-sectional study. J. Health Popul. Nutr. 2016, 35, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Bascaron, M. Establishment of a methodology for the determination of water quality. Bol Inf Medio Ambient. 1979, 9, 30–51. [Google Scholar]
- Couillard, D.; Lefebvre, Y. Analysis of water-quality indices. J. Environ. Manag. 1985, 21, 161–179. [Google Scholar]
- Ramos, J.A.L.; Medrano, C.N.; Silva, F.O.T.; García, J.T.S.; Gutiérrez, L.R.R. Assessing the inconsistency between groundwater vulnerability and groundwater quality: The case of Chapala Marsh, Mexico. Hydrogeol. J. 2012, 20, 591–603. [Google Scholar] [CrossRef]
- NOM-127-SSA. Mexican Official Norm Environmental Health, Water Use and Human Consumption: Permissible Limits of Quality and Treatments to be Bound Water for Drinking Water. 1994. Available online: http://www.salud.gob.mx/unidades/cdi/nom/m127ssa14.html (accessed on 20 September 2018).
- WHO. Guidelines for Drinking Water Quality; WHO: Geneva, Switzerland, 2011. [Google Scholar]
- Debels, P.; Figueroa, R.; Urrutia, R.; Barra, R.; Niell, X. Evaluation of water quality in the Chillán river (Central Chile) using physicochemical parameters and a modified water quality index. Environ. Monit. Assess. 2005, 110, 301–322. [Google Scholar] [CrossRef]
- Kannel, P.R.; Lee, S.; Lee, Y.S.; Kanel, S.R.; Khan, S.P. Application of water quality indices and dissolved oxygen as indicators for river water classification and urban impact assessment. Environ. Monit. Assess. 2007, 132, 93–110. [Google Scholar] [CrossRef]
- Massoud, M.A. Assessment of water quality along a recreational section of the Damour river in Lebanon using the water quality index. Environ. Monit. Assess. 2012, 184, 4151–4160. [Google Scholar] [CrossRef]
- Pesce, S.F.; Wunderlin, D.A. Use of water quality indices to verify the impact of Córdoba city (Argentina) on Suquía river. Water Res. 2000, 34, 2915–2926. [Google Scholar] [CrossRef]
- Sánchez, E.; Colmenarejo, M.F.; Vicente, J.; Rubio, A.; García, M.G.; Travieso, L.; Borja, R. Use of the water quality index and dissolved oxygen deficit as simple indicators of watersheds pollution. Ecol. Indic. 2007, 7, 315–328. [Google Scholar] [CrossRef]
- Barrón, R.L.E. Evaluación de la contaminación del agua subterránea basado en índices de calidad del agua. In Caso Acuífero Penjamo-Abasolo; Facultad de Ciencias UNAM: Mexico City, Mexico, 2004. [Google Scholar]
- Dojlido, J.; Raniszewski, J.; Woyciechowska, J. Water quality index applied to rivers in the Vistula river basin in Poland. Environ. Monit. Assess. 1994, 33, 33–42. [Google Scholar] [CrossRef]
- Jonnalagadda, S.B.; Mhere, G. Water quality of the Odzi river in the eastern highlands of Zimbabwe. Water Res. 2001, 35, 2371–2376. [Google Scholar] [CrossRef]
- Leal, J.A.R.; Silva, F.O.T.; Montes, I.S. Analysis of aquifer vulnerability and water quality using SINTACS and geographic weighted regression. Environ. Earth Sci. 2012, 66, 2257–2271. [Google Scholar] [CrossRef]
- Ramos, L.J.A.; Noyola Medrano, C.; Tapia Silva, F.O. Aquifer vulnerability and groundwater quality in mega cities: Case of the Mexico basin. Environ. Earth Sci. 2010, 61, 1309–1320. [Google Scholar] [CrossRef]
- Vanhatalo, E.; Kulahci, M. Impact of autocorrelation on principal components and their use in statistical process control. Qual. Reliab. Eng. Int. 2016, 32, 1483–1500. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, Y.; Guo, H. Application of multivariate statistical methods to water quality assessment of the watercourses in northwestern new territories, Hong Kong. Environ. Monit. Assess. 2007, 132, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kim, S.K. Comparing patterns of component loadings: Principal component analysis (PCA) versus independent component analysis (ICA) in analyzing multivariate non-normal data. Behav. Res. Methods. 2012, 44, 1239–1243. [Google Scholar] [CrossRef]
- Oppong, F.B.; Agbedra, S.Y. Assessing univariate and multivariate normality. A guide for non-statisticians. Math. Theory Model. 2016, 6, 26–33. [Google Scholar]
- Marín, C.A.E.; Martínez Cruz, D.A.; Otazo Sánchez, E.; Gavi Reyes, F.; Vásquez Soto, D. Groundwater quality assessment: An improved approach to k-means clustering, principal component analysis and spatial analysis: A case study. Water 2018, 10, 437. [Google Scholar] [CrossRef]
- Ayed, B.; Jmal, I.; Sahal, S.; Mokadem, N.; Saidi, S.; Boughariou, E.; Bouri, S. Hydrochemical characterization of groundwater using multivariate statistical analysis: The Maritime Djeffara shallow aquifer (Southeastern Tunisia). Environ. Earth Sci. 2017, 76, 1–22. [Google Scholar] [CrossRef]
- Papatheodorou, G.; Demopoulou, G.; Lambrakis, N. A long-term study of temporal hydrochemical data in a shallow lake using multivariate statistical techniques. Ecol. Model. 2006, 193, 759–776. [Google Scholar] [CrossRef]
- Manoj, K.; Padhy, P.K. Multivariate statistical techniques and water quality assessment: Discourse and review on some analytical models. Int. J. Environ. Sci. 2014, 5, 607. [Google Scholar]
- Steinley, D. K-means clustering: A half-century synthesis. Br. J. Math. Stat. Psychol. 2006, 59, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Royston, J.P. Some techniques for assessing multivarate normality based on the Shapiro-Wilk W. J. R. Stat. Soc. Ser. C Appl. Stat. 1983, 32, 121–133. [Google Scholar] [CrossRef]
- Ruppert, D. Multivariate transformations. In Encyclopedia of Environmetrics; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Davis, J.C.; Sampson, R.J. Statistics and Data Analysis in Geology; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Rizvi, N.; Katyal, D.; Joshi, V. Assessment of water quality of Hindon river in Ghaziabad and Noida, India by using multivariate statistical methods. J. Glob. Ecol. Environ. 2015, 3, 80–90. [Google Scholar]
- Karthikeyan, P.; Venkatachalapathy, R.; Vennila, G. Multivariate analysis for river water quality assessment of the Cauvery river, Tamil Nadu, India. Indian J. Mar. Sci. 2017, 46, 785–790. [Google Scholar]
- Nematollahi, M.J.; Ebrahimi, P.; Razmara, M.; Ghasemi, A. Hydrogeochemical investigations and groundwater quality assessment of Torbat-Zaveh plain, Khorasan Razavi, Iran. Environ. Monit. Assess. 2015, 188, 2. [Google Scholar] [CrossRef]
- Sarmadi, F.; Shokoohi, A. Regionalizing precipitation in Iran using GPCC gridded data via multivariate analysis and L-moment methods. Theor. Appl. Climatol. 2015, 122, 121–128. [Google Scholar] [CrossRef]
- Bonansea, M.; Ledesma, C.; Rodriguez, C.; Pinotti, L. Water quality assessment using multivariate statistical techniques in Río Tercero reservoir, Argentina. Hydrol. Res. 2015, 46, 377–388. [Google Scholar] [CrossRef]
- Hancer, E.; Karaboga, D. A comprehensive survey of traditional, merge-split and evolutionary approaches proposed for determination of cluster number. Swarm Evolut. Comput. 2017, 32, 49–67. [Google Scholar] [CrossRef]
- Majkić, D.B.; Oros, I.; Boreli-Zdravković, Đ. Spatial distribution of groundwater quality parameters in the Velika Morava river basin, Central Serbia. Environ. Earth Sci. 2018, 77, 30. [Google Scholar] [CrossRef]
- Taoufik, G.; Khouni, I.; Ghrabi, A. Assessment of physico-chemical and microbiological surface water quality using multivariate statistical techniques: A case study of the Wadi el-Bey river, Tunisia. Arab. J. Geosci. 2017, 10, 181. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond k-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. Nbclust: An R package for determining the relevant number of clusters in a data set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Yadav, I.C.; Devi, N.L.; Mohan, D.; Shihua, Q.; Singh, S. Assessment of groundwater quality with special reference to arsenic in Nawalparasi district, Nepal using multivariate statistical techniques. Environ. Earth Sci. 2014, 72, 259–273. [Google Scholar] [CrossRef]
- Juahir, H.; Zain, S.M.; Yusoff, M.K.; Hanidza, T.I.T.; Armi, A.S.M.; Toriman, M.E.; Mokhtar, M. Spatial water quality assessment of Langat river basin (Malaysia) using environmetric techniques. Environ. Monit. Assess. 2011, 173, 625–641. [Google Scholar] [CrossRef]
- Piper, A.M. A graphic procedure in the geochemical interpretation of water-analyses. Trans. Am. Geophys. Union 1944, 25, 914–928. [Google Scholar] [CrossRef]
- Stiff, J.H.A. The interpretation of chemical water analysis by means of patterns. Petrol. Technol. 1951, 3. [Google Scholar] [CrossRef]
- Aiuppa, A.; Bellomo, S.; Brusca, L.; D’Alessandro, W.; Federico, C. Natural and anthropogenic factors affecting groundwater quality of an active volcano (Mt. Etna, Italy). Appl. Geochem. 2003, 18, 863–882. [Google Scholar] [CrossRef]
- Kura, N.; Ramli, M.; Sulaiman, W.; Ibrahim, S.; Aris, A.; Mustapha, A. Evaluation of factors influencing the groundwater chemistry in a small tropical island of Malaysia. Int. J. Environ. Res. Public Health 2013, 10, 1861. [Google Scholar] [CrossRef] [PubMed]
- Thilagavathi, R.; Chidambaram, S.; Prasanna, M.V.; Thivya, C.; Singaraja, C. A study on groundwater geochemistry and water quality in layered aquifers system of Pondicherry region, Southeast India. Appl. Water Sci. 2012, 2, 253–269. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Ghione, R.; De Maio, M.; Lavy, M. Evaluation of hydrogeochemical processes and groundwater quality for suitability of drinking and irrigation purposes: A case study in the Aosta valley region, Italy. Arab. J. Geosci. 2017, 10, 264. [Google Scholar] [CrossRef]
- Martínez, C.D.A.; Chávez Morales, J.; Bustamante González, A.; Palacios Vélez, Ó.L.; de la Isla de Bauer, M.D.L.; Tijerina Chávez, L. Variación espacial de la calidad del agua para uso agrícola del acuífero costero del valle del mayo, sonora, méxico. Hidrobiológica 2016, 26, 109–119. [Google Scholar]
- Bonton, A.; Rouleau, A.; Bouchard, C.; Rodriguez, M.J. Assessment of groundwater quality and its variations in the capture zone of a pumping well in an agricultural area. Agric. Water Manag. 2010, 97, 824–834. [Google Scholar] [CrossRef]
- Gopinath, S.; Srinivasamoorthy, K.; Vasanthavigar, M.; Saravanan, K.; Prakash, R.; Suma, C.S.; Senthilnathan, D. Hydrochemical characteristics and salinity of groundwater in parts of Nagapattinam district of Tamil Nadu and the union territory of Puducherry, India. Carbonates Evaporites 2018, 33, 1–13. [Google Scholar] [CrossRef]
- Ravikumar, P.; Somashekar, R.K. Principal component analysis and hydrochemical facies characterization to evaluate groundwater quality in Varahi river basin, Karnataka State, India. Appl. Water Sci. 2017, 7, 745–755. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, Y.; Groves, C.; Yuan, D.; Kambesis, P. Natural and anthropogenic factors affecting the groundwater quality in the Nandong karst underground river system in Yunan, China. J. Contam. Hydrol. 2009, 109, 49–61. [Google Scholar] [CrossRef]
- Morán-Ramírez, J.; Ledesma-Ruiz, R.; Mahlknecht, J.; Ramos-Leal, J.A. Rock–water interactions and pollution processes in the volcanic aquifer system of Guadalajara, Mexico, using inverse geochemical modeling. Appl. Geochem. 2016, 68, 79–94. [Google Scholar] [CrossRef]
- Shrestha, S.; Kazama, F. Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan. Environ. Model. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
- Choi, B.Y.; Yun, S.T.; Yu, S.Y.; Lee, P.K.; Park, S.S.; Chae, G.T.; Mayer, B. Hydrochemistry of urban groundwater in Seoul, South Korea: Effects of land-use and pollutant recharge. Environ. Geol. 2005, 48, 979–990. [Google Scholar] [CrossRef]
- Varol, S.; Davraz, A. Evaluation of the groundwater quality with WQI (Water Quality Index) and multivariate analysis: A case study of the Tefenni plain (Burdur/Turkey). Environ. Earth Sci. 2015, 73, 1725–1744. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Singh, A.K.; Singh, A.K.; Singh, M.P. Hydrogeochemical analysis and evaluation of surface water quality of Pratapgarh district, Uttar Pradesh, India. Appl. Water Sci. 2017, 7, 1609–1623. [Google Scholar] [CrossRef]
Figure 1.
Location map of the study area, showing sampling locations, urban zones, agricultural areas, settlements, and the Tula River.
Figure 1.
Location map of the study area, showing sampling locations, urban zones, agricultural areas, settlements, and the Tula River.
Figure 2.
Piper and Stiff diagrams. (a) Piper diagram showing the water types according to geochemical differences; (b) Stiff diagrams projected spatially, showing the water types in the study zone.
Figure 2.
Piper and Stiff diagrams. (a) Piper diagram showing the water types according to geochemical differences; (b) Stiff diagrams projected spatially, showing the water types in the study zone.
Figure 3.
Spatial overlap between the distribution of groundwater quality and the clustering of sampling sites.
Figure 3.
Spatial overlap between the distribution of groundwater quality and the clustering of sampling sites.
Figure 4.
Bivariate plots of (a) Ca2+ + Mg2+ vs. SO42− + HCO3−, (b) HCO3− vs. Ca2+ + Mg2+, (c) Ca2+ vs. NO3−, (d) Cl− vs. total dissolved solids (TDS), (e) Ca2+ vs. TDS, and (f) Cl− vs. Ca2+ + Mg2+.
Figure 4.
Bivariate plots of (a) Ca2+ + Mg2+ vs. SO42− + HCO3−, (b) HCO3− vs. Ca2+ + Mg2+, (c) Ca2+ vs. NO3−, (d) Cl− vs. total dissolved solids (TDS), (e) Ca2+ vs. TDS, and (f) Cl− vs. Ca2+ + Mg2+.
Figure 5.
Screen plot from PCA loadings scores for dataset of water samples.
Figure 5.
Screen plot from PCA loadings scores for dataset of water samples.
Figure 6.
Spatial distribution map of cations (a) Ca2+, (b) Mg2+, (c) Na+, and (d) K+, as well as anions (e) SO42−, (f) Cl−, (g) NO3−, and (h) HCO3− in the study area.
Figure 6.
Spatial distribution map of cations (a) Ca2+, (b) Mg2+, (c) Na+, and (d) K+, as well as anions (e) SO42−, (f) Cl−, (g) NO3−, and (h) HCO3− in the study area.
Figure 7.
Spatial distribution map of (a) EC, (b) TDS, (c) pH, (d) temperature, (e) CO32−, and (f) CaCO3 in the study area.
Figure 7.
Spatial distribution map of (a) EC, (b) TDS, (c) pH, (d) temperature, (e) CO32−, and (f) CaCO3 in the study area.
Table 1.
Weight classification according to organoleptic characteristics of water.
Table 1.
Weight classification according to organoleptic characteristics of water.
| Weight (k) | Characteristic of Water |
|---|
| 1.0 | Water without apparent pollution—clear or with natural suspended solids |
| 0.75 | Water with slight color, scums, and apparent non-natural turbidity |
| 0.50 | Water with polluted aspect and strong odor |
| 0.25 | Highly polluted water with blackish color, hard odor, and visible fermentation |
Table 2.
Variables used in the water quality index (WQI) calculations, relative weights, and scores of normalization.
Table 2.
Variables used in the water quality index (WQI) calculations, relative weights, and scores of normalization.
| Variable | Relative Weight (Pi)
| Normalization Factor (Ci)
|
|---|
| 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 |
|---|
| Temperature | 0.0303 | <20 | <21 | <22 | <24 | <26 | <28 | <30 | <32 | <36 | ≤40 | >40 |
| EC | 0.0909 | <750 | <1000 | <1250 | <1500 | <2000 | <2500 | <3000 | <5000 | <8000 | ≤12,000 | >12,000 |
| TDS | 0.1212 | <100 | <500 | <750 | <1000 | <1500 | <2000 | <3000 | <5000 | <10,000 | ≤20,000 | >20,000 |
| pH | 0.0909 | 7 | 7–8 | 7–8.5 | 7–9 | 6.5–7 | 6–9.5 | 5–10 | 4–11 | 3–12 | 2–13 | 1–14 |
| Ca2+ | 0.0606 | <10 | <50 | <100 | <150 | <200 | <300 | <400 | <500 | <600 | ≤1000 | >1000 |
| Mg2+ | 0.0606 | <10 | <25 | <50 | <75 | <100 | <150 | <200 | <250 | <300 | ≤500 | >500 |
| Na+ | 0.0606 | <10 | <50 | <100 | <150 | <200 | <300 | <400 | <500 | <600 | ≤1000 | >1000 |
| K+ | 0.0606 | <10 | <25 | <50 | <75 | <100 | <150 | <200 | <250 | <300 | ≤500 | >500 |
| Cl− | 0.1212 | <25 | <50 | <100 | <150 | <200 | <300 | <500 | <700 | <1000 | ≤1500 | >1500 |
| NO3− | 0.1212 | <0.5 | <2.0 | <4.0 | <6.0 | <8.0 | <10 | <15 | <20 | <50 | ≤100 | >100 |
| HCO3− | 0.0303 | <25 | <100 | <200 | <300 | <400 | <500 | <600 | <800 | <1000 | ≤1500 | >1500 |
| TH (CaCO3) | 0.0303 | <25 | <100 | <200 | <300 | <400 | <500 | <600 | <800 | <1000 | ≤1500 | >1500 |
| SO42− | 0.1212 | <25 | <50 | <75 | <100 | <150 | <250 | <400 | <600 | <1000 | ≤1500 | >1500 |
Table 3.
Water quality classification according to the WQI ranges [
49].
Table 3.
Water quality classification according to the WQI ranges [
49].
| WQI Range | WQI Scale | Use |
|---|
| 90–100 | Excellent | Does not require purifying, and is safe for consumption |
| 80–89 | Acceptable | Requires minor purification for consumption |
| 70–79 | Slightly polluted | Requires intermediate purification for consumption |
| 50–69 | Polluted | Requires very significant purification for consumption |
| 40–49 | Strongly polluted | Is dubious for consumption |
| 0–39 | Extremely polluted | Is not acceptable for consumption at all |
Table 4.
Spearman´s rank correlation matrix, illustrating the relationship between the 16 variables determined in groundwater and surface water.
Table 4.
Spearman´s rank correlation matrix, illustrating the relationship between the 16 variables determined in groundwater and surface water.
| | Temp | Ca2+ | Mg2+ | Na+ | K+ | TH (CaCO3) | SAR | pH | EC | SO42− | HCO3− | CO32− | Cl− | NO3− | TDS | WQI |
|---|
| Temp | 1 | | | | | | | | | | | | | | | |
| Ca2+ | 0.006 | 1 | | | | | | | | | | | | | | |
| Mg2+ | 0.021 | 0.191 | 1 | | | | | | | | | | | | | |
| Na+ | 0.000 | 0.966 | 0.330 | 1 | | | | | | | | | | | | |
| K+ | 0.014 | 0.347 | 0.000 | 0.018 | 1 | | | | | | | | | | | |
| TH (CaCO3) | 0.001 | 0.000 | 0.001 | 0.708 | 0.783 | 1 | | | | | | | | | | |
| SAR | 0.000 | 0.235 | 0.913 | 0.000 | 0.046 | 0.294 | 1 | | | | | | | | | |
| pH | 0.514 | 0.004 | 0.127 | 0.426 | 0.952 | 0.002 | 0.055 | 1 | | | | | | | | |
| EC | 0.000 | 0.009 | 0.014 | 0.000 | 0.013 | 0.001 | 0.000 | 0.627 | 1 | | | | | | | |
| SO42− | 0.000 | 0.001 | 0.352 | 0.000 | 0.860 | 0.002 | 0.009 | 0.818 | 0.000 | 1 | | | | | | |
| HCO3− | 0.000 | 0.772 | 0.008 | 0.000 | 0.000 | 0.261 | 0.002 | 0.456 | 0.000 | 0.496 | 1 | | | | | |
| CO32− | 0.000 | 0.785 | 0.093 | 0.000 | 0.013 | 0.419 | 0.000 | 0.241 | 0.000 | 0.081 | 0.000 | 1 | | | | |
| Cl− | 0.000 | 0.009 | 0.015 | 0.000 | 0.024 | 0.001 | 0.000 | 0.429 | 0.000 | 0.000 | 0.004 | 0.000 | 1 | | | |
| NO3− | 0.000 | 0.870 | 0.172 | 0.000 | 0.041 | 0.316 | 0.000 | 0.506 | 0.000 | 0.048 | 0.027 | 0.002 | 0.000 | 1 | | |
| TDS | 0.000 | 0.030 | 0.019 | 0.000 | 0.014 | 0.006 | 0.000 | 0.622 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1 | |
| WQI | 0.000 | 0.029 | 0.008 | 0.000 | 0.004 | 0.004 | 0.000 | 0.939 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 1 |
Table 5.
Descriptive statistics for the two groups found from K-means clustering analysis.
Table 5.
Descriptive statistics for the two groups found from K-means clustering analysis.
| Parameter | Cluster 1 (n = 13) | Cluster 2 (n = 18) |
|---|
| Min | Max | Mean | Median | S.D. | Min | Max | Mean | Median | S.D. |
|---|
| Temp | 25.10 | 33.00 | 28.93 | 28.6 | 2.53 | 18.40 | 25.50 | 23.34 | 24.10 | 2.03 |
| Ca2+ | 41.08 | 188.78 | 91.24 | 82.97 | 39.17 | 21.64 | 113.03 | 53.21 | 49.70 | 23.73 |
| Mg2+ | 12.51 | 39.37 | 20.38 | 17.13 | 8.33 | 2.79 | 29.40 | 13.84 | 11.24 | 8.26 |
| Na+ | 55.41 | 440.95 | 184.45 | 156.1 | 100.74 | 5.56 | 185.76 | 73.69 | 57.76 | 50.60 |
| K+ | 0.12 | 24.48 | 15.38 | 15.37 | 7.21 | 1.60 | 19.35 | 9.82 | 10.11 | 5.15 |
| TH(CaCO3) | 163.13 | 528.92 | 311.75 | 309.25 | 96.14 | 73.06 | 322.26 | 189.87 | 188.90 | 78.16 |
| SAR | 1.25 | 13.02 | 4.93 | 3.78 | 3.31 | 0.14 | 8.42 | 2.61 | 2.00 | 2.22 |
| pH | 7.74 | 8.29 | 8.01 | 8.01 | 0.19 | 7.64 | 8.62 | 8.08 | 8.09 | 0.22 |
| EC | 1277.00 | 2280.00 | 1552.55 | 1503 | 259.62 | 412.00 | 1087.00 | 733.11 | 718.50 | 247.86 |
| SO42− | 57.78 | 448.94 | 158.41 | 123.05 | 111.56 | 4.08 | 164.12 | 53.74 | 48.85 | 39.55 |
| HCO3− | 89.24 | 479.01 | 292.43 | 281.91 | 108.27 | 103.73 | 355.75 | 215.54 | 195.26 | 66.82 |
| CO32− | 4.50 | 30.00 | 13.92 | 13.2 | 8.29 | 3.00 | 18.00 | 7.67 | 6.45 | 4.21 |
| Cl− | 139.53 | 268.85 | 185.22 | 190.58 | 34.70 | 34.03 | 125.92 | 71.37 | 68.07 | 31.63 |
| NO3− | 22.99 | 83.29 | 42.06 | 35.88 | 20.01 | 5.70 | 39.41 | 15.83 | 13.70 | 9.54 |
| TDS | 724.84 | 1643.47 | 1003.49 | 1007.91 | 249.21 | 295.12 | 736.75 | 513.92 | 488.84 | 165.30 |
| WQI | 52.00 | 67.00 | 61.82 | 62.00 | 4.60 | 68.00 | 87.00 | 79.33 | 80.00 | 6.82 |
Table 6.
Summary of the principal component analysis (PCA) loading after Varimax rotation.
Table 6.
Summary of the principal component analysis (PCA) loading after Varimax rotation.
| Variables | Component Matrix |
|---|
| PC1 | PC2 | PC3 |
|---|
| Temperature | −0.954 | 0.063 | −0.043 |
| Ca2+ | −0.129 | 0.981 | −0.176 |
| Mg2+ | −0.162 | 0.184 | 0.926 |
| Na+ | −0.870 | −0.228 | −0.110 |
| K+ | −0.173 | −0.153 | 0.951 |
| TH (CaCO3) | −0.167 | 0.963 | 0.029 |
| SAR | −0.236 | −0.760 | −0.174 |
| pH | 0.021 | −0.831 | −0.226 |
| EC | −0.984 | 0.046 | −0.056 |
| SO42− | −0.232 | 0.154 | −0.782 |
| HCO3− | −0.230 | −0.107 | 0.705 |
| CO32− | −0.249 | −0.191 | 0.107 |
| Cl− | −0.930 | 0.067 | −0.074 |
| NO3− | −0.253 | −0.131 | −0.077 |
| TDS | −0.988 | 0.006 | −0.046 |
| WQI | 0.960 | −0.013 | 0.060 |
| Eigenvalue | 3.0016 | 1.7217 | 1.2815 |
| Variability (%) | 56.31 | 18.53 | 10.26 |
| Cumulative (%) | 56.31 | 74.84 | 85.10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).