Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation
Abstract
1. Introduction
2. Numerical Setup
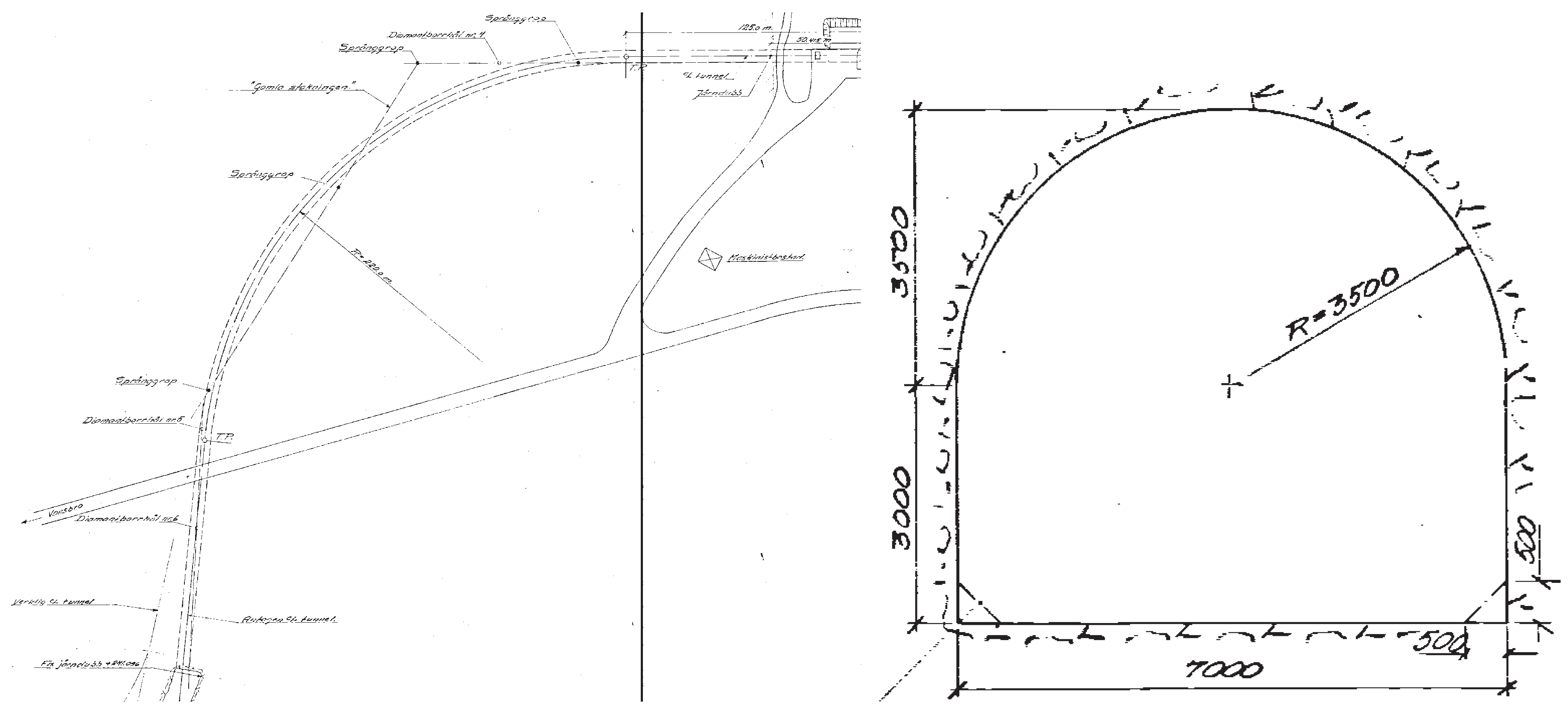
2.1. Gävunda-Tunnel
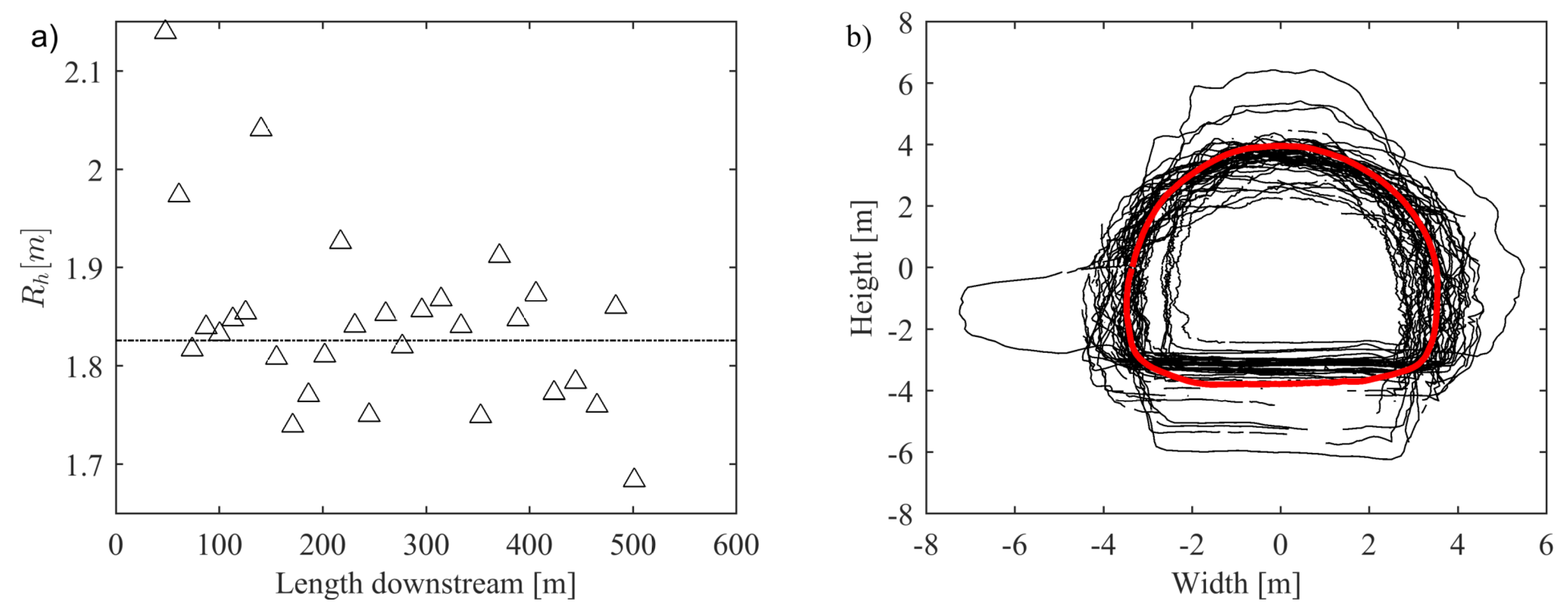
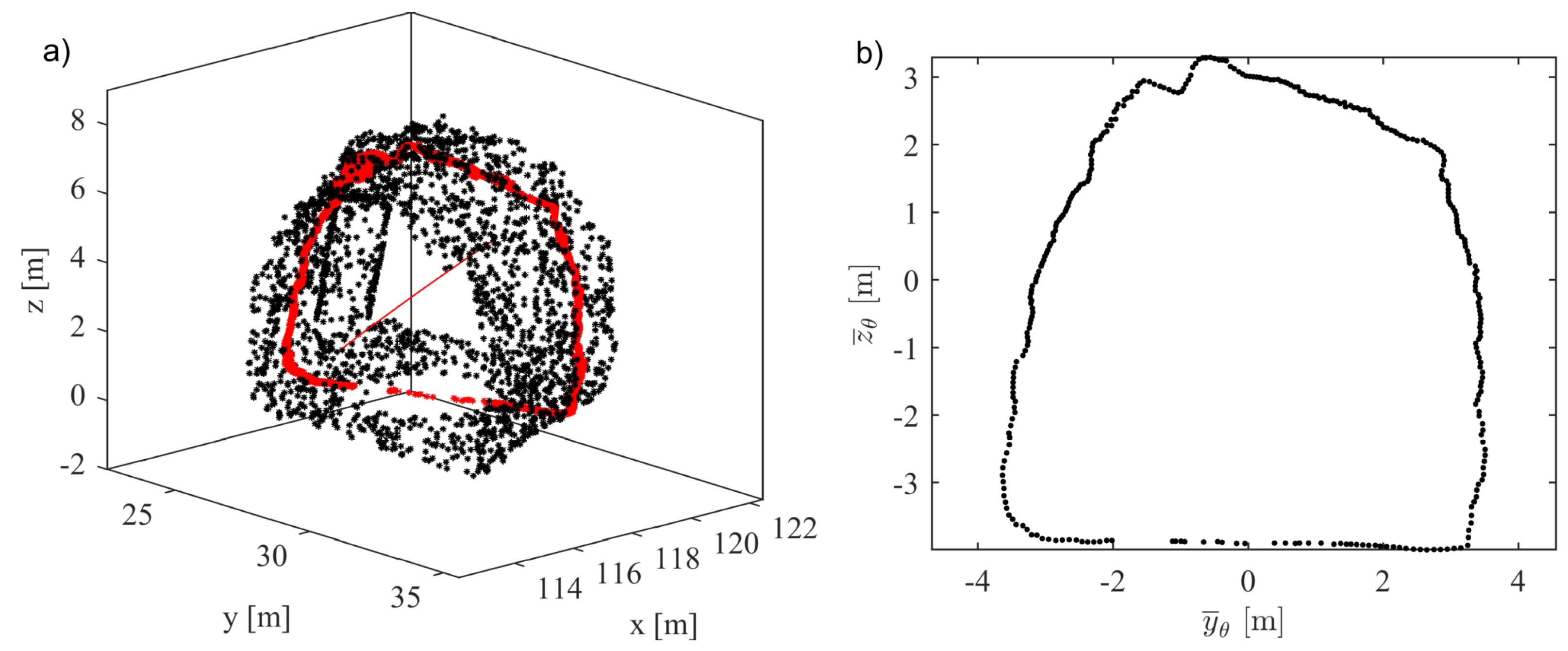
2.2. Determining Rough Surface Statistics
2.3. Discretization and Simulation Setup
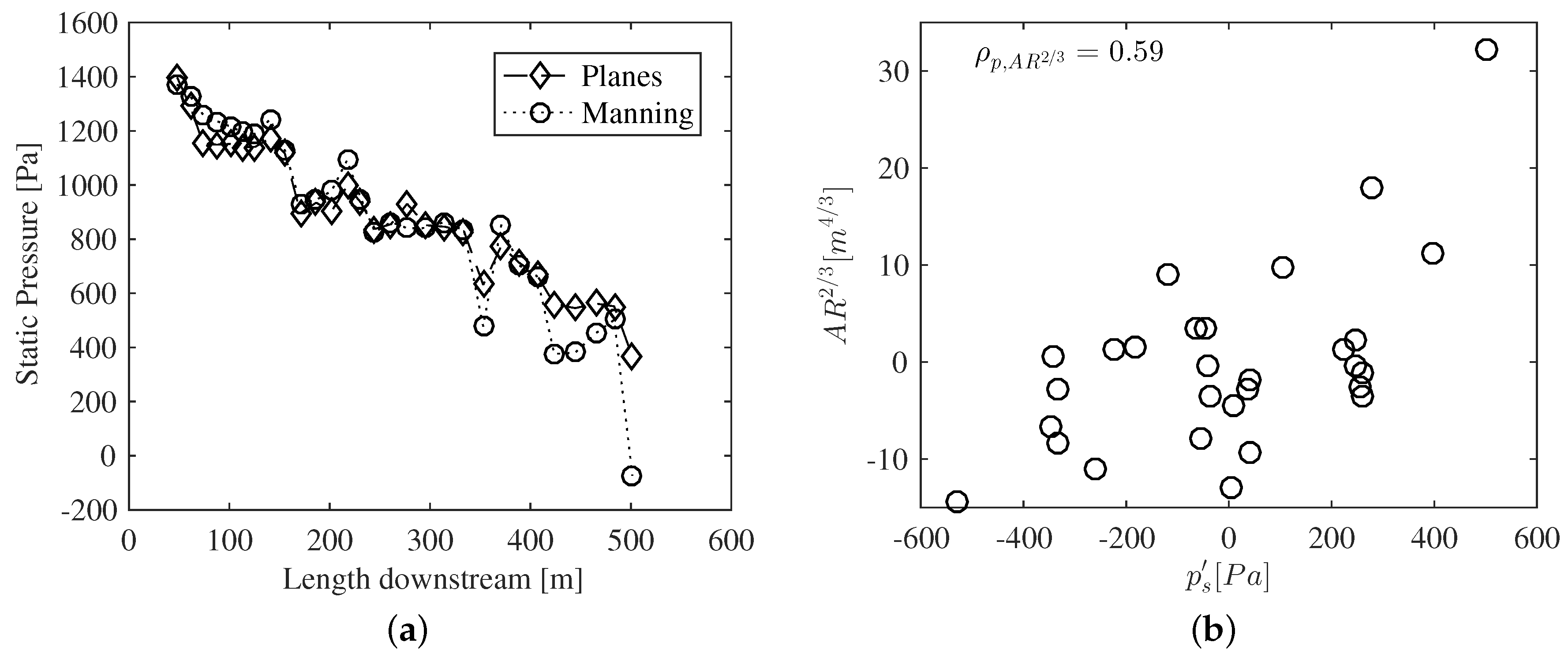
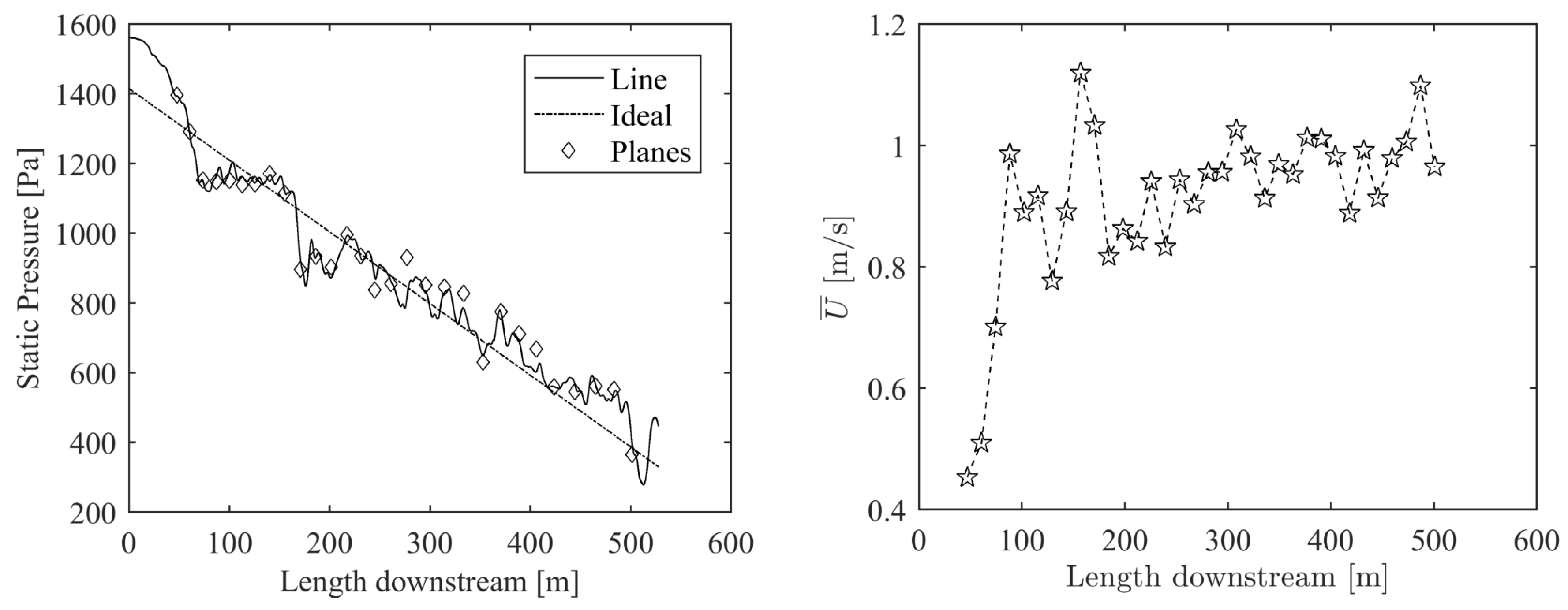
3. Results and Discussion
Head Loss
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bråtveit, K.; Bruland, A.; Brevik, O. Rock falls in selected Norwegian hydropower tunnels subjected to hydropeaking. Tunn. Undergr. Space Technol. 2016, 52, 202–207. [Google Scholar] [CrossRef]
- Reinius, E. Rock Erosion. Int. Water Power Dam Constr. 1986, 38, 43–48. [Google Scholar]
- Andersson, L.R.; Larsson, I.A.S.; Hellström, J.G.I.; Andreasson, P.; Andersson, A.G. Experimental study of head loss over laser scanned rock tunnel. In Proceedings of the 6th International Symposium on Hydraulic Structures, DigitalCommons@USU, Portland, OR, USA, 27–30 June 2016. [Google Scholar]
- Andersson, L.R.; Hellström, J.G.I.; Andreasson, P.; Andersson, A.G. Numerical Simulation of Artificial and Natural Rough Surfaces; American Physical Society: College Park, MD, USA, 2015. [Google Scholar]
- Patel, S.M.; Sondergeld, C.H.; Rai, C.S. Laboratory studies of hydraulic fracturing by cyclic injection. Int. J. Rock Mech. Min. Sci. 2017, 95, 8–15. [Google Scholar] [CrossRef]
- Jimenez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 2004, 36, 173–196. [Google Scholar] [CrossRef]
- Andersson, L.R.; Larsson, I.A.S.; Hellström, J.G.I.; Andreasson, P.; Andersson, A.G. Characterization of Flow Structures Induced by Highly Rough Surface Using Particle Image Velocimetry, Proper Orthogonal Decomposition and Velocity Correlations. Engineering 2018, 10, 399–416. [Google Scholar] [CrossRef]
- Andersson, A.G.; Andreasson, P.; Hellström, J.G.I.; Lundström, T.S. Modelling and validation of flow over a wall with large surface roughness. In Proceedings of the 9th European Fluid Mechanics Conference, Roma, Italy, 9–13 September 2012. [Google Scholar]
- Sarkar, S.; Dey, S. Double-averaging turbulence characteristics in flows over a gravel bed. J. Hydraul. Res. 2010, 48, 801–809. [Google Scholar] [CrossRef]
- Bråtveit, K.; Lia, L.; Bøe-Olsen, N.R. An efficient method to describe the geometry and the roughness of an existing unlined hydro power tunnel. Energy Procedia 2012, 20, 200–206. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Wang, G.C.; Lu, T.M. Characterization of Amorphous and Crystalline Rough Surface: Principles and Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Råde, L.; Westergren, B. Mathematics Handbook for Science and Engineering; Studentlitteratur: Lund, Sweden, 2004. [Google Scholar]
- Chanson, H. The Hydraulics of Open Channel Flow: An Introduction, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andersson, L.R.; Hellström, J.G.I.; Andreasson, P.; Lundström, T.S. Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation. Water 2019, 11, 1562. https://doi.org/10.3390/w11081562
Andersson LR, Hellström JGI, Andreasson P, Lundström TS. Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation. Water. 2019; 11(8):1562. https://doi.org/10.3390/w11081562
Chicago/Turabian StyleAndersson, L. Robin, J. Gunnar I. Hellström, Patrik Andreasson, and T. Staffan Lundström. 2019. "Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation" Water 11, no. 8: 1562. https://doi.org/10.3390/w11081562
APA StyleAndersson, L. R., Hellström, J. G. I., Andreasson, P., & Lundström, T. S. (2019). Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation. Water, 11(8), 1562. https://doi.org/10.3390/w11081562