1. Introduction
While water resources play an important role in human society, the world suffers from all types of natural disasters [
1]. In many countries, floods are the most likely natural disaster, and compared with other natural disasters, they are easily predicted and prevented [
2]. Therefore, it is very important for flood disaster management departments to formulate scientific and comprehensive plans for flood control. Consequently, government agencies spend massive amounts of money and manpower on flood control and rescue.
Floods are easily predicted, which means that preparations can be made to prevent flooding from actually happening. Developed countries such as England, the United States, Holland, Denmark, Germany, France, Belgium, and Austria have invested significant time and effort into flood control and disaster mitigation research since the 1960s and have achieved significant results in meteorology, hydrology, water conservancy, water quality, topography, the influence of social and economic activities on the prevention of flood damages, the runoff-conflux model of floods and its prediction and analysis, and other fields. During the process, the Wallingford National Institute of England, the Delft Hydraulics Institute, the Danish Hydraulic Institute, (DHI, Hesholm, Denmark), the United States Environmental Protection Agency, (EPA, Washington, DC, USA) and Army Corps of Engineers, (ACE, Washington, DC, USA), and other research institutes have stood out [
3,
4]. In the 1970s, the United States proposed flood control that used non-structural measures, which realized flood management through legislation, flood forecasting, flood dispatching, flood detention, flood insurance, floodplain management, and soil and water conservation, developed flood contingency plans and other methods, standardized people’s precautions and preparations against heavy rain and flooding, and provided guidance according to actual circumstances so that the losses from floods could be reduced and better social and economic benefits could be achieved. Compared with structural measures, non-structural measures were no longer the focus of flood control; instead, they emphasized the timely and scientific implementation of flood control command and dispatch through the collection, analysis, and processing of relevant flood information. This was done in order to improve the potential capability of the existing flood-fighting structural measures and standardize people’s actions against floods and the developmental activities within the floodplain, thus realizing flood control and disaster mitigation [
5]. Non-structural measures were important supplements to structural measures.
Among these non-structural measures, flood control material and emergency logistics were important for fighting floods. Flood control material is one of the three major elements of flood control and rescue, including material for preparation, response, and mitigation phases, and the reserve management of flood control materials is the key link in carrying out flood control work and plays an irreplaceable role in national flood control and rescue work. However, flood emergency preparedness lacks logistical insights [
6,
7], and relevant scholars have already conducted some primary studies. Garrido, Lamas, and Pino (2015) put forward a flood logistics model. The model attempts to optimize emergency supply inventories and vehicle availability [
8]. Leeuw, Vis, and Jonkman (2012) developed an emergency logistics framework that supports preventing catastrophic breaches of flood defenses during extreme situations [
9]. Alem, Clark, and Moreno (2016) developed a new two-stage stochastic network flow model to determine how to rapidly supply humanitarian aid to victims of floods [
10].
Intelligent storage is an important element of intelligent logistics and a key development trend in modern warehousing and logistics. The effectiveness of intelligent storage is chiefly influenced by the storage location allocation, and optimal storage location allocation can enhance the storage space utilization rate, shorten the storage and retrieval distances and times, accelerate the turnover of goods, ensure inventory stability, and increase the operating performance of an intelligent storage system.
The key to effective storage is optimizing the storage location allocation strategies, and scholars have performed in-depth, systematic studies of storage location allocation. Roodbergen et al. analyzed storage location strategies [
11] and found that the storage location allocation methods of commercial intelligent storage systems chiefly consist of the following types: fixed storage location assignment [
12,
13,
14,
15], random storage location assignment [
16,
17,
18], class-based storage location assignment [
19,
20], random class-based storage location assignment [
21], and shared storage location assignment. Most of these studies assume that a warehouse is initially empty, which is clearly not in accordance with the needs of real projects. Furthermore, even when the studies in the literature consider a warehouse with a non-empty initial state, they perform simulation experiments only involving a single batch of goods entering the warehouse. However, available empty storage locations will be abundant when a single batch of goods is put into storage, and there will thus be considerable freedom when selecting an optimal storage location. Consequently, it is possible that only sub-optimal locations will be left for the next batches of goods entering storage, and the arrangement of the storage locations as a whole will be irrational. Lee et al. proposed similarity coefficients to cluster goods and then assigned goods to storage locations in accordance with the clustering results [
15]. As for algorithms, most studies have adopted intelligent optimization algorithms, such as the genetic algorithm [
22], the simulated annealing algorithm [
23], the tabu search method [
24], the data mining-based algorithm [
25], and other algorithms [
26,
27], which can greatly shorten the computing time and enable optimal solutions to be found after relatively few iterations.
The foregoing review reveals that most scholars have constructed intelligent storage systems via a systems engineering approach and synergistically applied technologies, including message identification, communications technology, automatic control, and intelligent algorithms, in their intelligent storage systems. In particular, many scholars have used mathematical modelling to construct mathematical models of intelligent storage systems and then used simulation experiments to validate the models [
28,
29,
30]. Furthermore, operation optimization methods are most commonly used in intelligent storage analysis and decision-making [
31], and the development of commercial intelligent storage location allocation methods has provided a foundation for research and development (R&D) related to intelligent storage for emergency logistics.
Because emergency supplies tend to be infrequently used, intelligent storage systems are seldom used for emergency supplies, and therefore, there has been little research on storage location allocation in intelligent emergency logistics [
32,
33,
34,
35,
36]. The emergency supply reserve warehouses of some power agencies have used the Internet of Things to construct intelligent storage systems for their emergency power supplies [
37], which has enabled substantial increases in storage automation and storage and retrieval performance, reduced injuries and supply losses, and enhanced the emergency response capabilities.
There has been relatively little research on the application of intelligent storage in emergency logistics, and no research on key intelligent storage technologies for emergency disaster relief supplies has yet been published. Furthermore, because intelligent storage systems have not been used for flood control, there have been few studies concerning this aspect. However, the research on the key intelligent storage technologies that are used in commercial logistics and particularly the research on the storage strategies that are used in intelligent storage systems are already quite mature. However, because of the characteristics of the storage and management of flood control materials, including limited types of supplies, large quantities, low batch numbers, large quantities in a batch, the need for quick retrieval in the event of an emergency, and strong constraints on response times, the findings of the research on the application of intelligent storage systems to commercial logistics are not fully applicable to flood control materials. Therefore, there is an urgent need for research on the practical application of technologies for the intelligent storage of emergency flood control materials.
Based on the characteristics of flood control materials and their intelligent storage, this study established a flood control material storage location allocation model with the multiple objectives of retrieval efficiency and shelf stability and used a weighting method to transform a multi-objective optimization problem into a single-objective optimization problem. The study then optimized the storage location allocation of provincial flood prevention supplies using MATLAB. The optimized allocation can comprehensively improve the support ability, utilization efficiency, technical level, and management level of the flood control material reserve system, reduce the losses and hazards caused by emergencies, and achieve remarkable social and economic benefits.
3. Intelligent Storage Location Allocation Model for Flood Control Materials
3.1. Construction of a Multi-Objective Optimization Model
The types of the flood control materials include motor oil, life jackets, tents, boats, portable lights, etc., and the material specifications cover the lengths, widths, heights, and importance of the materials. Here, in order to simplify the problem, a certain number of single-class materials will be grouped as a single standard pallet group based on their size. The combination is the standard pallet group of the material and the length, width, height, and weight of the standard pallet group of the various materials satisfy the shelf restrictions.
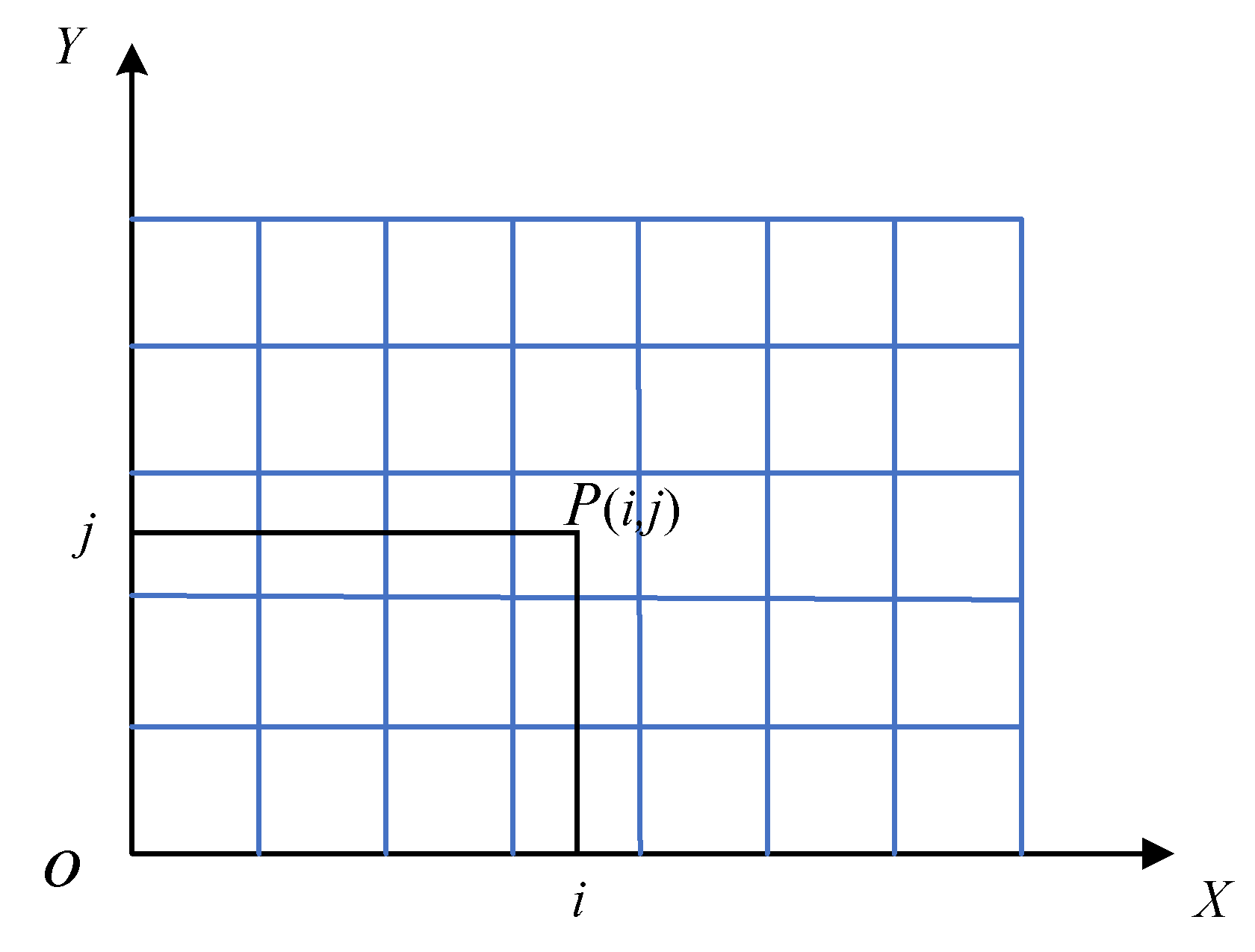
The paper takes single-row shelves as the research target, and we establish a multi-layer shelf coordinate system in the optimization module with the starting position of the work vehicle at the exit table as the origin O(0,0), the X-axis is the longitudinal axis direction of the shelf, the Y-axis is the vertical direction of the shelf, each column and each layer of the shelf is one unit in length in the X-axis and Y-axis directions, and the position of the materials is determined as P(i,j).
The main variables and parameters are defined as follows.
We assume that a certain set of shelves in a warehouse has rows, and the position of the materials is determined as P(i,j) (0 ≤ i ≤ m, 0 ≤ j ≤ n).
The flood control materials include r total categories; Wk is the material weight (single standard pallet group weight) of the type-k material (0 ≤ k ≤ r);is the time that is needed for a forklift to transport the goods at the storage location at the th row and th level; are, respectively, the horizontal and vertical operating speeds of the shuttle vehicles or forklifts; are respectively, the length and height of a storage location; pk is the calling frequency of the materials (0 ≤ k ≤ r), the total number of times the materials are used within a certain period of time, which is equivalent to the number of times that the materials are retrieved divided by the time.
We define the decision variable as xijk. When the type-k material (0 ≤ k ≤ r) is stored in P(i,j), xijk = 1; otherwise, , where 0 ≤ i ≤ m, 0 ≤ j ≤ n, 0 ≤ k ≤ r.
Based on the classification of materials, different materials should be stored in different warehouse areas, and storage location allocation must be performed in different warehouse areas. Based on storage location allocation principles, this study constructed the following model.
- (1)
In accordance with the principle of lighter materials on top and heavier materials on the bottom, assuming that a certain set of shelves in a warehouse has
rows, where the level closest to the floor is the first level and the row closest to the exit is the first row, the goal of storage location allocation optimization is to minimize the sum
of the products of the weights of the materials on pallets and the levels on which the materials are located. The first objective function of the shortest optimization objective function is as follows:
- (2)
In accordance with the principles of close access and quick turnover, minimizing the sum
of the transport times of the materials in each storage location and minimizing the sum of the products of the usage frequency of each material and the forklift operating time when retrieving the material. The second objective function that optimizes the shelf stability is as follows:
Based on the weighting method, the weights
α and
β (where 0 ≤
α ≤ 1, 0 ≤
β ≤ 1, and
α +
β = 1) of the fusion model are determined according to the importance of the shortest delivery time and shelf stability. The two objective functions for the shortest delivery time and shelf stability are merged, and the final warehouse optimization multi-objective model is established as follows:
3.2. Simplifying the Storage Location Allocation Model
Storage location allocation is a composite multi-objective optimization problem, and multi-objective optimization problems are typically solved in two ways. One way uses a weighting method, a maximum method, a constraint method, or goal programming to quantitatively address the multiple objectives and obtain a unique feasible solution. The second way uses a multi-objective optimization algorithm based on artificial intelligence, such as a multi-objective genetic algorithm, an ant colony optimization algorithm, or a simulated annealing algorithm, to perform the optimization.
In this study, considering the characteristics of a flood control materials warehouse, a weighting method was used to transform the multi-objective problem into a single-objective problem. In view of the equal importance of the two objectives of the shortest delivery time and shelf stability, in this study, the two objectives were both assigned weights of 0.5, which resulted in the following objective function:
Each side is multiplied by 2 to yield the final optimization model for location allocation as follows:
3.3. Determining the Parameters
3.3.1. Facility and Equipment Status and Their Parameters
In accordance with the distances of shelves from the exit and their lifting heights, an optimal storage location is a location in an intelligent storage system that is at a height within 20% of the storage area that is closest to the floor and within the 20% of the storage area that is closest to the exit. These storage areas have the characteristics of easy storage, short pathways, and low mechanical operating losses. An intelligent storage system is chiefly composed of a material storage and transport system and a warehouse management system. Here, the material storage and transport system comprises shelves, the storage and retrieval entrance/exit, and warehousing equipment.
- (1)
Shelves: Multi-level shelves are closely spaced, and individual shelves may function independently. To facilitate this research, this study assumed a single set of shelves with a shelf height of and length of . Because the shelves had rows and levels, there were storage locations, and the storage locations had identical specifications, namely, a height of and a length of . Thus, .
- (2)
Storage and retrieval entrance/exit: The material storage and retrieval system included a shuttle vehicle system and forklift. One storage and retrieval entrance/exit was located outside of each set of shelves. Because vehicles can typically drive directly into flood control material warehouses for loading or unloading, this study considered only the transport of materials from shelves to a storage and retrieval entrance/exit.
- (3)
Warehousing transport equipment: Only one shuttle vehicle was used for single pick-up actions and was responsible for serving one set of shelves. The shuttle vehicle was located at a fixed initial position at the storage and retrieval entrance/exit in the beginning, and the time that is needed for the shuttle vehicle to leave its initial position, complete the placement (retrieval) of goods and return to its initial position was defined as the operation time. The warehousing equipment includes a shuttle car and a forklift. The shuttle car is responsible for the horizontal work. The forklift is responsible for the vertical work and other forklift operations. The working speed of the vehicle includes the maximum idle speed of the shuttle vx1 and the maximum speed of the shuttle load vx2. The vehicle’s horizontal acceleration is denoted as ax, the forklift’s vertical speed is denoted as vy, and the forklift’s speed is denoted as vf. Here, we can refer to the forklift’s basic operating parameters to calculate the value or use our experience to set the value.
The shuttle’s movement consists of its horizontal movement, the shelves, and the use of a forklift to move vertically up and down the shelves. The speed of a loaded shuttle vehicle is different from that of an empty shuttle vehicle. Its linear acceleration rate when starting is identical to the linear deceleration rate when stopping. After the shuttle vehicle reaches its maximum speed, it maintains that speed during its operations. See
Table 1 for the warehouse shelving parameters.
3.3.2. Determining the Storage Location Operation Time
In the coordinate system encompassing multiple levels of shelves, the X-axis represents the length of the shelves, and the Y-axis represents the height of the shelves. Goods were stored within storage locations. The time that is needed for the transport system consisting of shuttles and forklifts to move to individual storage locations on the fixed shelves was calculated using kinematics. We constructed a time-minimization model to obtain the amount of time that is needed to access goods at each storage location.
Storage locations were designated using two-dimensional coordinates, where
indicated the row coordinate and
indicated the level coordinate. The origin
was set as the shuttle’s initial location on the entrance/exit platform, and the shuttle’s movement from
to the storage location
and back again completed an operating cycle (see
Figure 1).
The horizontal movement distance is calculated as follows:
The vertical operating distance is calculated as follows:
The horizontal operating times were designated as is the time for the loaded shuttle vehicle to reach the storage location, and is the return time of the loaded shuttle vehicle. The vertical operating time was designated as , and the time-minimization model assumed that the shuttle vehicle accelerated uniformly until reaching the maximum velocity and then continued to move at its maximum velocity. The shuttle vehicle decelerated at a uniform rate after approaching its target storage location. Here, it was also necessary to consider the situations where the shuttle vehicle did not reach its maximum velocity when travelling a short route and where it travelled a sufficiently long route to reach its maximum velocity.
When the horizontal movement distance was too short, the shuttle vehicle could not reach the maximum velocity before it had to decelerate uniformly from its original velocity. When the movement distance was sufficiently long, the shuttle vehicle accelerated until reaching the maximum velocity , then moved at a uniform velocity and finally decelerated at a uniform rate. While the shuttle vehicle moved in the same manner when returning, it was loaded and therefore could not reach the maximum velocity of the unloaded condition. At this time, the maximum velocity that it reached was .
In the vertical direction, the forklift lifted the shuttle vehicle from the entrance/exit platform at a constant velocity of
, and the operation time was calculated using the data parameters in
Table 1 as follows:
When operating, the shuttle vehicle first moved vertically to the level of the target storage location and then moved horizontally to the appropriate location. The total time needed by the shuttle vehicle for a single operation was therefore calculated as follows:
Taking shelves with three levels and 10 rows as an example, the operation time for the shuttle vehicle to reach each storage location is as shown in
Table 2.
4. Empirical Analysis
This study empirically analyzed the storage location allocation in the intelligent storage area for flood control materials at the Zhenjiang warehouse of the Jiangsu water conservancy and flood control material reserve center [
1].
4.1. Case Warehouse
To emphasize the issues in intelligent storage location allocation with multiple objectives in Chinese flood control material reserve management, a case study was conducted.
The Jiangsu Provincial Hydraulic and Flood Control Material Reserve Centre (HFCMRC) Zhenjiang Warehouse is the only central- and provincial-level flood-fighting material warehouse in Jiangsu Province. It is one of the most representative flood-fighting material reserve warehouses in China. For this reason, this study chose the HFCMRC Zhenjiang Warehouse as the case example.
Interviews, document analyses, and observations were used for the data collection in this case study. A series of face-to-face semi-structured interviews with managers and staff members from the government sector (flood control and food control materials) and the business sector (food control materials) were conducted from September 2017 to August 2018. The inventory, invocation, and warehousing data of Jiangsu provincial flood control materials were provided by HFCMRC and the HFCMRC Zhenjiang Warehouse.
4.2. Retrieval of Materials in Storage
In accordance with the types and quantities of materials that were used at the Jiangsu provincial water conservancy and flood control material reserve center and in line with the warehouse’s size and shelving arrangement, we selected five types of supplies: motor oil, life jackets, tents, outboard motors, and powerful handheld flashlights. These supplies are most frequently used, have regular shapes, and can be suitably placed on multi-level shelves. See
Table 3 for the specific quantities of these items in storage.
4.3. Determining of the Intelligent Storage Area Location, Size, and Dimensions
According to the general construction plan of the Zhenjiang warehouse of the Jiangsu water conservancy and flood control material reserve center, the warehouse’s storage room has a minimum length and width of 30 m and 18 m, respectively. Because the location of the warehouse has not yet been determined, the warehouse’s dimensions were set as 30 m × 18 m, which provided a total of 540 m2. This ensured that the design would be applicable to any storage area in the warehouse.
4.4. Facility Layout and Equipment Types of Intelligent Storage Area
(1) Selection of shelves
There are limited types of stored flood control materials. They have large batch quantities, are often heavy and bulky, are not easily to manually carry, are not frequently used, and must be accessed quickly when needed. In view of these characteristics, we considered the use of pallet racks, drive-in racks, shuttle racks, and cantilever racks.
The specifications of the intelligent shelf storage locations in this study were preliminarily set as 1.5 m × 1.1 m × 1.5 m.
Table 4 lists the advantages and disadvantage of the various types of shelves and the other equipment required.
From the above types of shelves, pallet racks and drive-in racks must be equipped with forklift shuttle racks, and these warehouses must possess shuttles and forklifts. Intelligent access warehouse shelves also must be equipped with forklifts. Among these types of shelves, the order of space utilization of warehouses from large to small is as follows: intelligent access warehouse shelves, shuttle racks, drive-in racks, and pallet racks. The total valuation of shelves in descending order is as follows: intelligent access warehouse shelves, shuttle racks, drive-in racks, and pallet racks. The price of a shuttle is 100,000 yuan, and a 500 square meter warehouse needs to be equipped with two to three sets. The shelves can be customized. Here, they are specified to be 1.5 m × 1.1 m × 1.5 m. The prices of each type of shelf are different, and the price of pallet racks is the lowest. A 500 square meter warehouse needs three to four shuttles. Considering the low utilization rate of the flood control warehouse, we can rent forklifts, which can save costs and avoid idle assets. The price of a forklift is approximately 500,000 yuan. If the decision is made to purchase a forklift, a Linde forklift or Zhejiang Nori forklift is recommended. Furthermore, electric forklifts are economical and environmentally friendly and require narrower lanes compared with diesel forklifts, thereby making electric forklifts more preferable. Their price is between 60,000 yuan and 80,000 yuan.
(2) Selection of pallets
Different countries have different pallet specifications. The most common pallet specification in China is 1200 mm × 1000 mm, which is also one of the most common pallet specifications in Europe. These pallets are low-price, flat, wooden pallets with good durability, which makes them well suited to flood control materials, and they have a price of approximately Renminbi (RMB) 35–60 each.
When pallets are used to store materials, attention should be paid to the reasonableness of the materials that are stored on the pallets. The materials should cover at least 80% of the pallet area, the height of the center of gravity of the stored materials should not exceed two-thirds of the pallet width, and the height of the materials above the pallet should not exceed 1200 mm. In this study, the various types of materials, their quantities, and their stacking arrangements are given in
Table 5. The materials in this table were placed on shuttle racks, and generators and towed water pumps were stored on the floor. If more materials are added in the future, they can be placed on shuttle racks and placed at an upper level.
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 present the schematic diagrams of the arrangements of the materials.
4.5. Storage Location Allocation in the Intelligent Storage Area
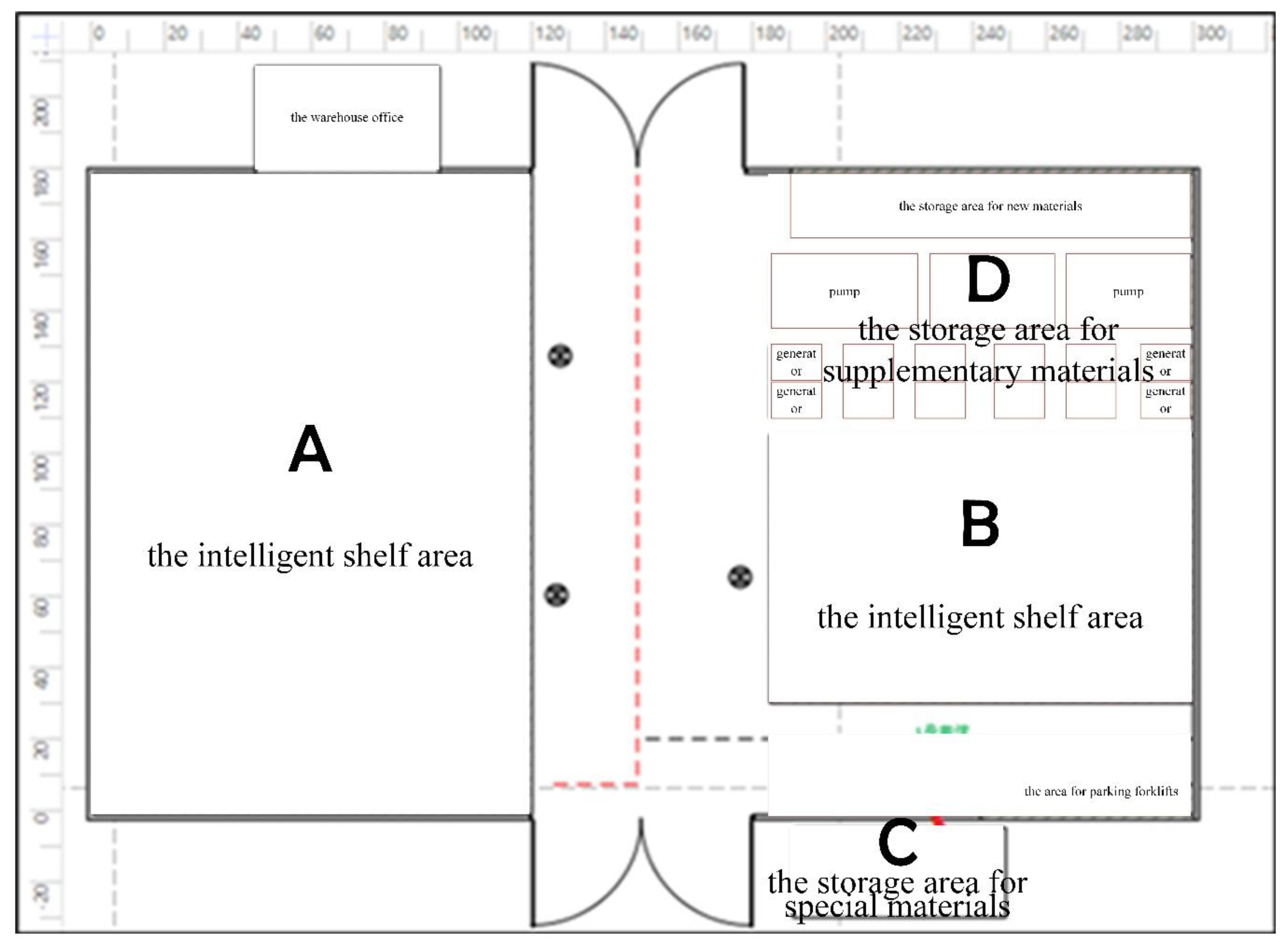
We first arranged the warehouse’s internal layout (see
Figure 7) in accordance with the existing intelligent warehouse area and material storage needs.
Compartment A and compartment B are both intelligent shelf areas, and compartment C is for storing special materials, such as tent poles and very small amounts of materials. It is equipped with ordinary shelves and cantilevered shelves. Compartment D is the pending area, which can be used as the storage area for supplementary materials, such as generators, pumps, and other supplies. Compartment A is approximately 11 × 18 = 198 square meters, compartment B is approximately 12.1 × 7.5 = 84 square meters, compartment C is approximately 12 × 1 = 12 square meters, and compartment D is approximately 12 × 6.5 = 78 square meters. The blank areas are the lanes. The middle lane is 6 meters wide, and the other lane is approximately 3 meters wide. The upper part is the entrance, and the bottom is the exit. Temporary sorting areas can be established on both sides of the entrance and exit. If a one-time delivery is sufficient, the upper entrance can be used as a temporary exit to improve the distributional efficiency of flood control materials. In addition, if the warehouse is subject to realistic conditions, the entrances and exits can also be combined together, and the exit can be used as the entrance.
Based on our storage location allocation model and the flood control material warehouse’s material use records, we assigned outboard motors, life jackets, tents, motor oil, and flashlights to one category, and generators and towed water pumps to another category. The materials that are suitable for storage in an intelligent warehouse were roughly divided into three areas: Area I contained outboard motors, life jackets, and tents; Area II contained motor oil and flashlights; and Area III contained generators, towed water pumps, and space for other materials that might be stored in the intelligent warehouse in the future. The materials in Area I were the most frequently used and had high inventory levels, the materials in Area II were frequently used but had low inventory levels, and the materials in Area III were moderately used, had low inventory levels, and were very heavy, bulky, and difficult to move.
Therefore, we arranged the storage area in accordance with the material types and quantities and the number of storage locations on the shelves. Type I materials were placed in areas A and B, with life jackets placed in Area A and outboard motors and tents placed in Area B. Type II materials consisted of tents, tent poles, and flashlights. Because of the close relationship between the tents and tent poles, they were placed in Area C. Type III materials consisting of generators and towed water pumps were placed sequentially on the floor in Area D.
After the materials had been placed in these sub-areas in accordance with the storage location allocation principles, the materials could be quickly and precisely located and retrieved from the warehouse, which increased the efficiency and facilitated their inspection, inventory, and maintenance.
Depending on their form, the shelves were classified into two main types. Type 1 consisted of pallet racks, which required many lanes and had a relatively low overall spatial utilization rate. Type 2 consisted of close-packed shelves, including drive-in racks, shuttle racks, and an intelligent 3-D storage area. These shelves required fewer lanes and used relatively little space.
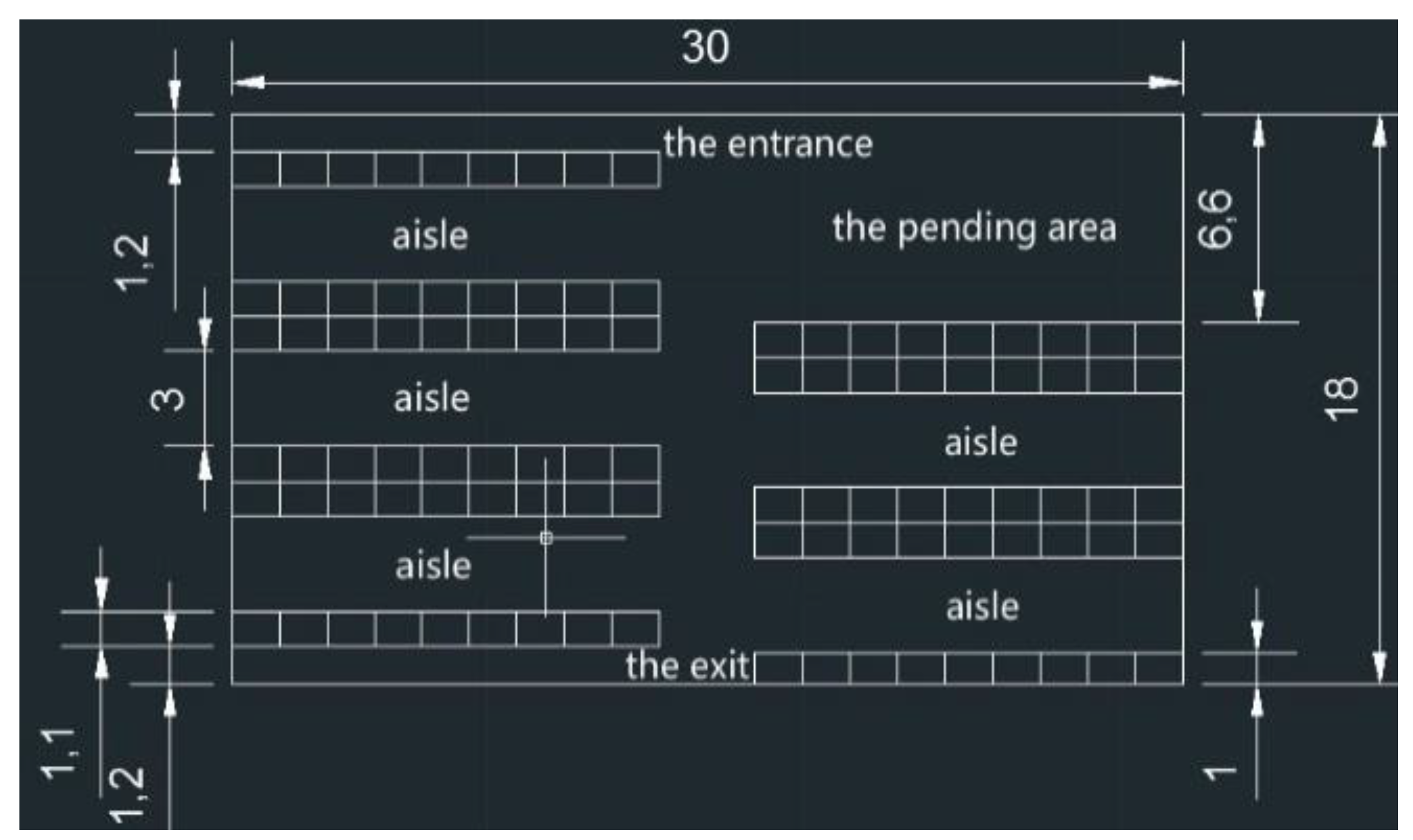
The storage locations on the pallet racks are shown in
Figure 8. A total of 90 storage locations were situated on each level in areas A and B, and five levels could be used for the storage of existing materials.
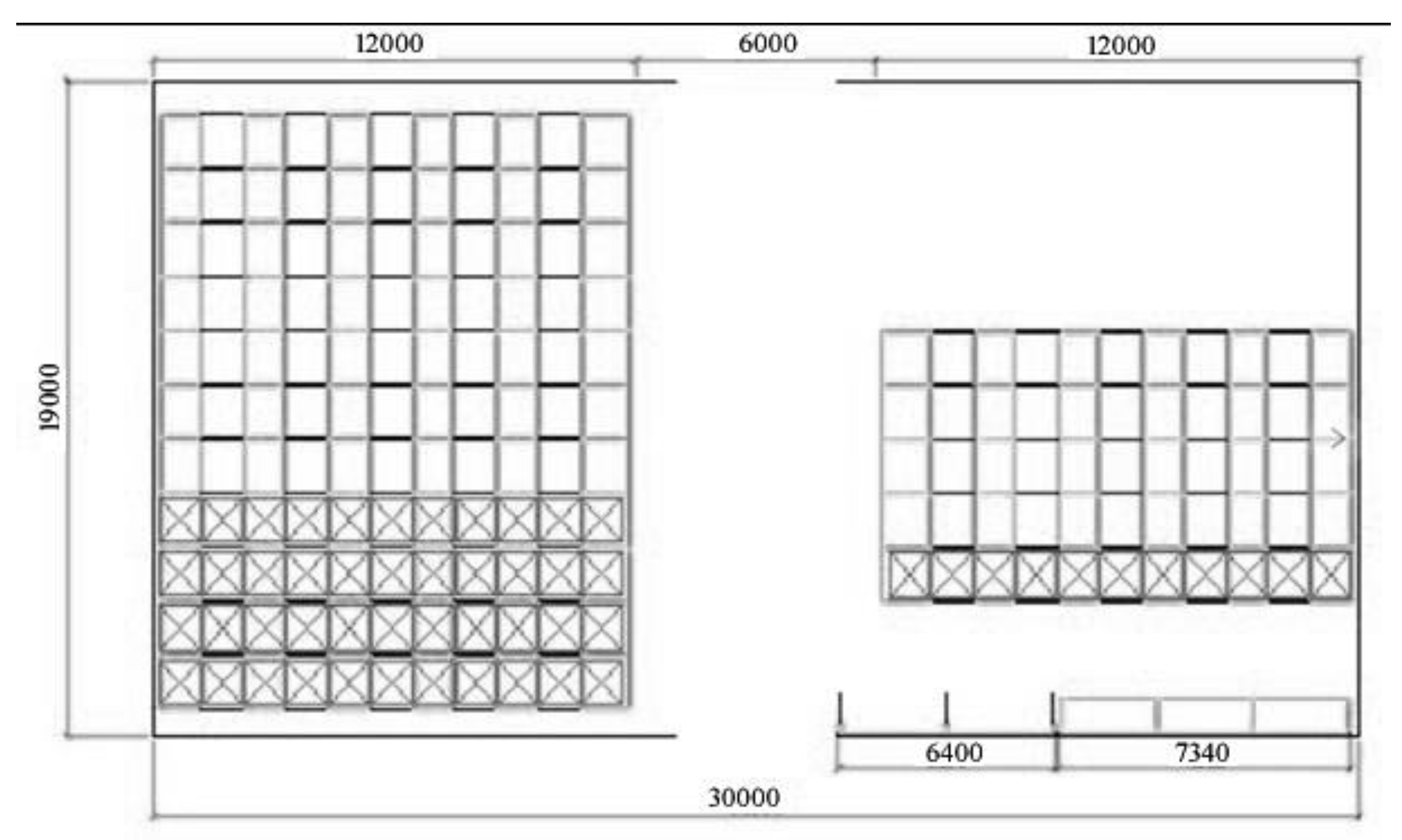
The type 2 close-packed shelves, including drive-in racks, shuttle racks, and intelligent 3-D storage area shelves, could be arranged in the following manner. Objects could be placed horizontally on the shelves, and the main aisles could be used to ensure that the life jackets could be stored and removed via separate pathways. There were 176 storage locations on each level and four levels of shelves, which resulted in a total of 704 storage locations. See
Figure 9 for a plan diagram of the storage locations.
Area C, which was used for the storage of tents and poles, had an overall volume of 5 m × 1.2 m × 4 mm and a floor area of approximately 12 m2. The tent poles were placed on the shelves in bundles of 10 poles. The storage locations were at a vertical distance of 0.5 m from each other, their total height was 3 m, and there were 12 storage locations. The size of the storage locations in the ordinary shelves located on the right was 1.4 m × 1.0 m × 1.5 m. Each level had five storage locations, and there were four levels. These shelves were used for the placement of small items, such as motor oil and flashlights that required convenient access. Area D contained 78 m2 of empty space that could be used for the storage of additional materials or to meet other needs in the future.
See
Table 6 for the material parameters at the Zhenjiang warehouse.
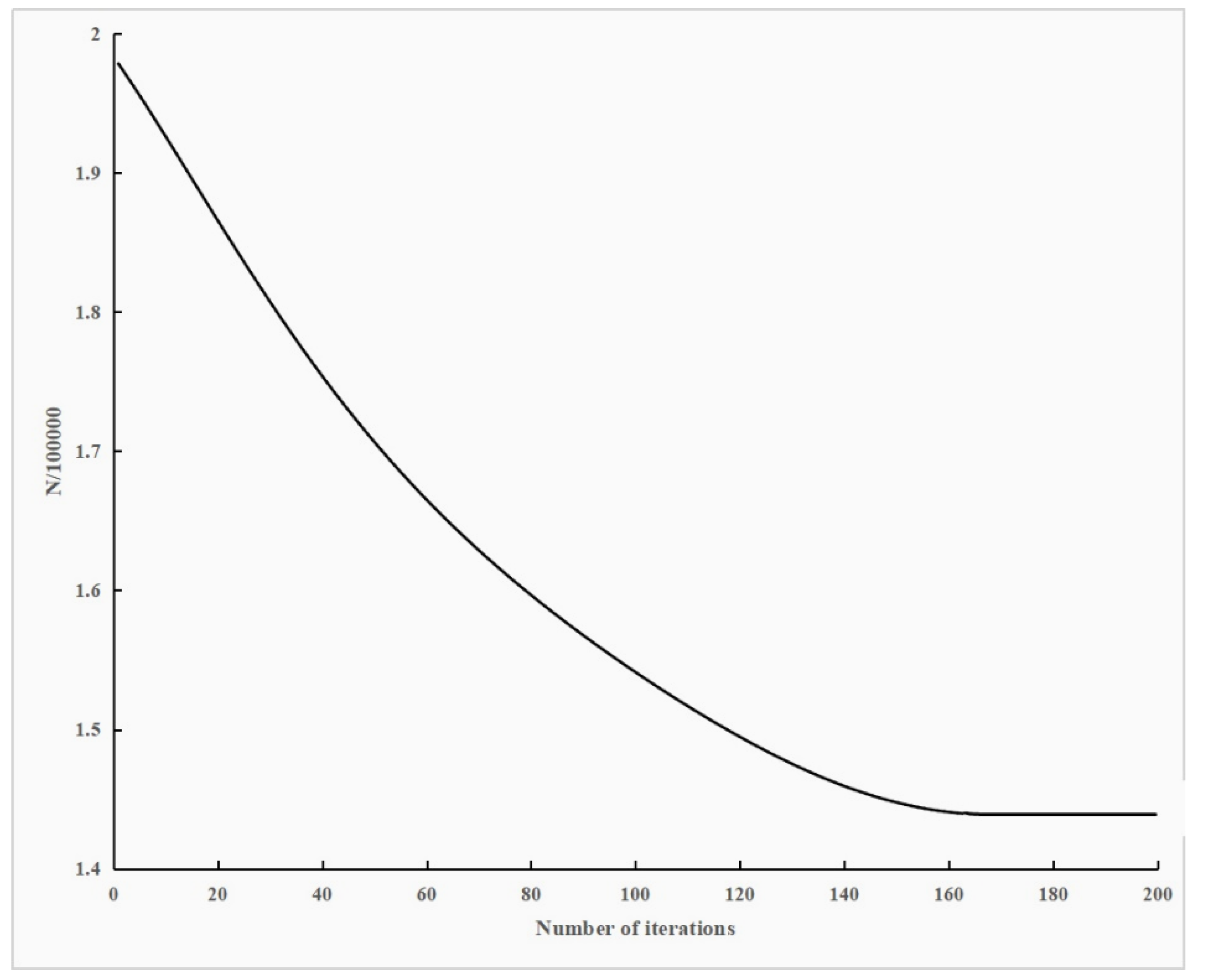
Our storage location optimization model was programmed using the MATLAB software and yielded an
H-function variation curve when run (see
Figure 10).
The following conclusions can be derived from the curve in
Figure 10. As the number of iterations increases, the objective function value
H steadily decreases and reaches a relatively constant value after the number of iterations reaches 170. This indicates that the objective function has basically achieved convergence. The final value was
.
The solution that was obtained above optimized the model using the genetic algorithm, and MATLAB yielded the storage location allocation results for the close-packed shelves in different areas at the Zhenjiang intelligent warehouse (see
Table 7).