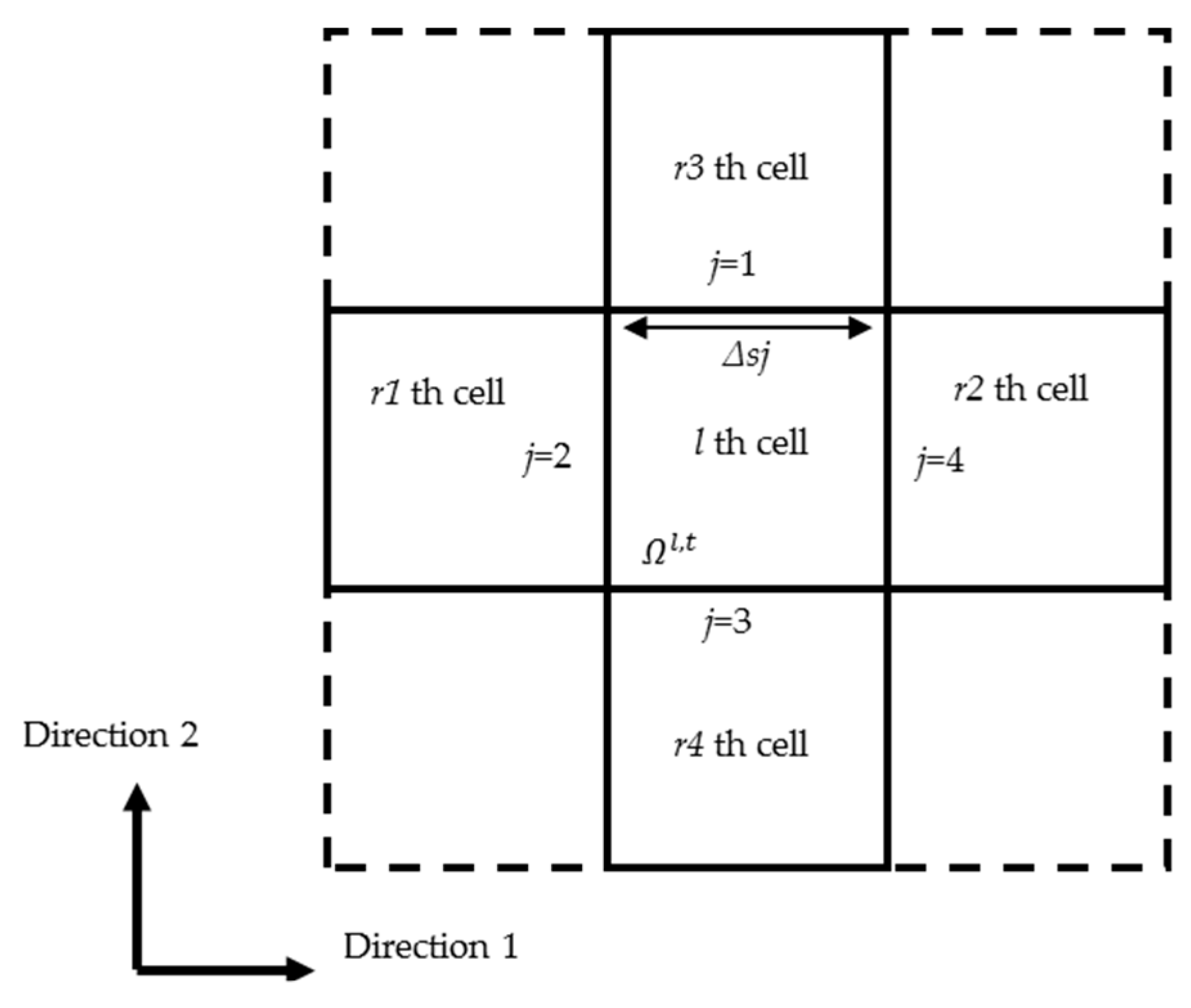
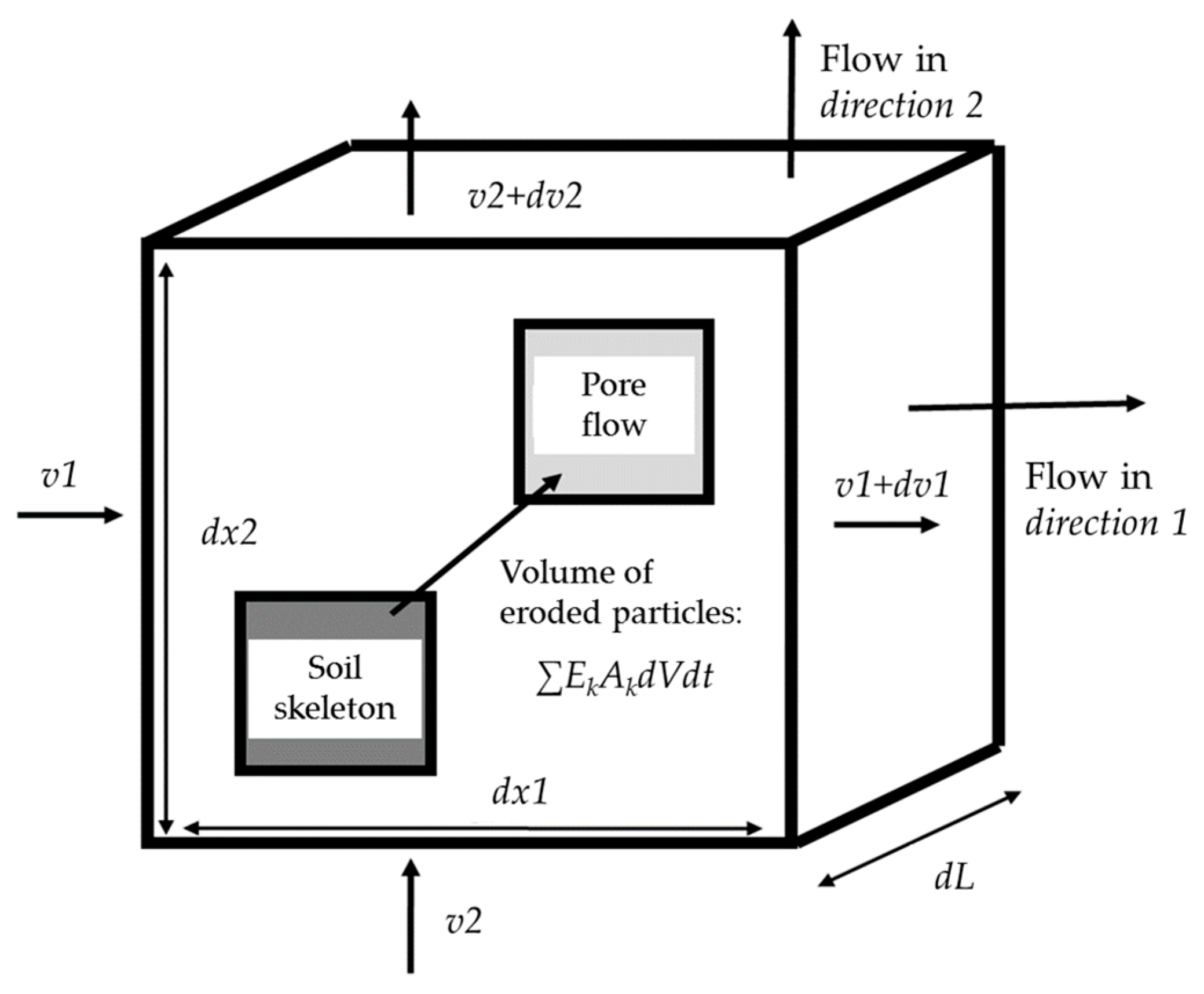
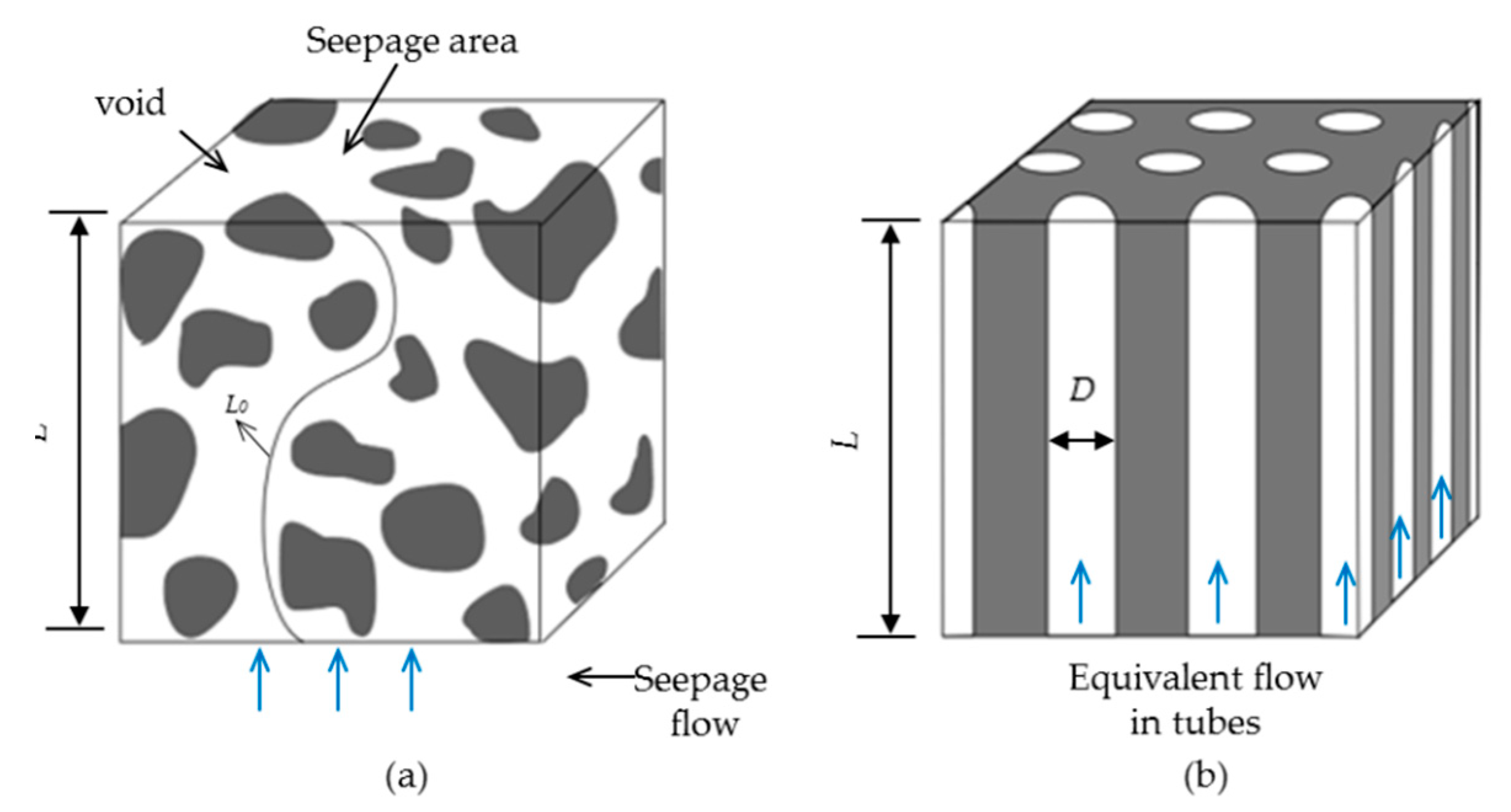
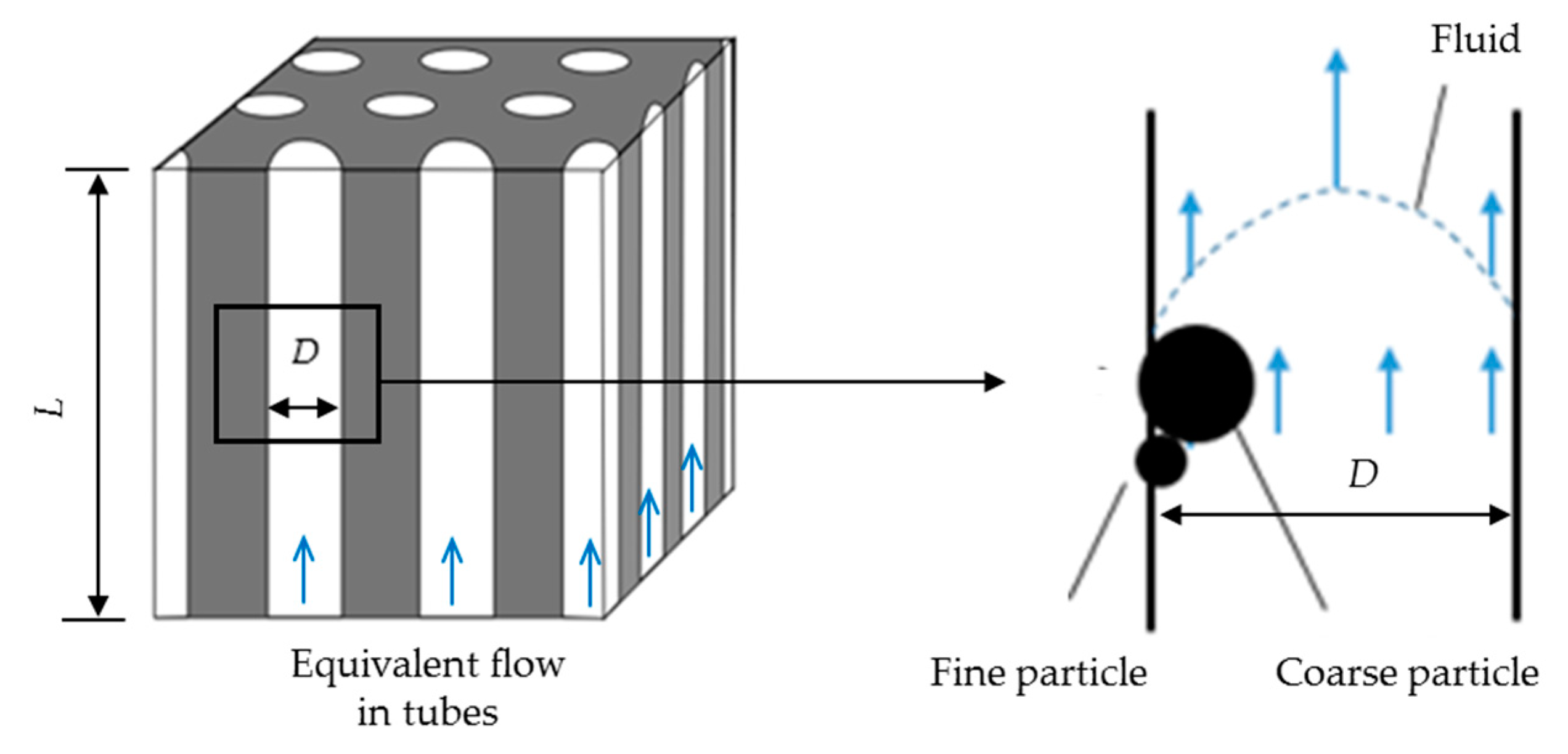
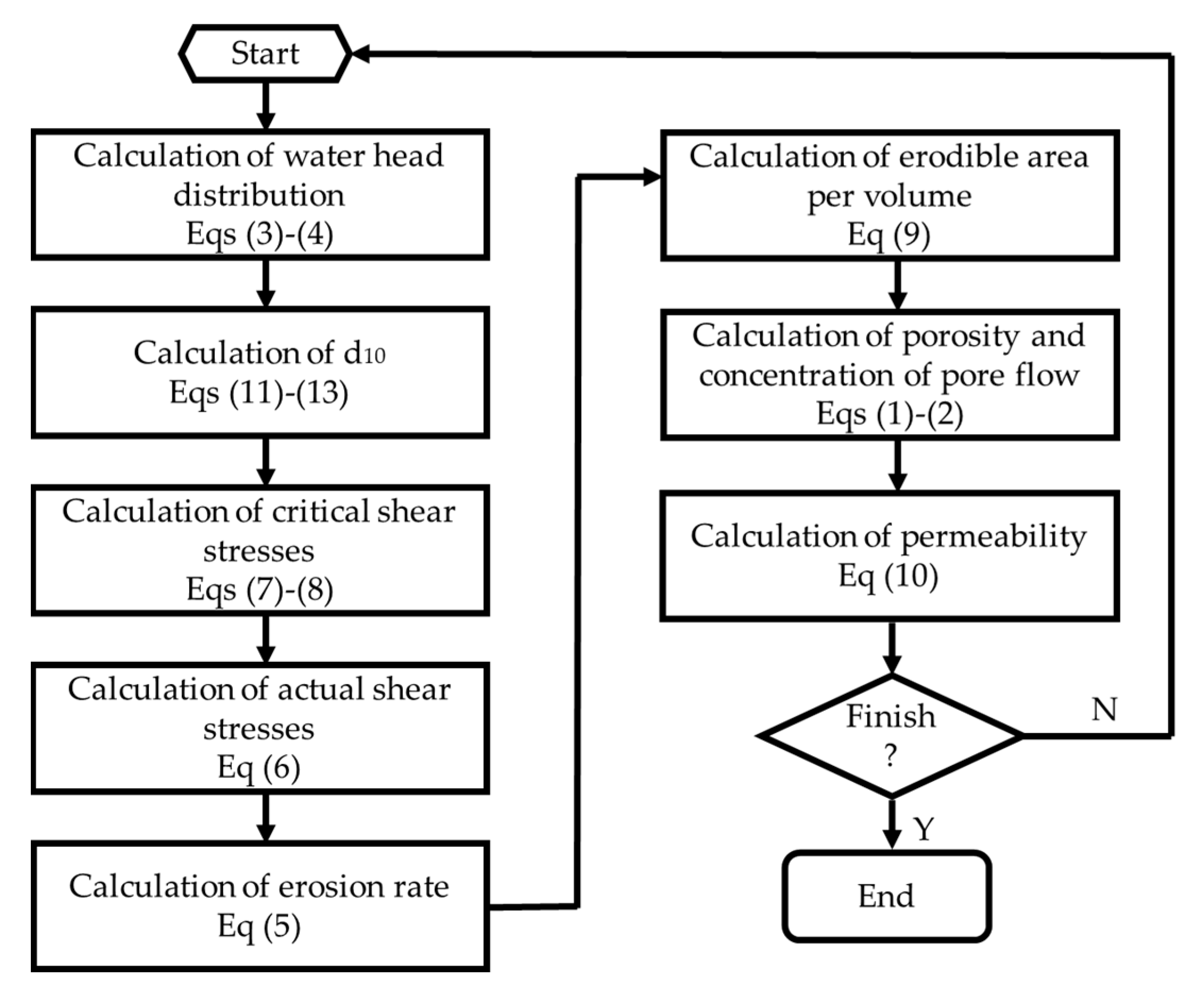
1. Introduction
Suffusion is the mass movement of fine particles through the pore space of a coarser matrix driven by seepage forces [
1]. It is one of the main mechanisms initiating internal erosion within levees, earth dams and foundations [
2,
3,
4] as well as watershed hillslopes [
5,
6].
A lot of experimental [
7,
8,
9,
10,
11,
12,
13,
14] and numerical (CFD) studies [
15,
16] were launched and expected to reveal the underlying mechanisms corresponding to suffusion. Most of these studies were macroscopic and under the important assumption that the movement of soil is a continuous process. This assumption has never been verified through or connected directly to a particle-scale study. However, some of following studies in granular system start to show their potential to support this assumption. For instance, as DEM models [
17,
18,
19] and CFD+DEM models [
20] are developed, the suspension, collision or spin of particles have been described in detail, but still seem to be irrelevant to the internal structure fracture (based on regime transition research [
21]) or massive movement (based on rheology research [
22,
23,
24]). Since then, macroscopic studies on suffusion are still mainstream, especially when focusing on engineering practices.
Suffusion can take on many forms, but it is particularly insidious when it occurs under a relatively low hydraulic gradient. Hydraulic engineers determine the internal stability by examining the critical gradient of a soil which directly affects the likelihood of diffusion. Generally, the soil is internally stable if
ic < 0.7 [
7].
The internal stability of soils is closely related to its grain size distribution (GSD). As pointed out by Wan and Fell [
1], internally unstable soils are usually broadly graded soils with particles from silt (or clay) to gravel size, whose GSD curves are concave upward (or known as gap-graded soils). GSD-based assessment approaches, based on experimental evidence, have been used extensively in practice [
8,
9,
10,
11,
12,
13,
14]. Most of them distinguish coarse and fine particles within the soil and incorporate characteristic sizes into an assessment index or indices.
Early studies accounted for two particles sizes with an additional division size. For example, Kézdi [
25] divided soils into coarse and fine components. The maximum value of
D15/
d85, which depends on the division size, is used as the index of internal stability.
D15 (
d85) is the size for which 85% (15%) by weight is finer in the coarse (fine) components, respectively. The soil is evaluated as unstable if
D15/
d85 > 4. Similarly, Kenney and Lau [
26] introduced a “shape curve” to identify an internally unstable soil. They defined
F as the percentage of particles that are finer than an adjustable size
d and
H +
F as the percentage of particles finer than the size of 4
d. The material is assessed as internally unstable when the minimum value of
H/
F is less than 1.3 originally, [
26] and a modified lower value of 1.0 later [
27]. Different from the usage of an adjustable particle size, Burenkova [
28] considered three characteristic sizes and evaluated the soils unstable when
d90/
d60 is greater than 1.86log(
d90/
d15) + 1 or less than 0.76log(
d90/
d15), where
dx (
x = 15, 60 or 90) hereafter is the diameter for which
x% by weight of the soil particles are finer.
In recent decades, the idea of a more precise representation of the GSD curve has been further developed. Wan and Fell [
1] extracted four sizes from the GSD curve. Two are for coarse particles and the other two for the fine counterpart of the soils. They defined two variables,
s1 = 15/log(
d20/
d05) and
s2 = 30/log(
d90/
d60), for each soil sample. The well-known assessment criterion is that a soil sample is internally unstable when
s1 < 22 and
s2 > 80. That is, an internally unstable soil is featured as
d20/
d05 > 4.8 and
d90/
d60 < 2.4. Also, its accuracy is higher than any other GSD-based approaches mentioned above.
The accuracy of the GSD-based approaches has been improving since more and more GSD information has been added in. In terms of seepage flow dynamics, however, these approaches are still empirical and with ambiguous meaning. Early research suggests that the gap-graded soils are apt to being internally unstable since fine particles easily pass through, but do not fill in the voids between the coarse particles if subjected to seepage [
9]. The filtration of detached fine particles has therefore been well accepted as the mechanism responsible for the internal stability. Overall, suffusion appears as the combination of detachment, transport, and filtration of fine particles. They may depend on the excessive shear stress related to particle inception [
15,
29], sediment transport capacity if definable, and the size of the voids, respectively. In addition to the filtration effect, the other mechanisms may dominate in some cases, but have received less attention so far. Such incomplete understanding hampers the explanation of other important factors such as porosity [
30,
31] and loading history [
32].
This paper presents a numerical simulation of fine particle dynamics subjected to seepage flow, within an extended numerical framework of Fujisawa’s study [
15]. We take into account the combined effects of GSD and porosity. Wilcock and Crowe’s theory [
33] is adopted to quantify the inception and transport of each size group of soil particles. We reproduce the phenomena observed in seepage tests and explain why the soils with specific GSD behave more internally unstable, and we predict the internal stability of soil through the model.
3. Model Verification
In this section, the proposed model is examined by previous experiments (studies by Skempton and Brogan in 1994 [
9] and Wan and Fell in 2008 [
1]). The experimental works have detailed records of hydraulic gradient (or eroded soil mass) at different stage of seepage flow and are therefore used for model calibration and validation.
Furthermore, in the next section, more experiments (studies by Lau in 1984 [
36]; Lafleur et al. in 1989 [
8]; and Chapuis in 1996 [
10]) are also included when examining the model’s capability in predicting internal stability.
3.1. Overview of Experiments
3.1.1. Devices
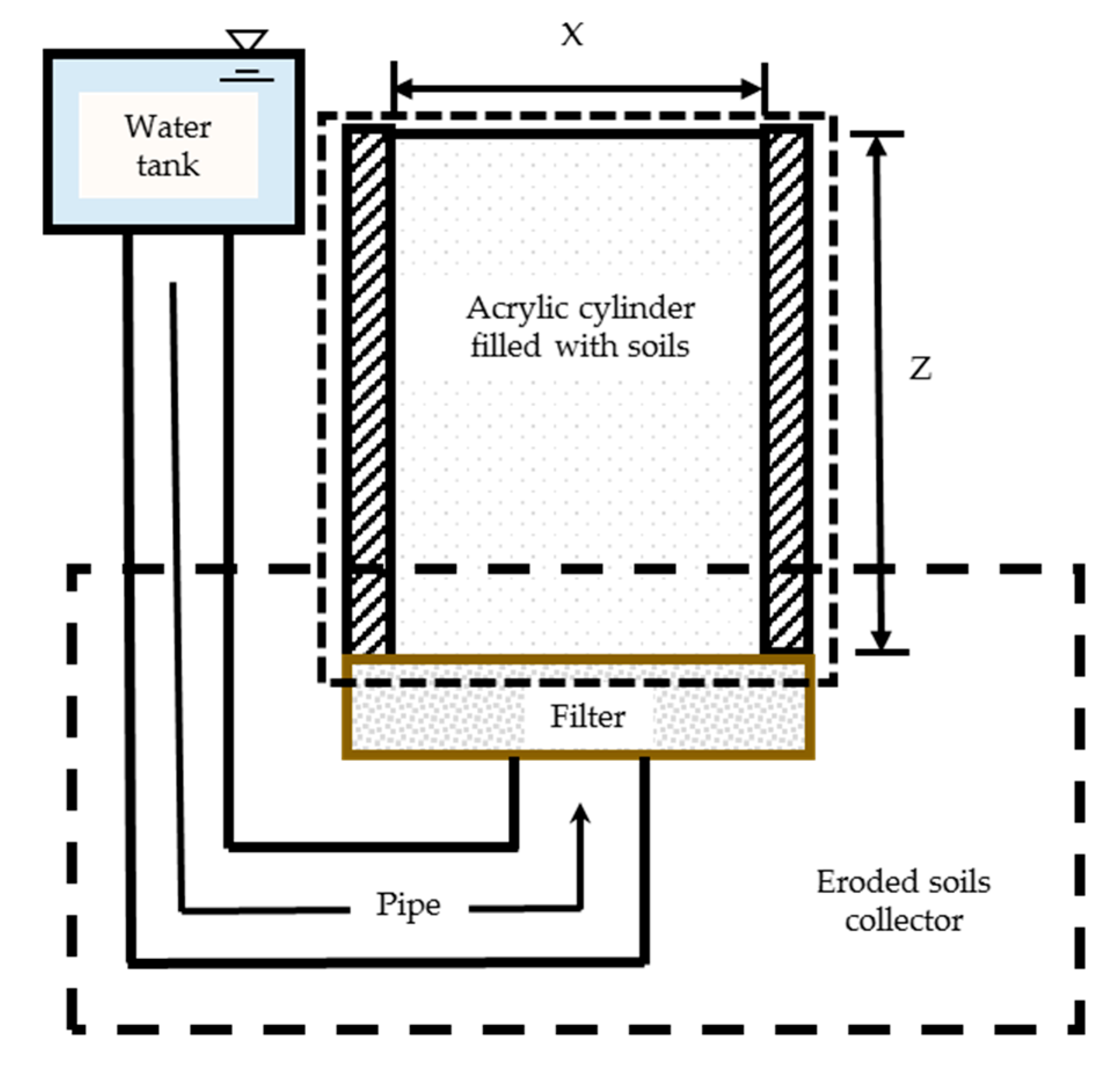
The designs in experimental devices between these studies were similar: their experiments were conducted using acrylic cylinders filled up with fully mixed soils (see
Figure 5). The upper end of the cylinder was the outlet of the seepage field, which allowed free outflow (also known as being downstream of the seepage field), and the discharge of the seepage flow was measured when running the experiment. The lower end was the inlet of the seepage field (also known as being upstream of seepage field), which connected the filter layer and the water pipe. The filter layer was designed to make the inflow distribution more stable, and the water pipe was used to connect the soil device with the water tank.
3.1.2. Observed Stages of Suffusion Process
With the increase of hydraulic gradient, Skempton and Brogan [
9] observed the seepage flow and identified three stages of suffusion: (1) the “dancing-like movement of particles” stage, during which initial signal demonstrating that the suffusion had begun; (2) the “slight but general movement of particles” stage, during which suffusion kept developing and formed the shape of the “pipe” started stretching towards the upstream, and (3) the “strong general piping of particles” stage, where the soil particles were strongly moving out of the soil fabric.
Wan and Fell [
1] gave similar characterizations. They identified the flow at the outlet as “clear”, “cloudy”, and “very cloudy” by manually observing and recording, because the degree of turbidity indicated the degree of suffusion, just like the judgment shown in Skempton and Brogan [
9]. The “clear” flow indicated no suffusion and other conditions meant erosion at different stages. The soil samples were evaluated as internally unstable when the stage of “slight but general movement of particles” or “cloudy” flow was reached below the hydraulic gradient of a manually fixed value which was set as the critical one (e.g., 0.7 mentioned in
Section 1).
3.1.3. Soil Samples
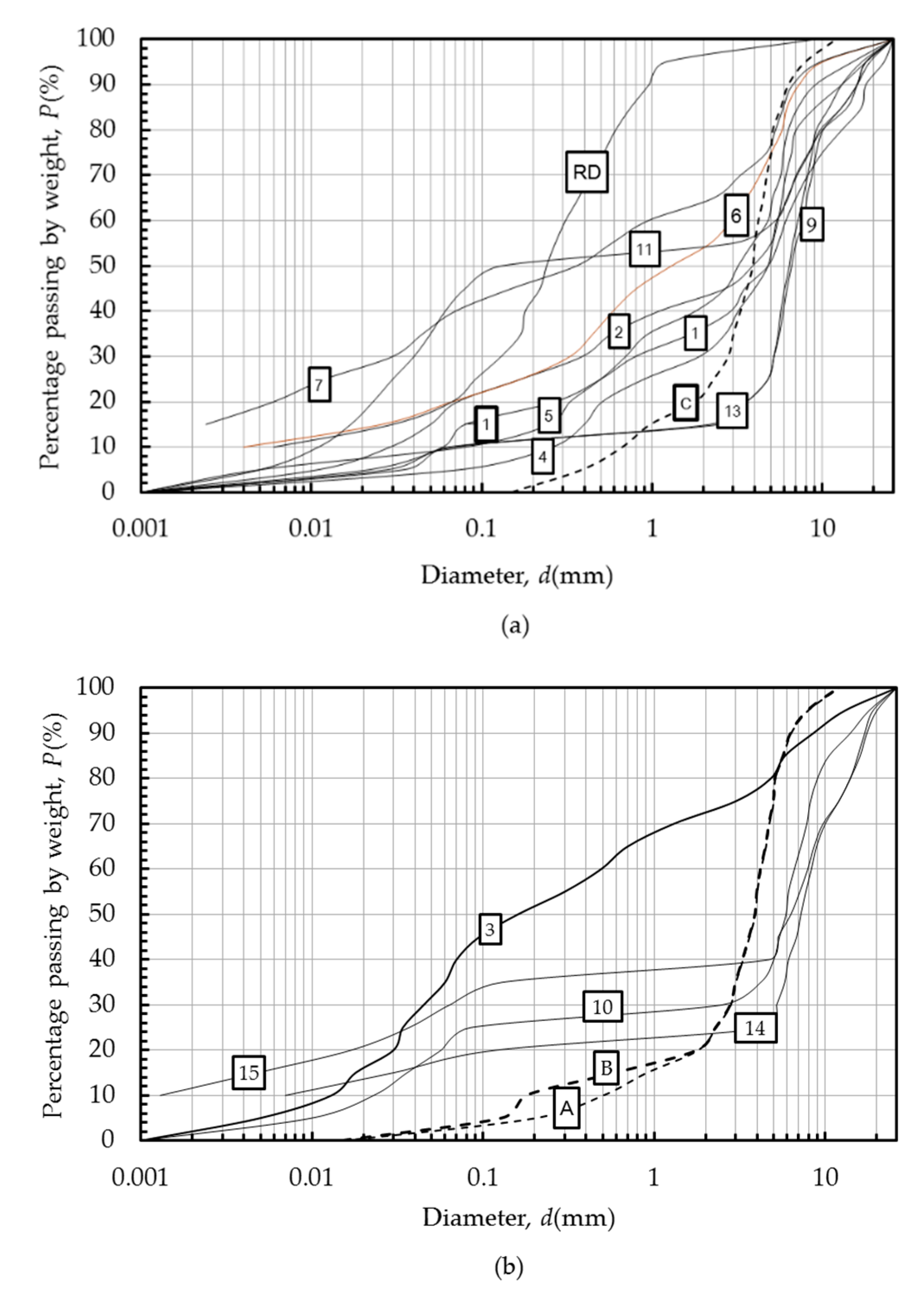
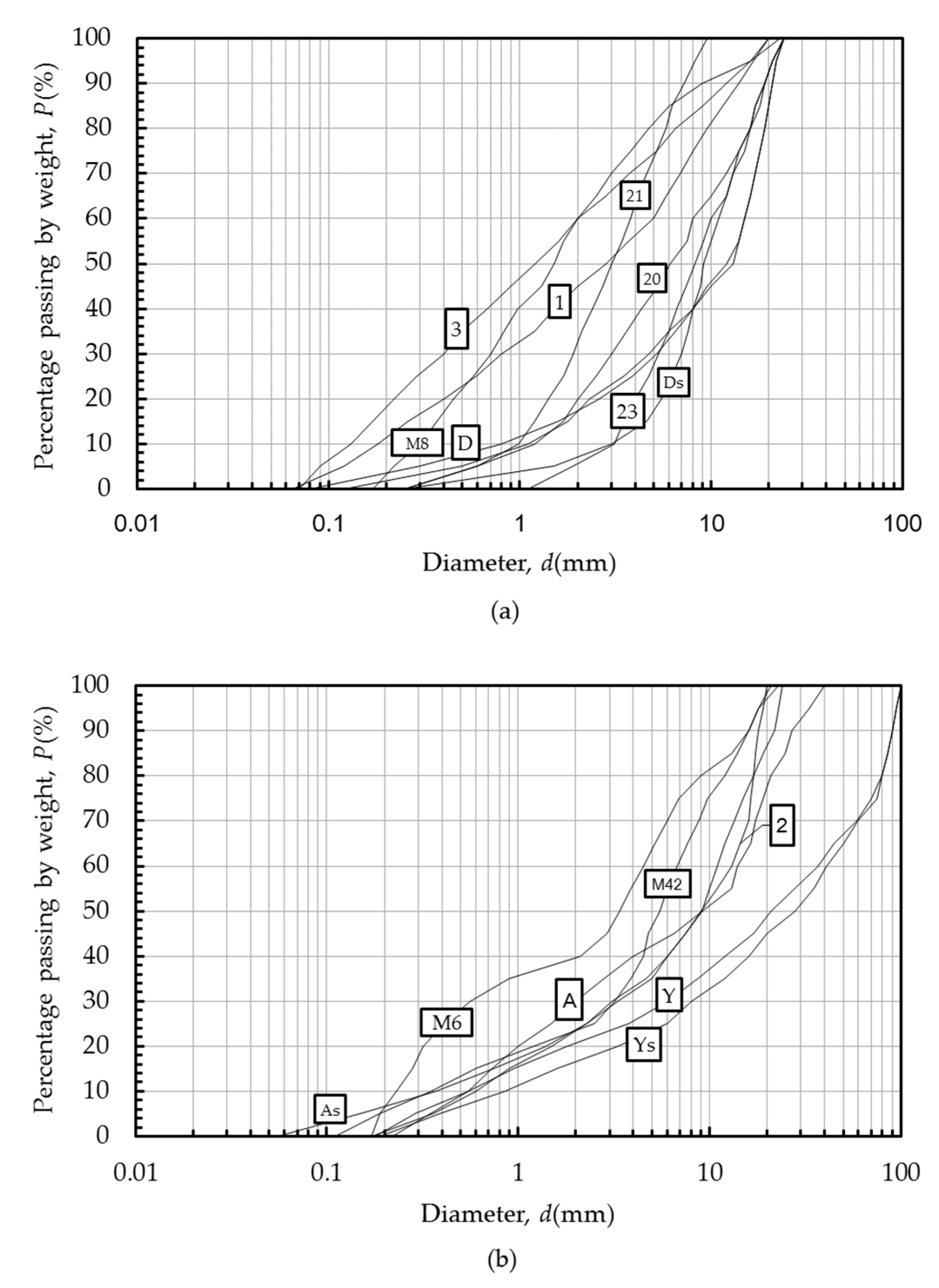
Skempton and Brogan [
9] used three different samples of non-cohesive soils and reported three runs of data, namely Runs A, B, C, respectively. In comparison, Wan and Fell [
1] presented 18 runs of experimental data with 14 soil samples (upward flow tests only), their soils contained a portion of cohesive particles (diameter
d < 0.02 mm). The maximum soil diameter was
d = 30 mm. Both gap-graded soils and continuous-graded soils were used in the experiments. (see
Figure 6).
The definition of gap-graded soils varies in different studies. However, among them, most gap-graded soils have irregular shapes. For instance, a horizontal part of the curve could be graded from 0.02 mm to 2 mm. Otherwise the soils are defined as continuous-graded.
For the runs that lacked complete curves (e.g., Runs 2 and 7), we assume that the diameter of particles in the missing part is the same size as the finest soil particles shown in curves, so that we can perform simulations for these runs.
3.2. Simulation Domain and Boundary Settings
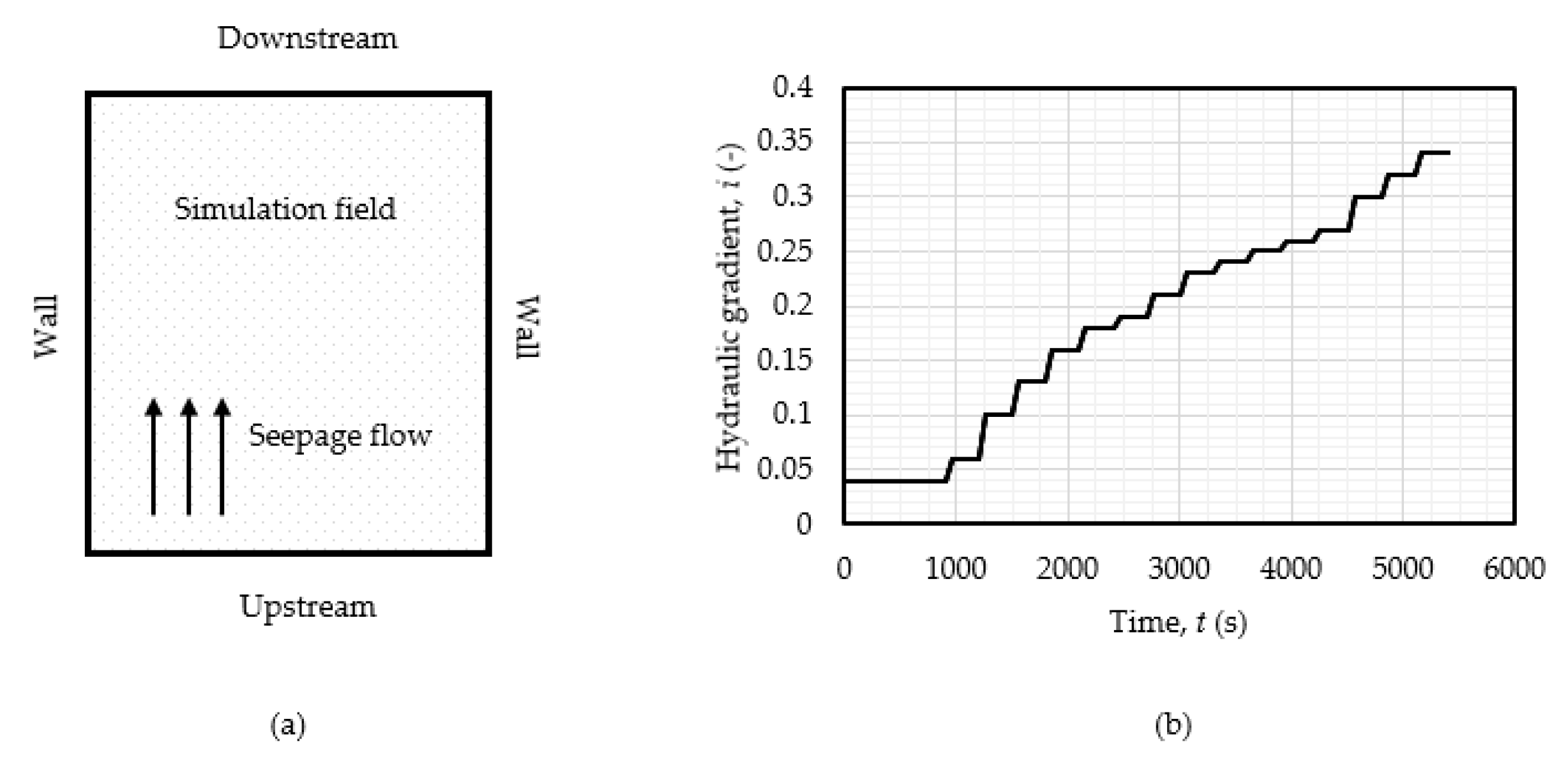
The simulation domain is proposed considering the circular symmetry of the seepage field, and assuming a two-dimensional flow at the vertical cross-section plane. As shown in
Figure 7a, the domain covers a rectangle cross-sectional area. The size of the area is corresponding to the actual size of experimental device. Therefore, for the runs in Skempton and Brogan [
9] the height of the domain is set as 155 mm and the width is set as 139 mm; and for the runs in Wan and Fell [
1] the height is set as 300 mm and the width is set as 300 mm. The inlet boundary is imposed with a stable, consistent water head at each stage of hydraulic gradient. Taking Run B in Skempton and Brogan [
9] as an example, the loading history is shown in
Figure 7b.
In 2017, Rochim et al. [
32] noted that the loading history might affect the experimental results of critical hydraulic gradient as well as the eroded mass. They found that if they set a longer duration time under a specific hydraulic gradient, they would record a lower critical hydraulic gradient and more eroded mass.
Such a phenomenon can be explained: when the duration time is not long enough under a specific hydraulic gradient, the erosion process may not reach a steady/stable status, which will lead to the unreliable judgment of critical hydraulic gradient.
To eliminate the effect of different loading histories, in our simulation, a long enough duration time and corresponding stable results are used to validate our model.
3.3. Parameter Calibration
During the simulation, the pure water density ρw is set as 1000 kg/m3, and the viscosity coefficient μw is set as 10−6 Pa·s. Besides GSD, other initial conditions of the soils (including initial porosity n0, initial permeability coefficient ks0, and density of soil particles ρs) are also reproduced according to the experimental records.
There are two ways to obtain the initial porosity n0 of the soil: (1) directly from the experimental records, and (2) by calculating n0 = 1 − Vs0/V, where Vs0 denotes the initial soil volume and V denotes the initial volume of seepage field.
Parameters need to be calibrated include
α in Equation (5),
b in Equation (7),
A and
B in Equation (8), and Γ in Equation (10). The calibrated parameters are presented in
Table 1. These parameters are calibrated using a part of experimental data, i.e., Runs A and B from Skempton and Brogan [
9] (for non-cohesive soils) and Runs 2 and 3 from Wan and Fell [
1] (for cohesive cases).
Based on these runs,
A,
B,
b and
α are calibrated by trial and error.
A0 = 0.021,
B0 = 0.015, and
b0 = 0.067, as suggested by Wilcock and Crowe [
33] are used as initial values for
A,
B, and
b, and
α0 = 0.0000021, as suggested by Fujisawa et al. [
15], is used as the initial value of
α.
It should be noted again that Wan and Fell [
1] did not record the amount of soil erosion, and
α ranges from 0.0001 to 0.01 would not affect the calculation results in
Section 3.4.1. However, Skempton and Brogan [
9] did record the amount of soil erosion during the experiment, the model can reasonably reproduce the
q-i relationship as well as the eroded mass when
α = 0.005 is subtracted. Therefore,
α is fixed as 0.005 in our model. Value of Γ is calculated based on Equation (14):
3.4. Calibration Results
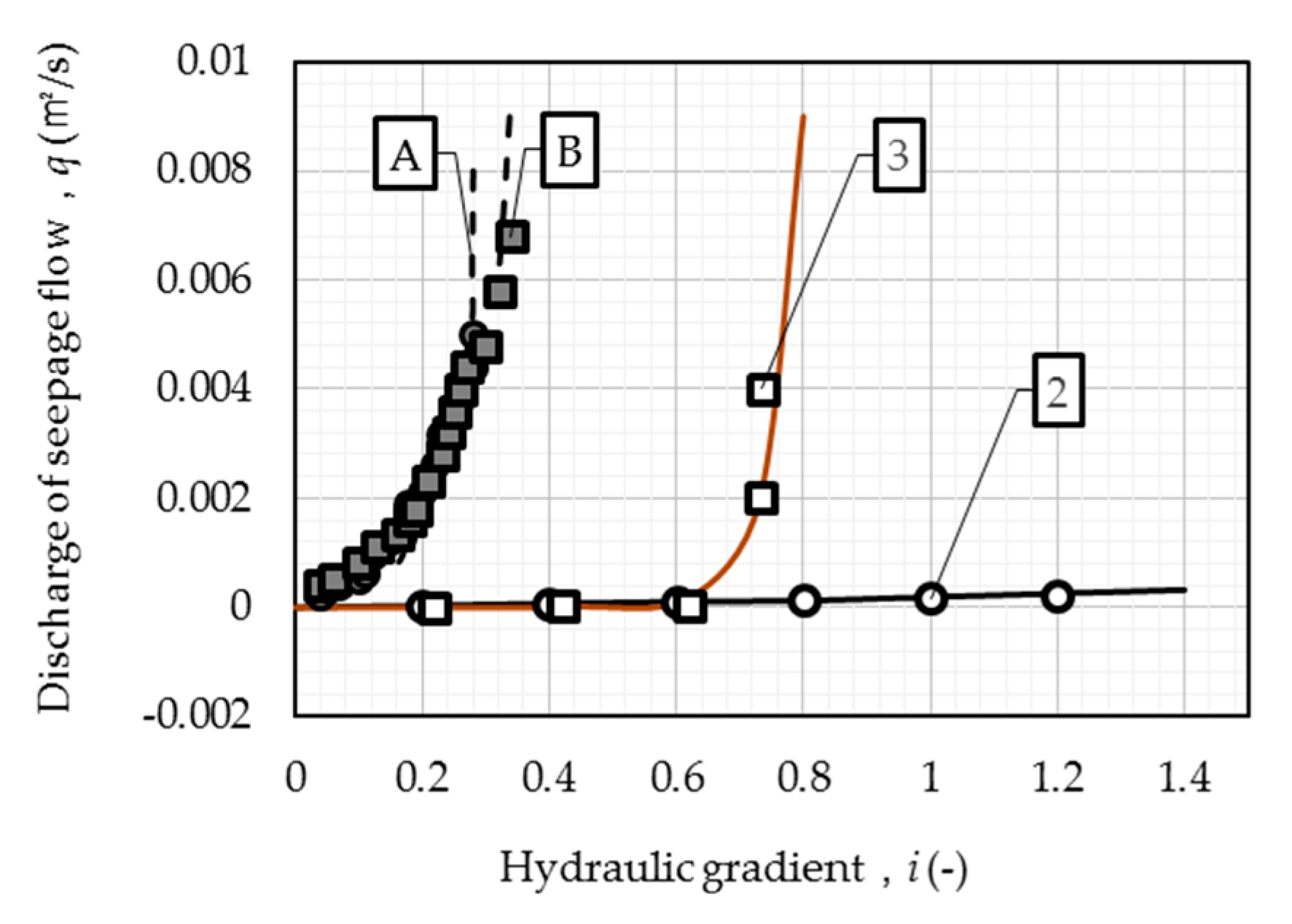
3.4.1. q-i Relationship
It shows that the computed q-i relationships agrees well with measured ones. It should be noted that ±10% change of these parameters will not affect the calibration results.
3.4.2. Eroded Mass
The computed eroded mass in Run A (duration time, 80 min; last hydraulic gradient,
i = 0.28) and Run B (duration time, 90 min; last hydraulic gradient,
i = 0.34) in Skempton and Brogan [
9] are 220.40 g and 77.16 g, which are close to the measured mass 225 g and 75 g, with relative errors less than 3%.
3.5. Model Verification
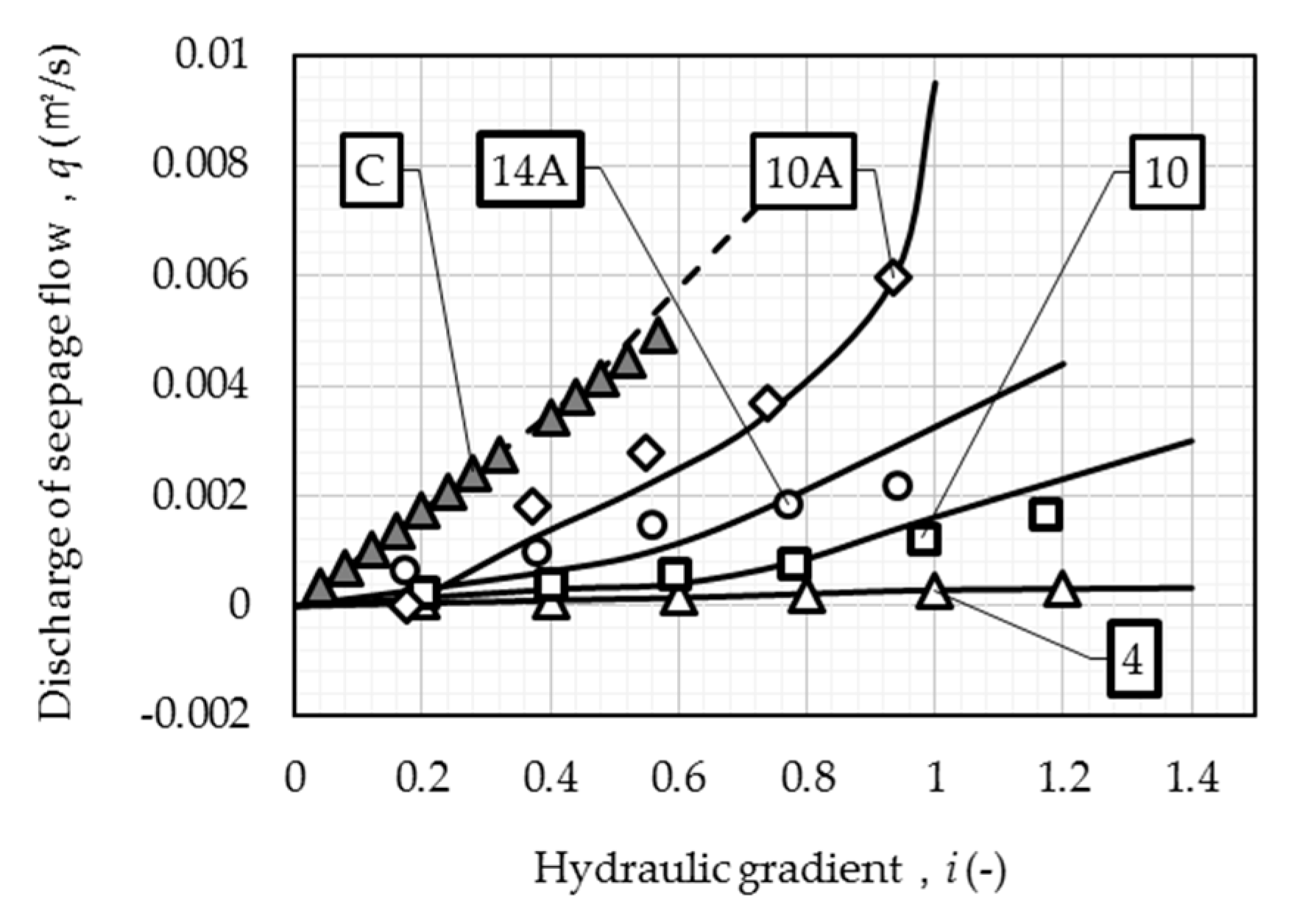
3.5.1. q-i Relationship in Other Runs
Using the calibrated parameters, we conducted the simulation with the data from other runs, the results of representative runs are shown in
Figure 9.
The internally unstable runs (e.g., Runs A and B) and internally stable runs (e.g., Run C) in Skempton and Brogan [
9] show obvious difference in shape of
q-
i curves. For example, when
i = 0.28 and 0.34, curves of Runs A and B show a sudden rise, respectively, whereas the curve of Run C shows a stable trend all over the experiment. The explanation is as follows: for Runs A and B, as particles are massively eroded by the seepage flow under a specific hydraulic gradient
i, the porosity
n and the hydraulic conductivity
ks increases, as well as the discharge
q; while for Run C, less soil particles are eroded under such a hydraulic gradient which triggers massive suffusion in Runs A and B, or an even higher hydraulic gradient. The simulation result of the data by Wan and Fell [
1] show a similar phenomenon.
3.5.2. Eroded Mass for Run C in Skempton and Brogan
The computed eroded mass for Run C in Skempton and Brogan [
9] is 57.4 g, close to the measurement of 55 g. The relative error is less than 5%.
3.6. Determination of Critical Hydraulic Gradient
When
i reaches critical hydraulic gradient
ic, it can be inferred that the soil has undergone a sudden, irreversible, and largely destructive adjustment due to suffusion. Run 10 in Wan and Fell [
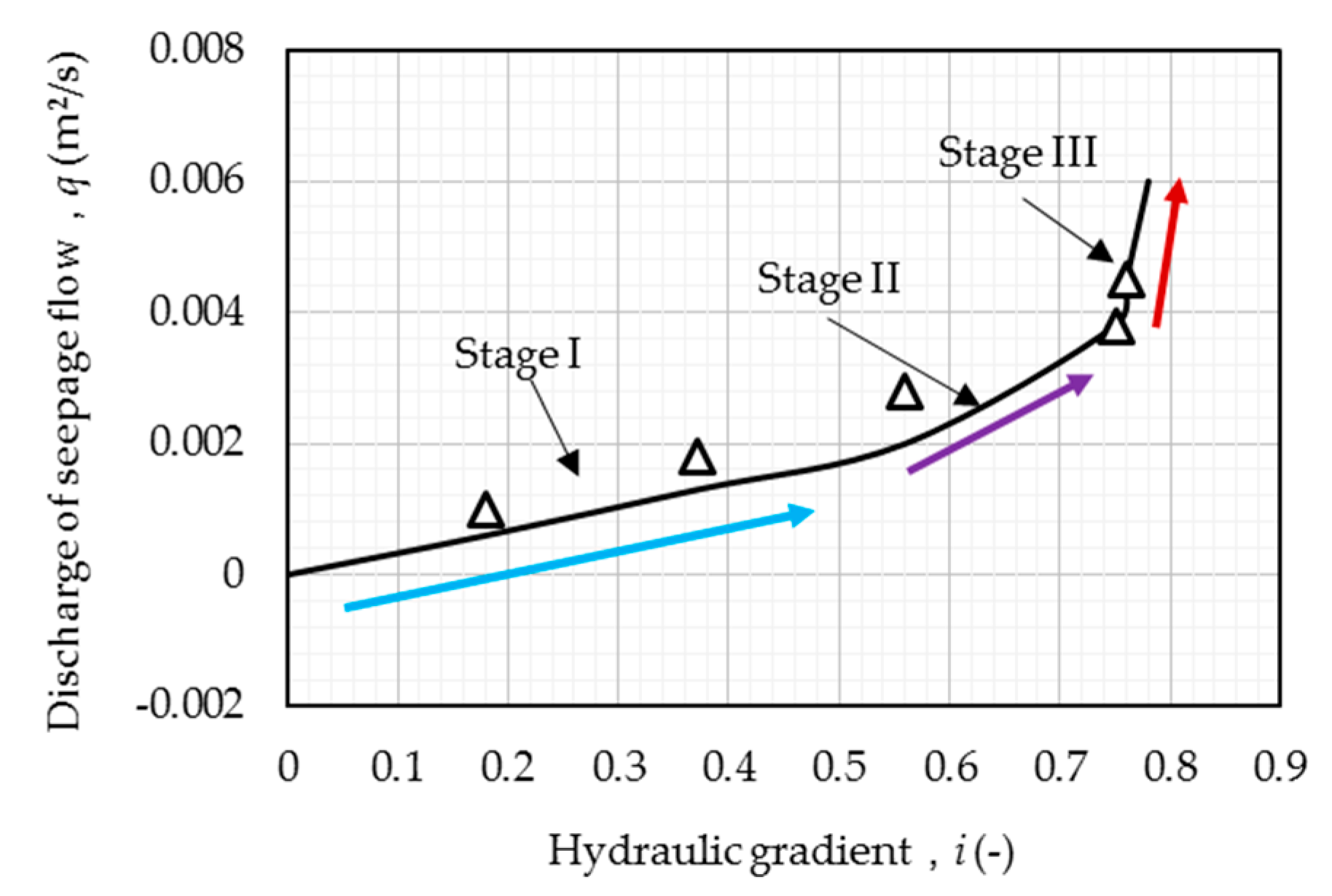
1] is used as an example to reveal the reason. In
Figure 10, the suffusion process can be divided into three different stages according to the different slopes of the
q-
i curve:
In stage I (i < 0.55), discharge of seepage flow q grows linearly with the hydraulic gradient i, during this stage the out flow is “clear” according to the corresponding experimental record; and in stage II (0.55 < i < 0.76), q grows in a nonlinear, but controlled, trend with i, during this stage the outflow is “cloudy” according to the corresponding experimental record; and in stage III (i > 0.76 = ic), one may notice an abrupt change of q-i curve, and this abrupt change may indicate the failure of soil fabrics.
When i < ic, the suffusion behavior has already taken place in the formation of losses of fine particles in limited scale, and such losses will not affect the stability of the whole soil fabrics. When i = ic or i > ic, more particles are lost until the failure of whole structure occurs.
Following the justification,
ic is evaluated by observing the boundary between stage II and stage III for all the runs in the three studies.
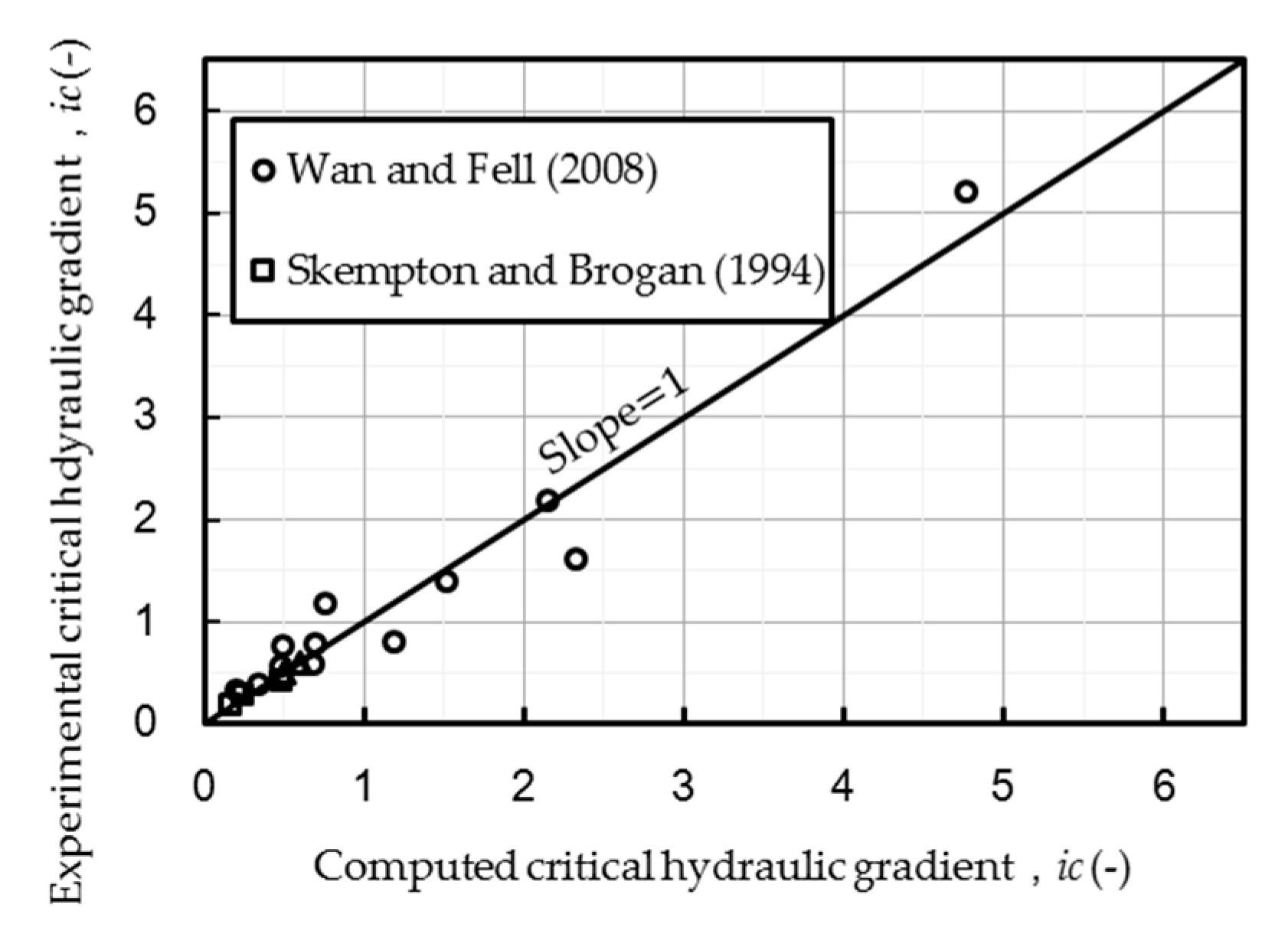
Figure 11 compares the computed critical gradients with the measured gradients. 18 of the total 21 runs are reproduced satisfactorily (relative error <10%). The three exceptions are Runs 5, 11, 13 in Wan and Fell [
1].
3.7. Porosity Distribution in Different Suffusion Stages
In this study, taking Run A in the study by Skempton and Brogan [
9] as an example in order to describe the suffusion process more directly and concretely, we present the spatial distribution of porosity corresponding to stage I, II, and III in 3.6 (see
Figure 12 and
Figure 13), respectively:
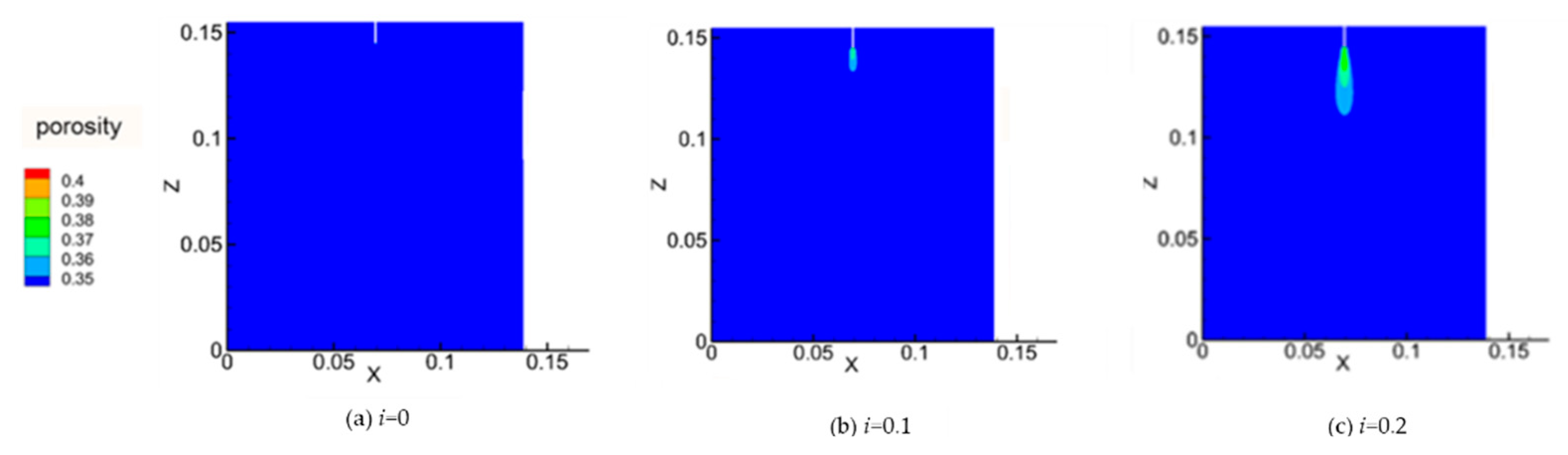
Figure 12a denotes the initial porosity distribution (corresponding to stage I),
Figure 12b,c denotes the porosity distribution when it reaches a stable one under hydraulic gradient
i = 0.1 and
i = 0.2 respectively (corresponding to stage II since
i <
ic = 0.28). When
i = 0.1, the high-porosity zone only appears limitedly in the local region near the outlet, which means that there is no significant erosion in the seepage field. When
i = 0.2, the high-porosity zone expands for a while, however, it is still limited to the local region near the outlet.
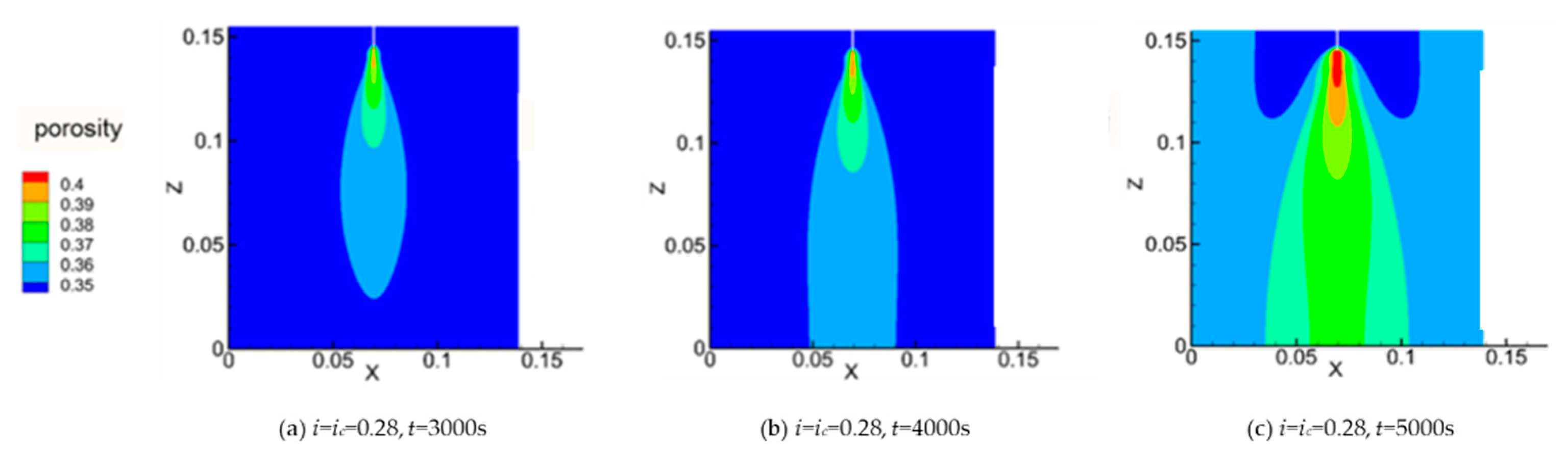
Figure 13a–c denotes porosity distribution when
i = ic = 0.28 (corresponding to stage III), during the loading time
t = 3000 s, 4000 s and 5000 s. The high-porosity zone grows so rapidly and intensely that it connects the upstream to the downstream. Such a phenomenon indicates an unsteady status under the massive suffusion behavior.
4. Predicting Internal Stability
In
Section 3, we describe the suffusion process numerically and evaluate the critical hydraulic gradient
ic, and in this section we attempt to give a further investigation in predicting internal stability.
4.1. Shear Stress Comparison Approach
Averagely, suffusion will be triggered when τ > τcr, where τcr denotes the critical shear stress of the finest soil particles (particle size dr) remaining in soil fabrics. According to Equation (7), τcr = min(τck) as it has been already known that dr = min(dk), and it will increase when suffusion proceeds. Meanwhile, as the particles are continuously eroded out of the seepage field, the porosity ρ and hydraulic conductivity ks of the soils become higher, and based on Equation (10), τ will also increase. When i = ic, τ will keep exceeding τcr as the suffusion continues. The suffusion will develop inevitably until the whole fabrics are destroyed.
For each of the soils, there must exist a hydraulic gradient ik < ic, when i = ik, if the loading time is long enough, and all the particles with sizes d < dk will be eroded out of the soil fabrics. Under this assumed situation, dr = dk, and τcr = τck. At the moment, the volume of the soils Vs will be decreased by k% (ρs is a constant), and the porosity of the soil will be n = n0 + (1 − n0)k%.
Therefore, when n = n0 + (1 − n0)k% is given, τcr = τck; where τck is determined by Equations (7) and (8). Since then, a quantitative τcr-n relationship can be computed. A τ-n relationship can also be obtained through Equation (6).
Here, an approach to predict S (stable) and U (unstable) based on the comparison of the relationship between τcr-n and τ-n is illustrated: when i is given, by comparing the relative locations of the τcr-n curve and the τ-n curve in the same coordinate system, we can judge whether suffusion starts, stops or proceeds irreversibly.
4.2. Evaluation Results
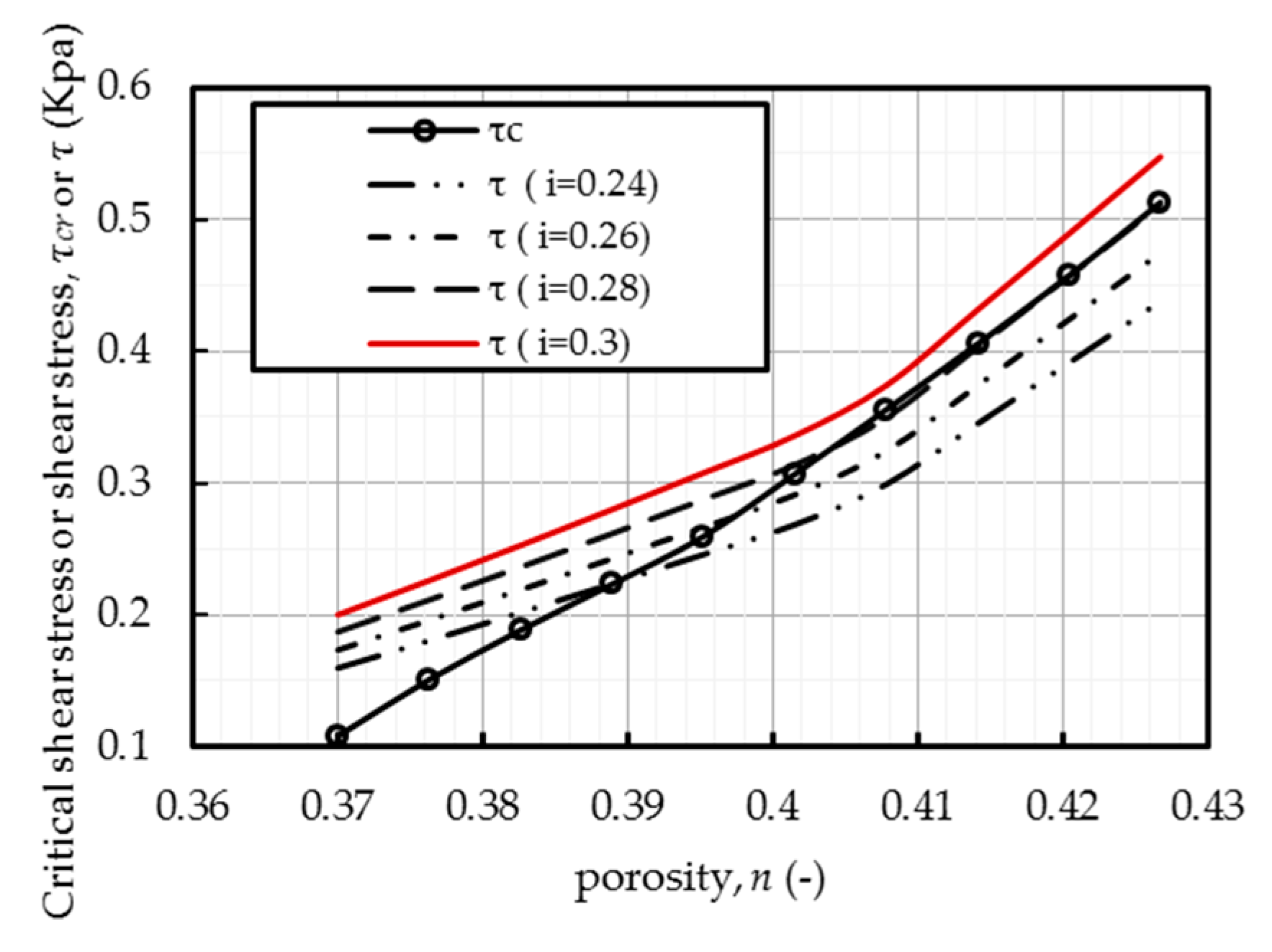
Taking Run A in Skempton and Brogan [
9] as an example (see
Figure 14), under the hydraulic gradient
i = 0.28, when
n < 0.405,
τ > τc, which means suffusion is triggered and developed; when
n > 0.405, the
τ-
n curve almost coincides with the
τc-
n curve, which means that the suffusion process is irreversible. When
i = 0.30, the
τ-
n curve is always above the
τc-
n curve and there is no intersection between the two curves. This indicates that under this hydraulic gradient, the suffusion process of the soil is still irreversible.
According to the results shown in
Figure 14, the critical hydraulic gradient is
ic = 0.28, which is in accordance to the experimental data of Skempton and Brogan [
9], and since
ic < 0.7, according to the study by Hillel [
34], the internal stability of soils in this run is
U. It should be noted that
α does not involve with the analysis process, which indicates that it does not affect the results of internal stability prediction.
To verify the approach, experimental data from Lau [
36], Lafleur et al. [
8], and Chapuis et al. [
10] are also studied. The GSD curves are presented in
Appendix B. This approach is able to distinguish the internal stability of 30 runs out of 36, indicating 83.33% of accuracy, while the most accepted traditional GSD-based approach based on the study by Wan and Fell [
1] is 75%.
5. Conclusions
In this study, a new numerical model taking combined effects of GSD and porosity into account is developed to describe the suffusion process. The theory by Wilcock and Crowe [
33] in field of sediment transportation is adopted to quantitively describe the inception and transport of finer soil particles. During the simulation, all of the related parameters are calibrated in a solid way. The numerical results showed satisfactory performance when validating with the experimental data of Skempton and Brogan [
9] and Wan and Fell [
1].
The model can reproduce the q-i relationships of experiments as well as critical hydraulic gradients ic of runs, and describe the suffusion process by showing porosity spatial distribution at different stages.
Inspired by the modeling work, an approach to predicting internal stability is also proposed. Disclosing the relationships among the factors, we found that the soils with specific GSD and porosity are prone to induce the suffusion. The model demonstrates better performance in the judgments of the internal stability (83.33% of correctness) of 36 experimental runs. The accuracy is higher than most of traditional GSD-based approaches. The results provide useful guidelines in macroscopic engineering practice.