Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application
Abstract
1. Introduction
2. Data and Methods
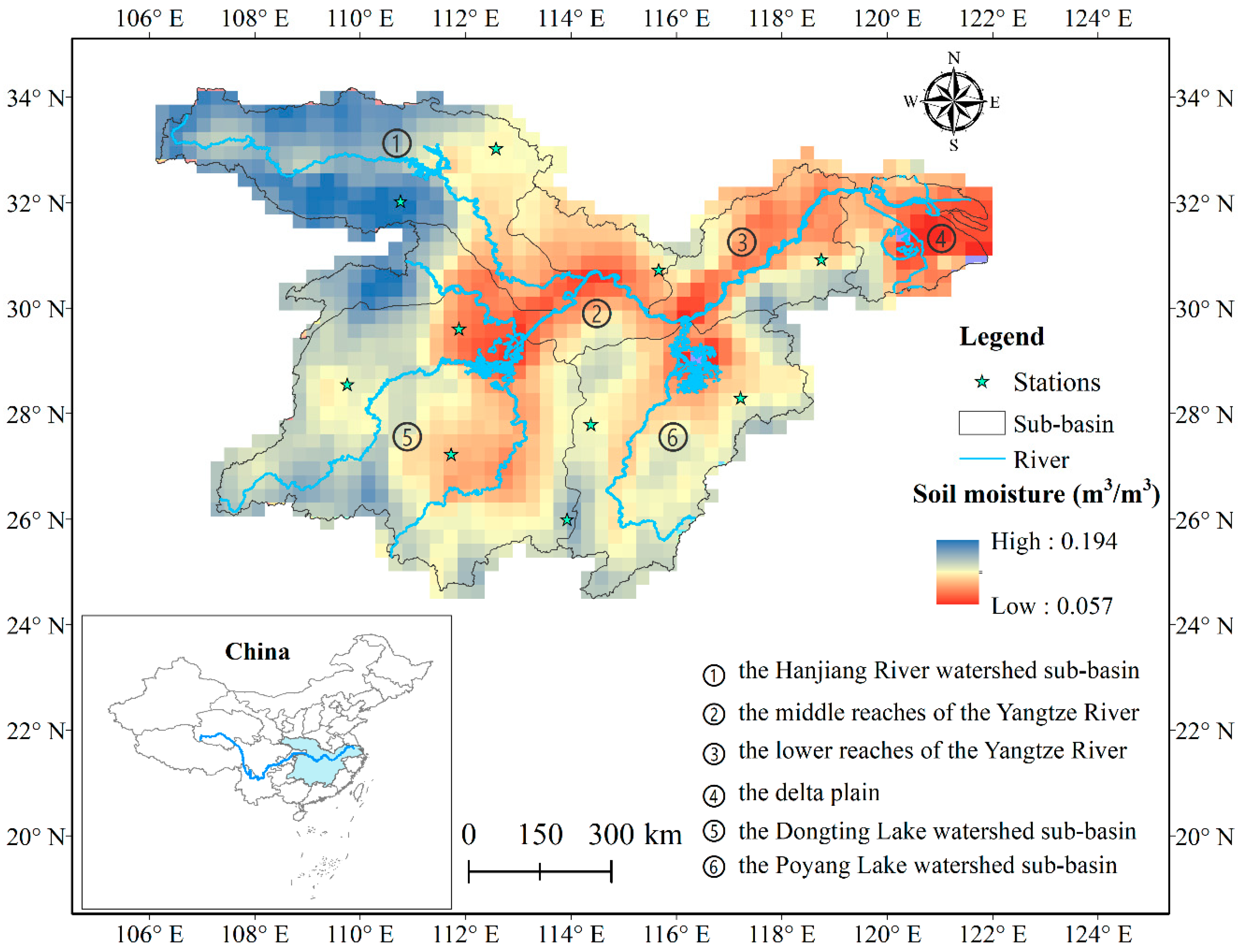
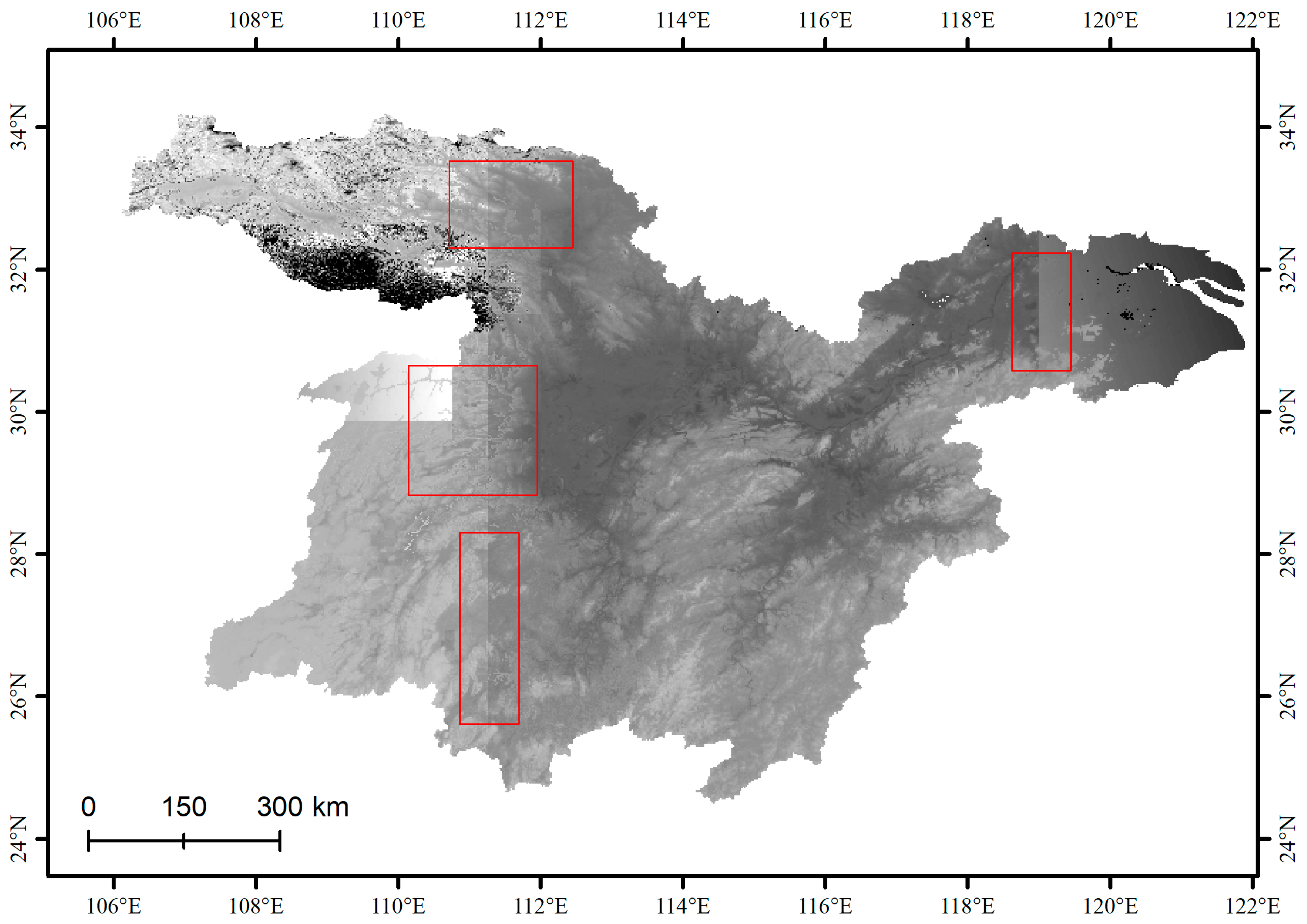
2.1. Study Area
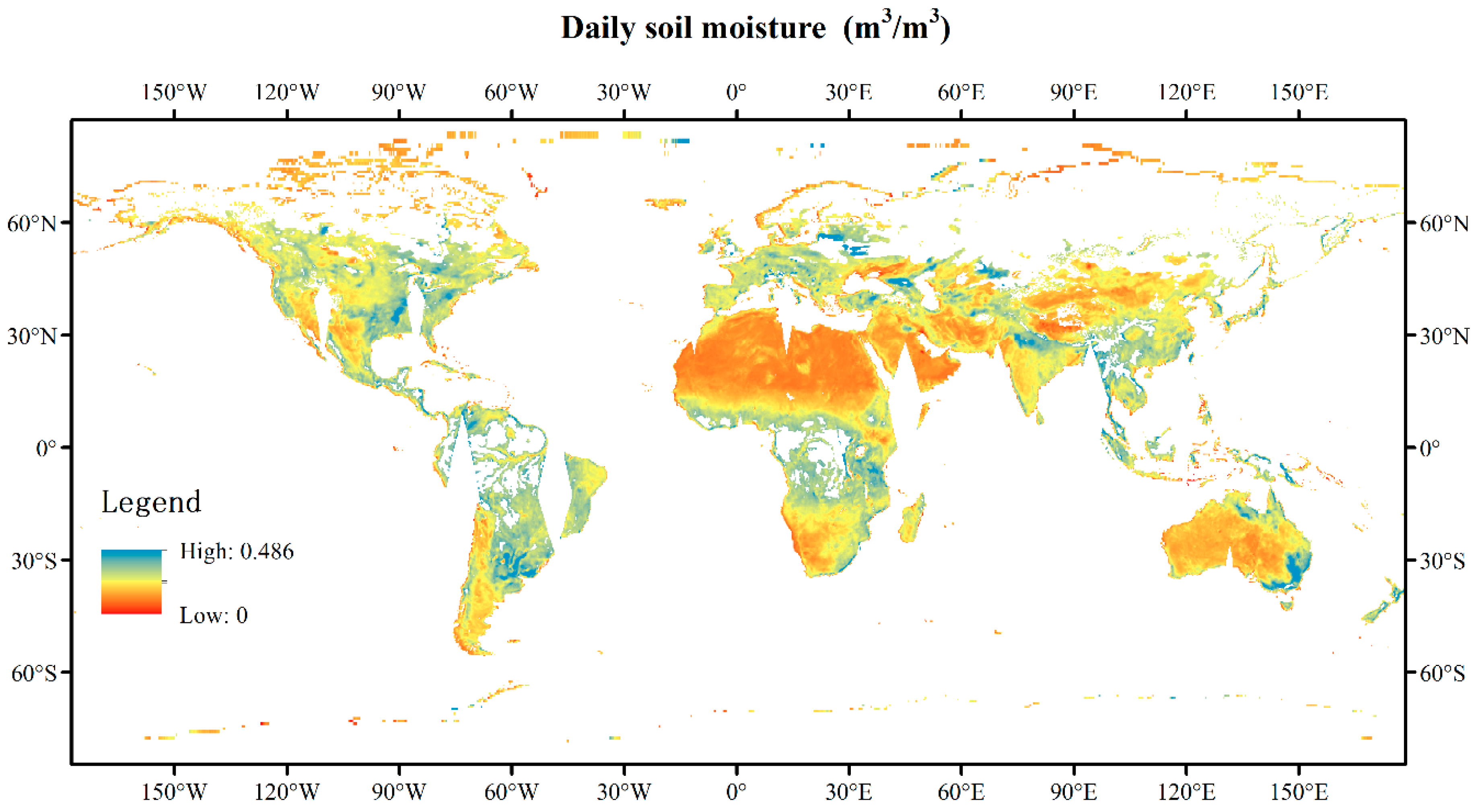
2.2. Data
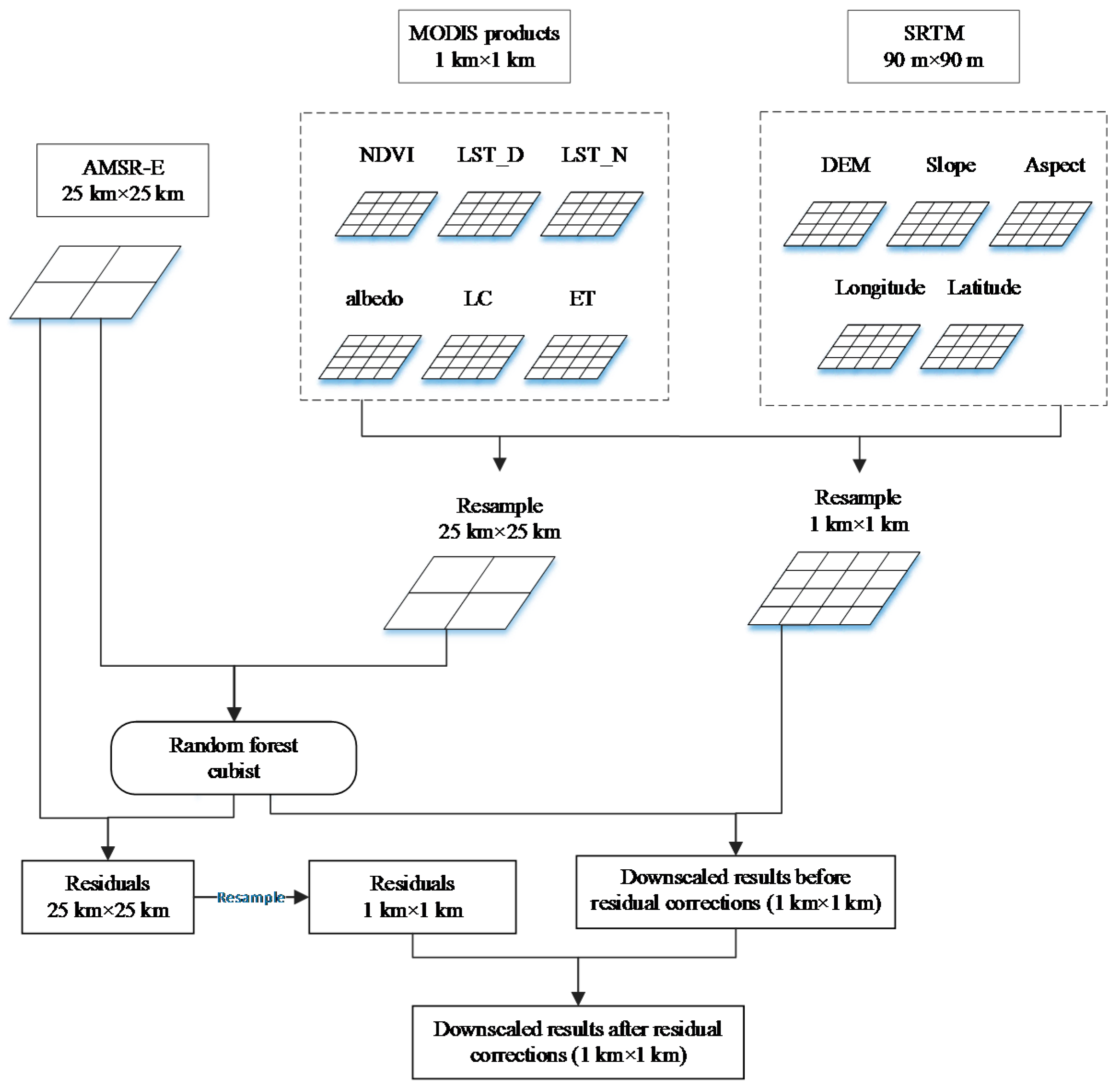
2.3. Methodology
3. Results and Discussion
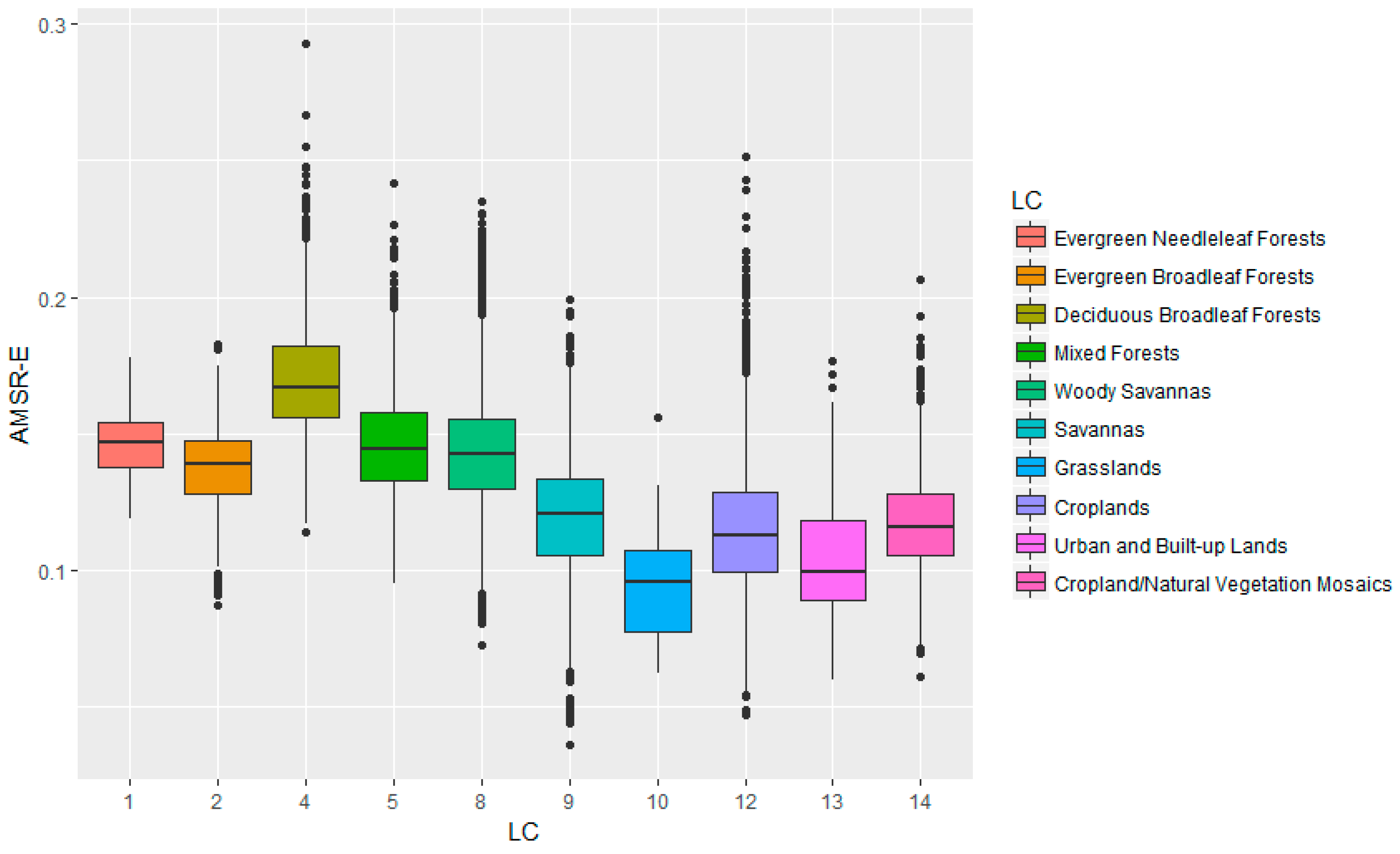
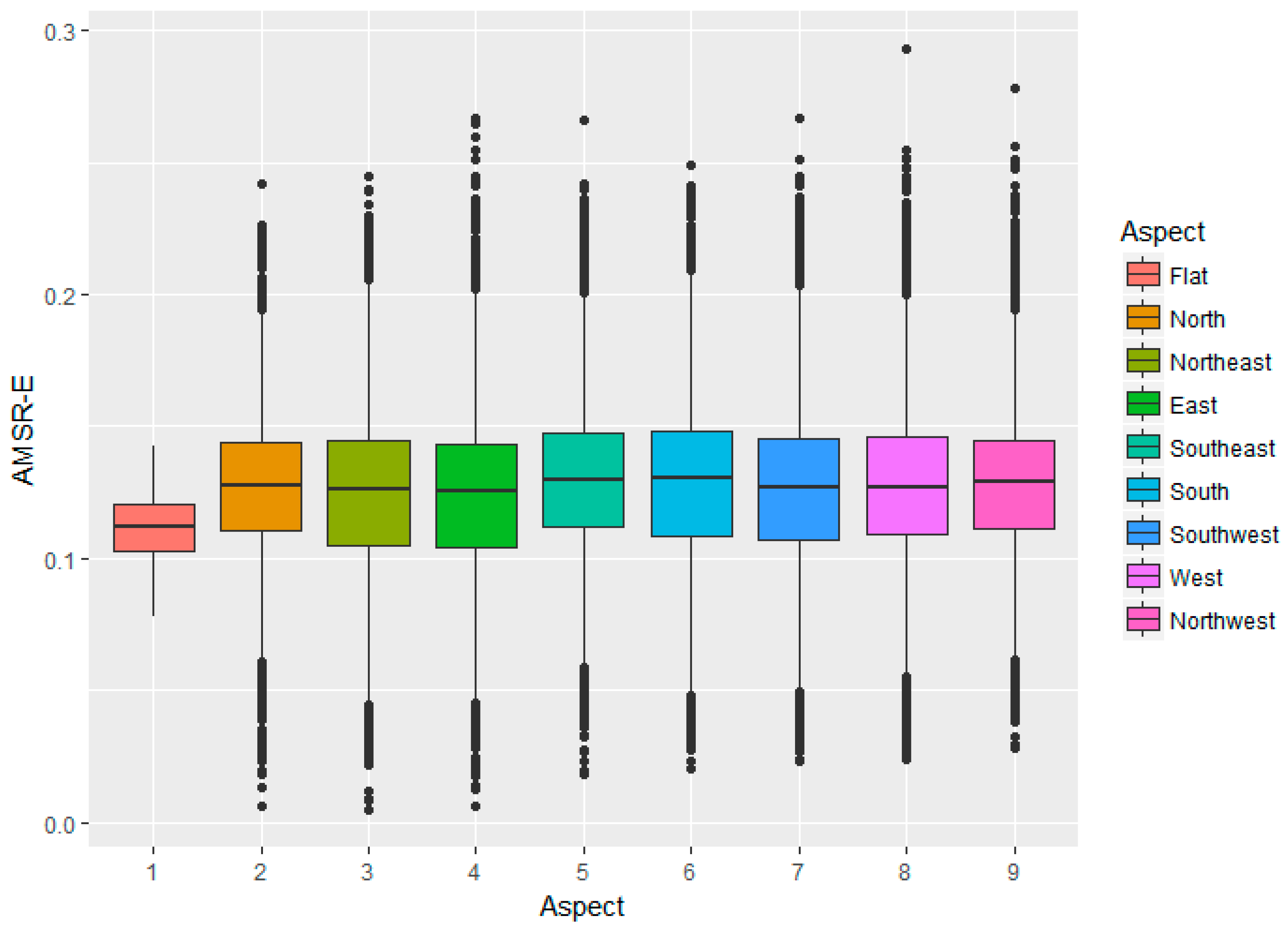
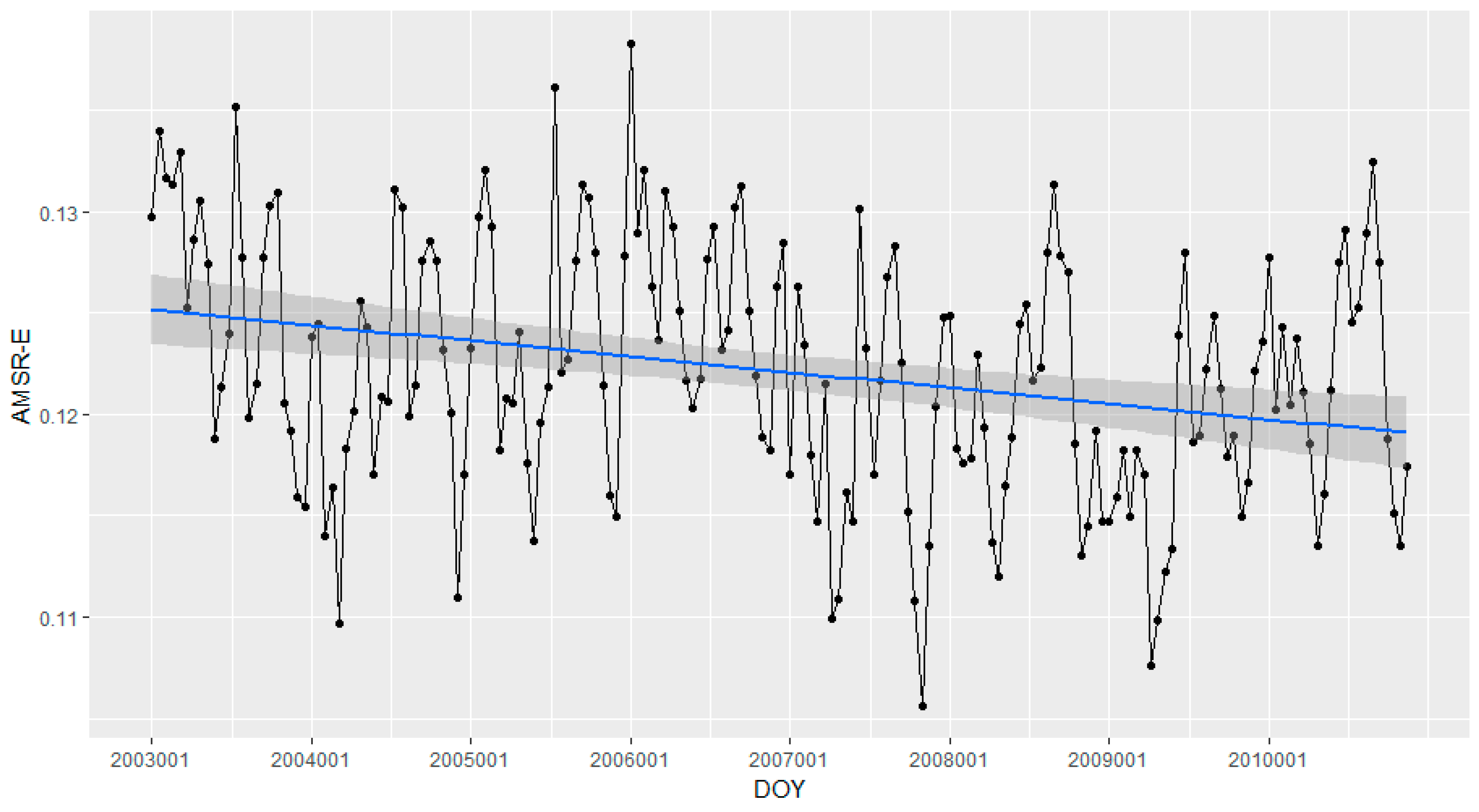
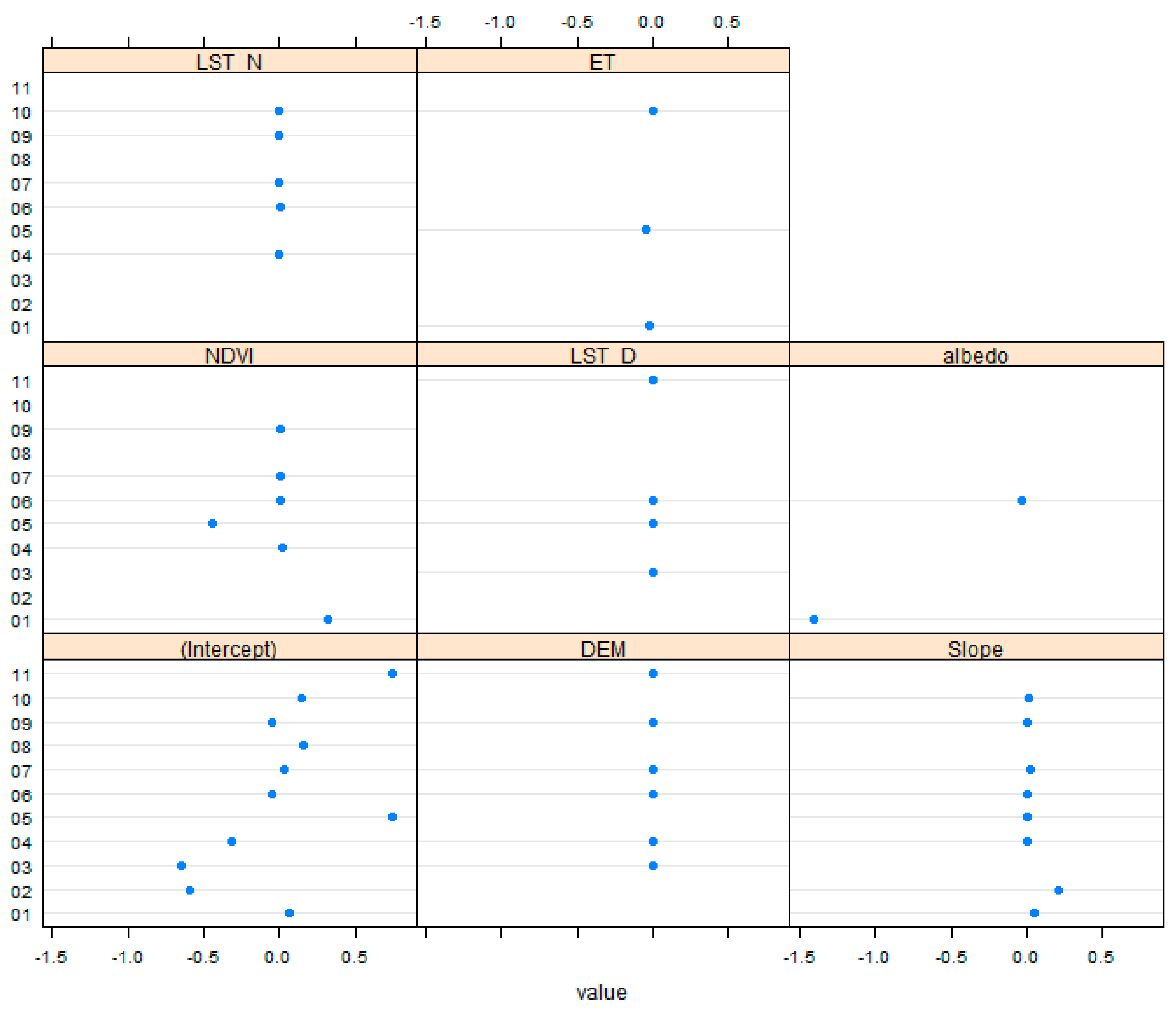
3.1. Relationship between Soil Moisture and Environmental Variables
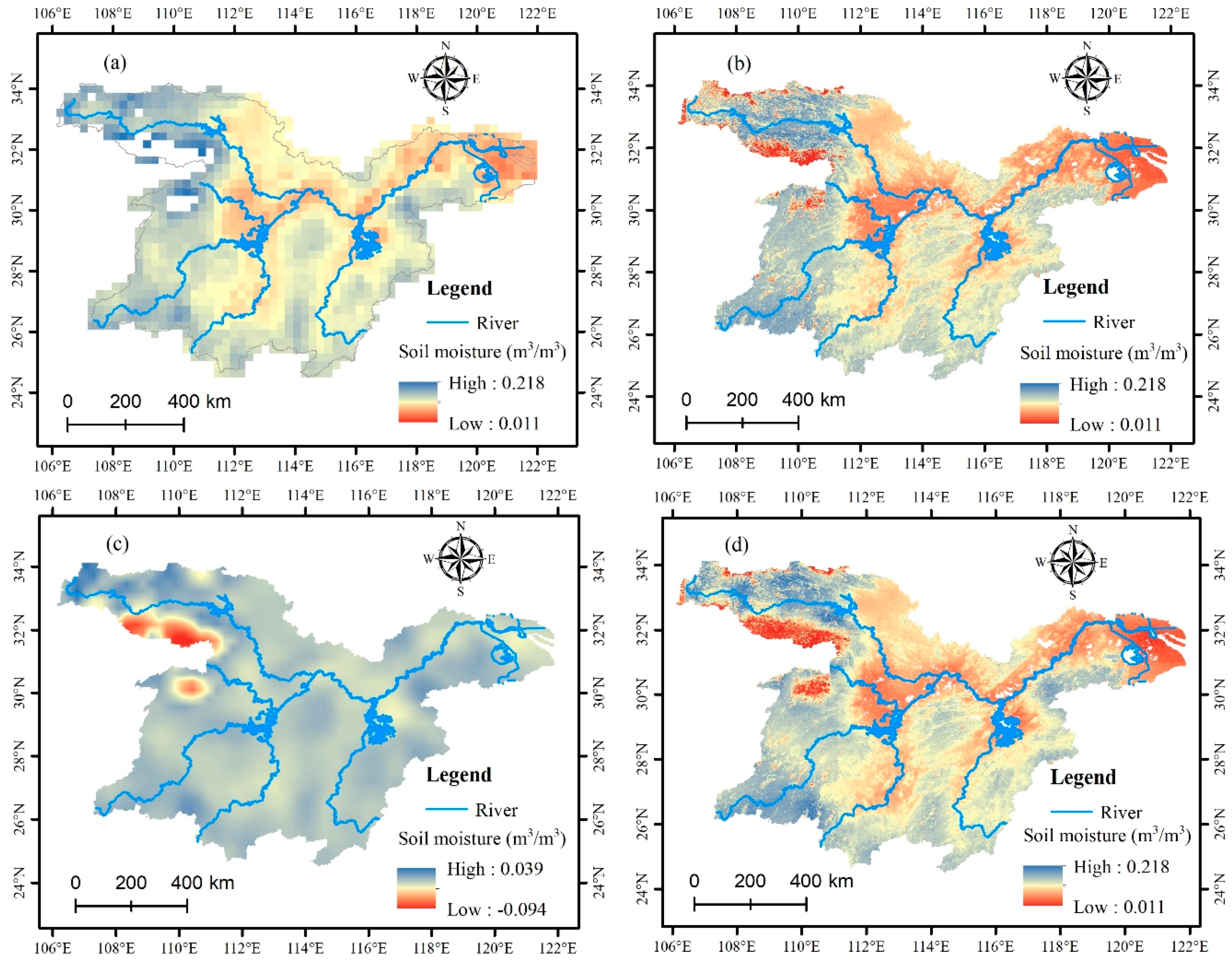
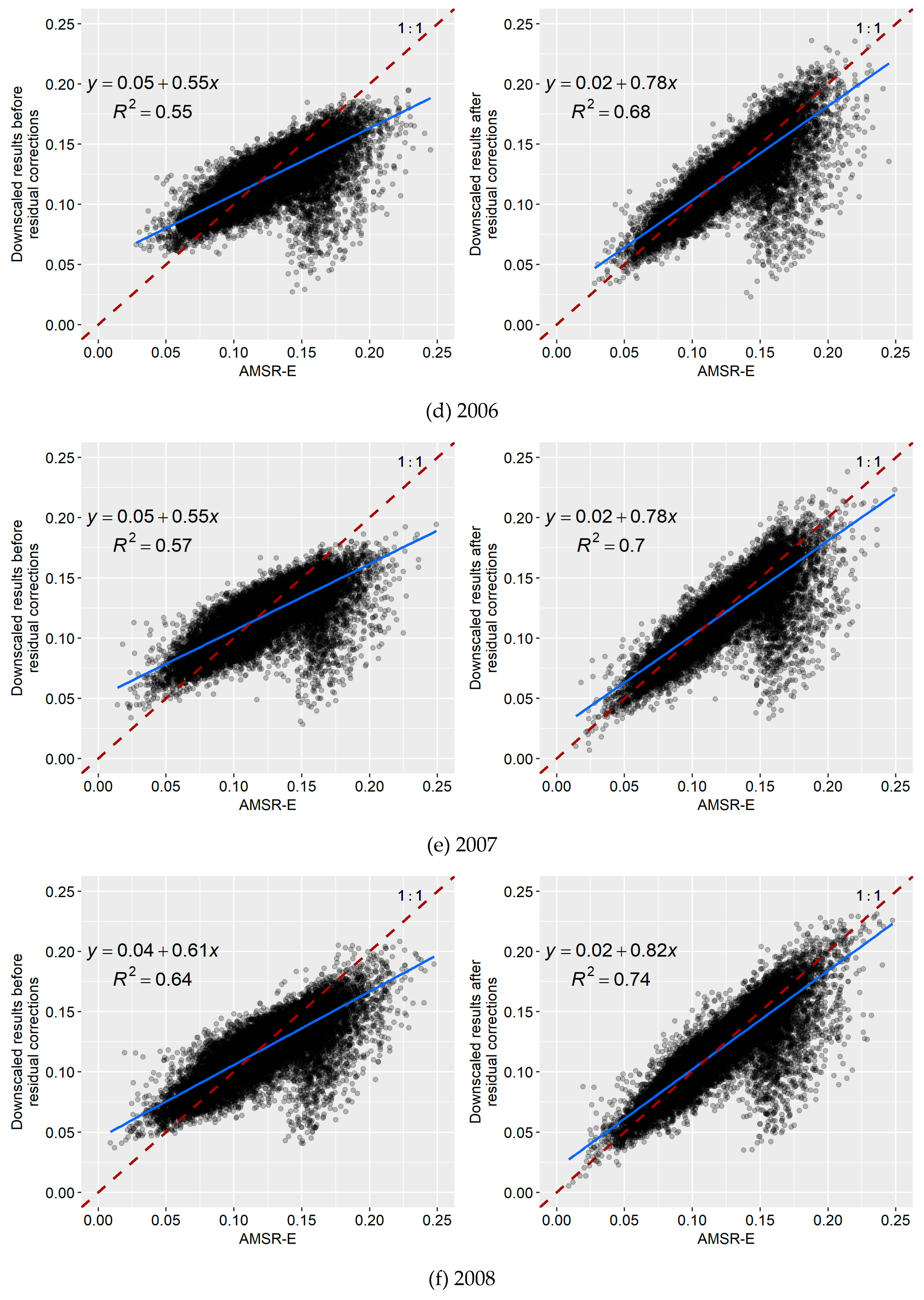
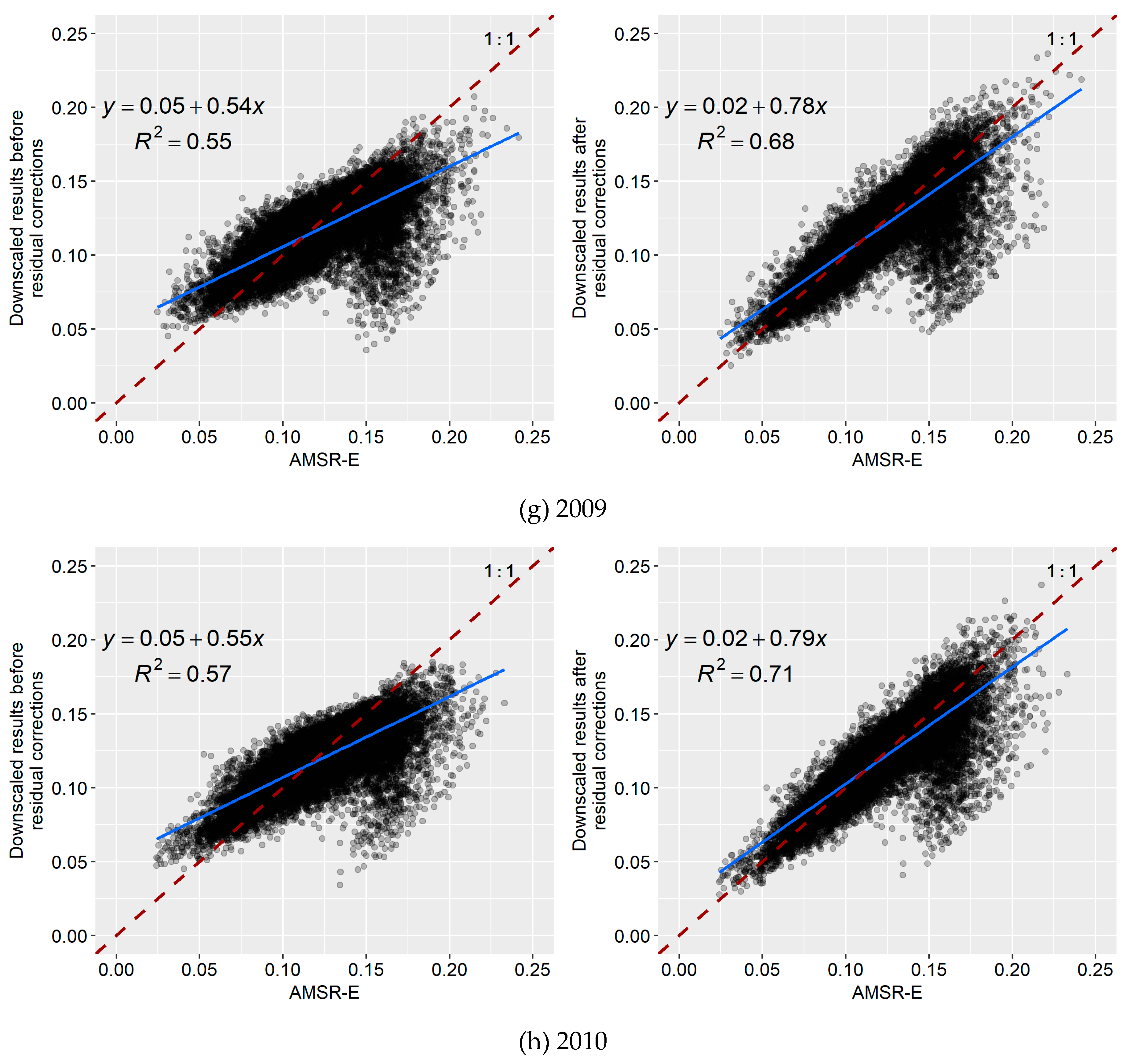
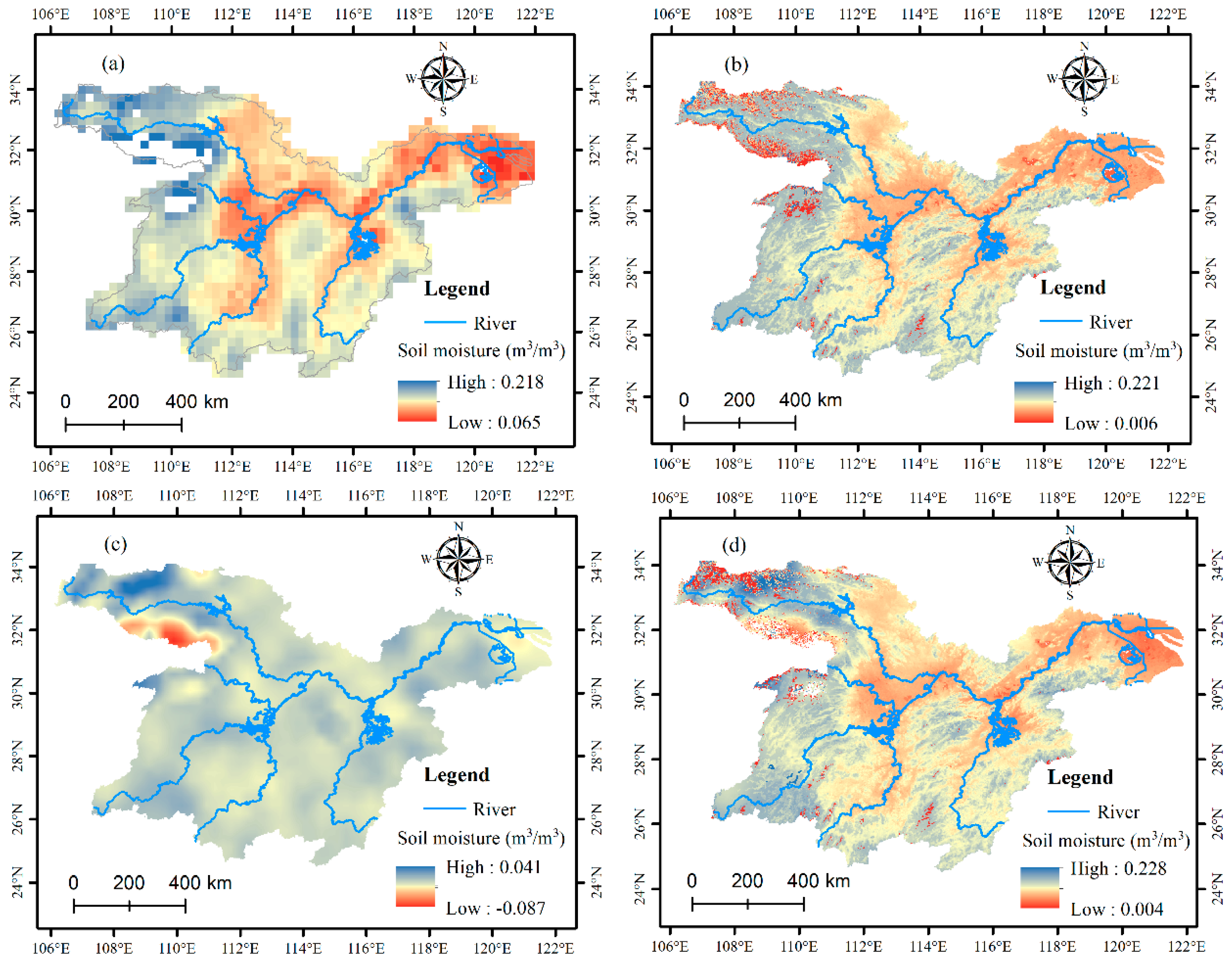
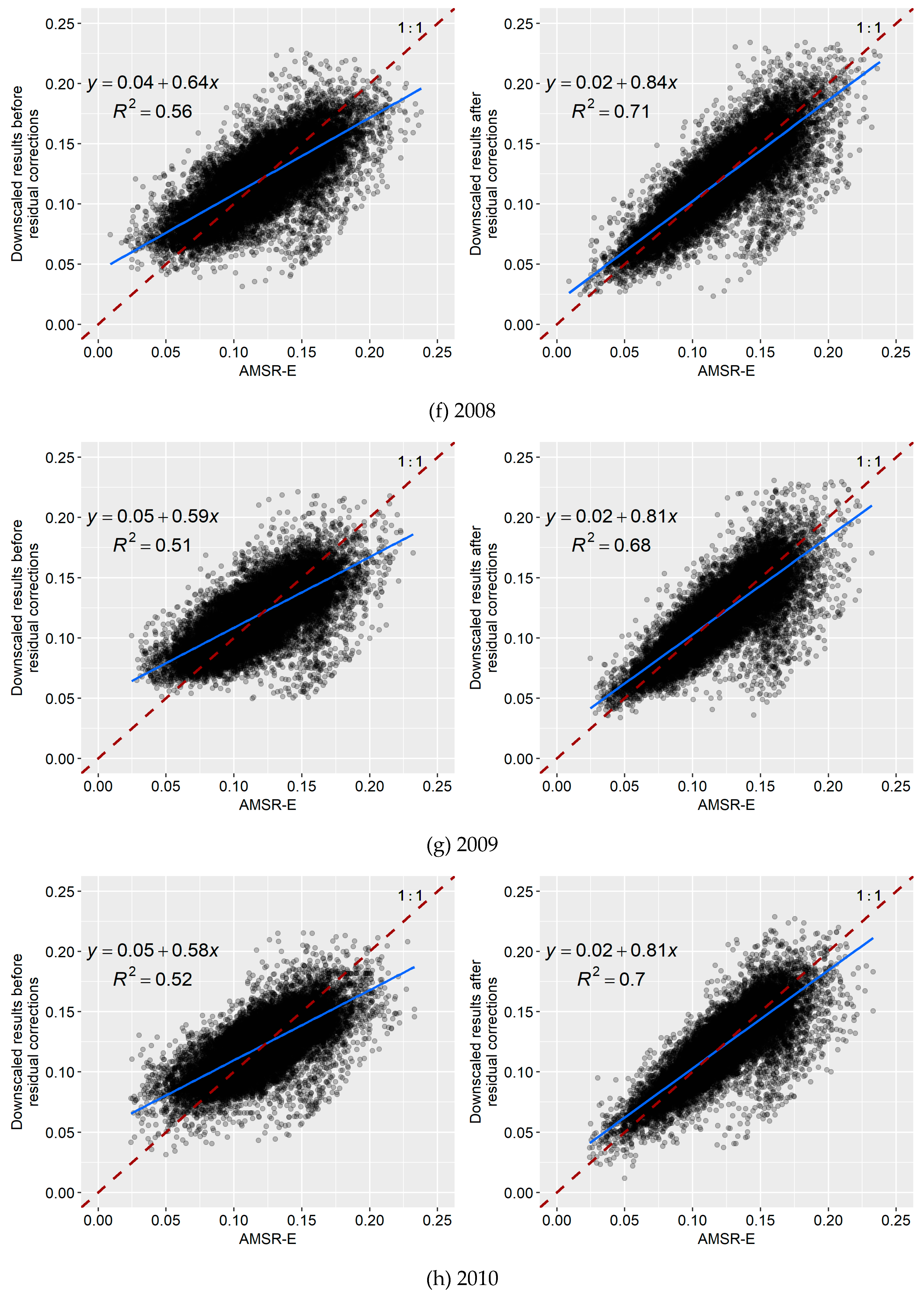
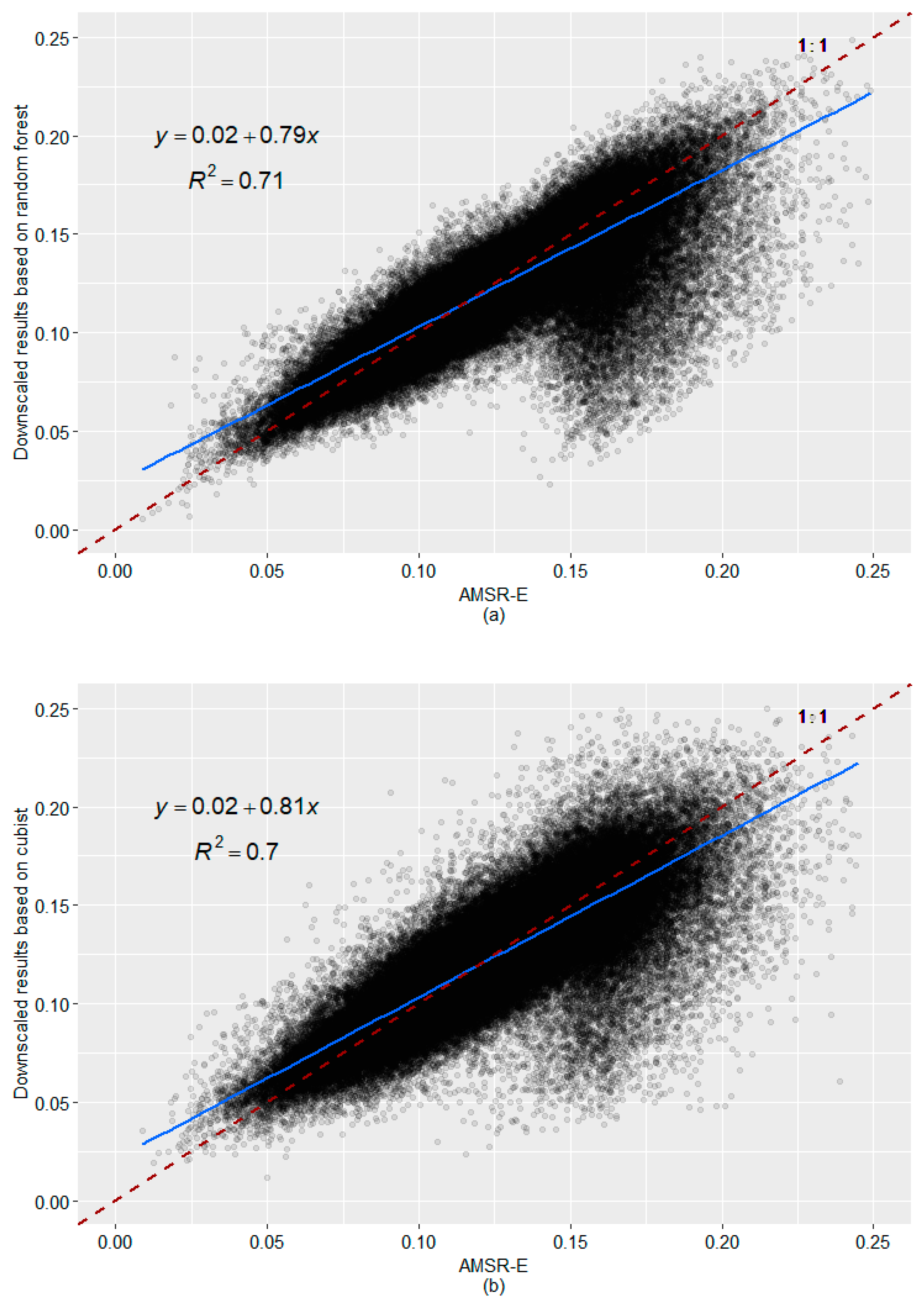
3.2. Downscaling Results Based on the Random Forest Algorithm
3.3. Downscaling Results Based on the Cubist Model
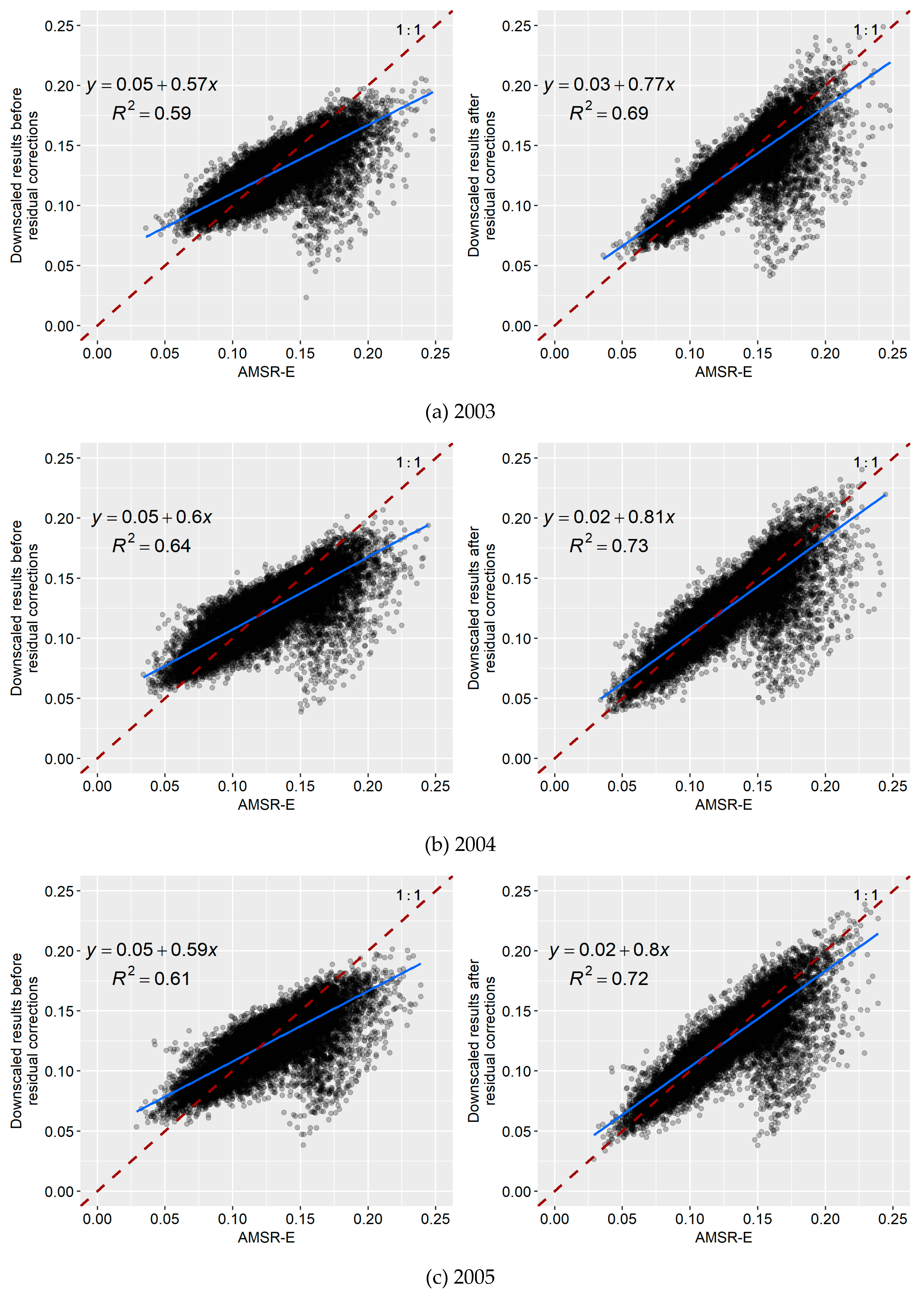
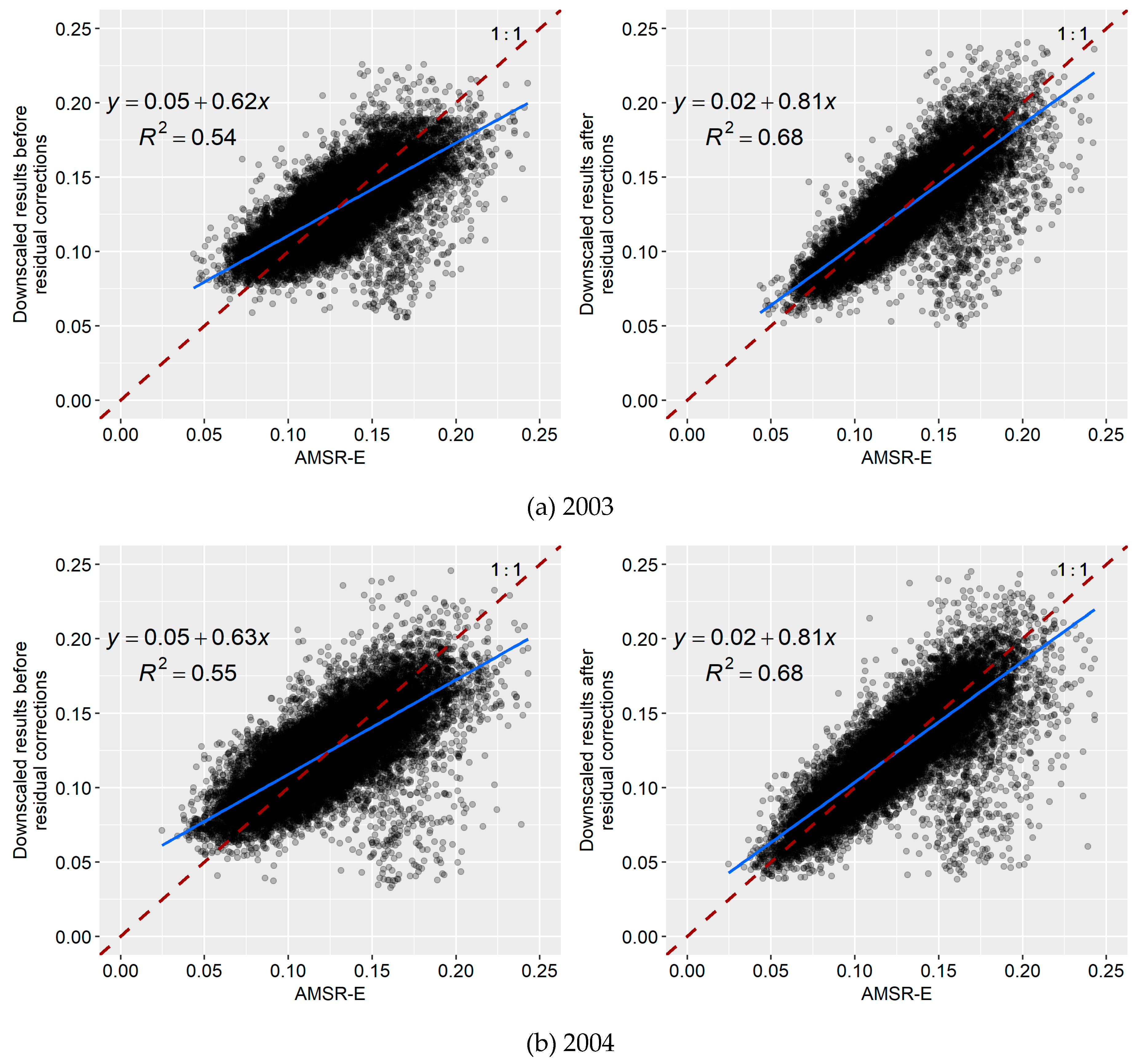
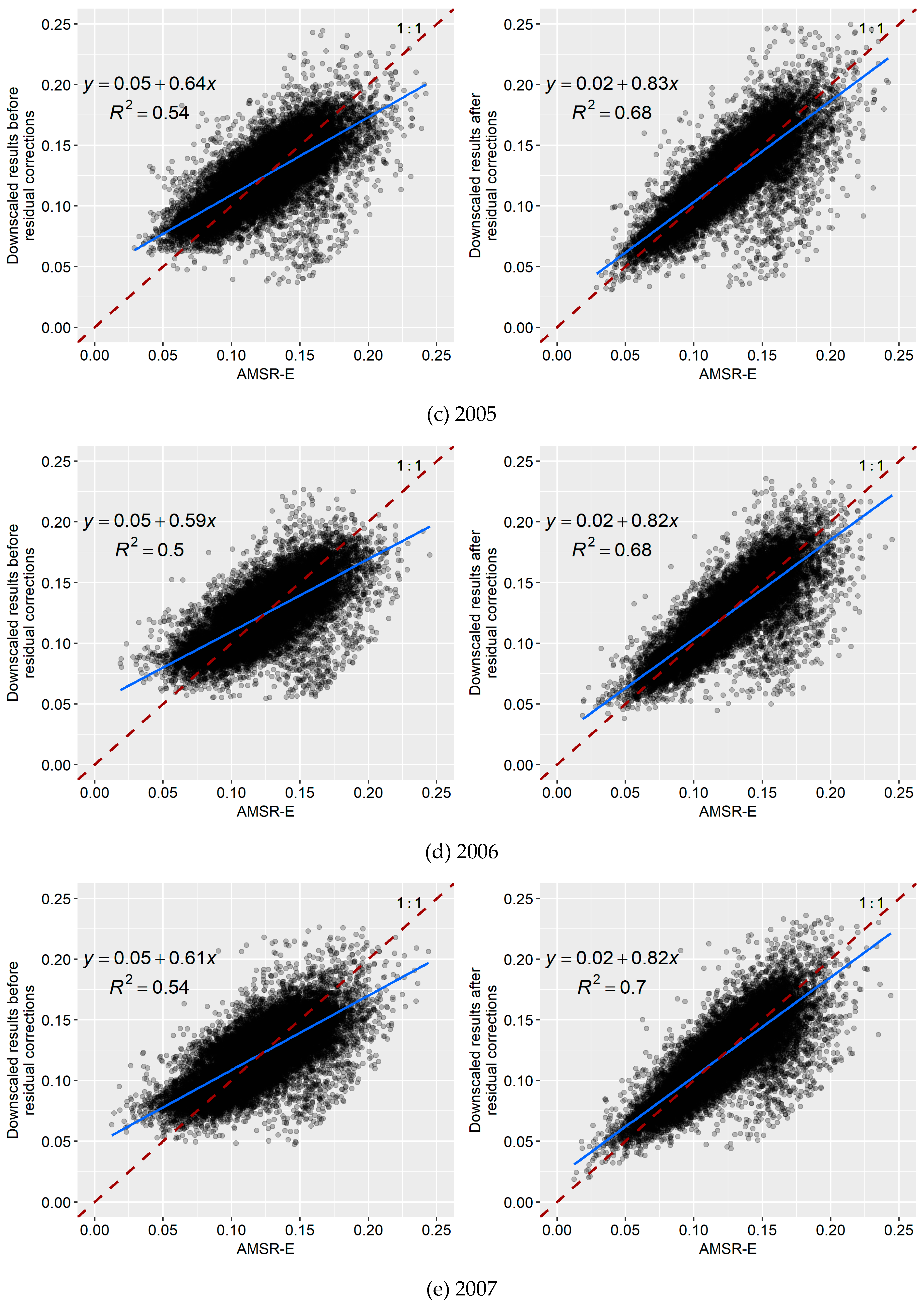
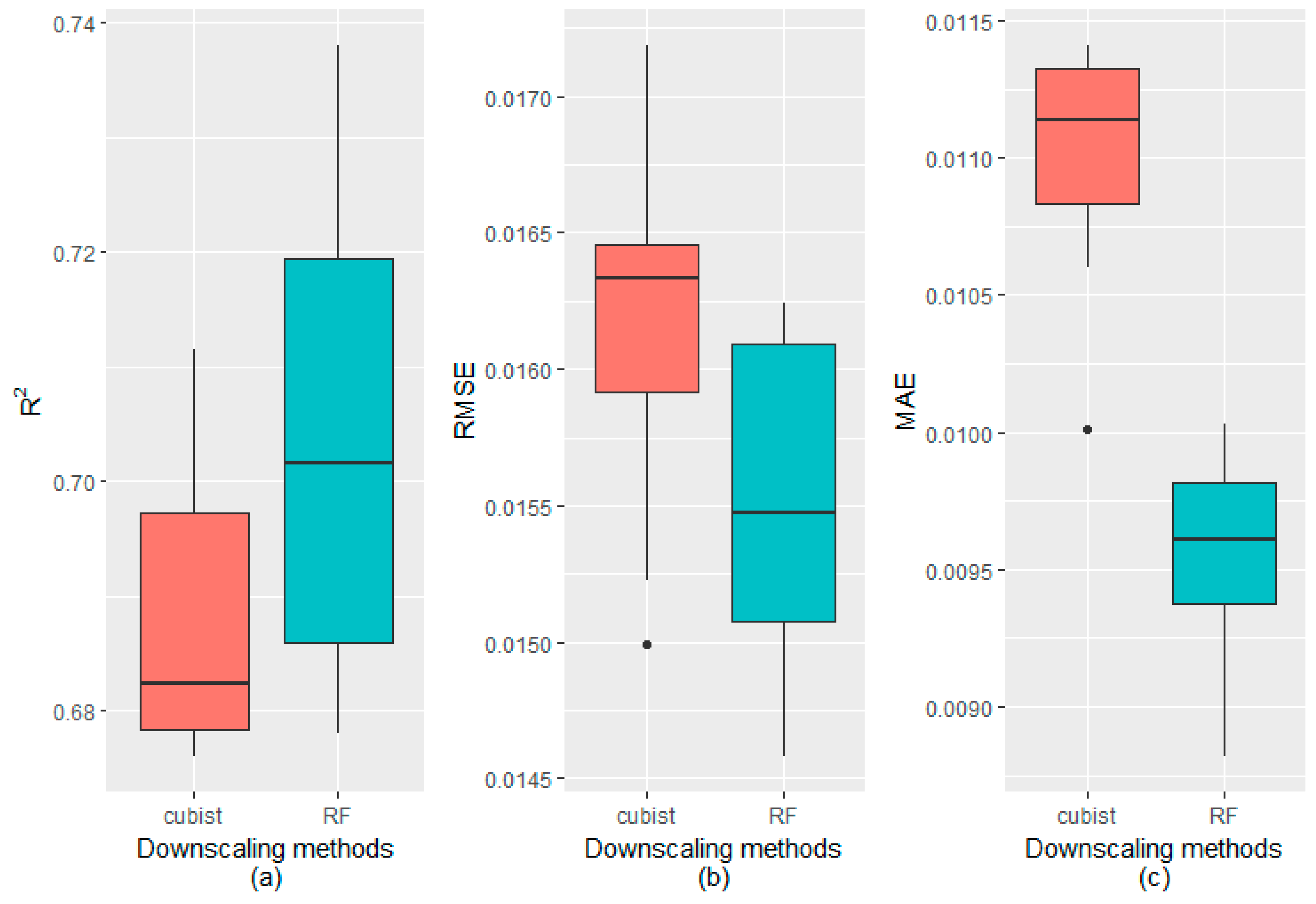
3.4. Comparative Analysis of the Downscaling Results Based on the Random Forest and Cubist Algorithms
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Merlin, O.; Walker, J.; Chehbouni, A.; Kerr, Y. Towards deterministic downscaling of SMOS soil moisture using MODIS derived soil evaporative efficiency. Remote Sens. Environ. 2008, 112, 3935–3946. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Kolassa, J.; Prigent, C.; Aires, F.; Gentine, P. Global downscaling of remotely sensed soil moisture using neural networks. Hydrol. Earth Syst. Sci. 2018, 22, 5341–5356. [Google Scholar] [CrossRef]
- Berg, A.; Lintner, B.R.; Findell, K.L.; Malyshev, S.; Loikith, P.C.; Gentine, P. Impact of Soil Moisture–Atmosphere Interactions on Surface Temperature Distribution. J. Clim. 2014, 27, 7976–7993. [Google Scholar] [CrossRef]
- Pablos, M.; Martínez-Fernández, J.; Sánchez, N.; González-Zamora, Á. Temporal and Spatial Comparison of Agricultural Drought Indices from Moderate Resolution Satellite Soil Moisture Data over Northwest Spain. Remote Sens. 2017, 9, 1168. [Google Scholar] [CrossRef]
- Kang, Y.H.; Khan, S.; Ma, X.Y. Climate change impacts on crop yield, crop water productivity and food security—A review. Prog. Nat. Sci. 2009, 19, 1665–1674. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Van doninck, J.; Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E.C. The potential of multitemporal Aqua and Terra MODIS apparent thermal inertia as a soil moisture indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Assessment of Evapotranspiration and Soil Moisture Content Across Different Scales of Observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Mitra, D.S.; Majumdar, T.J. Thermal inertia mapping over the Brahmaputra basin, India using NOAA-AVHRR data and its possible geological applications. Int. J. Remote Sens. 2004, 25, 3245–3260. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Zhao, W.; Sanchez, N.; Lu, H.; Li, A. A spatial downscaling approach for the SMAP passive surface soil moisture product using random forest regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SMMR). J. Geophys. Res. Atmos. 2007, 112, 112. [Google Scholar] [CrossRef]
- Guha, A.; Lakshmi, V. Use of the scanning multichannel microwave radiometer (SMMR) to retrieve soil moisture and surface temperature over the central United States. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1482–1494. [Google Scholar] [CrossRef]
- Yan, F.H.; Jin, Y.Q. Monitoring flooding of the Huaihe River, China, in summer 2003 using characteristic indices derived from special sensor microwave/imager (SSM/I) multitemporal observations. Can. J. Remote Sens. 2004, 30, 764–768. [Google Scholar] [CrossRef]
- De Ridder, K. Surface soil moisture monitoring over Europe using Special Sensor Microwave/Imager (SSM/I) imagery. J. Geophys. Res. Atmos. 2003, 108, 4422. [Google Scholar] [CrossRef]
- De Ridder, K. Quantitative estimation of skin soil moisture with the Special Sensor Microwave/Imager. Bound. Layer Meteorol. 2000, 96, 421–432. [Google Scholar] [CrossRef]
- Wen, J.; Su, Z.; Ma, Y. Determination of land surface temperature and soil moisture from Tropical Rainfall Measuring Mission/Microwave Imager remote sensing data. J. Geophys. Res. Atmos. 2003, 108, 4038–4050. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Kirstetter, P.E.; Maggioni, V.; Hong, Y.; Gourley, J.J. Incorporating Surface Soil Moisture Information in Error Modeling of TRMM Passive Microwave Rainfall. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6226–6240. [Google Scholar] [CrossRef]
- Lee, K. A combined passive/active microwave remote sensing approach for surface variable retrieval using Tropical Rainfall Measuring Mission observations. Remote Sens. Environ. 2004, 92, 112–125. [Google Scholar] [CrossRef]
- Jackson, T.; Hsu, A. Soil moisture and TRMM microwave imager relationships in the Southern Great Plains 1999 (SGP99) experiment. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1632–1642. [Google Scholar] [CrossRef]
- Wu, S.L.; Zhu, X.X. USING AMSR-E land product to monitor the drought process in China. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3894–3897. [Google Scholar] [CrossRef]
- Sridhar, V.; Jaksa, W.; Fang, B.; Lakshmi, V.; Hubbard, K.G.; Jin, X. Evaluating Bias-Corrected AMSR-E Soil Moisture using in situ Observations and Model Estimates. Vadose Zone J. 2013, 12, 12. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M. Relationships among remotely sensed soil moisture, precipitation and landslide events. Nat. Hazards 2007, 43, 211–222. [Google Scholar] [CrossRef]
- Mikai, H.; Arai, Y.; Mutoh, T.; Imaoka, K.; Shibata, A. A comparison of in situ precipitation with soil moisture retrieved from AMSR-E. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29–29 July 2005; pp. 3460–3461. [Google Scholar]
- Choi, M.; Hur, Y.M.; Kim, H.; Kim, T.W.; Ahn, J.H. Passive microwave soil moisture evaluations by ground based measurements in Korea. In 100 Years Isprs Advancing Remote Sensing Science; Wagner, W., Szekely, B., Eds.; ISPRS: Vienna, Austri, 2010; Volume 38, pp. 132–136. [Google Scholar]
- Chakraborty, A.; Sai, M.S.; Murthy, C.; Roy, P.; Behera, G. Assessment of area favourable for crop sowing using AMSR-E derived Soil Moisture Index (AMSR-E SMI). Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 537–547. [Google Scholar] [CrossRef]
- Al-Jassar, H.K.; Rao, K.S. Monitoring of soil moisture over the Kuwait desert using remote sensing techniques. Int. J. Remote Sens. 2010, 31, 4373–4385. [Google Scholar] [CrossRef]
- Usowicz, B.; Marczewski, W.; Usowicz, J.B.; Lukowski, M.I.; Lipiec, J. Comparison of Surface Soil Moisture from SMOS Satellite and Ground Measurements. Int. Agrophys. 2014, 28, 359–369. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Design of an optimum soil moisture monitoring network using SMOS. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Park, S.; Park, S.; Im, J.; Rhee, J.; Shin, J.; Park, J.D. Downscaling GLDAS Soil Moisture Data in East Asia through Fusion of Multi-Sensors by Optimizing Modified Regression Trees. Water 2017, 9, 332. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Zhan, C.; Han, J.; Hu, S.; Liu, L.; Dong, Y. Spatial Downscaling of GPM Annual and Monthly Precipitation Using Regression-Based Algorithms in a Mountainous Area. Adv. Meteorol. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.B.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping Annual Precipitation across Mainland China in the Period 2001–2010 from TRMM3B43 Product Using Spatial Downscaling Approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef]
- Ma, Z.; Shi, Z.; Zhou, Y.; Xu, J.; Yu, W.; Yang, Y. A spatial data mining algorithm for downscaling TMPA 3B43 V7 data over the Qinghai–Tibet Plateau with the effects of systematic anomalies removed. Remote Sens. Environ. 2017, 200, 378–395. [Google Scholar] [CrossRef]
- Draper, C.S.; Walker, J.P.; Steinle, P.J.; De Jeu, R.A.; Holmes, T.R. An evaluation of AMSR–E derived soil moisture over Australia. Remote Sens. Environ. 2009, 113, 703–710. [Google Scholar] [CrossRef]
- Im, J.; Park, S.; Rhee, J.; Baik, J.; Choi, M. Downscaling of AMSR-E soil moisture with MODIS products using machine learning approaches. Environ. Earth Sci. 2016, 75, 1120. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A Comparison of Different Regression Algorithms for Downscaling Monthly Satellite-Based Precipitation over North China. Remote Sens. 2016, 8, 835. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, Y.; Hu, B.; Liang, Z.; Shi, Z. Downscaling annual precipitation with TMPA and land surface characteristics in China. Int. J. Clim. 2017, 37, 5107–5119. [Google Scholar] [CrossRef]
- Lee, Y.J.; Park, C.; Lee, M.L. Identification of a Contaminant Source Location in a River System Using Random Forest Models. Water 2018, 10, 391. [Google Scholar] [CrossRef]
| Scientific Data Sets (SDS) | Spatial Resolution | Scale Factor |
|---|---|---|
| MOD13A2 (MODIS/Terra Vegetation Indices 16-Day L3 Global 1 km SIN Grid V006) | 1 km | 0.0001 |
| MOD11A2 (MODIS/Terra Land Surface Temperature/Emissivity 8-Day L3 Global 1 km SIN Grid V006) | 1 km | 0.02 |
| MCD43A3 (MODIS/Terra+Aqua BRDF/Albedo Daily L3 Global-500 m V006) | 500 m | 0.001 |
| MCD12Q1 (MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 500 m SIN Grid V006) | 500 m | N/A |
| MOD16A2 (MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500 m SIN Grid V006) | 500 m | 0.1 |
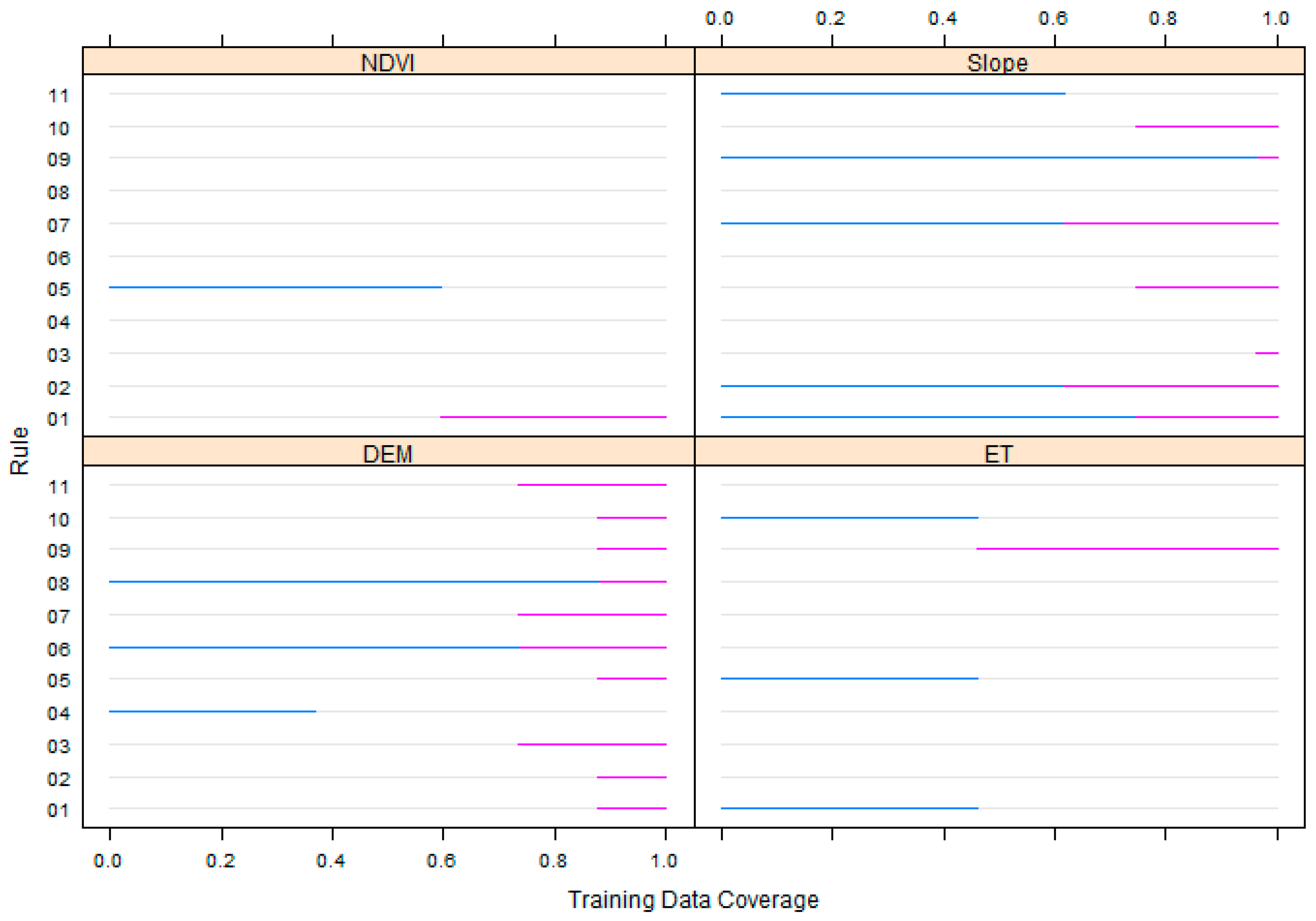
| Rule 1: if {DEM > 1062, Slope > 3.82698, Slope ≤ 8.79908, Aspect in {4, 5, 6, 7, 9}, NDVI > 0.42153, ET ≤ 14.8708} then outcome = 0.0623238 + 0.0426 × Slope − 0.0217 × ET − 1.412 × albedo + 0.315 × NDVI |
| Rule 2: if {DEM > 1062, Slope > 2.77987, Slope ≤ 3.82698, LC in {4, 5}} then outcome = −0.5929961 + 0.2089 × Slope |
| Rule 3: if {DEM > 646, Slope > 8.79908} then outcome = −0.6552099 − 1.79 × 10−5 × DEM + 0.0025 × LST_D |
| Rule 4: if {DEM ≤ 136} then outcome = −0.3143938 + 0.0002028 × DEM + 0.0015 × LST_N + 0.0015 × Slope + 0.019 × NDVI |
| Rule 5: if {DEM > 1062, Slope > 3.82698, Aspect in {4, 5, 6, 7, 9}, NDVI ≤ 0.42153, ET ≤ 14.8708} then outcome = 0.7520723 − 0.0417 × ET − 0.444 × NDVI + 0.0061 × Slope + 0.0002 × LST_D |
| Rule 6: if {DEM > 136, DEM ≤ 646} then outcome = −0.0459537 + 0.00228 × LST_N + 3.57 × 10−5 × DEM − 0.0016 × LST_D + 0.0012 × Slope − 0.035 × albedo + 0.003 × NDVI |
| Rule 7: if {DEM > 646, Slope > 2.77987, Slope ≤ 3.82698, LC in {8, 9, 12}} then outcome = 0.0276217 + 0.0255 × Slope + 5.8 × 10−6 × DEM + 0.00016 × LST_N + 0.003 × NDVI |
| Rule 8: if {DEM > 646, DEM ≤ 1062} then outcome = 0.1565938 |
| Rule 9: if {DEM > 1062, Slope > 3.82698, Slope ≤ 8.79908, ET > 14.8708} then outcome = −0.0548823 + 0.0008 × LST_N + 5.5 × 10−6 × DEM + 0.0003 × Slope + 0.003 × NDVI |
| Rule 10: if {DEM > 1062, Slope > 3.82698, Aspect in {3, 8}, ET ≤ 14.8708} then outcome = 0.1484353 + 0.0081 × Slope − 0.0044 × ET + 0.00014 × LST_N |
| Rule 11: if {DEM > 646, Slope ≤ 2.77987} then outcome = 0.7492527 − 0.0021 × LST_D + 8 × 10−7 × DEM |
| Station Name | AMSR-E | Random Forest | Cubist | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| Nanyang | 0.6836 | 0.0066 | 0.0053 | 0.8545 | 0.0064 | 0.0045 | 0.7331 | 0.0077 | 0.0059 |
| Fangxian | 0.4002 | 0.0161 | 0.0120 | 0.5024 | 0.0126 | 0.0104 | 0.4673 | 0.0132 | 0.0104 |
| Lixian | 0.8234 | 0.0125 | 0.0107 | 0.8757 | 0.0074 | 0.0061 | 0.7390 | 0.0088 | 0.0062 |
| Guzhang | 0.7278 | 0.0085 | 0.0070 | 0.8632 | 0.0059 | 0.0047 | 0.8368 | 0.0052 | 0.0039 |
| Shaodong | 0.5923 | 0.0151 | 0.0134 | 0.8569 | 0.0070 | 0.0056 | 0.6687 | 0.0176 | 0.0160 |
| Yichun | 0.7286 | 0.0120 | 0.0102 | 0.8375 | 0.0061 | 0.0047 | 0.8145 | 0.0055 | 0.0043 |
| Guidong | 0.5469 | 0.0084 | 0.0075 | 0.6758 | 0.0109 | 0.0096 | 0.6202 | 0.0203 | 0.0195 |
| Yingshan | 0.4692 | 0.0242 | 0.0228 | 0.7510 | 0.0179 | 0.0172 | 0.5008 | 0.0265 | 0.0256 |
| Xuancheng | 0.4979 | 0.0116 | 0.0095 | 0.7959 | 0.0077 | 0.0059 | 0.6706 | 0.0095 | 0.0076 |
| Guixi | 0.5484 | 0.0162 | 0.0144 | 0.8063 | 0.0084 | 0.0071 | 0.6708 | 0.0134 | 0.0120 |
| Mean values | 0.6018 | 0.0131 | 0.0113 | 0.7819 | 0.0090 | 0.0076 | 0.6722 | 0.0128 | 0.0111 |
| Year | Random Forest | Cubist | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| 2003 | 0.6866 | 0.0146 | 0.0088 | 0.6759 | 0.0150 | 0.0100 |
| 2004 | 0.7311 | 0.0153 | 0.0094 | 0.6783 | 0.0172 | 0.0113 |
| 2005 | 0.7155 | 0.0151 | 0.0093 | 0.6841 | 0.0164 | 0.0109 |
| 2006 | 0.6780 | 0.0162 | 0.0098 | 0.6808 | 0.0161 | 0.0110 |
| 2007 | 0.6965 | 0.0162 | 0.0100 | 0.6950 | 0.0163 | 0.0114 |
| 2008 | 0.7381 | 0.0156 | 0.0097 | 0.7115 | 0.0166 | 0.0114 |
| 2009 | 0.6840 | 0.0161 | 0.0099 | 0.6783 | 0.0163 | 0.0112 |
| 2010 | 0.7066 | 0.0150 | 0.0095 | 0.7036 | 0.0152 | 0.0106 |
| Mean values | 0.7045 | 0.0155 | 0.0096 | 0.6884 | 0.0162 | 0.0110 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; She, D.; Zhang, L.; Guo, M.; Liu, X. Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application. Water 2019, 11, 1401. https://doi.org/10.3390/w11071401
Chen S, She D, Zhang L, Guo M, Liu X. Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application. Water. 2019; 11(7):1401. https://doi.org/10.3390/w11071401
Chicago/Turabian StyleChen, Shaodan, Dunxian She, Liping Zhang, Mengyao Guo, and Xin Liu. 2019. "Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application" Water 11, no. 7: 1401. https://doi.org/10.3390/w11071401
APA StyleChen, S., She, D., Zhang, L., Guo, M., & Liu, X. (2019). Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application. Water, 11(7), 1401. https://doi.org/10.3390/w11071401






