Relationships between Spatial and Temporal Variations in Precipitation, Climatic Indices, and the Normalized Differential Vegetation Index in the Upper and Middle Reaches of the Heihe River Basin, Northwest China
Abstract
1. Introduction
2. Study Area
3. Data and Methods
3.1. Data
3.2. Methods
3.2.1. Theil-Sen Median Trend Analysis and Mann–Kendall Test Statistic
3.2.2. Wavelet Coherence
3.2.3. Other Methods
4. Results and Discussion
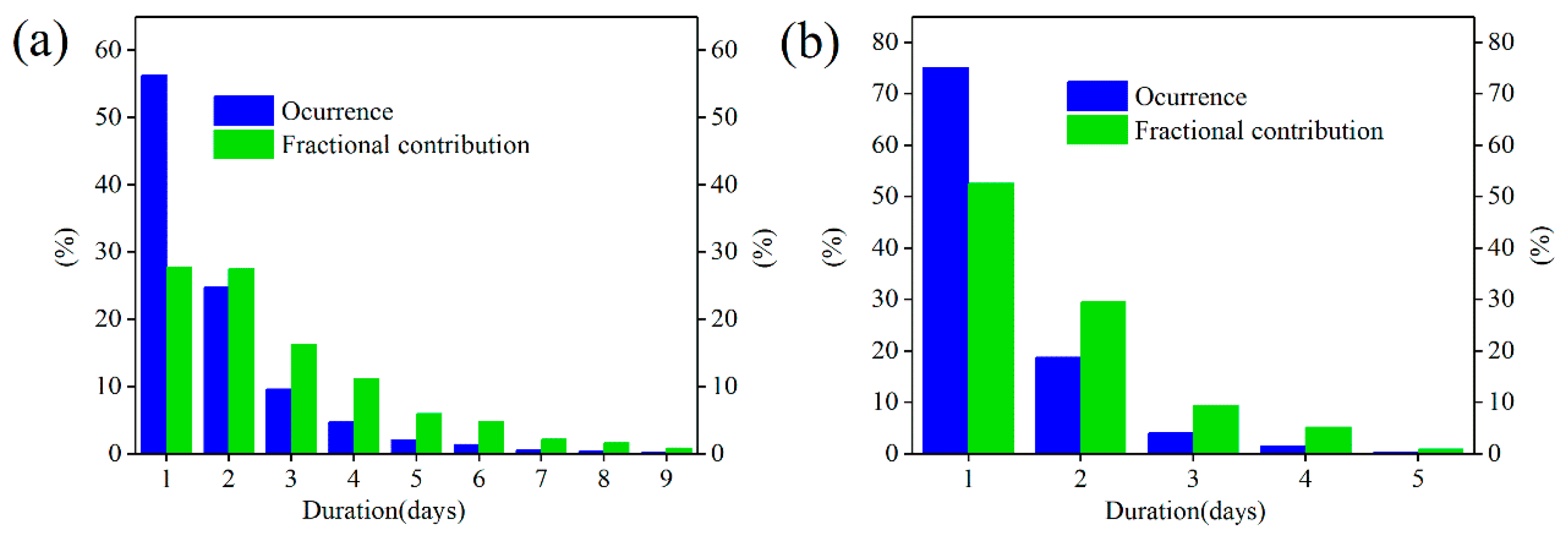
4.1. Occurrence and Fractional Contribution of WPs
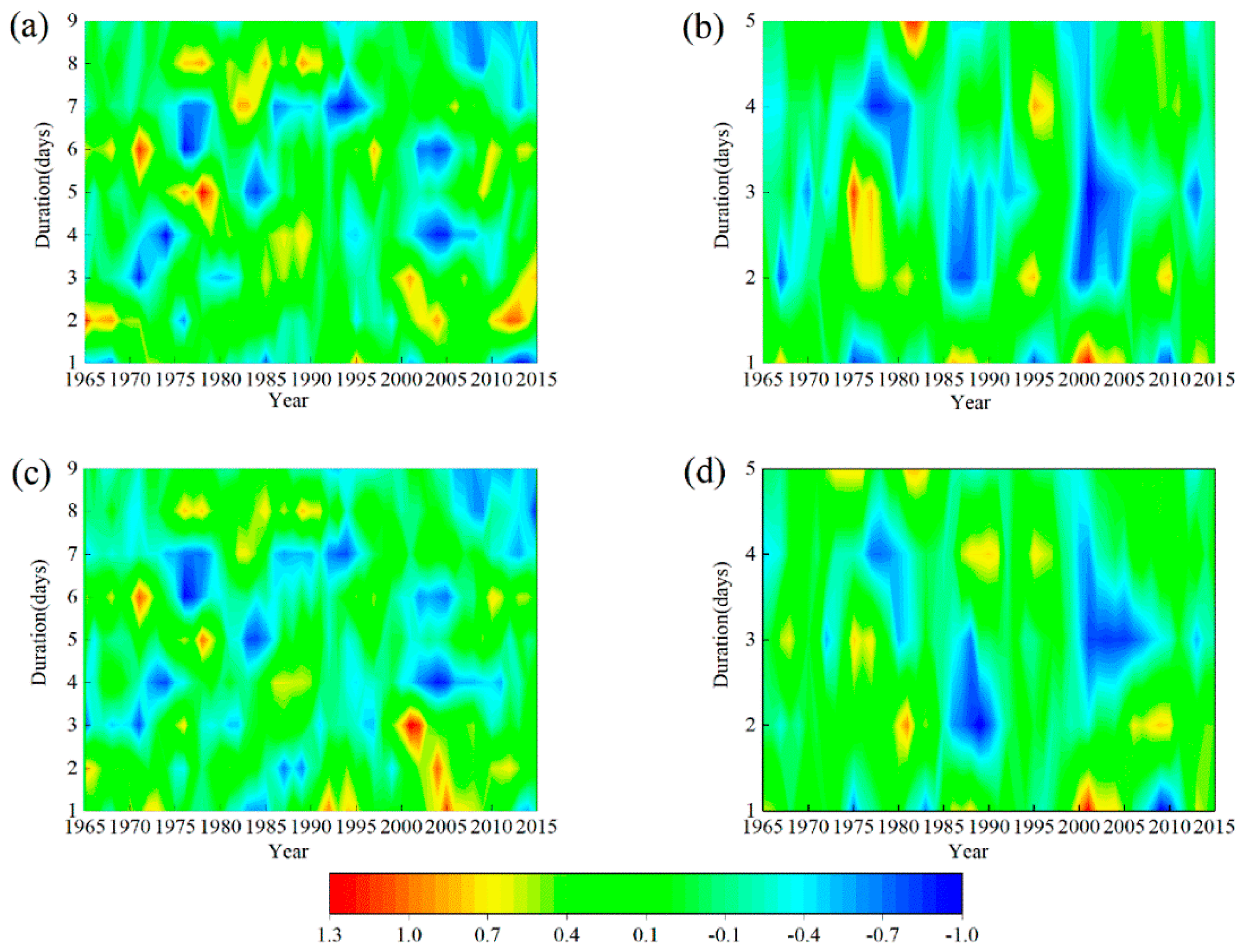
4.2. Temporal Changes in the Occurrence and Fractional Contribution of WPs
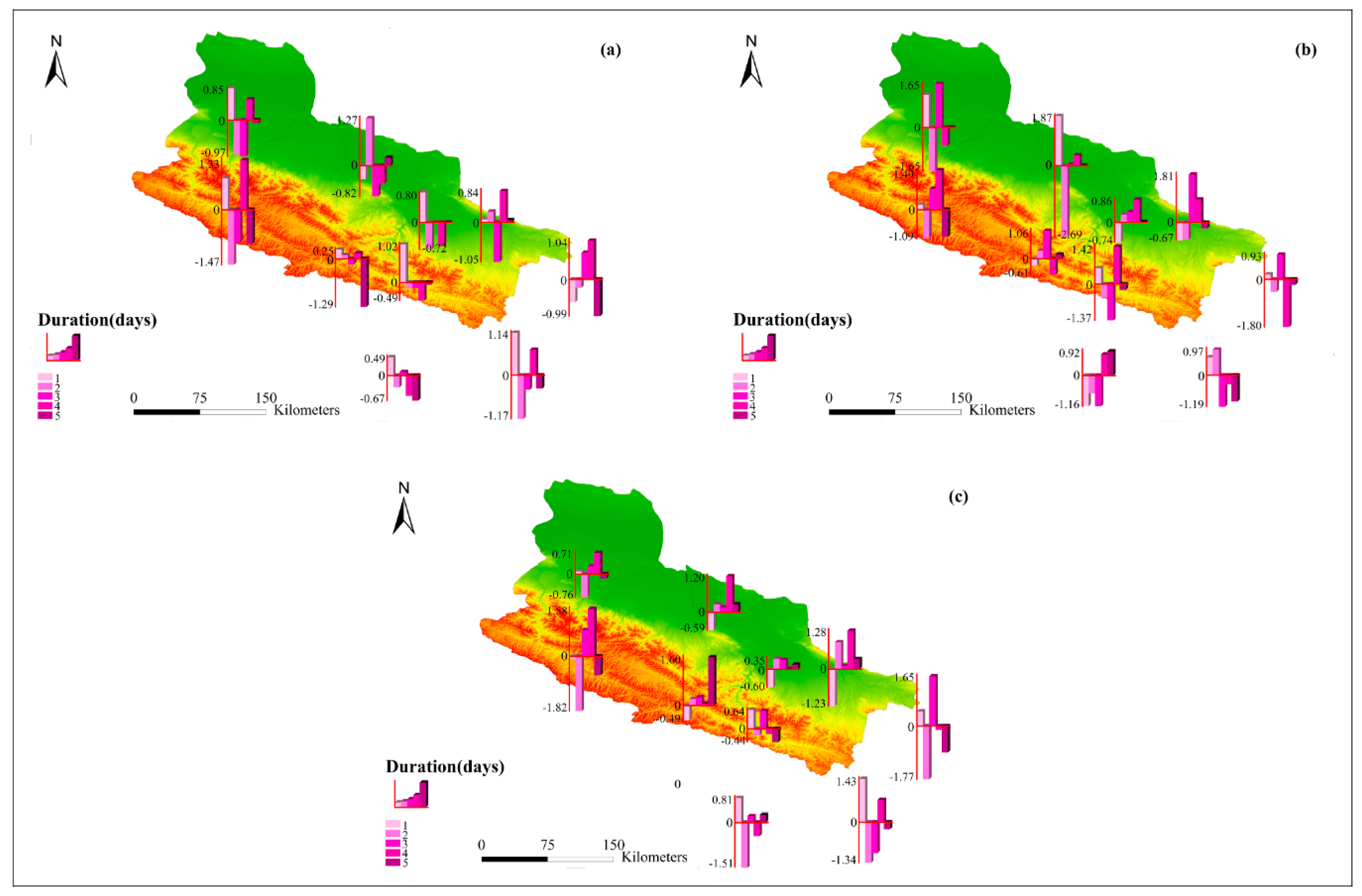
4.3. Spatial Distribution of Normalized Occurrences and Fractional Contributions for WPs
4.4. Trends in Precipitation Indices
4.5. Changes in the Attributes of the Precipitation Regimes
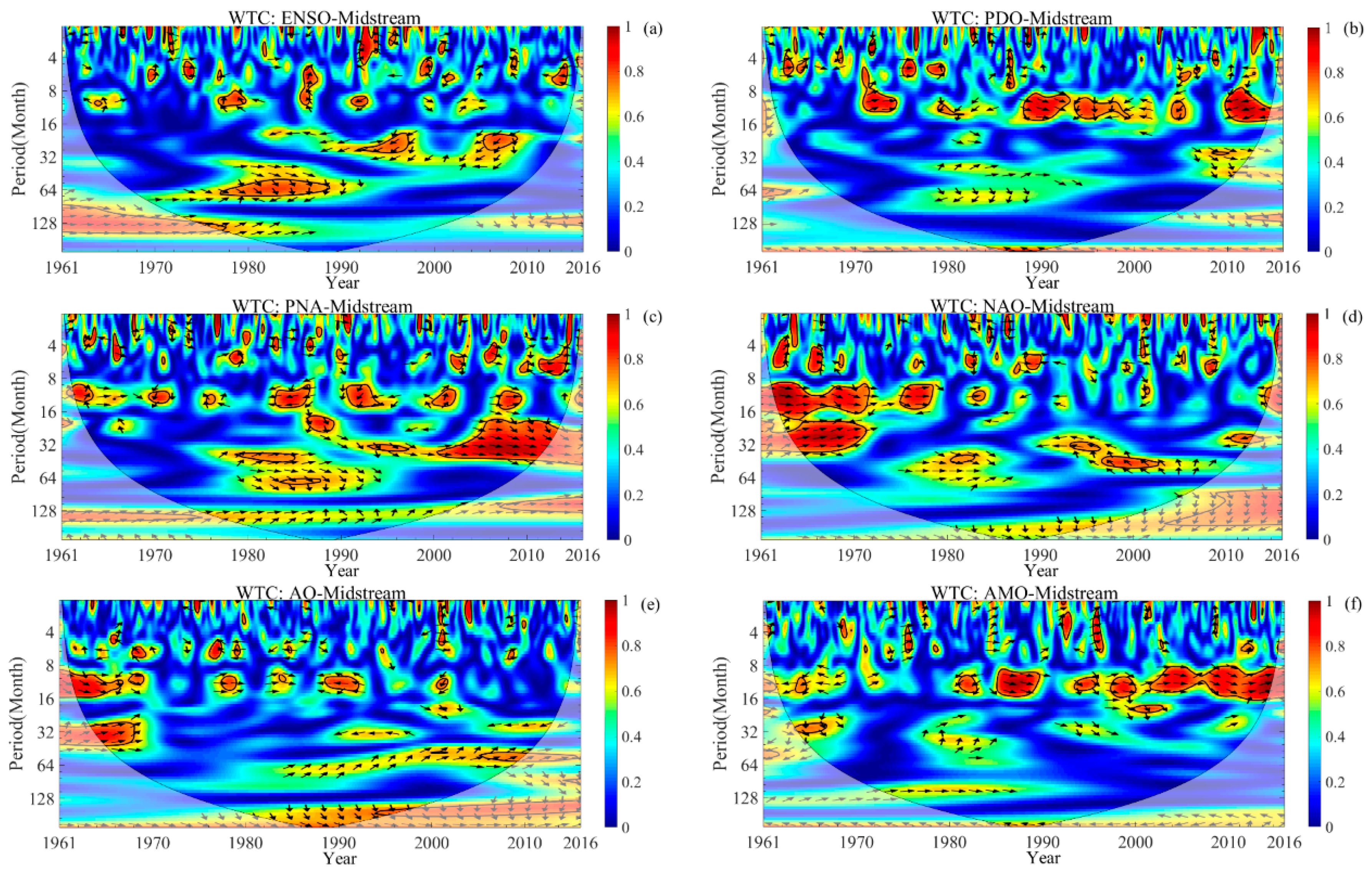
4.6. Wavelet Coherence between the Monthly Precipitation and Large-Scale Climate Indices
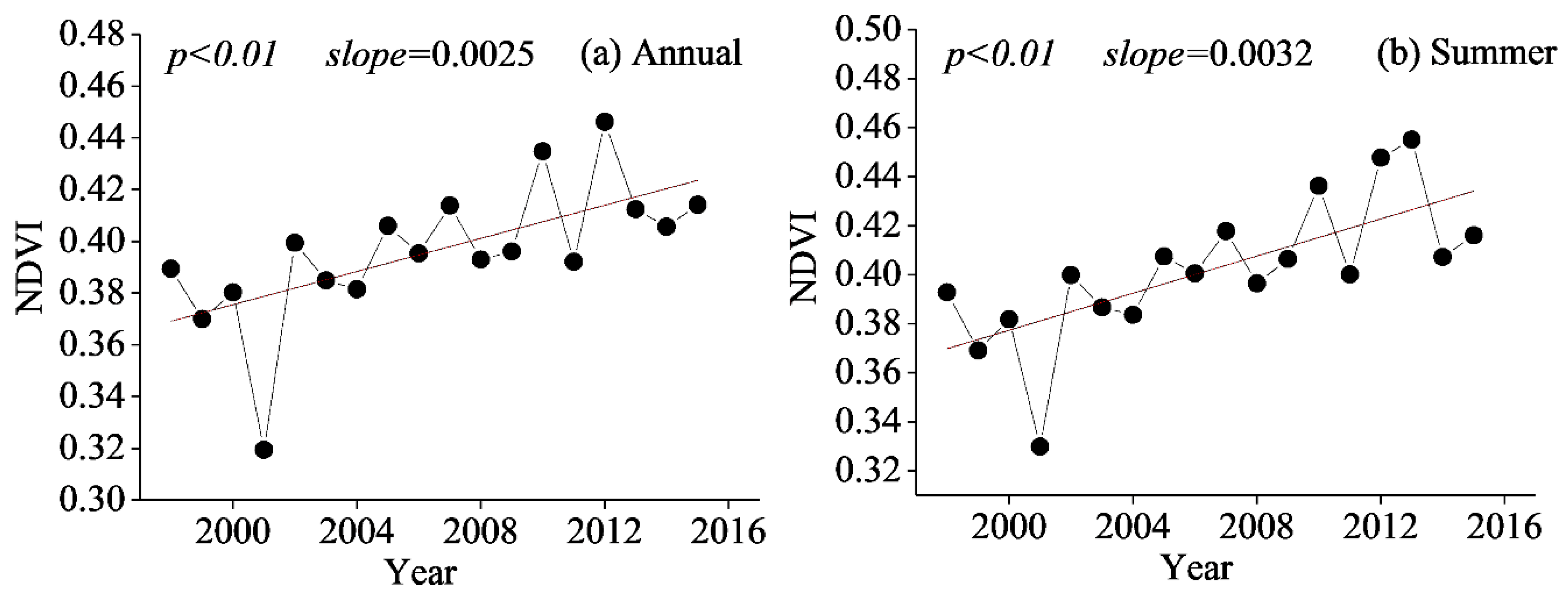
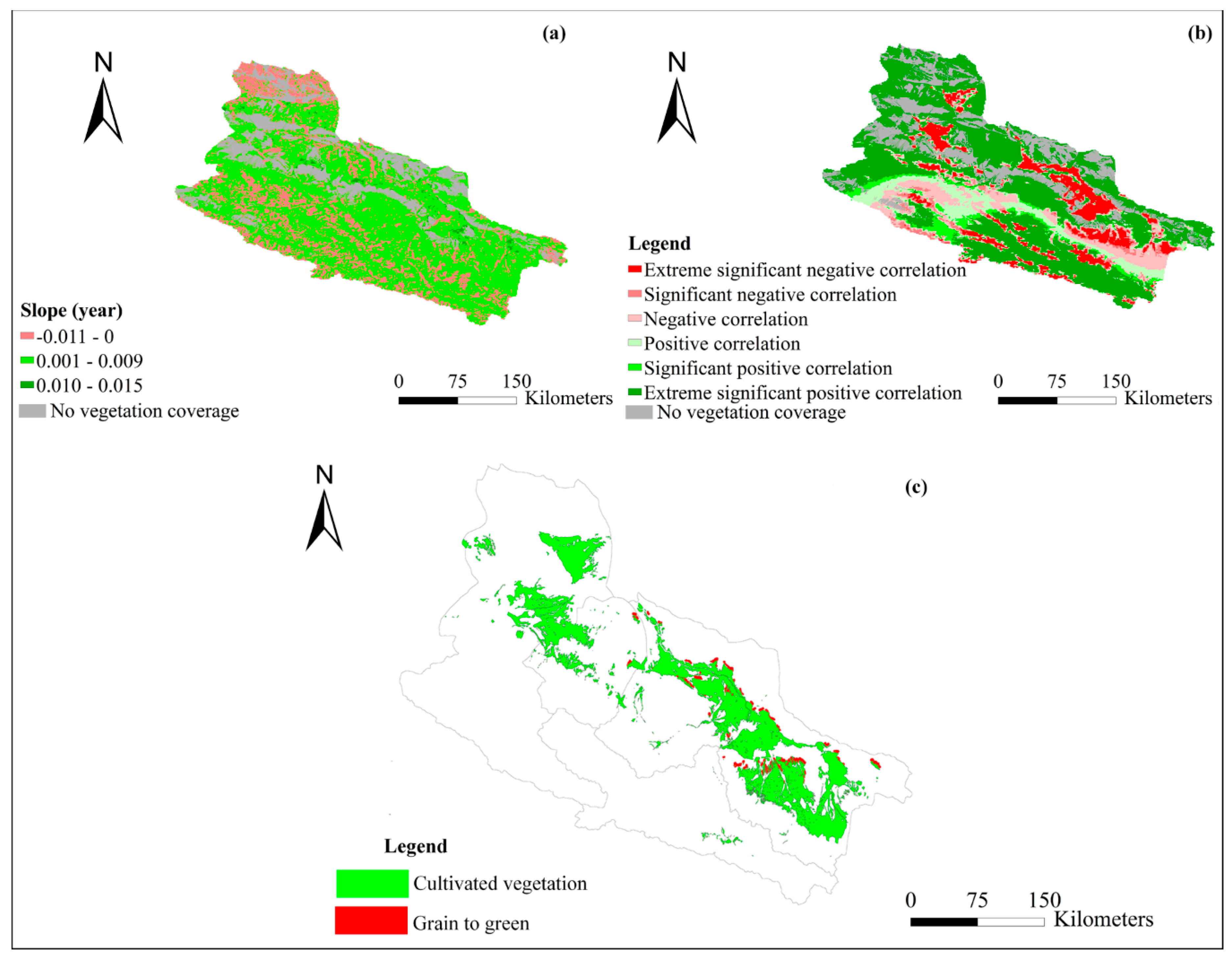
4.7. Relationship between Precipitation and the NDVI
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Y.; He, N.; Wang, Q.; Miao, C.Y. Increase of external nutrient input impact on carbon sinks in Chinese coastal seas. Environ. Sci. Technol. 2013, 47, 13215–13216. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Miao, C.Y.; Xi, Y.; Duan, Q.Y.; Lei, X.H.; Li, H. Analysis of precipitation characteristics on the loess plateau between 1965 and 2014, based on high-density gauge observations. Atmos. Res. 2018, 213, 264–274. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2013; p. 1535. [Google Scholar]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.L.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Sayemuzzaman, M.; Jha, M.K. Seasonal and annual precipitation time series trend analysis in North Carolina, United States. Atmos. Res. 2014, 137, 183–194. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhang, Y.Y.; Hong, S. Temporal and spatial variations of precipitation in northwest China during 1960–2013. Atmos. Res. 2017, 183, 283–295. [Google Scholar] [CrossRef]
- Xing, Z.Q.; Yan, D.H.; Zhang, C.; Wang, G.; Zhang, D.D. Spatial characterization and bivariate frequency analysis of precipitation and runoff in the upper Huai River Basin, China. Water Resour. Manag. 2015, 29, 3291–3304. [Google Scholar] [CrossRef]
- Liu, J.Y.; Zhang, Q.; Singh, V.P.; Shi, P.J. Contribution of multiple climatic variables and human activities to streamflow changes across China. J. Hydrol. 2016, 545, 145–162. [Google Scholar] [CrossRef]
- Wu, J.W.; Miao, C.Y.; Wang, Y.M.; Duan, Q.Y.; Zhang, X.M. Contribution analysis of the long-term changes in seasonal runoff on the loess plateau, China, using eight budyko-based methods. J. Hydrol. 2016, 545, 263–275. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F.L. Contributions of climate change and human activities to runoff change in seven typical catchments across China. Sci. Total Environ. 2017, 605–606, 219–229. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Peng, J.; Chen, Y.D.; Li, J.F. Spatial–temporal changes of precipitation structure across the pearl river basin, China. J. Hydrol. 2012, 440–441, 113–122. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Li, J.F.; Chen, X.H. Analysis of the periods of maximum consecutive wet days in China. J. Geophys. Res. Atmos. 2011, 116, 1–18. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.H.; Singh, V.P.; Xu, C.Y.; Kong, D.D.; Xiao, M.Z.; Chen, X.H. Homogenization of precipitation and flow regimes across China: Changing properties, causes and implications. J. Hydrol. 2015, 530, 462–475. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Xiao, W.H.; Chen, L.H.; Yan, D.H.; Zhou, Y.Y.; Yang, M.Z. Spatial and temporal variability in the precipitation concentration in the upper reaches of the hongshui river basin, southwestern China. Adv. Meteorol. 2018, 2018, 4329757. [Google Scholar] [CrossRef]
- Sarricolea, P.; Meseguer-Ruiz, Ó.; Serrano-Notivoli, R.; Soto, M.V.; Martin-Vide, J. Trends of daily precipitation concentration in Central-Southern Chile. Atmos. Res. 2019, 215, 285–298. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Gulev, S.; Kollet, K.S. Changing structure of European precipitation: Longer wet periods leading to more abundant rainfalls. Geophys. Res. Lett. 2010, 37, L06704. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Singh, V.P. Spatiotemporal patterns of precipitation regimes in the Huai river basin, China, and possible relations with ENSO events. Nat. Hazards 2016, 82, 1–19. [Google Scholar] [CrossRef]
- Huang, J.; Chen, X.; Xue, Y.; Lin, J.; Zhang, J. Changing characteristics of wet/dry spells during 1961–2008 in Sichuan province, southwest China. Theor. Appl. Climatol. 2017, 127, 129–141. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Ji, W.; Guo, Q.H.; Ke, J.H.; Tao, S. Variation in a satellite-based vegetation index in relation to climate in China. J. Veg. Sci. 2004, 15, 219–226. [Google Scholar] [CrossRef]
- Cleland, E.E.; Chuine, I.; Menzel, A.; Mooney, H.A.; Schwartz, M.D. Shifting plant phenology in response to global change. Trends Ecol. Evol. 2007, 22, 357–365. [Google Scholar] [CrossRef]
- Mao, D.H.; Wang, Z.M.; Luo, L.; Ren, C.Y. Integrating AVHRR and MODIS data to monitor NDVI changes and their relationships with climatic parameters in Northeast China. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 528–536. [Google Scholar] [CrossRef]
- Li, J.; Peng, S.; Li, Z. Detecting and attributing vegetation changes on China’s loess plateau. Agric. For. Meteorol. 2017, 247, 260–270. [Google Scholar] [CrossRef]
- Xin, Z.; Xu, J.; Zheng, W. Spatiotemporal variations of vegetation cover on the Chinese loess plateau (1981–2006): Impacts of climate changes and human activities. Sci. China Ser. D Earth Sci. 2008, 51, 67–78. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, Q.; Zhang, C.B.; Li, J.L. Spatiotemporal variation of grassland vegetation NDVI in the middle and upper reaches of the Heihe river and its response to climatic factors. Acta Pratacult. Sin. 2013, 22, 138–147. (In Chinese) [Google Scholar]
- Chuai, X.W.; Huang, X.J.; Wang, W.J.; Bao, G. NDVI temperature and precipitation changes and their relationships with different vegetation types during 1998–2007 in Inner Mongolia, China. Int. J. Climatol. 2013, 33, 1696–1706. [Google Scholar] [CrossRef]
- Liu, Y.L.; Lei, H.M. Responses of natural vegetation dynamics to climate drivers in China from 1982 to 2011. Remote Sens. 2015, 7, 10243–10268. [Google Scholar] [CrossRef]
- Sun, W.Y.; Song, X.Y.; Mu, X.M.; Gao, P.; Wang, F.; Zhao, GJ. Spatiotemporal vegetation cover variations associated with climate change and ecological restoration in the Loess plateau. Agricu. For. Meteorol. 2015, 209–210, 87–99. [Google Scholar] [CrossRef]
- Sun, W.C.; Song, H.; Yao, X.L.; Ishidaira, H.; Xu, Z.X. Changes in remotely sensed vegetation growth trend in the Heihe basin of arid northwestern China. PLoS ONE 2015, 10, e0135376. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.L.; Li, L.H.; Chen, X.; Shi, H. Effects of precipitation intensity and temperature on, NDVI-based grass change over northern China during the period from 1982 to 2011. Remote Sens. 2015, 7, 10164–10183. [Google Scholar] [CrossRef]
- Yuan, X.L.; Li, L.H.; Chen, X. Increased grass NDVI under contrasting trends of precipitation change over north China during 1982–2011. Remote Sens. Let. 2015, 6, 69–77. [Google Scholar] [CrossRef]
- Jiang, L.L.; Jiapaer, G.; Bao, A.M.; Guo, H.; Ndayisaba, F. Vegetation dynamics and responses to climate change and human activities in central Asia. Sci. Total Environ. 2017, 599–600, 967–980. [Google Scholar] [CrossRef]
- Wen, Z.F.; Wu, S.J.; Chen, J.L.; Lü, M.Q. NDVI indicated long-term interannual changes in vegetation activities and their responses to climatic and anthropogenic factors in the three gorges reservoir region, China. Sci. Total Environ. 2017, 574, 947–959. [Google Scholar] [CrossRef] [PubMed]
- Zhao, A.Z.; Zhang, A.B.; Liu, X.F.; Cao, S. Spatiotemporal changes of normalized difference vegetation index (NDVI) and response to climate extremes and ecological restoration in the Loess Plateau, China. Theor. Appl. Climatol. 2017, 132, 555–567. [Google Scholar] [CrossRef]
- Cui, L.; Wang, L.; Singh, R.P.; Lai, Z.; Jiang, L.; Yao, R. Association analysis between spatiotemporal variation of vegetation greenness and precipitation/temperature in the Yangtze river basin (China). Environ. Sci. Pollut. Res. 2018, 25, 21867–21878. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.Y.; Yang, L.Q.; Guan, W.Q.; Wang, F.F.; Liu, Z.Y.; Xu, C.Q. Assessing vegetation response to climatic variations and human activities: Spatiotemporal NDVI variations in the Hexi corridor and surrounding areas from 2000 to 2010. Theor. Appl. Climatol. 2018, 135, 1179–1193. [Google Scholar] [CrossRef]
- Qu, S.; Wang, L.C.; Lin, A.W.; Zhu, H.J.; Yuan, M.X. What drives the vegetation restoration in Yangtze river basin, China: Climate change or anthropogenic factors? Ecol. Indic. 2018, 90, 438–450. [Google Scholar] [CrossRef]
- Li, B.F.; Chen, Y.N.; Chen, Z.S.; Xiong, H.G.; Lian, L.S. Why does precipitation in northwest China show a significant increasing trend from 1960 to 2010. Atmos. Res. 2016, 167, 275–284. [Google Scholar] [CrossRef]
- Li, C.; Wang, R.H. Recent changes of precipitation in Gansu, northwest China: An index-based analysis. Theor. Appl. Climatol. 2017, 129, 1–16. [Google Scholar] [CrossRef]
- Wang, H.J.; Pan, Y.P.; Chen, Y.N.; Ye, Z.W. Linear trend and abrupt changes of climate indices in the arid region of northwestern China. Atmos. Res. 2017, 196, 108–118. [Google Scholar] [CrossRef]
- Wen, X.H.; Wu, X.Q.; Gao, M. Spatiotemporal variability of temperature and precipitation in Gansu province (Northwest China) during 1951–2015. Atmos. Res. 2017, 197, 132–149. [Google Scholar] [CrossRef]
- Gao, R.; Li, F.; Wang, X.; Liu, T.; Du, D.; Yong, B. Spatiotemporal variations in precipitation across the Chinese Mongolian plateau over the past half century. Atmos. Res. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Qin, Y.H.; Li, B.F.; Chen, Z.S.; Chen, Y.N.; Lian, L.S. Spatio-temporal variations of nonlinear trends of precipitation over an arid region of northwest China according to the extreme-point symmetric mode decomposition method. Int. J. Climatol. 2017, 38, 1–11. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.C.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Wang, L.; Chen, R.S.; Song, Y.; Yang, Y.; Liu, J.F.; Han, C.T.; Liu, J.F. Precipitation–altitude relationships on different timescales and at different precipitation magnitudes in the Qilian mountains. Theor. Appl. Climatol. 2018, 134, 875–884. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.D.; Ge, Y.C.; Li, H.Y.; Han, F.; Hu, X.L.; Tian, Y. Hydrological cycle in the Heihe river basin and its implication for water resource management in endorheic basins. J. Geophys. Res. Atmos. 2018, 123, 890–914. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.X.; Chen, C.F.; Zhao, M.W.; Fan, Z.M. An improved statistical downscaling scheme of tropical rainfall measuring mission precipitation in the Heihe river basin, China. Int. J. Climatol. 2018, 38, 1–14. [Google Scholar] [CrossRef]
- Zhang, M.M.; Wang, S.; Fu, B.J.; Gao, G.Y.; Shen, Q. Ecological effects and potential risks of the water diversion project in the Heihe river basin. Sci. Total Environ. 2018, 619–620, 794–803. [Google Scholar] [CrossRef]
- Yin, Z.L.; Xiao, H.L.; Zou, S.B.; Zhu, R.; Lu, Z.X.; Lan, Y.C.; Shen, Y.P. Simulation of hydrological processes of mountainous watersheds in inland river basins: Taking the Heihe Mainstream River as an example. J. Arid Land 2014, 6, 16–26. [Google Scholar] [CrossRef]
- Yang, L.S.; Feng, Q.; Yin, Z.L.; Wen, X.H.; Si, J.H.; Li, C.B.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2016, 31, 1100–1112. [Google Scholar] [CrossRef]
- Li, Z.L.; Xu, Z.X.; Shao, Q.X.; Yang, J. Parameter estimation and uncertainty analysis of swat model in upper reaches of the heihe river basin. Hydrol. Process. 2009, 23, 2744–2753. [Google Scholar] [CrossRef]
- Ge, Y.C.; Li, X.; Huang, C.L.; Nan, Z.T. A decision support system for irrigation water allocation along the middle reaches of the Heihe River Basin, Northwest China. Environ. Model. Softw. 2013, 47, 182–192. [Google Scholar] [CrossRef]
- Qiu, L.H.; Peng, D.Z.; Xu, Z.X.; Liu, W.F. Identification of the impacts of climate changes and human activities on runoff in the upper and middle reaches of the Heihe river basin, China. J. Water Clim. Chang. 2015, 7, 251–262. [Google Scholar] [CrossRef]
- Nian, Y.Y.; Li, X.; Zhou, J.; Hu, X.L. Impact of land use change on water resource allocation in the middle reaches of the Heihe River Basin in north-western China. J. Arid Land 2014, 6, 273–286. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. I, II, III. Nederl. Akad. Wetensch. Proc. 1950, 53, 386–392. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 39, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H. Nonparametric tests against trend. Econometrica 1945, 13, 124–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Carey, S.K.; Tetzlaff, D.; Buttle, J.; Laudon, H.; McDonnell, J.; McGuire, K.; Shanley, J. Use of color maps and wavelet coherence to discern seasonal and interannual climate influences on streamflow variability in northern catchments. Water Resour. Res. 2013, 49, 6194–6207. [Google Scholar] [CrossRef]
- Holman, I.P.; Rivas-Casado, M.; Bloomfield, J.P.; Gurdak, J.J. Identifying non-stationary groundwater level response to North Atlantic Ocean-atmosphere teleconnection patterns using wavelet coherence. Hydrogeol. J. 2011, 19, 1269–1278. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Processes. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Mengistu, S.G.; Creed, I.F.; Kulperger, R.; Quick, C.G. Russian nesting dolls effect-using wavelet analysis to reveal non-stationary and nested stationary signals in water yield from catchments on a northern forested landscape. Hydrol. Process. 2013, 27, 669–686. [Google Scholar] [CrossRef]
- Partal, T. Wavelet analysis and multi-scale characteristics of the runoff and precipitation series of the Aegean region (Turkey). Int. J. Climatol. 2012, 32, 108–120. [Google Scholar] [CrossRef]
- Dash, M.K.; Pandey, P.C.; Vyas, N.K.; Turner, J. Variability in the ENSO-induced southern hemispheric circulation and Antarctic sea ice extent. Int. J. Climatol. 2013, 33, 778–783. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B.; Biswas, A. Inter-annual to inter-decadal streamflow variability in Quebec and Ontario in relation to dominant largescale climate indices. J. Hydrol. 2016, 536, 426–446. [Google Scholar] [CrossRef]
- De Oliveirajunior, J.F.; Gois, G.; Terassi, P.M.; Junior, C.A.; Blanco, C.J.; Sobral, B.S.; Gasparini, K.A. Drought severity based on the SPI index and its relation to the ENSO and PDO climatic variability modes in the regions North and Northwest of the State of Rio de Janeiro—Brazil. Atmos. Res. 2018, 212, 91–105. [Google Scholar] [CrossRef]
- Mariotti, L.; Coppola, E.; Sylla, M.B.; Giorgi, F.; Piani, C. Regional climate model simulation of projected 21st century climate change over an all-Africa domain: Comparison analysis of nested and driving model results. J. Geophys. Res. Atmos. 2011, 116, D15111. [Google Scholar] [CrossRef]
- Sun, F.; Roderick, M.L.; Farquhar, G.D.; Lim, W.H. Partitioning the variance between space and time. Geophys. Res. Lett. 2010, 37, L12704. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.M.; Salama, M.S.; Su, Z.B. Assessment of vegetation dynamics and their response to variations in precipitation and temperature in the Tibetan plateau. Clim. Chang. 2010, 103, 519–535. [Google Scholar] [CrossRef]
- Han, H.B.; Ma, M.G.; Yan, P. Periodicity analysis of NDVI time series and its relationship with climatic factors in the Heihe river basin in China. Rem. Sen. Tech. Appl. 2011, 26, 554–560. (In Chinese) [Google Scholar]
- Xu, X.; Jiang, Y.; Liu, M.H.; Huang, Q.Z.; Huang, G.H. Modeling and assessing Agro-hydrological processes and irrigation water saving in the middle Heihe River basin. Agric. Water Manag. 2019, 211, 152–164. [Google Scholar] [CrossRef]
- Zou, M.Z.; Kang, S.Z.; Niu, J.; Lu, H.N. A new technique to estimate regional irrigation water demand and driving factor effects using an improved SWAT model with LMDI factor decomposition in an arid basin. J. Clean. Prod. 2018, 185, 814–828. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Paruelo, J.M.; Burke, I.C. Land use impacts on the normalized difference vegetation index in temperate Argentina. Ecol. Appl. 2003, 13, 616–628. [Google Scholar] [CrossRef]
- Jung, M.; Chang, E. NDVI-based land-cover change detection using harmonic analysis. Int. J. Remote Sens. 2015, 36, 1097–1113. [Google Scholar]
- Xu, L.L.; Li, B.L.; Yuan, Y.C.; Gao, X.Z.; Zhang, T.; Sun, Q.L. Detecting different types of directional land cover changes using MODIS NDVI time series dataset. Remote Sens. 2016, 8, 495. [Google Scholar] [CrossRef]
- Liu, X.R.; Shen, Y.J. Quantification of the impacts of climate change and human agricultural activities on oasis water requirements in an arid region: A case study of the Heihe River basin, China. Earth Syst. Dynam 2018, 9, 211–225. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 418, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.F.; Shen, Y.P.; Li, D.L.; Zhang, G.W.; Ding, Y.J.; Hu, R.J.; Kang, E. Discussion on the present climate change from warm-dry to warm-wet in Northwest China. Quat. Sci. 2003, 23, 152–164. (In Chinese) [Google Scholar]
- Zhang, X.Z.; Li, P.; Li, D.S. Spatiotemporal Variations of Precipitation in the Southern Part of the Heihe River Basin (China). 1984–2014. Water 2018, 10, 410. [Google Scholar] [CrossRef]
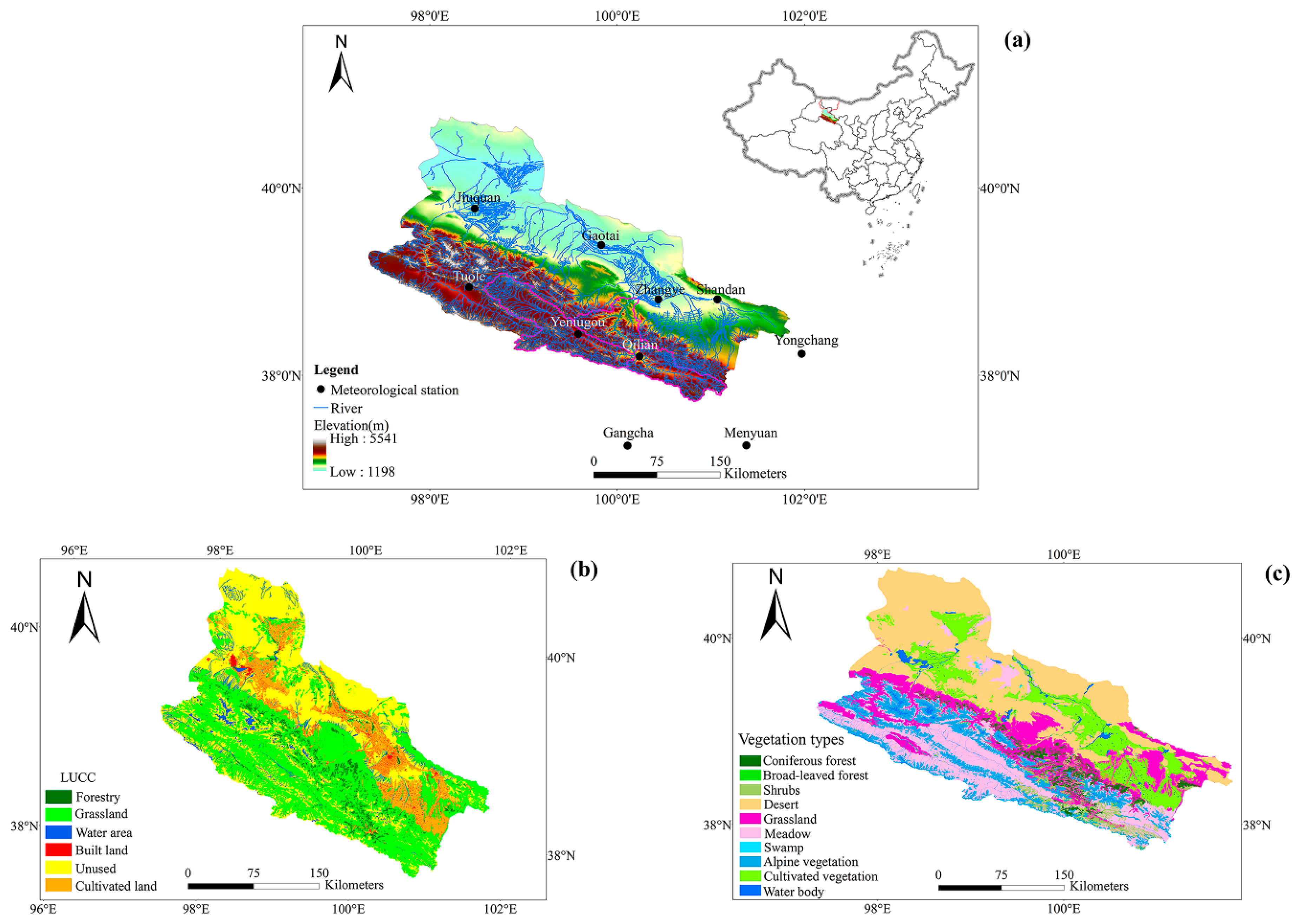
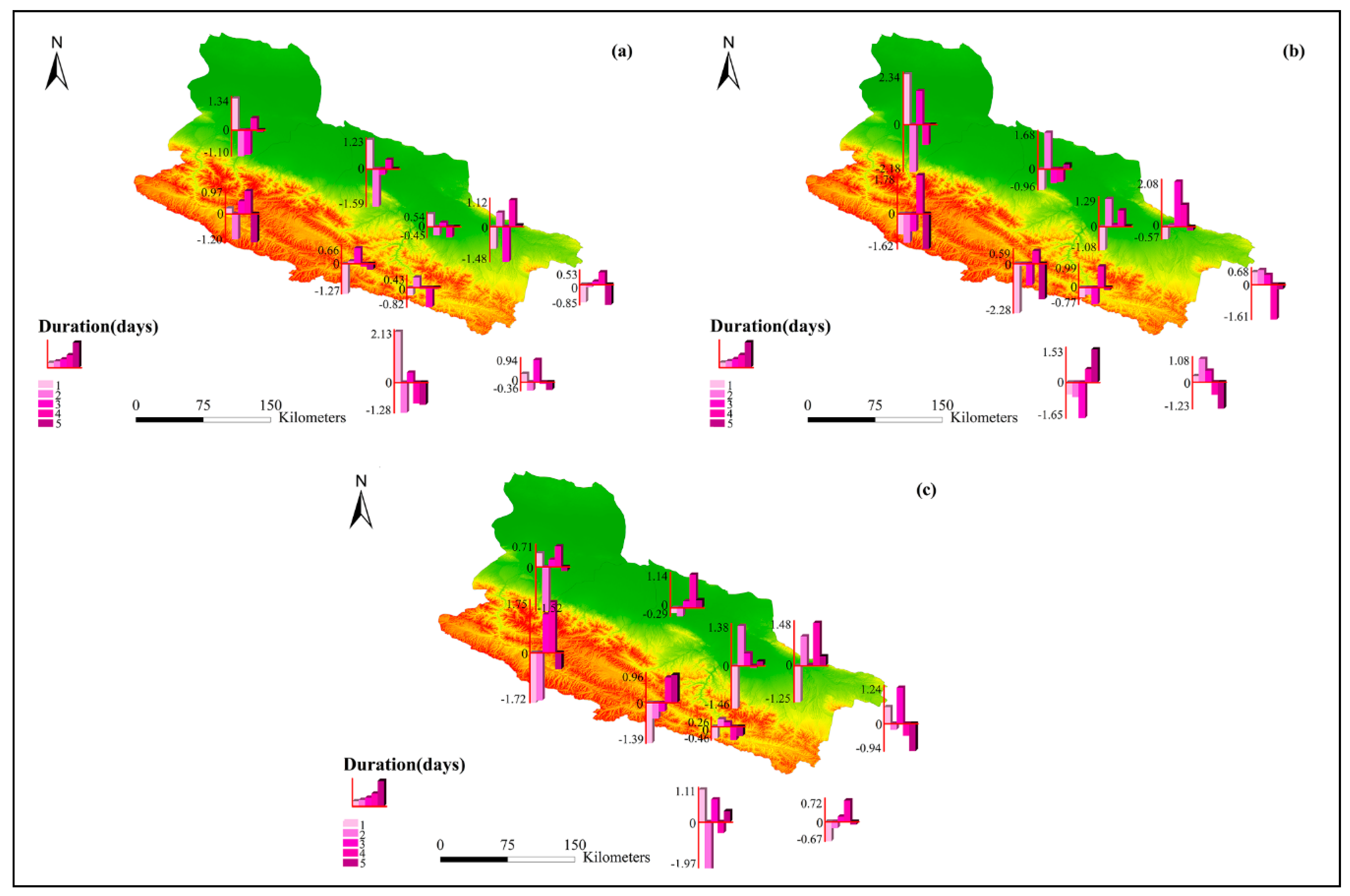
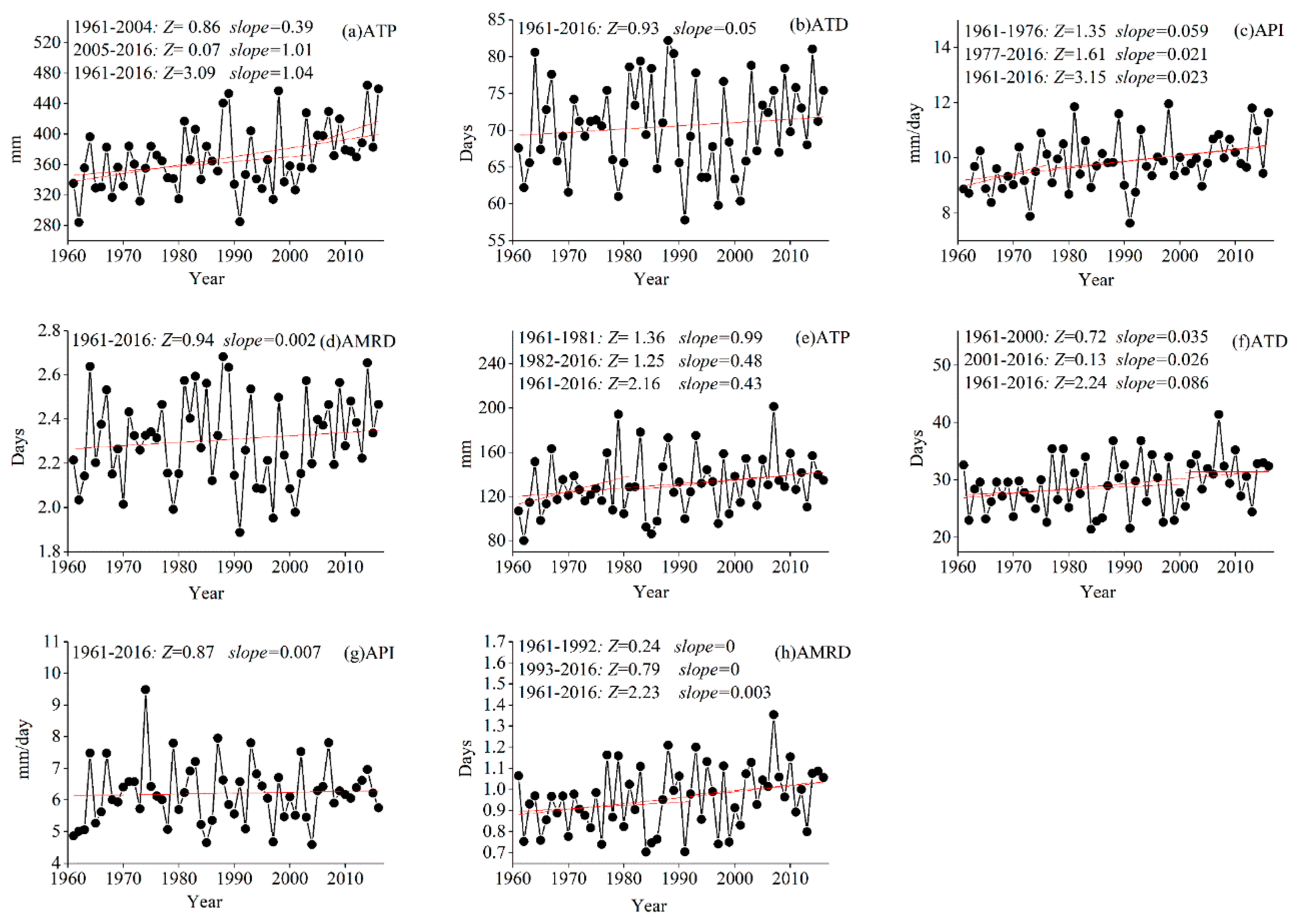
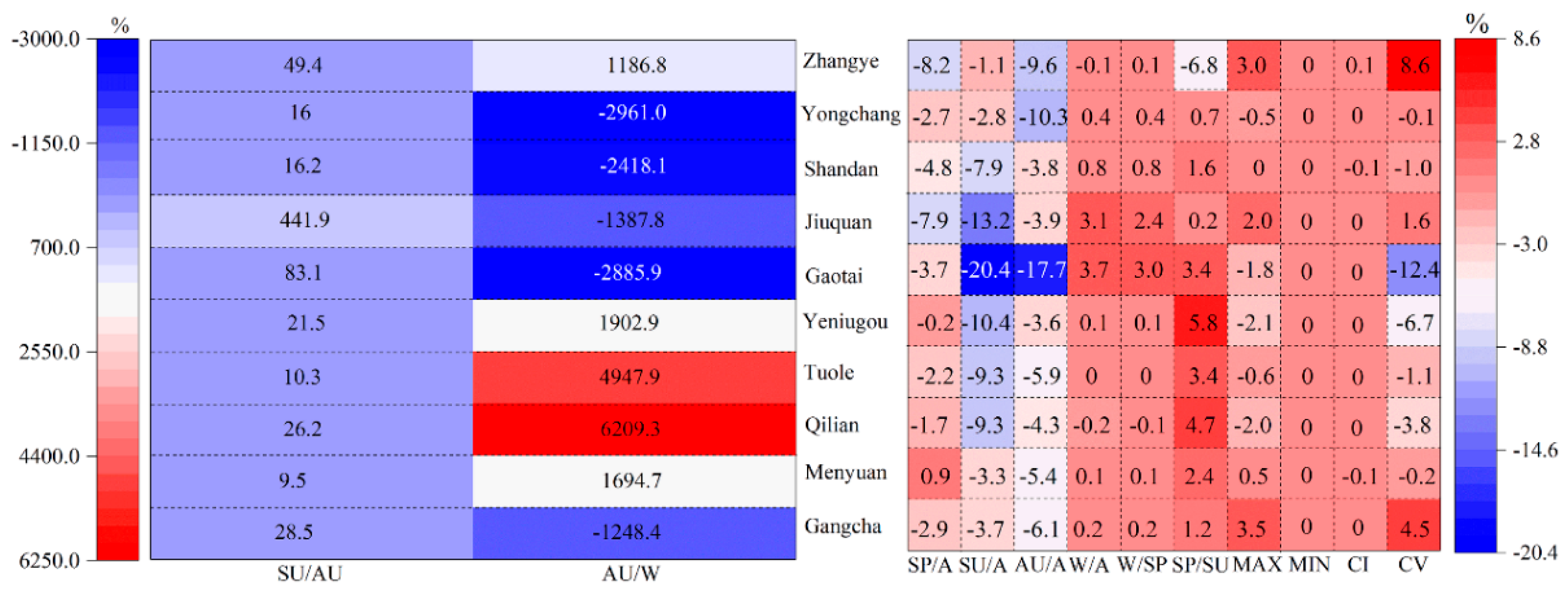
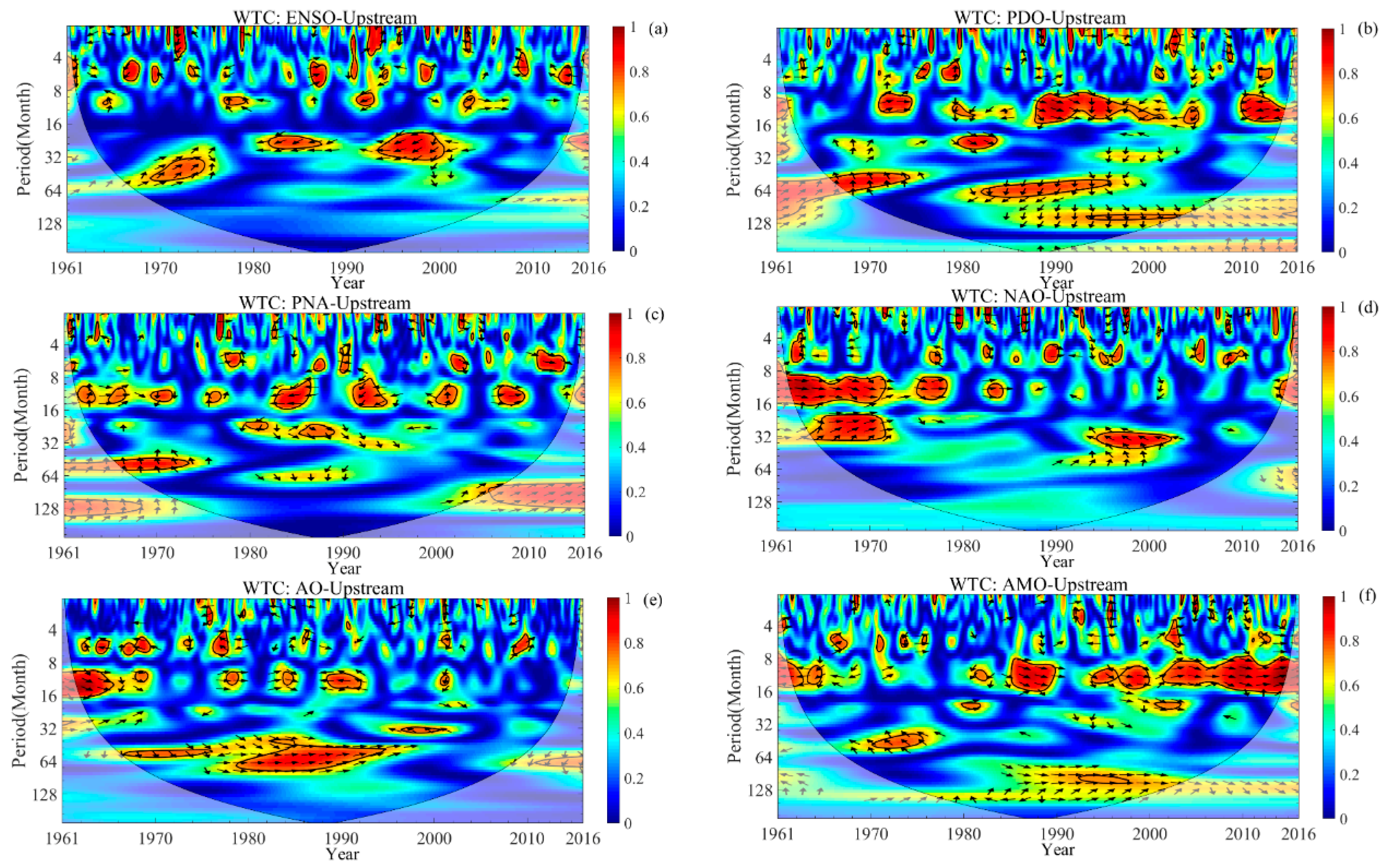
| Station | Longitude (E) | Latitude (N) | Elevation (m) | ATP | ATD | API | AMRD |
|---|---|---|---|---|---|---|---|
| Qilian | 100.24° | 38.19° | 2787.4 | 368.13 | 70.82 | 10.11 | 0.10 |
| Yeniugou | 99.58° | 38.41° | 3286.0 | 270.98 | 75.73 | 10.00 | 0.10 |
| Tuole | 98.01° | 39.03° | 3283.0 | 374.78 | 52.96 | 9.23 | 0.08 |
| Gangcha | 100.11° | 37.25° | 3309.0 | 354.59 | 67.46 | 9.40 | 0.10 |
| Menyuan | 101.38° | 37.25° | 2867.0 | 475.45 | 85.73 | 10.40 | 0.13 |
| Gaotai | 99.79° | 39.36° | 1332.2 | 97.30 | 23.32 | 5.70 | 0.05 |
| Shandan | 101.08° | 38.77° | 1764.6 | 179.87 | 36.71 | 7.25 | 0.07 |
| Yongchang | 101.58° | 38.18° | 1976.1 | 184.98 | 39.43 | 6.98 | 0.07 |
| Jiuquan | 98.49° | 39.70° | 1477.2 | 78.61 | 19.86 | 5.26 | 0.04 |
| Zhangye | 100.46° | 38.91° | 1482.7 | 114.08 | 26.77 | 5.86 | 0.05 |
| Station | ATP | ATD | API | AMRD |
|---|---|---|---|---|
| Qilian | 1.96 a | 0.35 | 1.48 | 0.91 |
| Yeniugou | 3.56 b | 1.82 | 2.72 b | 1.61 |
| Tuole | 3.27 b | 2.11 a | 2.44 a | 1.99 a |
| Gangcha | 2.18 a | 0.66 | 1.51 | −0.76 |
| Menyuan | 0.88 | −1.31 | 1.34 | 0.93 |
| Gaotai | 1.28 | 2.7 b | −0.05 | 2.3 a |
| Shandan | 1.36 | 1.53 | 1.86 | 0.42 |
| Yongchang | 2.27 a | 2.62 b | 0.29 | 2.45 a |
| Jiuquan | 1.18 | 1.78 | 0.25 | 1.77 |
| Zhangye | 0.49 | 0.44 | 0.54 | 0.37 |
| Precipitation Indices | Definitions | Units |
|---|---|---|
| ATP | Annual total precipitation amount when precipitation ≥1 mm | mm |
| ATD | Annual total rainy days | day |
| API | Annual precipitation intensity | mm/day |
| AMRD | Annual mean rainy days | day |
| W/A | The ratio between the average of the total monthly precipitation during December and February of the next year and the total annual precipitation | % |
| SP/A | The ratio between the average of the total monthly precipitation during March and May of the next year and the total annual wet precipitation | % |
| SU/A | The ratio between the average of the total monthly precipitation during June and August of the next year and the total annual wet precipitation | % |
| AU/A | The ratio between the average of the total monthly precipitation during September and November of the next year and the total annual wet precipitation | % |
| W/SP | Ratio between winter precipitation and spring precipitation | % |
| SP/SU | Ratio between spring precipitation and summer precipitation | % |
| SU/AU | Ratio between summer precipitation and autumn precipitation | % |
| AU/W | Ratio between autumn precipitation and winter precipitation | % |
| MAX | Ratio between the maximum monthly average precipitation and total annual precipitation | % |
| MIN | Ratio between the minimum monthly average precipitation and total annual precipitation | % |
| CI | Ratio between the minimum and the maximum monthly average precipitation | % |
| CV | Ratio between the standard deviation and the average monthly precipitation | % |
| Regions | Lag Time (Months) | Correlations | ENSO | AO | NAO | PNA | PDO | AMO |
|---|---|---|---|---|---|---|---|---|
| UHRB | 0 | Pearson | −0.016 | 0.033 | 0.077 a | 0.019 | −0.020 | 0.168 b |
| Kendall | 0.009 | 0.024 | 0.072 b | −0.016 | −0.014 | 0.082 b | ||
| Spearman | 0.014 | 0.041 | 0.106 b | −0.025 | −0.021 | 0.122 b | ||
| 1 | Pearson | −0.016 | 0.052 | 0.053 | −0.014 | 0.039 | 0.162 b | |
| Kendall | 0.012 | 0.040 | 0.064 a | −0.024 | 0.033 | 0.087 b | ||
| Spearman | 0.019 | 0.065 | 0.094 a | −0.034 | 0.050 | 0.130 b | ||
| 3 | Pearson | −0.003 | 0.063 | 0.014 | −0.058 | 0.145 b | 0.084 | |
| Kendall | 0.015 | 0.022 | −0.001 | −0.021 | 0.095 b | 0.056 a | ||
| Spearman | 0.022 | 0.031 | −0.001 | −0.030 | 0.14 b | 0.081 a | ||
| 6 | Pearson | 0.006 | −0.042 | −0.094 a | 0.044 | 0.060 | −0.065 | |
| Kendall | −0.009 | 0.001 | −0.061 a | 0.017 | 0.035 | −0.038 | ||
| Spearman | −0.015 | −0.007 | −0.090 a | 0.027 | 0.053 | −0.056 | ||
| 9 | Pearson | 0.047 | −0.019 | 0.015 | 0.027 | −0.106 b | −0.036 | |
| Kendall | 0.002 | −0.029 | −0.002 | 0.038 | −0.070 b | −0.021 | ||
| Spearman | 0.004 | −0.043 | −0.004 | 0.055 | −0.103 b | −0.030 | ||
| 12 | Pearson | 0.030 | 0.013 | 0.058 | 0.023 | 0.006 | 0.143 b | |
| Kendall | 0.019 | 0.004 | 0.068 b | −0.016 | −0.005 | 0.076 b | ||
| Spearman | 0.027 | 0.012 | 0.100 b | −0.024 | −0.007 | 0.113 b | ||
| MHRB | 0 | Pearson | −0.013 | 0.048 | 0.032 | 0.027 | 0.024 | 0.112 b |
| Kendall | 0.027 | 0.039 | 0.056 a | 0.010 | 0.010 | 0.090 b | ||
| Spearman | 0.044 | 0.069 | 0.085 a | 0.018 | 0.015 | 0.133 b | ||
| 1 | Pearson | −0.003 | 0.059 | 0.037 | −0.025 | 0.099 a | 0.104 b | |
| Kendall | 0.036 | 0.020 | 0.015 | −0.014 | 0.053 a | 0.093 b | ||
| Spearman | 0.059 | 0.029 | 0.022 | -.022 | 0.079 a | 0.139 b | ||
| 3 | Pearson | 0.040 | 0.031 | −0.019 | −0.005 | 0.153 b | 0.032 | |
| Kendall | 0.050 | 0.019 | −0.024 | 0.001 | 0.101 b | 0.043 | ||
| Spearman | 0.076 a | 0.030 | −0.036 | 0.003 | 0.148 b | 0.066 | ||
| 6 | Pearson | 0.067 | −0.059 | −0.070 | 0.051 | 0 | −0.076 | |
| Kendall | 0.038 | −0.021 | −0.063 a | 0.038 | 0.013 | −0.031 | ||
| Spearman | 0.056 | −0.033 | −0.092 a | 0.058 | 0.020 | −0.046 | ||
| 9 | Pearson | 0.090 a | 0.016 | 0.026 | −0.007 | −0.063 | 0.001 | |
| Kendall | 0.050 | 0.008 | 0.027 | 0.035 | −0.037 | 0.004 | ||
| Spearman | 0.075 | 0.011 | 0.041 | 0.051 | −0.055 | 0.007 | ||
| 12 | Pearson | 0.038 | 0.042 | 0.066 | 0.015 | 0.028 | 0.087 a | |
| Kendall | 0.034 | 0.026 | 0.063 a | −0.015 | 0.011 | 0.065 a | ||
| Spearman | 0.049 | 0.045 | 0.094 a | −0.022 | 0.017 | 0.096 a |
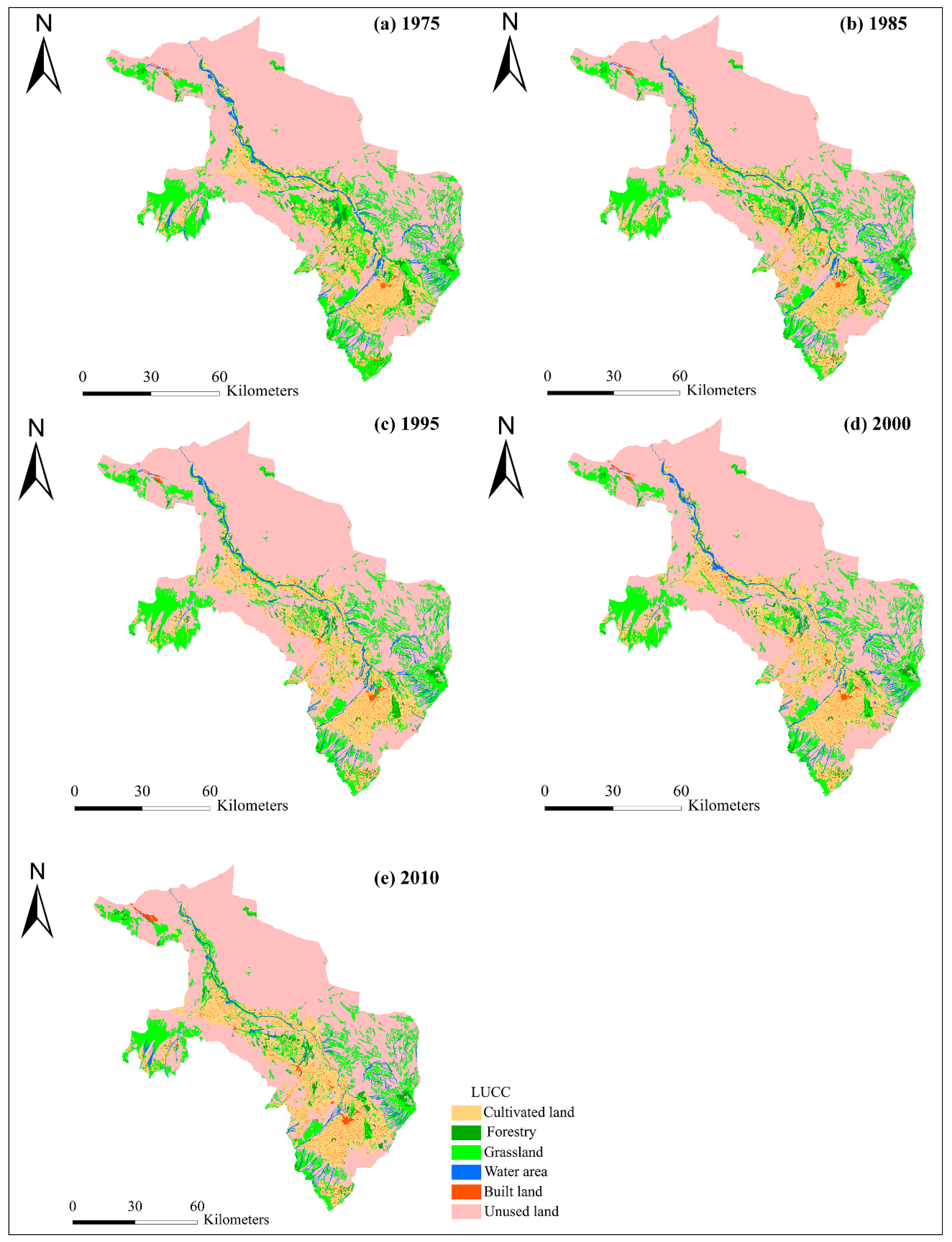
| Land Use Types | Cultivated Land | Woodland | Grassland | Water Area | Built on Land | Unused Land |
| Cultivated land | 0.04 | 0.26 | 0.05 | 0.28 | 0.15 | |
| Woodland | 0.42 | 0.21 | 0.01 | 0.01 | 0.12 | |
| Grassland | 3.97 | 0.26 | 0.16 | 0.06 | 1.71 | |
| Water area | 0.53 | 0.02 | 0.34 | 0.01 | 0.19 | |
| Built land | 0.06 | 0.00 | 0.00 | 0.01 | 0.00 | |
| Unused land | 1.84 | 0.38 | 1.46 | 0.14 | 0.22 | |
| Cultivated Land | Woodland | Grassland | Water Area | Built on Land | Unused Land | |
| 1975–1987 | 14.40 | 1.52 | 15.33 | 2.22 | 1.60 | 65.52 |
| 1987–1992 | 15.25 | 1.21 | 14.49 | 2.04 | 1.34 | 66.88 |
| 1992–2001 | 16.48 | 1.23 | 14.29 | 2.11 | 1.41 | 67.04 |
| 2000–2010 | 17.88 | 1.25 | 13.03 | 1.80 | 1.71 | 63.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, F.; Cheng, Q.; Ge, Y. Relationships between Spatial and Temporal Variations in Precipitation, Climatic Indices, and the Normalized Differential Vegetation Index in the Upper and Middle Reaches of the Heihe River Basin, Northwest China. Water 2019, 11, 1394. https://doi.org/10.3390/w11071394
Zhong F, Cheng Q, Ge Y. Relationships between Spatial and Temporal Variations in Precipitation, Climatic Indices, and the Normalized Differential Vegetation Index in the Upper and Middle Reaches of the Heihe River Basin, Northwest China. Water. 2019; 11(7):1394. https://doi.org/10.3390/w11071394
Chicago/Turabian StyleZhong, Fanglei, Qingping Cheng, and Yinchun Ge. 2019. "Relationships between Spatial and Temporal Variations in Precipitation, Climatic Indices, and the Normalized Differential Vegetation Index in the Upper and Middle Reaches of the Heihe River Basin, Northwest China" Water 11, no. 7: 1394. https://doi.org/10.3390/w11071394
APA StyleZhong, F., Cheng, Q., & Ge, Y. (2019). Relationships between Spatial and Temporal Variations in Precipitation, Climatic Indices, and the Normalized Differential Vegetation Index in the Upper and Middle Reaches of the Heihe River Basin, Northwest China. Water, 11(7), 1394. https://doi.org/10.3390/w11071394







