Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting
Abstract
1. Introduction
2. Methodology
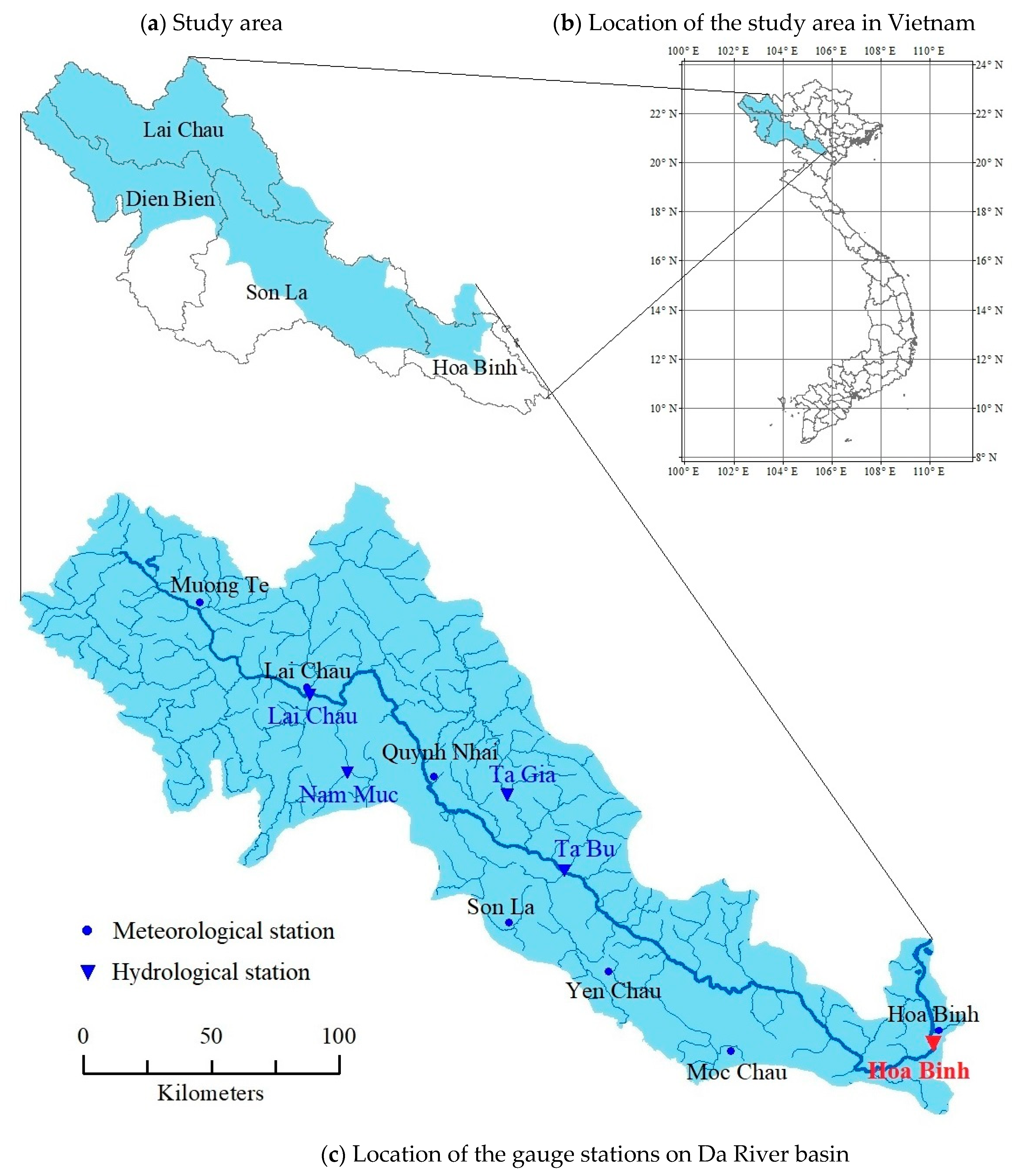
2.1. Study Area and Data
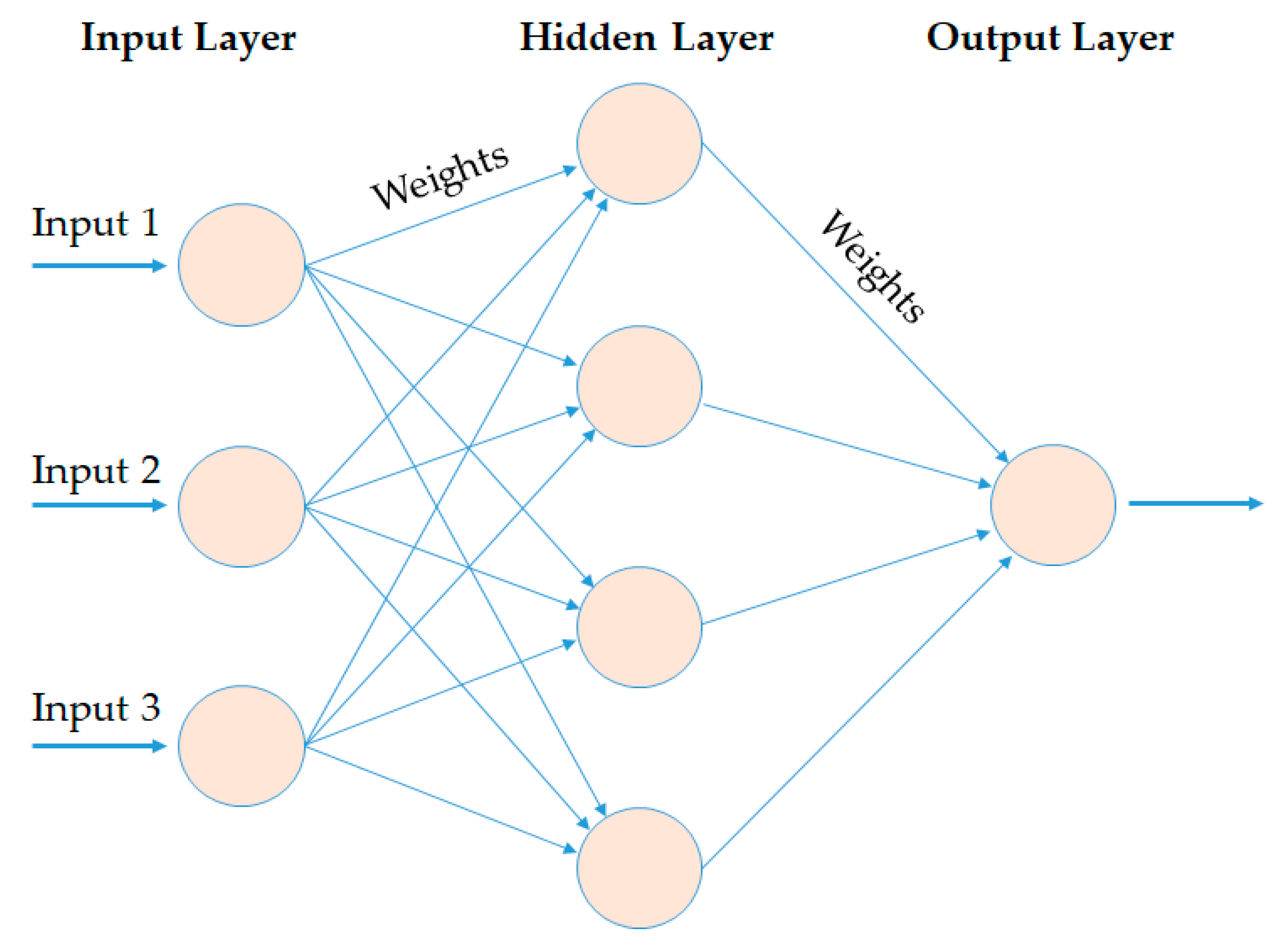
2.2. Artificial Neural Network (ANN)
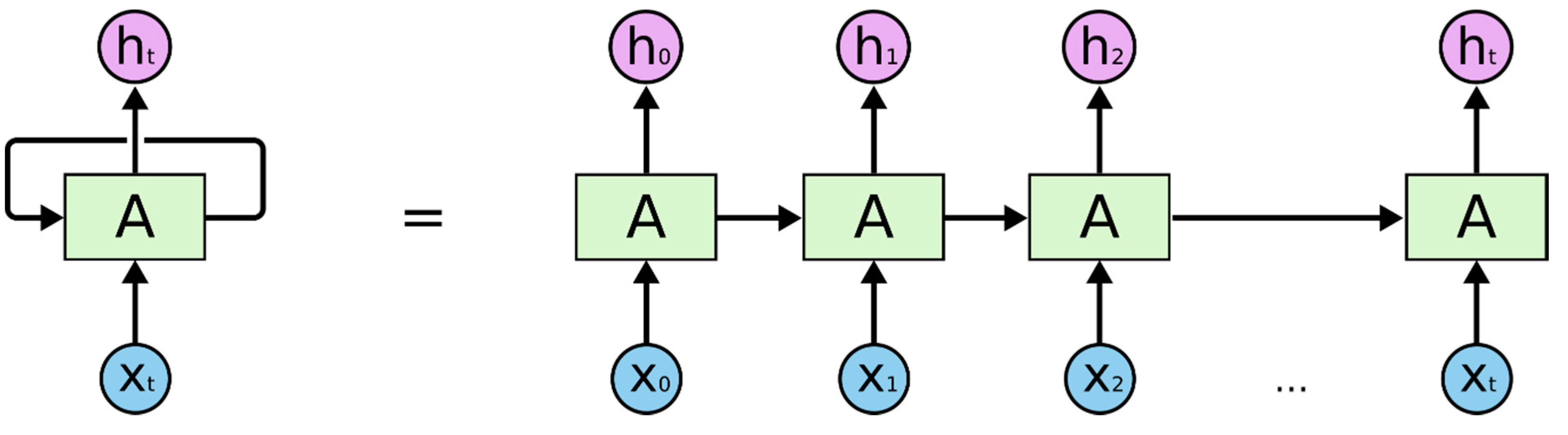
2.3. Recurrent Neural Network (RNN)
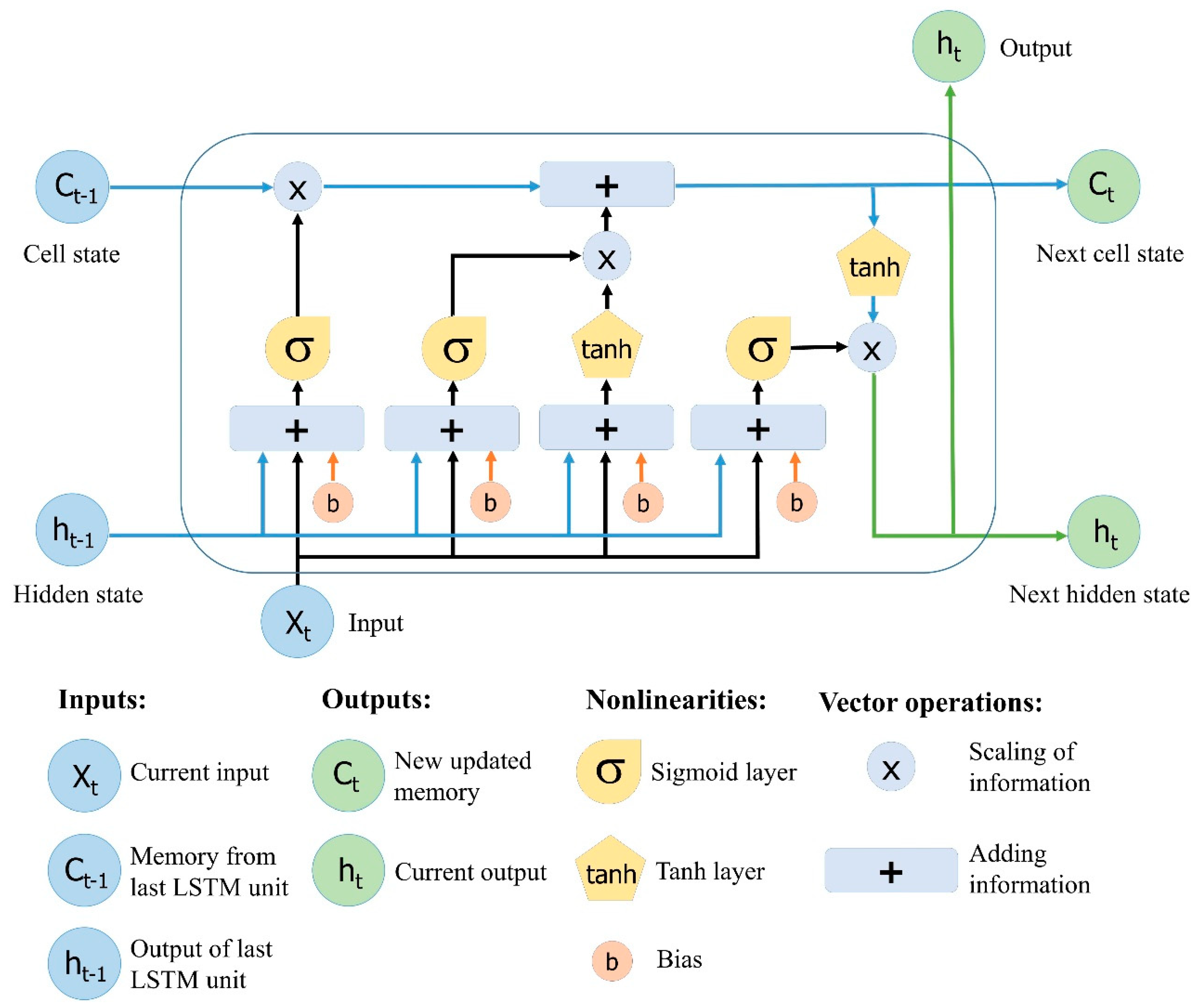
2.4. Long Short-Term Memory (LSTM) Neural Network
2.5. Model Evaluation Criteria
3. Model Structure
3.1. Scenarios
3.2. Model Design
4. Results and Discussion
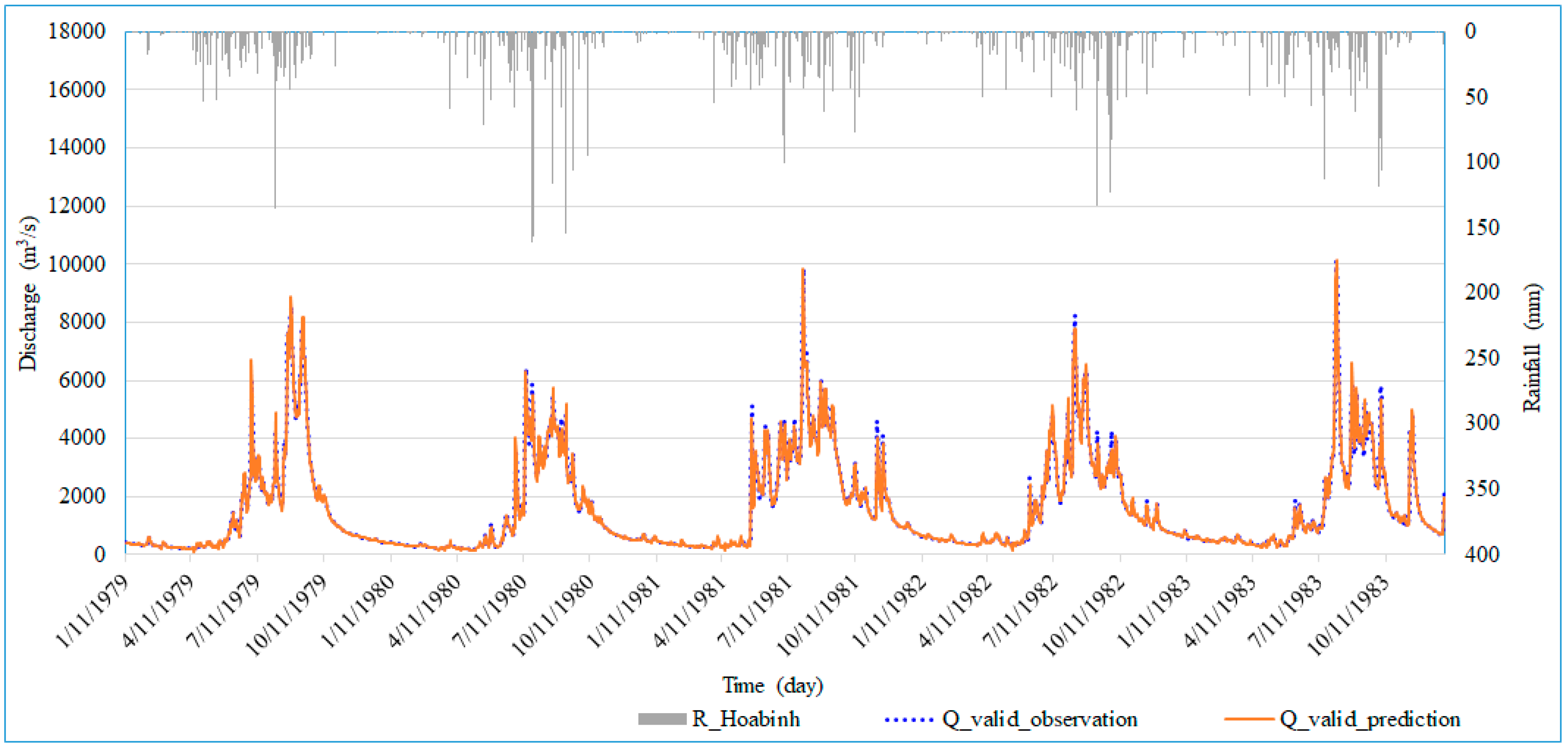
4.1. Validation Results
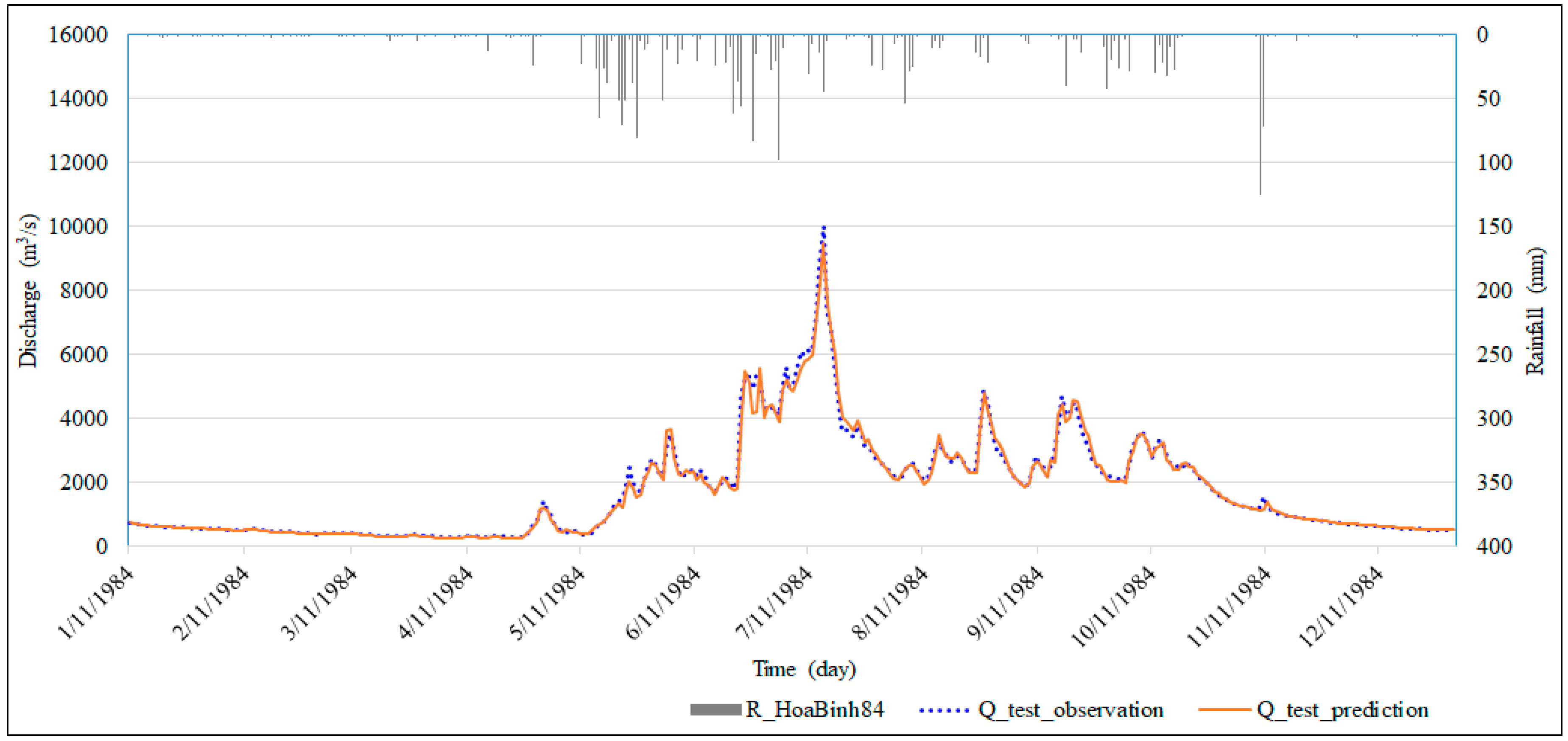
4.2. Test Results
4.2.1. Results for Testing Phase
4.2.2. Results for Flood Peak Forecasts
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thirumalaiah, K.C.; Deo, M. Hydrological forecasting using neural networks. J. Hydrol. Eng. 2000, 5, 180–189. [Google Scholar] [CrossRef]
- Kişi, Ö. A combined generalized regression neural network wavelet model for monthly streamflow prediction. KSCE J. Civ. Eng. 2011, 15, 1469–1479. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Hidayat, H.; Hoitink, A.J.F.; Sassi, M.G.; Torfs, P.J.J.F. Prediction of discharge in a tidal river using artificial neural networks. J. Hydrol. Eng. 2014, 19, 04014006. [Google Scholar] [CrossRef]
- Elsafi, S.H. Artificial neural networks (ANNs) for flood forecasting at Dongola station in the River Nile, Sudan. Alex. Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
- Khan, M.Y.A.; Hasan, F.; Panwar, S.; Chakrapani, G.J. Neural network model for discharge and water-level prediction for Ramganga River catchment of Ganga basin, India. Hydrol. Sci. J. 2016, 61, 2084–2095. [Google Scholar] [CrossRef]
- Sung, J.; Lee, J.; Chung, I.-M.; Heo, J.-H. Hourly water level forecasting at tributary affected by main river condition. Water 2017, 9, 644. [Google Scholar] [CrossRef]
- Yu, P.-S.; Chen, S.-T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Improving real time flood forecasting using fuzzy inference system. J. Hydrol. 2014, 509, 25–41. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP neural network algorithm in traditional hydrological model for flood forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Sahay, R.R.; Srivastava, A. Predicting monsoon floods in rivers embedding wavelet transform, genetic algorithm and neural network. Water Resour. Manag. 2014, 28, 301–317. [Google Scholar] [CrossRef]
- Londhe, S.; Charhate, S. Comparison of data-driven modelling techniques for river flow forecasting. Hydrol. Sci. J. 2010, 55, 1163–1174. [Google Scholar] [CrossRef]
- Makwana, J.J.; Tiwari, M.K. Intermittent streamflow forecasting and extreme event modelling using wavelet based artificial neural networks. Water Resour. Manag. 2014, 28, 4857–4873. [Google Scholar] [CrossRef]
- Govindaraju, R.S. Artificial neural networks in hydrology. II: Hydrologic applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Govindaraju, R.S. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 2, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Mikolov, T.; Joulin, A.; Chopra, S.; Mathieu, M.; Ranzato, M.A. Learning longer memory in recurrent neural networks. arXiv 2014, arXiv:1412.7753. [Google Scholar]
- Li, Y.; Cao, H. Prediction for tourism flow based on LSTM neural network. Procedia Comput. Sci. 2018, 129, 277–283. [Google Scholar] [CrossRef]
- Yanjie, D.; Yisheng, L.; Fei-Yue, W. Travel time prediction with LSTM neural network. In Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1053–1058. [Google Scholar] [CrossRef]
- Nelson, D.M.Q.; Pereira, A.C.M.; de Oliveira, R.A. Stock market’s price movement prediction with LSTM neural networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1419–1426. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Le, X.-H.; Ho, V.H.; Lee, G.; Jung, S. A deep neural network application for forecasting the inflow into the Hoa Binh reservoir in Vietnam. In Proceedings of the 11th International Symposium on Lowland Technology (ISLT 2018), Hanoi, Vietnam, 26–28 September 2018. [Google Scholar]
- Aichouri, I.; Hani, A.; Bougherira, N.; Djabri, L.; Chaffai, H.; Lallahem, S. River flow model using artificial neural networks. Energy Procedia 2015, 74, 1007–1014. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Werbos, P.J. Generalization of backpropagation with application to a recurrent gas market model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Olah, C. Understanding LSTM Networks. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 26 June 2018).
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Hochreiter, S.; Bengio, Y.; Frasconi, P. Gradient flow in recurrent nets: The difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Networks; Kolen, J., Kremer, S., Eds.; Wiley-IEEE Press: Piscataway, NJ, USA, 2001. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. III-1310–III-1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yan, S. Understanding LSTM and Its Diagrams. Available online: https://medium.com/mlreview/understanding-lstm-and-its-diagrams-37e2f46f1714 (accessed on 26 June 2018).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models Part I—A discussion of principles. J. Hydrol. Eng. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rossum, G. Python Tutorial; CWI (Centre for Mathematics and Computer Science): Amsterdam, The Netherlands, 1995. [Google Scholar]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
| No. | Stations | Items | Value | Unit | Period (24 years) | Time |
|---|---|---|---|---|---|---|
| 1 | Muong Te | Maximum Daily Precipitation | 197.4 | mm | 1961–1984 | 14 July1970 |
| 2 | Lai Chau | Maximum Daily Precipitation | 197.5 | mm | 1961–1984 | 13 June 1961 |
| 3 | Quynh Nhai | Maximum Daily Precipitation | 169.9 | mm | 1961–1984 | 13 June 1980 |
| 4 | Son La | Maximum Daily Precipitation | 198 | mm | 1961–1984 | 29 June 1980 |
| 5 | Yen Chau | Maximum Daily Precipitation | 172 | mm | 1961–1984 | 16 July 1965 |
| 6 | Moc Chau | Maximum Daily Precipitation | 166.7 | mm | 1961–1984 | 13 June 1965 |
| 7 | Hoa Binh | Maximum Daily Precipitation | 176.2 | mm | 1961–1984 | 9 July 1973 |
| 8 | Ta Gia | Peak Flood Discharge | 3320 | m3/s | 1961–1984 | 15 July 1970 |
| 9 | Nam Muc | Peak Flood Discharge | 1680 | m3/s | 1961–1984 | 8 July 1964 |
| 10 | Lai Chau | Peak Flood Discharge | 10,200 | m3/s | 1961–1984 | 18 August 1971 |
| 11 | Ta Bu | Peak Flood Discharge | 15,300 | m3/s | 1961–1984 | 8 July 1964 |
| 12 | Hoa Binh 1 | Peak Flood Discharge | 16,900 | m3/s | 1961–1984 | 9 July 1964 |
| No | Stations | Items | Latitude | Longitude | Period (24 Years) | Correlation Coefficient of Data | Location (Province) |
|---|---|---|---|---|---|---|---|
| 1 | Muong Te | R | 22°22′ | 102°50′ | 1961–1984 | 0.30 | Lai Chau |
| 2 | Lai Chau | R | 22°04′ | 103°09′ | 1961–1984 | 0.24 | Dien Bien |
| 3 | Quynh Nhai | R | 21°51′ | 103°34′ | 1961–1984 | 0.18 | Son La |
| 4 | Son La | R | 21°20′ | 103°54′ | 1961–1984 | 0.23 | Son La |
| 5 | Yen Chau | R | 21°03′ | 104°18′ | 1961–1984 | 0.24 | Son La |
| 6 | Moc Chau | R | 20°50′ | 104°41′ | 1961–1984 | 0.25 | Son La |
| 7 | Hoa Binh | R | 20°49′ | 105°20′ | 1961–1984 | 0.21 | Hoa Binh |
| 8 | Ta Gia | Q | 21°47′ | 103°48′ | 1961–1984 | 0.77 | Lai Chau |
| 9 | Nam Muc | Q | 21°52′ | 103°17′ | 1961–1984 | 0.83 | Dien Bien |
| 10 | Lai Chau | Q | 22°04′ | 103°09′ | 1961–1984 | 0.95 | Dien Bien |
| 11 | Ta Bu | Q | 21°26′ | 104°03′ | 1961–1984 | 0.97 | Son La |
| 12 | Hoa Binh 1 | Q | 20°49′ | 105°19′ | 1961–1984 | 1.00 | Hoa Binh |
| Items | Detail |
|---|---|
| Prediction Target | Discharge forecasting at Hoa Binh Station for: - Day one - Day two - Day three |
| Input Variable | Observed daily rainfall and flow data include: - Rainfall data at seven meteorological stations - Flow rate data at five hydrological stations |
| Training Parameters | - Learning rate: 0.0001 - Number of units: 20; 30; 50 - Number of epochs: 100,000 |
| Forecast for | Case | Input Variable | Number of Units | Number of Epochs | RMSE (m3/s) | NSE (%) | |
|---|---|---|---|---|---|---|---|
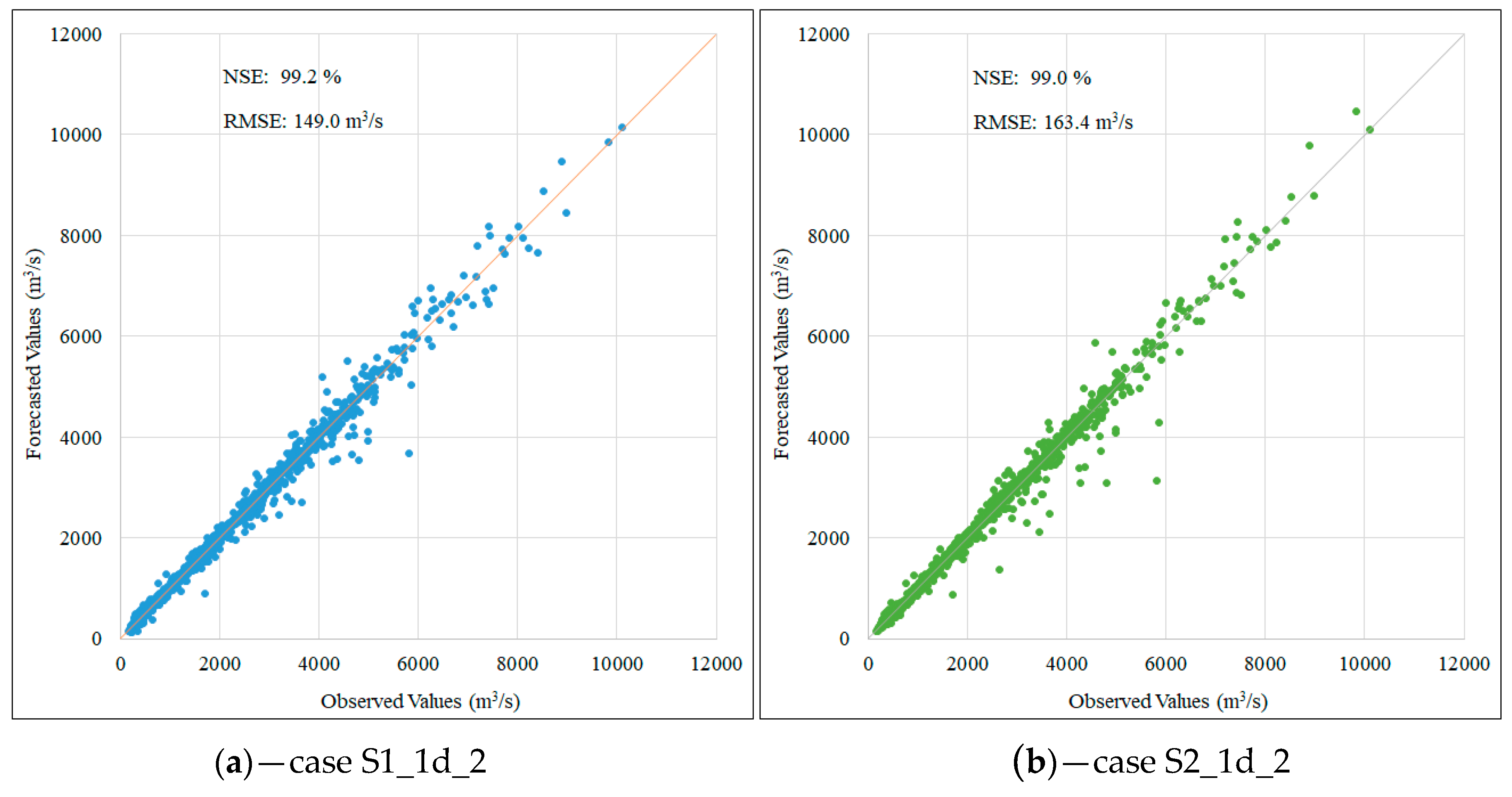
| One day | 1st scenario | S1_1d_1 | 12 | 20 | 6500 | 149.6 | 99.1 |
| S1_1d_2 | 12 | 30 | 8628 | 149.0 | 99.2 | ||
| S1_1d_3 | 12 | 50 | 6971 | 151.3 | 99.1 | ||
| 2nd scenario | S2_1d_1 | 5 | 20 | 7887 | 165.0 | 99.0 | |
| S2_1d_2 | 5 | 30 | 8474 | 163.4 | 99.0 | ||
| S2_1d_3 | 5 | 50 | 10,132 | 164.0 | 99.0 | ||
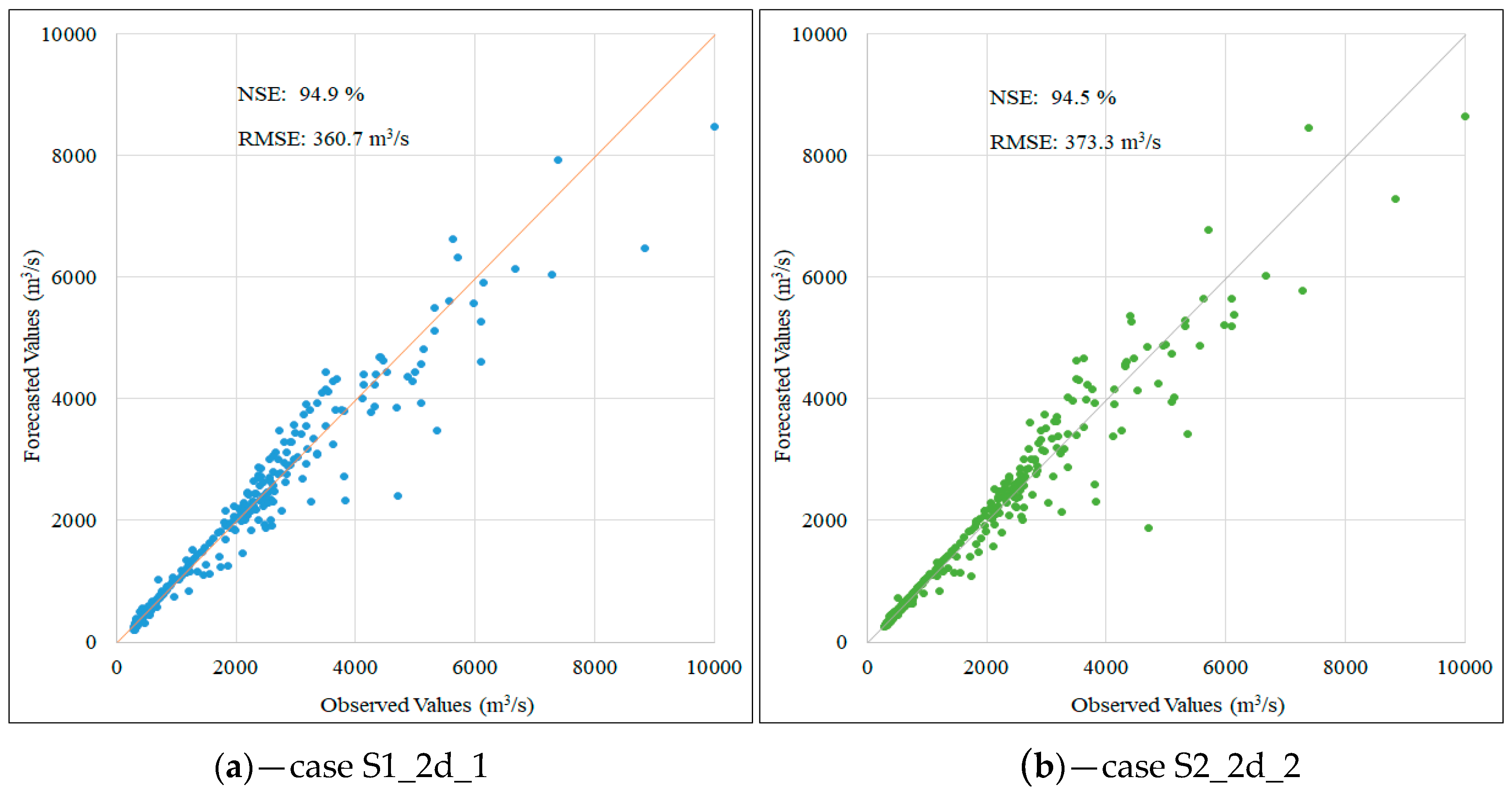
| Two days | 1st scenario | S1_2d_1 | 12 | 20 | 3636 | 366.1 | 94.9 |
| S1_2d_2 | 12 | 30 | 5494 | 367.7 | 94.9 | ||
| S1_2d_3 | 12 | 50 | 4772 | 367.4 | 94.9 | ||
| 2nd scenario | S2_2d_1 | 5 | 20 | 7683 | 374.2 | 94.7 | |
| S2_2d_2 | 5 | 30 | 7361 | 370.9 | 94.8 | ||
| S2_2d_3 | 5 | 50 | 7438 | 373.7 | 94.7 | ||
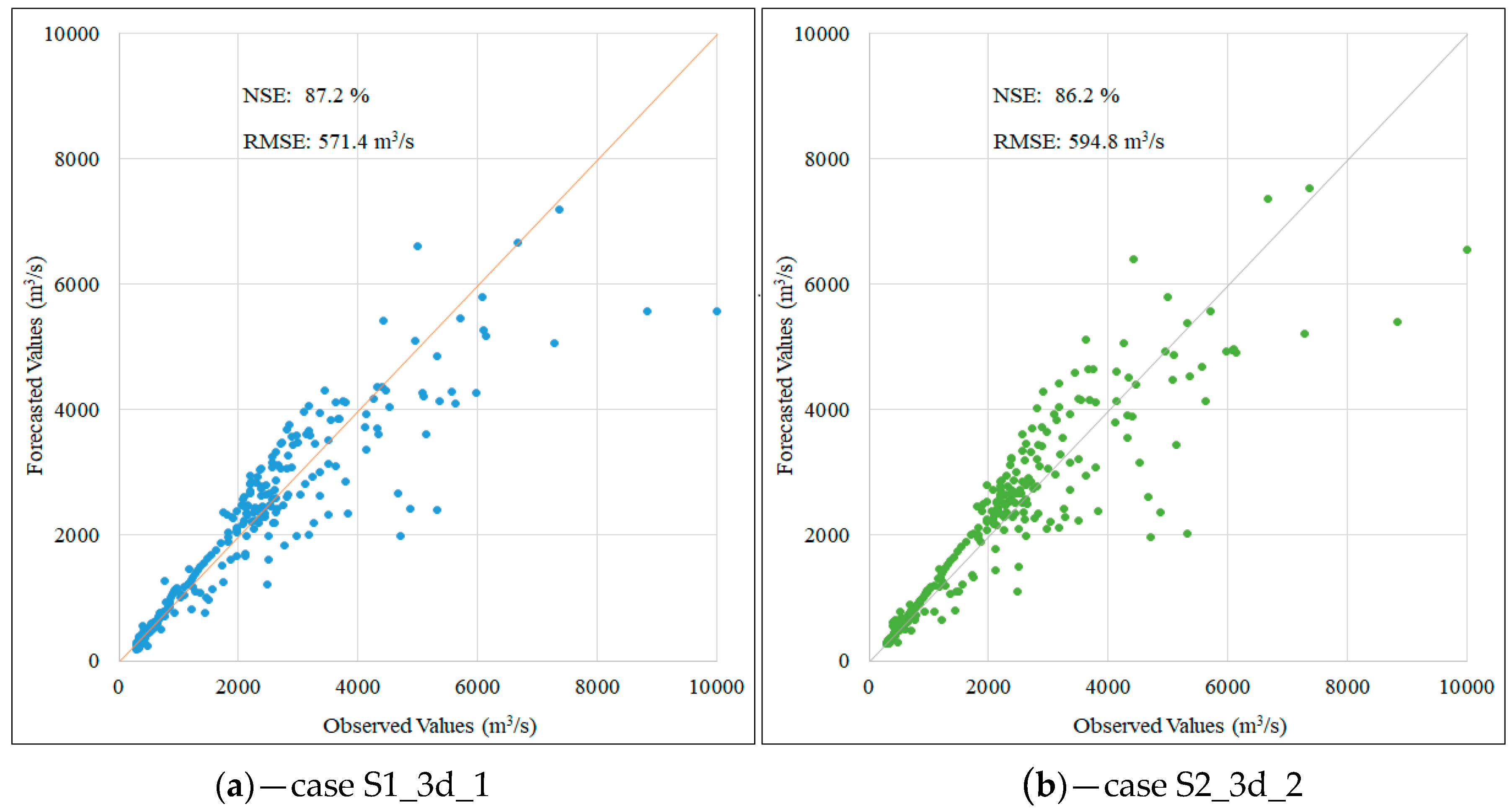
| Three days | 1st scenario | S1_3d_1 | 12 | 20 | 2654 | 567.3 | 87.8 |
| S1_3d_2 | 12 | 30 | 3075 | 573.1 | 87.5 | ||
| S1_3d_3 | 12 | 50 | 2296 | 584.8 | 87.0 | ||
| 2nd scenario | S2_3d_1 | 5 | 20 | 3655 | 589.7 | 86.8 | |
| S2_3d_2 | 5 | 30 | 4620 | 589.0 | 86.8 | ||
| S2_3d_3 | 5 | 50 | 4864 | 590.3 | 86.8 | ||
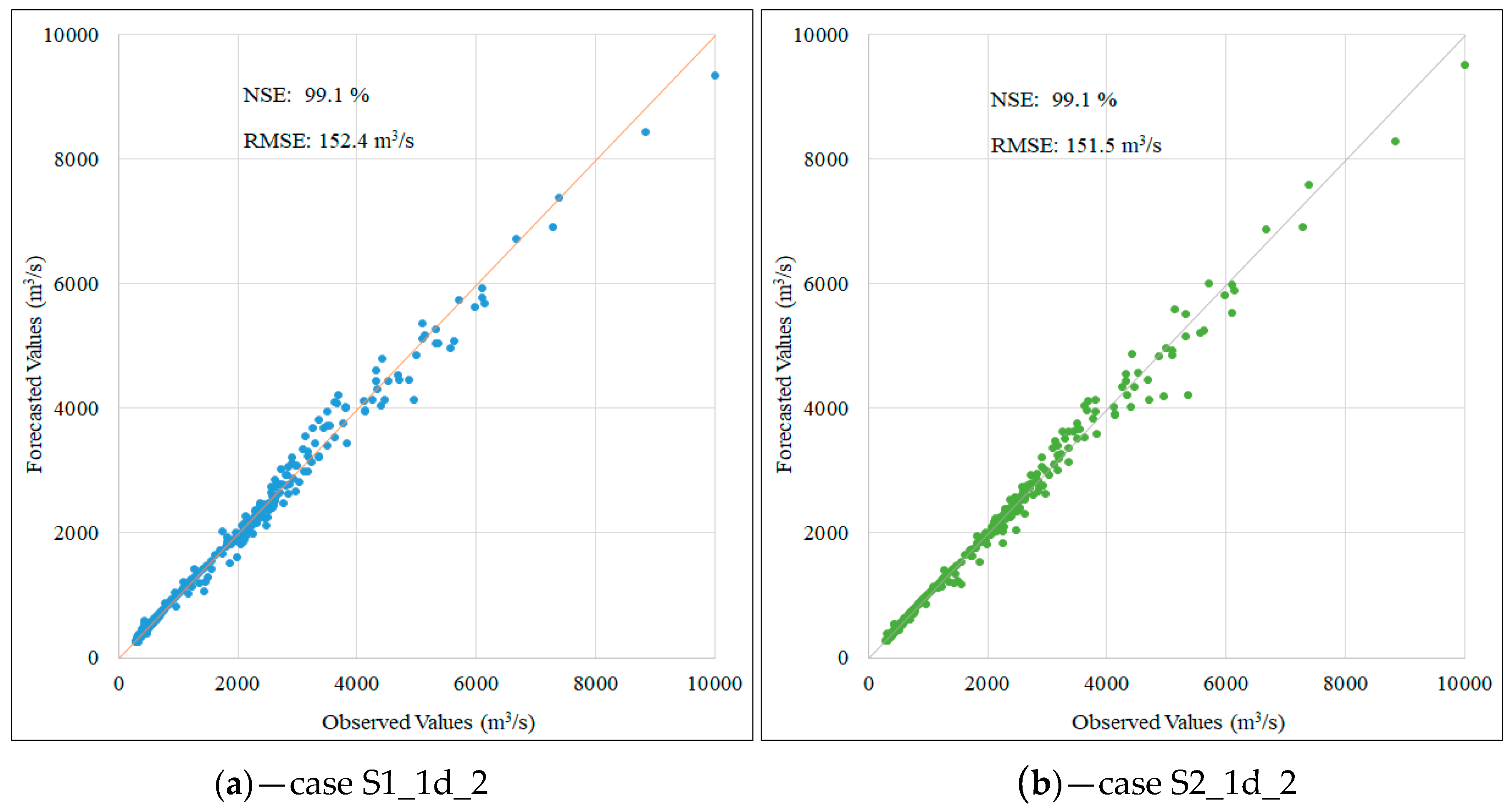
| Predict for | Case | RMSE Test (m3/s) | NSE Test (%) | Forecasted Peak (m3/s) | Observed Peak (m3/s) | Relative Error (%) |
|---|---|---|---|---|---|---|
| One day | S1_1d_2 | 152.4 | 99.1 | 9340 | 10,000 | 6.6 |
| S2_1d_2 | 151.5 | 99.1 | 9510 | 10,000 | 4.9 | |
| Two days | S1_2d_1 | 360.7 | 94.9 | 8477 | 10,000 | 15.2 |
| S2_2d_2 | 373.3 | 94.5 | 8632 | 10,000 | 13.7 | |
| Three days | S1_3d_1 | 571.4 | 87.2 | 7181 | 10,000 | 28.2 |
| S2_3d_2 | 594.0 | 86.2 | 7527 | 10,000 | 24.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, X.-H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. https://doi.org/10.3390/w11071387
Le X-H, Ho HV, Lee G, Jung S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water. 2019; 11(7):1387. https://doi.org/10.3390/w11071387
Chicago/Turabian StyleLe, Xuan-Hien, Hung Viet Ho, Giha Lee, and Sungho Jung. 2019. "Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting" Water 11, no. 7: 1387. https://doi.org/10.3390/w11071387
APA StyleLe, X.-H., Ho, H. V., Lee, G., & Jung, S. (2019). Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water, 11(7), 1387. https://doi.org/10.3390/w11071387







