Numerical Simulation and Experiment Study on the Characteristics of Non-Darcian Flow and Rheological Consolidation of Saturated Clay
Abstract
1. Introduction
2. Experimental Study on the Permeability Characteristics of Saturated Clay
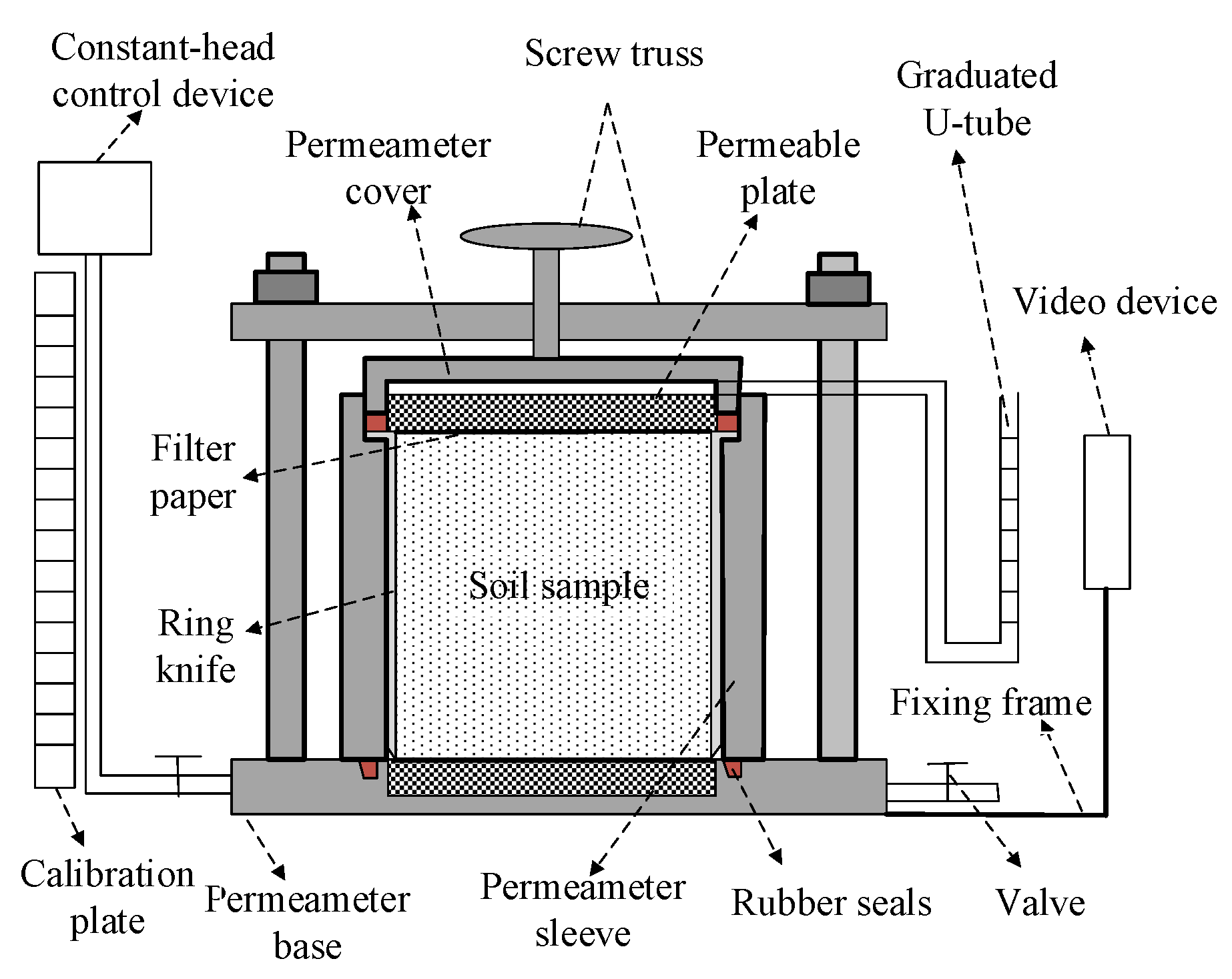
2.1. Constant-Head Permeability Test Device
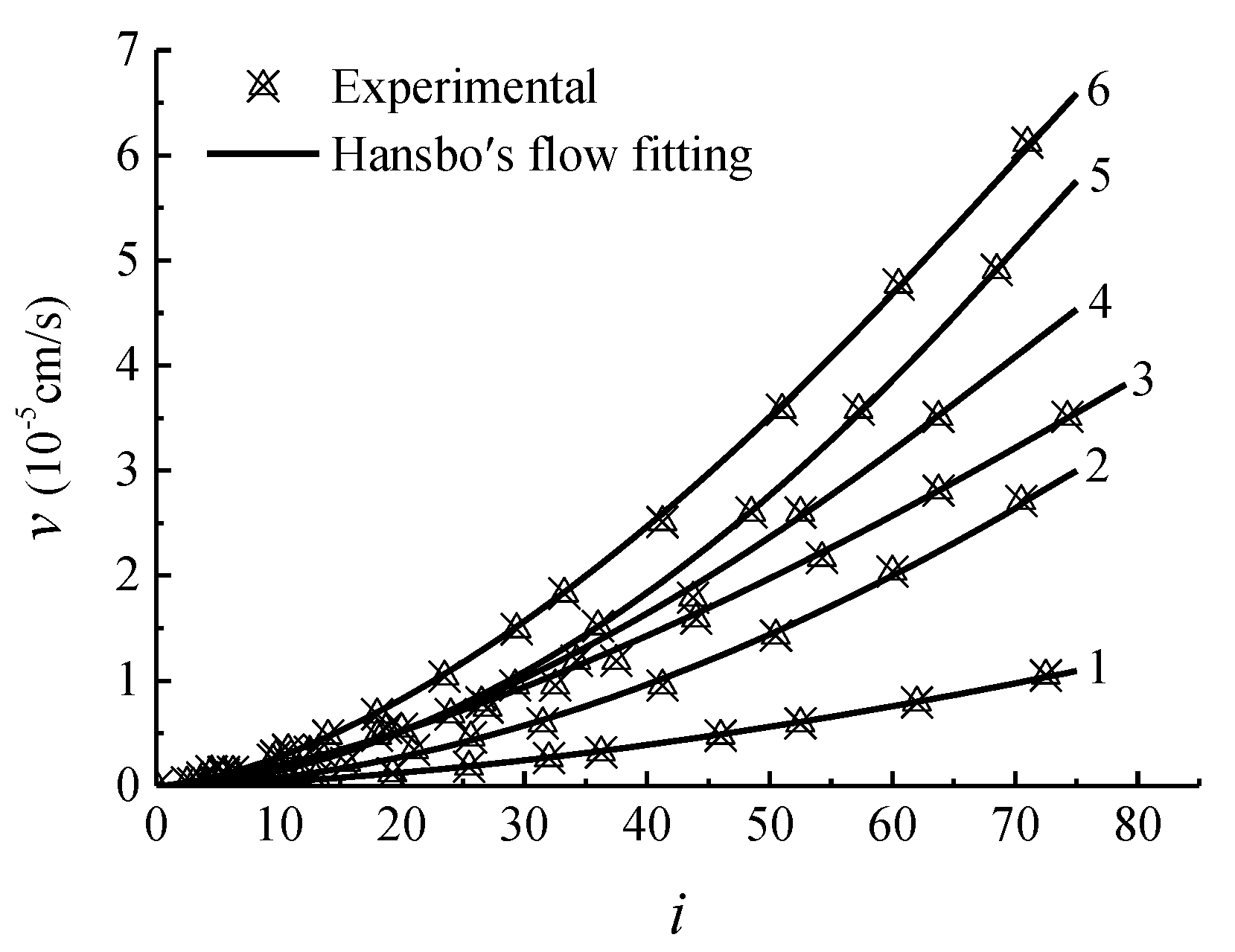
2.2. Permeability Test and Data Processing
3. Experimental Study on Rheological Consolidation Characteristics of Saturated Clay
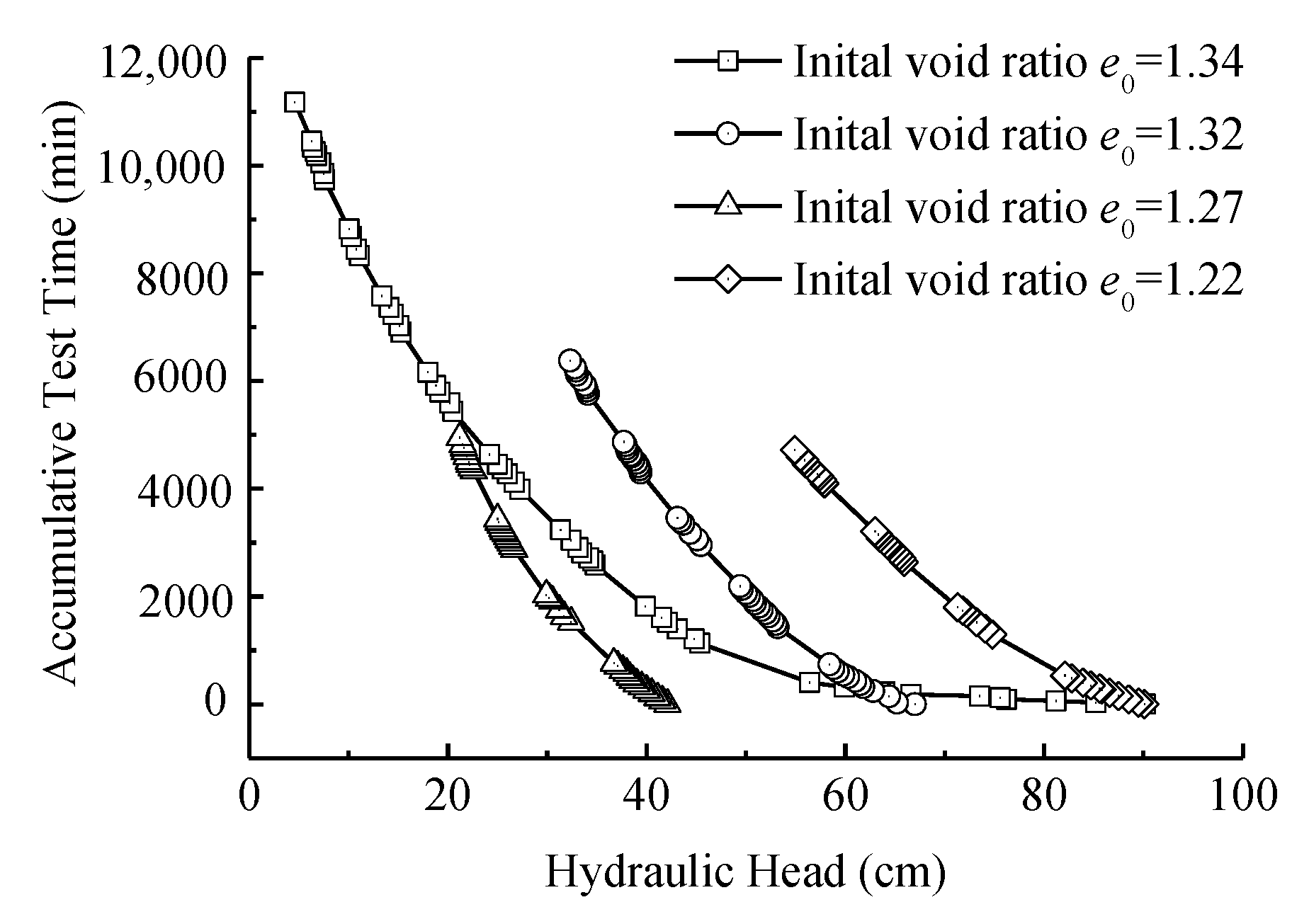
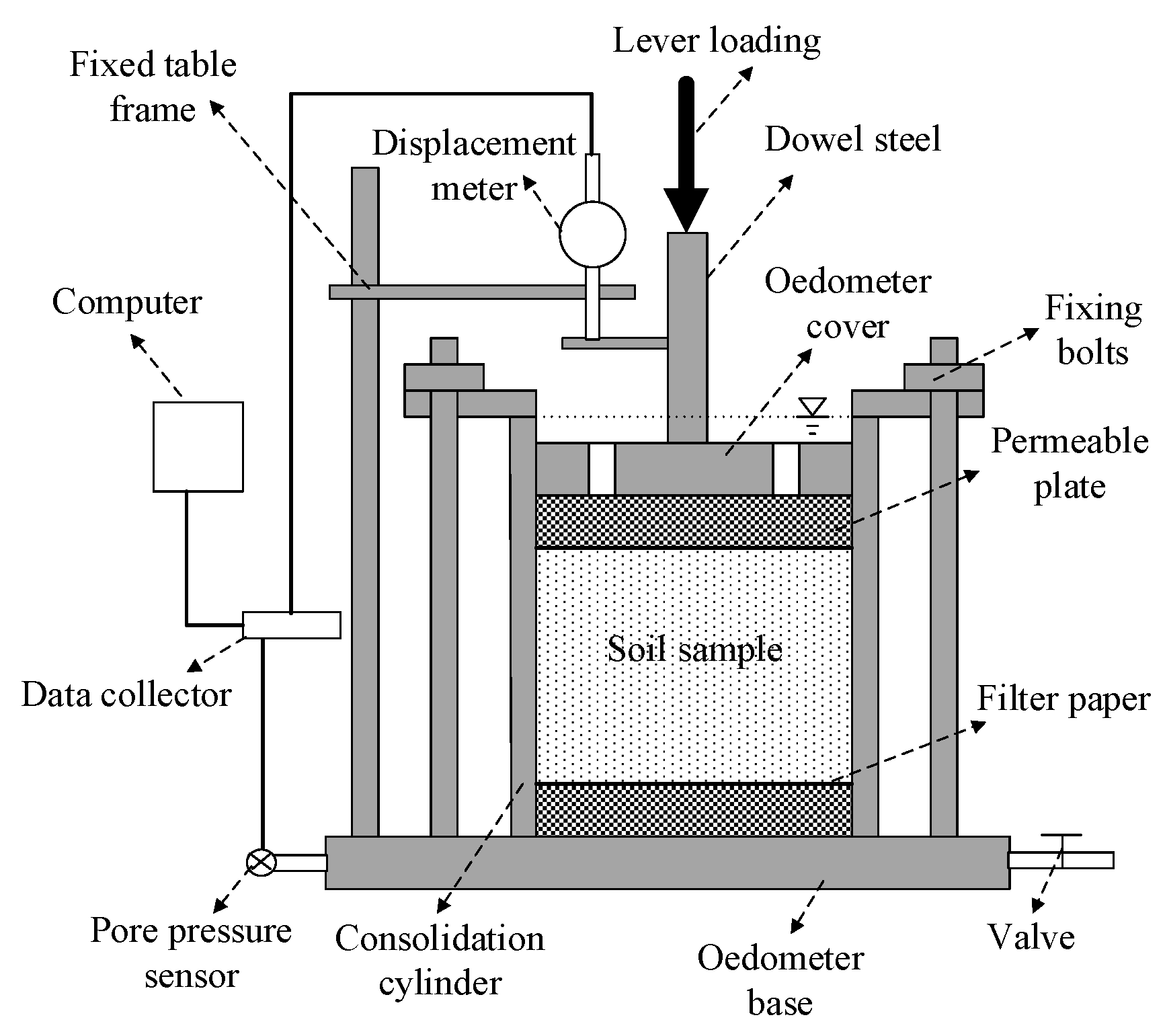
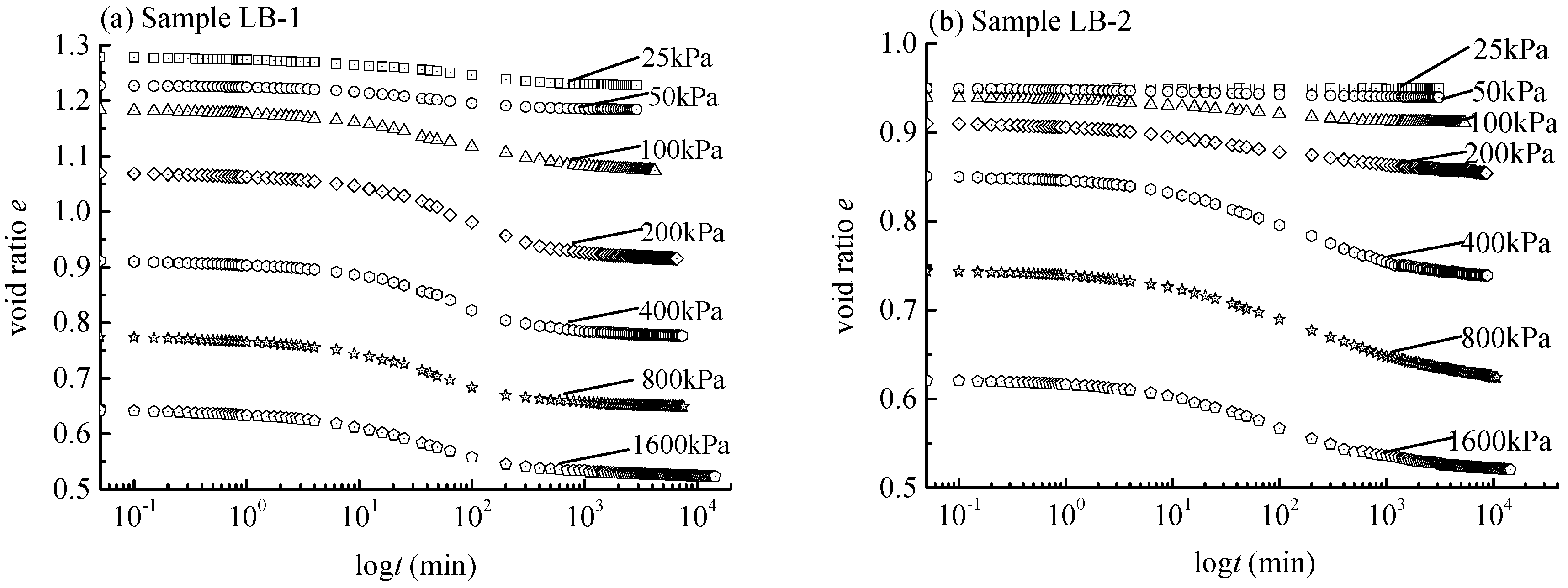
3.1. One-Dimensional Rheological Consolidation Test
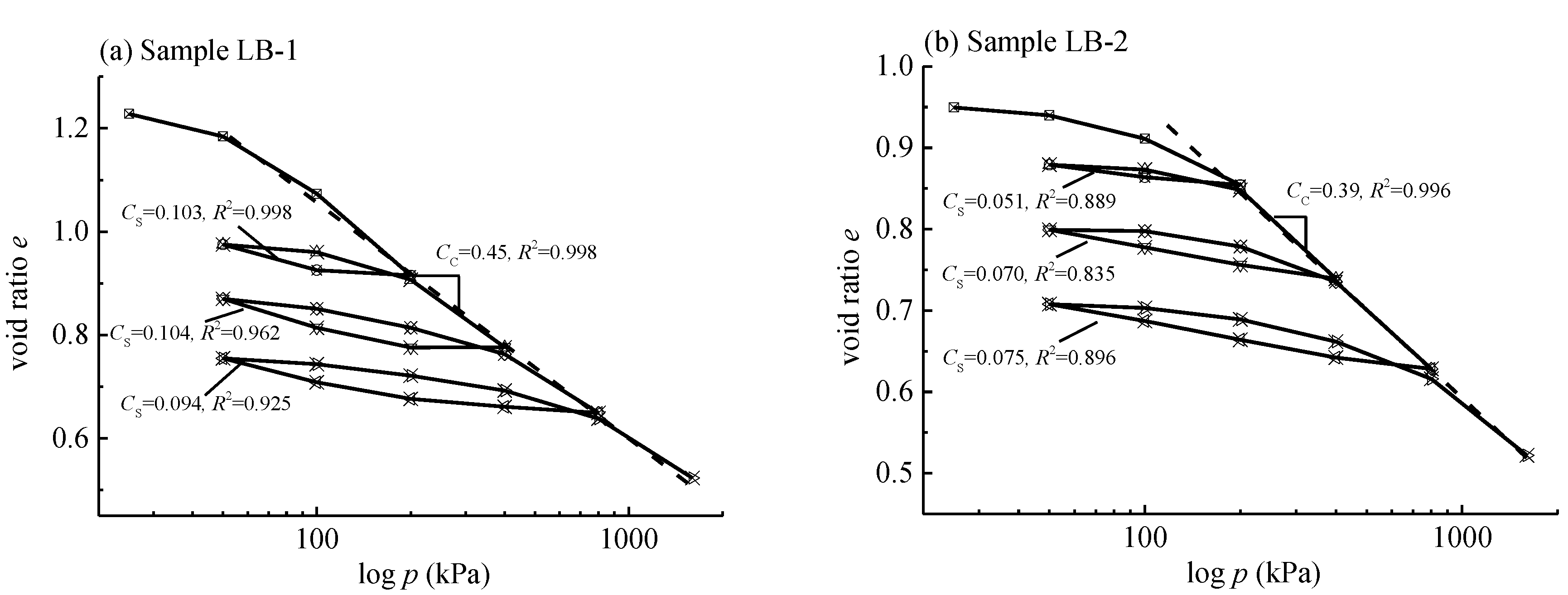
3.2. One-Dimensional Rheological Consolidation Test Data Processing
4. Derivation of Governing Equations
4.1. UH Model Considering Time Effect
4.2. One-Dimensional Rheological Consolidation Equation of UH Model
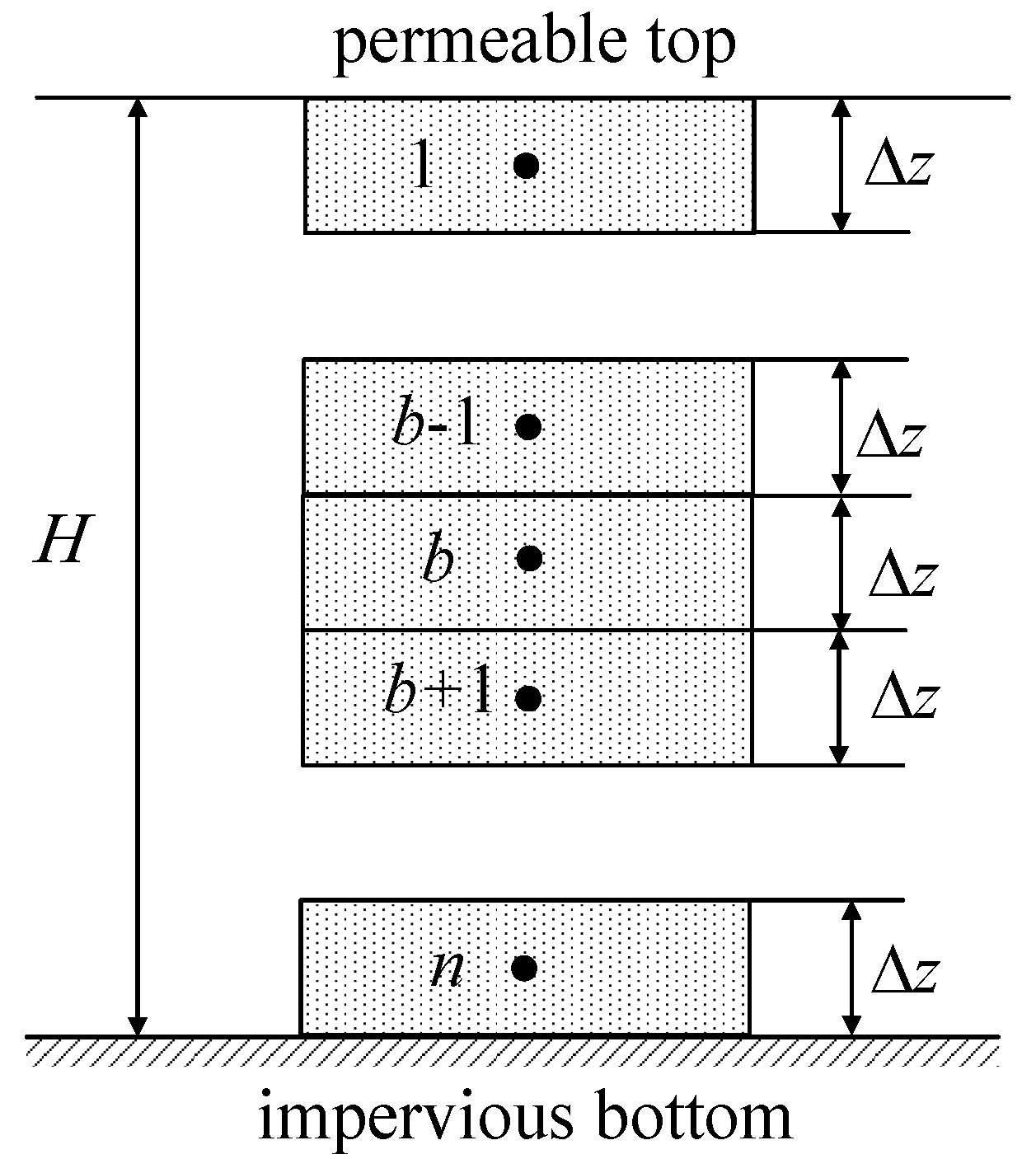
4.3. Discretization of the Governing Equation
5. Verification of the Suitability of UH Model
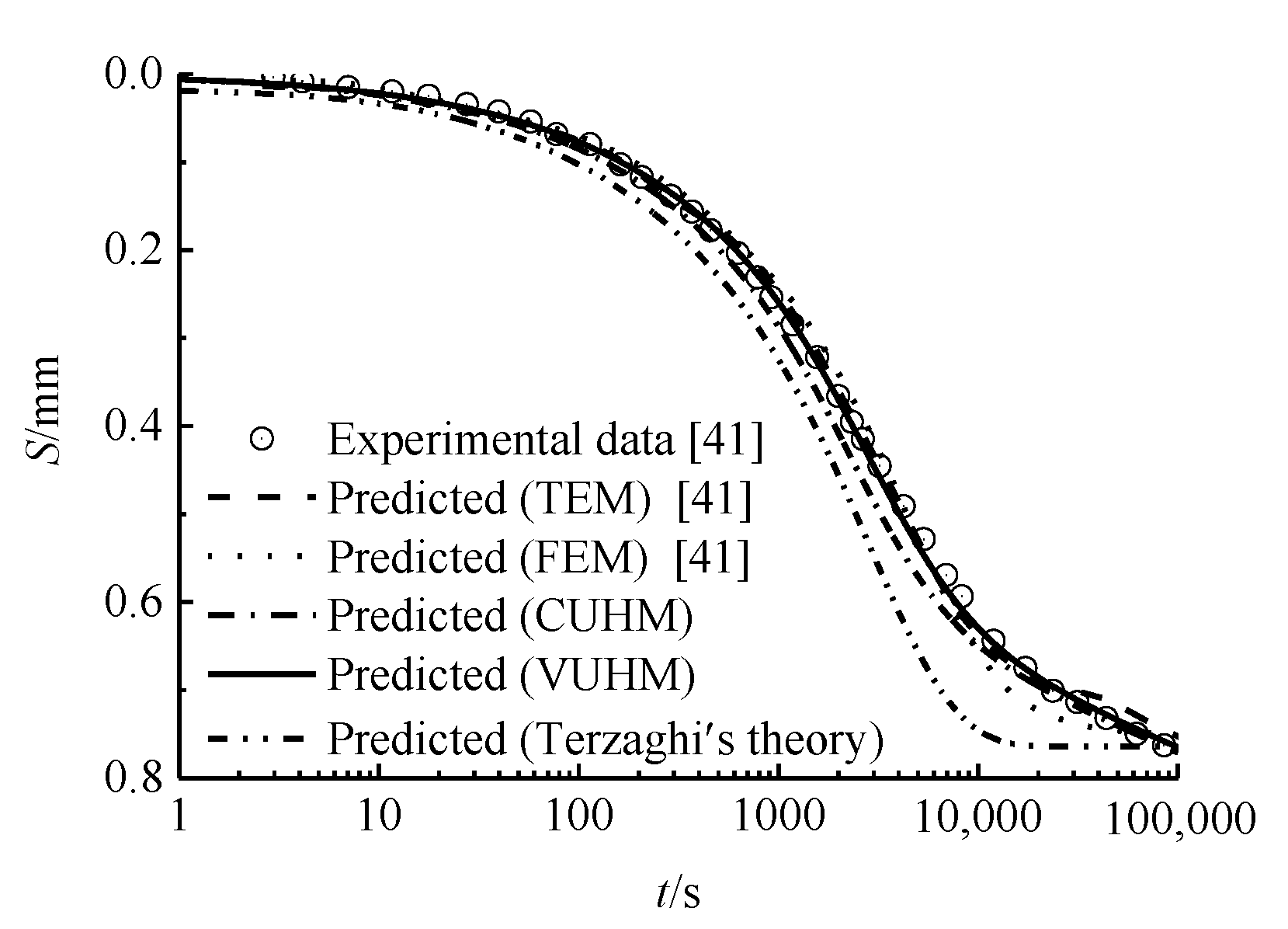
5.1. Verification of the Experimental Results in this Paper
5.2. Verification of Experimental Results obtained by Li's
6. Conclusions
- (1)
- Compared to the traditional falling-head permeability experiment, the improved constant-head experimental device for insignificant amounts of water flow saturated clays requires shorter time and has less experimental error.
- (2)
- The water flow of saturated clay pores deviated from Darcy flow and Hansbo’s flow equations had good applicability to clay samples used in this experiment.
- (3)
- Saturated clay had significant rheological properties. The predicted results of Terzaghi’s theory were quite different from the experimental results, and the UH constitutive model agreed well with experimental results and had good applicability in predicting the rheological deformation of saturated clay samples.
7. Patents
- Zhongyu Liu; Yangyang Xia; Jiachao Zhang; Xinmu Zhu; Jiandong Wei. A device for preparing saturated remolded clay ring knife sample. China Patent, CN201,721,820,336.8, 2018-08-07.
- Jiandong Wei; Yangyang Xia; Zhongyu Liu; Jiachao Zhang; Xinmu Zhu. A triple saturated clay constant-head permeability test device. China Patent, CN201,821,335,366.4, 2019-04-12.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Terzaghi, K. Theoretical Soil Mechanics; Wiley and Sons: New York, NY, USA, 1943. [Google Scholar]
- King, F.H. Principles and Conditions of the Movement of Ground Water; United States Geological Survey: Reston, VA, USA, 1898. [Google Scholar]
- Hansbo, S. Consolidation of clay with special reference to influence of vertical sand drain. Swed. Geotech. Inst. 1960, 18, 45–50. [Google Scholar]
- Swartzendruber, D. Modification of darcy’s law for the flow of water in soils. Soil Sci. 1962, 93, 22–29. [Google Scholar] [CrossRef]
- Slepicka, F. Contribution to the Solution of the Filtration Law; International Union of Geodesy and Geophysics, Commission of Subterranean Waters: Helsinkl, Finland, 1960; pp. 245–258. [Google Scholar]
- Miller, R.J.; Low, P.E. Threshold gradient for water flow in clay systems. Soil Sci. Soc. Am. J. 1963, 27, 605–609. [Google Scholar] [CrossRef]
- Qi, T.; Xie, K.H.; Hu, A.F.; Zhang, Z.Q. Laboratorial study on non-Darcy permeability in Xiaoshan clay. J. Zhejiang Univ. Eng. Sci. 2007, 41, 1023–1028. [Google Scholar]
- Dubin, B.; Moulin, G. Influence of a critical gradient on the consolidation of clays. In Consolidation of Soils: Testing and Evaluation (STP 892); ASTM: West Conshochen, PA, USA, 1986; pp. 354–377. [Google Scholar]
- Wang, X.Y.; Liu, C.L. New understanding of the regularity of water permeability in cohesive soil. Acta Geosci. Sin. 2003, 24, 91–95. [Google Scholar]
- Deng, Y.E.; Xie, H.P.; Huang, R.Q.; Liu, C.Q. Law of nonlinear flow in saturated clays and radial consolidation. Appl. Math. Mech. 2007, 28, 1427–1436. [Google Scholar] [CrossRef]
- Sun, L.Y.; Yue, J.C.; Zhang, J. Experimental study on non-Darcian permeability characteristics of saturated clays. J. Zhengzhou Univ. Eng. Sci. 2010, 31, 31–34. [Google Scholar]
- Hansbo, S. Deviation from Darcy’s law observed in one dimensional consolidation. Geotechnique 2003, 53, 601–605. [Google Scholar] [CrossRef]
- E, J.; Chen, G.; Sun, A.R. One-dimensional consolidation of saturated cohesive soil considering non-Darcy flows. Chin. J. Geotech. Eng. 2009, 31, 1115–1119. [Google Scholar]
- Li, C.X.; Xie, K.H. One-dimensional nonlinear consolidation of soft clay with the non-Darcian flow. J. Zhejiang Univ. Sci. 2013, 14, 435–446. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Sun, L.Y.; Yue, J.C.; Ma, C.W. One-dimensional consolidation theory of saturated clay based on non-Darcy flow. Chin. J. Rock Mech. Eng. 2009, 28, 973–979. [Google Scholar]
- Liu, Z.Y.; Zhang, J.C.; Zheng, Z.L.; Guan, C. Finite element analysis of two-dimensional Biot’s consolidation with Hansbo’s flow. Rock Soil Mech. 2018, 39, 4617–4626. [Google Scholar]
- Liu, Z.Y.; Jiao, Y. Consolidation of ground with ideal sand drains based on Hansbo’s flow. Chin. J. Geotech. Eng. 2015, 37, 792–801. [Google Scholar]
- Davis, E.H.; Raymond, G.P. A non-linear theory of consolidation. Géotechnique 1965, 15, 161–173. [Google Scholar] [CrossRef]
- Zhuang, Y.C.; Xie, K.H.; Li, X.B. Nonlinear analysis of consolidation with variable compressibility and permeability. J. Zhejiang Univ. Eng. Sci. 2005, 6, 181–187. [Google Scholar] [CrossRef]
- Conte, E. Consolidation of anisotropic soil deposits. Soils Found. 1998, 38, 227–237. [Google Scholar] [CrossRef]
- Bartholomeeusen, G.; Sills, G.C.; Znidarčiċ, D.; Van Kesteren, W.; Merckelbach, L.M.; Pyke, R.; Carrier, W.D.; Lin, H.; Penumadu, D.; Winterwerp, H.; et al. Sidere: Numerical prediction of large-strain consolidation. Géotechnique 2002, 52, 639–648. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. Nonlinear consolidation of thin layers subjected to time-dependent loading. Can. Geotech. J. 2007, 44, 717–725. [Google Scholar] [CrossRef]
- Buisman, A.S. Results of long duration settlement tests. In Proceedings of the 1th International Conference on Soil Mechanics and Foundation Engineering, Cambridge, MA, USA, 22–26 June 1936; pp. 103–105. [Google Scholar]
- Taylor, D.W.; Merchant, W. A theory of clay consolidation accounting for secondary compression. J. Math. Phys. 1940, 19, 167–185. [Google Scholar] [CrossRef]
- Chen, Z.J. One dimensional problems of consolidation and secondary time effects. China Civ. Eng. J. 1958, 5, 1–3. [Google Scholar]
- Bjerrum, L. Engineering geology of normally consolidated marine clays as related to the settlement of buildings. Geotechnique 1967, 17, 83–118. [Google Scholar] [CrossRef]
- Bjerrum, L. Embankments on soft ground: State of threat report. In Proceedings of the Specialty Conference on Performance of Earth and Earth Supported Structures, Lafayette, Indiana, 11–14 June 1972; pp. 1–54. [Google Scholar]
- Nash, D.F.T.; Sills, G.C.; Davison, L.R. One-dimensional consolidation testing for soft clay from Bothkennar. Geotechnique 1992, 42, 241–256. [Google Scholar] [CrossRef]
- Chen, X.P.; Luo, Q.Z.; Zhou, Q. Time-dependent behaviour of interactive marine and terrestrial deposit clay. Geomech. Eng. 2014, 7, 279–295. [Google Scholar] [CrossRef]
- Yin, Z.Z.; Zhang, H.B.; Zhu, J.G.; Li, G.W. Secondary consolidation of soft soils. Chin. J. Geotech. Eng. 2003, 25, 521–526. [Google Scholar]
- Reddy, B.K.; Sahu, R.B.; Ghosh, S. Consolidation behavior of organic soil in normal Kolkata Deposit. Indian Geotech. J. 2014, 44, 341–350. [Google Scholar] [CrossRef]
- Yin, J.H. Non-linear creep of soils in oedometer tests. Geotechnique 1999, 49, 699–707. [Google Scholar] [CrossRef]
- Feng, W.Q.; Lalit, B.; Yin, Z.Y.; Yin, J.H. Long-term Non-linear creep and swelling behavior of Hong Kong marine deposits in oedometer condition. Comput. Geotech. 2017, 84, 1–15. [Google Scholar] [CrossRef]
- Yao, Y.P.; Kong, L.M.; Hu, J. An elastic-viscous-plastic model for overconsolidated clays. Sci. China Tech. Sci. 2013, 56, 441–457. [Google Scholar] [CrossRef]
- Hu, J.; Yao, Y.P. One-dimensional consolidation analysis of UH model considering time effect. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 1492–1498. [Google Scholar]
- GB/T50123-1999. Standard for Soil Test Method; China Planning Press: Beijing, China, 1999. [Google Scholar]
- Liu, Z.Y.; Xia, Y.Y.; Zhang, J.C.; Zhu, X.M.; Wei, J.D. Preparation Device for Saturated Remodeling Clay Soil Ring Knife Sample. China Henan CN207703568U, 7 August 2018. [Google Scholar]
- Taylor, D.W. Fundamentals of Soil Mechanics; John Wiley & Sons Inc.: New York, NY, USA, 1948. [Google Scholar]
- Beery, P.L.; Wilkinson, W.B. The radial consolidation of caly soils. Geotechnique 1969, 19, 253–254. [Google Scholar] [CrossRef]
- Wong, R.C.; Varatharajan, S. Viscous behaviour of clays in one-dimensional compression. Can. Geotech. J. 2014, 51, 795–809. [Google Scholar] [CrossRef]
- Li, X.B. Theoretical and Experimental Studies on Rheological Consolidation of Soft Soil; Zhejiang University: Hangzhou, China, 2005. [Google Scholar]
- Chen, F.; Drumm, E.C.; Guiochon, G. Coupled discrete element and finite volume solution of two classical soil mechanics problems. Comput. Geotech. 2011, 38, 638–647. [Google Scholar] [CrossRef]
- Sorensen, K.K.; Okkels, N. Correlation between Drained Shear Strength and Plasticity Index of Undisturbed Overconsolidated Clays. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; Volume 1, pp. 423–428. [Google Scholar]


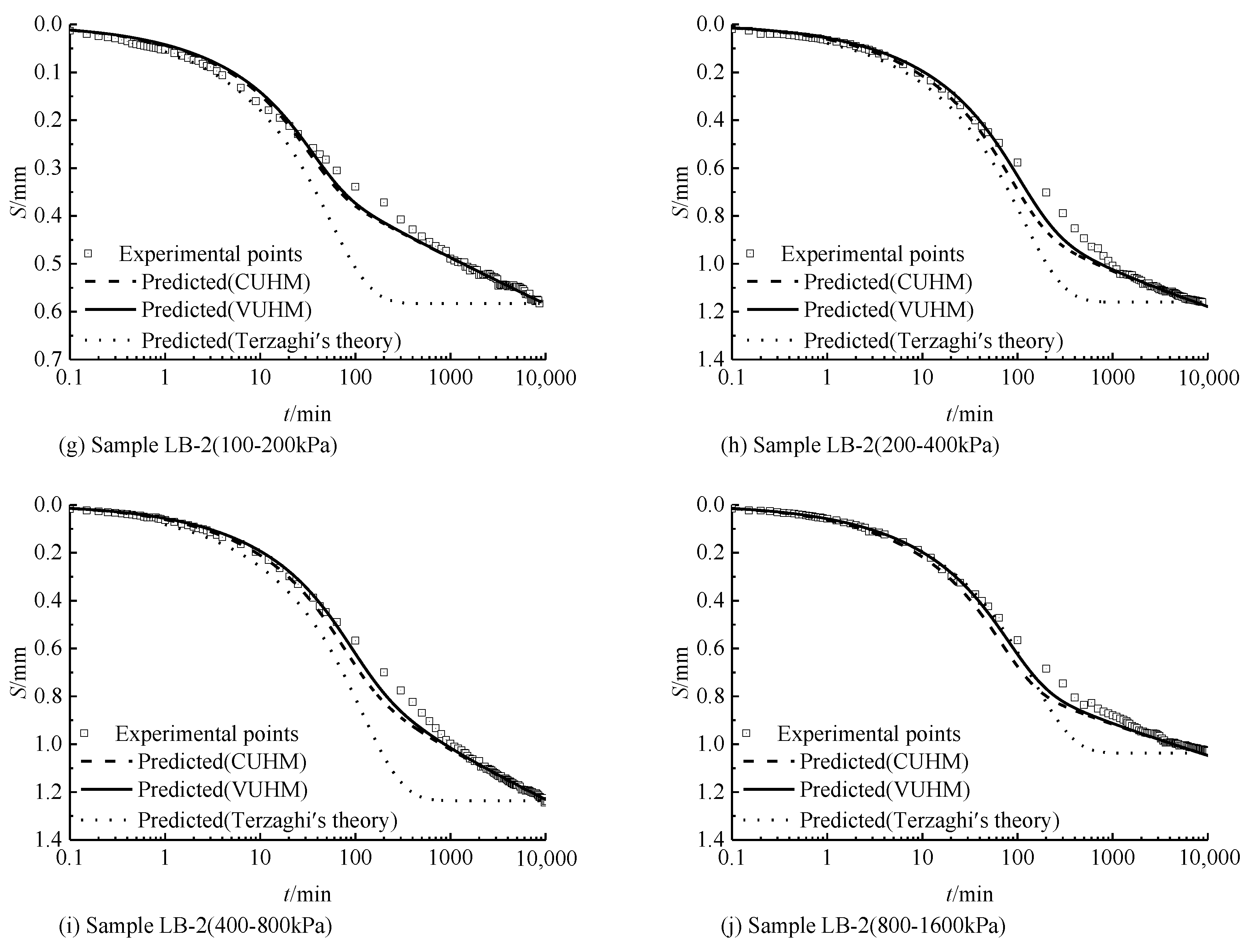
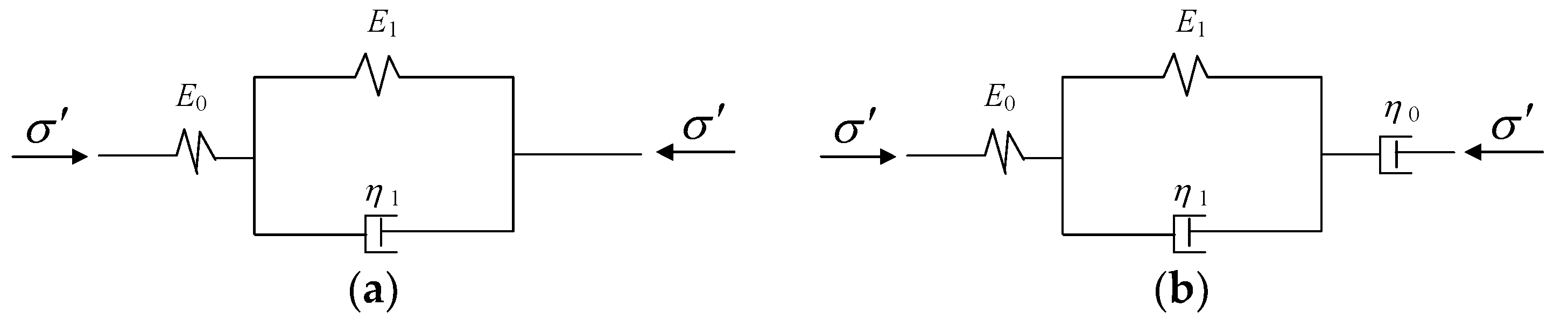
| Specific Gravity, Gs | Liquid Limit, wL (%) | Plastic Limit, wP (%) | Plastic Index, IP (%) |
|---|---|---|---|
| 2.71 | 39.4 | 22.3 | 17.1 |
| Soil Sample Number | e0 | k (cm/s) | i0 | m | R2 |
|---|---|---|---|---|---|
| SL-1 | 1.26 | 6.73 × 10−8 | 22.20 | 1.45 | 0.985 |
| SL-2 | 1.29 | 1.28 × 10−7 | 23.54 | 1.58 | 0.978 |
| SL-3 | 1.36 | 2.31 × 10−7 | 27.81 | 1.63 | 0.964 |
| SL-4 | 1.44 | 6.85 × 10−7 | 31.25 | 1.81 | 0.972 |
| SL-5 | 1.47 | 8.95 × 10−7 | 24.37 | 1.64 | 0.967 |
| SL-6 | 1.50 | 1.29 × 10−6 | 30.41 | 1.83 | 0.956 |
| Sample Number | Specific Gravity, Gs | Bulk Density, ρ (g/cm3) | Water Content, w (%) | Void Ratio, e0 |
|---|---|---|---|---|
| LB-1 | 2.71 | 1.738 | 47.77 | 1.30 |
| LB-2 | 2.71 | 1.864 | 34.14 | 0.95 |
| Order | Loading (kPa) |
|---|---|
| First loading | 0-25-50-100-200 |
| First Unloading | 200-100-50 |
| Second Loading | 50-100-200-400 |
| Second Unloading | 400-200-100-50 |
| Third Loading | 50-100-200-400-800 |
| Third Unloading | 800-400-200-100-50 |
| Fourth Loading | 50-100-200-400-800-1600 |
| Soil Sample Number | Loading (kPa) | ||||||
|---|---|---|---|---|---|---|---|
| 25 | 50 | 100 | 200 | 400 | 800 | 1600 | |
| LB-1 | 0.0040 | 0.0050 | 0.0120 | 0.0110 | 0.0091 | 0.0085 | 0.0080 |
| LB-2 | 0.0009 | 0.0015 | 0.0030 | 0.0092 | 0.0135 | 0.0208 | 0.0134 |
| Loading Interval/(kPa) | H/mm | e0 | CC | Ck | CS | Cα | R0 | k0/(m/min) |
|---|---|---|---|---|---|---|---|---|
| 50–100 | 18.99 | 1.184 | 0.42 | 0.66 | 0.100 | 0.0120 | 0.65 | 1.2 × 10−8 |
| 100–200 | 18.01 | 1.070 | 0.0110 | 0.92 | 0.70 × 10−8 | |||
| 200–400 | 16.63 | 0.913 | 0.0091 | 0.83 | 0.40 × 10−8 | |||
| 400–800 | 15.44 | 0.776 | 0.0085 | 0.79 | 0.25 × 10−8 | |||
| 800–1600 | 14.29 | 0.644 | 0.0080 | 0.76 | 0.12 × 10−8 |
| Loading Interval/(kPa) | H/mm | e0 | CC | Ck | CS | Cα | R0 | k0/(m/min) |
|---|---|---|---|---|---|---|---|---|
| 50–100 | 1.988 | 0.940 | 0.42 | 0.66 | 0.065 | 0.0030 | 0.58 | 1.0 × 10−8 |
| 100–200 | 1.959 | 0.911 | 0.0092 | 0.53 | 0.85 × 10−8 | |||
| 200–400 | 1.899 | 0.852 | 0.0135 | 0.65 | 0.39 × 10−8 | |||
| 400–800 | 1.789 | 0.745 | 0.0190 | 0.60 | 0.19 × 10−8 | |||
| 800–1600 | 1.512 | 0.622 | 0.0135 | 0.66 | 0.06 × 10−8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xia, Y.; Shi, M.; Zhang, J.; Zhu, X. Numerical Simulation and Experiment Study on the Characteristics of Non-Darcian Flow and Rheological Consolidation of Saturated Clay. Water 2019, 11, 1385. https://doi.org/10.3390/w11071385
Liu Z, Xia Y, Shi M, Zhang J, Zhu X. Numerical Simulation and Experiment Study on the Characteristics of Non-Darcian Flow and Rheological Consolidation of Saturated Clay. Water. 2019; 11(7):1385. https://doi.org/10.3390/w11071385
Chicago/Turabian StyleLiu, Zhongyu, Yangyang Xia, Mingsheng Shi, Jiachao Zhang, and Xinmu Zhu. 2019. "Numerical Simulation and Experiment Study on the Characteristics of Non-Darcian Flow and Rheological Consolidation of Saturated Clay" Water 11, no. 7: 1385. https://doi.org/10.3390/w11071385
APA StyleLiu, Z., Xia, Y., Shi, M., Zhang, J., & Zhu, X. (2019). Numerical Simulation and Experiment Study on the Characteristics of Non-Darcian Flow and Rheological Consolidation of Saturated Clay. Water, 11(7), 1385. https://doi.org/10.3390/w11071385





