The Capacity of the Hydrological Modeling for Water Resource Assessment under the Changing Environment in Semi-Arid River Basins in China
Abstract
:1. Introduction
2. Data Source and Methods
2.1. Study Areas and Data Sources
2.2. Mann–Kendall Rank Test
2.3. Average-Difference T-Test
2.4. Hydrological Models
2.4.1. Xin’anjiang Model
2.4.2. SIMHYD Model
2.4.3. GR4J Model
2.4.4. RCCC-WBM Model
2.5. Model Calibration and Objective Functions
3. Results and Discussion
3.1. Variability and Trends of Precipitation and Temperature in 1951–2013
3.2. Inter-Annual Variations and Abrupt Change of Observed Runoff
3.3. Relationships between Runoff and Precipitation in a Changing Environment
3.4. Hydrological Simulation for Stream Flow
3.4.1. Hydrological Modeling under Natural Period
3.4.2. Hydrological Modeling under a Changing Environment
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, Z.X. Hydrological models: Past, present and future. J. Beijing Norm. Univ. 2010, 46, 278–289. [Google Scholar]
- Elsawah, S.; Pierce, S.A.; Hamilton, S.H.; Delden, H.V.; Haase, D.; Elmahdi, A.; Jakeman, A.J. An overview of the system dynamics process for integrated modelling of socio-ecological systems: Lessons on good modelling practice from five case studies. Environ. Model. Softw. 2017, 93, 127–145. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, J.; Yang, Q. Attribution of runoff change for the Xinshui River catchment on the Loess pPateau of cCina in a changing environment. Water 2016, 8, 267. [Google Scholar] [CrossRef]
- Montanari, A.; Young, G.; Savenije, H.H.G.; Hughes, D.; Wagener, T.; Ren, L.L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S.; et al. “Panta rhei—Everything flows”: Change in hydrology and society—The IAHS scientific decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Liu, D.L.; Zhang, M.; Feng, P.; Cheng, L.; Yu, Q.; Eamus, D. Impacts of future climate change on water resource availability of eastern Australia: A case study of the Manning River basin. J. Hydrol. 2019, 573, 49–59. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Impacts Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- IPCC. Climate Change and Water; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Bao, Z.; Zhang, J.; Wang, G.; Fu, G.; Liu, C.; Yan, X. Pan evaporation trend for the Haihe River basin and its response to climate change. Pan 2011, 237, 1. [Google Scholar]
- Bao, Z.; Zhang, J.; Wang, G.; Fu, G.; He, R.; Yan, X.; Jin, J.; Liu, Y.; Zhang, A. Attribution for decreasing streamflow of the haihe river basin, northern China: Climate variability or human activities? J. Hydrol. 2012, 460, 117–129. [Google Scholar] [CrossRef]
- Albergel, C.; Dorigo, W.; Reichle, R.H.; Balsamo, G.; de Rosnay, P.; Muñoz-Sabater, J.; Isaksen, L.; de Jeu, R.; Wagner, W. Skill and global trend analysis of soil moisture from reanalyses and microwave remote sensing. J. Hydrometeorol. 2013, 14, 1259–1277. [Google Scholar] [CrossRef]
- Datta, S.; Satten, G.A. Rank-sum tests for clustered data. J. Am. Stat. Assoc. 2005, 100, 908–915. [Google Scholar] [CrossRef]
- Yang, Y.; Fei, T. Abrupt change of runoff and its major driving factors in Haihe River catchment, China. J. Hydrol. 2009, 374, 373–383. [Google Scholar] [CrossRef]
- Bassingthwaighte, J.B.; Raymond, G.M. Evaluating rescaled range analysis for time series. Ann. Biomed. Eng. 1994, 22, 432–444. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.C.; Zhou, C.H.; Bao-Lin, L.I. Brown-forsythe based method for detectingchange points in hydrological time series. Geogr. Res. 2005, 6, 14–18. [Google Scholar]
- Lee, A.F.S.; Heghinian, S.M. A shift of the mean level in a sequence of independent normal random variables: A bayesian approach. Technometrics 1977, 19, 503–506. [Google Scholar]
- Guan, X.X.; Zhang, J.Y.; Ju, Q.; Wang, G.Q.; Guan, T.S. Comparison of consistency testing for key hydrological elements by using multiple statistical methods. J. North China Univ. Water Resour. Electr. Power 2018, 39, 51–56. [Google Scholar]
- Hou, Q.L.; Bai, H.Y.; Ren, Y.Y.; He, Y.N.; Ma, X.P. Analysis of variation in runoff of the main stream of the Weihe River and related driving forces over the last 50 years. Resour. Sci. 2011, 33, 1505–1512. [Google Scholar]
- Guan, X.X.; Liu, Y.; Jin, J.L.; Liu, C.S.; Liu, Y.L.; Wang, G.Q. Characteristics of hydrological changes of typical catchments in different climatic regions of China. J. North China Univ. Water Resour. Electr. Power 2018, 39, 13–17. [Google Scholar]
- Bao, W.M. Hydrological Forecasting, 4th ed.; China Water and Hydropower Press: Beijing, China, 2009. [Google Scholar]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Liu, Y.L.; He, R.M.; Bao, Z.X.; Liu, C.S.; Li, Y. Regional calibration of a water balance model for estimating stream flow in ungauged areas of the Yellow River basin. Quat. Int. 2014, 336, 65–72. [Google Scholar] [CrossRef]
- Zhan, C.S.; Jiang, S.S.; Sun, F.B.; Jia, Y.W.; Yue, W.F.; Niu, C.W. Quantitative contribution of climate change and human activities to runoff changes in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2014, 11, 2149–2175. [Google Scholar] [CrossRef]
- Zeng, S.; Zhan, C.; Sun, F.; Du, H.; Wang, F. Effects of climate change and human activities on surface runoff in the Luan River basin. Adv. Meteorol. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Nash, L.L.; Gleick, P.H. Sensitivity of streamflow in the Colorado Basin to climatic changes. J. Hydrol. 1991, 125, 221–241. [Google Scholar] [CrossRef]
- Legesse, D.; Vallet-Coulomb, C.; Gasse, F. Hydrological response of a catchment to climate and land use changes in tropical Africa: Case study south central Ethiopia. J. Hydrol. 2003, 275, 67–85. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Luedeling, E.; Zhang, M. Climate change sensitivity assessment of a highly agricultural watershed using SWAT. J. Hydrol. 2009, 374, 16–29. [Google Scholar] [CrossRef]
- Wen, D.; Cui, B.; Liu, Z.; Zhang, K. Relative effects of human activities and climate change on the river runoff in an arid basin in northwest China. Hydrol. Process. 2015, 28, 4854–4864. [Google Scholar]
- Liu, X.M.; Liu, W.H.; Xia, J. Comparison of the streamflow sensitivity to aridity index between the Danjiangkou Reservoir basin and Miyun Reservoir basin, China. Theor. Appl. Climatol. 2013, 111, 683–691. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Pagano, T.C. Assessing water resources in China using precise projections and VIC model. Hydrol. Earth Syst. Sci. Discuss. 2012, 16, 231–240. [Google Scholar] [CrossRef]
- Xu, Z.X.; Cheng, L. Progress on studies and applications of the distributed hydrological models. J. Hydraul. Eng. 2010, 41, 1009–1017. [Google Scholar]
- Zhao, J.; Wang, D.; Yang, H.; Sivapalan, M. Unifying catchment water balance models for different time scales through the maximum entropy production principle. Water Resour. Res. 2016, 52, 7503–7512. [Google Scholar] [CrossRef]
- Guo, F.; Ma, J.J. An analysis of applying SIMHYD model in the Yellow River basin. China Rural Water Hydropower 2015, 6, 75–80. [Google Scholar]
- Arsenault, R.; Gatien, P.; Renaud, B.; Brissette, F.; Martel, J.-L. A comparative analysis of 9 multi-model averaging approaches in hydrological continuous streamflow simulation. J. Hydrol. 2015, 529, 754–767. [Google Scholar] [CrossRef]
- Bao, Z.; Fu, G.; Wang, G.; Jin, J.; He, R.; Yan, X.; Liu, C. Hydrological projection for the Miyun Reservoir basin with the impact of climate change and human activity. Quat. Int. 2012, 282, 96–103. [Google Scholar] [CrossRef]
- Wang, G.Q.; Yan, X.L.; Zhang, J.Y.; Liu, C.S.; Jin, J.L.; Liu, Y.L.; Bao, Z.X. Detecting evolution trends in the recorded runoffs from the major rivers in China during 1950–2010. J. Water Clim. Chang. 2013, 4, 252–264. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Wang, G.Q.; He, R.M.; Liu, C.S. Variation trends of runoffs in the Middle Yellow River basin and its response to climate change. Adv. Water Sci. 2009, 20, 153–158. [Google Scholar]
- Andersen, F.; Jensen, K.H.; Sandholt, I.; Stisen, S.; Jorreto, S.; Pulido-Bosch, A. Hydrological modelling in a semi-arid region using remote sensing data. AGU Fall Meet. 2006. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.621.5983&rep=rep1&type=pdf (accessed on 6 May 2019).
- Alkhoury, W.; Toll, M.; Gunkel, A.; Lange, J.; Sauter, M. The effect of space-time variations and measurement accuracy of precipitation on hydrological modelling in arid and semi-arid regions—A case study from Jordan. EGU Gen. Assem. Conf. 2010, 12, 1009. [Google Scholar]
- Molina-Navarro, E.; Hallack-Alegría, M.; Martínez-Pérez, S.; Ramírez-Hernández, J.; Mungaray-Moctezuma, A.; Sastre-Merlín, A. Hydrological modeling and climate change impacts in an agricultural semiarid region. Case study: Guadalupe River basin, Mexico. Agric. Water Manag. 2016, 175, 29–42. [Google Scholar] [CrossRef]
- Bhatti, A.M.; Jaranillasanchez, P.A.; Koike, T. Modeling hydrological responses to climate change in semi-arid region watershed. AGU Fall Meet. 2013. Available online: http://adsabs.harvard.edu/abs/2013AGUFM.H52B..04B (accessed on 6 May 2019).
- Kateb, H.E.; Zhang, H.; Zhang, P.; Mosandl, R. Soil erosion and surface runoff on different vegetation covers and slope gradients: A field experiment in southern Shaanxi province, China. Catena 2013, 105, 1–10. [Google Scholar] [CrossRef]
- Peng, Y.; Li, C.X.; Li, J. Assessment on the ecological security of the Yellow River Basin in Ningxia Province from 2000 to 2012. Resour. Sci. 2015, 37, 2480–2490. [Google Scholar]
- Zhang, R.; Wang, Y.M.; Chang, J.X.; Li, Y.Y. Response of land use change to human activities in the Yellow River Basin based on water resources division. J. Nat. Resour. 2019, 34, 274–287. [Google Scholar]
- Liu, F.; Chen, S.; Dong, P.; Peng, J. Spatial and temporal variability of water discharge in the Yellow River basin over the past 60 years. J. Geogr. Sci. 2012, 22, 1013–1033. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Yong, B.; Singh, V.P.; Yang, X.; Yuan, F. Quantifying the effects of climate variability and human activities on runoff from the Laohahe basin in northern China using three different methods. Hydrol. Process. 2011, 25, 2492–2505. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhang, J.Y.; Pagano, T.C.; Liu, Y.L.; Liu, C.S.; Bao, Z.X.; Jin, J.L.; He, R.M. Using hydrological simulation to detect human-disturbed epoch in runoff series. Water Sci. Technol. 2015, 71, 691–699. [Google Scholar] [CrossRef] [PubMed]
- Bao, W.M.; Shen, D.D.; Ni, P.; Zhou, J.W.; Sun, Y.Q. Proposition and certification of moving mean difference method for detecting abrupt change points. J. Geogr. Sci. 2018, 73, 2075–2085. [Google Scholar]
- Zhang, X.; Fang, Y.; Qu, B. Key techniques and challenges of developing real-time flood forecasting systems based on the xin’anjiang model. AGU Fall Meet. 2015. Available online: http://adsabs.harvard.edu/abs/2015AGUFM.H43J..05Z (accessed on 6 May 2019).
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Lü, H.; Hou, T.; Horton, R.; Zhu, Y.; Chen, X.; Jia, Y.; Wang, W.; Fu, X. The streamflow estimation using the xinanjiang rainfall runoff model and dual state-parameter estimation method. J. Hydrol. 2013, 480, 102–114. [Google Scholar] [CrossRef]
- Song, X.; Kong, F.; Zhan, C.; Han, J.; Zhang, X. Parameter identification and global sensitivity analysis of Xin’anjiang model using meta-modeling approach. Water Sci. Eng. 2013, 6, 1–17. [Google Scholar]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W.; Singh, V.P.; Frevert, D. Application and Testing of the Simple Rainfall-Runoff Model Simhyd; Water Resources Publication: Littleton, CO, USA, 2002. [Google Scholar]
- Kachroo, R.K. River flow forecasting. Part 5. Applications of a conceptual model. J. Hydrol. 1992, 133, 141–178. [Google Scholar] [CrossRef]
- Nascimento, N.; Yang, X.; Makhlouf, Z.; Michel, C. GR3J: A daily watershed model with three free parameters. Hydrol. Sci. J. 1999, 44, 263–277. [Google Scholar]
- Xu, C.-Y.; Singh, V.P. A review on monthly water balance models for water resources investigations. Water Resour. Manag. 1998, 12, 20–50. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Wang, G.Q. Variation of Stream Flow and Attribution Analysis; China Science Press: Beijing, China, 2014. [Google Scholar]
- Li, C.B.; Wang, S.B.; Yang, L.S.; Yang, W.J.; Li, W.Y. Spatial and temporal variation of main hydrologic meteorological elements in the Taohe River basin from 1951 to 2010. J. Glaciol. Geocryol. 2013, 35, 1259–1266. [Google Scholar]
- Wang, F.; Mu, X.M.; Zhang, X.P.; Li, Y. Effect of soil and water conservation on runoff and sediment in Pianguan River. Sci. Soil Water Conserv. 2005, 2, 10–14. [Google Scholar]
- Zheng, H.X.; Zhang, L.; Zhu, R.R.; Liu, C.M.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the yellow river basin. Water Resour. Res. 2009, 45, 641–648. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Lan, T.; Shi, J.; Lu, S. Change-point detection and variation assessment of the hydrologic regime of the Wenyu River. Toxicol. Environ. Chem. 2016, 98, 358–375. [Google Scholar] [CrossRef]
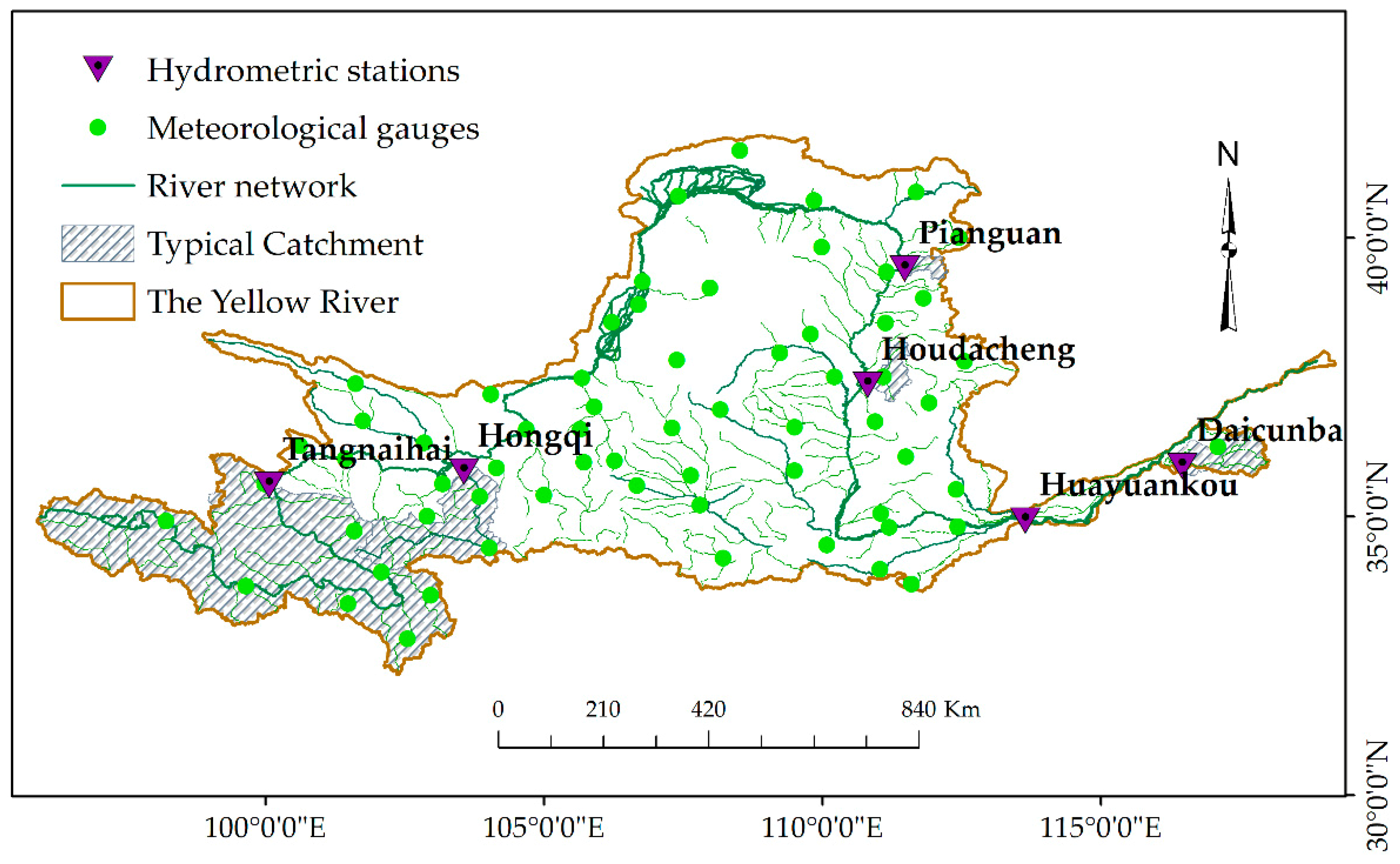
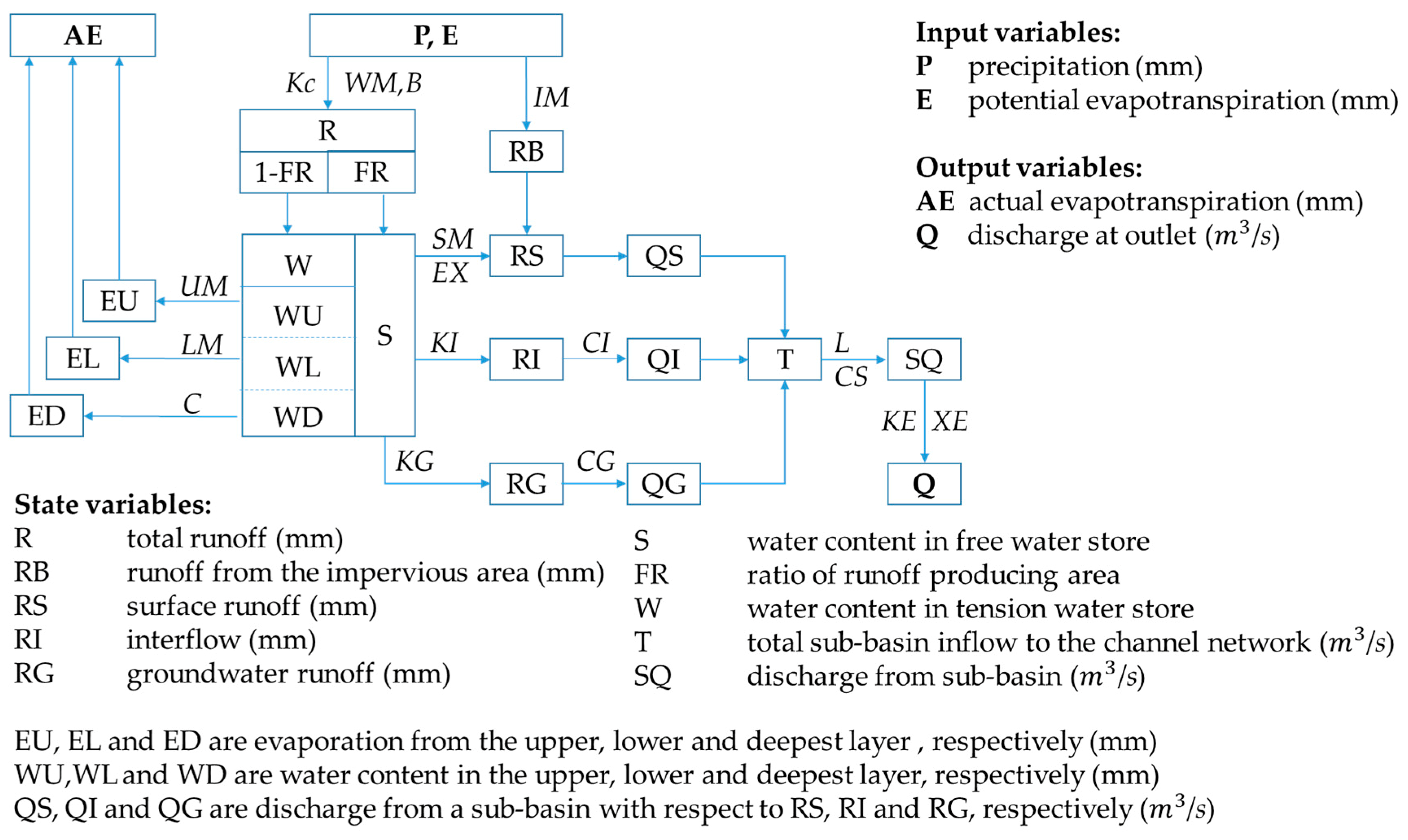
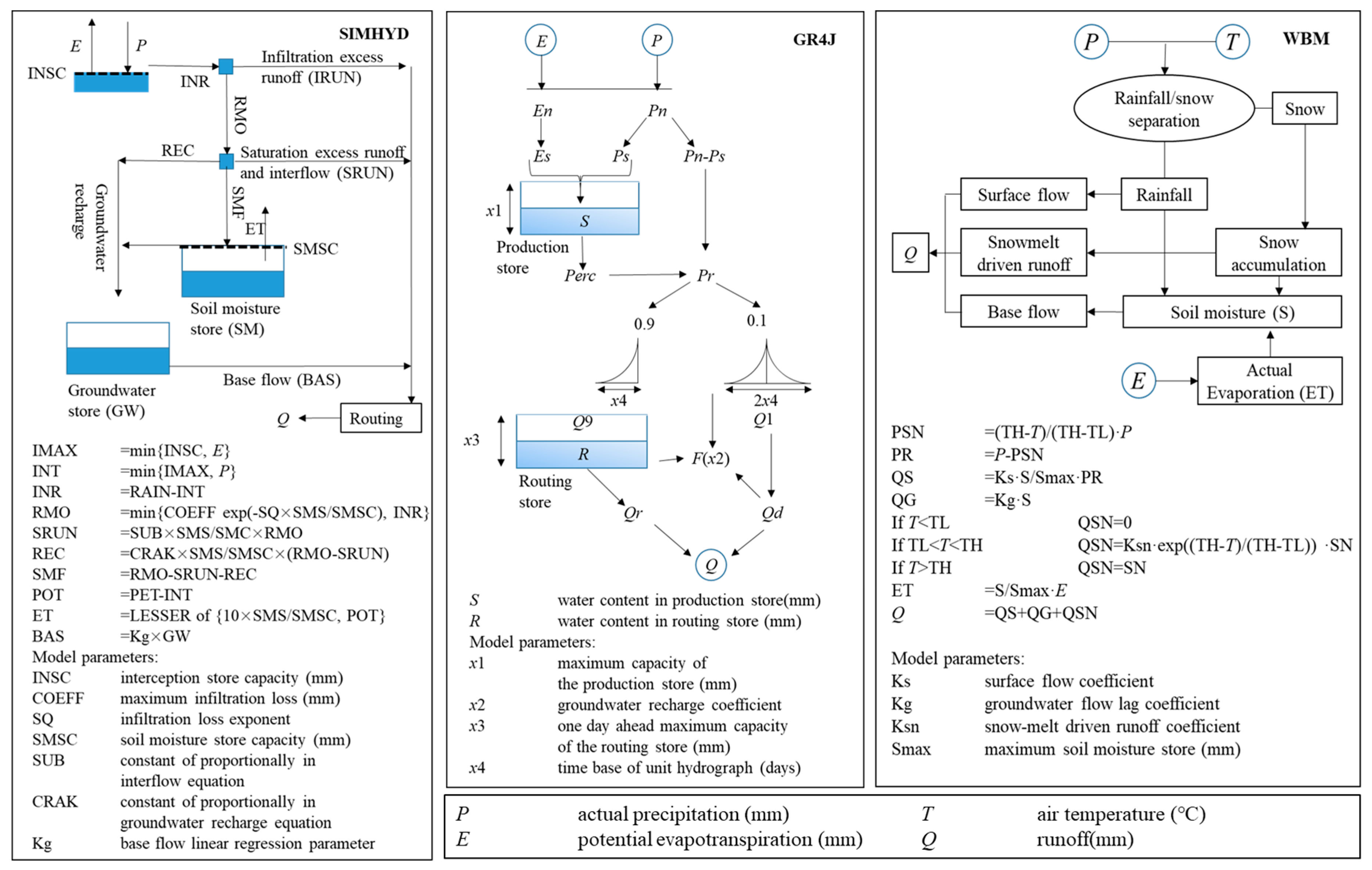
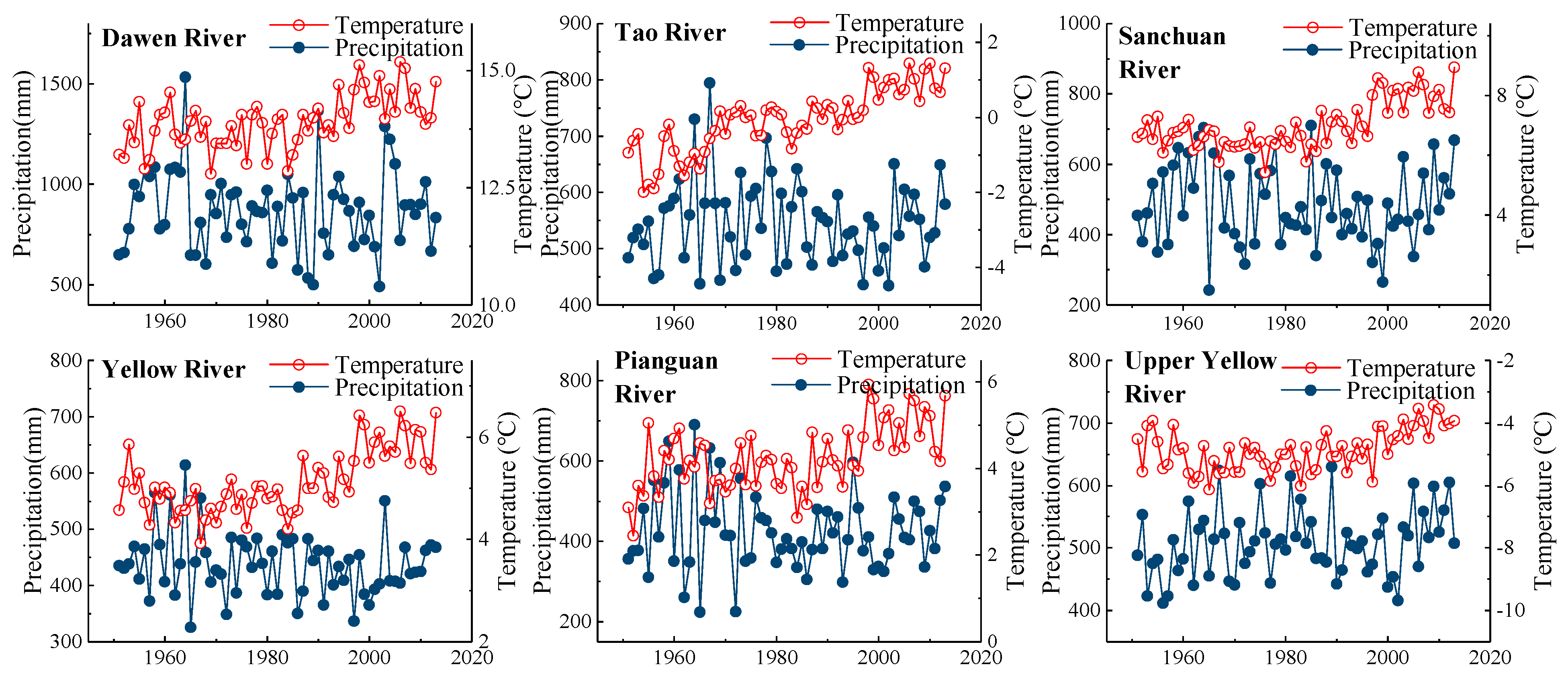
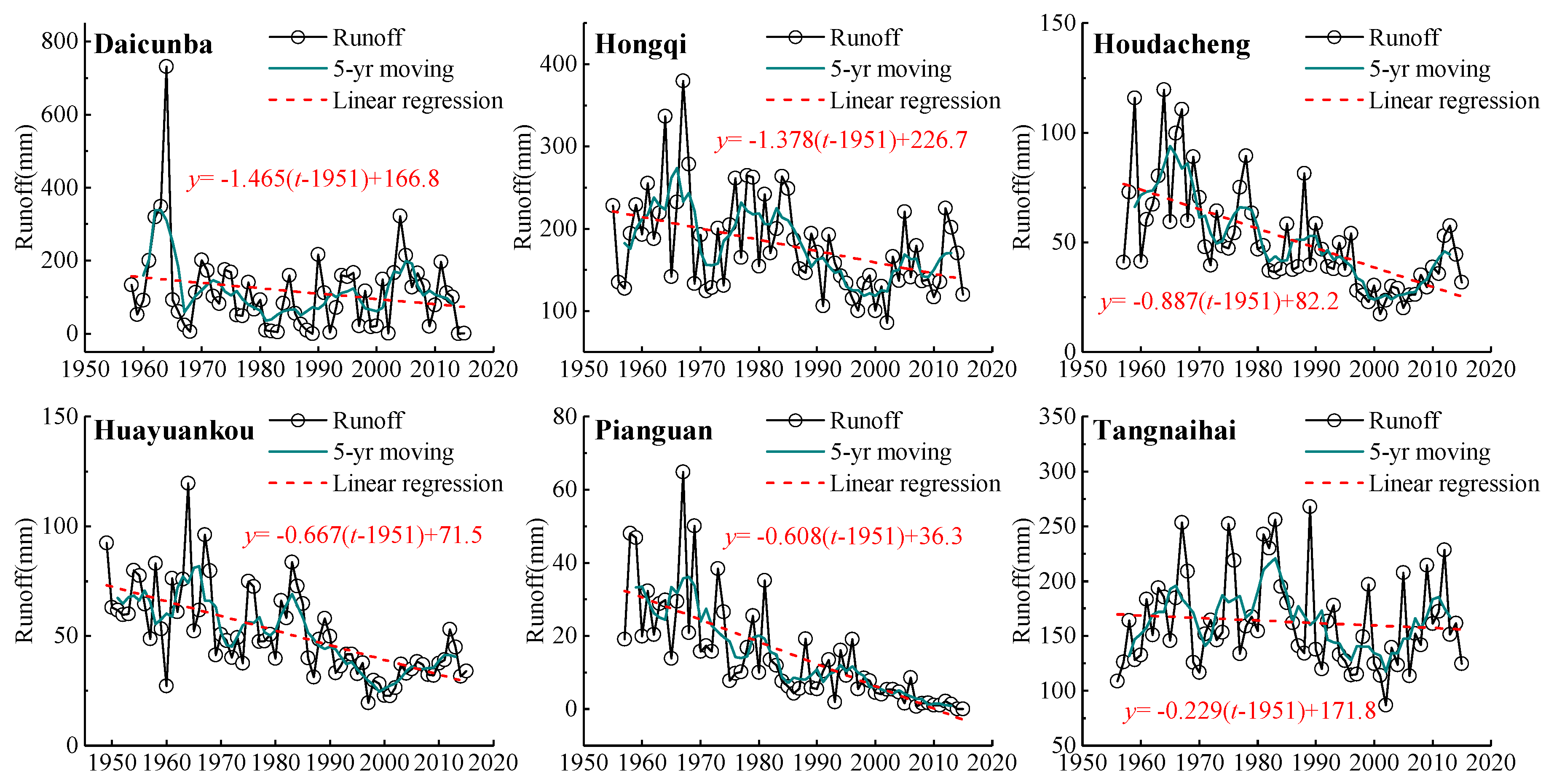
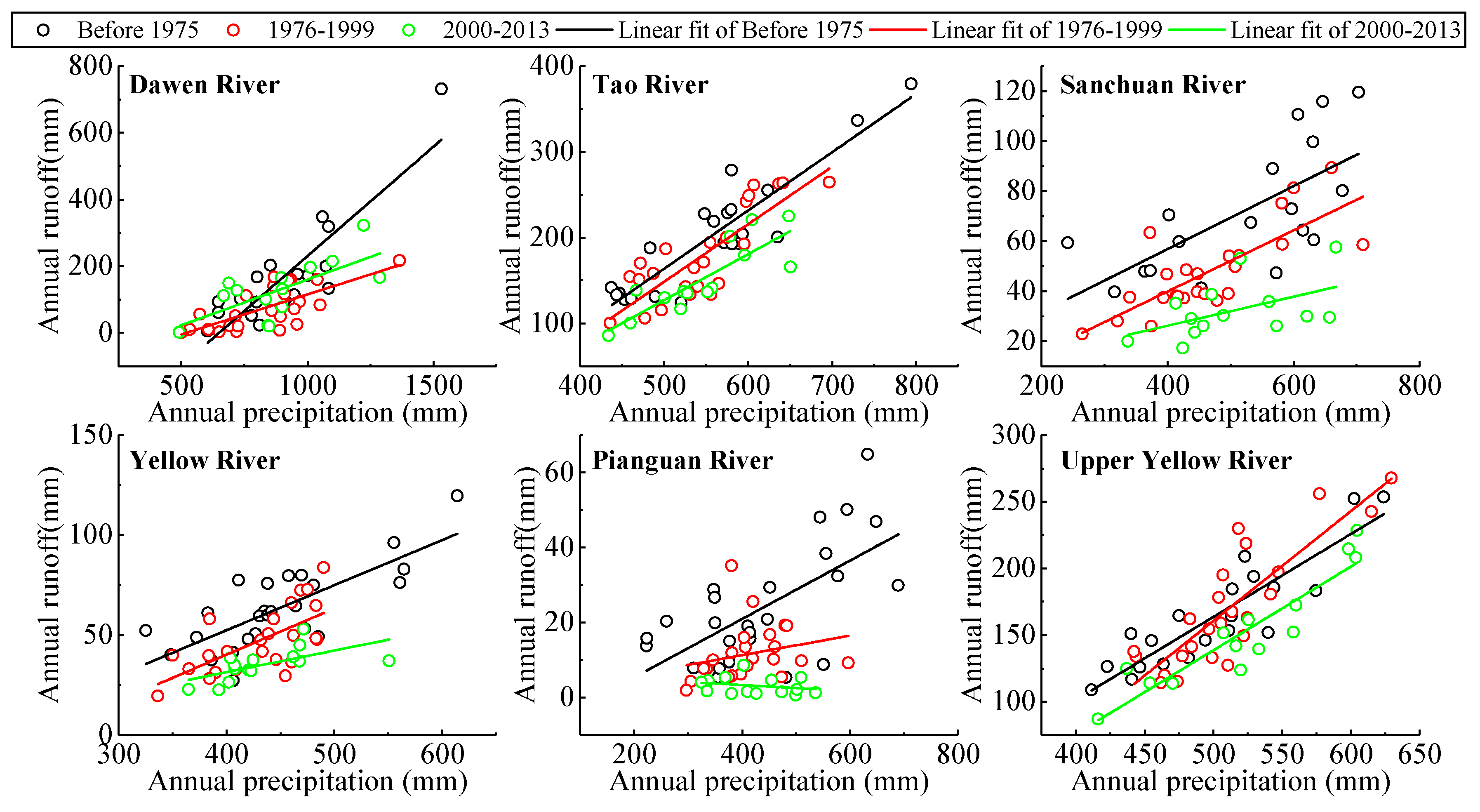
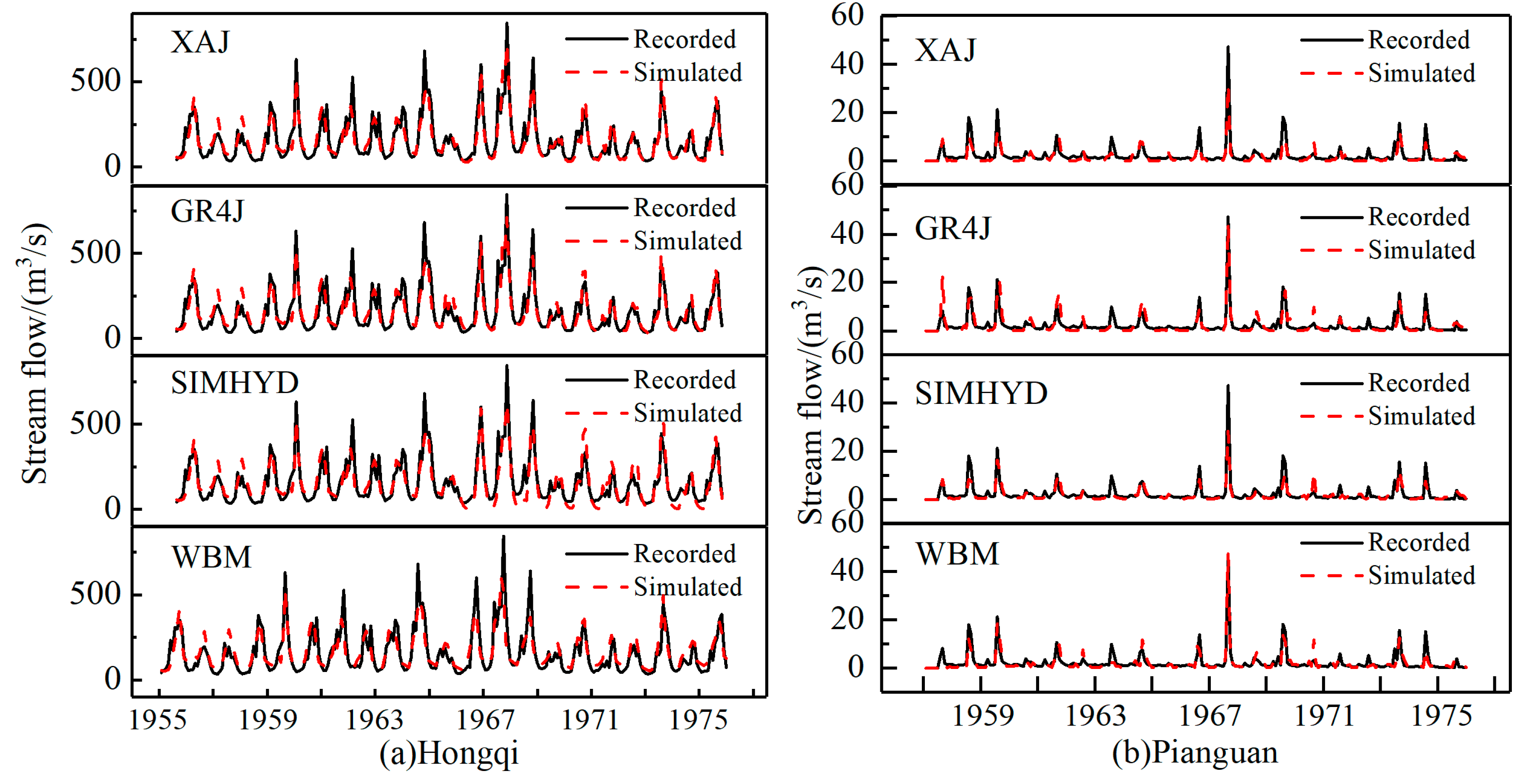
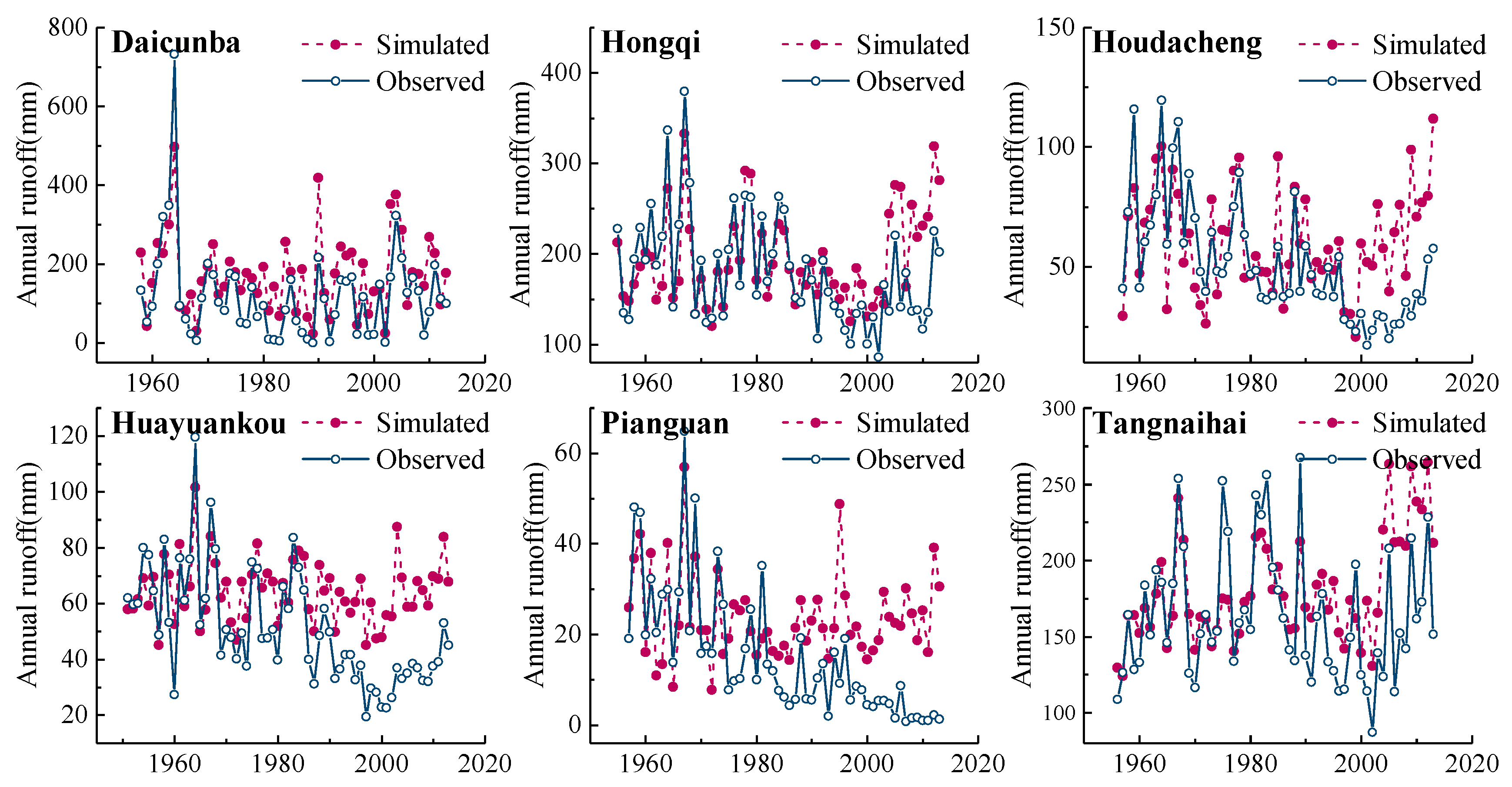
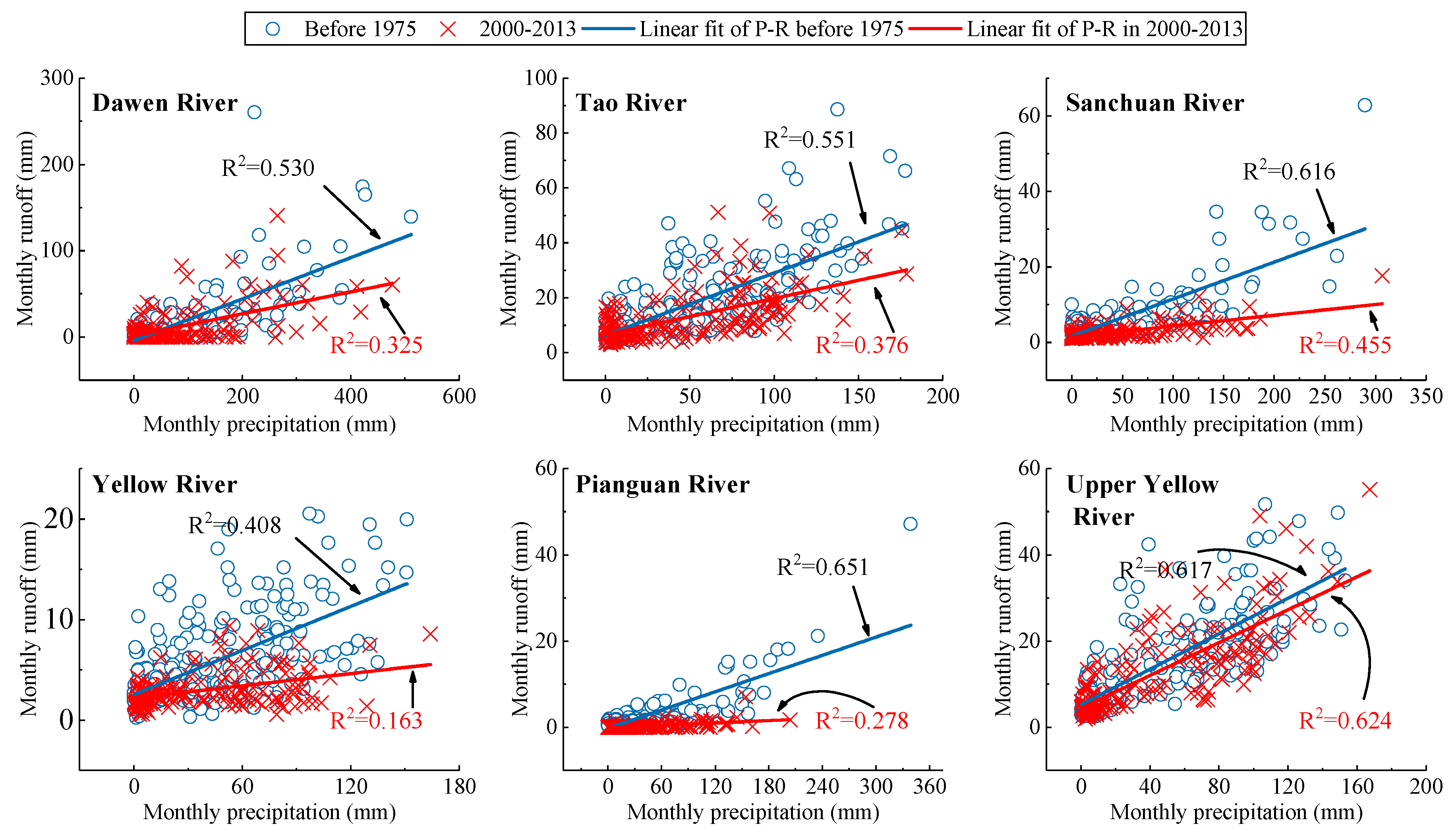
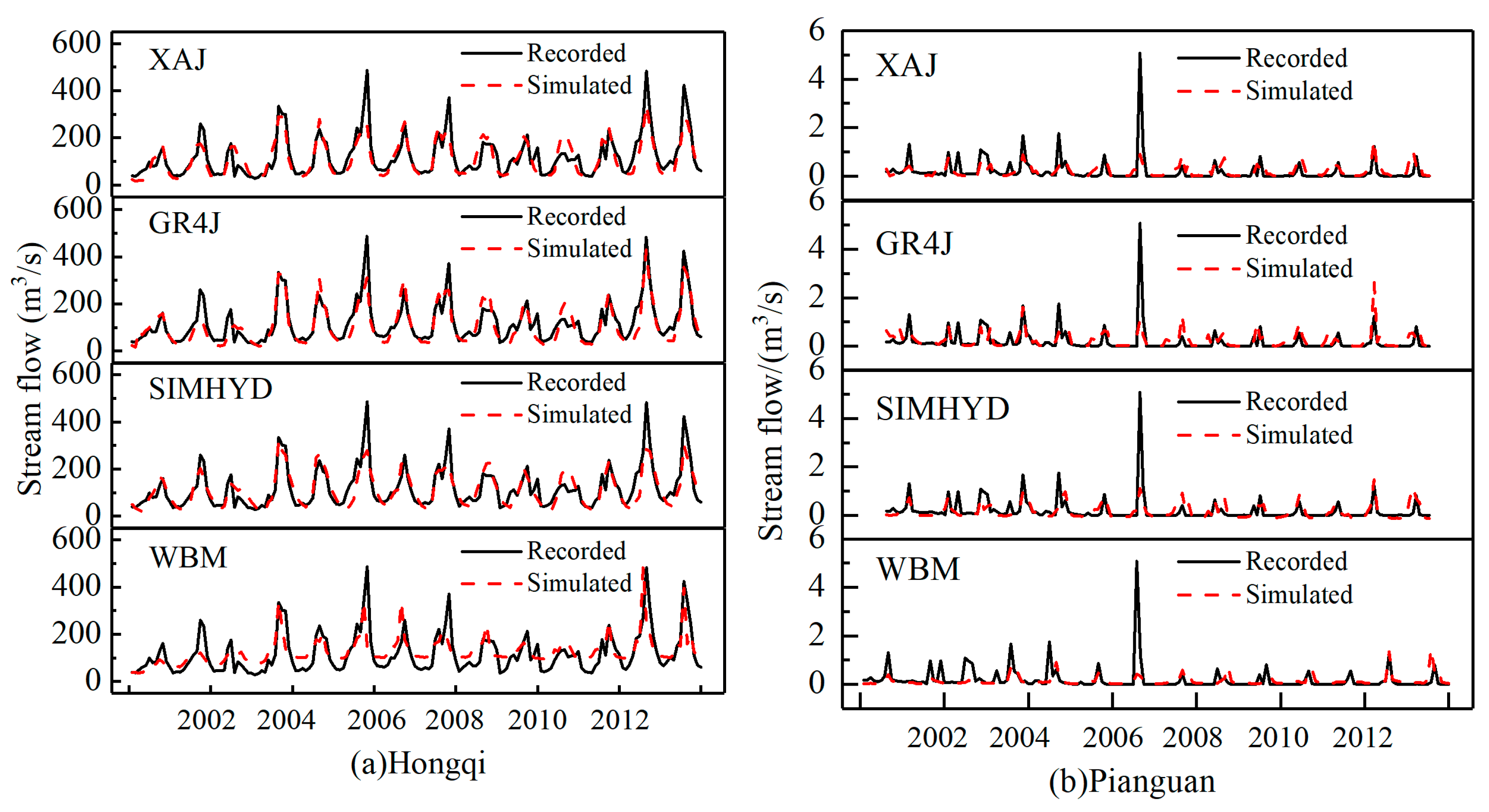
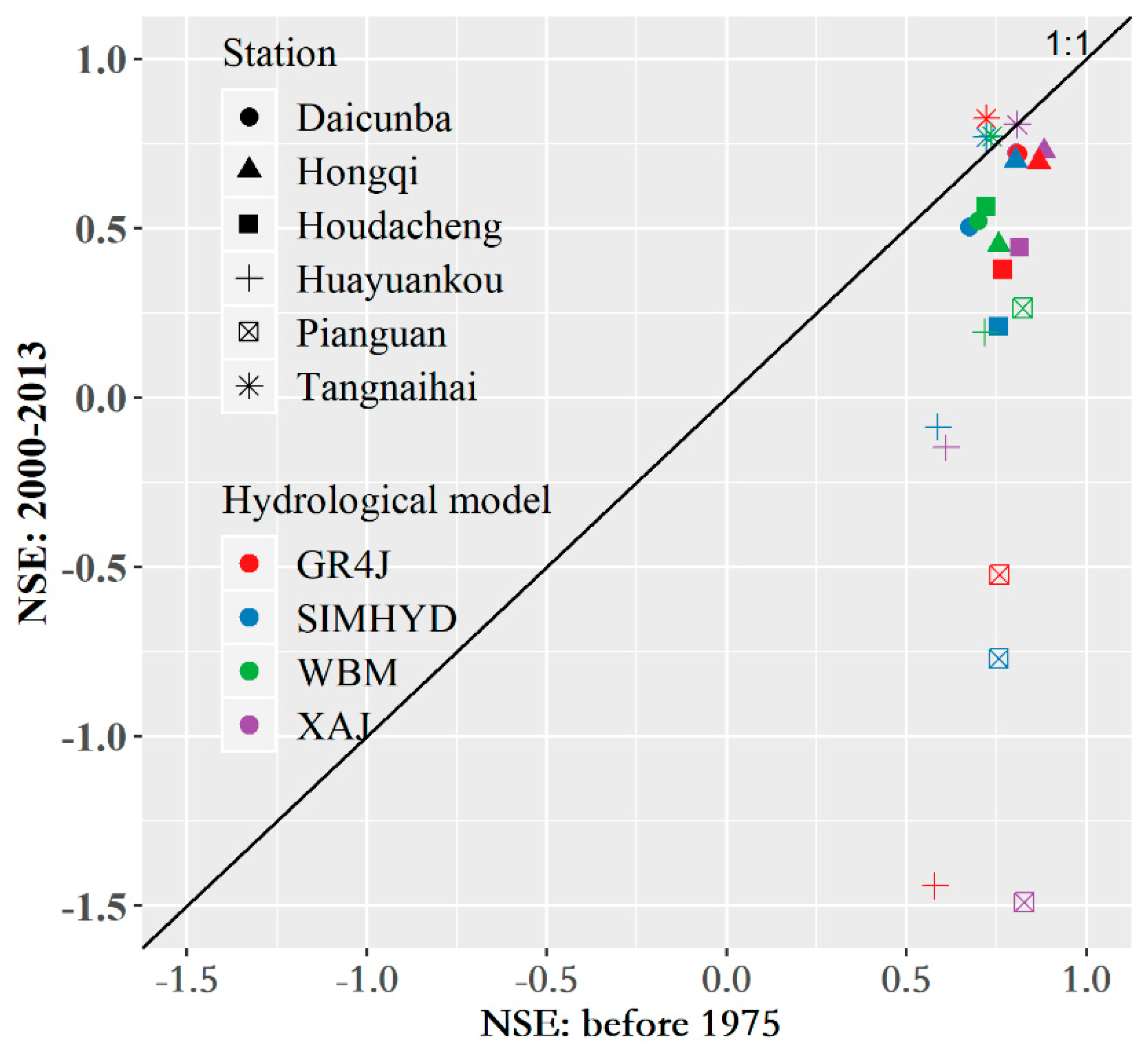
| River | Stations | Drainage Area/km2 | Discharge Series | Precipitation/mm | Runoff/mm | Annual Average Temperature/°C |
|---|---|---|---|---|---|---|
| Upper Yellow River | Tangnaihai | 121,973 | 1956–2013 | 507.9 | 166.9 | −4.9 |
| Tao River | Hongqi | 24,973 | 1955–2015 | 547.2 | 180.6 | 0.2 |
| Pianguan River | Pianguan | 1896 | 1951–2013 | 425.3 | 14.7 | 4.3 |
| Sanchuan River | Houdacheng | 4105 | 1957–2015 | 487.1 | 51.1 | 7.0 |
| Yellow River | Huayuankou | 730,036 | 1951–2013 | 437.8 | 56.7 | 5.1 |
| Dawen River | Daicunba | 8264 | 1958–2015 | 870.9 | 73.9 | 13.9 |
| River/Basins | Hydrometric Station | Annual Precipitation | Annual Temperature | ||||
|---|---|---|---|---|---|---|---|
| S (mm/year) | Trend | U | S (°C/year) | Trend | U | ||
| Dawen River | Daicunba | −1.031 | ↓ | −0.88 | 0.017 | ↑ | 4.18 |
| Tao River | Hongqi | −0.226 | ↓ | −0.05 | 0.019 | ↑ | 4.15 |
| Sanchuan River | Houdacheng | −0.462 | ↓ | −0.41 | 0.029 | ↑ | 4.74 |
| Yellow River | Huayuankou | −0.483 | ↓ | −0.72 | 0.022 | ↑ | 4.78 |
| Pianguan River | Pianguan | −0.433 | ↓ | −0.23 | 0.022 | ↑ | 3.7 |
| Upper Yellow River | Tangnaihai | 0.703 | ↑ | 1.8 | 0.013 | ↑ | 3.36 |
| River | Stations | U | Abrupt Change Year | Statistics | P-Value | Previous Studies | |
|---|---|---|---|---|---|---|---|
| Change Year | References | ||||||
| Dawen River | Daicunba | −1.19 | 1975 | 1.866 | 7.78 × 10−2 | 1975 | [58] |
| Tao River | Hongqi | −3.02 | 1986 | 3.168 | 3.50 × 10−3 | 1989 | [59] |
| Sanchuan River | Houdacheng | −3.60 | 1997 | −17.18 | 1.74 × 10−5 | 1995 | [58] |
| Yellow River | Huayuankou | −5.57 | 1986 | 3.505 | 5.02 × 10−3 | 1986 | [58] |
| Pianguan River | Pianguan | −7.41 | 1983 | 6.166 | 1.30 × 10−7 | 1984 | [60] |
| Upper Yellow River | Tangnaihai | −1.13 | 1990 | −3.432 | 7.62 × 10−3 | 1990 | [61] |
| River | Station | Calibration Period | NSE 1 | RE (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| XAJ | GR4J | SIMHYD | WBM | XAJ | GR4J | SIMHYD | WBM | |||
| Dawen River | Daicunba | 1958–1968 | 0.827 | 0.870 | 0.709 | 0.703 | −0.68 | −0.36 | −10.2 | −6.73 |
| Tao River | Hongqi | 1955–1965 | 0.849 | 0.852 | 0.779 | 0.732 | −5.48 | −5.46 | −9.26 | 5.15 |
| Sanchuan River | Houdacheng | 1957–1967 | 0.814 | 0.754 | 0.747 | 0.728 | −4.58 | −9.63 | 1.64 | −11.9 |
| Yellow River | Huayuankou | 1958–1968 | 0.665 | 0.560 | 0.647 | 0.752 | −7.57 | −7.60 | −9.35 | 0.10 |
| Pianguan River | Pianguan | 1957–1967 | 0.838 | 0.729 | 0.799 | 0.812 | −4.11 | −9.27 | −2.13 | −10.9 |
| Upper Yellow River | Tangnaihai | 1956–1966 | 0.834 | 0.725 | 0.738 | 0.735 | 4.80 | −0.55 | −6.95 | −2.02 |
| River | Station | Verification Period | NSE | RE (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| XAJ | GR4J | SIMHYD | WBM | XAJ | GR4J | SIMHYD | WBM | |||
| Dawen River | Daicunba | 1969–1975 | 0.784 | 0.750 | 0.638 | 0.696 | 9.00 | 9.17 | −13.9 | 15.4 |
| Tao River | Hongqi | 1966–1975 | 0.915 | 0.883 | 0.828 | 0.781 | 4.72 | 11.6 | 5.17 | 11.0 |
| Sanchuan River | Houdacheng | 1968–1975 | 0.816 | 0.782 | 0.764 | 0.714 | 7.47 | −14.9 | 6.79 | −10.9 |
| Yellow River | Huayuankou | 1969–1975 | 0.555 | 0.599 | 0.529 | 0.686 | 16.9 | 8.54 | 13.1 | 23.3 |
| Pianguan River | Pianguan | 1968–1975 | 0.815 | 0.788 | 0.713 | 0.834 | −8.48 | −16.1 | 15.6 | −16.7 |
| Upper Yellow River | Tangnaihai | 1967–1975 | 0.781 | 0.718 | 0.705 | 0.739 | 8.30 | 0.33 | 8.81 | −2.45 |
| River | Station | Calibration Period | NSE | RE (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| XAJ | GR4J | SIMHYD | WBM | XAJ | GR4J | SIMHYD | WBM | |||
| Dawen River | Daicunba | 2000–2010 | 0.748 | 0.726 | 0.544 | 0.486 | −3.42 | 16.8 | 35.1 | 8.06 |
| Tao River | Hongqi | 2000–2010 | 0.661 | 0.652 | 0.705 | 0.409 | −11.8 | −6.61 | −1.26 | 4.16 |
| Sanchuan River | Houdacheng | 2000–2010 | 0.341 | 0.199 | 0.416 | 0.490 | −14.6 | −28.7 | −3.40 | 4.25 |
| Yellow River | Huayuankou | 2000–2010 | 0.065 | −0.885 | 0.099 | 0.217 | −3.15 | −28.4 | 0.35 | 0.46 |
| Pianguan River | Pianguan | 2000–2010 | 0.293 | 0.271 | 0.352 | 0.265 | 4.16 | 12.2 | −19.6 | −25.9 |
| Upper Yellow River | Tangnaihai | 2000–2010 | 0.824 | 0.818 | 0.761 | 0.776 | −10.9 | −6.70 | 0.27 | −0.87 |
| River | Station | Verification Period | NSE | RE (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| XAJ | GR4J | SIMHYD | WBM | XAJ | GR4J | SIMHYD | WBM | |||
| Dawen River | Daicunba | 2011–2013 | 0.701 | 0.719 | 0.465 | 0.558 | −10.5 | −1.57 | 27.9 | −11.0 |
| Tao River | Hongqi | 2011–2013 | 0.794 | 0.740 | 0.695 | 0.495 | −11.3 | 8.42 | −17.9 | −16.4 |
| Sanchuan River | Houdacheng | 2011–2013 | 0.549 | 0.560 | 0.005 | 0.640 | −34.2 | −18.3 | −59.8 | −9.25 |
| Yellow River | Huayuankou | 2011–2013 | −0.359 | −1.99 | -0.270 | 0.170 | −29.5 | −9.52 | −31.3 | −22.1 |
| Pianguan River | Pianguan | 2011–2013 | v3.27 | v1.32 | −1.89 | 0.264 | 296 | 157 | 213 | 193 |
| Upper Yellow River | Tangnaihai | 2011–2013 | 0.791 | 0.832 | 0.778 | 0.769 | −18.8 | 13.3 | −15.0 | −11.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Zhang, J.; Elmahdi, A.; Li, X.; Liu, J.; Liu, Y.; Jin, J.; Liu, Y.; Bao, Z.; Liu, C.; et al. The Capacity of the Hydrological Modeling for Water Resource Assessment under the Changing Environment in Semi-Arid River Basins in China. Water 2019, 11, 1328. https://doi.org/10.3390/w11071328
Guan X, Zhang J, Elmahdi A, Li X, Liu J, Liu Y, Jin J, Liu Y, Bao Z, Liu C, et al. The Capacity of the Hydrological Modeling for Water Resource Assessment under the Changing Environment in Semi-Arid River Basins in China. Water. 2019; 11(7):1328. https://doi.org/10.3390/w11071328
Chicago/Turabian StyleGuan, Xiaoxiang, Jianyun Zhang, Amgad Elmahdi, Xuemei Li, Jing Liu, Yue Liu, Junliang Jin, Yanli Liu, Zhenxin Bao, Cuishan Liu, and et al. 2019. "The Capacity of the Hydrological Modeling for Water Resource Assessment under the Changing Environment in Semi-Arid River Basins in China" Water 11, no. 7: 1328. https://doi.org/10.3390/w11071328
APA StyleGuan, X., Zhang, J., Elmahdi, A., Li, X., Liu, J., Liu, Y., Jin, J., Liu, Y., Bao, Z., Liu, C., He, R., & Wang, G. (2019). The Capacity of the Hydrological Modeling for Water Resource Assessment under the Changing Environment in Semi-Arid River Basins in China. Water, 11(7), 1328. https://doi.org/10.3390/w11071328







