An Endorheic Lake in a Changing Climate: Geochemical Investigations at Lake Trasimeno (Italy)
Abstract
:1. Introduction
2. Materials and Methods
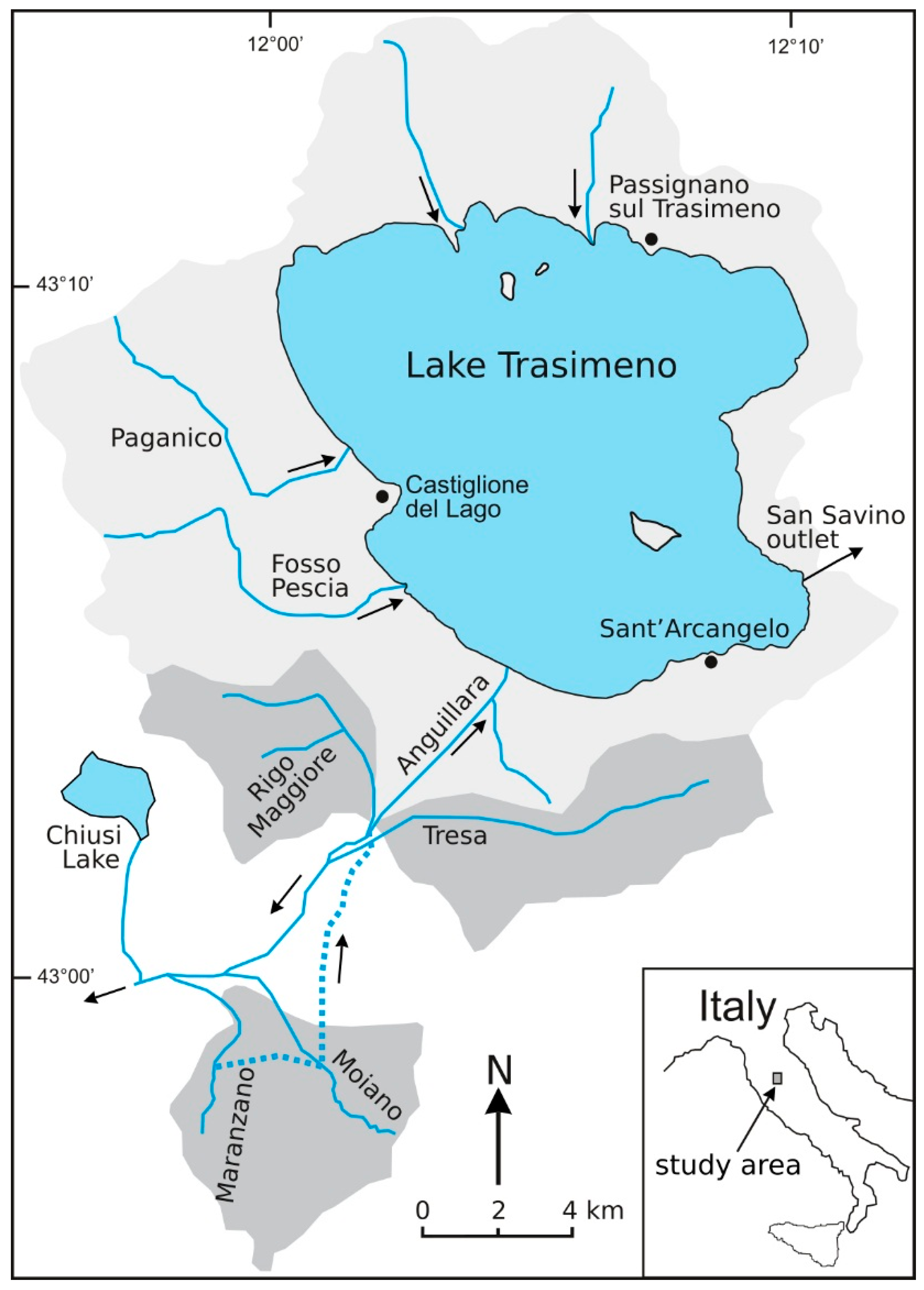
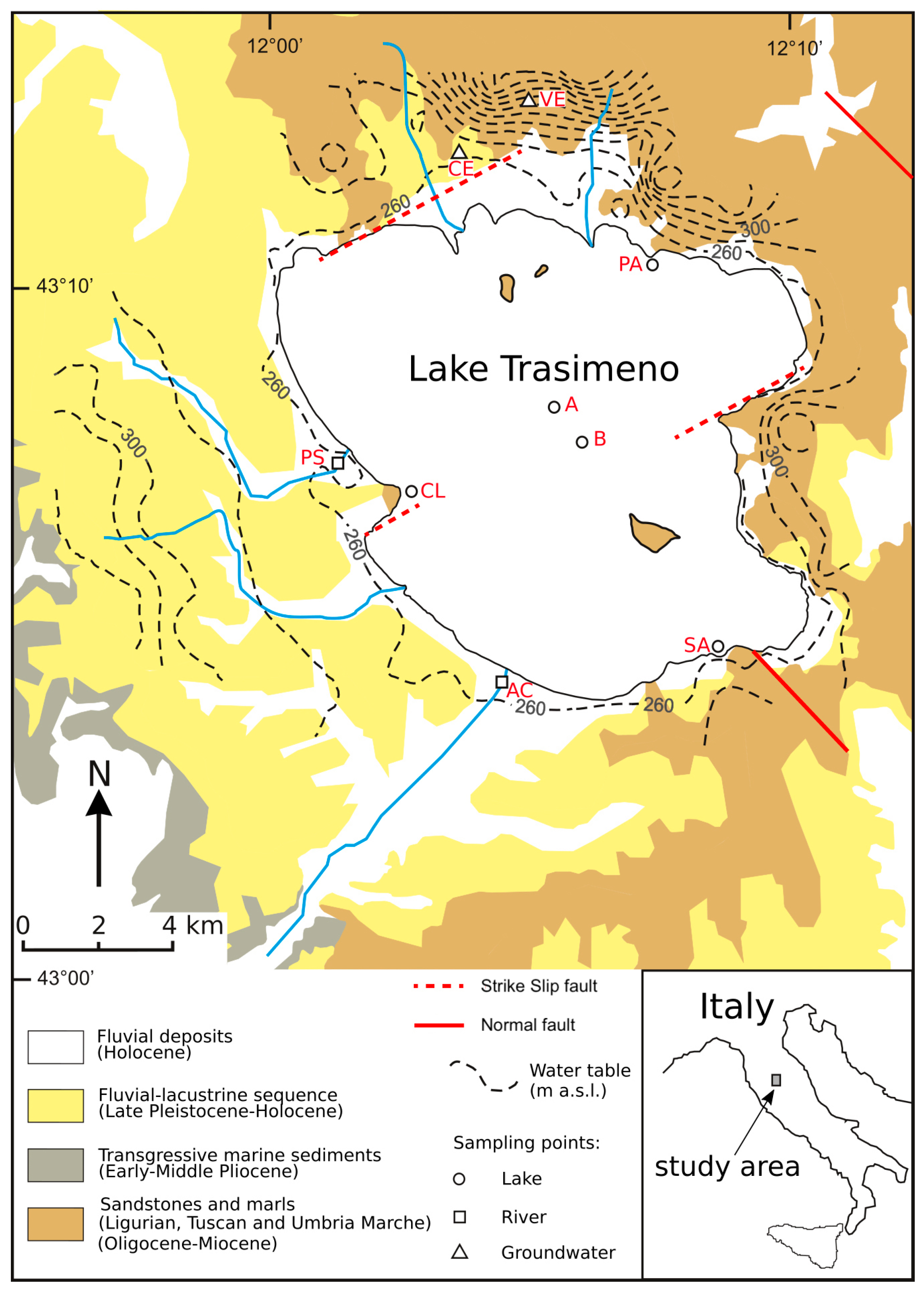
2.1. The Study Area: Geological, Hydrogeological and Hydrological Setting
2.2. Sampling and Analyses
3. Results
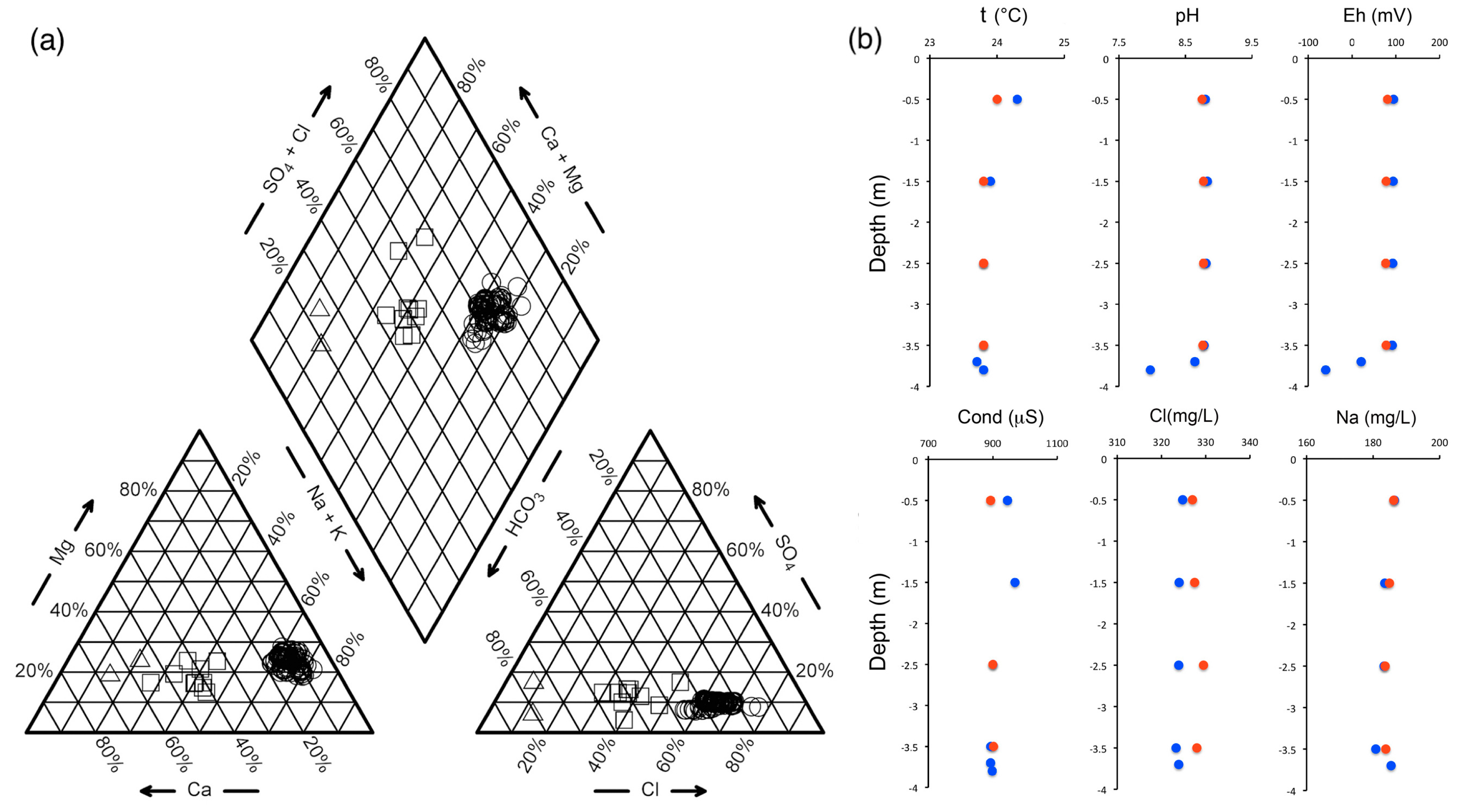
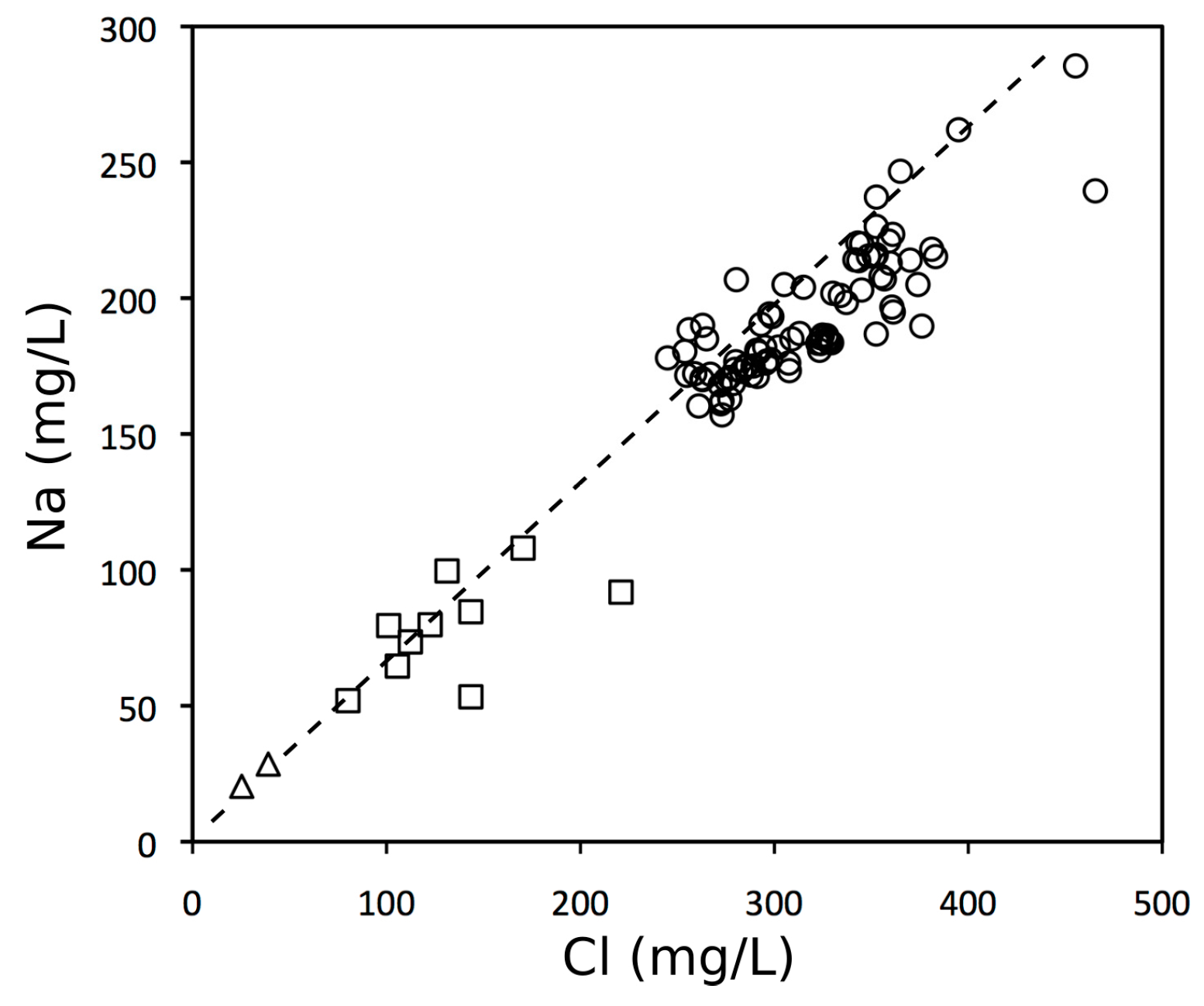
3.1. Chemical Composition of Lake Water, River Waters and Groundwater
3.2. Aqueous Speciation Calculations
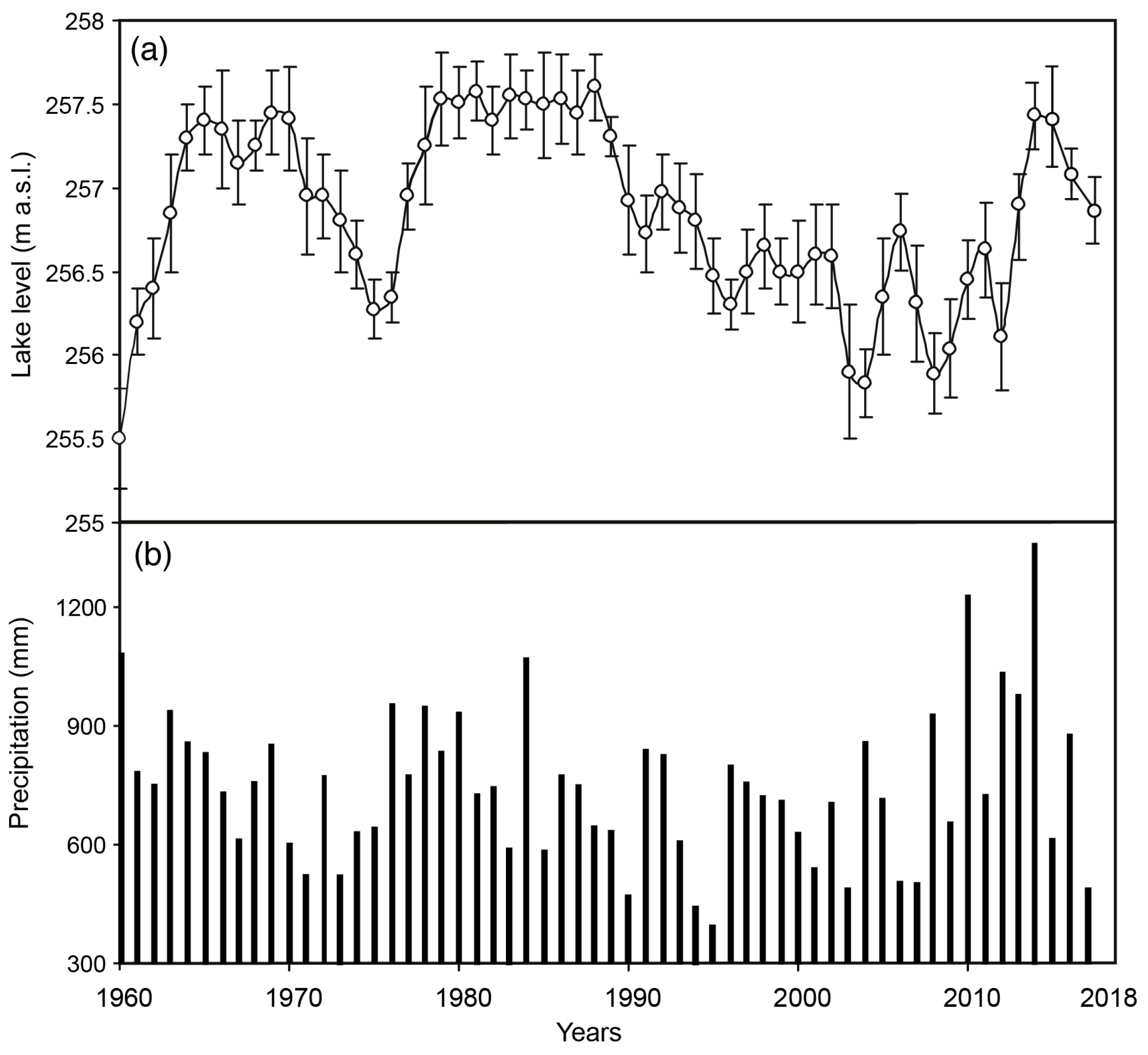
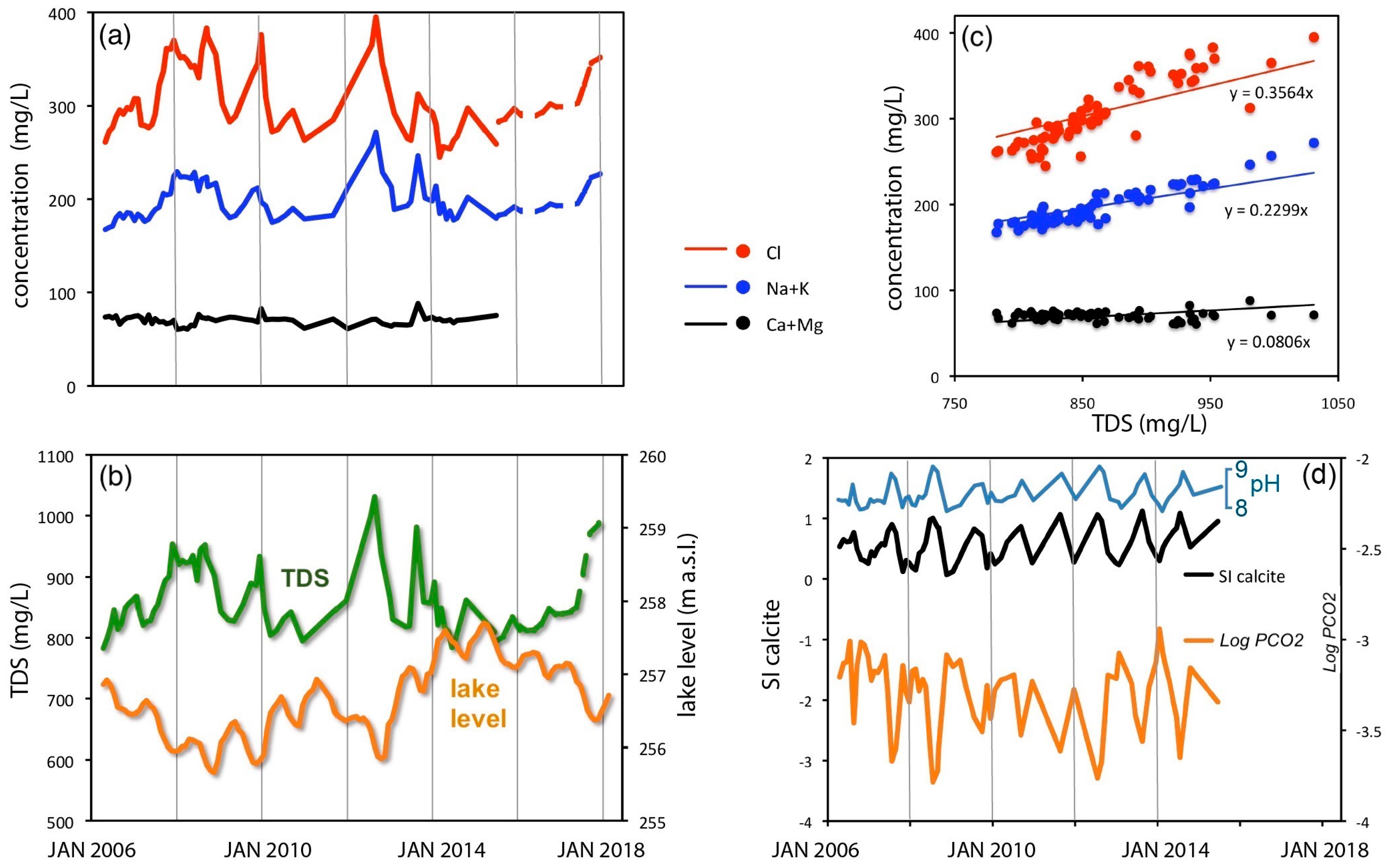
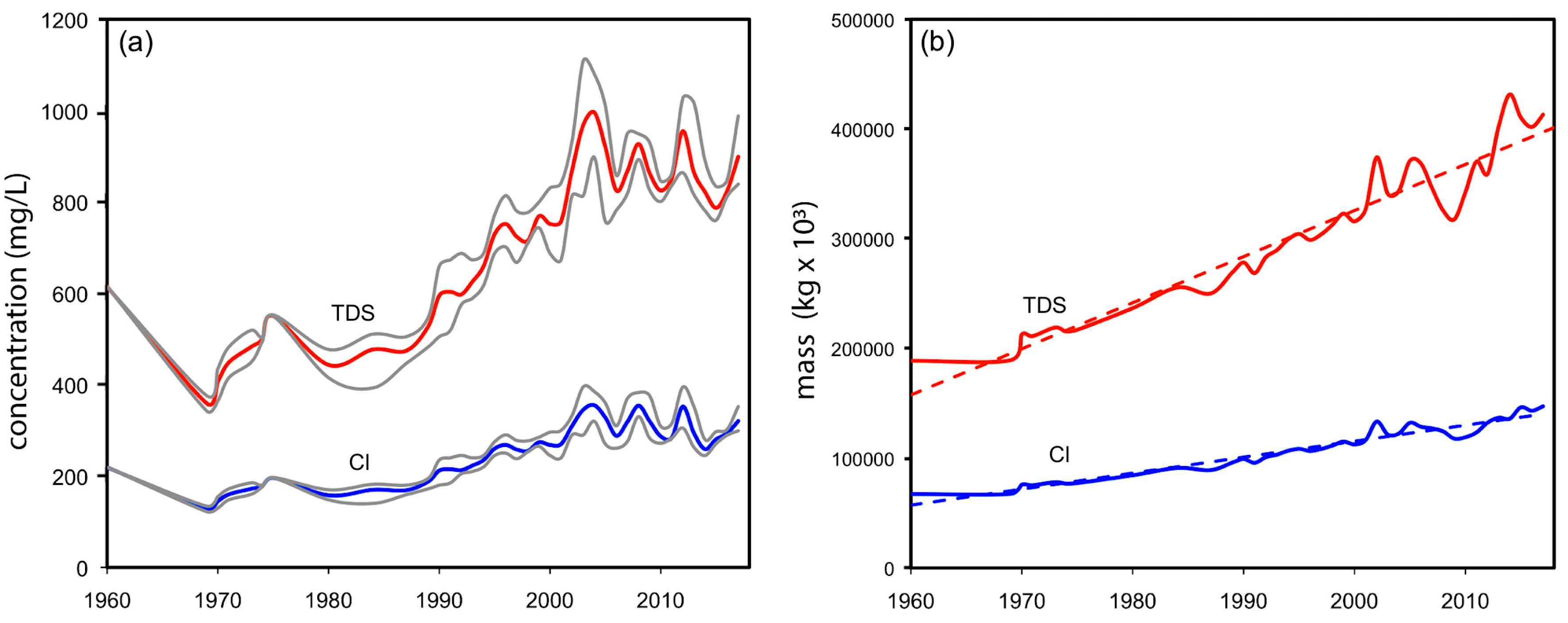
3.3. Chemical Variations of Lake Water from 2006 to 2018
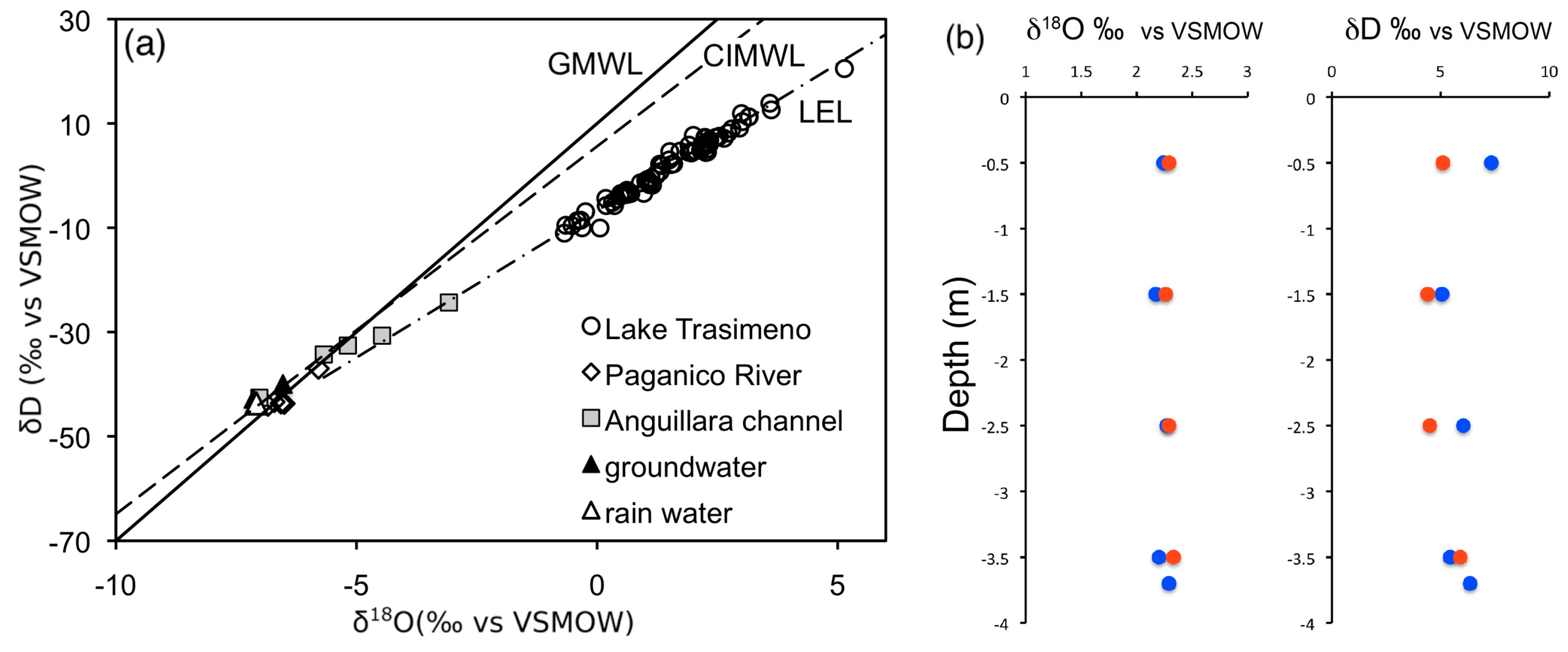
3.4. Isotopic Composition of Water and Total Dissolved Inorganic Carbon
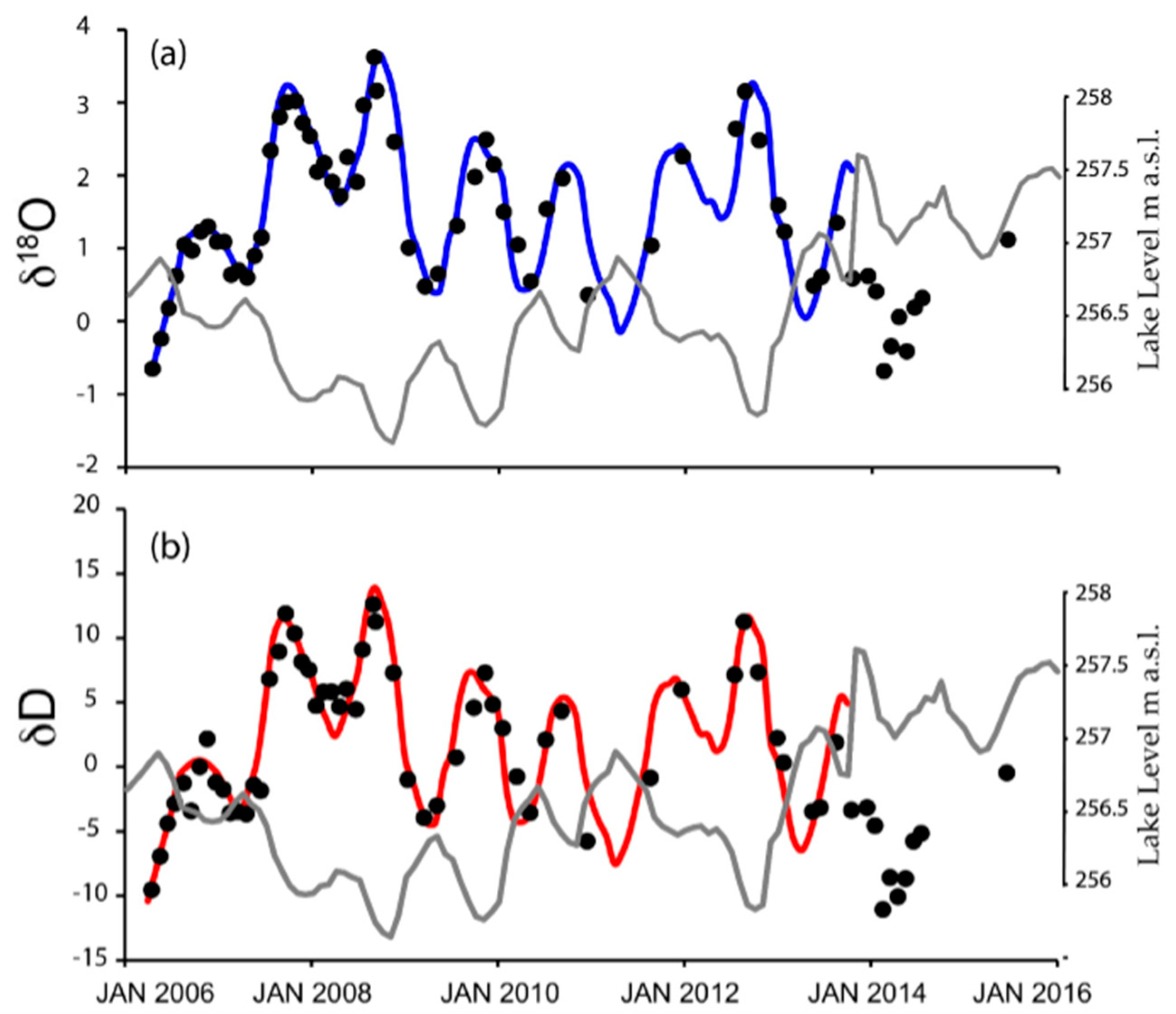
3.5. Isotopic Variations of Lake Water from 2006 to 2015
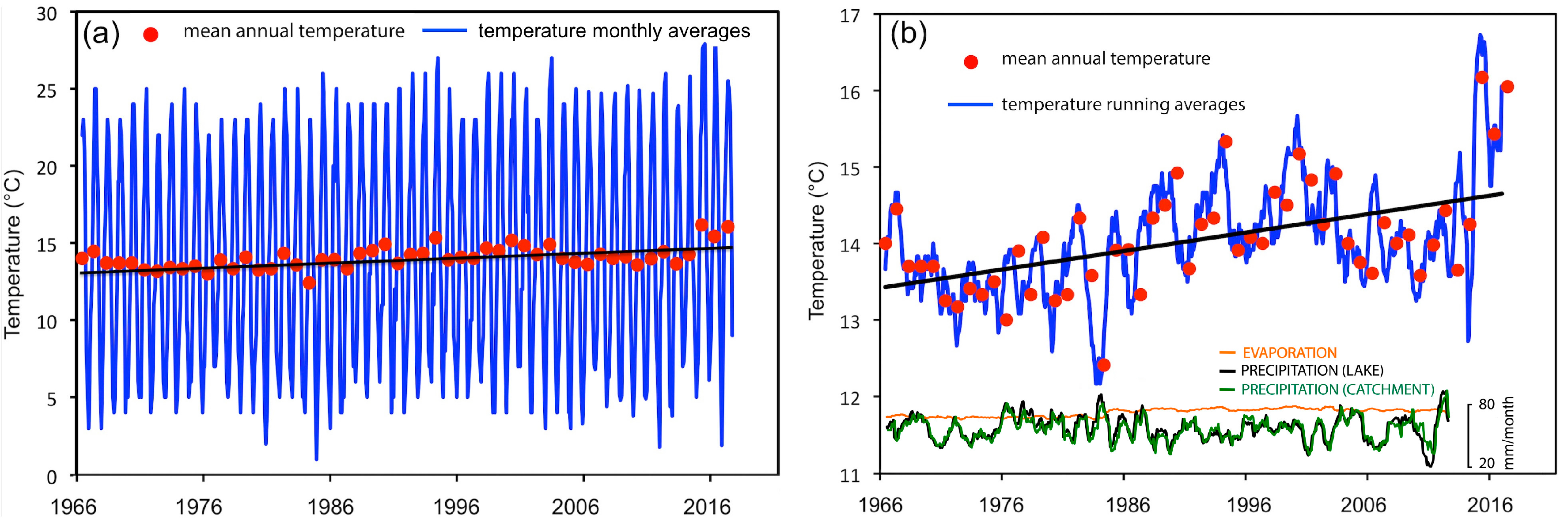
3.6. Long-Term Physical and Chemical Variations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mason, I.M.; Guzkowska, M.A.J.; Rapley, C.G.; Street-Perrott, F.A. The response of lake levels and areas to climate change. Clim. Chang. 1994, 27, 161–197. [Google Scholar] [CrossRef]
- Vance, R.E.; Wolfe, S.A. Geological indicators of water resources in semi-arid environments: Southwestern interior of Canada. In Geoindicators: Assessing Rapid Environmental Changes in Earth Systems; Berger, A.R., Iams, W.J., Eds.; A.A. Balkema: Rotterdam, The Netherlands, 1996; pp. 237–250. [Google Scholar]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A. Paleolimnology: The History and Evolution of Lake Systems, 1st ed.; Oxford University Press: Oxford, UK, 2003; 528p. [Google Scholar]
- Ludovisi, A.; Gaino, E. Meteorological and water quality changes in Lake Trasimeno (Umbria, Italy) during the last fifty years. J. Limnol. 2010, 69, 174–188. [Google Scholar] [CrossRef]
- Dragoni, W. Il Lago Trasimeno e le Variazioni Climatiche; Progetto informativo dell’assessorato all’Ambiente della Provincia di Perugia; Provincia di Perugia, Servizio Gestione e Difesa Idraulica: Perugia, Italy, 2004; 60p. [Google Scholar]
- Burzigotti, R.; Dragoni, W.; Evangelisti, C.; Gervasi, L. The role of lake Trasimeno (central Italy) in the history of hydrology and water management. In Proceedings of the Third IWHA Conference, Bibliotheca Alexandrina, Alexandria, Egypt, 11–14 December 2003. [Google Scholar]
- Gambini, E. Le Oscillazioni di Livello del Lago Trasimeno; Quaderni del Museo della Pesca 2; Edizioni Era Nova: Perugia, Italy, 1995; p. 139. [Google Scholar]
- Beadle, L.C. The Inland Waters of Tropical Africa; Longman: London, UK, 1974; 365p. [Google Scholar]
- IPCC. AR4 WG2. Climate Change 2007: Impacts, Adaptation and Vulnerability, Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; 976p. [Google Scholar]
- IPCC. AR5 WG2. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; 688p. [Google Scholar]
- Dragoni, W. Some considerations on Climatic Changes, Water Resources and Water Needs in the Italian Region South of the 43° N. In Water, Environment and Society in Times of Climatic Change; Brown, N., Issar, A., Eds.; Kluwer: Dordrecht, The Netherlands, 1998; pp. 241–271. [Google Scholar]
- Cambi, C.; Dragoni, W. Groundwater yield, climatic changes and recharge variability: Considerations arising from the modelling of a spring in the Umbria – Marche Apennines. Hydrogéologie 2000, 4, 11–25. [Google Scholar]
- Ludovisi, A.; Gaino, E.; Bellezza, M.; Casadei, S. Impact of climate change on the hydrology of shallow Lake Trasimeno (Umbria, Italy): History, forecasting and management. Aquat. Ecosyst. Health 2013, 16, 190–197. [Google Scholar] [CrossRef]
- Dragoni, W.; Melillo, M.; Giontella, C. Bilancio idrico del Lago Trasimeno. In Tutela Ambientale del Lago Trasimeno; Martinelli, A., Ed.; ARPA Umbria: Perugia, Italy, 2012; pp. 70–85. [Google Scholar]
- Cortecci, G. Oxygen-isotope variations in sulfate ions in the water of some Italian lakes. Geochim. Cosmochim. Acta 1973, 37, 1531–1542. [Google Scholar] [CrossRef]
- Cortecci, G.; Dinelli, E. Sulfur isotopic composition of sulfate from Trasimeno, Chiusi, Montepulciano and Corbara lakes (central Italy). Miner. Petrogr. Acta 1999, 42, 17–28. [Google Scholar]
- Mearelli, M.; Lorenzoni, M.; Mantilacci, L. Il lago Trasimeno. Riv. Idrobiol. 1990, 29, 353–389. [Google Scholar]
- Giovanardi, F.; Poletti, A.; Micheli, A. Indagine sulla qualità della acque del lago Trasimeno—Idrochimica. Acqua-Aria 1995, 5, 519–526. [Google Scholar]
- Giovanardi, F.; Poletti, A.; Micheli, A. Indagine sulla qualità della acque del lago Trasimeno—Definizione dei livelli trofici. Acqua-Aria 1995, 6, 627–633. [Google Scholar]
- Cingolani, L.; Charavgis, F.; Bodo, G.; Neri, N. Monitoraggio qualitativo del reticolo superficiale del Lago Trasimeno. In Piano di Tutela delle Acque; Allegati/Monografia 6; ARPA Umbria—Regione Umbria: Perugia, Italy, 2012; 68p. [Google Scholar]
- Giardino, C.; Bresciani, M.; Villa, P.; Martinelli, A. Application of remote sensing in water resource management: The case study of Lake Trasimeno, Italy. Water Resour. Manag. 2010, 24, 3885–3899. [Google Scholar] [CrossRef]
- Doglioni, C.; Mongelli, F.; Pialli, G. Appenninic back arc lithospheric boudinage on the former alpine belt. Mem. Soc. Geol. Ital. 1998, 52, 457–468. [Google Scholar]
- Barchi, M. The Neogene-Quaternary evolution of the Northern Apennines: Crustal structure, style of deformation and seismicity. In The Geology of Italy: Tectonics and Life Along Plate Margins; Journal of the Virtual Explorer, Electronic Edition; Beltrando, M., Peccerillo, A., Mattei, M., Conticelli, S., Doglioni, C., Eds.; The Virtual Explorer Pty. Ltd.: Conder, Australia, 2010; Volume 36, p. 11. [Google Scholar] [CrossRef]
- Brozzetti, F.; Boncio, P.; Lavecchia, G. A new interpretation of the CROP03 seismic profile across the Northern Tiber Valley and inferences about the seismotectonics of the Citta’ di Castello-San Sepolcro area. In Proceedings of the Geoitalia 2001: 3. Forum italiano di scienze della terra, Chieti, Italy, 5–8 September 2001; Carmina, B., Orlando, A., Pasero, M., Eds.; Federazione Italiana di Scienze della Terra: Chieti, Italy, 2001; pp. 337–338. [Google Scholar]
- Pascucci, V.; Merlini, S.; Martini, I.P. Seismic stratigraphy of the Miocene-Pleistocene sedimentary basinsof the Northern Tyrrhenian Sea and western Tuscany (Italy). Basin Res. 1999, 4, 337–356. [Google Scholar] [CrossRef]
- Pauselli, C.; Barchi, M.R.; Federico, C.; Magnani, M.B.; Minelli, G. The crustal structure of the Northern Apennines (Central Italy): An insight by the Crop03 seismic line. Am. J. Sci. 2006, 306, 428–450. [Google Scholar] [CrossRef]
- Gasperini, L.; Barchi, M.R.; Bellucci, L.G.; Bortoluzzi, G.; Ligi, M.; Pauselli, C. Tectonostratigraphy of Lake Trasimeno (Italy) and the geological evolution of the Northern Apennines. Tectonophysics 2010, 492, 164–174. [Google Scholar] [CrossRef]
- ISPRA—Servizio Geologico d’Italia. Carta Geologica d’Italia Alla Scala 1:50.000, Foglio 310 Passignano sul Trasimeno; Barchi, M., Marroni, M., Eds.; Istituto Superiore per la Protezione e la Ricerca Ambientale: Rome, Italy, 2014; ISBN 8893110342. [Google Scholar]
- Ambrosetti, P.; Cattuto, C.; Gregori, L. Lineamenti geomorfologici dell’area a sud del Lago Trasimeno: Bacino di Tavernelle/Pietrafitta. Il Quat. 1989, 2, 57–64. [Google Scholar]
- Deffenu, L.; Dragoni, W. Caratteristiche idrogeologiche del Lago Trasimeno. Mem. Soc. Geol. Ital. 1978, 19, 295–302. [Google Scholar]
- Dragoni, W. Idrogeologia del Lago Trasimeno: Sintesi, problemi, aggiornamenti. Geogr. Fis. Dinam. Quat. 1982, 5, 192–206. [Google Scholar]
- Cardellini, C.; Frondini, F.; Peruzzi, L. Caratteristiche idrogeochimiche degli acquiferi nel bacino del Lago Trasimeno (Italy). In Proceedings of the 2nd International Workshop Aquifer Vulnerability and Risk, and 4th Congress on the Protection and Management of Groundwater, Parma, Italy, 21–23 September 2005; Reggia di Colorno: Colorno, Italy, 2005; p. 7. [Google Scholar]
- Club Velico Trasimeno. Available online: http://www.clubvelicotrasimeno.it/Home.aspx (accessed on 20 December 2018).
- ARPA Umbria—Elenco Monitoraggi. Available online: http://www.arpa.umbria.it/pagine/elenco-monitoraggi (accessed on 10 December 2018).
- Parkhurst, D.L. User’s Guide to PHREEQC: A Computer Program for Speciation, Reaction-Path, Advective-Transport, and Inverse Geochemical Calculations; Water-Resources Investigations Report 95-4227; U.S. Geological Survey, Earth Science Information Center, Open-File Reports Section: Lakewood, CO, USA, 1995; 143 p.
- Wolery, T.J. Calculation of Chemical Equilibrium between Aqueous Solution and Minerals - The EQ3/6 Software Package; Lawrence Livermore National Laboratory Report UCRL-52658; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1979; 41 p.
- Italian Republic. Decreto legislativo 3 aprile 2006, n. 152, Norme in materia ambientale. Gazzetta Ufficale 2006, 88, 13–374. [Google Scholar]
- European Union. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for Community action in the field of water policy. Off. J. 2000, L 327, 1–73. [Google Scholar]
- Reeder, R.J.; Nakajima, Y. The nature of ordering and ordering defects in dolomite. Phys. Chem. Miner. 1982, 8, 29–35. [Google Scholar] [CrossRef]
- Zucchini, A.; Comodi, P.; Katerinopoulou, A.; Balic-Zunic, T.; McCammon, C.; Frondini, F. Order-disorder-reorder process in thermally treated dolomite samples: A combined powder and singlecrystal X-ray diffraction study. Phys. Chem. Miner. 2012, 39, 319–328. [Google Scholar] [CrossRef]
- Land, L.S. Failure to precipitate dolomite at 25 °C from dilute solution despite 1000 fold oversaturation after 32 years. Aquat. Geochem. 1998, 4, 361–368. [Google Scholar] [CrossRef]
- Arvidson, R.S.; Mackenzie, F.T. The dolomite problem: Control of precipitation kinetics by temperatureand saturation state. Am. J. Sci. 1999, 299, 257–288. [Google Scholar] [CrossRef]
- Frondini, F. Geochemistry of regional aquifer systems hosted by carbonate-evaporite formations in Umbria and southern Tuscany (central Italy). Appl. Geochem. 2008, 23, 2091–2104. [Google Scholar] [CrossRef]
- Longinelli, A.; Selmo, E. Isotopic composition of precipitation in Italy: A first overall map. J. Hydrol. 2003, 70, 75–88. [Google Scholar]
- Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
- Gibson, J.J.; Birks, S.J.; Edwards, T.W.D. Global prediction of δA and δ2H-δ18O evaporation slopes for lakes and soil water accounting for seasonality. Glob. Biogeochem. Cycles 2008, 22, GB2031. [Google Scholar] [CrossRef]
- Brabanti, L.; Carollo, A.; Libera, V. Carta Batimetrica del Lago Trasimeno; Istituto Italiano di Idrobiologia: Pallanza, Italy, 1968. [Google Scholar]
- Giustini, F.; Brilli, M.; Patera, A. Mapping oxygen stable isotopes of precipitation in Italy. J. Hydrol. Reg. Stud. 2016, 8, 162–181. [Google Scholar] [CrossRef] [Green Version]
- Craig, H.; Gordon, L.I. Deuterium and oxygen-18 variations in the ocean and marine atmosphere. In Stable Isotopes in Oceanographic Studies and Paleo-Temperatures; Tongiorgi, E., Ed.; Lab. Geol. Nucl.: Pisa, Italy, 1965; pp. 9–130. [Google Scholar]
- Gat, J.R.; Mook, W.G.; Meijer, H.A.J. Atmospheric Water. In Environmental Isotopes in the Hydrological Cycle: Principles and Applications; IAEA-UNESCO Series; IHP-V Technical Documents in Hydrology, No.39, Vol. II; Mook, W.G., Ed.; UNESCO: Paris, France, 2001; Volume 2, p. 113. [Google Scholar]
- Rozanski, K.; Froehlich, K.; Mook, W.G. Surface Water. In Environmental Isotopes in the Hydrological Cycle: Principles and Applications; IAEA-UNESCO Series; IHP-V Technical Documents in Hydrology, N.39, Vol. III; Mook, W.G., Ed.; UNESCO: Paris, France, 2001; Volume 3, p. 117. [Google Scholar]
- Gibson, J.J.; Birks, S.J.; Yi, Y. Stable isotope mass balance of lakes: A contemporary perspective. Quat. Sci. Rev. 2016, 131, 316–328. [Google Scholar] [CrossRef]
- Regione Umbria. Servizio Idrografico Regionale. Available online: http://www.regione.umbria.it/ambiente/servizio-idrografico (accessed on 20 December 2018).
- Skrzypek, G.; Mydłowski, A.; Dogramaci, S.; Hedley, P.; Gibson, J.J.; Grierson, P.F. Estimation of evaporative loss based on the stable isotope composition of water using Hydrocalculator. J. Hydrol. 2015, 523, 781–789. [Google Scholar] [CrossRef] [Green Version]
- Horita, J.; Wesolowski, D.J. Liquid-vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature. Geochim. Cosmochim. Acta 1994, 58, 3425–3437. [Google Scholar] [CrossRef]
- Wessa, P. Multivariate Correlation Matrix (v1.0.11) in Free Statistics Software (v1.2.1), Office for Research Development and Education. 2016. Available online: http://www.wessa.net/Patrick.Wessa/rwasp_pairs.wasp/ (accessed on 2 April 2019).
- Mannelli, G.; Mancini, P. Forme di inquinamento delle acque del Lago Trasimeno. Riv. Idrobiol. 1962, 2, 113–126. [Google Scholar]
- Tiberi, O. Fluoruri e cloruri nel lago Trasimeno. Riv. Idrobiol. 1980, 19, 37–59. [Google Scholar]
- Tiberi, O. Analisi di componenti abiotiche nei sedimenti del lago Trasimeno. Riv. Idrobiol. 1991, 30, 303–337. [Google Scholar]
- Tiberi, O.; Taticchi-Viganò, M.I.; Di Giovanni, M.V. Ragguagli sulle condizioni fisiche, chimiche, planctologiche del Lago Trasimeno (febbraio 1969–febbraio 1970). Riv. Idrobiol. 1971, 10, 39–233. [Google Scholar]
- Yapiyev, V.; Sagintayev, Z.; Inglezakis, V.J.; Samarkhanov, K.; Verhoef, A. Essentials of endorheic basins and lakes: A review in the context of current and future water resource management and mitigation activities in Central Asia. Water 2017, 9, 798. [Google Scholar] [CrossRef]
- Finch, J.W.; Hall, R.L. Evaporation from Lakes. In Encyclopedia of Hydrological Sciences, Part 4 Hydrometeorology; Anderson, M.G., McDonnell, J.J., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hartmann, D.L.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 159–254. [Google Scholar]
- Wang, W.; Lee, X.; Xiao, W.; Liu, S.; Shultz, N.; Wang, Y.; Zang, M.; Zhao, L. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nat. Geosci. 2018, 11, 410–414. [Google Scholar] [CrossRef]
- Livingstone, D.M.; Lotter, A.F. The relationship between air and water temperatures in lakes of the Swiss Plateau: A case study with palaeolimnological implications. J. Paleolimnol. 1998, 19, 181–198. [Google Scholar] [CrossRef]
- Schneider, P.; Hook, S.J. Space observations of inland water bodies show rapid surface warming since 1985. Geophys. Res. Lett. 2010, 37, L22405. [Google Scholar] [CrossRef]
- Sharma, S.; Gray, D.K.; Read, J.S.; O’Reilly, C.M.; Schneider, P.; Qudrat, A.; Gries, C.; Stefanoff, S.; Hampton, S.E.; Hook, S.; et al. A global database of lake surface temperatures collected by in situ and satellite methods from 1985–2009. Sci. Data 2015, 2, 150008. [Google Scholar] [CrossRef] [PubMed]
- Austin, J.; Colman, S. A century of temperature variability in Lake Superior. Limnol. Oceanogr. 2008, 53, 2724–2730. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
| Samples | Calcite | Dolomite (Ordered) | Gypsum | Fluorite | Halite | Quartz | Chalcedony | Amorphous Silica | log10 PCO2 |
|---|---|---|---|---|---|---|---|---|---|
| Lake | 0.75 (0.29) | 2.94 (0.65) | −2.31 (0.08) | −2.05 (0.12) | −5.79 (0.09) | −0.32 (0.35) | −0.60 (0.35) | −1.68 (0.35) | −3.34 (0.22) |
| Groundwater | −0.11 (0.14) | 0.44 (0.14) | −2.03 (0.31) | −2.75 (0.68) | −7.68 (0.31) | 0.56 (0.14) | 0.28 (0.14) | −0.82 (0.15) | −1.73 (0.19) |
| Rivers | 0.59 (0.26) | 1.93 (0.46) | −1.97 (0.28) | −2.35 (0.19) | −6.58 (0.22) | 0.20 (0.30) | −0.08 (0.30) | 1.17 (0.30) | −2.61 (0.17) |
| Variable | t (°C) | P (mm) | E (mm) | ∆D‰ | ∆18O‰ |
|---|---|---|---|---|---|
| t (°C) | 1 (0.000) | −0.352 (0.001) | 0.913 (0.000) | 0.788 (0.000) | 0.798 (0.000) |
| P (mm) | 1 (0.000) | −0.367 (0.001) | −0.632 (0.000) | −0.638 (0.000) | |
| E (mm) | 1 (0.000) | 0.870 (0.000) | 0.877 (0.000) | ||
| ∆D‰ | 1 (0.000) | 0.994 (0.000) | |||
| ∆18O‰ | 1 (0.000) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frondini, F.; Dragoni, W.; Morgantini, N.; Donnini, M.; Cardellini, C.; Caliro, S.; Melillo, M.; Chiodini, G. An Endorheic Lake in a Changing Climate: Geochemical Investigations at Lake Trasimeno (Italy). Water 2019, 11, 1319. https://doi.org/10.3390/w11071319
Frondini F, Dragoni W, Morgantini N, Donnini M, Cardellini C, Caliro S, Melillo M, Chiodini G. An Endorheic Lake in a Changing Climate: Geochemical Investigations at Lake Trasimeno (Italy). Water. 2019; 11(7):1319. https://doi.org/10.3390/w11071319
Chicago/Turabian StyleFrondini, Francesco, Walter Dragoni, Nicola Morgantini, Marco Donnini, Carlo Cardellini, Stefano Caliro, Massimo Melillo, and Giovanni Chiodini. 2019. "An Endorheic Lake in a Changing Climate: Geochemical Investigations at Lake Trasimeno (Italy)" Water 11, no. 7: 1319. https://doi.org/10.3390/w11071319
APA StyleFrondini, F., Dragoni, W., Morgantini, N., Donnini, M., Cardellini, C., Caliro, S., Melillo, M., & Chiodini, G. (2019). An Endorheic Lake in a Changing Climate: Geochemical Investigations at Lake Trasimeno (Italy). Water, 11(7), 1319. https://doi.org/10.3390/w11071319





