Analysis of Drought-Sensitive Areas and Evolution Patterns through Statistical Simulations of the Indian Ocean Dipole Mode
Abstract
1. Introduction
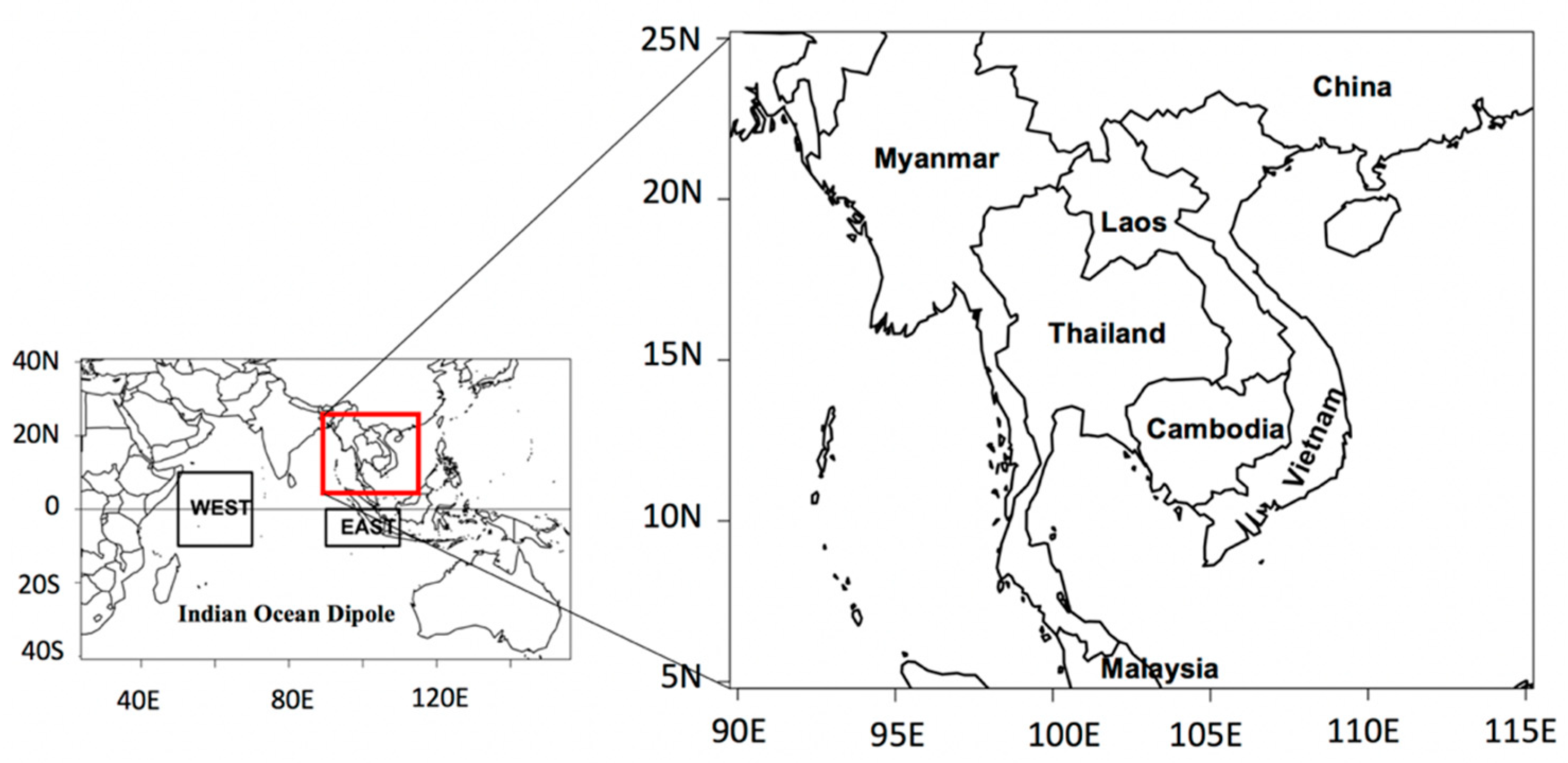
2. Data and Methods
3. Results of the Analysis
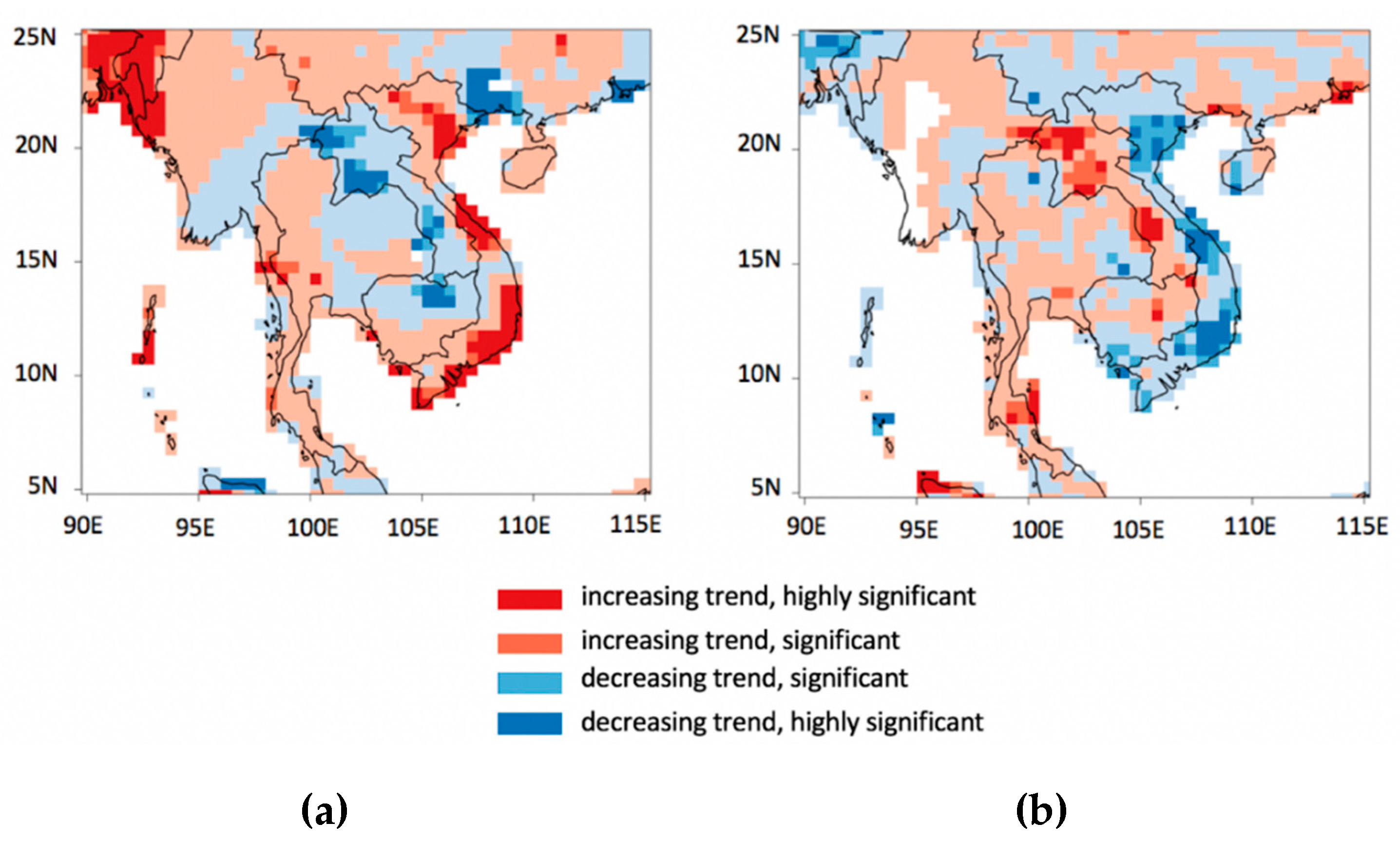
3.1. Trends in Spring Precipitation and Extreme Drought
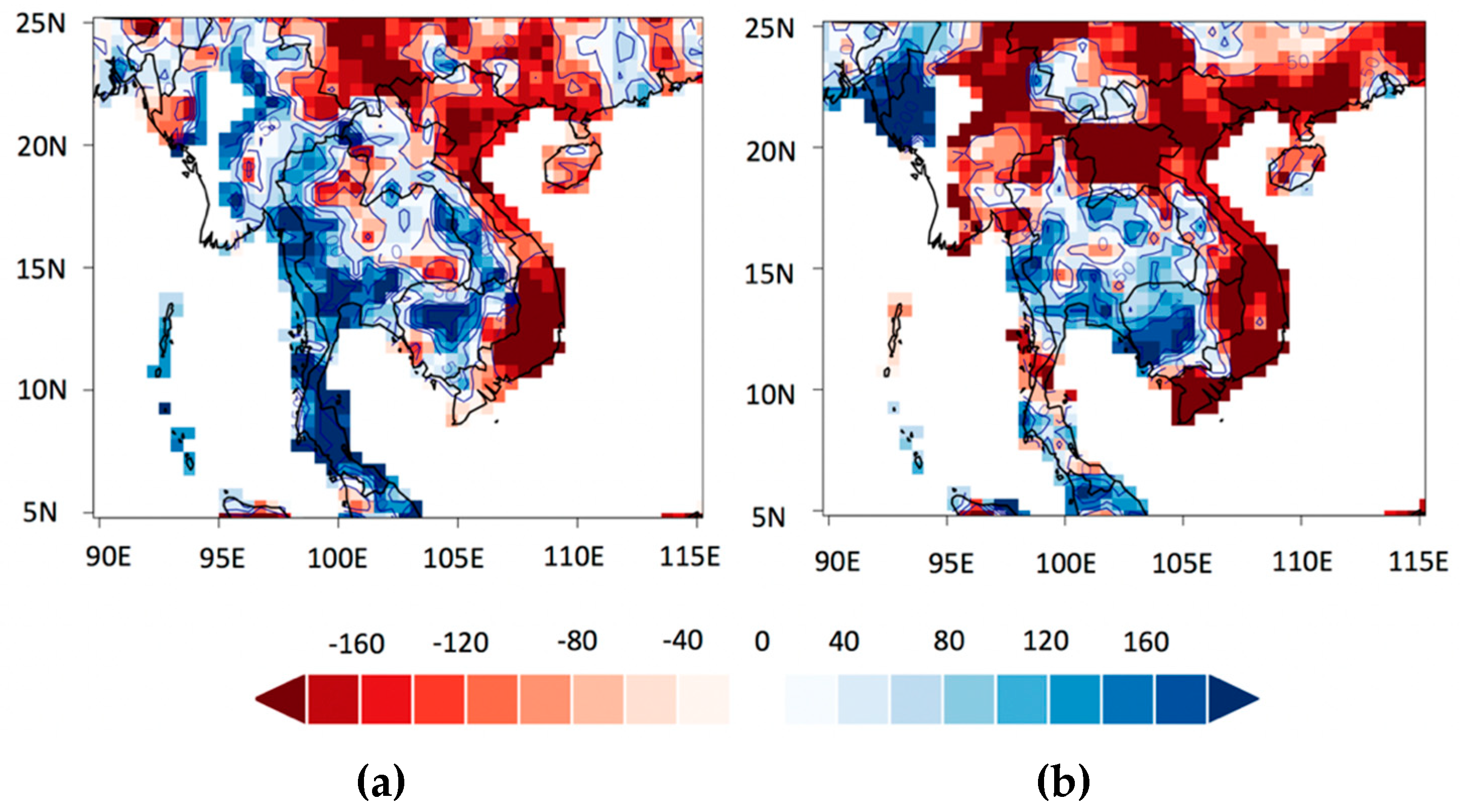
3.2. Composite Anomaly of Extreme Drought for IOD Modes
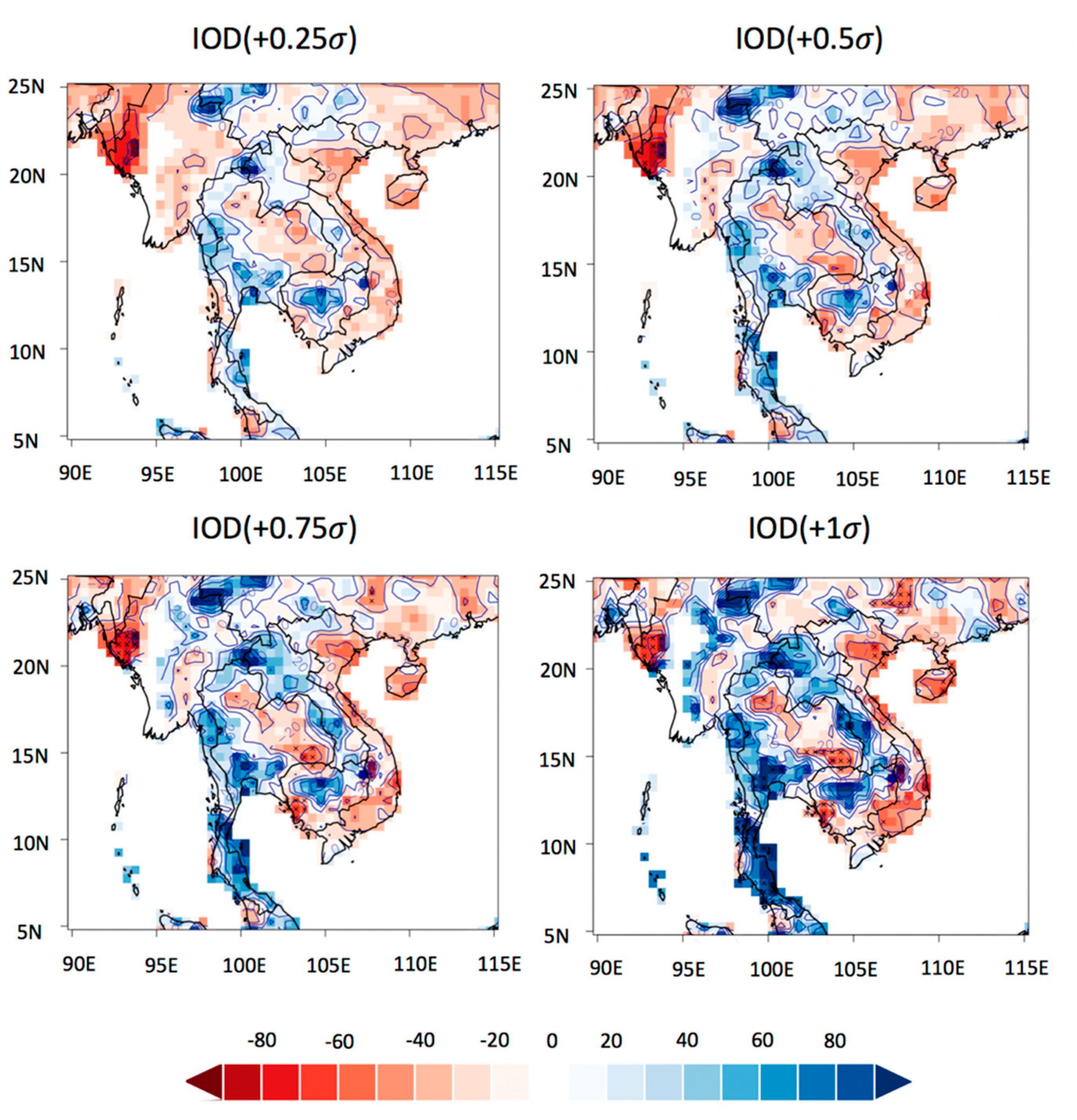
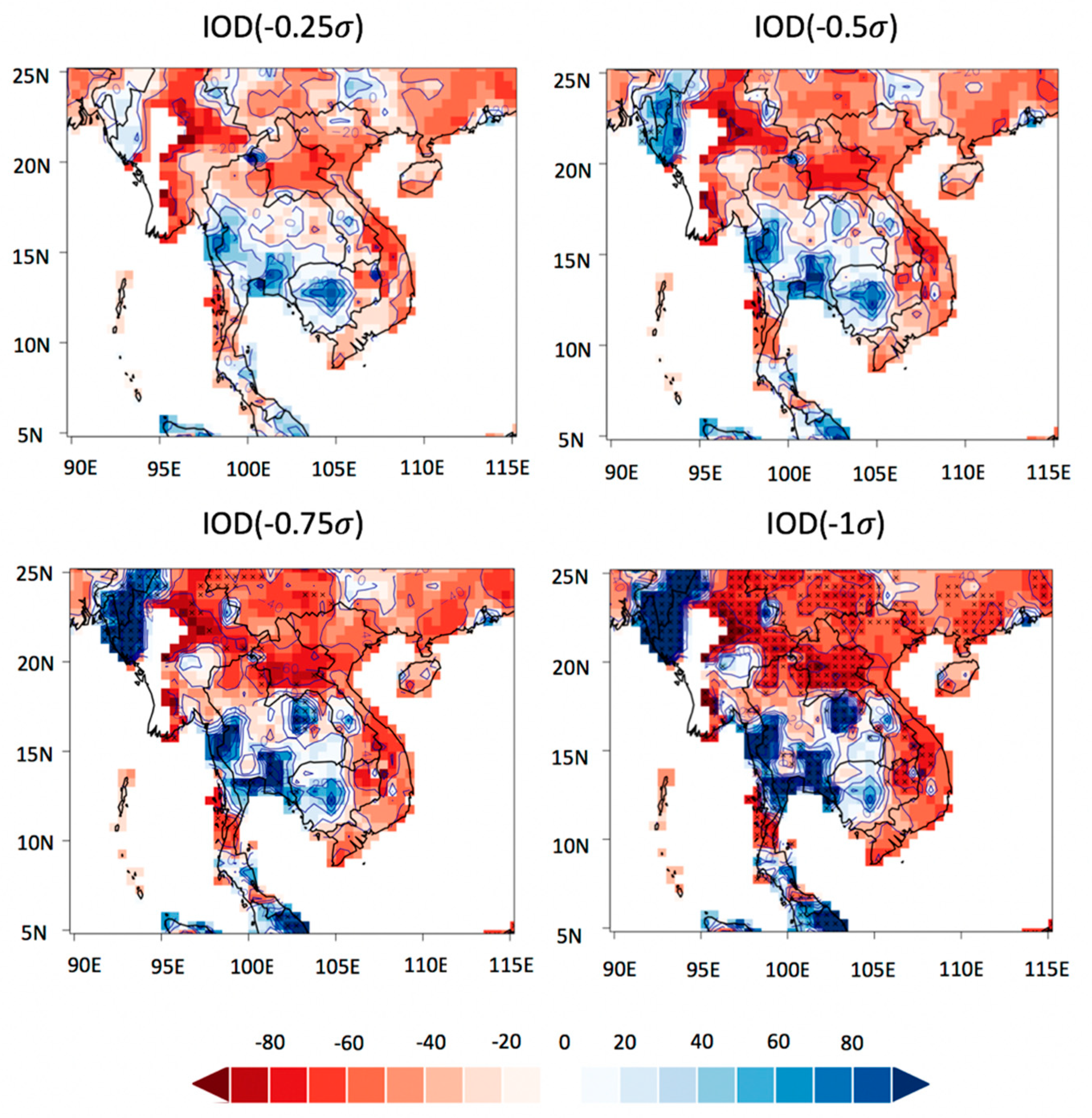
3.3. Changes in Extreme Drought Using the IBB method
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Change 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Change 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Rind, D.; Goldberg, R.; Hansen, J.; Rosenzweig, C.; Ruedy, R. Potential evapotranspiration and the likelihood of future drought. J. Geophys. Res.: Atmos. 1990, 95, 9983–10004. [Google Scholar] [CrossRef]
- Wang, G. Agricultural drought in a future climate: results from 15 global climate models participating in the IPCC 4th assessment. Clim. Dyn. 2005, 25, 739–753. [Google Scholar] [CrossRef]
- Richard, R.; Heim, J. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar]
- Gao, Q.; Kim, J.-S.; Chen, J.; Chen, H.; Lee, J.-H. Atmospheric Teleconnection-Based Extreme Drought Prediction in the Core Drought Region in China. Water 2019, 11, 232. [Google Scholar] [CrossRef]
- Le, M.H.; Perez, G.C.; Solomatine, D. Meteorological Drought Forecasting Based on Climate Signals Using Artificial Neural Network — A Case Study in Khanhhoa Province Vietnam. Procedia Eng. 2016, 154, 1169–1175. [Google Scholar] [CrossRef]
- Nguyen, H.; Shaw, R. Chapter 8 Drought Risk Management in Vietnam. In Droughts in Asian Monsoon Region; Emerald Group Publishing Limited: Bingley, UK, 2011; pp. 141–161. [Google Scholar]
- Hundertmark, W.J.I. Building drought management capacity in the Mekong river basin. Irrig. Drain. 2008, 57, 279–287. [Google Scholar] [CrossRef]
- Vu, M.T.; Raghavan, V.S.; Liong, S.-Y. Ensemble Climate Projection for Hydro-Meteorological Drought over a river basin in Central Highland, Vietnam. KSCE J. Civ. Eng. 2015, 19, 427–433. [Google Scholar] [CrossRef]
- Shu, F.; Prasoot, S.; Monthathip, C. Increasing Production of Rainfed Lowland Rice in Drought Prone Environments. Plant Prod. Sci. 1998, 1, 75–82. [Google Scholar]
- Kim, J.-S.; Seo, G.-S.; Jang, H.-W.; Lee, J.-H. Correlation analysis between Korean spring drought and large-scale teleconnection patterns for drought forecasting. KSCE J. Civ. Eng. 2017, 21, 458–466. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Q.; Chen, X.; Xu, C.-Y.; Jiang, S.J. On the Linkage between the Extreme Drought and Pluvial Patterns in China and the Large-Scale Atmospheric Circulation. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Jin, F.-F. An Equatorial Ocean Recharge Paradigm for ENSO. Part I: Conceptual Model. J. Atmos. Sci. 1997, 54, 811–829. [Google Scholar] [CrossRef]
- Black, E.; Slingo, J.; Sperber, K.R. An Observational Study of the Relationship between Excessively Strong Short Rains in Coastal East Africa and Indian Ocean SST. Mon. Weather Rev. 2003, 131, 74–94. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. Impact of the Indian Ocean Dipole on the Relationship between the Indian Monsoon Rainfall and ENSO. Geophys. Res. Lett. 2001, 28, 4499–4502. [Google Scholar] [CrossRef]
- Saji, N.; Yamagata, T. Possible impacts of Indian Ocean Dipole mode events on global climate. Clim. Res. 2003, 25, 151–169. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. Influence of the Indian Ocean Dipole on the Australian winter rainfall. Geophys. Res. Lett. 2003, 30, 1821. [Google Scholar] [CrossRef]
- Liess, S.; Kumar, A.; Snyder, P.K.; Kawale, J.; Steinhaeuser, K.; Semazzi, F.H.M.; Ganguly, A.R.; Samatova, N.F.; Kumar, V. Different Modes of Variability over the Tasman Sea: Implications for Regional Climate. J. Clim. 2014, 27, 8466–8486. [Google Scholar] [CrossRef]
- Cai, W.; Cowan, T.; Sullivan, A. Recent unprecedented skewness towards positive Indian Ocean Dipole occurrences and its impact on Australian rainfall. Geophys. Res. Lett. 2009, 36, 245–253. [Google Scholar] [CrossRef]
- Chan, S.C.; Behera, S.K.; Yamagata, T. Indian Ocean Dipole influence on South American rainfall. Geophys. Res. Lett. 2008, 35, L14S12. [Google Scholar] [CrossRef]
- Zanchettin, D.; Bothe, O.; Müller, W.; Bader, J.; Jungclaus, J.H. Different flavors of the Atlantic Multidecadal Variability. Clim. Dyn. 2014, 42, 381–399. [Google Scholar] [CrossRef]
- Cai, W.; Zheng, X.-T.; Weller, E.; Collins, M.; Cowan, T.; Lengaigne, M.; Yu, W.; Yamagata, T. Projected response of the Indian Ocean Dipole to greenhouse warming. Nat. Geosci. 2013, 6, 999–1007. [Google Scholar] [CrossRef]
- Ihara, C.; Kushnir, Y.; Cane, M.A. Warming Trend of the Indian Ocean SST and Indian Ocean Dipole from 1880 to 2004. J. Clim. 2008, 21, 2035–2046. [Google Scholar] [CrossRef]
- Ren, H.-L.; Jin, F.-F. Niño indices for two types of ENSO. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–183. [Google Scholar]
- Guttman, N.B. ACCEPTING THE STANDARDIZED PRECIPITATION INDEX: A CALCULATION ALGORITHM. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank correlation methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Hall, P.; Presnell, B. Intentionally biased bootstrap methods. J. R. Stat. Soc. 1999, 61, 143–158. [Google Scholar] [CrossRef]
- Lee, T. Climate change inspector with intentionally biased bootstrapping (CCIIBB ver. 1.0) — methodology development. Geosci. Model Dev. 2017, 10, 525–536. [Google Scholar] [CrossRef]
- Piechota, T.C.; Chiew, F.H.S.; Dracup, J.A.; McMahon, T.A. Seasonal streamflow forecasting in eastern Australia and the El Niño–Southern Oscillation. Water Resour. Res. 1998, 34, 3035–3044. [Google Scholar] [CrossRef]
- Mahala, B.K.; Nayak, B.K.; Mohanty, P.K. Impacts of ENSO and IOD on tropical cyclone activity in the Bay of Bengal. Nat. Hazards 2015, 75, 1105–1125. [Google Scholar] [CrossRef]
- Pradhan, P.K.; Preethi, B.; Ashok, K.; Krishna, R.; Sahai, A.K. Modoki, Indian Ocean Dipole, and western North Pacific typhoons: Possible implications for extreme events. J. Geophys. Res. 2011, 116, D18108. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Ando, K.; Bourles, B.; Freitag, H.; Lumpkin, R.; Masumoto, Y.; Murty, V.; Nobre, P.; Ravichandran, M.; Vialard, J.J.P.O.O. The Global Tropical Moored Buoy Array. In Proceedings of the “OceanObs’09: Sustained Ocean Observations and Information for Society” Conference, OceanObs’09, Venice, Italy, 21–25 September 2009. [Google Scholar]
- Kim, J.-S.; Son, C.-Y.; Moon, Y.-I.; Lee, J.-H. Seasonal rainfall variability in Korea within the context of different evolution patterns of the central Pacific El Niño. J. Water Clim. Change 2017, 8, 412–422. [Google Scholar] [CrossRef]
- Kim, J.-S.; Kim, S.T.; Wang, L.; Wang, X.; Moon, Y.-I. Tropical cyclone activity in the northwestern Pacific associated with decaying Central Pacific El Niños. Stochastic Environ. Res. Risk Assess. 2016, 30, 1335–1345. [Google Scholar] [CrossRef]
- Kim, J.-S.; Zhou, W.; Wang, X.; Jain, S. El Niño Modoki and the Summer Precipitation Variability over South Korea: A Diagnostic Study. J. Meteorolog. Soc. Jpn. 2012, 90, 673–684. [Google Scholar] [CrossRef]
- Ashok, K.; Yamagata, T. Climate change: The El Niño with a difference. Nature 2009, 461, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Chiodi, A.M.; Harrison, D.E. Observed El Niño SSTA Development and the Effects of Easterly and Westerly Wind Events in 2014/15. J. Clim. 2017, 30, 1505–1519. [Google Scholar] [CrossRef]
- Juneng, L.; Tangang, F.T. Evolution of ENSO-related rainfall anomalies in Southeast Asia region and its relationship with atmosphere–ocean variations in Indo-Pacific sector. Clim. Dyn. 2005, 25, 337–350. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.-P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403. [Google Scholar] [CrossRef]
- Lee, S.-K.; Park, W.; Baringer, M.O.; Gordon, A.L.; Huber, B.; Liu, Y. Pacific origin of the abrupt increase in Indian Ocean heat content during the warming hiatus. Nat. Geosci. 2015, 8, 445–449. [Google Scholar] [CrossRef]
- Liu, W.; Xie, S.-P.; Lu, J. Tracking ocean heat uptake during the surface warming hiatus. Nat. Commun. 2016, 7, 10926. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.-G.; Sombutmounvong, V.; Xiong, L.; Lee, J.-H.; Kim, J.-S. Analysis of Drought-Sensitive Areas and Evolution Patterns through Statistical Simulations of the Indian Ocean Dipole Mode. Water 2019, 11, 1302. https://doi.org/10.3390/w11061302
Gao Q-G, Sombutmounvong V, Xiong L, Lee J-H, Kim J-S. Analysis of Drought-Sensitive Areas and Evolution Patterns through Statistical Simulations of the Indian Ocean Dipole Mode. Water. 2019; 11(6):1302. https://doi.org/10.3390/w11061302
Chicago/Turabian StyleGao, Qing-Gang, Vonevilay Sombutmounvong, Lihua Xiong, Joo-Heon Lee, and Jong-Suk Kim. 2019. "Analysis of Drought-Sensitive Areas and Evolution Patterns through Statistical Simulations of the Indian Ocean Dipole Mode" Water 11, no. 6: 1302. https://doi.org/10.3390/w11061302
APA StyleGao, Q.-G., Sombutmounvong, V., Xiong, L., Lee, J.-H., & Kim, J.-S. (2019). Analysis of Drought-Sensitive Areas and Evolution Patterns through Statistical Simulations of the Indian Ocean Dipole Mode. Water, 11(6), 1302. https://doi.org/10.3390/w11061302






