Comparative Study of Methods for Delineating the Wellhead Protection Area in an Unconfined Coastal Aquifer
Abstract
1. Introduction
2. Material and Methods
2.1. Delineation Methods Selection
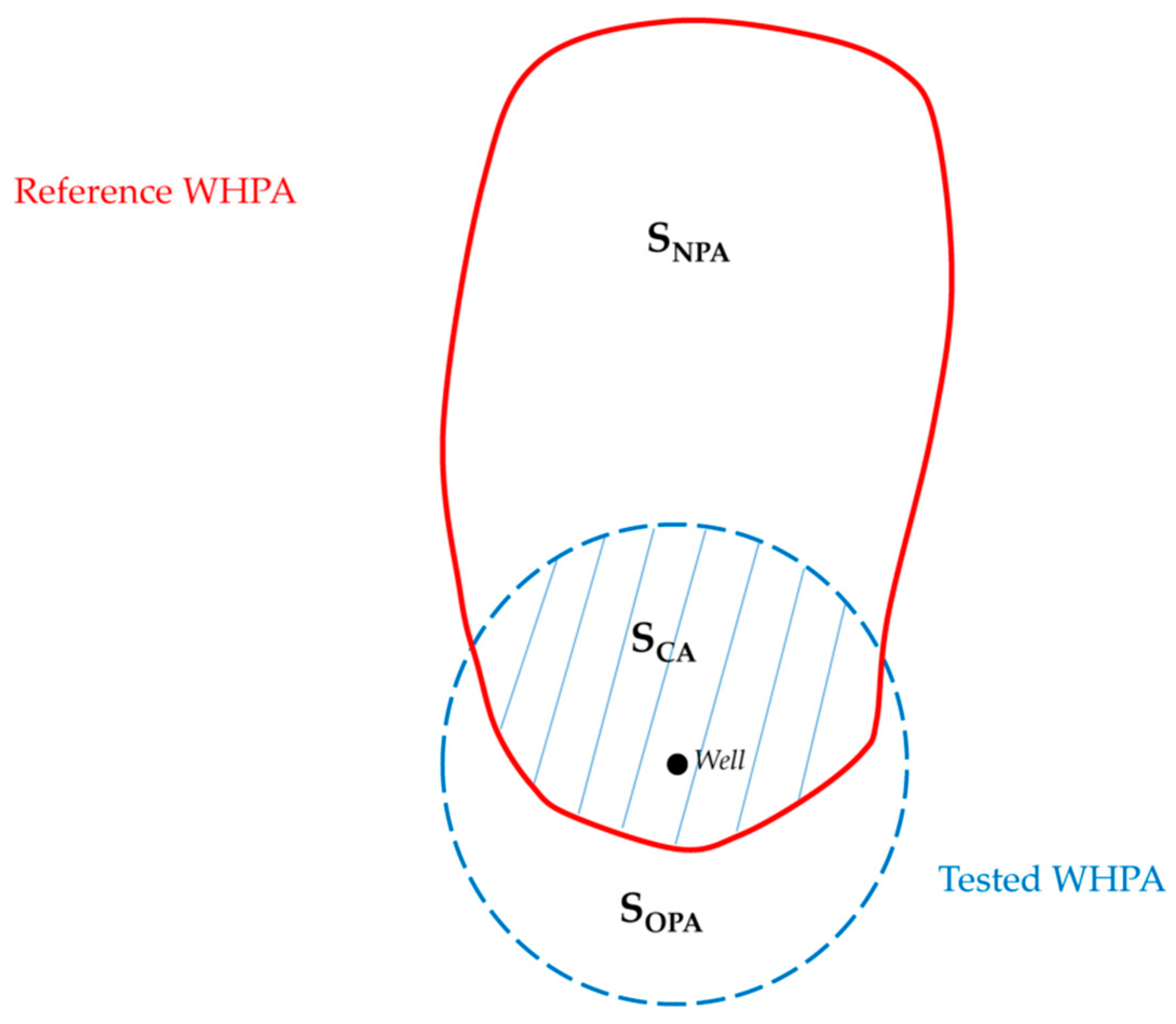
2.2. Reference WHPA
2.3. Stochastic Modeling for Uncertainty Analysis
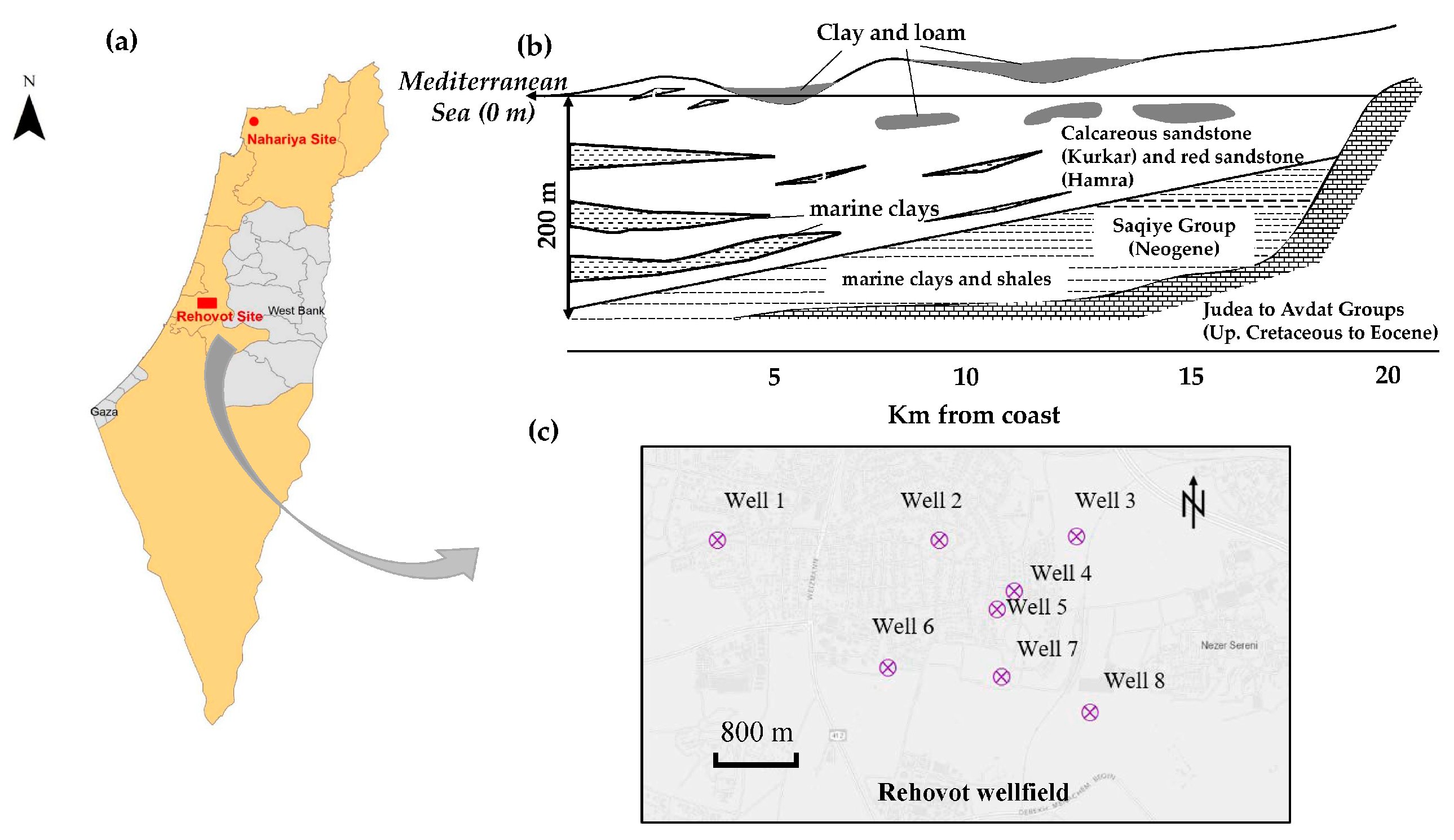
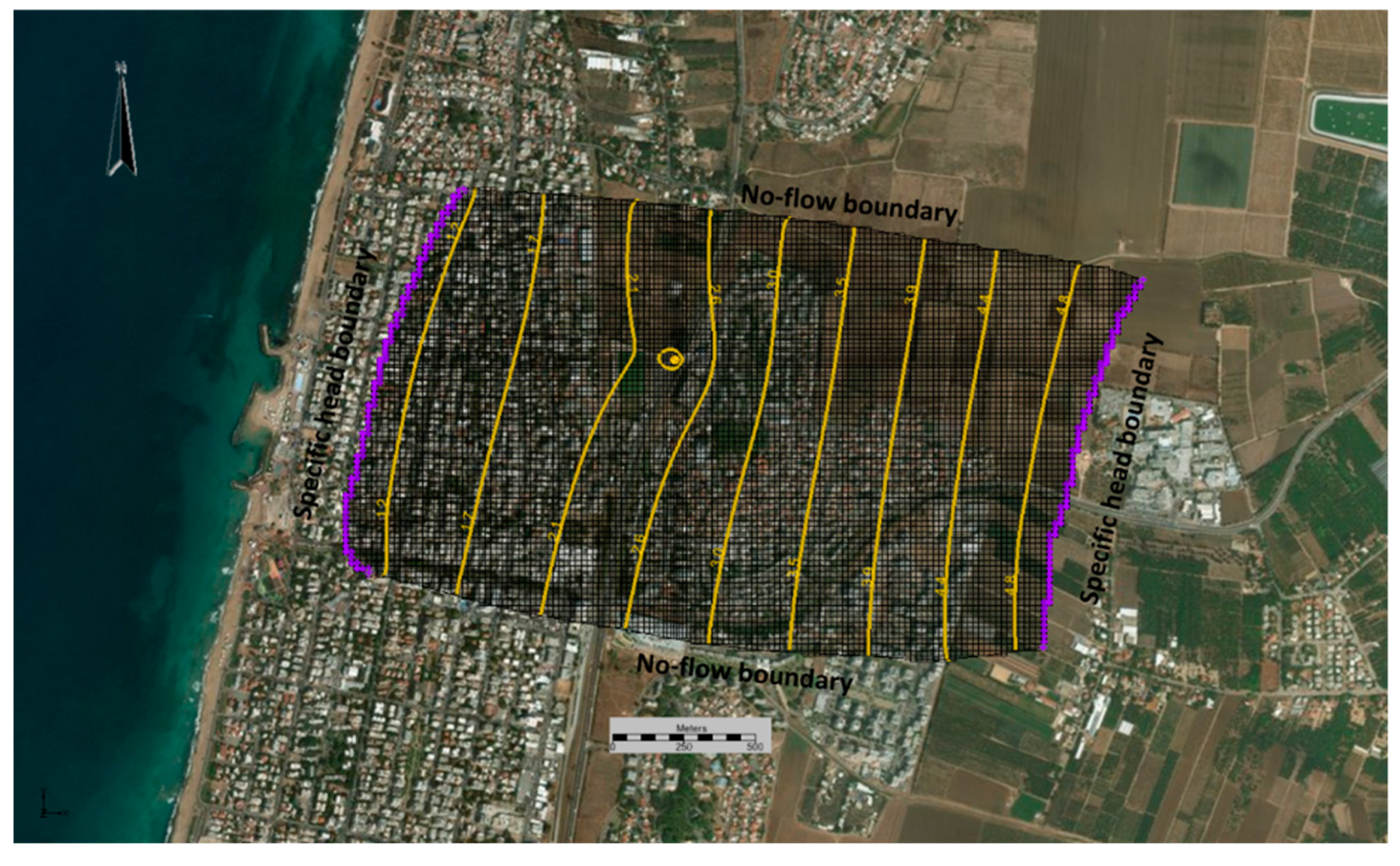
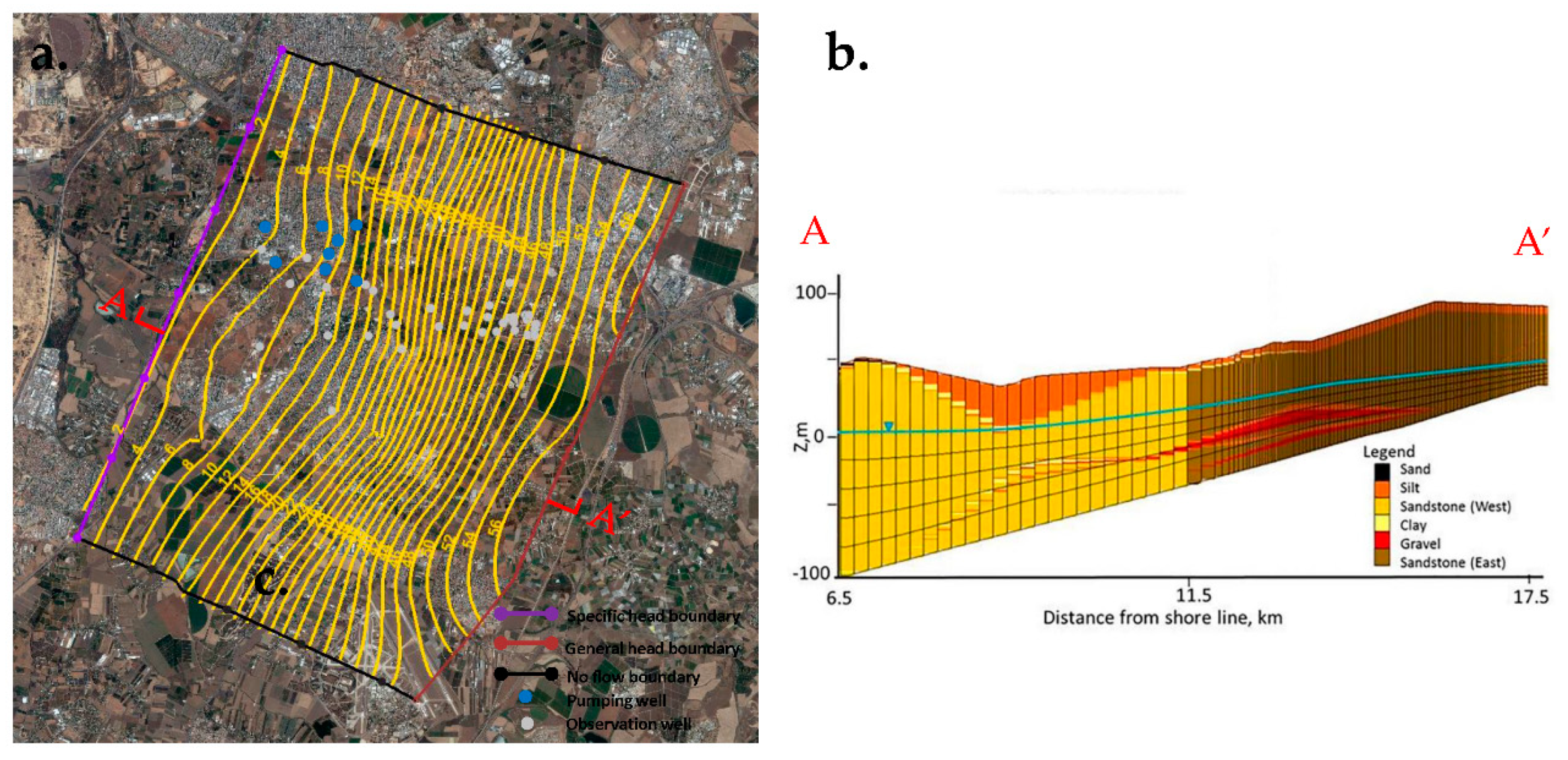
2.4. Study Area
3. Results
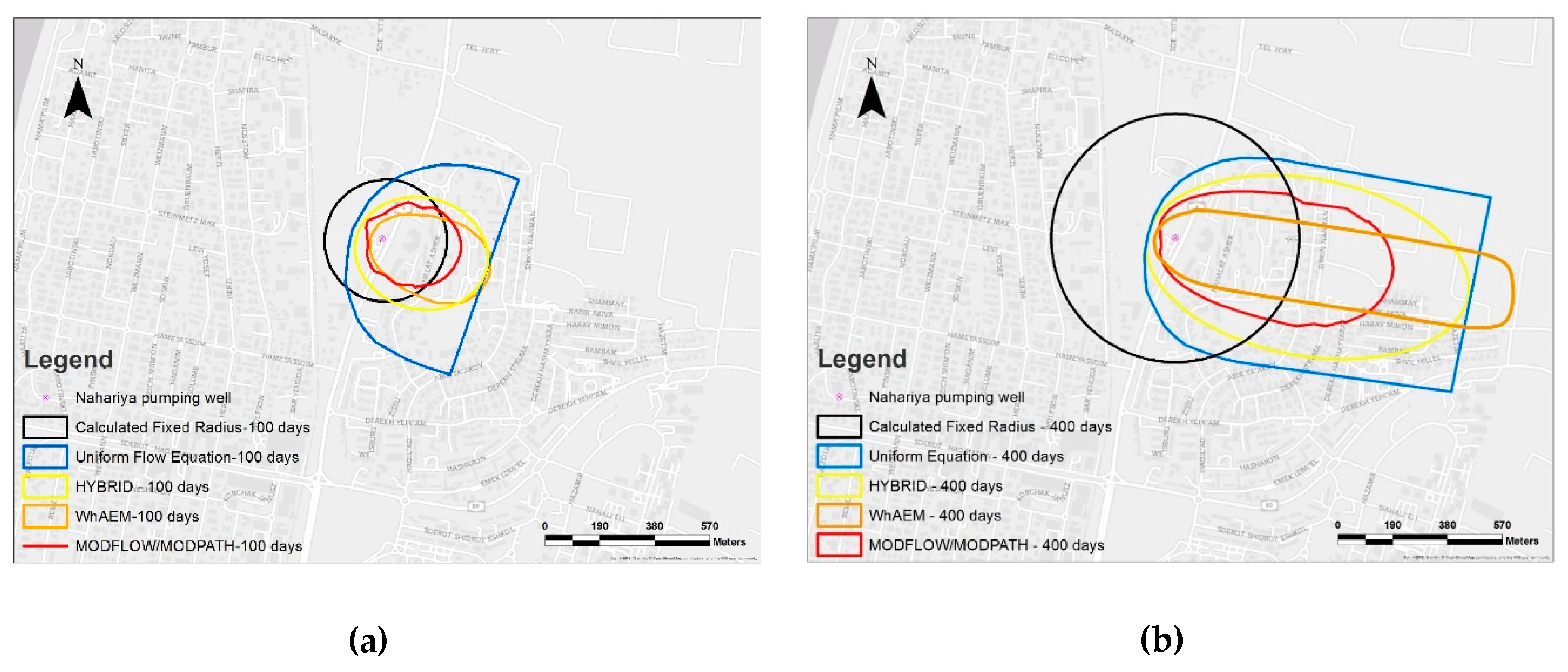
3.1. WHPA Delineation of the Nahariya Site (Single Well)
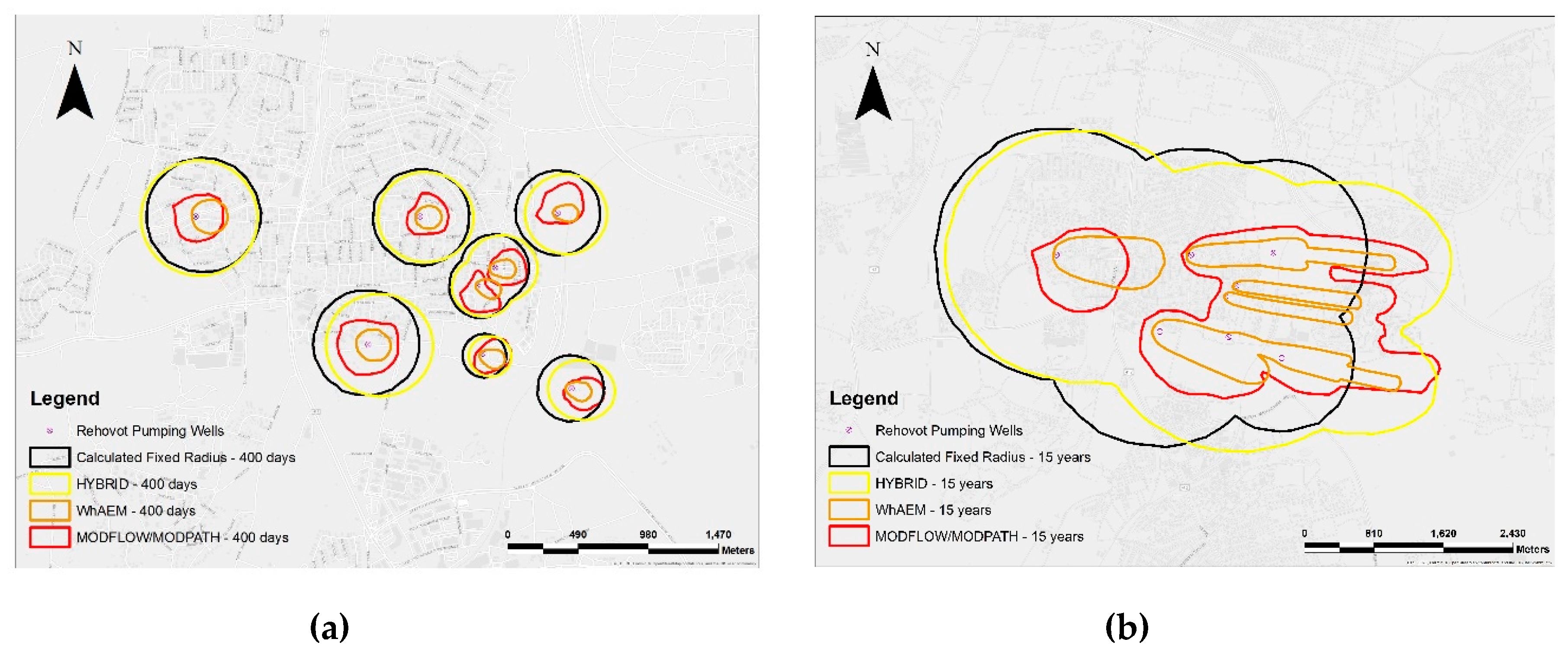
3.2. WHPA Delineation of the Rehovot Site (Multi-Well Field)
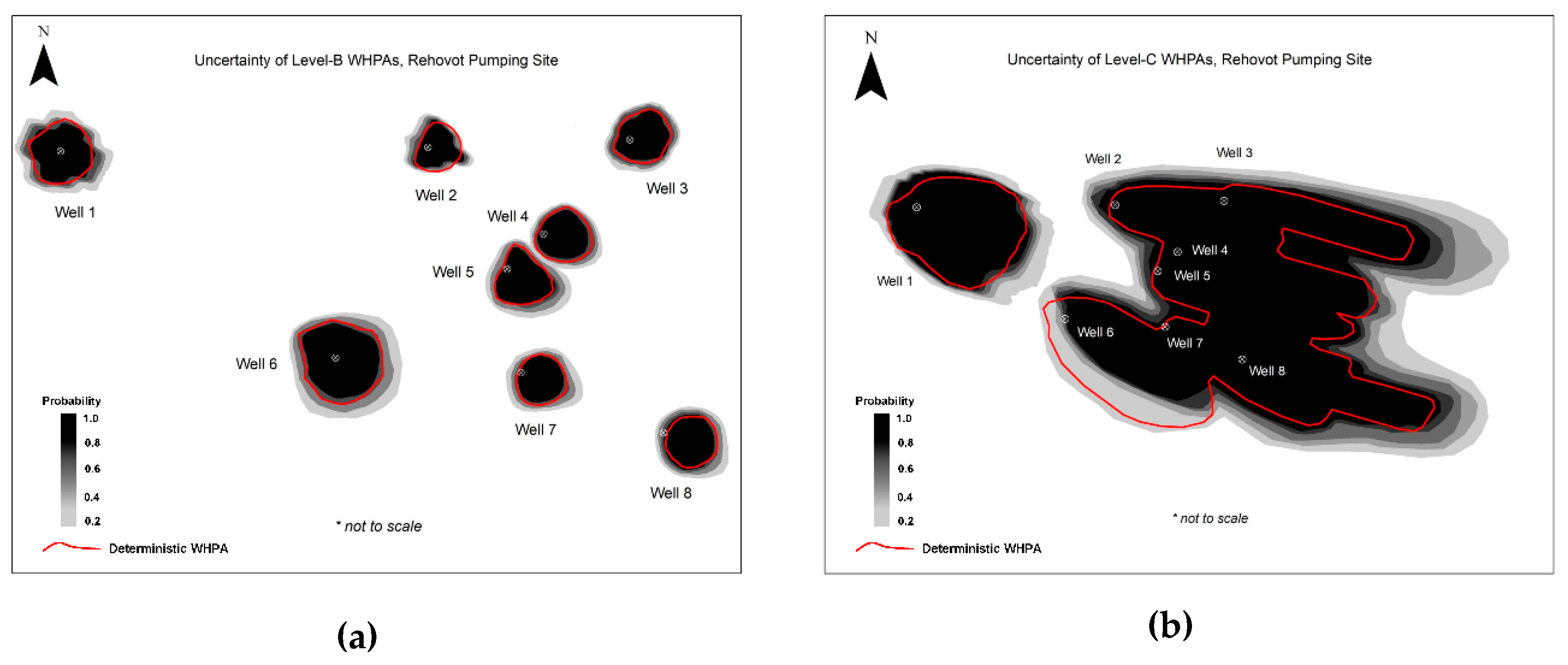
3.3. Uncertainty Analysis Results of Numerical Modeling (MODFLOW-MODPATH) Method
4. Discussion and Recommendation
4.1. Comparison of WHPA Delineation Results
4.1.1. Comparison of Level-B Protection Zones
4.1.2. Comparison of Level-C Protection Zones
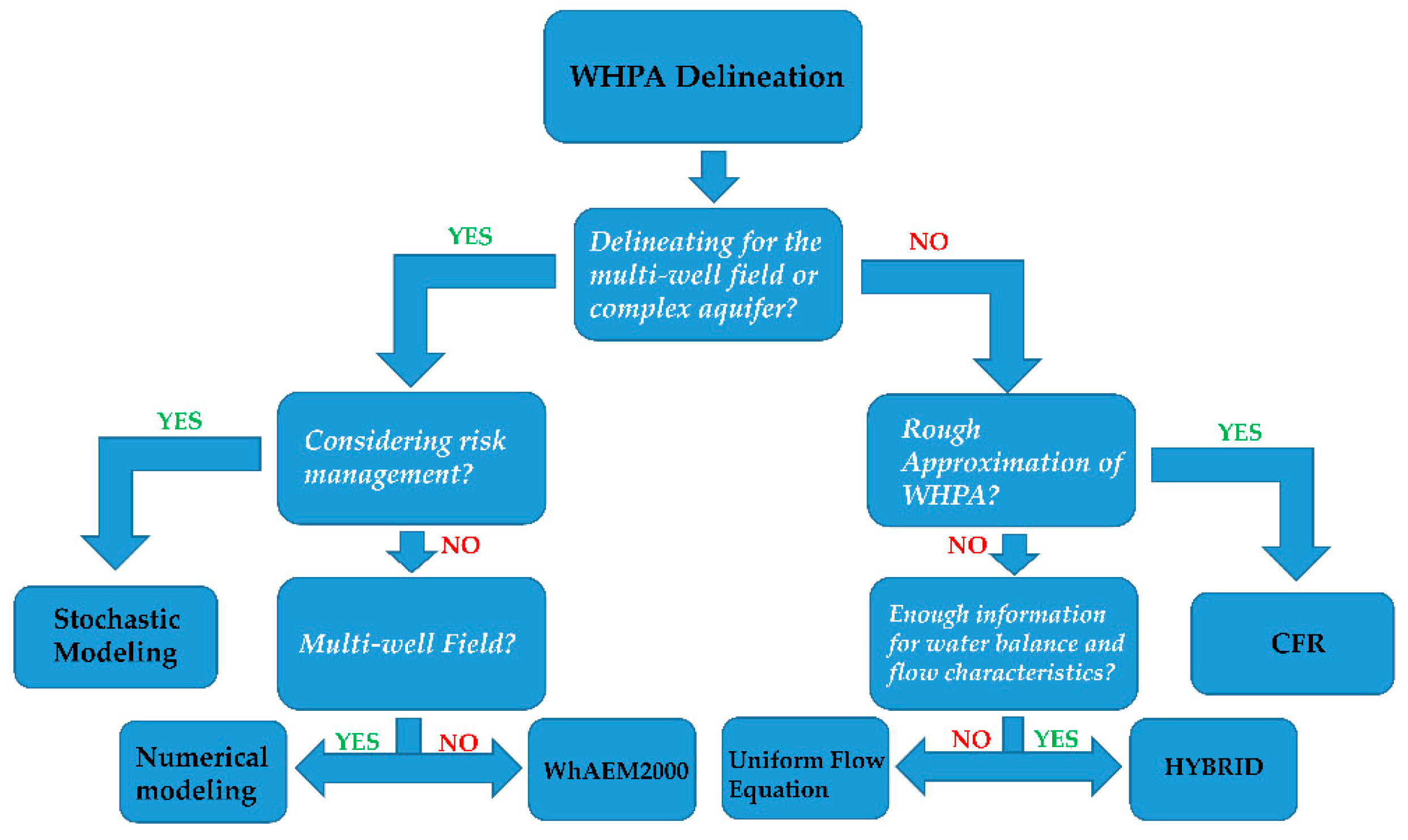
4.2. Recommendation for Selecting Delineation Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Shah, T.; Burke, J.; Villholth, K.G.; Angelica, M.; Custodio, E.; Daibes, F.; Hoogesteger, J.; Giordano, M.; Girman, J.; Van Der Gun, J.; et al. Groundwater: A Global Assessment of Scale and Significance; Earthscan: London, UK; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2007; pp. 395–423. [Google Scholar]
- World Water Assessment Programme (United Nations). Water: A Shared Responsibility; the United Nations World Water Development Report 2; UN-HABITAT: Nairobi, Kenya, 2006. [Google Scholar]
- EPA. Guidelines for Delineation of Wellhead Protection Areas; EPA-440/5-93-001; United States Environmental Protection Agency: Washington, DC, USA, 1987; p. 212.
- Cleary, T.C.B.F.; Cleary, R.W. Delineation of Wellhead Protection Areas: Theory and Practice. Water Sci. Technol. 1991, 24, 239–250. [Google Scholar] [CrossRef]
- Vassolo, S.; Kinzelbach, W.; Schafer, W. Determination of a well head protection zone by stochastic inverse modelling. J. Hydrol. 1998, 206, 268–280. [Google Scholar] [CrossRef]
- Schleyer, R.; Milde, G.; Milde, K. Wellhead Protection Zones in Germany—Delineation, Research and Management. J. Inst. Water Environ. Manag. 1992, 6, 303–311. [Google Scholar] [CrossRef]
- EPA. Handbook—Groundwater and Wellhead Protection; United States Environmental Protection Agency: Washington, DC, USA, 1994; p. 288.
- Harter, T. Delineating Groundwater Sources and Protection Zones; Rollins, L., Ed.; University of California at Davis: Davis, CA, USA, 2002. [Google Scholar]
- EPA. Literature Review of Methods for Delineating Wellhead Protection Areas; United States Environmental Protection Agency: Washington, DC, USA, 1998; p. 48.
- Rock, G.; Kupfersberger, H. Numerical delineation of transient capture zones. J. Hydrol. 2002, 269, 134–149. [Google Scholar] [CrossRef]
- Piccinini, L.; Fabbri, P.; Pola, M.; Marcolongo, E.; Rosignoli, A. Numerical modeling to well-head protection area delineation, an example in Veneto Region (NE Italy). Rend. Online Soc. Geol. Ital. 2015, 35, 232–235. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005: The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005.
- Forster, C.B.; Lachmar, T.E.; Oliver, D.S. Comparison of Models for Delineating Wellhead Protection Areas in Confined to Semiconfined Aquifers in Alluvial Basins. Groundwater 1997, 35, 689–697. [Google Scholar] [CrossRef]
- Pollock, D.W. User Guide for MODPATH Version 7—A Particle-Tracking Model for MODFLOW; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2016; p. 41.
- Evers, S.; Lerner, D.N. How uncertain is our estimate of a wellhead protection zone? Ground Water 1998, 36, 49–57. [Google Scholar] [CrossRef]
- Theodossiou, N.; Fotopoulou, E. Delineating well-head protection areas under conditions of hydrogeological uncertainty. A case-study application in northern Greece. Environ. Process. 2015, 2, 113–122. [Google Scholar] [CrossRef]
- Fadlelmawla, A.A.; Dawoud, M.A. An approach for delineating drinking water wellhead protection areas at the Nile Delta, Egypt. J. Environ. Manag. 2006, 79, 140–149. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, F.; Guadagnini, A.; Butler, A.; Franssen, H.J.H.; Van den Wiel, N.; Bakr, M.; Riva, M.; Guadagnini, L. Delineation of source protection zones using statistical methods. Water Resour. Manag. 2005, 19, 163–185. [Google Scholar] [CrossRef][Green Version]
- Schmoll, O.; World Health Organization. Protecting Groundwater for Health: Managing the Quality of Drinking-Water Sources; IWA Pub.: London, UK, 2006. [Google Scholar]
- Paradis, D.; Martel, R.; Karanta, G.; Lefebvre, R.; Michaud, Y.; Therrien, R.; Nastev, M. Comparative study of methods for WHPA delineation. Ground Water 2007, 45, 158–167. [Google Scholar] [CrossRef] [PubMed]
- Landmeyer, J.E. Description and Application of Capture Zone Delineation for A Wellfield at Hilton Head Island, South Carolina. Water-Resour. Investig. Rep. 1994, 94, 4012. [Google Scholar]
- ANWQMS. National Water Quality Management Strategies: Guidelines for Groundwater Protection in Australia; Agriculture and Resources Management Council of Australia and New Zealand: Canberra, Australia, 1995.
- DoELG. Groundwater Protection Schemes; Environmental Protection Agency and Geological Survey of Ireland, Department of Environment and Local Government: Dublin, Ireland, 1999.
- DVGW. Code of Practice W101 for Drinking Water Protection Areas Part 1, Protective Areas for Groundwater; German Association of Gas and Water Experts: Bonn, Germany, 1995. [Google Scholar]
- Government of Oman. Water Resources of the Sultanate of Oman; Ministry of Water Resources: Muscat, Oman, 1991.
- Bear, J.; Jacobs, M. On the movement of water bodies injected into aquifers. J. Hydrol. 1965, 3, 37–57. [Google Scholar] [CrossRef]
- Todd, D.K.; Mays, L.W. 4.3 WELL IN A UNIFORM FLOW. In Groundwater Hydrology, 3rd ed.; Bill, Z., Ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2004; p. 656. [Google Scholar]
- Haitjema, H.M.; Wittman, J.; Kelson, V.; Bauch, N. WhAEM: Program Documentation for the Wellhead Analytic Element Model; EPA/600/R-94/210 (NTIS PB95-167373); U.S. Environmental Protection Agency: Washington, DC, USA, 1994.
- Paradis, D.; Martel, R. HYBRID: A Wellhead Protection Delineation Method for Aquifers of Limited Extent; Geological Survey of Canada: Ottawa, ON, Canada, 2007; p. 5.
- Israel Ministry of Health. Public Health Regulations 2013—The Sanitary Quality of Drinking Water and Drinking Water Facilities; Collection of Regulations 7262; Department of Environmental Health, Public Health Services, Ministry of Health: Jerusalem, Israel, 2013; p. 34.
- Miller, C.; Chudek, P.; Babcock, S. A Comparison of wellhead Protection Area Delineation Methods for Public Drinking Water Systems in Whatcom County, Washington. J. Environ. Health 2003, 66, 17. [Google Scholar] [PubMed]
- Loucks, D.P.; van Beek, E.; Stedinger, J.R.; Dijkman, J.P.M.; Villars, M.T. 9. Model Sensitivity and Uncertainty Analysis. In Water Resources Systems Planning and Management: An Introduction to Methods, Models and Applications; Springer International Publishing AG: Basel, Switzerland, 2005. [Google Scholar] [CrossRef]
- Guha, H. A Stochastic Modeling Approach to Address Hydrogeologic Uncertainties in Modeling Wellhead Protection Boundaries in Karst Aquifers1. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 654–662. [Google Scholar] [CrossRef]
- Weinberger, G.; Livshitz, Y.; Givati, A.; Zilberbrand, M.; Tal, A.; Weiss, M.; Zurieli, A. The Natural Water Resources Between the Mediterranean Sea and the Jordan River; Hydro Report 11/1; Israel Hydrological Service: Jerusalem, Israel, 2011; p. 63.
- Eriksson, E.; Khunakasem, V. Chloride concentration in groundwater, recharge rate and rate of deposition of chloride in the Israel Coastal Plain. J. Hydrol. 1969, 7, 178–197. [Google Scholar] [CrossRef]
- Kass, A.; Gavrieli, I.; Yechieli, Y.; Vengosh, A.; Starinsky, A. The impact of freshwater and wastewater irrigation on the chemistry of shallow groundwater: A case study from the Israeli Coastal Aquifer. J. Hydrol. 2005, 300, 314–331. [Google Scholar] [CrossRef]
- Nativ, R.; Weisbrod, N. Hydraulic Connections among Subaquifers of the Coastal-Plain Aquifer, Israel. Ground Water 1994, 32, 997–1007. [Google Scholar] [CrossRef]
- Yosef, B. The Hydrogeology of the Coastal Plain of Western Galilee (in Hebrew); TAHAL: Tel Aviv, Israel, 1967. [Google Scholar]
- Wexler, A. Hydrogeological Plan for the Water Development, Production, and Utilization in the Kavri Basin; GSI/36/2001; Water Commission & Planning Department: Tel Aviv, Israel, 2001.
- Dvory, N. Hydrographic Survey in the Production Field of Nahariya Municipality Drilling Etgar Engineering LTD Report; Etgar: Tel Aviv, Israel, 2009. [Google Scholar]
- Yakirevich, A.; Kuznetsov, M.; Adar, E. Modeling Contaminant Migration in Coastal Aquifer (Givon Region)—Internal Report; Ben-Gurion University of the Negev: Beersheba, Israel, 2015. [Google Scholar]
| Analytical Methods | Equations | Note |
|---|---|---|
| CFR | r (L): radius of the circular WHPA, Q (L3/T): pumping rate, t (T): time of travel, n (-): aquifer porosity, H (L): aquifer thickness, N (L/T): infiltration rate. | |
| Uniform flow equation | XL (L): down-gradient flow boundary, YL (L): max. width of up-gradient zone, tx (T): time of travel, rx(±) (L): distance to up-gradient boundary (+), or to down-gradient boundary (−), K (L/T): hydraulic conductivity, b (L): aquifer thickness, i (-): hydraulic gradient, n (-): aquifer porosity, Q (L3/T): pumping rate. | |
| HYBRID | w/2 (L): vertical dimension of ellipse, d/2 (L): horizontal dimension of ellipse, other parameters are the same as the parameters from uniform flow equation method. |
| Method | Pumping Rate (m3/day) | Saturated Thickness (m) | Porosity (%) | Recharge Rate (mm/year) | Conductivity (m/day) | Hydraulic Gradient |
|---|---|---|---|---|---|---|
| Nahariya site | ||||||
| CFR | 6600 | 15.5 | 30 | 250 | - | - |
| Uniform flow equation | 6600 | 15.5 | 30 | - | 250 | 0.0025 |
| WhAEM2000 | 6600 | 15.5 | 30 | 250 | 250 | - |
| HYBRID | 6600 | 15.5 | 30 | 250 | 250 | 0.0025 |
| MODFLOW-MODPATH | 6600 | 15.5 | 30 | 250 | 250 | - |
| Rehovot site | ||||||
| CFR | 1000–3000 | 4.9–18.5 | 30 | 208 | - | - |
| WhAEM2000 | 1000–3000 | 85 | 30 | 208 | 10.5 | - |
| HYBRID | 1000–3000 | 4.9–18.5 | 30 | 208 | 10.5 | 0.0019–0.0068 |
| MODFLOW-MODPATH | 1000–3000 | 4.9–18.5 | 30 | 0.1–475 | 0.006–30 | - |
| Well Number | Analytical Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CFR | Uniform Flow Equation | HYBRID | |||||||
| Level-B WHPA | |||||||||
| r (m) | S (km2) | XL (m) | YL (m) | rx (m) | S (km2) | w/2(m) | d/2 (m) | S (km2) | |
| Well 1 | 397 | 0.49 | 3002 | 9431 | 415 | - | 398 | 397 | 0.50 |
| Well 2 | 335 | 0.35 | 1173 | 3686 | 367 | - | 334 | 336 | 0.35 |
| Well 3 | 295 | 0.27 | 462 | 1450 | 361 | - | 292 | 298 | 0.27 |
| Well 4 | 238 | 0.18 | 374 | 1176 | 291 | - | 236 | 241 | 0.18 |
| Well 5 | 221 | 0.15 | 323 | 1014 | 274 | - | 219 | 224 | 0.15 |
| Well 6 | 367 | 0.42 | 707 | 2223 | 433 | - | 365 | 370 | 0.42 |
| Well 7 | 152 | 0.07 | 160 | 505 | 203 | - | 148 | 156 | 0.07 |
| Well 8 | 231 | 0.17 | 289 | 907 | 296 | - | 227 | 235 | 0.16 |
| Level-C WHPA | |||||||||
| Well 1 | 1467 | 6.76 | 3002 | 9431 | 1715 | - | 1457 | 1477 | 6.76 |
| Well 2 | 1236 | 4.80 | 1173 | 3686 | 1704 | - | 1120 | 1275 | 4.48 |
| Well 3 | 1089 | 3.72 | 462 | 1450 | 2069 | - | 941 | 1260 | 3.72 |
| Well 4 | 880 | 2.43 | 374 | 1176 | 1670 | - | 761 | 1018 | 2.43 |
| Well 5 | 817 | 2.10 | 323 | 1014 | 1613 | - | 692 | 965 | 2.10 |
| Well 6 | 1356 | 5.77 | 707 | 2223 | 2330 | - | 1229 | 1497 | 5.78 |
| Well 7 | 560 | 0.98 | 160 | 505 | 1336 | - | 420 | 748 | 0.99 |
| Well 8 | 852 | 2.28 | 289 | 907 | 1833 | - | 685 | 1060 | 2.28 |
| Parameters | Mean(Starting) Value | Value Range | Distribution Pattern |
|---|---|---|---|
| Nahariya Site | |||
| K (m/day) | 200 | 100–300 | Lognormal |
| Rehovot Site | |||
| Kwest (m/day) | 10.43 | 5.0–15.0 | Lognormal |
| Keast (m/day) | 7.30 | 3.5–10.5 | Lognormal |
| Pumping Sites | Surface Area (S) | CFR | Uniform Flow Equation | WhAEM2000 | HYBRID | MODFLOW-MODPATH |
|---|---|---|---|---|---|---|
| Nahariya Site (Level-B: 100 days) | ||||||
| Nahariya well | S (km2) | 0.14 | 0.29 | 0.097 | 0.14 | 0.073 |
| (%) | 43.1 | 25.0 | 58.6 | 51.7 | Reference | |
| Rehovot Site (Level-B: 400 days) | ||||||
| Well 1 | S (km2) | 0.49 | - | 0.05 | 0.51 | 0.09 |
| (%) | 18.4 | - | 43.3 | 17.7 | Reference | |
| Well 2 | S (km2) | 0.35 | - | 0.02 | 0.33 | 0.06 |
| (%) | 17.1 | - | 33.3 | 18.2 | Reference | |
| Well 3 | S (km2) | 0.27 | - | 0.02 | 0.25 | 0.07 |
| (%) | 25.9 | - | 28.6 | 28.00 | Reference | |
| Well 4 | S (km2) | 0.18 | - | 0.02 | 0.18 | 0.05 |
| (%) | 27.8 | - | 40.0 | 27.8 | Reference | |
| Well 5 | S (km2) | 0.15 | - | 0.02 | 0.15 | 0.05 |
| (%) | 33.3 | - | 16.7 | 33.3 | Reference | |
| Well 6 | S (km2) | 0.42 | - | 0.04 | 0.41 | 0.13 |
| (%) | 31.0 | - | 30.8 | 31.7 | Reference | |
| Well 7 | S (km2) | 0.07 | - | 0.02 | 0.06 | 0.05 |
| (%) | 51.2 | - | 40.0 | 33.3 | Reference | |
| Well 8 | S (km2) | 0.17 | - | 0.02 | 0.15 | 0.05 |
| (%) | 29.4 | - | 40.0 | 33.3 | Reference | |
| Average | S (km2) | - | - | - | - | - |
| (%) | 28.8 | - | 34.1 | 27.03 | Reference | |
| Sum | S (km2) | 2.00 | - | 0.21 | 1.91 | 0.55 |
| (%) | - | - | - | - | - | |
| Pumping Sites | Surface Area (S) | CFR | Uniform Flow Equation | WhAEM2000 | HYBRID | MODFLOW-MODPATH | |
|---|---|---|---|---|---|---|---|
| Nahariya Site (Level-B: 100 days) | |||||||
| Nahariya well | S (km2) | 0.56 | 0.75 | 0.37 | 0.55 | 0.29 | |
| (%) | 25.1 | 38.6 | 54.3 | 53.2 | Reference | ||
| Rehovot Site (Level-B: 400 days) | |||||||
| Entire wellfield | S (km2) | 14.38 | - | 2.62 | 16.04 | 5.66 | |
| (%) | 30.2 | - | 40.6 | 35.3 | Reference | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Weisbrod, N.; Yakirevich, A. Comparative Study of Methods for Delineating the Wellhead Protection Area in an Unconfined Coastal Aquifer. Water 2019, 11, 1168. https://doi.org/10.3390/w11061168
Liu Y, Weisbrod N, Yakirevich A. Comparative Study of Methods for Delineating the Wellhead Protection Area in an Unconfined Coastal Aquifer. Water. 2019; 11(6):1168. https://doi.org/10.3390/w11061168
Chicago/Turabian StyleLiu, Yue, Noam Weisbrod, and Alexander Yakirevich. 2019. "Comparative Study of Methods for Delineating the Wellhead Protection Area in an Unconfined Coastal Aquifer" Water 11, no. 6: 1168. https://doi.org/10.3390/w11061168
APA StyleLiu, Y., Weisbrod, N., & Yakirevich, A. (2019). Comparative Study of Methods for Delineating the Wellhead Protection Area in an Unconfined Coastal Aquifer. Water, 11(6), 1168. https://doi.org/10.3390/w11061168






