Modeling the Influence of Outflow and Community Structure on an Endangered Fish Population in the Upper San Francisco Estuary
Abstract
1. Introduction
2. Material and Methods
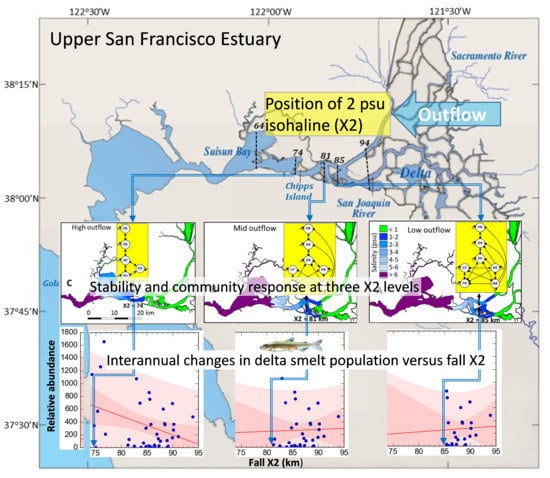
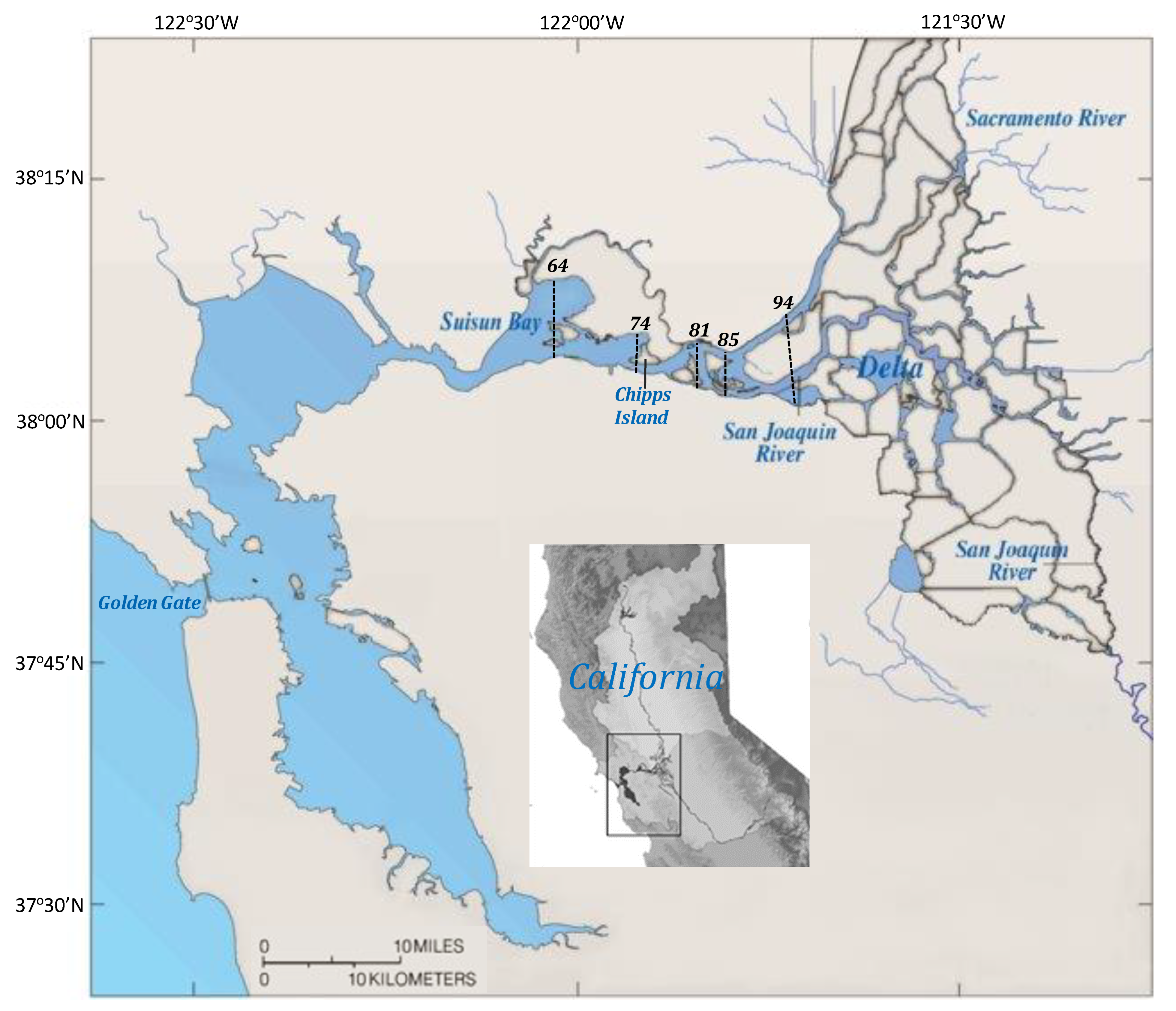
2.1. Study Area
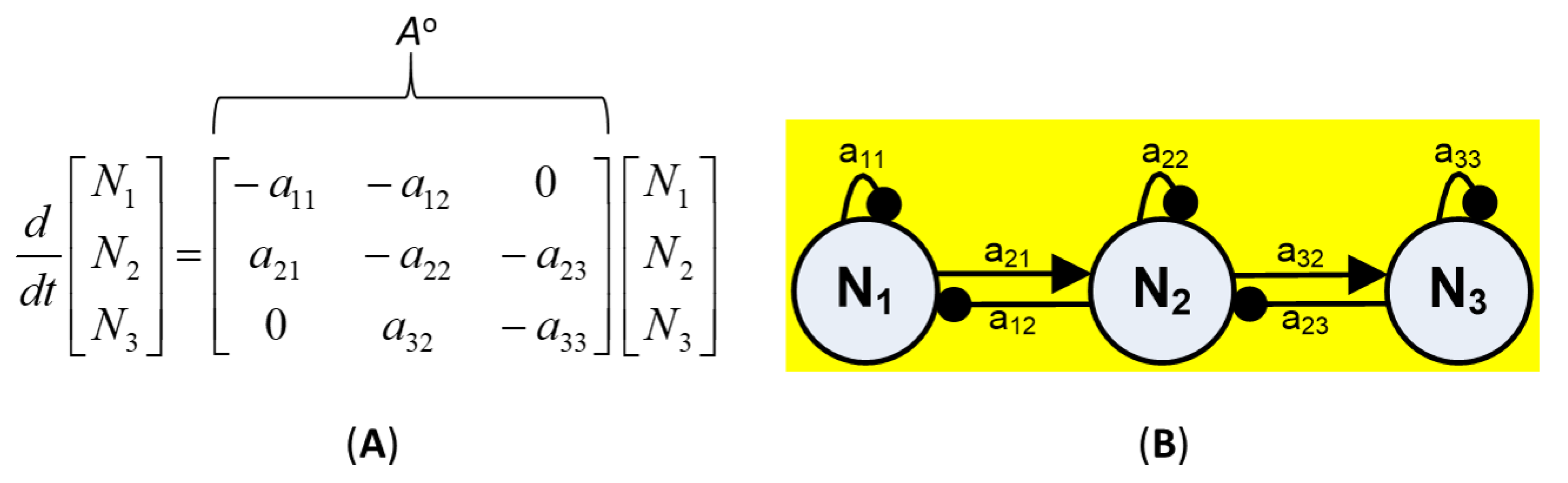
2.2. Community Matrix Models
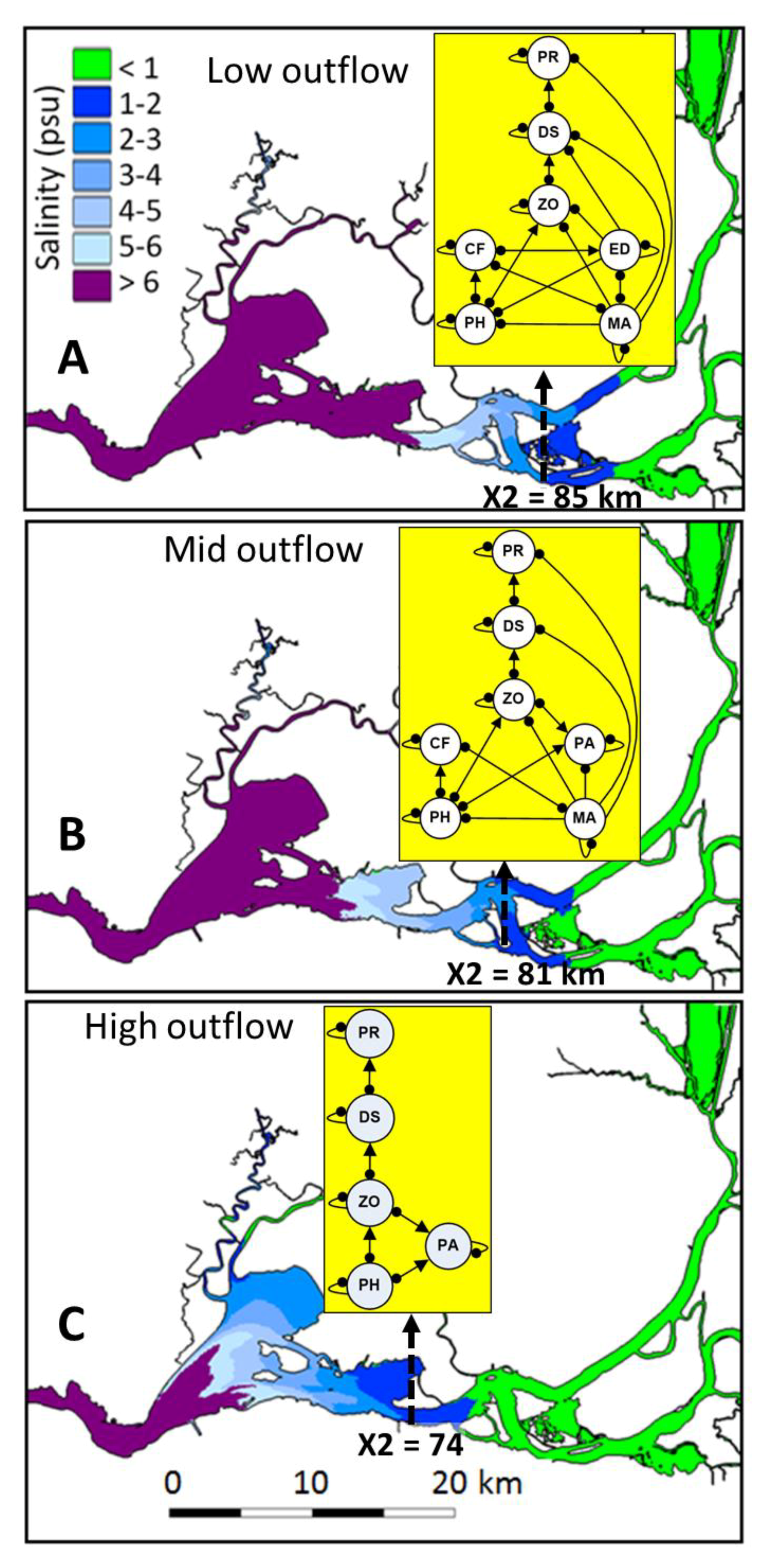
2.3. Community Structure and Outflow Scenarios
- (1)
- Compilation of long-term data and studies in the upper SF Estuary, including: monitoring data for delta smelt and other species [53], outflow and X2 data [51], interpretation of the spatio-temporal distribution of the salinity field in the LSZ based on the three-dimensional UnTRIM hydrodynamic model for the upper SF Estuary [24,75], and baseline knowledge of the modeled ecosystem (e.g., [6,10,39,40,54,55,63,76,77]).
- (2)
- Consideration of dynamic and stationary factors for developing conceptual models of estuarine communities [78], where dynamic factors include physico-chemical and biological characteristics of the low salinity habitat corresponding to the LSZ each X2 position, and stationary factors include geographically fixed habitat features at each X2 position such as substrate, erodible sediment, and bathymetry in the low salinity habitat [24,38].
- (3)
- Refinement of conceptual models into different subsystems describing the essential community variables influencing subadult delta smelt based on ecological syntheses of long-term field data and studies [24,38]. Community variables selected for each of the three modeled subsystems were based on functional groups (e.g., [74,79]), and their predominant spatio-temporal overlap with dynamic and stationary abiotic and biotic factors. Except for delta smelt and species with significant ecological impacts (the cyanobacterium M. aeruginosa [80], the clams P. amurensis and C. fluminea [56], and the macrophyte E. densa [58], Table 1), other functional groups included trophic levels to minimize redundant species interactions (e.g., [74,81]), (Table 1).
- (4)
- Reformulation of conceptual models into signed digraphs based on qualitative model guidelines (e.g., [71,79,93]). Negative self-effect (self-damping) was assumed to arise for each variable from density-dependent growth rate or a limited source, as in the case of nutrients [71]. Each community variable was then implicitly connected to other variables or abiotic factors through negative feedback [71,74]. Reported community interactions considered for the modeled subsystem included: predation (+, −); interference competition (−, −); and amensalism (0, −), (Appendix A).
- (5)
- Estimation of the direction of change of community variables (+, 0, −) in response to increased outflow (Table 1). Four outflow input scenarios were modeled, with the first scenario accounting for the effect of outflow on the previously referred species having significant ecological impacts. The outflow inputs for the three subsequent scenarios were used to evaluate whether cumulative outflow inputs in each subsystem could reinforce or reverse potential responses on delta smelt and other community variables. These scenarios included: scenario 1 + phytoplankton (scenario 2), scenario 2 + zooplankton (scenario 3), and scenario 3 + delta smelt (scenario 4).
2.4. Qualitative Analyses
2.5. Quantitative Simulations
2.6. Statistical Analyses
3. Results
3.1. Community Stability
3.2. Community Response to Outflow
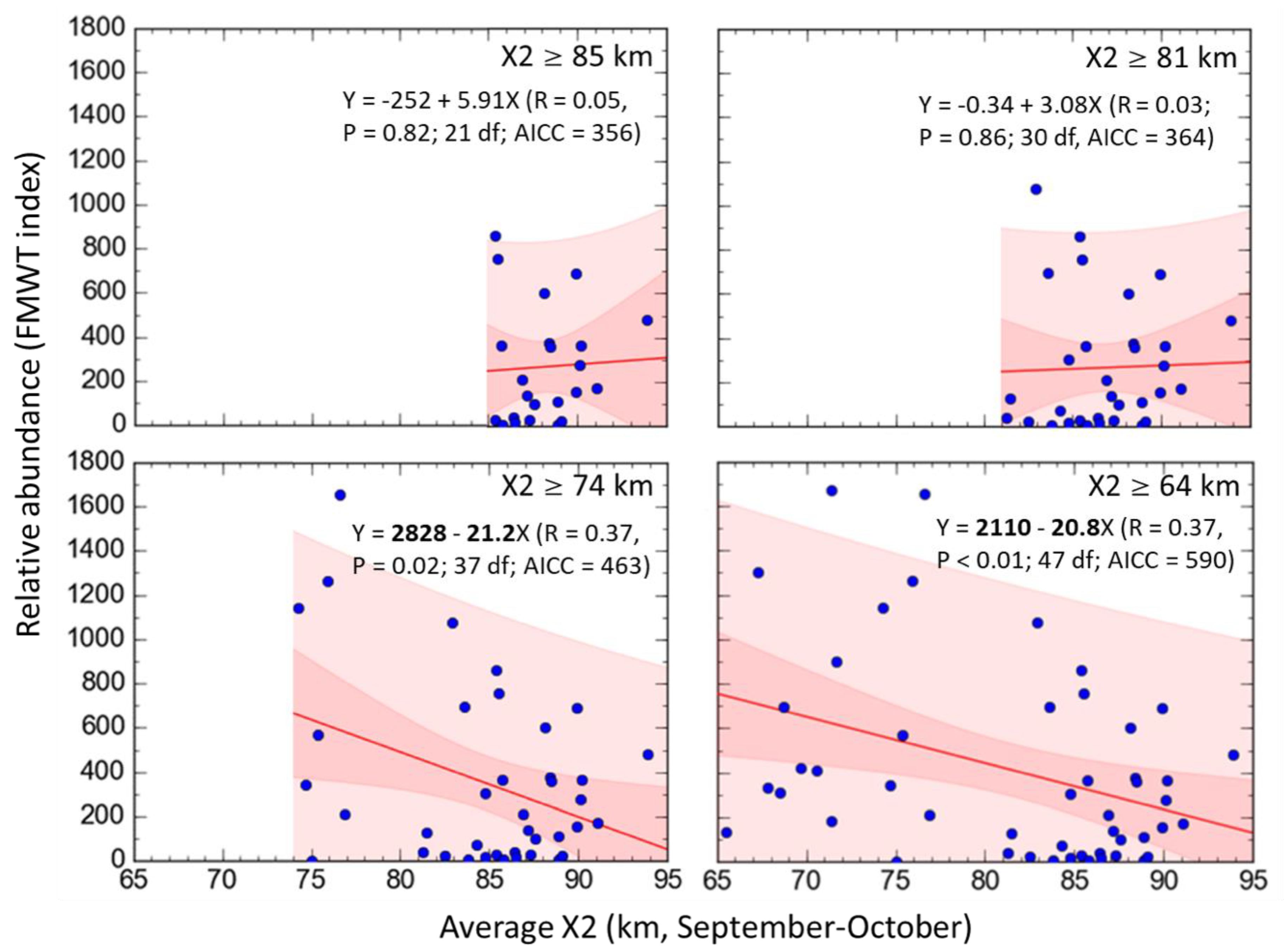
3.3. Delta Smelt Abundance and X2
4. Discussion
4.1. Community Stability
4.2. Community Model Predictions
4.3. Delta Smelt Abundance under Different Ranges of X2
4.4. Community Models and Prediction Metrics
4.5. Management Implications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| High-X2 Variables | DS | ZO | PH | ED | PR | CF | MA |
| DS | −1 [71] | 1 [41] | 0 | −1 [64] | −1 [92] | 0 | −1 [70] |
| ZO | −1 [41] | −1 [71] | 1 [113] | −1 [114] | 0 | 0 | −1 [69] |
| PH | 0 | −1 [113] | −1 [71] | −1 [85] | 0 | −1 [115] | −1 [80] |
| ED | 0 | 0 | 0 | −1 [71] | 0 | 1 [116] | −1 [117] |
| PR | 1 [92] | 0 | 0 | 0 | −1 [71] | 0 | −1 [80] |
| CF | 0 | 0 | 1 [115] | −1 [100] | 0 | −1 [71] | −1 [118] |
| MA | 0 | 0 | 0 | −1 [119] | 0 | −1 [120] | −1 [71] |
| Mid-X2 Variables | DS | ZO | PH | PA | PR | CF | MA |
| DS | −1 [71] | 1 [41] | 0 | 0 | −1 [92] | 0 | −1 [70] |
| ZO | −1 [41] | −1 [71] | 1 [113] | −1 [66,88] | 0 | 0 | −1 [69] |
| PH | 0 | −1 [113] | −1 [71] | −1 [60] | 0 | −1 [115] | −1 [80] |
| PA | 0 | 1 [66,88] | 1 [60] | −1 [71] | 0 | 0 | −1 [118] |
| PR | 1 [92] | 0 | 0 | 0 | −1 [71] | 0 | −1 [80] |
| CF | 0 | 0 | 1 [115] | 0 | 0 | −1 [71] | −1 [118] |
| MA | 0 | 0 | 0 | 0 | 0 | −1 [120] | −1 [71] |
| Low-X2 Variables | DS | ZO | PH | PA | PR | ||
| DS | −1 [71] | 1 [41] | 0 | 0 | −1 [92] | ||
| ZO | −1 [41] | −1 [71] | 1 [113] | −1 [66,88] | 0 | ||
| PH | 0 | −1 [113] | −1 [71] | −1 [60] | 0 | ||
| PA | 0 | 1 [66,88] | 1 [60] | −1 [71] | 0 | ||
| PR | 1 [92] | 0 | 0 | 0 | −1 [71] |
References
- Townend, I.H. Identifying change in estuaries. J. Coast. Conserv. 2004, 10, 5–12. [Google Scholar] [CrossRef]
- Lotze, H.K.; Lenihan, H.S.; Bourque, B.J.; Bradbury, R.H.; Cooke, R.G.; Kay, M.C.; Kidwell, S.M.; Kirby, M.X.; Peterson, C.H.; Jackson, J.B.C. Depletion, degradation, and recovery potential of estuaries and coastal seas. Science 2006, 312, 1806–1809. [Google Scholar] [CrossRef]
- Borja, A.; Dauer, D.M.; Elliott, M.; Simenstad, C.A. Medium- and long-term recovery of estuarine and coastal ecosystems: Patterns, rates and restoration effectiveness. Estuaries Coasts 2010, 33, 1249–1260. [Google Scholar] [CrossRef]
- Gillson, J. Freshwater flow and fisheries production in estuarine and coastal systems: Where a drop of rain is not lost. Rev. Fish. Sci. 2011, 19, 168–186. [Google Scholar] [CrossRef]
- Grimaldo, L.F.; Sommer, T.; Van Ark, N.; Jones, G.; Holland, E.; Moyle, P.B.; Herbold, B.; Smith, P. Factors affecting fish entrainment into massive water diversions in a tidal freshwater estuary: Can fish losses be managed? N. Am. J. Fish. Manag. 2009, 29, 1253–1270. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D. Drivers of change in estuarine-coastal ecosystems: Discoveries from four decades of study in San Francisco Bay. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Hobbs, J.A.; Moyle, P.B.; Fangue, N.; Connon, R.E. Is extinction inevitable for delta smelt and longfin smelt? An opinion and recommendations for recovery. SFEWS 2017, 15. [Google Scholar] [CrossRef]
- Cohen, A.N.; Carlton, J.T. Accelerating invasion rate in a highly invaded estuary. Science 1998, 279, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Castillo, G.C.; Damon, L.J.; Hobbs, J.A. Community patterns and environmental associations for pelagic fishes in a highly modified estuary. Mar. Coast. Fish. 2018, 10, 508–524. [Google Scholar] [CrossRef]
- Feyrer, F.; Newman, K.; Nobriga, M.; Sommer, T. Modeling the effects of future outflow on the abiotic habitat of an imperiled estuarine fish. Estuaries Coasts 2011, 34, 120–128. [Google Scholar] [CrossRef]
- Komoroske, L.M.; Connon, R.E.; Lindberg, J.; Cheng, B.S.; Castillo, G.; Hasenbein, M.; Fangue, N.A. Ontogeny influences sensitivity to climate change stressors in an endangered fish. Conserv. Physiol. 2014, 2, cou008. [Google Scholar] [CrossRef] [PubMed]
- Schlacher, T.A.; Wooldridge, T.H. Ecological responses to reductions in freshwater supply and quality in South Africa’s estuaries: Lessons for management and conservation. J. Coast. Conserv. 1996, 2, 115–130. [Google Scholar] [CrossRef]
- Moyle, P.B.; Bennett, W.A.; Fleenor, W.E.; Lund, J.R. Habitat variability and complexity in the upper San Francisco Estuary. SFEWS 2010, 8. [Google Scholar] [CrossRef]
- Reinert, T.R.; Peterson, J.T. Modeling the effects of potential salinity shifts on the recovery of striped bass in the Savannah River Estuary, Georgia-South Carolina, United States. Environ. Manag. 2008, 41, 753–765. [Google Scholar] [CrossRef] [PubMed]
- Guenther, C.B.; MacDonald, T.C. Comparison of estuarine salinity gradients and associated nekton community change in the Lower St. Johns River Estuary. Estuaries Coasts 2012, 35, 1443–1452. [Google Scholar] [CrossRef]
- Wissel, B.; Fry, B. Tracing Mississippi River influences in estuarine food webs of coastal Louisiana. Oecologia 2005, 144, 659–672. [Google Scholar] [CrossRef] [PubMed]
- Vinagre, C.; Salgado, J.; Cabral, H.N.; Costa, M.J. Food web structure and habitat connectivity in fish estuarine nurseries—Impact of river flow. Estuaries Coasts 2011, 34, 663–674. [Google Scholar] [CrossRef]
- Estevez, E.D. Review and assessment of biotic variables and analytical methods used in estuarine inflow studies. Estuaries 2002, 25, 1291–1303. [Google Scholar] [CrossRef]
- Sakaris, P.C. A review of the effects of hydrologic alteration on fisheries and biodiversity and the management and conservation of natural resources in regulated river systems. In Current Perspectives in Contaminant Hydrology and Water Resources Sustainability; Bradley, P.M., Ed.; Tech: Rijeka, Croatia, 2013; pp. 273–297. [Google Scholar]
- Rowell, K.; Flessa, K.W.; Dettmana, D.L.; Román, M.J.; Gerberc, L.R.; Findley, L.T. Diverting the Colorado River leads to a dramatic life history shift in an endangered marine fish. Biol. Conserv. 2008, 141, 1138–1148. [Google Scholar] [CrossRef]
- Purtlebaugh, C.H.; Allen, M.C. Relative abundance, growth, and mortality of five Age-0 estuarine fishes in relation to discharge of the Suwannee River, Florida. Trans. Am. Fish. Soc. 2010, 139, 1233–1246. [Google Scholar] [CrossRef]
- Livingston, R.J. Trophic response of estuarine fishes to long-term changes of river runoff. Bull. Mar. Sci. 1997, 60, 984–1004. [Google Scholar]
- Kimmerer, W.J. Effects of freshwater flow on abundance of estuarine organisms: Physical effects or trophic linkages? Mar. Ecol. Prog. Ser. 2002, 243, 39–55. [Google Scholar] [CrossRef]
- Brown, L.R.; Baxter, R.; Castillo, G.; Conrad, L.; Culberson, S.; Erickson, G.; Feyrer, F.; Fong, S.; Gehrts, K.; Grimaldo, L.; et al. Synthesis of Studies in the Fall Low-Salinity Zone of the San Francisco Estuary, September–December 2011; US Geological Survey Scientific Investigations Report 2014–5041; US Geological Survey: Reston, VA, USA, 2014.
- Wootton, J.T.; Emmerson, M. Measurement of interaction strength in nature. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 419–444. [Google Scholar] [CrossRef]
- Lane, P.; Levins, R. The dynamics of aquatic systems. The effects of nutrient enrichment on model plankton communities. Limnol. Oceanogr. 1977, 22, 454–471. [Google Scholar]
- Dambacher, J.M.; Li, H.W.; Rossignol, P.A. Qualitative predictions in model ecosystems. Ecol. Model. 2003, 161, 79–93. [Google Scholar] [CrossRef]
- Fox, J.W. Current food web models cannot explain the overall topological structure of observed food webs. Oikos 2006, 115, 97–109. [Google Scholar] [CrossRef]
- Levins, R. The qualitative analysis of partially specified systems. Ann. N. Y. Acad. Sci. 1974, 231, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Li, H.W.; Moyle, P.B. Ecological analysis of species introductions into aquatic ecosystems. Trans. Am. Fish. Soc. 1981, 110, 772–782. [Google Scholar] [CrossRef]
- Dambacher, J.M.; Luh, H.K.; Li, H.W.; Rossignol, P.A. Qualitative stability and ambiguity in model ecosystems. Am. Nat. 2003, 161, 876–888. [Google Scholar] [CrossRef]
- Hosack, G.R.; Hayes, K.R.; Dambacher, J.M. Assessing model structure uncertainty through an analysis of system feedback and Bayesian networks. Ecol. Appl. 2008, 18, 1070–1082. [Google Scholar] [CrossRef]
- Li, H.W.; Rossignol, P.A.; Castillo, G. Risk analysis of species introduction: Insights from qualitative modeling. In Non-Indigenous Fresh Water Organisms in North America; Vectors of Introduction, Biology and Impact; Claudi, R., Leach, J., Eds.; Lewis Press: Boca Raton, FL, USA, 1999; pp. 431–447. [Google Scholar]
- Montano-Moctezuma, G.; Li, H.W.; Rossignol, P.A. Alternative community structures in a kelp-urchin community: A qualitative modeling approach. Ecol. Model. 2007, 205, 343–354. [Google Scholar] [CrossRef]
- Dambacher, J.M.; Brewer, D.T.; Dennis, D.M.; Macintyre, M.; Foale, S. Qualitative modelling of gold mine impacts on Lihir Island’s socioeconomic system and reef-edge fish community. Environ. Sci. Technol. 2007, 41, 555–562. [Google Scholar] [CrossRef]
- Ramos-Jiliberto, R.; Garay-Narváez, L.; Medina, M.H. Retrospective qualitative analysis of ecological networks under environmental perturbation: A copper-polluted intertidal community as a case study. Ecotoxicology 2012, 21, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Reum, J.C.P.; Ferriss, B.E.; McDonald, P.S.; Farrell, D.M.; Harvey, C.J.; Klinger, T.; Levin, P.S. Evaluating community impacts of ocean acidification using qualitative network models. Mar. Ecol. Prog. Ser. 2015, 536, 11–24. [Google Scholar] [CrossRef]
- IEP (Interagency Ecological Program). An Updated Conceptual Model of Delta Smelt Biology: Our Evolving Understanding of an Estuarine Fish; Interagency Ecological Program for the San Francisco Bay/Delta Estuary. Technical Report 90; IEP: Sacramento, CA, USA, 2015. [Google Scholar]
- Jassby, A.D.; Kimmerer, W.J.; Monismith, S.G.; Armor, C.; Cloern, J.E.; Powell, T.M.; Schubel, J.R.; Vendlinski, T.J. Isohaline position as a habitat indicator for estuarine populations. Ecol. Appl. 1995, 5, 272–289. [Google Scholar] [CrossRef]
- Bennett, W.A. Critical assessment of the delta smelt population in the San Francisco Estuary, California. SFEWS 2005, 3. [Google Scholar] [CrossRef]
- Slater, S.B.; Baxter, R.D. Diet, prey selection, and body condition of age-0 delta smelt, Hypomesus transpacificus, in the Upper San Francisco Estuary. SFEWS 2014, 12. [Google Scholar] [CrossRef]
- Department of Fish and Wildlife. State and Federally Listed endangered and Threatened Animals of California; State of California, Natural Resources Agency, Department of Fish and Wildlife, Biogeographic Data Branch, California Natural Diversity Database: Sacramento, CA, USA, 2018.
- U.S. Fish and Wildlife Service. Formal Endangered Species Act Consultation on the Proposed Coordinated Operations of the Central Valley Project (CVP) and State Water Project (SWP); U.S. Fish and Wildlife Service, California and Nevada Region: Sacramento, CA, USA, 2008.
- Kimmerer, W.J.; MacWilliams, M.L.; Gross, E.S. Variation of fish habitat and extent of the low-salinity zone with freshwater flow in the San Francisco Estuary. SFEWS 2013, 11. [Google Scholar] [CrossRef]
- Sommer, T.; Mejia, F.H.; Nobriga, M.L.; Feyrer, F.; Grimaldo, L. The spawning migration of delta smelt in the upper San Francisco Estuary. SFEWS 2011, 9. [Google Scholar] [CrossRef]
- Moyle, P.B.; Brown, L.R.; Durand, J.R.; Hobbs, J.A. Delta smelt: Life history and decline of a once-abundant species in the San Francisco Estuary. SFEWS 2016, 14. [Google Scholar] [CrossRef]
- Dambacher, J.M.; Li, H.W.; Rossignol, P.A. Relevance of community structure in assessing indeterminacy of ecological predictions. Ecology 2002, 83, 1372–1385. [Google Scholar] [CrossRef]
- Cloern, J.E. Habitat connectivity and ecosystem productivity: Implications from a simple model. Am. Nat. 2007, 169, E21–E33. [Google Scholar] [CrossRef] [PubMed]
- Sommer, T.; Armor, C.; Baxter, R.; Breuer, R.; Brown, L.; Chotkowski, M.; Culberson, S.; Feyrer, F.; Gingras, M.; Herbold, B.; et al. The collapse of pelagic fishes in the upper San Francisco Estuary. Fisheries 2007, 32, 270–277. [Google Scholar] [CrossRef]
- Arthur, J.F.; Ball, M.D.; Baughman, S.Y. Summary of federal and state water project environmental impacts in the San Francisco Bay-Delta estuary, California. In The San Francisco Bay: The Ecosystem. Further Investigations into the Natural History of San Francisco Bay and Delta with Reference to the Influence of Man; Hollibaugh, J.T., Ed.; Friesen Printers: Altona, MB, Canada, 1996; pp. 445–495. [Google Scholar]
- California Department of Water Resources. Dayflow Data. Available online: https://water.ca.gov/Programs/Environmental-Services/Compliance-Monitoring-And-Assessment/Dayflow-Data (accessed on 14 May 2019).
- CDEC (California Data Exchange Center). The California Data Exchange Center. California Department of Water Resources. Available online: http://cdec.water.ca.gov (accessed on 29 April 2019).
- IEP (Interagency Ecological Program). Portal to IEP Data and Metadata. Available online: https://water.ca.gov/Programs/Environmental-Services/Interagency-Ecological-Program/Data-Portal (accessed on 29 April 2019).
- Feyrer, F.; Nobriga, M.L.; Sommer, T.R. Multidecadal trends for three declining fish species: Habitat patterns and mechanisms in the San Francisco Estuary, California, USA. Can. J. Fish. Aquat. Sci. 2007, 64, 723–734. [Google Scholar] [CrossRef]
- MacNally, R.; Thomson, J.R.; Kimmerer, W.J.; Feyrer, F.; Newman, K.B.; Sih, A.; Bennett, W.A.; Brown, L.; Fleishman, E.; Culberson, S.D.; et al. Analysis of pelagic species decline in the upper San Francisco Estuary using multivariate autoregressive modeling (MAR). Ecol. Appl. 2010, 20, 1417–1430. [Google Scholar] [CrossRef]
- Peterson, H.A.; Vayssieres, M. Benthic assemblage variability in the upper San Francisco Estuary: A 27-year retrospective. SFEWS 2010, 8. [Google Scholar] [CrossRef]
- Kratina, P.; MacNally, R.; Kimmerer, W.J.; Thomson, J.R.; Winder, M. Human-induced biotic invasions and changes in plankton interaction networks. J. Appl. Ecol. 2014, 51, 1066–1074. [Google Scholar] [CrossRef]
- Santos, M.J.; Anderson, L.W.; Ustin, S.L. Effects of invasive species on plant communities: An example using submersed aquatic plants at the regional scale. Biol. Invasions 2011, 13, 443–457. [Google Scholar] [CrossRef]
- Durand, J.; Fleenor, W.; McElreath, R.; Santos, M.J.; Moyle, P. Physical controls on the distribution of the submersed aquatic weed Egeria densa in the Sacramento–San Joaquin Delta and implications for habitat restoration. SFEWS 2016, 14. [Google Scholar] [CrossRef]
- Nichols, F.H.; Thompson, J.K.; Schemmel, L.E. Remarkable invasion of San Francisco Bay (California, USA) by the Asian clam Potamocorbula amurensis. II. Displacement of a former community. Mar. Ecol. Prog. Ser. 1990, 66, 95–101. [Google Scholar] [CrossRef]
- Winder, M.; Jassby, A.D. Shifts in zooplankton community structure: Implications for food web processes in the Upper San Francisco Estuary. Estuaries Coasts 2011, 34, 675–690. [Google Scholar] [CrossRef]
- Nobriga, M.L.; Feyrer, F.; Baxter, R.D.; Chotkowski, M. Fish community ecology in an altered river delta: Species composition, life history strategies, and biomass. Estuaries 2005, 28, 776–785. [Google Scholar] [CrossRef]
- Light, T.; Grosholz, T.; Moyle, P. Delta Ecological Survey (Phase I): Nonindigenous Aquatic Species in the Sacramento-San Joaquin Delta, a Literature Review; U.S. Fish and Wildlife Service: Stockton CA, USA, 2005. [Google Scholar]
- Ferrari, M.C.; Ranåker, L.; Weinersmith, K.L.; Young, M.J.; Sih, A.; Conrad, J.L. Effects of turbidity and an invasive waterweed on predation by introduced largemouth bass. Environ. Biol. Fishes 2014, 97, 79–90. [Google Scholar] [CrossRef]
- Hestir, E.L.; Schoellhamer, D.H.; Greenberg, J.; Morgan-King, T.; Ustin, S.L. The Effect of submerged aquatic vegetation expansion on a declining turbidity trend in the Sacramento-San Joaquin River Delta. Estuaries Coasts 2016, 39, 1110–1112. [Google Scholar] [CrossRef]
- Kimmerer, W.J. Response of anchovies dampens effects of the invasive bivalve Corbula amurensis on the San Francisco Estuary foodweb. Mar. Ecol. Prog. Ser. 2006, 324, 207–218. [Google Scholar] [CrossRef]
- Carlton, J.T.; Thompson, J.K.; Schemel, L.E.; Nichols, F.H. Remarkable invasion of San Francisco Bay (California, USA) by the Asian clam Potamocorbula amurensis. I. Introduction and dispersal. Mar. Ecol. Prog. Ser. 1990, 66, 81–94. [Google Scholar] [CrossRef]
- Lehman, P.W.; Boyer, G.; Hall, C.; Waller, S.; Gehrts, K. Distribution and toxicity of a new colonial Microcystis aeruginosa bloom in the San Francisco Bay Estuary, California. Hydrobiologia 2005, 541, 87–90. [Google Scholar] [CrossRef]
- Ger, K.A.; Teh, S.J.; Goldman, C.R. Microcystin-LR toxicity on dominant copepods Eurytemora affinis and Pseudodiaptomus forbesi of the upper San Francisco Estuary. Sci. Total Environ. 2009, 407, 4852–4857. [Google Scholar] [CrossRef] [PubMed]
- Acuña, S.; Baxa, D.; Teh, S. Sublethal dietary effects of microcystin producing Microcystis on threadfin shad, Dorosoma petenense. Toxicon 2014, 60, 1191–1202. [Google Scholar] [CrossRef]
- Puccia, C.J.; Levins, R. Qualitative Modeling of Complex Systems. An Introduction to Loop Analysis and Time Averaging; Harvard University Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Levins, R. Evolution in Changing Environments. Some Theoretical Explorations. Monographs in Population Biology; McArthur, R.H., Ed.; Princeton University Press: Princeton, NJ, USA, 1968. [Google Scholar]
- Puccia, C.J.; Levins, R. Qualitative Modeling in Ecology: Loop Analysis, Signed Digraphs and Time Averaging. In Qualitative Simulation Modeling and Analysis; Fishwick, P.A., Luker, P.A., Eds.; Advances in Simulation; Springer: New York, NY, USA, 1991; pp. 119–143. [Google Scholar]
- Castillo, G.C.; Li, H.W.; Rossignol, P.A. Absence of overall feedback in a benthic estuarine community: A system potentially buffered from impacts of biological invasions. Estuaries 2000, 23, 275–291. [Google Scholar] [CrossRef]
- MacWilliams, M.L.; Bever, A.J.; Gross, E.S.; Ketefian, G.S.; Kimmerer, W.J. Three-dimensional modeling of hydrodynamics and salinity in the San Francisco Estuary: An evaluation of model accuracy, X2, and the low–salinity zone. SFEWS 2015, 13. [Google Scholar] [CrossRef]
- Castillo, G. Annotated Bibliography of the Delta Smelt (Hypomesus transpacificus). Programmatic Review of Delta Smelt Program Elements (2005–06). Interagency Ecological Program. Available online: https://www.researchgate.net/publication/332725919 (accessed on 28 April 2019).
- Sommer, T.; Mejia, F.H. A place to call home: A synthesis of delta smelt habitat in the upper San Francisco Estuary. SFEWS 2013, 11. [Google Scholar] [CrossRef]
- Peterson, M.S. A conceptual view of environment-habitat-production linkages in tidal river estuaries. Rev. Fish. Sci. 2003, 11, 291–313. [Google Scholar] [CrossRef]
- Lane, P.A. Preparing Marine Plankton Data Sets for Loop Analysis. ESA Supplement. Available online: http://esapubs.org/archive/ecol/E067/001/suppl-1B.pdf (accessed on 29 April 2019).
- Lehman, P.W.; Teh, S.J.; Boyer, G.L.; Nobriga, M.L.; Bass, E.; Hogle, C. Initial impacts of Microcystis aeruginosa blooms on the aquatic food web in the San Francisco Estuary. Hydrobiologia 2010, 637, 229–248. [Google Scholar] [CrossRef]
- Simberloff, D.; Dayan, T. The guild concept and the structure of ecological communities. Annu. Rev. Ecol. Syst. 1991, 22, 115–143. [Google Scholar] [CrossRef]
- Lucas, L.V.; Cloern, J.E.; Thompson, J.K.; Monsen, N.E. Functional variability of habitats within the Sacramento-San Joaquin Delta: Restoration implications. Ecol. Appl. 2002, 12, 1528–1547. [Google Scholar]
- Lopez, C.B.; Cloern, J.E.; Schraga, T.S.; Little, A.J.; Lucas, L.V.; Thompson, J.K.; Burau, J.R. Ecological values of shallow-water habitats: Implications for restoration of disturbed ecosystems. Ecosystems 2006, 9, 422–440. [Google Scholar] [CrossRef]
- Brown, L.R.; Michniuk, D. Littoral fish assemblages of the alien-dominated Sacramento–San Joaquin Delta, California, 1980–1983 and 2001–2003. Estuaries Coasts 2007, 30, 186–200. [Google Scholar] [CrossRef]
- Yarrow, M.; Marin, V.H.; Finlayson, M.; Tironi, A.; Delgado, L.E.; Fisher, F. The ecology of Egeria densa Planchón (Liliopsida: Alismatales): A wetland ecosystem engineer? Rev. Chil. Hist. Nat. 2009, 82, 299–313. [Google Scholar] [CrossRef]
- Lehman, P.W.; Boyer, G.; Satchwell, M.; Waller, S. The influence of environmental conditions on the seasonal variation of Microcystis cell density and microcystins concentration in San Francisco Estuary. Hydrobiologia 2008, 600, 187–204. [Google Scholar] [CrossRef]
- Alpine, A.E.; Cloern, J.E. Trophic interactions and direct physical effects control phytoplankton biomass and production in an estuary. Limnol. Oceanogr. 1992, 37, 946–955. [Google Scholar] [CrossRef]
- Kimmerer, W.J.; Gartside, E.; Orsi, J.J. Predation by an introduced clam as the probable cause of substantial declines in zooplankton in San Francisco Bay. Mar. Ecol. Prog. Ser. 1994, 113, 81–93. [Google Scholar] [CrossRef]
- Kimmerer, W.J.; Parker, A.E.; Lidström, U.; Carpenter, E.J. Short-term and interannual variability in primary production in the low-salinity zone of the San Francisco Estuary. Estuaries Coasts 2012, 35, 913–929. [Google Scholar] [CrossRef][Green Version]
- Sobczak, W.V.; Cloern, J.E.; Jassby, A.D.; Muller-Solger, A.B. Bioavailability of organic matter in a highly disturbed estuary: The role of detrital and algal resources. Proc. Natl. Acad. Sci. USA 2002, 99, 8101–8105. [Google Scholar] [CrossRef] [PubMed]
- Jassby, A.D. Phytoplankton in the upper San Francisco Estuary: Recent biomass trends, their causes and their trophic significance. SFEWS 2008, 6. [Google Scholar] [CrossRef]
- Nobriga, M.L.; Loboschefsky, E.; Feyrer, F. Common predator, rare prey: Exploring juvenile striped bass predation on delta smelt in California’s San Francisco Estuary. Trans. Am. Fish. Soc. 2014, 142, 1563–1575. [Google Scholar] [CrossRef]
- Novak, M.; Wootton, J.T.; Doak, D.F.; Emmerson, M.; Estes, J.A.; Tinker, M.T. Predicting community responses to perturbations in the face of imperfect knowledge and network complexity. Ecology 2011, 92, 836–846. [Google Scholar] [CrossRef] [PubMed]
- Gantmacher, F.R. Applications of the Theory of Matrices; Dover Publications. Inc.: Mineola, NY, USA, 2005. [Google Scholar]
- Nakajima, H. Sensitivity and stability of flow networks. Ecol. Model. 1992, 62, 123–133. [Google Scholar] [CrossRef]
- Luh, H.K. Oregon State University. Loop Analysis Program in Microsoft.NET 3.5 Framework. Available online: http://ipmnet.org/loop/loopanalysis.aspx (accessed on 12 March 2019).
- California Department of Fish and Wildlife. Fall Midwater Trawl Index. Available online: http://www.dfg.ca.gov/delta/data/fmwt/indices.asp (accessed on 12 March 2019).
- Maceda-Veiga, A. Towards the conservation of freshwater fish: Iberian Rivers as an example of threats and management practices. Rev. Fish. Biol. Fisher. 2013, 23, 1–22. [Google Scholar] [CrossRef]
- Nobriga, M.L.; Sommer, T.R.; Feyrer, F.; Fleming, K. Long-term trends in summertime habitat suitability for delta smelt, Hypomesus transpacificus. SFEWS 2008, 6, 6. [Google Scholar] [CrossRef]
- Yamamuro, M. Herbicide-induced macrophyte-to-phytoplankton shifts in Japanese lagoons during the last 50 years: Consequences for ecosystem services and fisheries. Hydrobiologia 2012, 699, 5–19. [Google Scholar] [CrossRef]
- Kimmerer, W.J.; Thompson, J.K. Phytoplankton growth balanced by clam and zooplankton grazing and net transport into the low-salinity zone of the San Francisco Estuary. Estuaries Coasts 2014, 37, 1202–1218. [Google Scholar] [CrossRef]
- Bennett, W.A.; Moyle, P.B. Where have all the fishes gone? Interactive factors producing fish declines in the Sacramento-San Joaquin Estuary. In The San Francisco Bay: The Ecosystem. Further Investigations into the Natural History of San Francisco Bay and Delta with Reference to the Influence of Man; Hollibaugh, J.T., Ed.; Friesen Printers: Altona, MB, Canada, 1996; pp. 519–542. [Google Scholar]
- Rose, K.A.; Kimmerer, W.J.; Edwards, K.P.; Bennett, W.A. Individual-based modeling of delta smelt population dynamics in the upper San Francisco Estuary I. Model description and baseline results. Trans. Am. Fish. Soc. 2013, 142, 1238–1259. [Google Scholar] [CrossRef]
- Rose, K.A.; Kimmerer, W.J.; Edwards, K.P.; Bennett, W.A. Individual-based modeling of delta smelt population dynamics in the upper San Francisco Estuary II. Alternative baselines and good versus bad years. Trans. Am. Fish. Soc. 2013, 142, 1260–1272. [Google Scholar] [CrossRef]
- Kimmerer, W.J.; Rose, K.A. Individual-based modeling of delta smelt population dynamics in the upper San Francisco Estuary III. Effects of entrainment mortality and changes in prey. Trans. Am. Fish. Soc. 2018, 147, 223–243. [Google Scholar] [CrossRef]
- Hammock, B.G.; Moose, S.P.; Sandoval Solis, S.; Goharian, E.; Swee, J.T. Hydrodynamic modeling coupled with long-term field data provide evidence for suppression of phytoplankton by invasive clams and freshwater exports in the San Francisco Estuary. J. Environ. Manag. 2019, 63, 703–717. [Google Scholar] [CrossRef] [PubMed]
- Cottingham, A.; Huang, P.; Hipsey, M.R.; Hall, N.G.; Ashworth, E.; Williams, J.; Potter, I.C. Growth, condition, and maturity schedules of an estuarine fish species change in estuaries following increased hypoxia due to climate change. Ecol. Evol. 2018, 8, 7111–7130. [Google Scholar] [CrossRef]
- Baustian, M.M.; Clark, F.R.; Jerabek, A.S.; Wang, Y.; Bienn, H.C.; White, E.D. Modeling current and future freshwater inflow needs of a subtropical estuary to manage and maintain forested wetland ecological conditions. Ecol. Indic. 2018, 85, 791–807. [Google Scholar] [CrossRef]
- Martins, I.; Antunes, C.; Dias, E.; Campuzano, F.J.; Pinto, L.; Santos, M.M.; Antunes, C. Antagonistic effects of multiple stressors on macroinvertebrate biomass from a temperate estuary (Minho estuary, NW Iberian Peninsula). Ecol. Indic. 2019, 101, 792–803. [Google Scholar] [CrossRef]
- Allen, C.R.; Gunderson, L.H. Pathology and failure in the design and implementation of adaptive management. J. Environ. Manag. 2011, 92, 1379–1384. [Google Scholar] [CrossRef]
- Cartwright, J.; Caldwell, C.; Nebiker, S.; Knight, R. Putting flow-ecology relationships into practice: A decision-support system to assess fish community response to water-management scenarios. Water 2017, 9, 196. [Google Scholar] [CrossRef]
- Arthington, A.H.; Bhaduri, A.; Bunn, S.E.; Jackson, S.E.; Tharme, R.E.; Tickner, D.; Young, B.; Acreman, B.; Baker, N.; Capon, S.; et al. The Brisbane declaration and global action agenda on environmental flows. Front. Environ. Sci. 2018, 6, 45. [Google Scholar] [CrossRef]
- Gifford, S.M.; Rollwagen Bollens, G.C.; Bollens, S.M. Mesozooplankton omnivory in the upper San Francisco Estuary. Mar. Ecol. Prog. Ser. 2007, 348, 33–46. [Google Scholar] [CrossRef]
- Burks, R.L.; Jeppesen, E.; Lodge, D.M. Macrophyte and fish chemicals suppress Daphnia growth and alter life-history traits. Oikos 2000, 88, 139–148. [Google Scholar] [CrossRef]
- Lucy, F.E.; Karatayev, A.Y.; Burlakova, L.E. Predictions for the spread, population density, and impacts of Corbicula fluminea in Ireland. Aquat. Invasions 2012, 7, 465–474. [Google Scholar] [CrossRef]
- Sousa, R.; Gutierrez, J.L.; Aldridge, D.C. Non-indigenous invasive bivalves as ecosystem engineers. Biol. Invasions 2009, 11, 2367–2385. [Google Scholar] [CrossRef]
- Pflugmacher, S. Promotion of oxidative stress in the aquatic macrophyte Ceratophyllum demersum during biotransformation of the cyanobacterial toxin microcystin-LR. Aquat. Toxicol. 2004, 70, 169–178. [Google Scholar] [CrossRef]
- Hwang, S.J.; Kim, H.S.; Park, J.H.; Kim, B.H. Effects of cyanobacterium Microcystis aeruginosa on the filtration rate and mortality of the freshwater bivalve Corbicula leana. J. Environ. Biol. 2010, 31, 483–488. [Google Scholar]
- Gao, Y.N.; Dong, J.; Fu, Q.Q.; Wang, Y.P.; Chen, C.; Li, J.H.; Li, R.; Zhou, C.J. Allelopathic effects of submerged macrophytes on phytoplankton. Allelopath. J. 2017, 40, 1–22. [Google Scholar]
- Liu, Y.; Xie, P.; Wu, X.P. Grazing on toxic and non-toxic Microcystis aeruginosa PCC7820 by Unio douglasiae and Corbicula fluminea. Limnology 2009, 10, 1–5. [Google Scholar] [CrossRef]

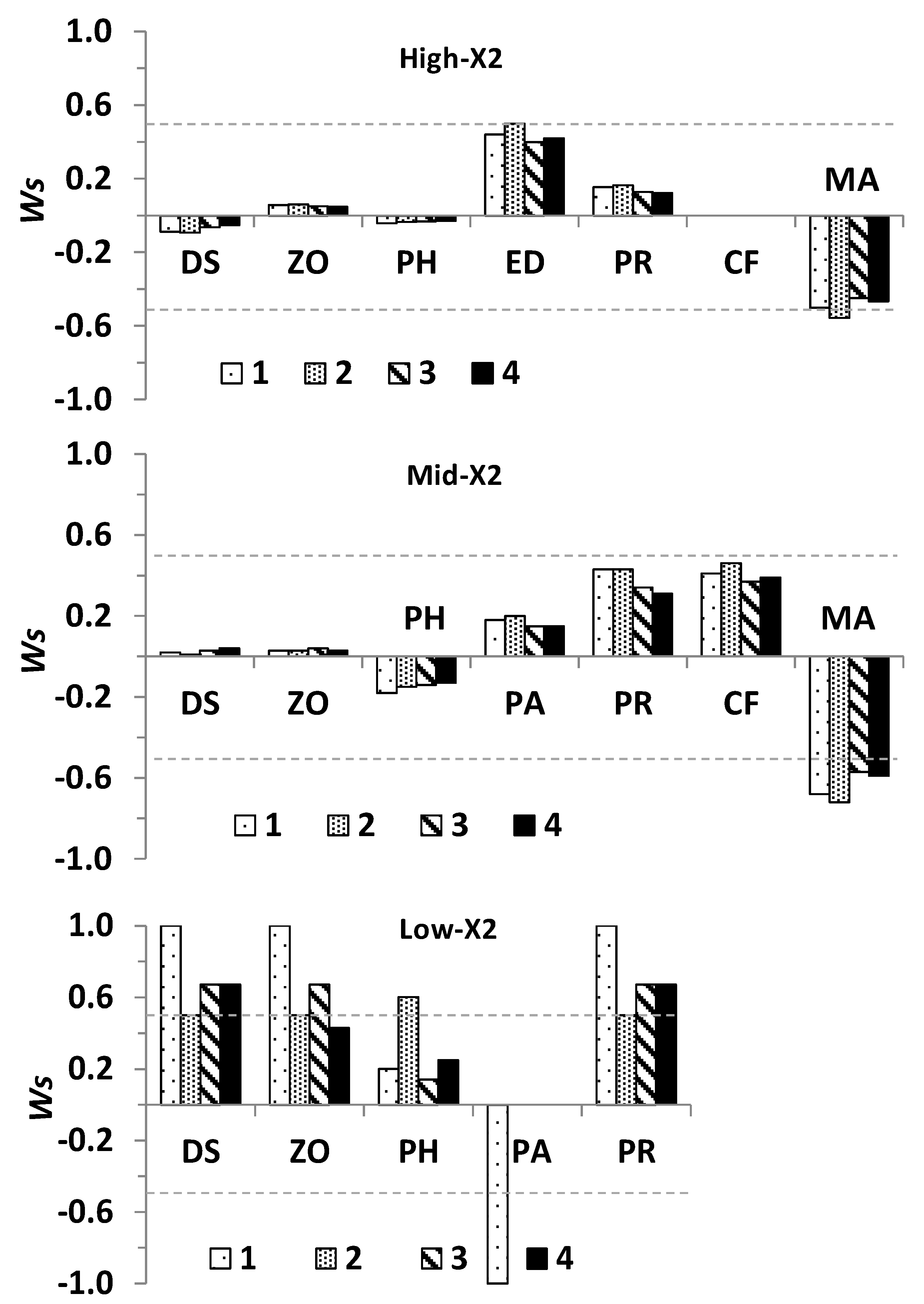
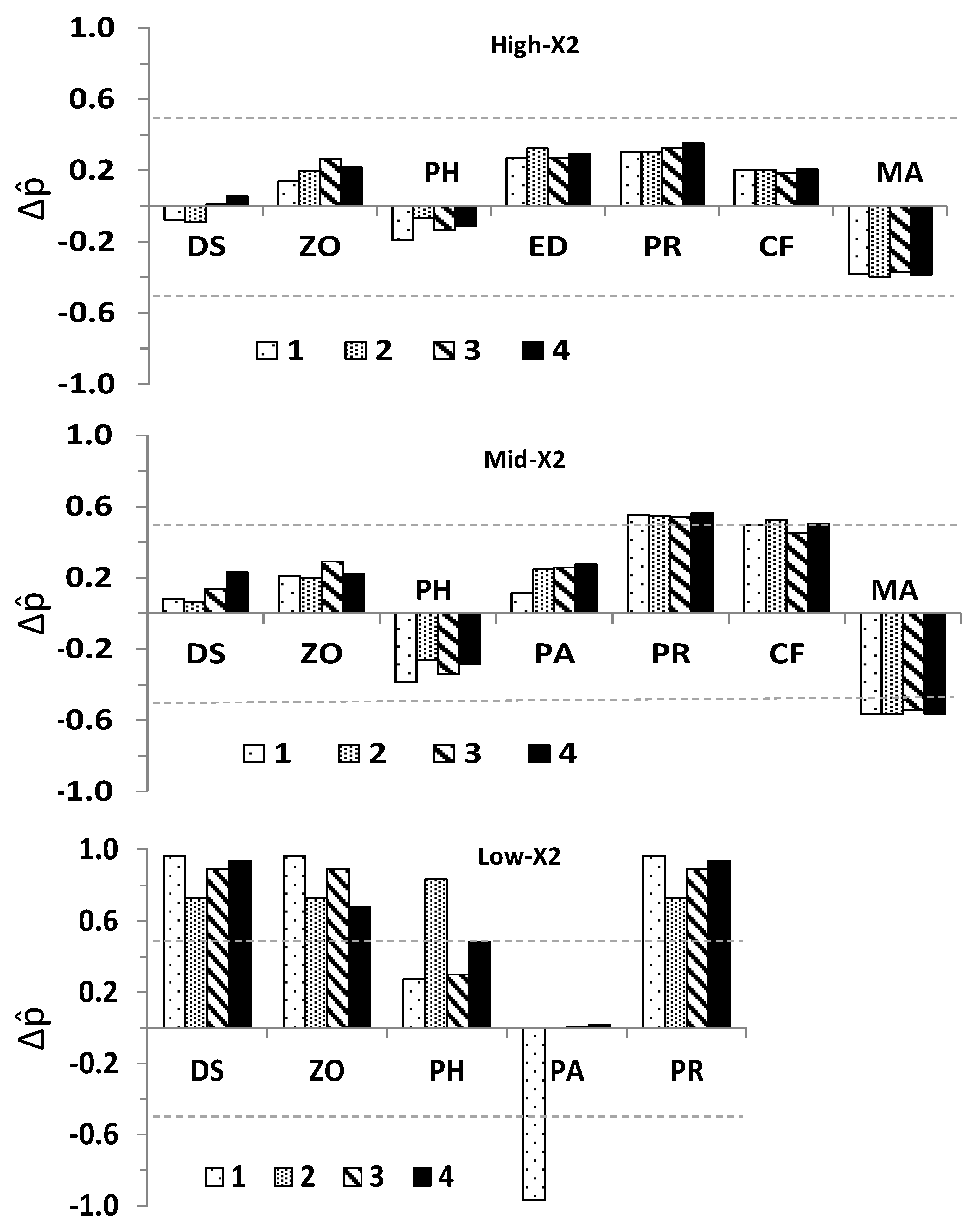
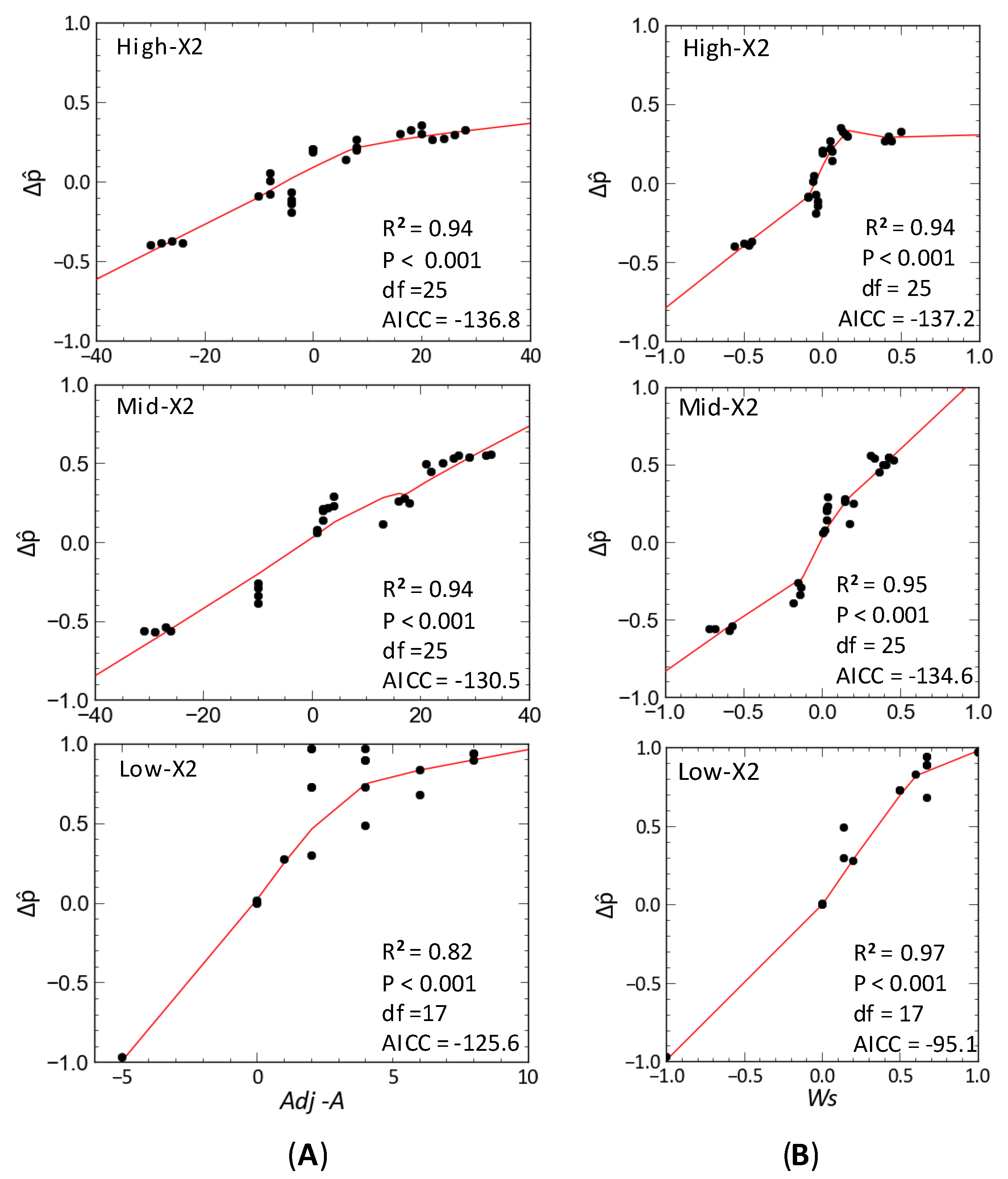
| Variable Type | Variable Code (Description) | Low X2 74 km | Mid X2 81 km | High X2 85 km | Functional Role | Community Response to Outflow |
|---|---|---|---|---|---|---|
| Explanatory | FL (Delta outflow, m3 s−1) | 323 [24] | 227 [24] | 142 [24] | Major abiotic forcing factor controlling the overlap between dynamic and stationary factors in the upper San Francisco Estuary, the position and size of the low salinity zone and the low salinity habitat of delta smelt and community interactions [24,38]. | |
| Response (Community variables) | CF (Corbicula fluminea, Asian clam) 1 | ● [24] | ● [24] | Filter feeder exerting grazing pressure on phytoplankton [82,83]. | (+) [56] | |
| DS (Hypomesus transpacificus, delta smelt) | ● [38,45] | ● [38,45] | ● [38,45] | Zooplanktivorous preying primarily on copepods, mysids, and cladocerans [40,41]. | (+) [10,54] | |
| ED (Egeria densa, Brazilian waterweed) 1 | ● [58,59] | Primary producer of dense submersed vegetation beds which reduce open water habitat, alter the habitat for other aquatic plants [58,65] and provide habitat for centrarchids [84]. | (−) [59,85] | |||
| MA (Microcystis aeruginosa, cyanobacterium) 2 | ● [24,86] | ● [24,86] | Biological contaminant due to its poor nutritional value and transfer of toxic microcystins into the aquatic food web [24,69,70,80]. | (−) [86] | ||
| PA (Potamocorbula amurensis, overbite clam) 1 | ● [24] | ● [24] | Filter feeder exerting grazing pressure on phytoplankton and zooplankton [87,88]. | (−) [56] | ||
| PH (Phytoplankton) | ● [38,89,90] | ● [38,89,90] | ● [38,89,90] | Primary producer fueling higher trophic levels of the food web in the open waters of the Delta and Suisun Bay [89,90]. | (+) [38,91] | |
| PR (Predators of delta smelt) | ● [24,38] | ● [24,38] | ● [24,38] | Piscivores deemed to exert predation pressure on delta smelt throughout the Delta and Suisun Bay [24], including two introduced species, striped bass Morone saxatilis [62,92] and largemouth bass Micropterus salmoides [64,84]. | (0) 3 [38] | |
| ZO (Zooplankton) | ● [24,38] | ● [24,38] | ● [24,38] | Primary and secondary consumer supporting pelagic and benthic food webs [41,88]. | (+) [55] |
| R–H Criteria | Low-X2 (74 km) | Mid-X2 (81 km) | High-X2 (85 km) |
|---|---|---|---|
| None | 2.7 | 39.9 | 48.2 |
| Only I | 0.3 | 3.5 | 10.6 |
| Only II | 0.0 | 0.0 | 0.0 |
| Both | 97 | 56.6 | 41.2 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo, G.C. Modeling the Influence of Outflow and Community Structure on an Endangered Fish Population in the Upper San Francisco Estuary. Water 2019, 11, 1162. https://doi.org/10.3390/w11061162
Castillo GC. Modeling the Influence of Outflow and Community Structure on an Endangered Fish Population in the Upper San Francisco Estuary. Water. 2019; 11(6):1162. https://doi.org/10.3390/w11061162
Chicago/Turabian StyleCastillo, Gonzalo C. 2019. "Modeling the Influence of Outflow and Community Structure on an Endangered Fish Population in the Upper San Francisco Estuary" Water 11, no. 6: 1162. https://doi.org/10.3390/w11061162
APA StyleCastillo, G. C. (2019). Modeling the Influence of Outflow and Community Structure on an Endangered Fish Population in the Upper San Francisco Estuary. Water, 11(6), 1162. https://doi.org/10.3390/w11061162