Experimental Investigation of Purging Saline Solution from a Dead-End Water Pipe
Abstract
1. Introduction
- -
- The network includes dead end pipes;
- -
- The pipe network is subjected to quite long periods of low pressure. One might think that this problem exists only in intermittent pipe network, but recent lab research [12] proved that continuous-supply pipe network with pipe leaking point might be vulnerable to external contamination ingress too.
- -
- Existence of salt/contaminated groundwater in the vicinity of the water network and this salty/contaminated groundwater might get intruded inside the pipe system during the low-pressure periods;
- -
- Inaccessibility of the dead-end point and thus purging should be conducted from other point.
2. Methodology
2.1. Preparation of Saline Solution
2.2. Experimental Setup
2.3. List of Experimental Runs
2.4. Apparatus and Software
2.5. Main Assumptions
- -
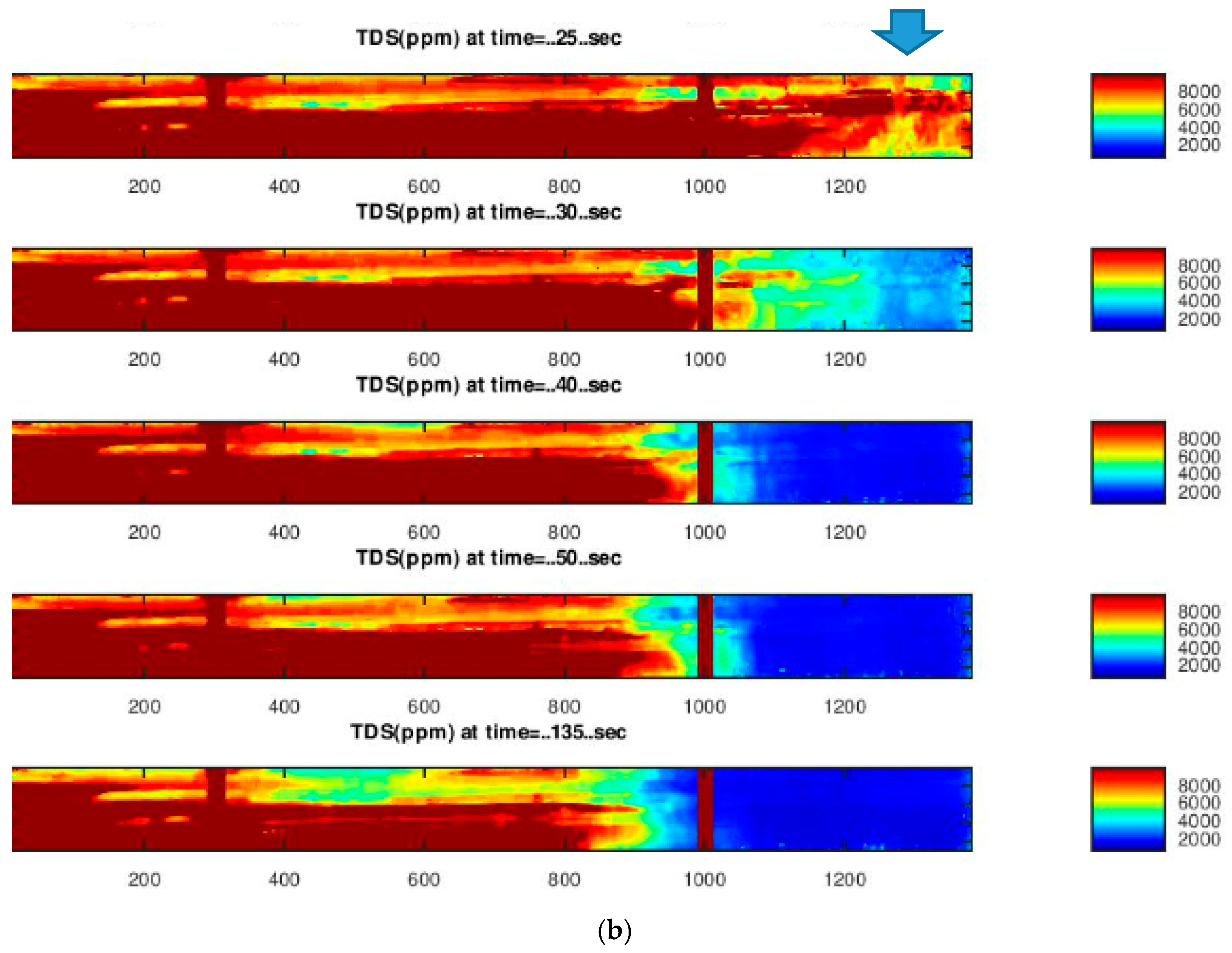
- It is claimed that imaging the pipe from outside will reveal a lot of information about the status of water quality in the dead end-leg during the purging process. The paper assumes that imaging the pipe from outside is significantly correlated to the average of what happens throughout the full pipe cross-section.
- -
- No additional measurement system to validate the results for this regard, authors conducted an extended 3D-numerical study for the same problem using ANSYS Fluent package and good agreement obtained [18].
- -
- The study neglected the effect of non-uniformity and unsteadiness in illumination from the used light sources.
- -
- The study also assumes that there is no access to the front of the dead zone (on site) and therefore direct insertion of clear purging water from the front of the dead end is not possible.
- -
- The influence of the pressure level on the purging process is not investigated.
2.6. Work Flow
- -
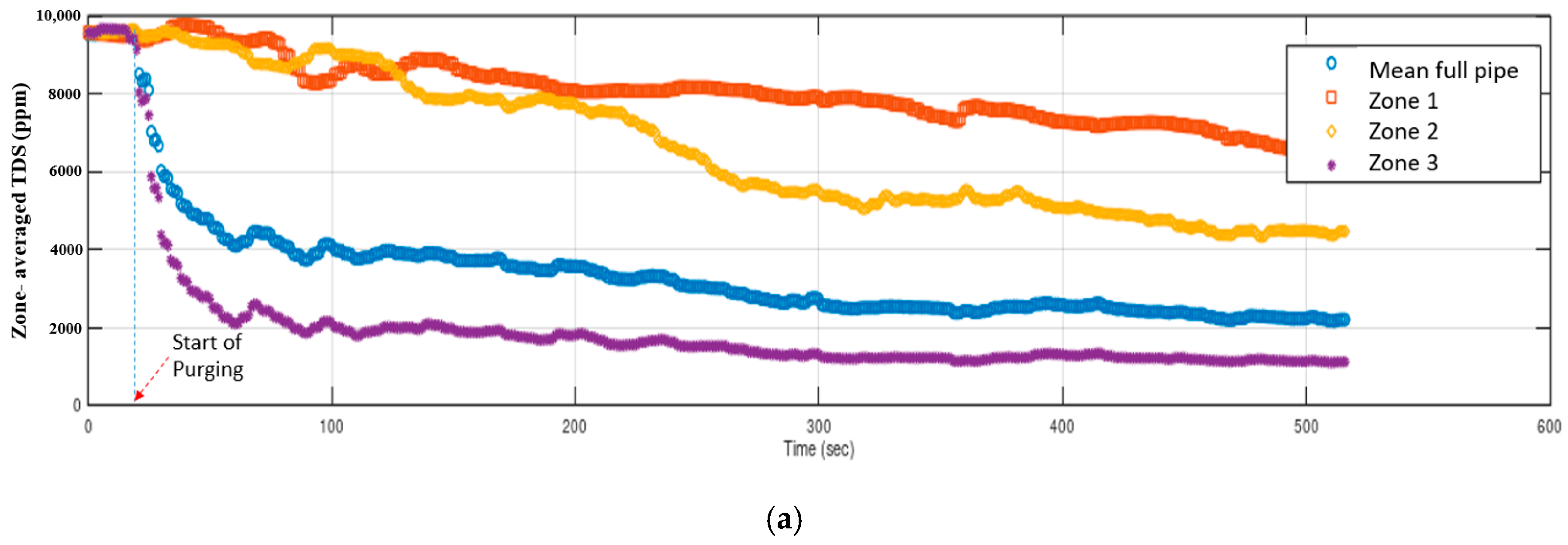
- Filling the dead leg pipe by the saline solution (TDS = 1867 ppm or TDS = 9600 ppm);
- -
- Selecting the purging location by opening the switch valve of one of the three purging pipes (making sure that the remaining purging pipes are closed);
- -
- Start video recording the purging process then start purging saline by using tap water and;
- -
- Convert the recorded mp4 video file to avi file using VLC freeware software [19]. This step is important since most of the video analysis packages (such as SciLab and Octave) can only read avi files;
- -
- The next step is to read the avi file and to carry out video analysis and image processing using a script code compatible with Octave package and was specifically written for this regard (more details to follow);
- -
- The final step is to plot temporal variations of color intensities and corresponding TDS values then to carry out post processing analysis using Excel.
2.7. Removal of Light Streaks
3. Results and Discussion
3.1. Flow Structure and Eddy Formulation
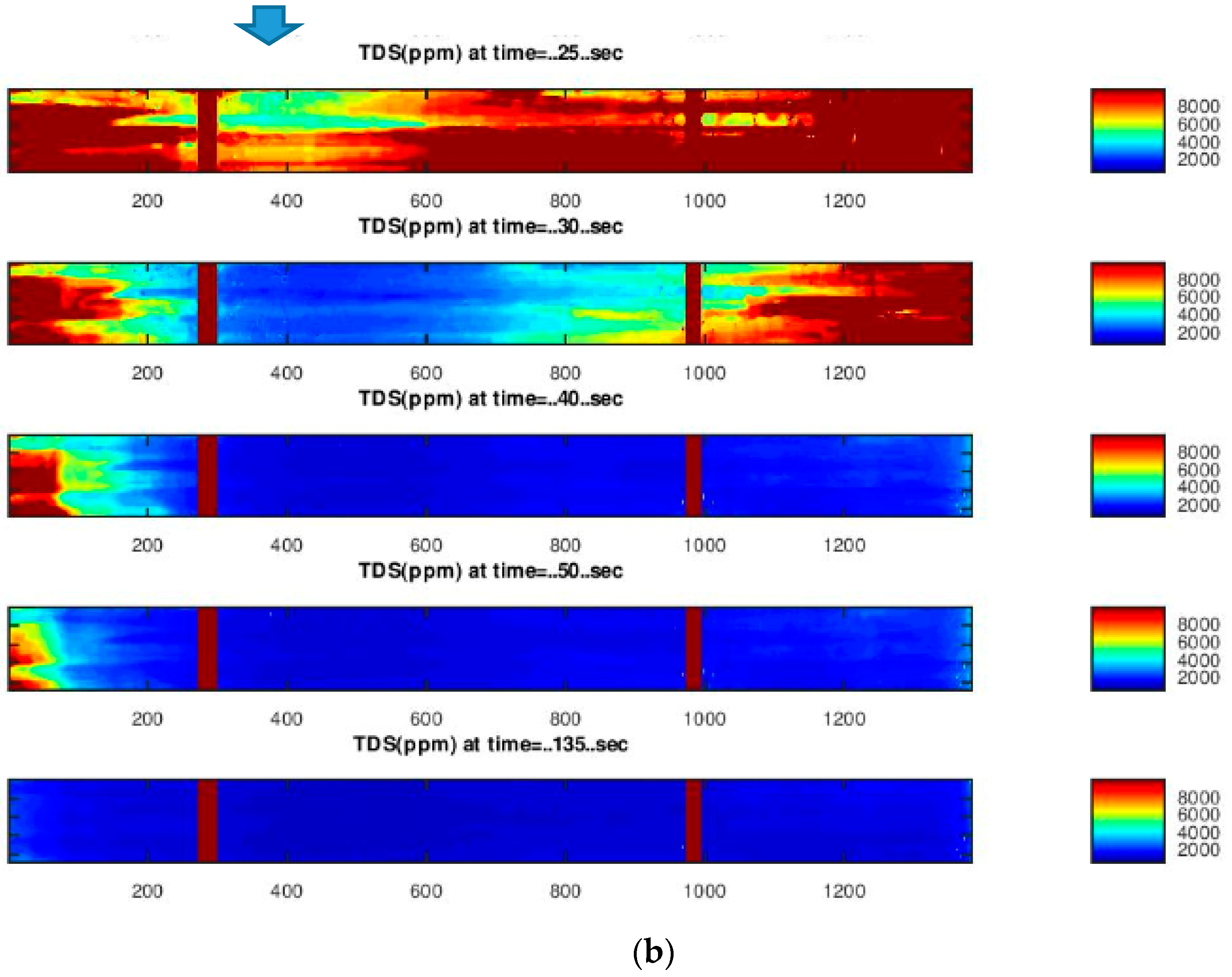
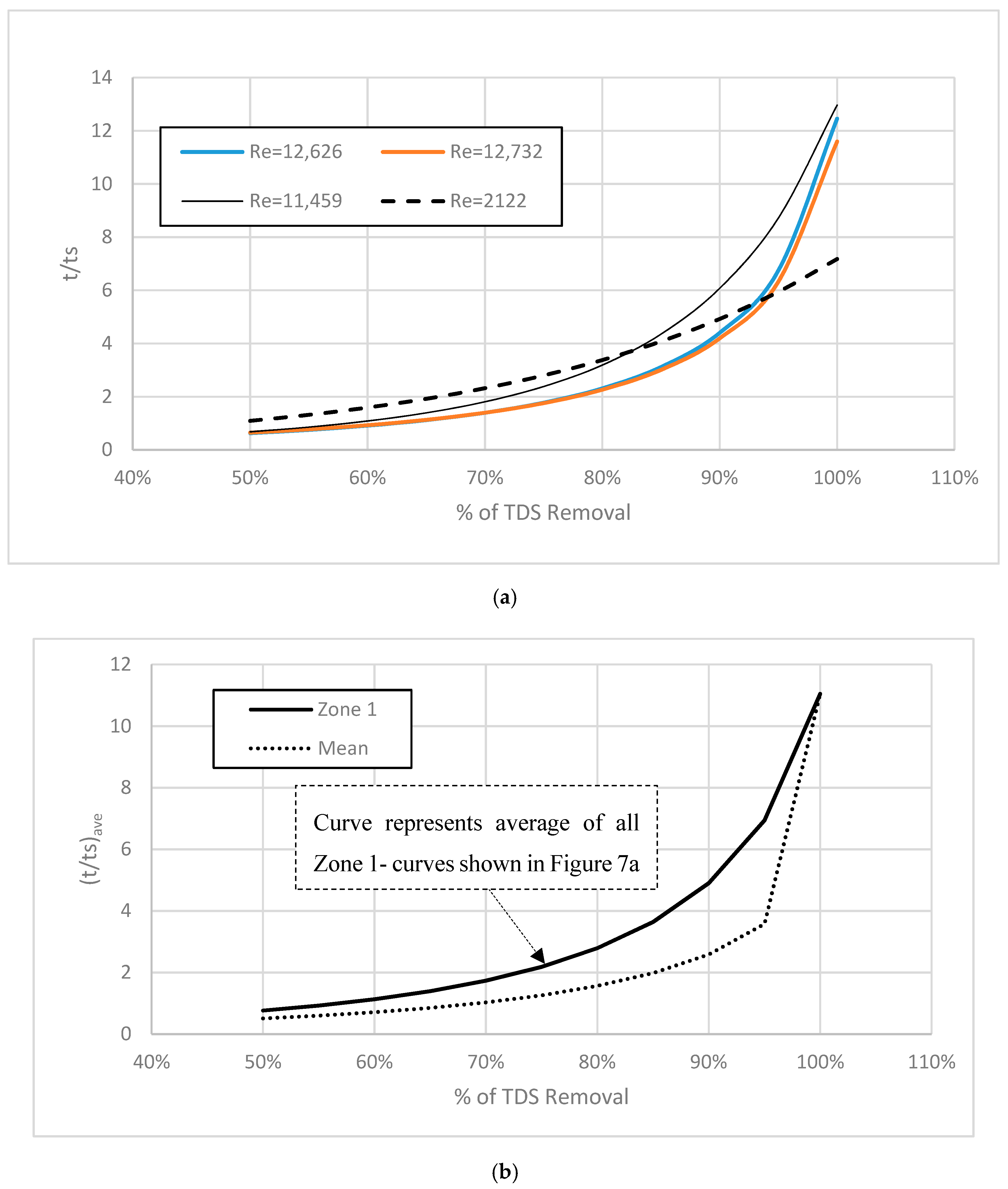
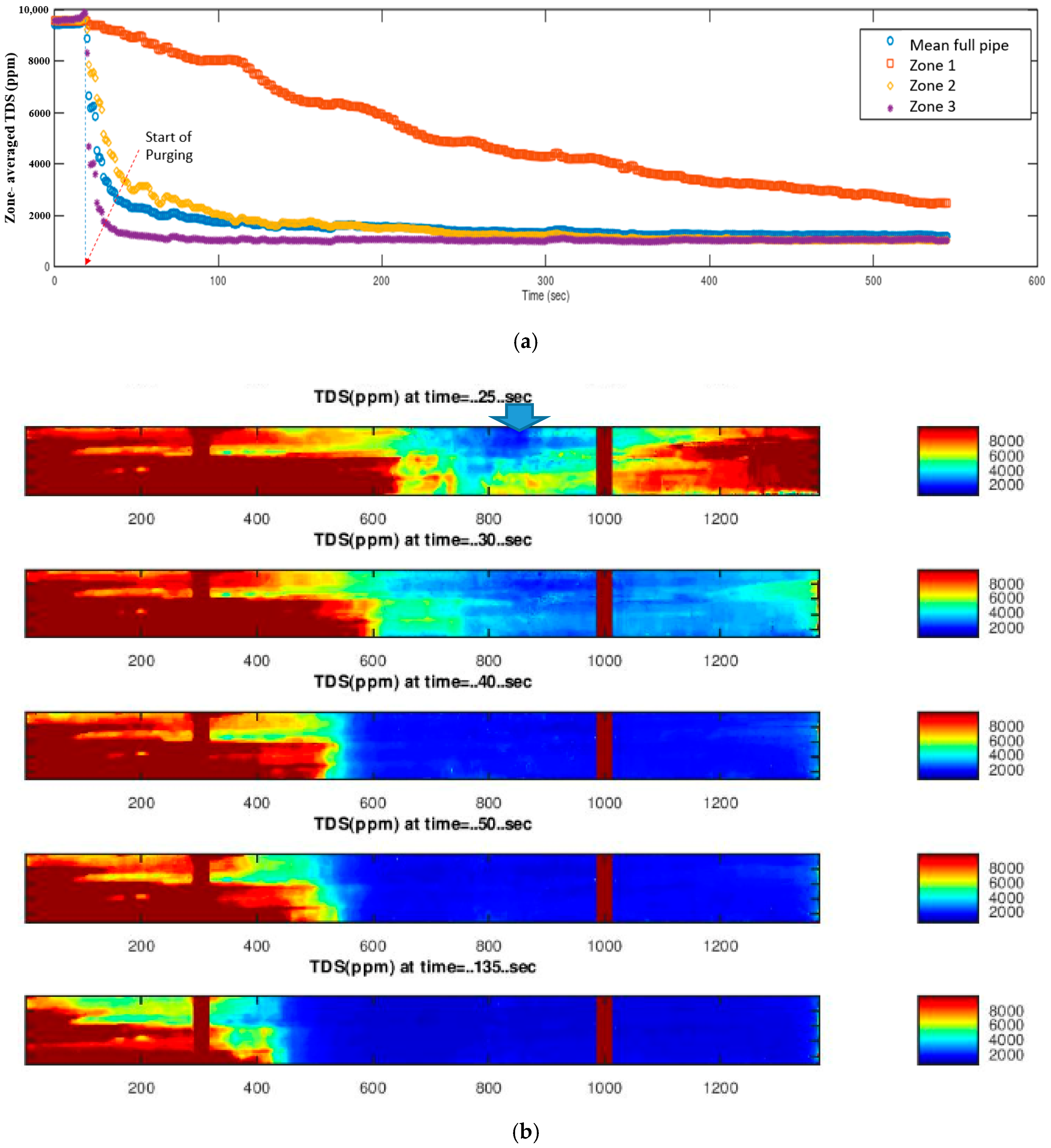
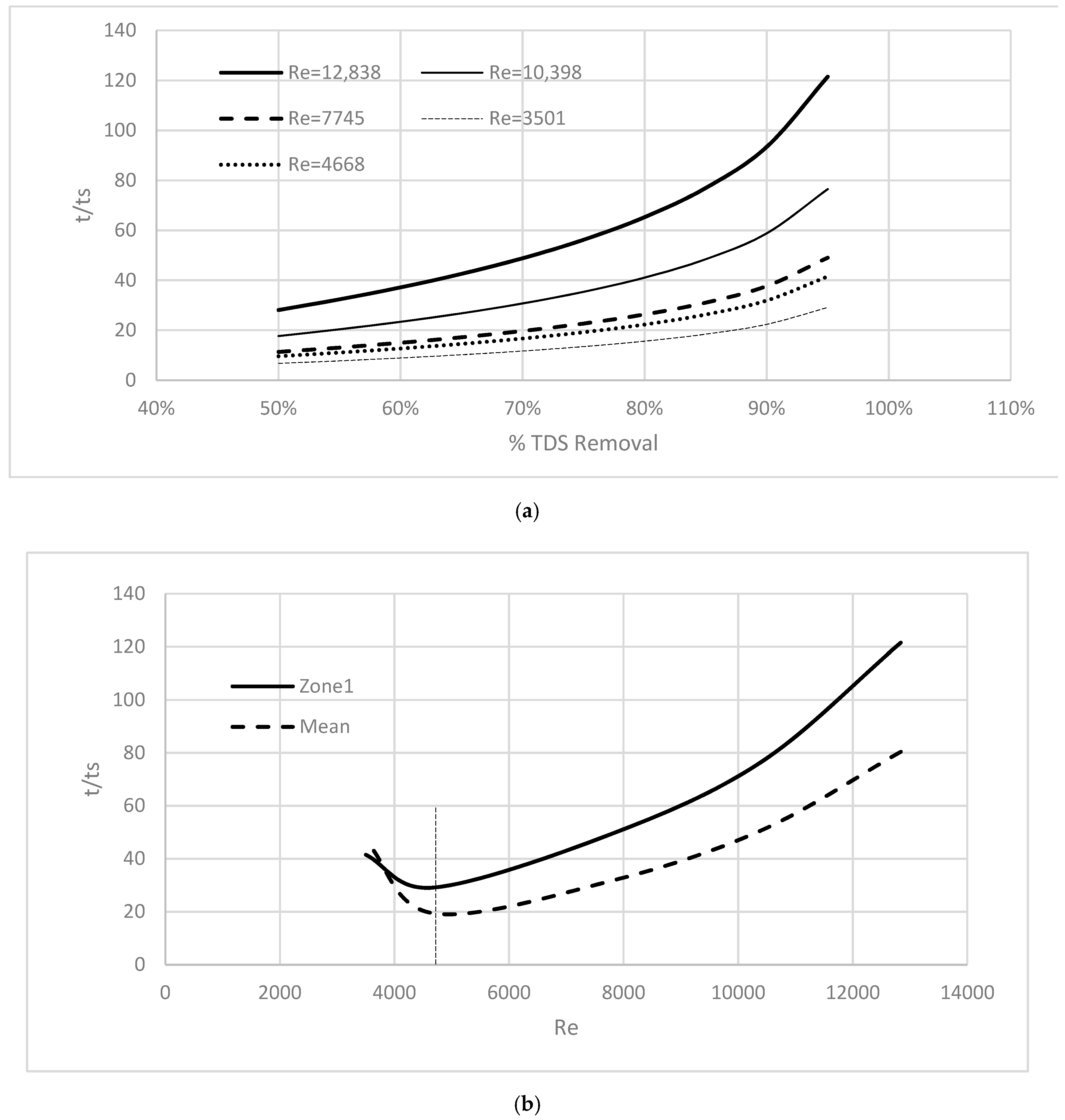
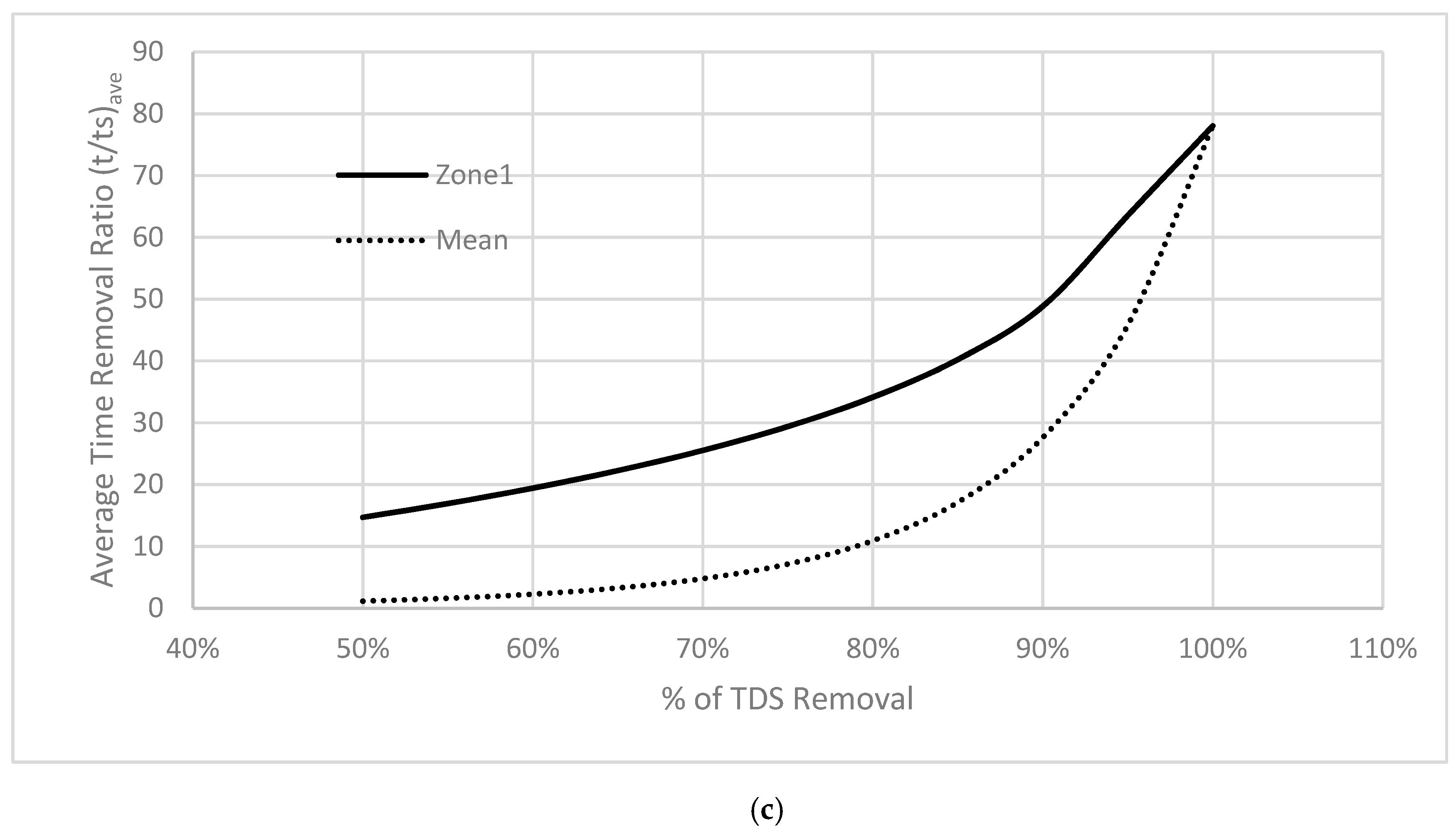
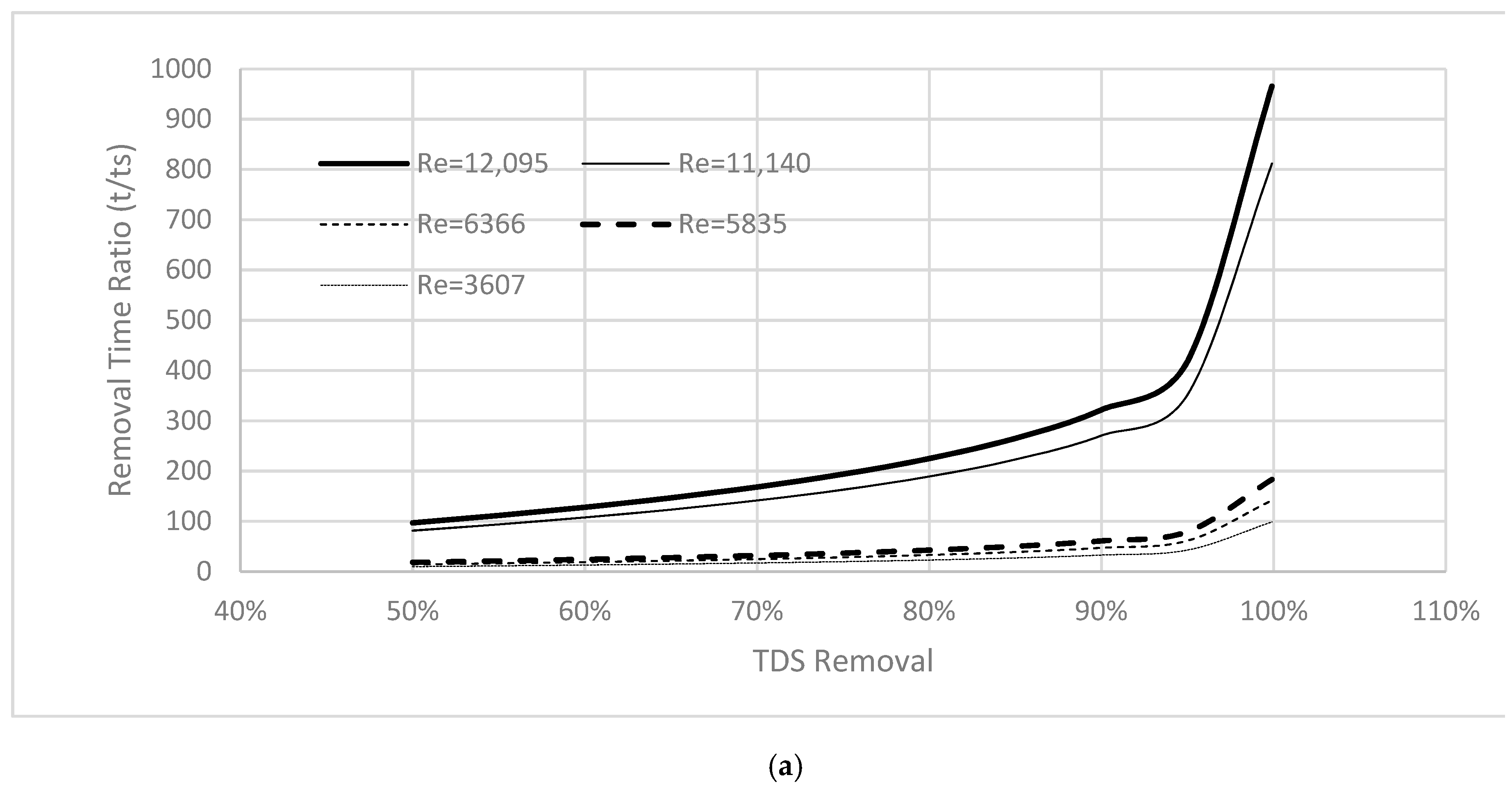
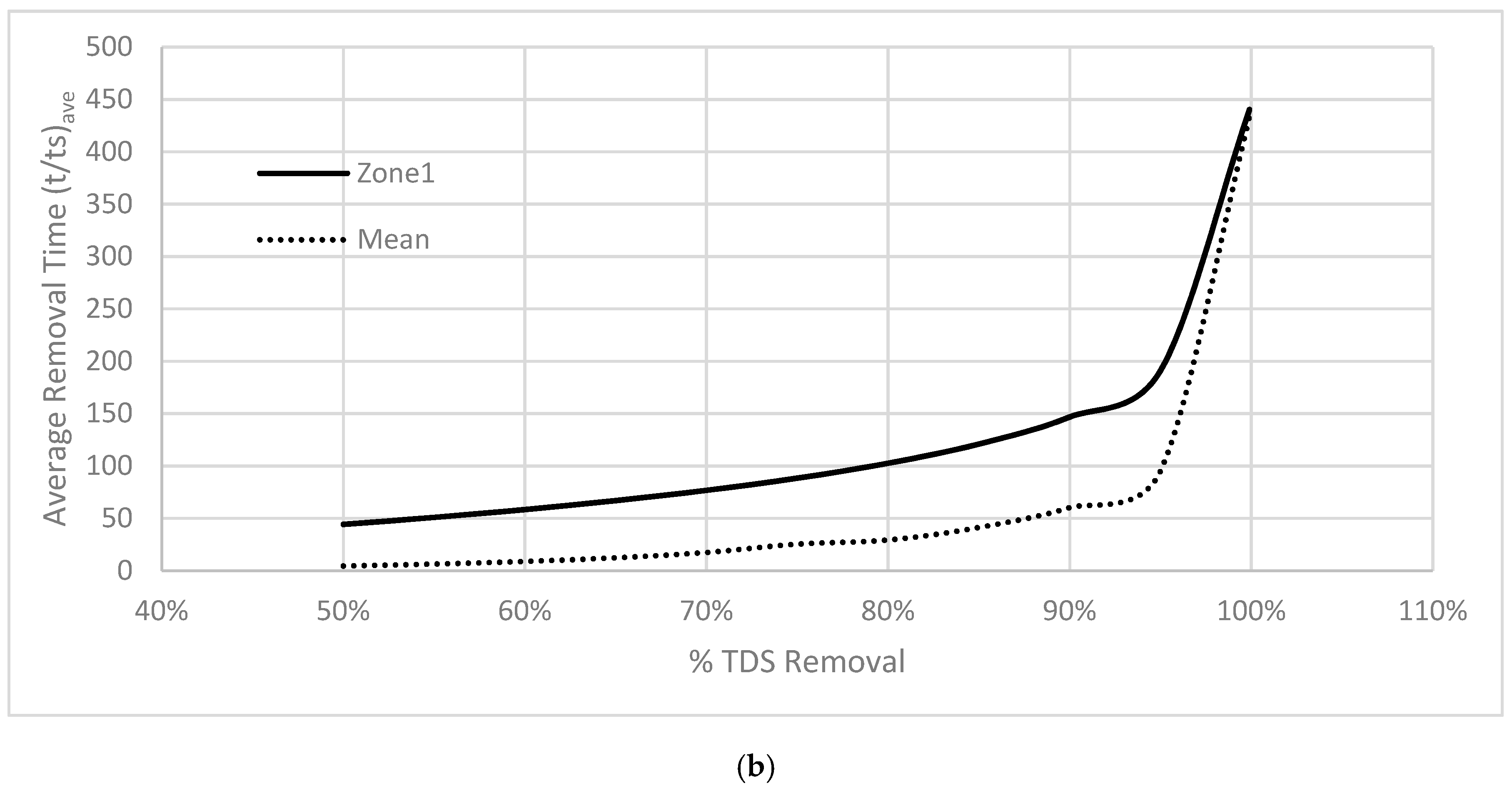
3.2. First Purging Location (Xp/D = 3)
3.3. Second Purging Location (Xp/D = 7)
3.4. Third Purging Location (Xp/D = 11)
4. Conclusions and Challenges
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| d | Diameter of the inlet purging pipe (d = 1 inch) |
| D | Diameter of the Pyrex pipe to be purged (D = 4 inches) |
| Gr | Grayness ratio, equation 1 |
| Grayi | The gray intensity of the water solution inside the pipe to be purged at any moment I (after commencement of purging) |
| Graym | The initial maximum gray intensity of the saline water (before purging starts) |
| Grayo | The average gray intensity of the tap water |
| GRB | Green-red-blue |
| GNU | is a free licensed operating system that stands for “GNU’s Not Unix!” |
| L | Length of the studied flow domain for the Pyrex pipe (L = 120 cm) |
| mL | Milliliters |
| ppm | Particles per million |
| Q | Purging flow rate |
| Re | Reynolds number of purging flow [Re = 4Q/(πDv)] where v is the kinematic viscosity of the purging fluid |
| Rex | Spatial Reynolds number, equation 4 |
| Sr | Salinity ratio, equation 2 |
| SSS | Saline solution standard |
| T | Time in seconds since start of recording |
| TDS | Total Dissolved Salt (units in ppm) |
| TDSi | The average TDS value of eater solution at any pixel inside the pipe and at any moment I after commencement of purging process |
| TDSm | Maximum TDS value of the solute (before dilution) (TDSm = 1867, 9600 and 14420 ppm for the three solutions) |
| TDSo | The average TDS value of original tap water before adding salt to it (TDSo = 300 ppm) |
| t | Time in seconds since start of purging process, equation 6 |
| to | Time for initiation of purging process |
| ts | Time scale = (πLD2/4Q) and it represents the time required to fill an empty pipe of length L and diameter D for an input flow rate equals the purging flow rate. |
| t/ts | The time ratio or the normalized time required to attain a specified TDS removal percentage |
| (t/ts)ave | The average time of removal ratio calculated to average the value for different purging flow rate |
| UDF | Uni-directional flushing of water network. |
| xp | The distance from the pipe dead end to the purging location and it is measured horizontally, Equation (4) |
| ∆Q | Entrained flow from resident saline water to the purging jet, Figure 4. |
References
- Carter, J.T.; Lee, Y.; Buchberger, S.G. Correlations between travel time and water quality in a dead-end loop. In Proceedings of the Water Quality Technology Conference, American Water Works Association, Denver, CO, USA, 9–12 November 1997. [Google Scholar]
- Galvin, R. Eliminate Dead-End Water. Opflow. 2011. Available online: http://midwestwatergroup.com/ownloads/Opflow%20-%20November%202011%20-%20Dead%20End%20Danger%20Zones.pdf (accessed on 12 March 2019).
- McVay, R.D. Effective Flushing Techniques for Water Systems. Florida Rural Water Association. Available online: http://www.frwa.net/uploads/4/2/3/5/42359811/effectiveflushingtechniquesforwatersystems051608.doc (accessed on 9 April 2019).
- MassDEP, Massachusetts Department of Environmental Protection Drinking Water Program. Fact Sheet Water Main Flushing FAQ for Consumers. 2018. Available online: https://www.mass.gov/files/documents/2018/05/07/Water%20Main%20Flushing%20-%20Fact%20Sheet%20-%20FAQ%20for%20Consumers.pdf (accessed on 6 April 2019).
- Kammereck, L.; Reisinger, D. Flushing Tips: Implementing Unidirectional Flushing Program. Water Finance and Environment, 2016. Available online: https://waterfm.com/implement-unidirectional-flushing-program-improve-efficiency-conservation/ (accessed on 9 April 2019).
- Yuan, W. Practical Analysis of Cleaning Water Supply Pipeline Using Air and Water Flushing Technology. In Proceedings of the 1st International WDSA/CCWI 2018 Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Barbeau, B.; Gauthier, V.; Julienne, K.; Carriere, A. Dead-end flushing of a distribution system: Short and long-term effects on water quality. J. Water Supply Res. Technol. Aqua 2005, 54, 371–383. [Google Scholar] [CrossRef]
- Ilaya-Ayza, A.; Martins, C.; Campbell, E.; Izquierdo, J. Implementation of DMAs in Intermittent Water Supply Networks Based on Equity Criteria. Water 2017, 9, 851. [Google Scholar] [CrossRef]
- Choe, K.; Varley, R.C.G.; Bijlani, H.U. Coping with Intermittent Water Supply, Problems and Prospects, Environmental Health Project. Activity Report No. 26; Dehra Dun, India, 1996. Available online: https://pdf.usaid.gov/pdf_docs/pnabz958.pdf (accessed on 18 March 2019).
- PNGRB, Petroleum and Natural Gas Regulatory Board, New Deli, India. Available online: http://www.pngrb.gov.in/pdf/public-notice/guidelines22122015.pdf (accessed on 11 may 2019).
- Firdausa, L.; Alwib, W.; Trinoveldib, F.; Rahayuc, I.; Rahmidard, L.; Warsito, K. Determination of Chromium and Iron Using Digital Image-based Colorimetry. Procedia Environ. Sci. 2014, 20, 298–304. [Google Scholar] [CrossRef]
- Fox, S.; Shepherd, W.; Collins, R.; Boxall, J. Experimental Quantification of Contaminant Ingress into a Buried Leaking Pipe during Transient Events. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Choodum, A.; Kanatharana, P.; Wongniramaikul, W.; Daeid, N. Using the iPhone as a device for a rapid quantitative analysis of trinitrotoluene in soil. Talanta 2013, 115, 143–149. [Google Scholar] [CrossRef]
- Elgamal, M.; Abdel-Mageed, N.; Helmy, A.; Ghanem, A. Hydraulic performance of sluice gate with unloaded upstream rotor. Water SA 2017, 43, 563–572. [Google Scholar] [CrossRef][Green Version]
- Stahel, A. Octave and MATLAB for Engineers; Bern University of Applied Sciences: Bern, Switzerland, 2018; Available online: https://web.ti.bfh.ch/~sha1/Labs/PWF/Documentation/OctaveAtBFH.pdf (accessed on 12 March 2019).
- Sony RX100 Cyber-Shot, Instruction Manual. Available online: https://www.docs.sony.com/release/DSCRX100_EN_ES.pdf (accessed on 12 March 2019).
- Coman, E.; Brewster, M.; Popuri, S.; Raim, A.; Gobbert, M. A Comparative Evaluation of Matlab, Octave, FreeMat, Scilab, R, and IDL on Tara. Technical Report HPCF-2012-15. Available online: www.umbc.edu/hpcf (accessed on 12 March 2019).
- Farouk, M.; Elgamal, M.H. CFD Simulation of Flushing the Dead-Ends of a Distribution System, submitted to Water SA. (unpublished).
- VLC for Dummies. Available online: https://wiki.videolan.org/Documentation:VLC_for_dummies/ (accessed on 12 March 2019).
- Yeh, K.C.; Kang, L.W.; Lee, M.S.; Lin, C.Y. Haze effect removal from image via haze density estimation in optical model. Opt. Express 2013. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, T.; Zhao, X.; Deng, L.; Wang, Y. FastDeRain: A Novel Video Rain Streak Removal Method Using Directional Gradient Priors. IEEE Trans. Image Process. 2018, 8, 2089–2102. [Google Scholar] [CrossRef] [PubMed]
- Rajaratnam, N. Turbulent Jets; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]

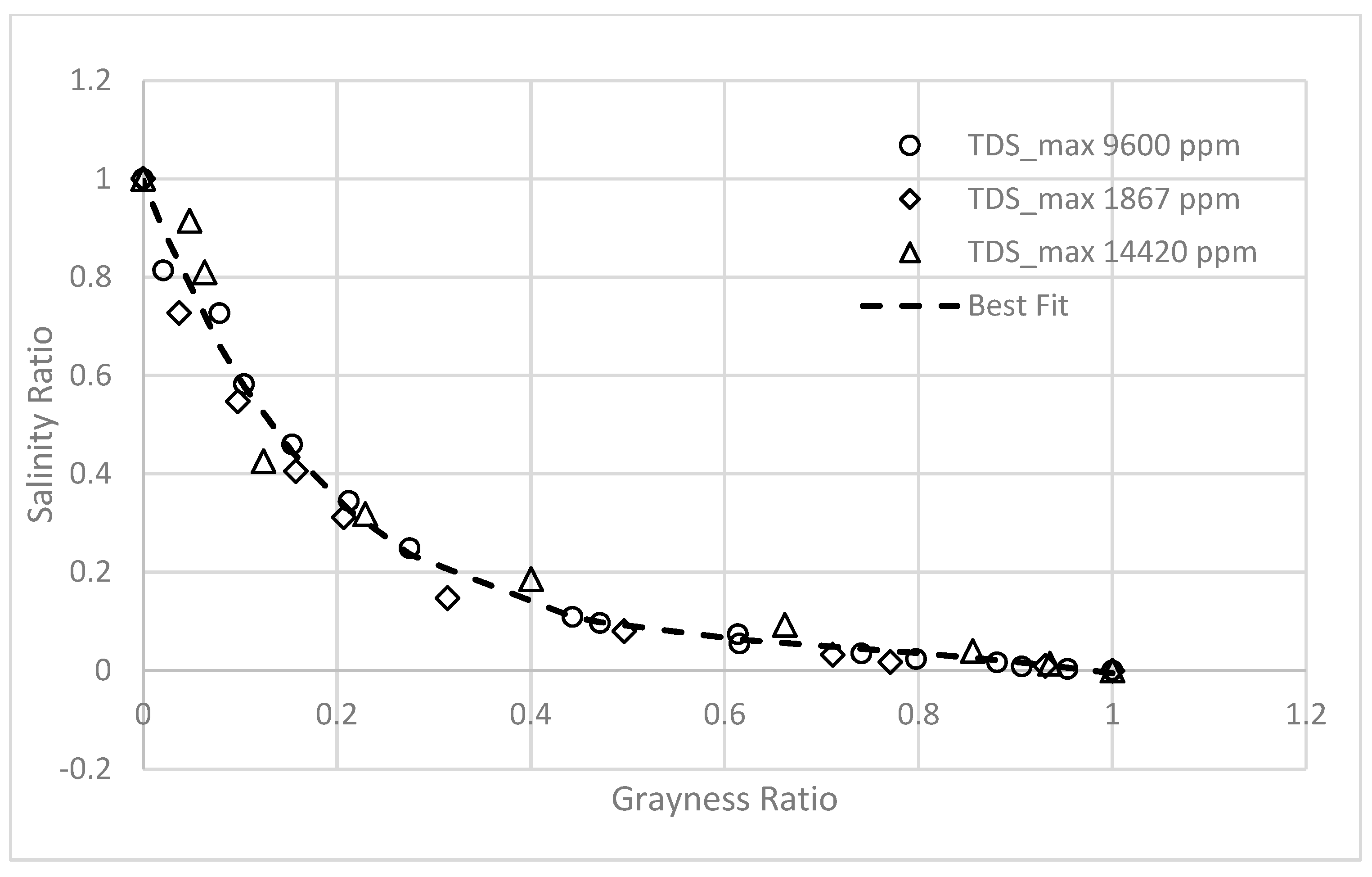

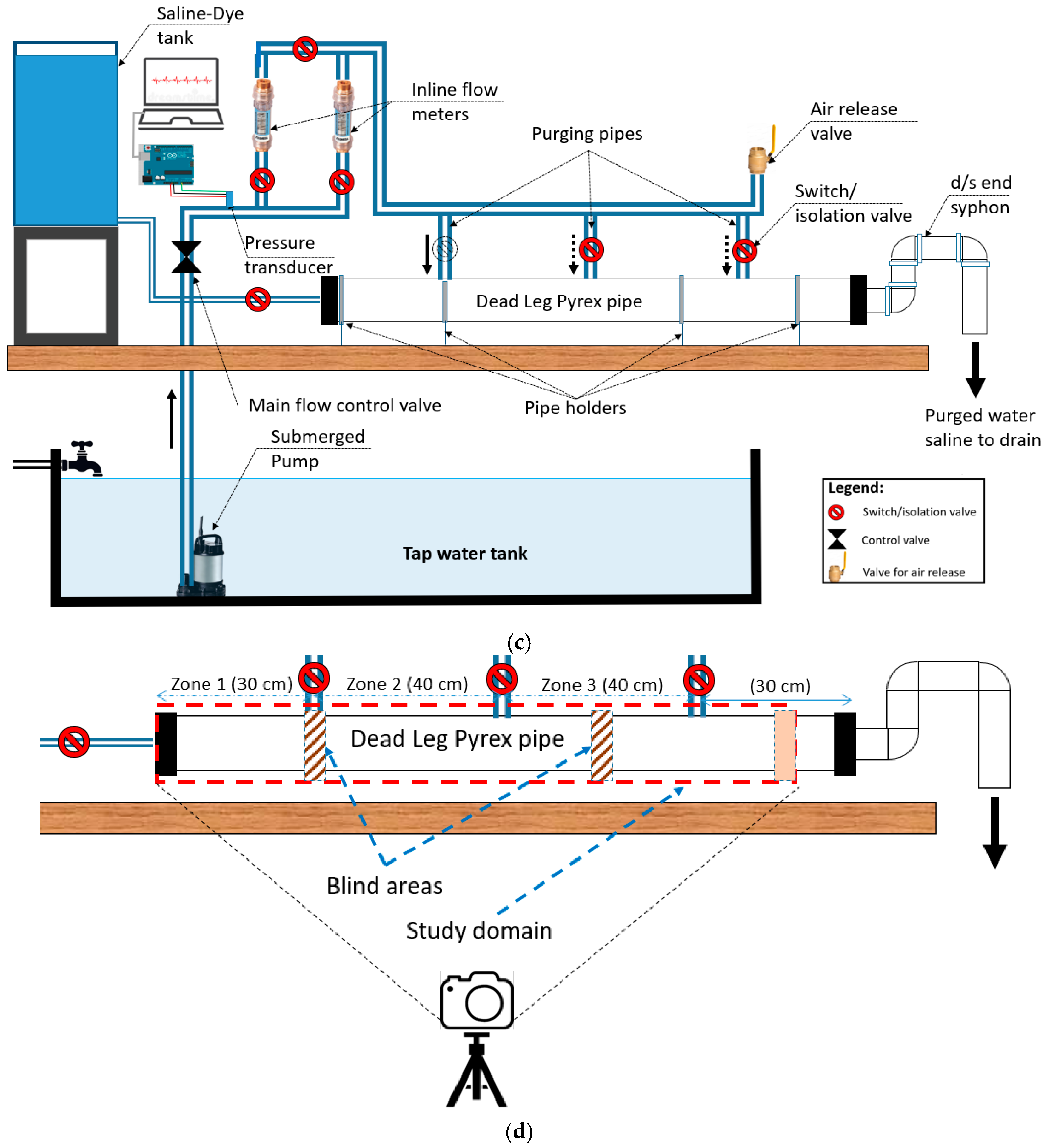
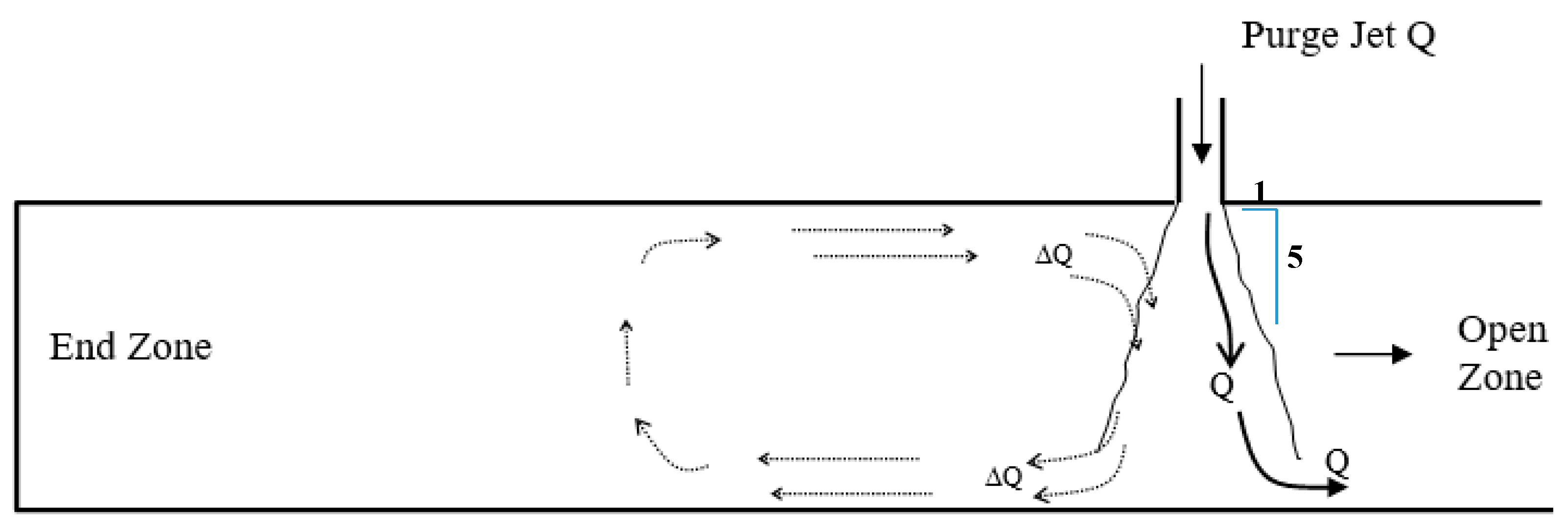
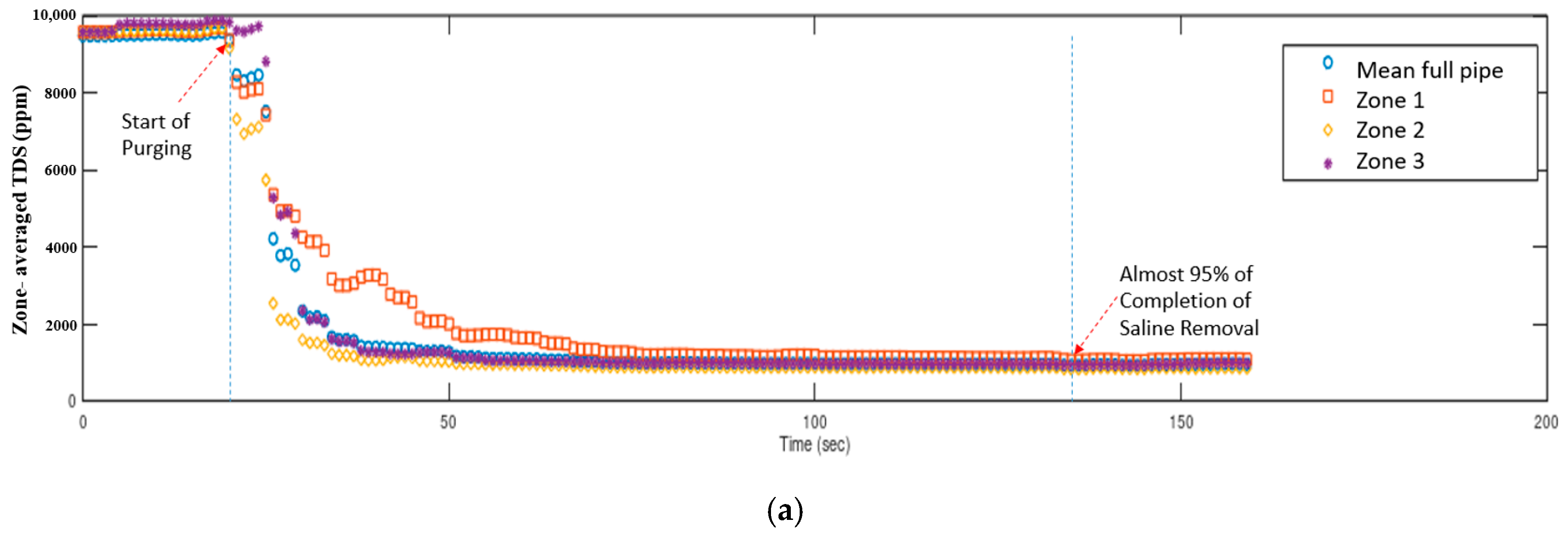
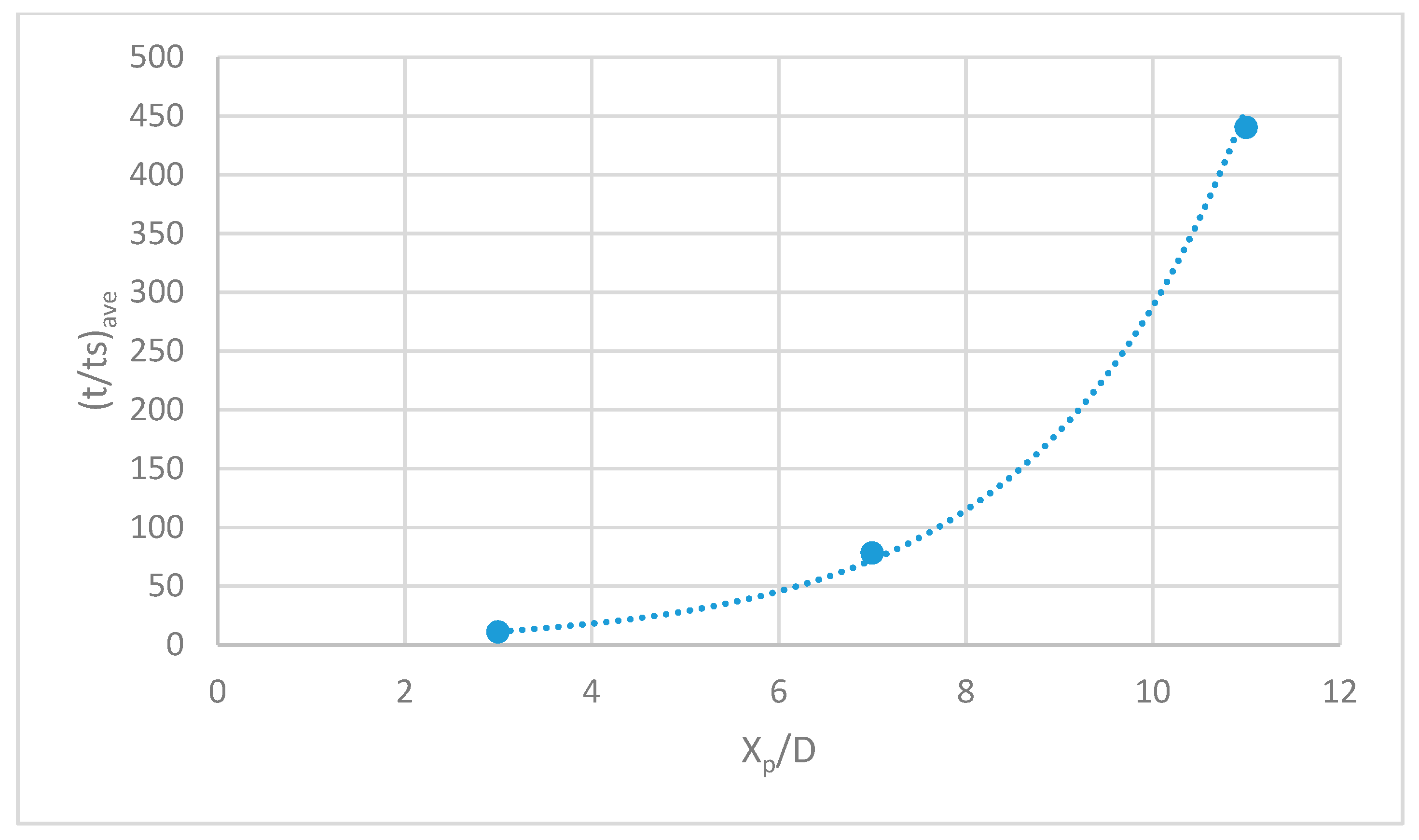
| Constant | a | b | c | d |
|---|---|---|---|---|
| Value | −4.39063 | 2.809594 | −0.7372 | 0.996435 |
| Run # | Run ID | Purging Flow(L/min) | Reynolds No (Re) | Purging Distance Ratio (Xp/D) | Spatial Reynolds No (Rex) | Purging Location | Initial Salinity of Purged Solution (ppm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1867 | 9600 | ||||||
| 1 | PPM1867Inj1Q1 | 60.8 | 12,902 | 3 | 38,706 | √ | √ | |||
| 2 | PPM1867Inj1Q2 | 10 | 2122 | 3 | 6366 | √ | √ | |||
| 3 | PPM1867Inj1Q3 | 10 | 2122 | 3 | 6366 | √ | √ | |||
| 4 | PPM1867Inj2Q1 | 56 | 11,884 | 7 | 83,188 | √ | √ | |||
| 5 | PPM1867Inj2Q2 | 46 | 9762 | 7 | 68,334 | √ | √ | |||
| 6 | PPM1867Inj2Q3 | 14 | 2971 | 7 | 20,797 | √ | √ | |||
| 7 | PPM1867Inj3Q1 | 60 | 12,732 | 11 | 140,052 | √ | √ | |||
| 8 | PPM1867Inj3Q2 | 58 | 12,308 | 11 | 135,388 | √ | √ | |||
| 9 | PPM1867Inj3Q3 | 46 | 9762 | 11 | 107,382 | √ | √ | |||
| 10 | PPM1867Inj3Q4 | 12 | 2546 | 11 | 28,006 | √ | √ | |||
| 11 | PPM9600Inj1Q1 | 59.5 | 12,626 | 3 | 37,878 | √ | √ | |||
| 12 | PPM9600Inj1Q2 | 59 | 12,520 | 3 | 37,560 | √ | √ | |||
| 13 | PPM9600Inj1Q3 | 54 | 11,459 | 3 | 34,377 | √ | √ | |||
| 14 | PPM9600Inj1Q4 | 10 | 2122 | 3 | 6366 | √ | √ | |||
| 15 | PPM9600Inj2Q1 | 60.5 | 12,838 | 7 | 89,866 | √ | √ | |||
| 16 | PPM9600Inj2Q2 | 49 | 10,398 | 7 | 72,786 | √ | √ | |||
| 17 | PPM9600Inj2Q3 | 36.5 | 7746 | 7 | 54,222 | √ | √ | |||
| 18 | PPM9600Inj2Q4 | 22 | 4669 | 7 | 32,683 | √ | √ | |||
| 19 | PPM9600Inj2Q5 | 16.5 | 3501 | 7 | 24,507 | √ | √ | |||
| 20 | PPM9600Inj3Q1 | 57 | 12,096 | 11 | 133,056 | √ | √ | |||
| 21 | PPM9600Inj3Q2 | 52.5 | 11,141 | 11 | 122,551 | √ | √ | |||
| 22 | PPM9600Inj3Q3 | 30 | 6366 | 11 | 70,026 | √ | √ | |||
| 23 | PPM9600Inj3Q4 | 27.5 | 5836 | 11 | 64,196 | √ | √ | |||
| 24 | PPM9600Inj3Q5 | 17 | 3608 | 11 | 39,688 | √ | √ | |||
| Digital Camera Model: | Sony RX100 Cyber-Shot |
|---|---|
| Camera Maximum Resolution: | 20.1 Mega Pixel |
| Camera Sensor: | BSI CMOS Sensor |
| Sensor size: | 1” |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgamal, M.; Farouk, M. Experimental Investigation of Purging Saline Solution from a Dead-End Water Pipe. Water 2019, 11, 994. https://doi.org/10.3390/w11050994
Elgamal M, Farouk M. Experimental Investigation of Purging Saline Solution from a Dead-End Water Pipe. Water. 2019; 11(5):994. https://doi.org/10.3390/w11050994
Chicago/Turabian StyleElgamal, Mohamed, and Mohamed Farouk. 2019. "Experimental Investigation of Purging Saline Solution from a Dead-End Water Pipe" Water 11, no. 5: 994. https://doi.org/10.3390/w11050994
APA StyleElgamal, M., & Farouk, M. (2019). Experimental Investigation of Purging Saline Solution from a Dead-End Water Pipe. Water, 11(5), 994. https://doi.org/10.3390/w11050994






