A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China
Abstract
1. Introduction
2. Methods
2.1. Multifractal Detrend Fluctuation Analysis (MFDFA)
2.1.1. MFDFA Algorithm
- Step 1: calculate the profile time series .where is the mean value of .
- Step 2: divide the profile time series into non-overlapping segments of equal length s. In segmentation, the total length n of time series data is often not an integer multiple of the segmentation length s, which causes the tail of the profile time series data to be discarded. To avoid this, the above segmentation process was repeated in reverse order of the profile time series data, and a total of segments were obtained.
- Step 3: Calculate the trend of each segment, and the detrended time series can be obtained by the following Equation:where and represent the segment time series and trend time series at each segment t, respectively.
- Step 4: Determine the variance by the following Equation:and then the qth-order fluctuation function of all segments are obtained by the following Equation:
- Step 5: There is a power-law relationship between the fluctuation function and scale s.
2.1.2. Multifractal Strength Analysis
2.2. Overlap Moving Window (OMW)
2.3. Ensemble Empirical Mode Decomposition (EEMD)
- Step 1: Add white noise to the original time series data .
- Step 2: Decompose the new time series data to many IMFs using the EMD method.
- Step 3: Repeat steps 1 and 2 with a different white noise each time.
- Step 4: Obtain the ensemble means of the corresponding IMFs of the decompositions as the final results.
2.4. The Modified OMW-EEMD-MFDFA Method
3. Experimental Analyses
4. Applications
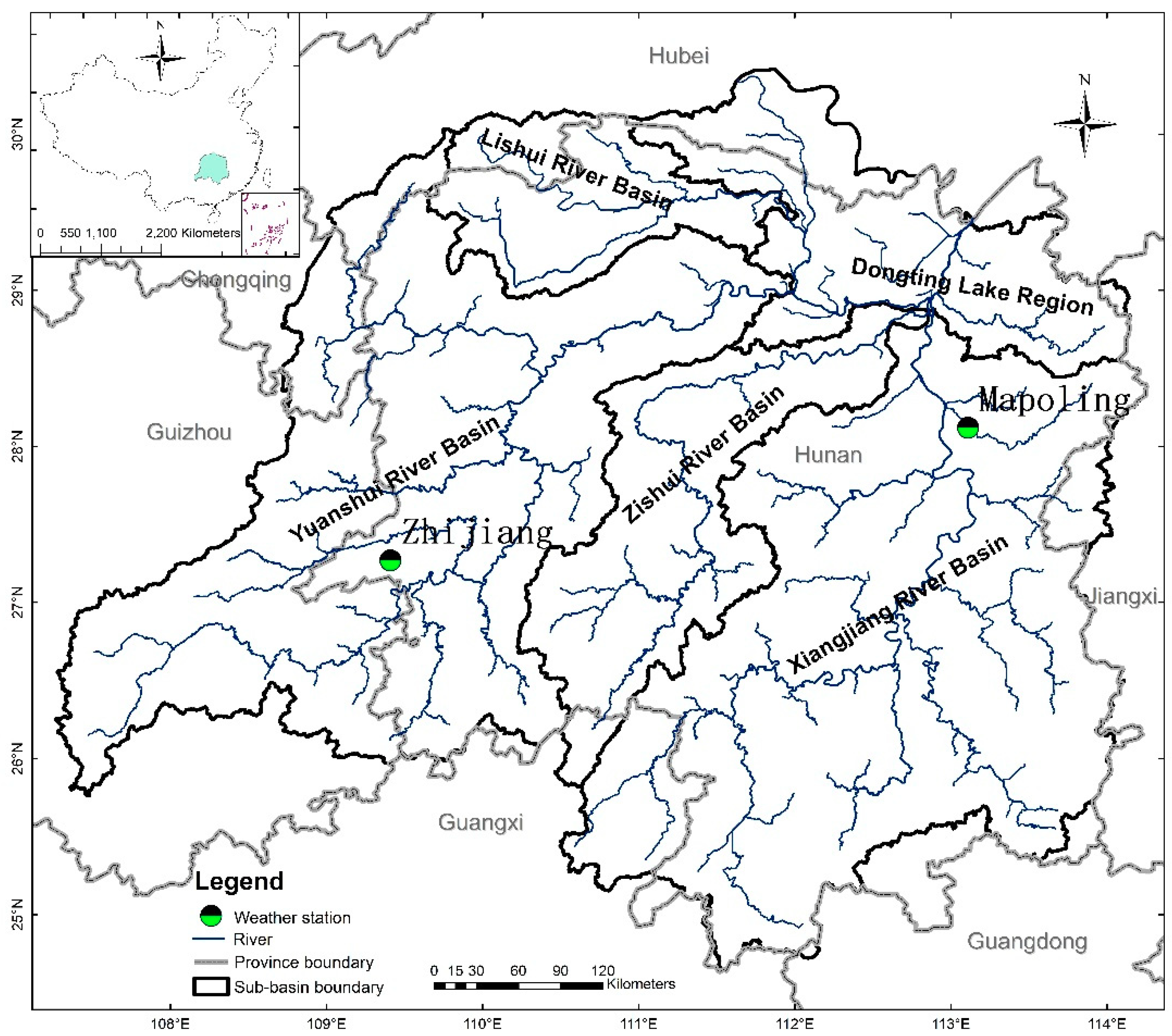
4.1. Data Collection and Preprocessing
4.1.1. Data Collection
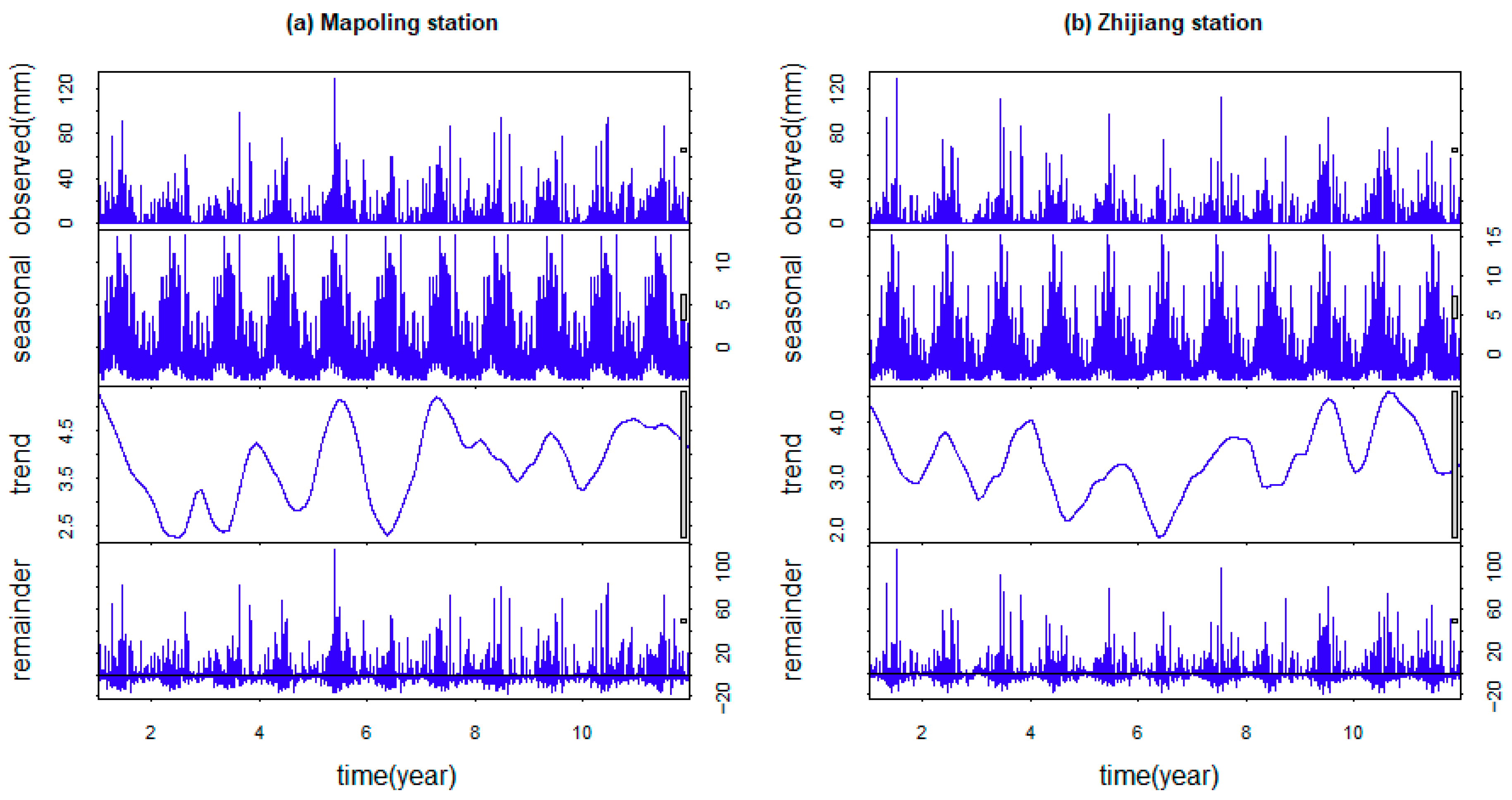
4.1.2. Data Preprocessing
4.2. Model Construction and Development
4.2.1. Segmentation using the OWM Algorithm
4.2.2. Detrending using the EEMD Method
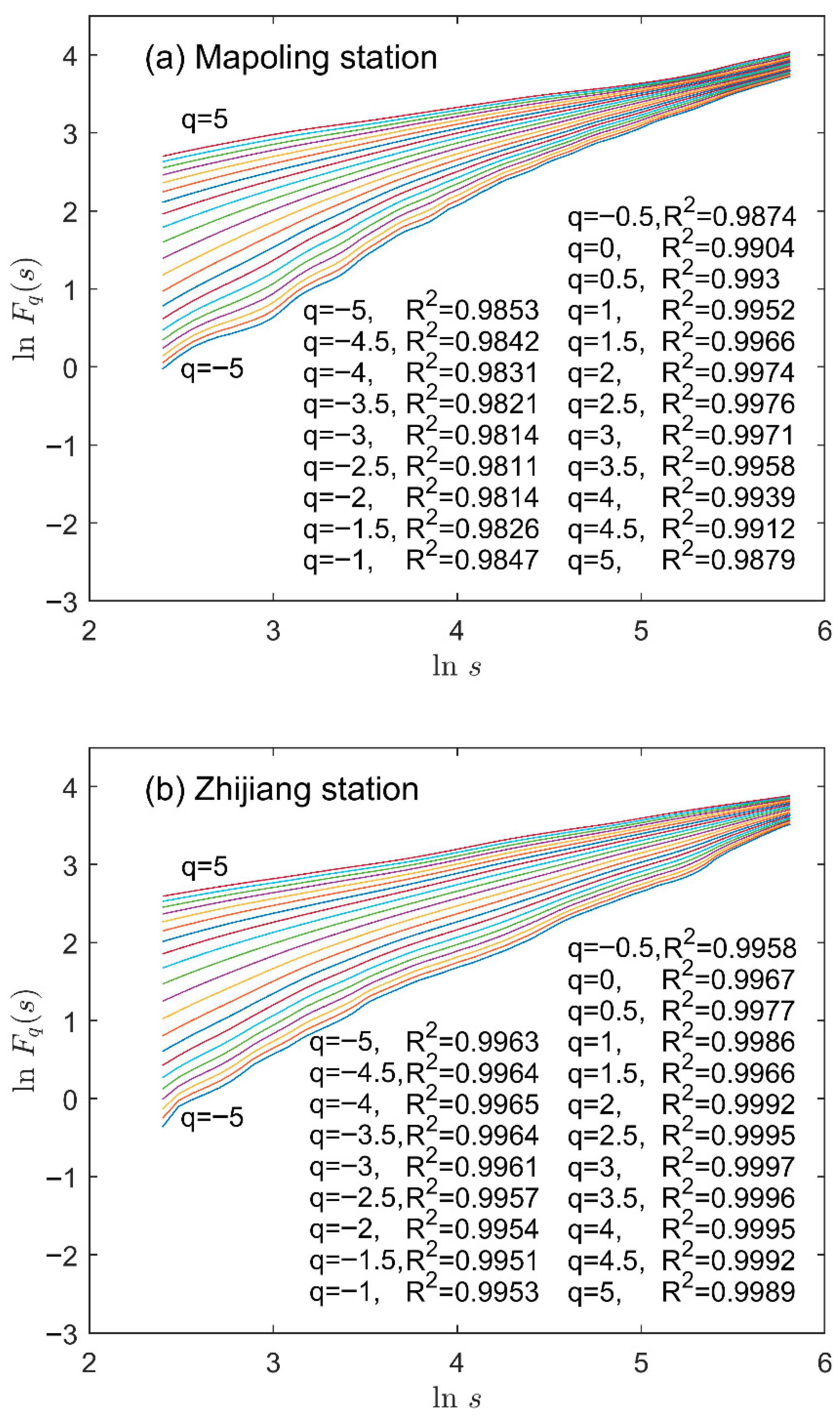
4.2.3. Selection of the Range of q
4.3. Results and Analysis
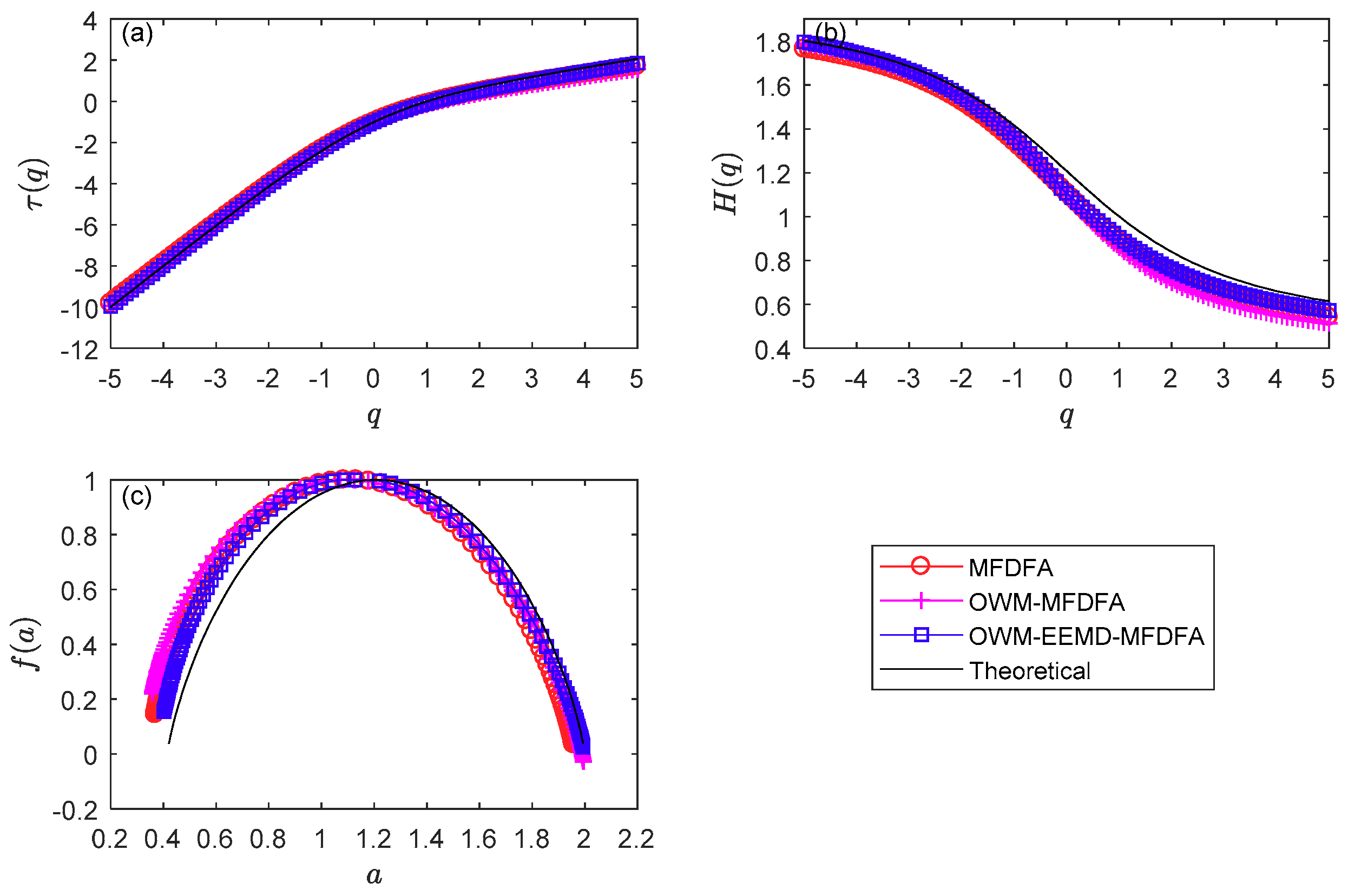
4.3.1. Multifractal Characteristics Analysis
4.3.2. Multifractal Source Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, K.-H.; Anagnostou, E.N. Investigation of the nonlinear hydrologic response to precipitation forcing in physically based land surface modeling. Can. J Remote Sens. 2004, 30, 706–716. [Google Scholar] [CrossRef]
- Li, E.H.; Mu, X.M.; Zhao, G.J.; Gao, P. Multifractal detrended fluctuation analysis of streamflow in the yellow river basin, china. Water 2015, 7, 1670–1686. [Google Scholar] [CrossRef]
- Kim, Z.; Singh, V.P. Assessment of environmental flow requirements by entropy-based multi-criteria decision. Water Resour. Manag. 2014, 28, 459–474. [Google Scholar] [CrossRef]
- Chen, P.-C.; Wang, Y.-H.; You, G.J.-Y.; Wei, C.-C. Comparison of methods for non-stationary hydrologic frequency analysis: Case study using annual maximum daily precipitation in Taiwan. J. Hydrol. 2017, 545, 197–211. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar]
- Lloyd, E.H.; Hurst, H.E.; Black, R.P.; Simaika, Y.M. Long-term storage: An experimental study. J. R. Stat. Soc. Ser. A 1966, 129, 591–593. [Google Scholar] [CrossRef]
- Lovejoy, S.; Mandelbrot, B. Fractal properties of rain and a fractal model. Tellus Ser. A 1985, 37, 209–232. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Multifractals and Rain, in New Uncertainty Concepts in Hydrology and Water Resources; Kunzewicz, Z.W., Ed.; Cambridge Univ: New York, NY, USA, 1995; pp. 61–103. [Google Scholar]
- Koscielny-Bunde, E.; Bunde, A.; Havlin, S.; Roman, H.E.; Goldreich, Y.; Schellnhuber, H.-J. Indication of a universal persistence law governing atmospheric variability. Phys. Rev. Lett. 1998, 81, 729–732. [Google Scholar] [CrossRef]
- Koscielny-Bunde, E.; Kantelhardt, J.W.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of river runoff records: Detrended fluctuation studies. J. Hydrol. 2006, 322, 120–137. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rybski, D.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. 2006, 111, D1. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, J.; Chen, Z.; Nie, Q.; Wei, C. Multifractal and long memory of humidity process in the tarim river basin. Stoch. Environ. Res. Risk A 2013, 28, 1383–1400. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. A multifractal walk down wall street. Sci. Am. 1999, 280, 70–73. [Google Scholar] [CrossRef]
- Livina, V.; Kizner, Z.; Braun, P.; Molnar, T.; Bunde, A.; Havlin, S. Temporal scaling comparison of real hydrological data and model runoff records. J. Hydrol. 2007, 336, 186–198. [Google Scholar] [CrossRef]
- Bunde, A.; Bogachev, M.I.; Lennartz, S. Precipitation and river flow: Long-term memory and predictability of extreme events. Geophys. Monogr. Ser. 2012, 196, 139–152. [Google Scholar]
- Yuan, X.H.; Ji, B.; Tian, H.; Huang, Y.H. Multiscaling analysis of monthly runoff series using improved mf-dfa approach. Water Resour. Manag. 2014, 28, 3891–3903. [Google Scholar] [CrossRef]
- Tessier, Y.; Lovejoy, S.; Hubert, P.; Schertzer, D.; Pecknold, S. Multifractal analysis and modeling of rainfall and river flows and scaling, causal transfer functions. J. Geophys. Res. Atmos. 1996, 101, 26427–26440. [Google Scholar] [CrossRef]
- Schmitt, F.; Vannitsem, S.; Barbosa, A. Modeling of rainfall time series using two-state renewal processes and multifractals. J. Geophys. Res. Atmos. 1998, 103, 23181–23193. [Google Scholar] [CrossRef]
- Olsson, J.; Singh, V.P.; Jinno, K. Effect of spatial averaging on temporal statistical and scaling properties of rainfall. J. Geophys. Res. Atmos. 1999, 104, 19117–19126. [Google Scholar] [CrossRef]
- Matsoukas, C.; Islam, S.; Rodriguez-Iturbe, I. Detrended fluctuation analysis of rainfall and streamflow time series. J. Geophys. Res.: Atmos. 2000, 105, 29165–29172. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climate change, the hurst phenomenon, and hydrological statistics. Hydrol. Sci. J. 2003, 48, 3–24. [Google Scholar] [CrossRef]
- Bhattacharya, R.N.; Waymire, G.E. The hurst effect under trends. J. App. Probab. 1983, 20, 649–662. [Google Scholar] [CrossRef]
- Künsch, H. Discrimination between monotonic trends and long-range dependence. J. App. Probab. 1986, 23, 1025–1030. [Google Scholar] [CrossRef]
- Mesa, O.J.; Poveda, G. The hurst effect: The scale of fluctuation approach. Water Resour. Res. 1993, 29, 3995–4002. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Rybski, D.; Bunde, A.; Havlin, S.; Kantelhardt, J.W.; Koscielny-Bunde, E. Detrended Fluctuation Studies of Long-Term Persistence and Multifractality of Precipitation and River Runoff Records; Springer: Berlin/Heidelberg, Germany, 2011; pp. 216–248. [Google Scholar]
- Avila, F.B.; Dong, S.Y.; Menang, K.P.; Rajczak, J.; Renom, M.; Donat, M.G.; Alexander, L.V. Systematic investigation of gridding-related scaling effects on annual statistics of daily temperature and precipitation maxima: A case study for south-east australia. Weather Clim. Extreme 2015, 9, 6–16. [Google Scholar] [CrossRef]
- de Lima, M.I.P.; de Lima, J.L.M.P. Investigating the multifractality of point precipitation in the madeira archipelago. Nonlinear Process. Geophys. 2009, 16, 299–311. [Google Scholar] [CrossRef]
- Garcia-Marin, A.P.; Jimenez-Hornero, F.J.; Ayuso, J.L. Applying multifractality and the self-organized criticality theory to describe the temporal rainfall regimes in andalusia (southern spain). Hydrol. Process. 2008, 22, 295–308. [Google Scholar] [CrossRef]
- Gemmer, M.; Fischer, T.; Jiang, T.; Su, B.D.; Liu, L.L. Trends in precipitation extremes in the zhujiang river basin, south china. J. Clim. 2011, 24, 750–761. [Google Scholar] [CrossRef]
- Liu, Y.H.; Zhang, K.X.; Zhang, W.C.; Shao, Y.H.; Pei, H.Q.; Feng, J.M. Multifractal analysis of 1-min summer rainfall time series from a monsoonal watershed in eastern china. Theor. Appl. Climatol. 2013, 111, 37–50. [Google Scholar]
- Rodriguez, R.; Casas, M.C.; Redano, A. Multifractal analysis of the rainfall time distribution on the metropolitan area of barcelona (spain). Meteorol. Atmos. Phys. 2013, 121, 181–187. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Fisher, A.J.; Calvet, L.E. A Multifractal Model of Asset Returns; Cowles Foundation for Research in Economics, Yale University: New Haven, CT, USA, 1997. [Google Scholar]
- Kantelhardt, J.W.; Rybski, D.; Zschiegner, S.A.; Braun, P.; Koscielny-Bunde, E.; Livina, V.; Havlin, S.; Bunde, A. Multifractality of river runoff and precipitation: Comparison of fluctuation analysis and wavelet methods. Phys. A Stat. Mech. Appl. 2003, 330, 240–245. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Chen, Y.Q.D.; Yu, Z.G. Multifractal detrended fluctuation analysis of streamflow series of the yangtze river basin, china. Hydrol. Process. 2008, 22, 4997–5003. [Google Scholar] [CrossRef]
- Zhou, Y.; Leung, Y. Multifractal temporally weighted detrended fluctuation analysis and its application in the analysis of scaling behavior in temperature series. J. Stat. Mech. Theory Exp. 2010, 2010, P0621. [Google Scholar] [CrossRef]
- Qian, X.Y.; Gu, G.F.; Zhou, W.X. Modified detrended fluctuation analysis based on empirical mode decomposition for the characterization of anti-persistent processes. Physica A 2011, 390, 4388–4395. [Google Scholar] [CrossRef][Green Version]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 01, 1–41. [Google Scholar] [CrossRef]
- Movahed, M.S.; Jafari, G.R.; Ghasemi, F.; Rahvar, S.; Tabar, M.R.R. Multifractal detrended fluctuation analysis of sunspot time series. J. Stat. Mech. Theory Exp. 2006, 2006, P02003. [Google Scholar] [CrossRef]
- Lopez, J.L.; Contreras, J.G. Performance of multifractal detrended fluctuation analysis on short time series. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 022918. [Google Scholar] [CrossRef]
- Sun, X.; Chen, H.; Wu, Z.; Yuan, Y. Multifractal analysis of hang seng index in hong kong stock market. Phys. A Stat. Mech. Appl. 2001, 291, 553–562. [Google Scholar] [CrossRef]
- Yu, S.; Stefan, T.; Klaus, E. Multifractal spectra as a measure of complexity in human posture. Fractals 2002, 10, 103–116. [Google Scholar]
- Kalamaras, N.; Tzanis, C.; Deligiorgi, D.; Philippopoulos, K.; Koutsogiannis, I. Distribution of air temperature multifractal characteristics over greece. Atmosphere-Basel 2019, 10, 45. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes. J. Geophys. Res. 1987, 92. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S.; Schmitt, F.; Chigirinskaya, Y.; Marsan, D. Multifractal cascade dynamics and turbulent intermittency. Fractals 1997, 5, 427–471. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424–1427. [Google Scholar] [CrossRef]
- Cleveland, R.; Cleveland, W.; McRae, J.; Terpenning, I. Stl: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–33. [Google Scholar]
- Chianca, C.; Ticona, A.; Penna, T. Fourier-detrended fluctuation analysis. Phys. A 2005, 357, 447–454. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Baranowski, P.; Krzyszczak, J.; Slawinski, C.; Hoffmann, H.; Kozyra, J.; Nierobca, A.; Siwek, K.; Gluza, A. Multifractal analysis of meteorological time series to assess climate impacts. Clim. Res. 2015, 65, 39–52. [Google Scholar] [CrossRef]

| MFDFA | OMW-MFDFA | OMW-EEMD-MFDFA | ||||
|---|---|---|---|---|---|---|
| 10 | 0.2955 | 1.0880 | 0.8365 | 5.7932 | 0.2006 | 0.6512 |
| 11 | 0.2578 | 1.0443 | 0.6661 | 4.6590 | 0.1139 | 0.3167 |
| 12 | 0.2335 | 0.9563 | 0.5571 | 3.9393 | 0.0774 | 0.2651 |
| 13 | 0.2178 | 0.9199 | 0.4875 | 3.4801 | 0.0695 | 0.1942 |
| 14 | 0.2112 | 0.9012 | 0.4428 | 3.1856 | 0.0616 | 0.1816 |
| Station | H(2) | B | |||
|---|---|---|---|---|---|
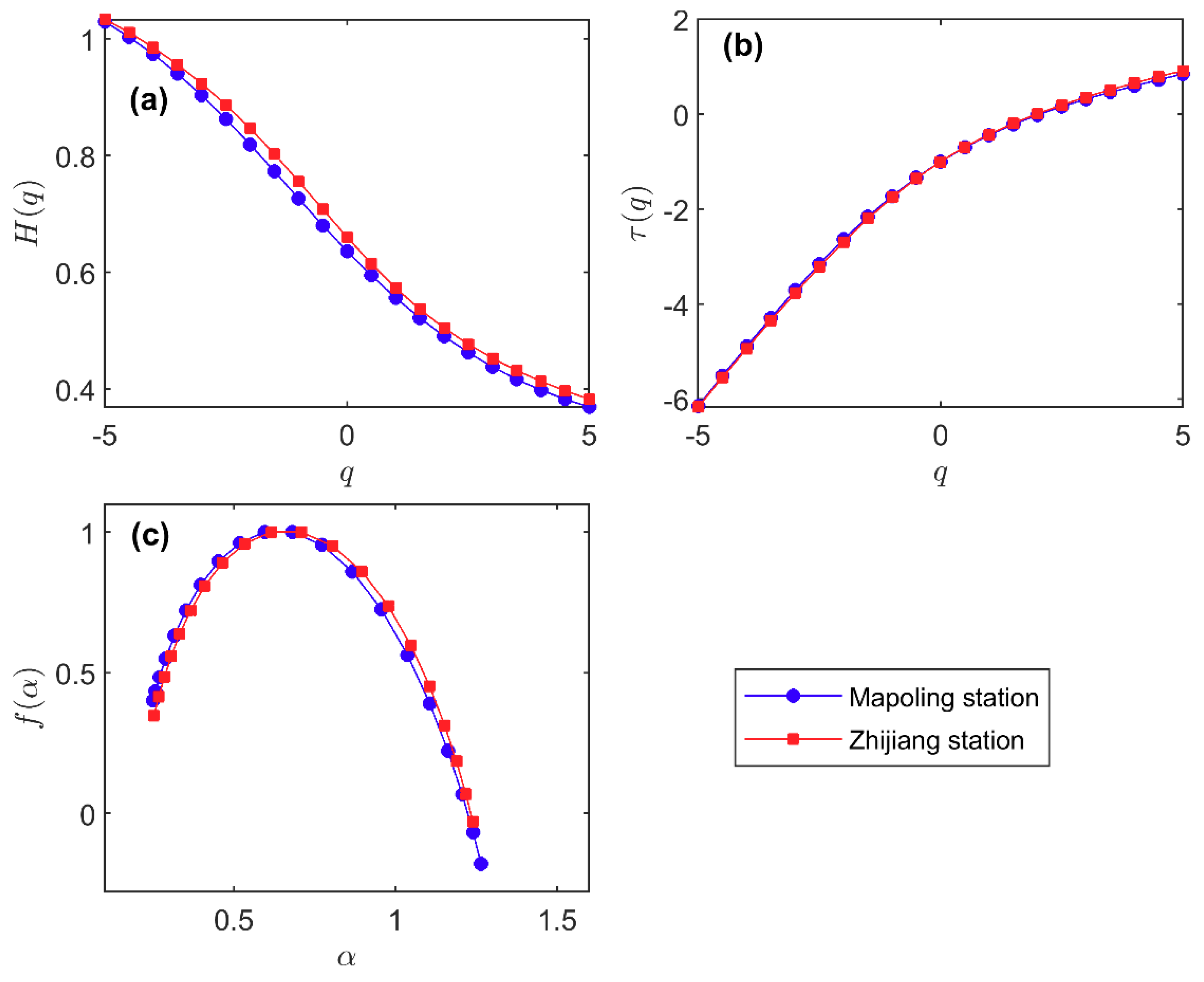
| Mapoling station | 0.5016 | 0.6599 | 1.0154 | 0.5798 | 0.4731 |
| Zhijiang station | 0.5046 | 0.6510 | 0.9870 | 0.3768 | 0.4695 |
| Station | ||||||
|---|---|---|---|---|---|---|
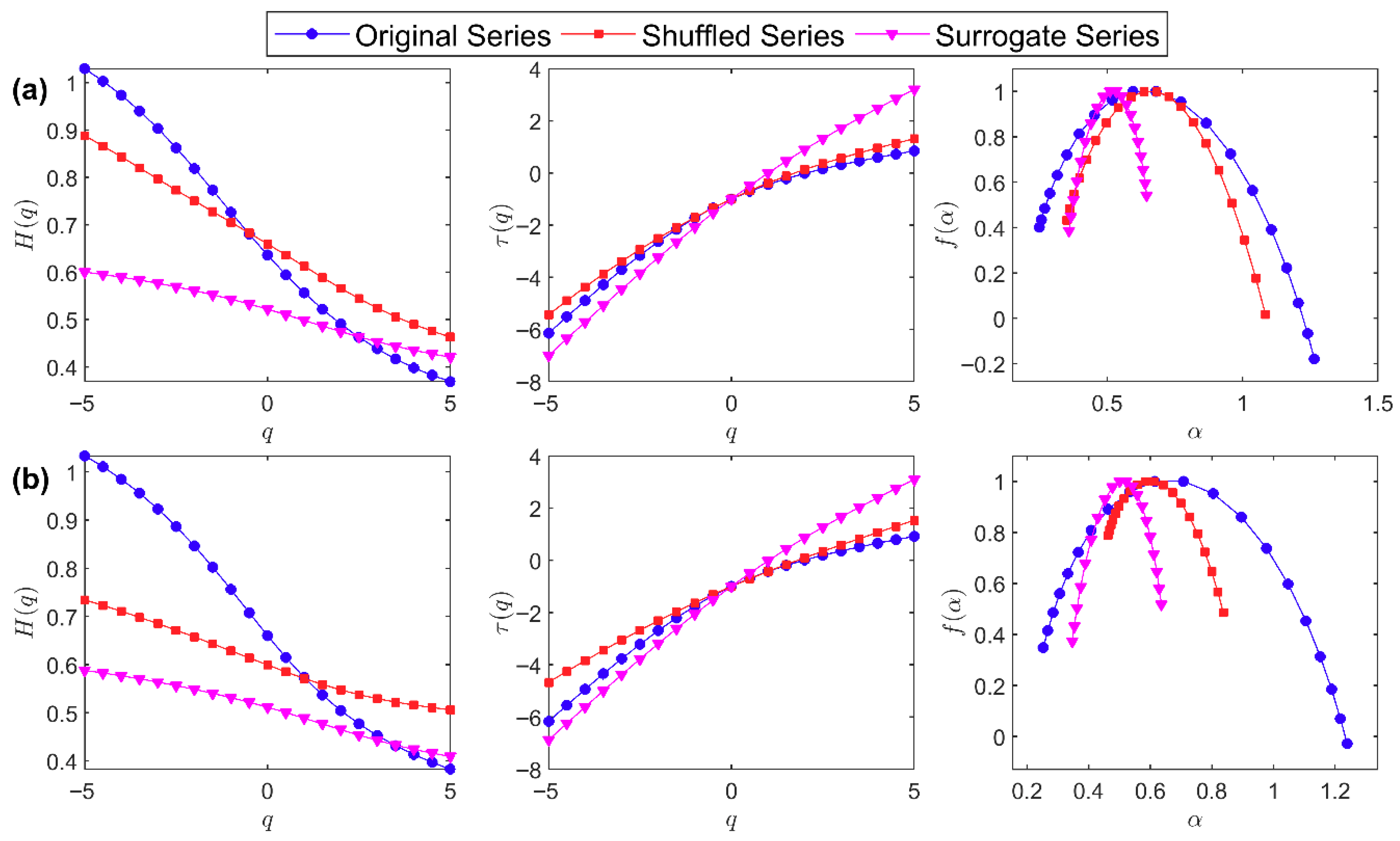
| Original | Shuffled | Surrogate | Original | Shuffled | Surrogate | |
| Mapoling station | 0.6599 | 0.4248 | 0.1794 | 1.0154 | 0.7349 | 0.2868 |
| Zhijiang station | 0.6510 | 0.2282 | 0.1789 | 0.9870 | 0.3735 | 0.2898 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, G.; Qiu, L.; Zhang, B.; Sun, Y.; Gui, Z.; Zhang, Q. A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China. Water 2019, 11, 891. https://doi.org/10.3390/w11050891
Zhang X, Zhang G, Qiu L, Zhang B, Sun Y, Gui Z, Zhang Q. A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China. Water. 2019; 11(5):891. https://doi.org/10.3390/w11050891
Chicago/Turabian StyleZhang, Xike, Gui Zhang, Luo Qiu, Bo Zhang, Yurong Sun, Zifan Gui, and Qiuwen Zhang. 2019. "A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China" Water 11, no. 5: 891. https://doi.org/10.3390/w11050891
APA StyleZhang, X., Zhang, G., Qiu, L., Zhang, B., Sun, Y., Gui, Z., & Zhang, Q. (2019). A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China. Water, 11(5), 891. https://doi.org/10.3390/w11050891




