Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria
Abstract
1. Introduction
- Factor Prioritization (FP): ranking the factor in terms of their relative sensitivity;
- Factor Fixing (FF), or screening: determining the factors are influential or not to the output uncertainty;
- Factor Mapping (FM): given specific output values or ranges, locating the regions in the factor space that produces them.
- In this study, we only focus on ranking and screening.
2. Global Sensitivity Analysis Methods
2.1. Classification of Global Sensitivity Analysis (GSA) Methods
2.1.1. Generalized (Regionalized) Sensitivity Analysis, and Other Density-Based Methods
2.1.2. Variance-Based Methods
2.1.3. Globally Aggregated Measure of Local Sensitivities (GLS) Method
2.2. Use of Meta-Modelling to Reduce Running Times of Global Sensitivity Analysis (GSA) Methods
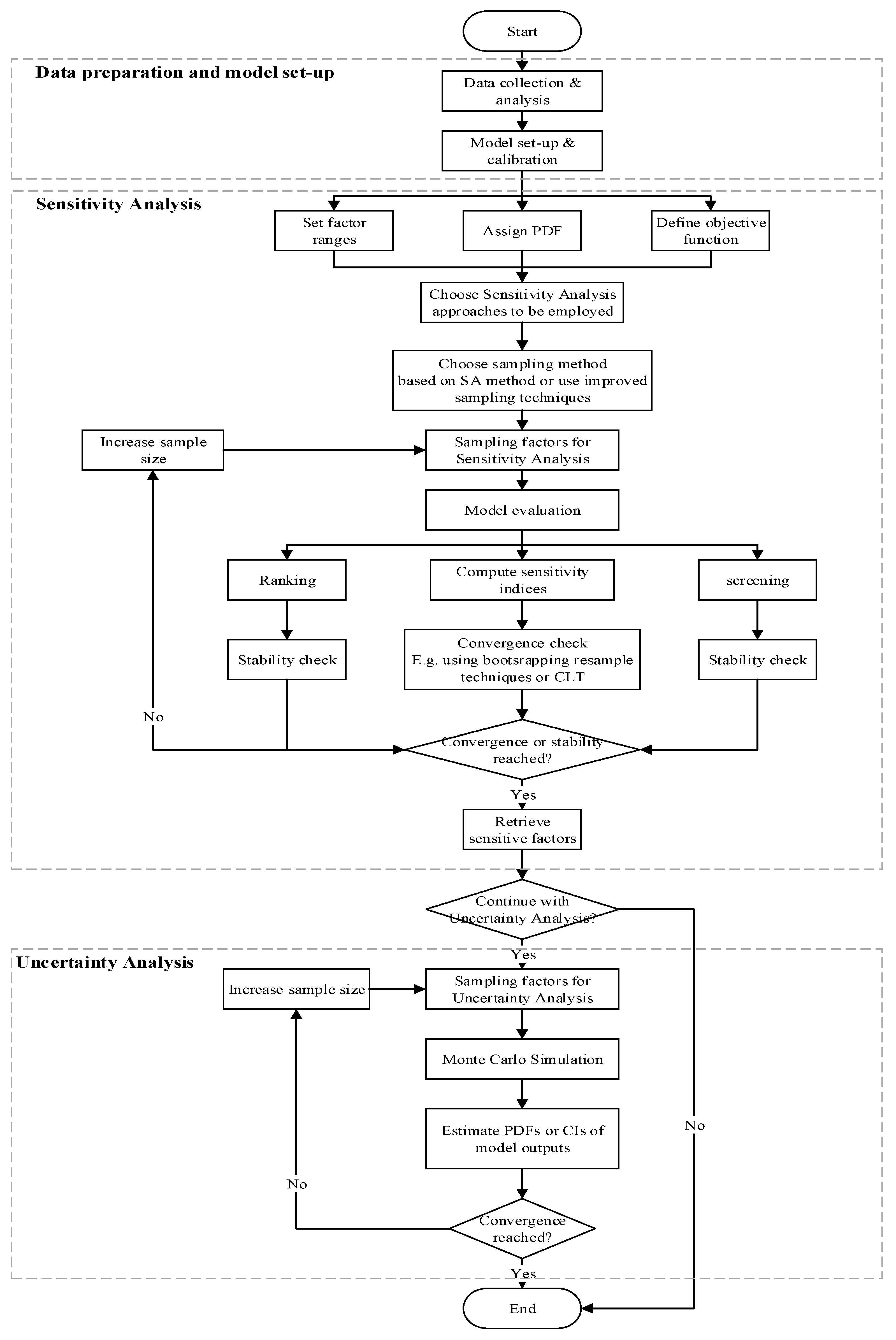
3. Methodology and Experimental Set-Up
3.1. Methodology for Evaluating SA Methods
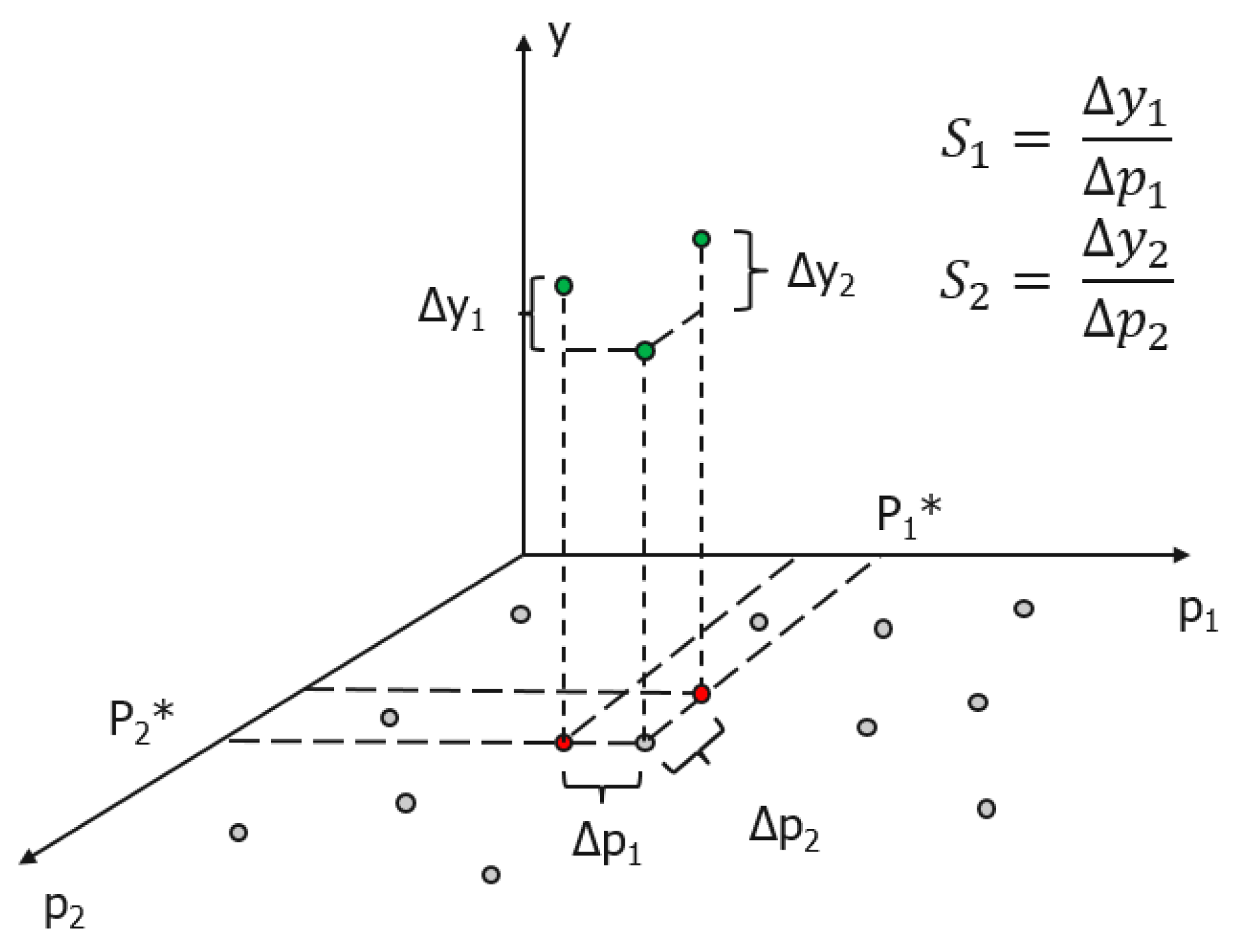
3.1.1. The Three Evaluation Criteria
3.1.2. Evaluation of Effectiveness
3.1.3. Evaluation of Efficiency
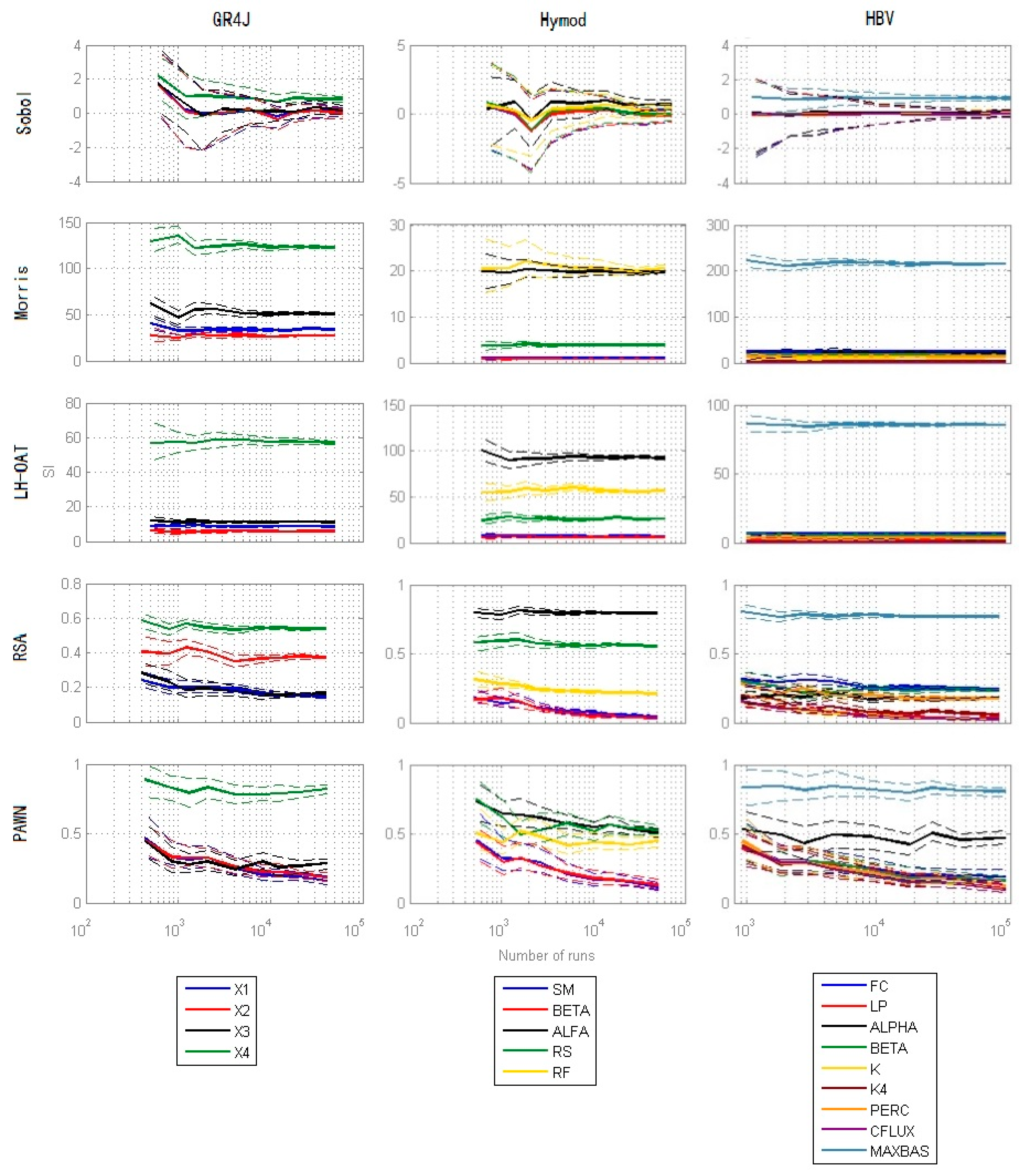
3.1.4. Evaluation of Convergence
- Generate N samples of parameters as the base sample set.
- The N base samples are re-sampled B times with replacement, and for each replica, the Sensitivity Indices are computed, producing B Sensitivity Indices to construct the distribution of them.
3.2. Case Study
3.3. Test Model
3.4. Experimental Set-Up
4. Results
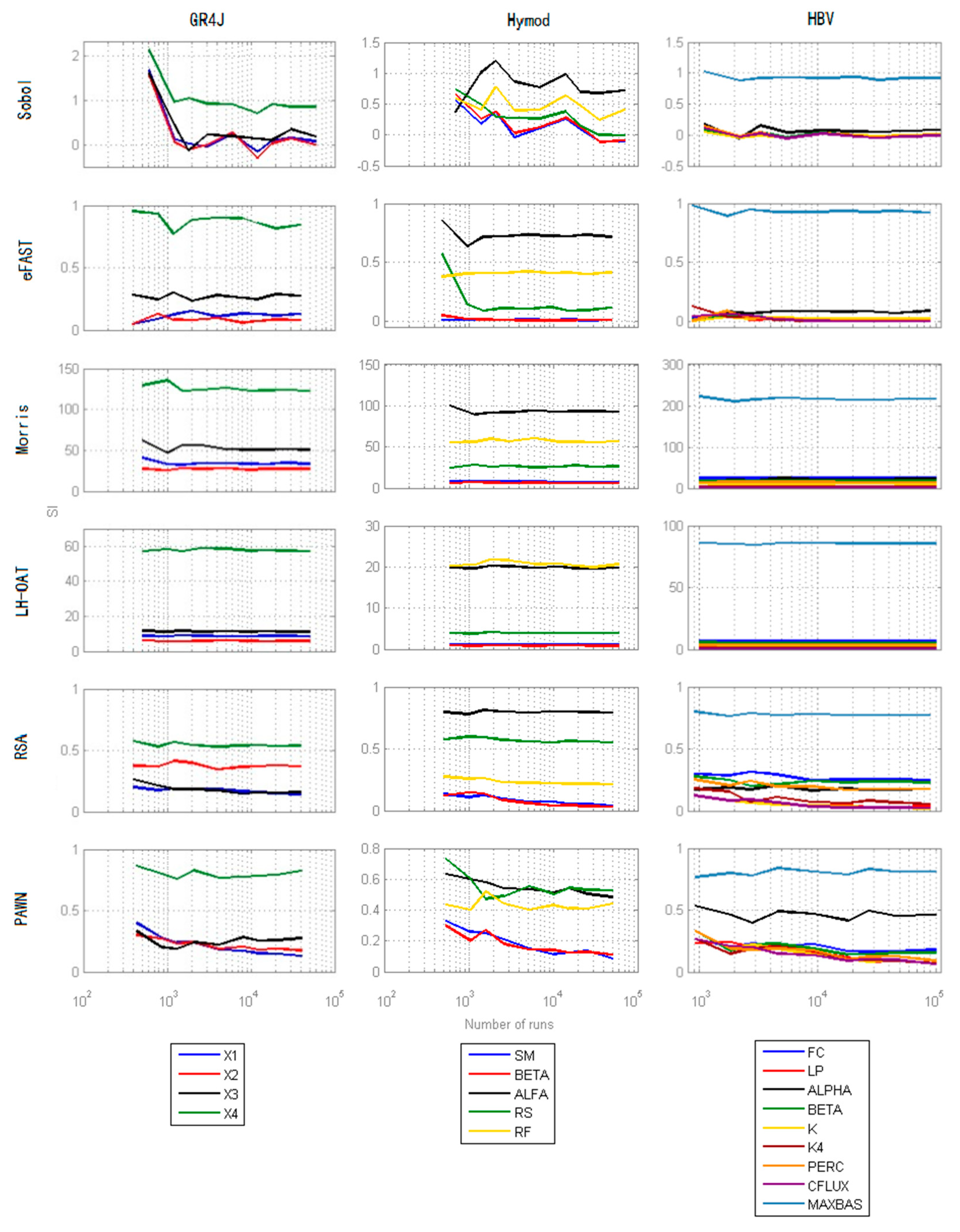
4.1. Preliminary Assessment of Sensitivity
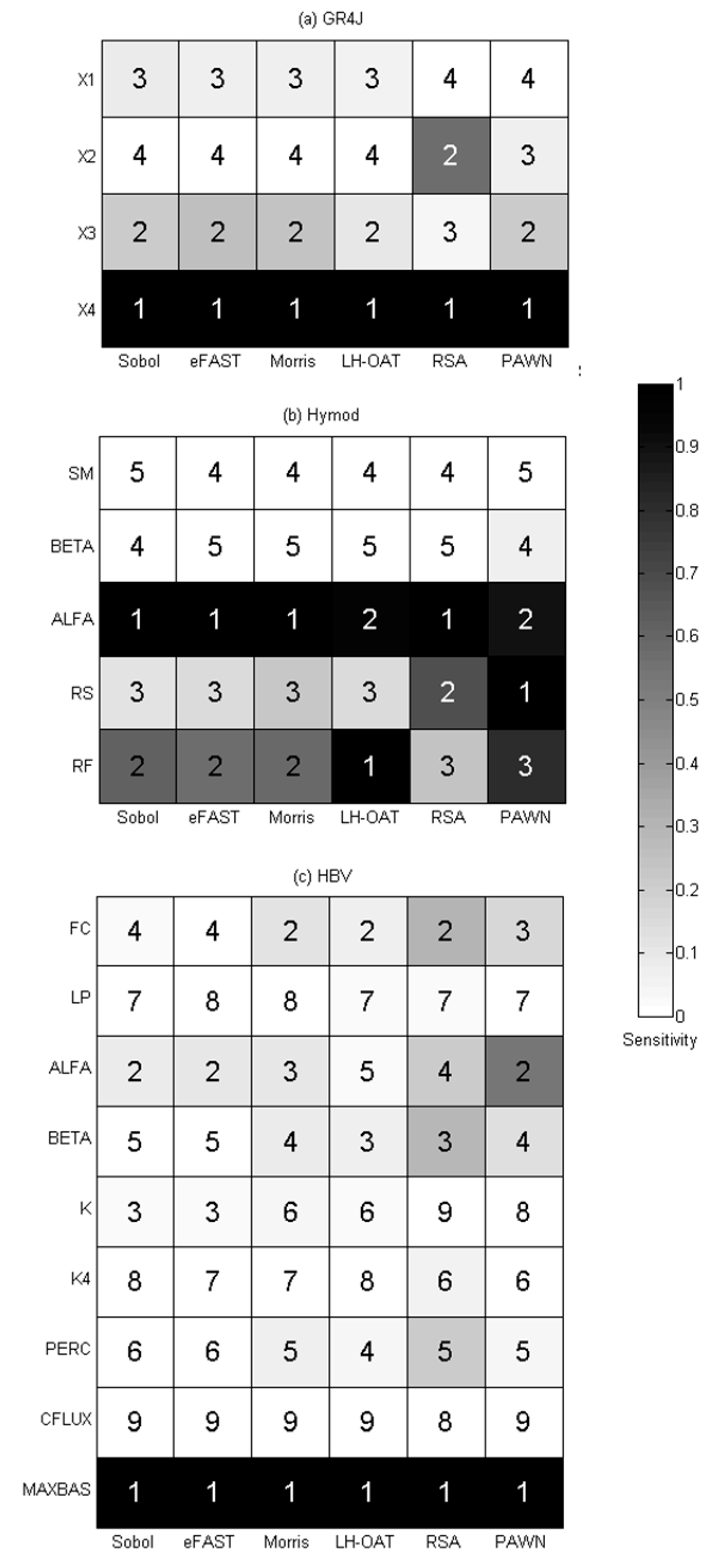
4.2. Effectiveness
- all the methods identify the same set of sensitive parameters (X3 and X4 for GR4J, ALFA, RS, and RF for Hymod, MAXBAS for HBV);
- for less influential or non-influential parameters, different methods show relatively large discrepancy in results;
- the results of Sobol and eFAST are close, and it is also so for Morris and LH-OAT, RSA and PAWN, which indicates that the methods of the same category have similar results. This is due to the reason that both Sobol and FAST are variance-based methods, they all calculate the contribution of the variance to the output. Both Morris and LH-OAT compute the first-order partial derivatives of the output. Similarly, RSA and PAWN use empirical CDFs and KS statistics to quantify the sensitivity. These groups of methods share the same principle;
- comparatively, the results of RSA and PAWN are always quite different from other methods. There may be two reasons: firstly, the generation of empirical CDFs may be inaccurate; secondly, the use of KS statistics to compute Sensitivity Index in both methods may also bring inaccuracy into the results (sensitivity to sampling) because KS statistics takes into account only the maximum difference between CDFs;
- ranking of parameters for the three models by different SA methods has many differences, but they are quite close in identifying sensitive and insensitive parameters, which means they are effective in screening.
4.3. Efficiency
4.4. Convergence
5. Discussion and Recommendations
5.1. Different Methods Are Based on Different Concepts
5.2. Recommendations for Choosing Sensitivity Analysis (SA) Methods
- For simple conceptual hydrological models (not requiring much time for running them multiple times), variance-based methods as Sobol and eFAST are recommended, because they have a strong theoretical background and provide more insight into sensitivity.
- For more complex hydrological or hydraulic models that need considerable time to run, GLS methods can be used, since they are more efficient.
- For distributed models, methods with simple concepts and sampling techniques are more suitable, such as RSA and LH-OAT.
- For very complex models, e.g., 2D (or even 3D) models, like flood inundation models, or high resolution groundwater models of large aquifers, the Local SA instead of Global SA can be used [52], or LSA at a selected limited number of points in the factor (sub)space, for a reduced number of factors.
- In situations when only relative sensitivity of the factors is needed, rather than the exact value of SI, it is advisable to aim only at determining ranking or screening of SA, which needs significantly less time than the calculation of global SI.
- If time allows, it is recommended, however, to employ several different SA methods rather than using only one method.
5.3. Practical Framework, with the Focus on Performance Analysis
5.4. Limitations
- The models used in this study are only conceptual rainfall-runoff models with similar structures, so the results may be different for other types of models.
- Evaluations of SA methods are still qualitative, so to evaluate each aspect of SA methods some more rigorous quantitative standard should be set. For example, when evaluating convergence, a threshold of the CI width should be defined for reaching convergence. Quantitative assessment will strengthen the conclusions of the comparisons.
- Only one performance metric (RMSE) is used in this study. Parameters that is not sensitive to RMSE may affect other metrics. Various performance metrics which capture different features of model behavior should be used in the future study.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cacuci, D.G.; Ionescu-Bujor, M. A comparative review of sensitivity and uncertainty analysis of large-scale systems—II: Statistical methods. Nucl. Sci. Eng. 2004, 147, 204–217. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J. Ignorance is bliss: Or seven reasons not to use uncertainty analysis. Water Resour. Res. 2006, 42, 1–8. [Google Scholar] [CrossRef]
- Tong, C. Refinement strategies for stratified sampling methods. Reliab. Eng. Syst. Saf. 2006, 91, 1257–1265. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The primer; Wiley Online Library: Chichester, UK, 2008; ISBN 978-0-470-05997-5. [Google Scholar]
- Bastin, L.; Cornford, D.; Jones, R.; Heuvelink, G.B.M.; Pebesma, E.; Stasch, C.; Nativi, S.; Mazzetti, P.; Williams, M. Managing uncertainty in integrated environmental modelling: The UncertWeb framework. Environ. Model. Softw. 2013, 39, 116–134. [Google Scholar] [CrossRef]
- Lemieux, C. Monte Carlo and Quasi-Monte Carlo Sampling; Springer: New York, NY, USA, 2009; ISBN 978-0-387-78164-8. [Google Scholar]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 1. Theory. Water Resour. Res. 2016, 52, 423–439. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 2. Application. Water Resour. Res. 2016, 52, 440–455. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Tang, Y.; Reed, P.; Van Werkhoven, K.; Wagener, T. Advancing the identification and evaluation of distributed rainfall-runoff models using global sensitivity analysis. Water Resour. Res. 2007, 43, 1–14. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J.; Ratto, M.; Matgen, P. Multi-method global sensitivity analysis of flood inundation models. Adv. Water Resour. 2008, 31, 1–14. [Google Scholar] [CrossRef]
- Gan, Y.; Duan, Q.; Gong, W.; Tong, C.; Sun, Y.; Chu, W.; Ye, A.; Miao, C.; Di, Z. A comprehensive evaluation of various sensitivity analysis methods: A case study with a hydrological model. Environ. Model. Softw. 2014, 51, 269–285. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. What do we mean by sensitivity analysis? The need for comprehensive characterization of “global” sensitivity in Earth and Environmental systems models. Water Resour. Res. 2015, 51, 3070–3092. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Yang, J. Convergence and uncertainty analyses in Monte-Carlo based sensitivity analysis. Environ. Model. Softw. 2011, 26, 444–457. [Google Scholar] [CrossRef]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- Baroni, G.; Tarantola, S. A General Probabilistic Framework for uncertainty and global sensitivity analysis of deterministic models: A hydrological case study. Environ. Model. Softw. 2014, 51, 26–34. [Google Scholar] [CrossRef]
- Spear, R.C.; Hornberger, G.M. Eutrophication in peel inlet—II. Identification of critical uncertainties via generalized sensitivity analysis. Water Resour. Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Hornberger, G.M.; Spear, R.C. Approach to the preliminary analysis of environmental systems. J. Environ. Mgmt. 1981, 12, 7–18. [Google Scholar]
- Whitehead, P.; Young, P.C. Water quality in river systems: Monte Carlo analysis. Water Resour. Res. 1979, 15, 451–459. [Google Scholar] [CrossRef]
- Spear, R.C. The application of Kolmogorov–Rényi statistics to problems of parameter uncertainty in systems design. Int. J. Control 1970, 11, 771–778. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Ghassemi, F.; Dietrich, C.R. Calibration and reliability of an aquifer system model using generalized sensitivity analysis. In Proceedings of the ModelCARE 90, The Hague, The Netherlands, 3–6 September 1990; pp. 43–51. [Google Scholar]
- Wagener, T.; Boyle, D.P.; Lees, M.J.; Wheater, H.S.; Gupta, H.V.; Sorooshian, S. A framework for development and application of hydrological models. Hydrol. Earth Syst. Sci. 2001, 5, 13–26. [Google Scholar] [CrossRef]
- Park, C.; Ahn, K. A new approach for measuring uncertainty importance and distributional sensitivity in probablistic safety assessment. Reliab. Eng. Syst. Saf. 1994, 46, 253–261. [Google Scholar] [CrossRef]
- Krykacz-Hausmann, B. Epistemic sensitivity analysis based on the concept of entropy. In Proceedings of the International Symposium on Sensitivity Analysis of Model Output, Madrid, Spain, 18–20 June 2001; pp. 31–35. [Google Scholar]
- Liu, H.; Sudjianto, A.; Chen, W. Relative entropy based method for probabilistic sensitivity analysis in engineering design. J. Mech. Des. 2006, 128, 326–336. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Plischke, E.; Borgonovo, E.; Smith, C.L. Global sensitivity measures from given data. Eur. J. Oper. Res. 2013, 226, 536–550. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.K. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Saltelli, A.; Bolado, R. An alternative way to compute Fourier amplitude sensitivity test (FAST). Comput. Stat. Data Anal. 1998, 26, 445–460. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Sirinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Radial Basis Functions, Multi-Variable Functional Interpolation and Adaptive Networks; Royal Signals and Radar Establishment Malvern: London, UK, 1988. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Advanced Lectures on Machine Learning; Bousquet, O., von Luxburg, U., Ratsch, G., Eds.; Springer: Berlin, Germany, 2004; pp. 63–71. ISBN 3-540-23122-6. [Google Scholar]
- Gramacy, R.B.; Lee, H.K.H. Bayesian treed Gaussian process models with an application to computer modeling. J. Am. Stat. Assoc. 2008, 103, 1119–1130. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard error, Confidence Intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 45–77. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Shrestha, D.L. A novel method to estimate model uncertainty using machine learning techniques. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Allen, R.G. Crop evapotranspiration-Guidelines for computing crop water requirements. Irrig. Drain 1998, 56, 300. [Google Scholar]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Boyle, D. Multicriteria Calibration of Hydrological Models. Ph.D. Thesis, Department of Hydrology and Water Resources, University of Arizona, Tucson, AZ, USA, 2001. [Google Scholar]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; Department of Water Resources Engineering, Lund Institute of Technology, University of Lund: Norrköping, Sweden, 1976. [Google Scholar]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- The James Hutton Institute. The HBV Model. Available online: http://macaulay.webarchive.hutton.ac.uk/hydalp/private/demonstrator_v2.0/models/hbv.html#History (accessed on 15 May 2019).
- Pianosi, F.; Sarrazin, F.; Wagener, T. A MATLAB toolbox for global sensitivity analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Calibration of Groundwater Models, with Analysis of Data, Sensitivities, Prediction, and Uncertainty; John Wiley: New York, NY, USA, 2007. [Google Scholar]


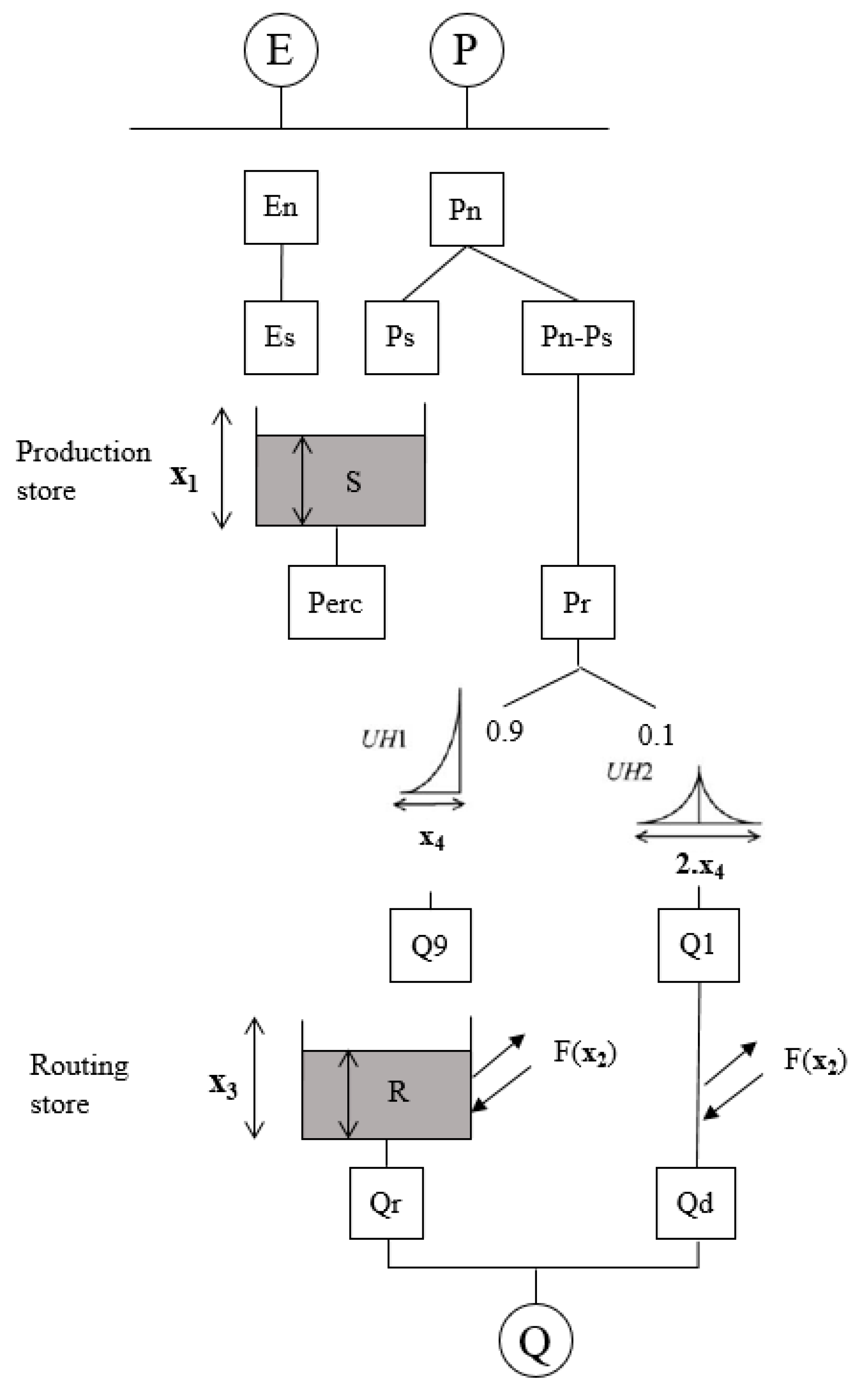
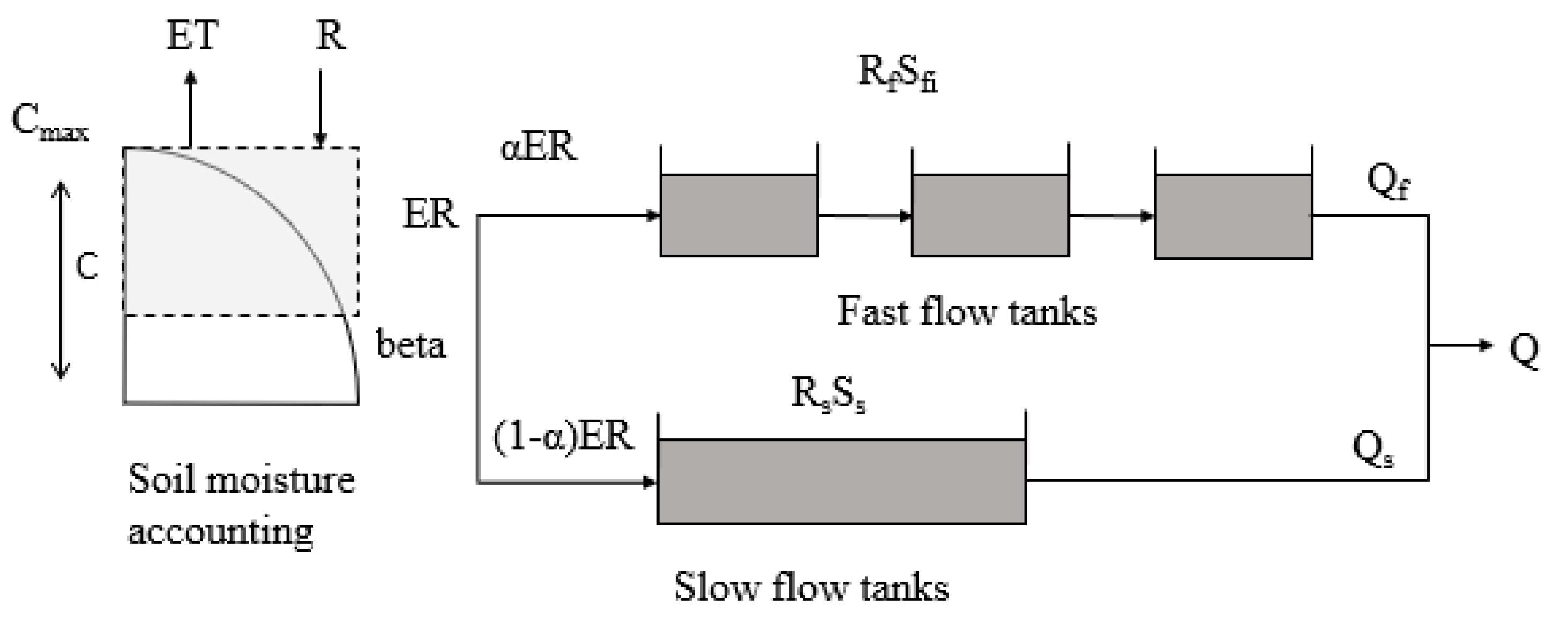
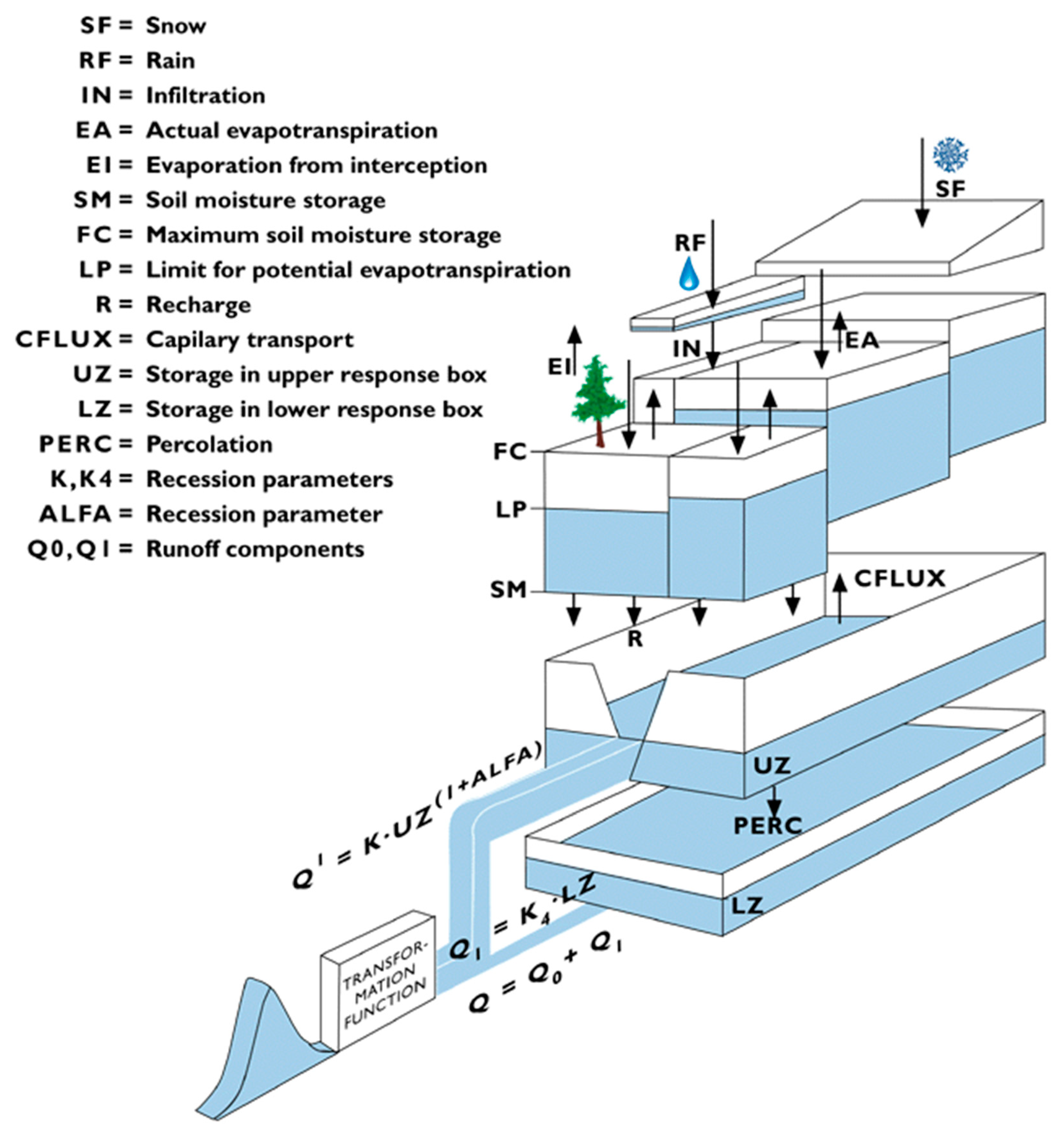
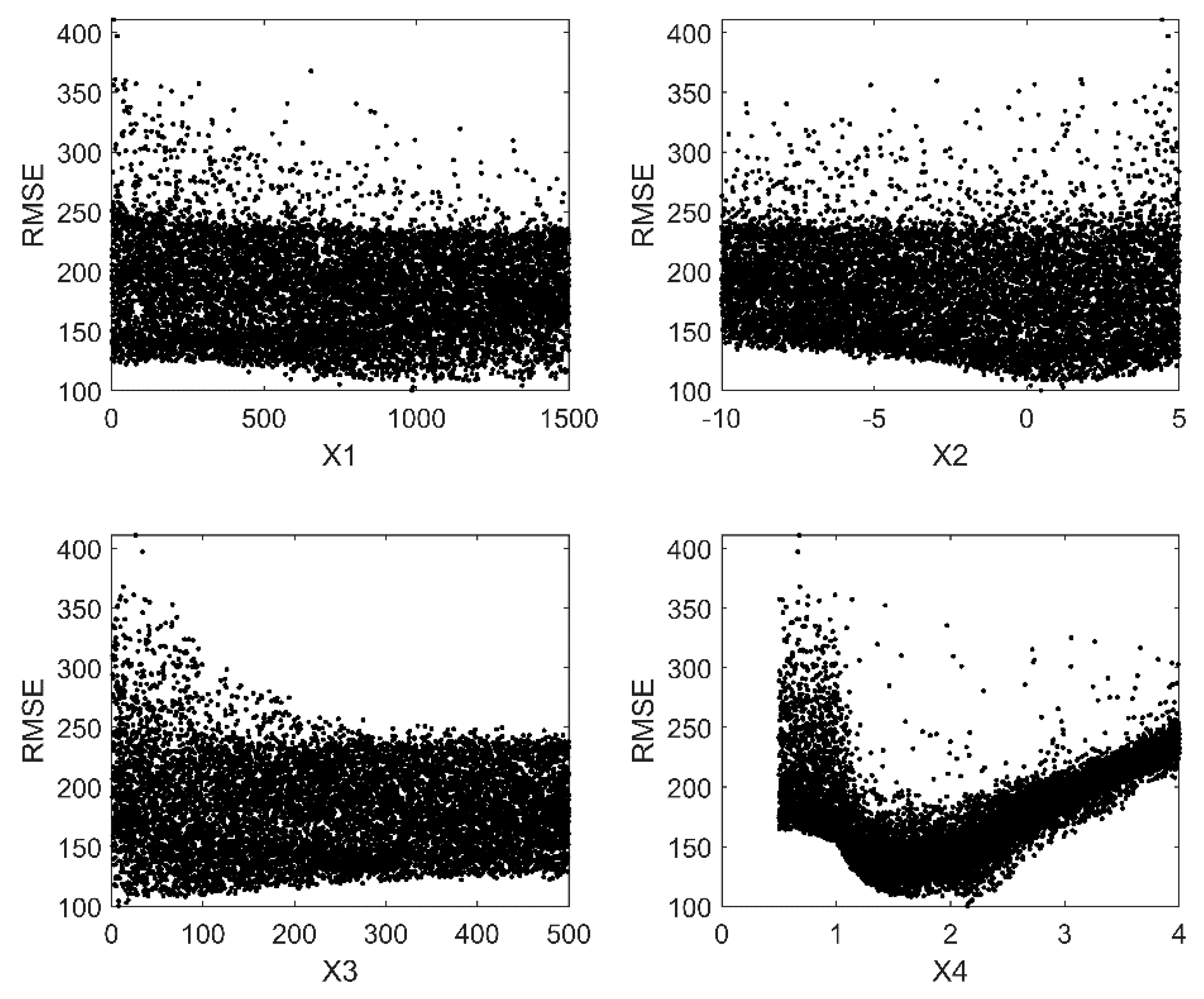
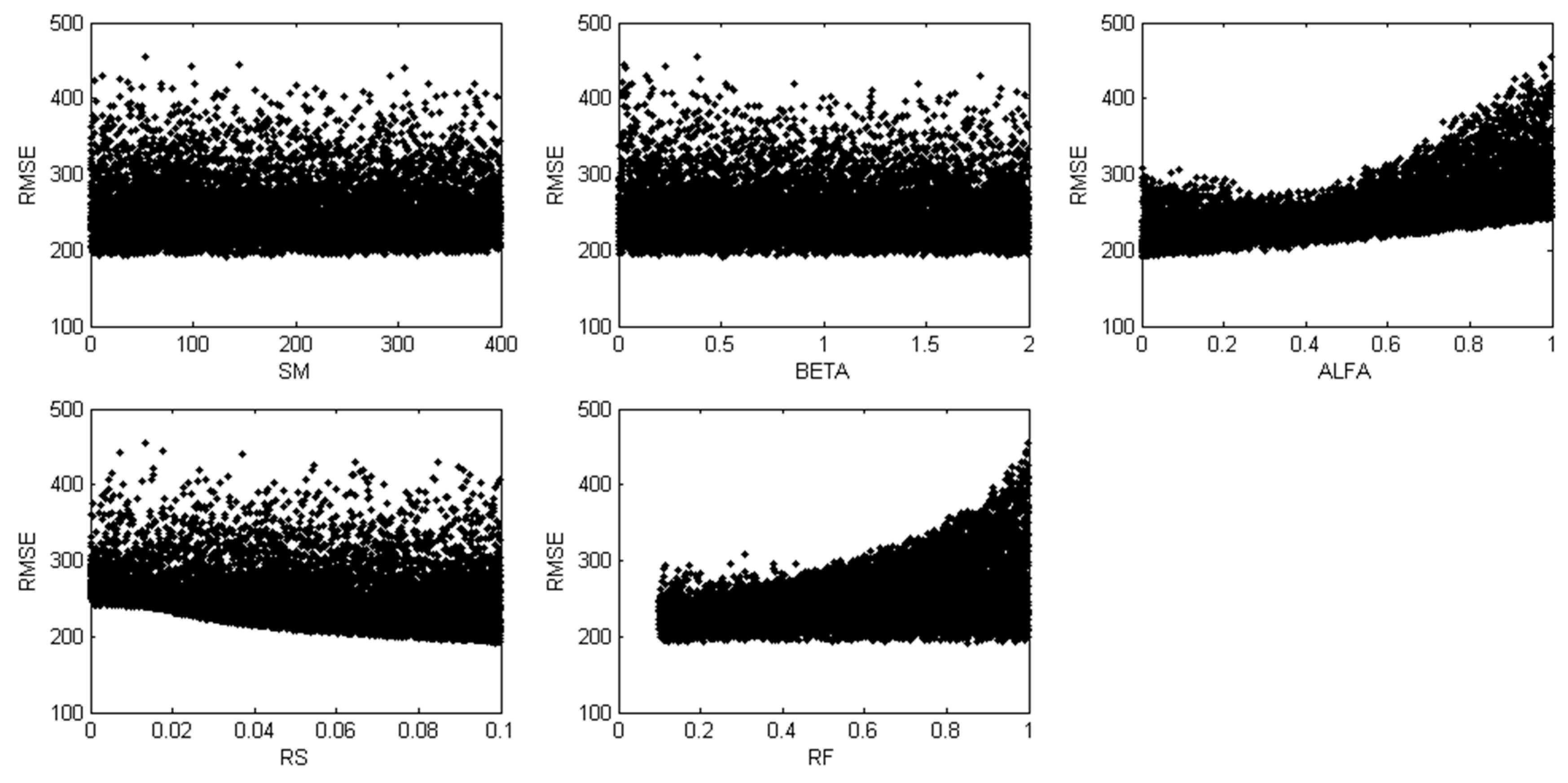
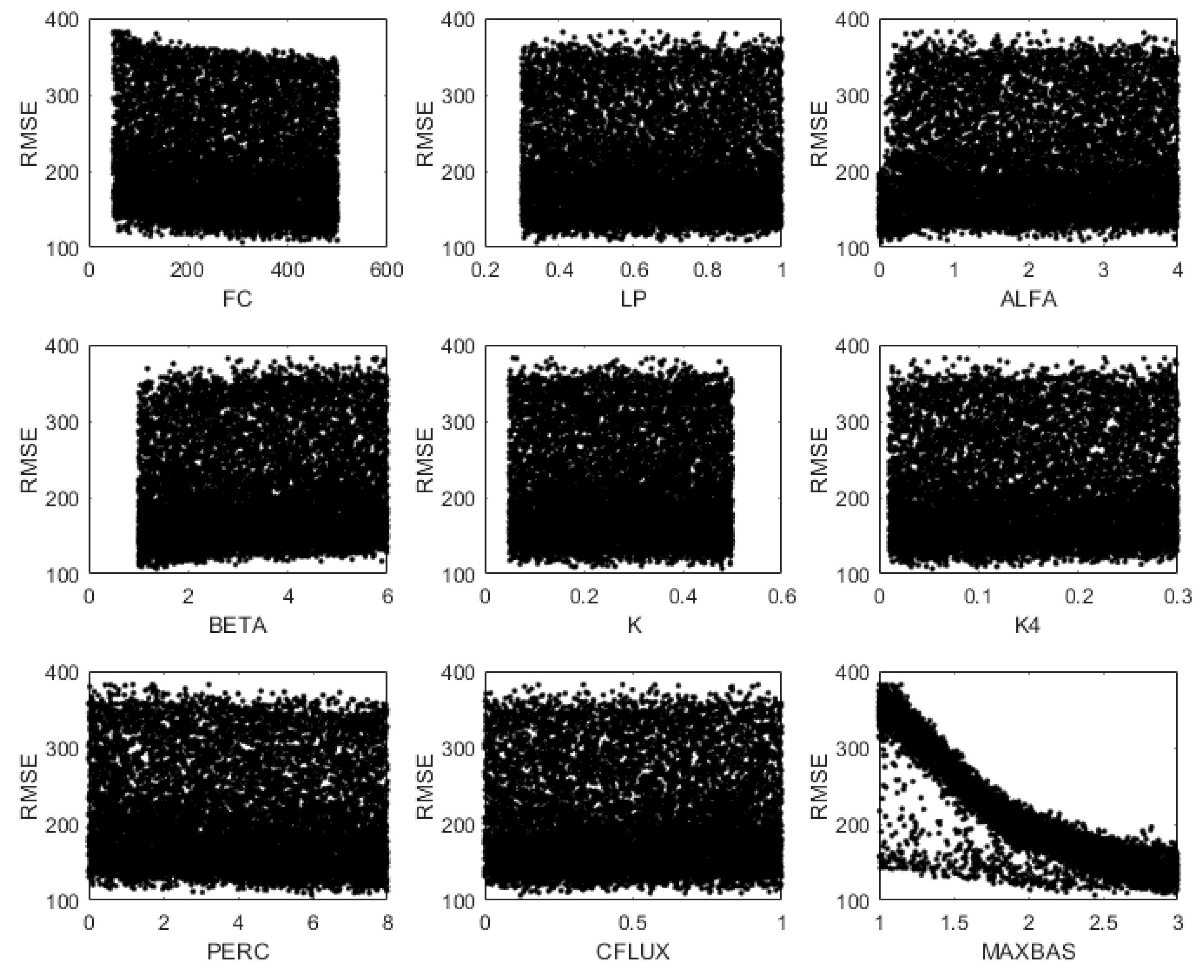
| Parameter | Description | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| X1 | Production store: Storage of rainfall in the surface of soil | mm | 1 | 1500 |
| X2 | Groundwater exchange coefficient: a function of groundwater exchange which influence routing store | mm | −10 | 5 |
| X3 | Routing storage: amount of water can be stored in soil porous | mm | 1 | 500 |
| X4 | Time peak: the time when the ordinate peak of flood hydrograph is created | day | 0.5 | 4 |
| Parameter | Description | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| SM | Maximum soil moisture | mm | 0 | 400 |
| BETA | Exponential parameter in soil routing | - | 0 | 2 |
| ALFA | Partitioning factor | - | 0 | 1 |
| RS | Slow reservoir outflow coefficient | - | 0 | 0.1 |
| RF | Fast reservoir outflow coefficient | - | 0.1 | 1 |
| Parameter | Description | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| FC | Maximum soil moisture content | mm | 50 | 500 |
| LP | Limit for potential evapotranspiration | - | 0.3 | 1 |
| ALFA | Response box parameter | - | 0 | 4 |
| BETA | Exponential parameter in soil moisture | - | 1 | 6 |
| K | Recession coefficient for upper tank | mm/d | 0.05 | 0.5 |
| K4 | Recession coefficient for lower tank | mm/d | 0.01 | 0.3 |
| PERC | Percolation from upper to lower tank | mm/d | 0 | 8 |
| CFLUX | Maximum value of capillary flow | mm/d | 0 | 1 |
| MAXBAS | Transfer function parameter | d | 1 | 3 |
| Method | Measure | Sampling Method | Required Number of Runs | Parameters within the Method | Benchmark Run | Number of Base Samples for Evaluation |
|---|---|---|---|---|---|---|
| Sobol | Sobol total-order index | LHS | (k + 2) × N | - | N = 10,000 | N = 100/200/300/500/1000/2000/3000/5000 |
| eFAST | FAST total-order index | Fourier Amplitude Sensitivity Test (FAST) sampling | K × N | Ms = 4 Ncs = 1 | N = 10,000 | N = 100/200/300/500/1000/2000/3000/5000 |
| Morris | Modified mean of Effect Elementary | Morris one at a time | (k + 1) × N | p = 32 Δ = 0.5161 | N = 10000 | N = 100/200/300/500/1000/2000/3000/5000 |
| LH-OAT | Effect S | LHS | (k + 1) × N | Δ = 0.05 | N = 10000 | N = 100/200/300/500/1000/2000/3000/5000 |
| RSA | Mean of KS statistics | LHS | N | - | N = k × 10000 | N = 100/200/300/500/1000/2000/3000/5000 |
| PAWN | Max of KS statistics | LHS | Nu + k × n × Nc | - | Nu =500 n =40 Nc = 250 | [Nu, n, Nc] = [30,10,10]/[50,10,20]/[100,15,20]/[100,20,25]/[200,25,40]/[200,25,80]/[200,30,100]/[500,50,100] |
| Method | Minimum Number of Run for GR4J | Minimum Number of Run for Hymod | Minimum Number of Run for HBV | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sensitivity Index (SI) | Rank | Conver-Gence | SI | Rank | Conver-Gence | SI | Rank | Conve-Gence | |
| Sobol | 15,000 | 6000 | 60,000 | 35,000 | 2100 | 70,000 | 11,000 | 22,000 | 110,000 |
| eFAST | 1188 | 388 | - | 2485 | 485 | - | 8937 | 8937 | - |
| Morris | 1000 | 500 | 10,000 | 1200 | 600 | 18,000 | 5000 | 2000 | 20,000 |
| LH-OAT | 1000 | 500 | 10,000 | 1200 | 600 | 18,000 | 5000 | 5000 | 20,000 |
| RSA | 4000 | 400 | 8000 | 2500 | 500 | 15,000 | 10,000 | 10,000 | 30,000 |
| PAWN | 12,200 | 8200 | 40,500 | 15,200 | 10,200 | 50,500 | 18,200 | 9200 | 100,500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Solomatine, D.P. Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria. Water 2019, 11, 1062. https://doi.org/10.3390/w11051062
Wang A, Solomatine DP. Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria. Water. 2019; 11(5):1062. https://doi.org/10.3390/w11051062
Chicago/Turabian StyleWang, Anqi, and Dimitri P. Solomatine. 2019. "Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria" Water 11, no. 5: 1062. https://doi.org/10.3390/w11051062
APA StyleWang, A., & Solomatine, D. P. (2019). Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria. Water, 11(5), 1062. https://doi.org/10.3390/w11051062






