Stability of Irrigation Canal Slopes Considering the Sea Level Rise and Dynamic Changes: Case Study El-Salam Canal, Egypt

Abstract

Stability of canals slopes are of paramount importance in engineering works due to its interaction with the infrastructure including roads networks and buildings. The failure of these slopes could cause human disaster, catastrophic environmental, and economic losses. The present study aims to investigate the stability of canals slopes considering the climate changes through sea level rise, fluctuation of groundwater level and the seismic actions. The study was simulated on the North Eastern part of Nile Delta aquifer, Egypt using the finite difference code of Visual MODFLOW. Moreover, the groundwater flow under the effect of sea level rise was investigated to study its effect on slope stability of El-Salam Canal, Egypt. Furthermore, the finite element program of Phase 2 was implemented, and safety factors were calculated using the shear strength reduction method (SSRM). The models are calibrated and verified through experimental work using permeability and seepage model. Moreover, the two models were applied on El-Salam Canal considering three scenarios to identify the safety factors including the effect of sea level rise (SLR), earthquake acceleration and a combination of the two scenarios. The results indicated that dynamic response values of the canal slope have different variation rules under near and far field earthquakes. Finally, the damage location and pattern of the slope failure are different in varying groundwater conditions.

1. Introduction

Failure of canal slopes are very dangerous problems in geotechnical engineering which lead to human, environmental, and economic problems. Many techniques are used for evaluating and analyzing slopes in order to invoke the remediation systems that overcome problems caused by slope failures. These slopes could be damaged under external loads, environmental conditions including changes in the groundwater table and canal stage, and many other reasons [1]. The failure surface in cohesion soils is deep while it is shallow in cohesionless soils, so the stabilizing systems were used to increase the safety of slope stability to avoid expected failure [2]. The slopes safety can be increased using drainage systems of surface and subsurface systems to modify the groundwater table, soil improvement techniques, and installing retaining structures such as concrete walls and sheet piles [3].

Sea level rise (SLR) is an important factor associated with global climate change [4]. Different sources of SLR measurements such as geologic indicators, tide gauges, and altimeters showed that the sea level has increased over the past 130 years [5]. Accurate measurements and prediction of sea level rise are complex due to being influenced, by other factors such as coastal subsidence, tectonic process and glacio-isostatic movements [4]. For the future, studies in 1996, 2001, and 2007 the Intergovernmental Panel on Climate Change (IPCC) [6,7,8] have estimated that the global sea to reach 0.94, 0.88, and 58 cm by 2100. The SLR is estimated to be 3 ± 0.4 mm/year with acceleration about 0.084 ± 0.025 mm/y² [9].

A number of world aquifer will be affected by these changes. In Egypt, the studies also indicated that the Nile Delta quaternary aquifer will be affected by SLR. This costal aquifer is connected by the Mediterranean Sea in the north while the aquifer productivity thickness is extending between an upper semi-permeable clay layer and lower impermeable rocky layer [10]. This productivity aquifer is a semi-confined aquifer [11] and the quaternary layer thickness varies from 1000 m in the northern parts to 200 m in the southern parts RIGW (1992a) [12]. The aquifer base slope is about 4 m/km to reach 40 times the average ground surface slope as presented in [13,14]. A number of studies were carried out to investigate the groundwater flow in the Nile Delta aquifer. Given the current conditions, the predicted impact of SLR by 25 and 50 cm on groundwater flow in the aquifer using 2D-FED model were simulated [15]. A numerical model was carried out using the FEFLOW model (a 3-D finite element variable density model) in Nile Delta aquifer under rising in sea level by 25, 50, and 100 cm [16]. The models results showed that the rise in sea level will effect on groundwater level and saltwater intrusion. Visual MODFLOW was used to simulate the effect of SLR in the northeastern Nile Delta, Egypt [17]; the study indicated that the salinity of groundwater abstraction will be increased from brackish water. A numerical study was developed [18] to simulate effects of climatic changes for increase in sea level by 25, 50, and 100 cm on the Nile delta aquifer using VISUAL MODFLOW. The results showed that the aquifer is sensitive for SLR and damaged large quantities of fresh water. The impact of SLR on design of subsurface drainage system in the Nile Delta, Egypt was studied [19], moreover the study indicated that climate change must be consider in the frame of the next water management strategies.

Evaluation of slope stability is an important part of geotechnical earthquake engineering due to its significant impact on infrastructure facilities such as buildings, bridges, roads, and lifelines and economic losses. Slopes failures are often observed following large earthquakes and the seismic slope stability methods can be divided into pseudo-static, sliding block, and stress-deformation [20]. Geo Studio software 2007 and 2-D finite element program of PLAXIS were used [21] to investigate the impact of earthquake shaking on stability safety and investigated the effect of embankment height and slopes on stability and liquefaction. The results showed that increasing embankment height and flattening could enhance stability and reduce the liquefaction zone. The seismic performance of slopes in pseudo-static designs with different safety factors was studied [22]. In this study the slope displacements obtained for different peak ground accelerations and safety factors are used to propose charts linking co-seismic slope displacements (D), seismic coefficients (K_h), and pseudo-static safety factors (FS), which are important parameters in pseudo-static approach. PLAXIS for modeling of bioreactor landfill was used [23]. The study showed that the factor of safety decreased as the solid waste was degraded with time, in both static and dynamic cases. The dynamic response and failure mode values were determined using finite element method for sandy slope subjected to fluctuation of groundwater conditions and the seismic forces actions [24]. The results indicated that these values have different variation rules.

This paper applies the finite element method, which is a fast and efficient design tool in modern engineering analysis, to evaluate the dynamic response of the slope when subjected simultaneously to seismic forces and variable groundwater conditions.

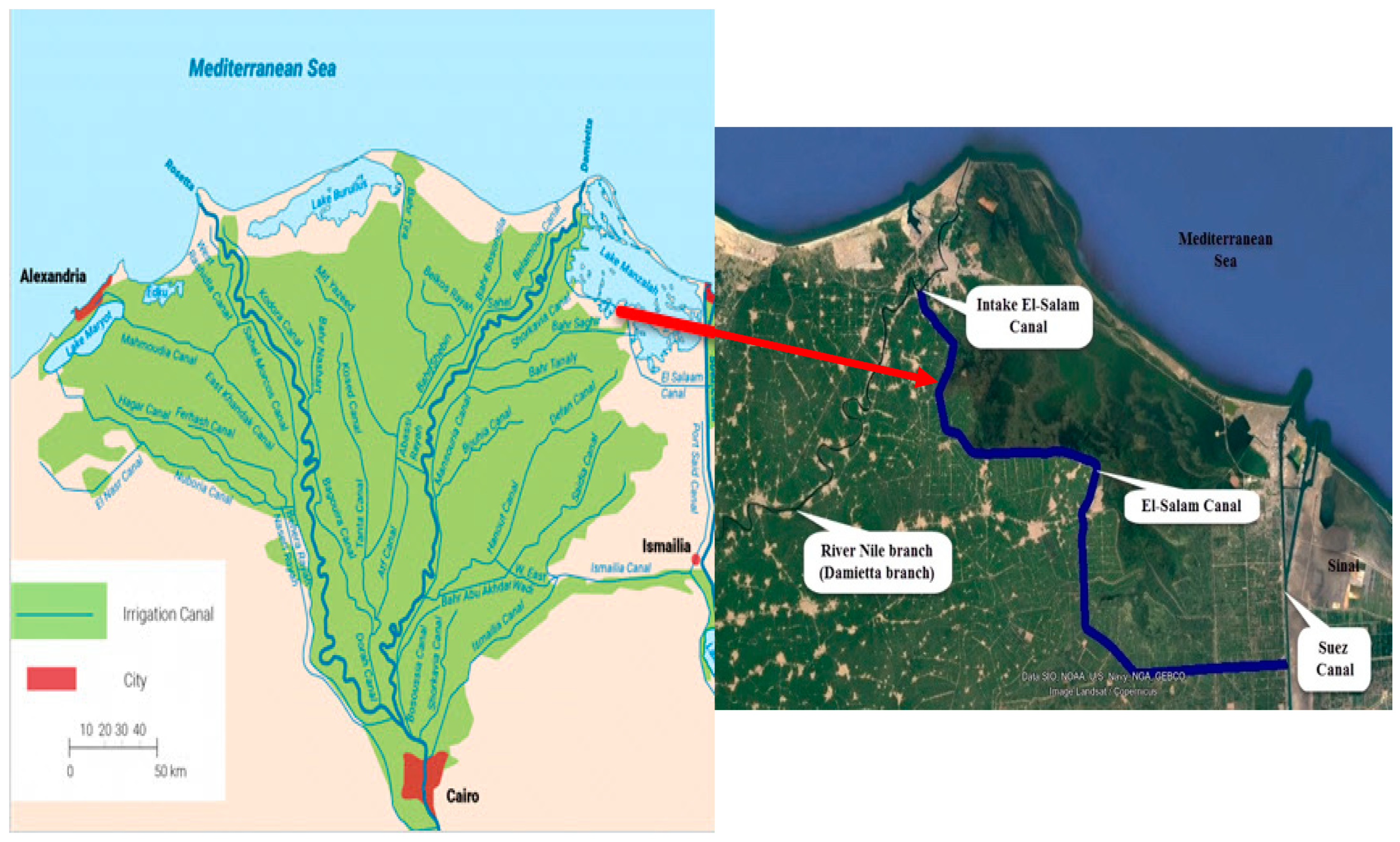
2. Description of Study Area

The current study area is a part of Nile Delta aquifer; this aquifer is one of the largest groundwater reservoirs [25] and this delta is one of the largest river deltas in worlds, covering an area of 22,000 km² EGSA (1997) [26]. It is bounded by the Mediterranean Sea in North, the Suez Canal in East, the Ismailia Canal in South Eastern, and the Nubaria Canal in South Western. Also, it is located between the latitudes of 30°00′ and 31°45′ N, and the longitudes of 29°30′ and 32°30′ E MWRI [27].

The current study was applied on El-Salam Canal, which is located in the North East of Egypt, where it supplies water for the reclamation of new lands in that part of the country see Figure 1. This artificial canal provides water from the Nile river and drainage water pumped from the main drains which is mixed by the Nile water to supply the new of reclamation lands in this part of the country. These areas are originally parts of the sedimentary formation of the ancient Nile branches. The intake of canal starts at the right bank of Nile River branch of Damietta branch at 219 km and 3 km upstream the Faraskur dam and passes through five governorates from Damietta, Dakahliya, Sharkiya, and Port Said to North Sinai [28]. The canal total length is about 277 km and and supplies its water to an area of 62 hectares which is divided into two main parts; the first part at Western knowns as El-Salam Canal has 86 km and 22 hectare, and the second part has 191 km and 44 hectare at Eastern part of Sinai [29].

The river Nile receives the back agricultural drainage water in Upper Egypt while this drainage water disposes to the Mediterranean Sea and North lakes in the Nile Delta. The collected drainage water is about 12 billion cubic meters (BCM) only about 5 BCM is currently being reused. Recently, the Egypt Government extended in newly reclaimed areas by using this water with a Nile water mix in a ratio of about 1:1 [31]. The water resources of the area west of Suez Canal and Sinai is supported by El-Salam Canal, the canals annual water supply is about 445 BCM milliard m³, about 2.11 BCM supplied from Nile water while 1.905 and 0.435 BCM from the Hadous drain and El-Serw drain [32]. The canal water salinity should not exceed 1250 mg/L [29].

In this study, VISUAL MODFLOW 2010 code is used to simulate groundwater flow SWI and assesses different scenarios for stability of canals slopes using the finite element software of Phase 2 in the North of Nile delta aquifer under SLR, an earthquake acceleration and a combination of the two scenarios.

3. Materials and Methods

3.1. Finite Difference Modelling

The groundwater flow models fell into two stages. The first was a conceptual model to understand the physical problem, the second was translating the physical system into mathematical terms. The current study was carried out to simulate the groundwater flow using VISUAL MODFLOW 2010. It is a 3-D finite difference model of combined groundwater flow and solute transport models. This models application includes groundwater head, abstraction well optimization, aquifer storage and recovery, groundwater remediation, and saltwater intrusion. The partial-differential equation used in MODFLOW to simulate the groundwater flow is McDonald and Harbaugh (1988) [33].

$$\frac{\partial }{\partial t}\left(K_{xx}\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left(K_{yy}\frac{\partial h}{\partial y}\right)+\frac{\partial }{\partial z}\left(K_{zz}\frac{\partial h}{\partial z}\right)+W=S_s\frac{\partial h}{\partial t}$$

(1)

where: K_xx, K_yy, and K_zz are the aquifer hydraulic conductivity in x, y, and z respectively (LT⁻¹), h is the potentiometric head (L), W is volumetric flux per unit volume (T⁻¹), S_S is specific storage (L⁻¹), and t is time (T).

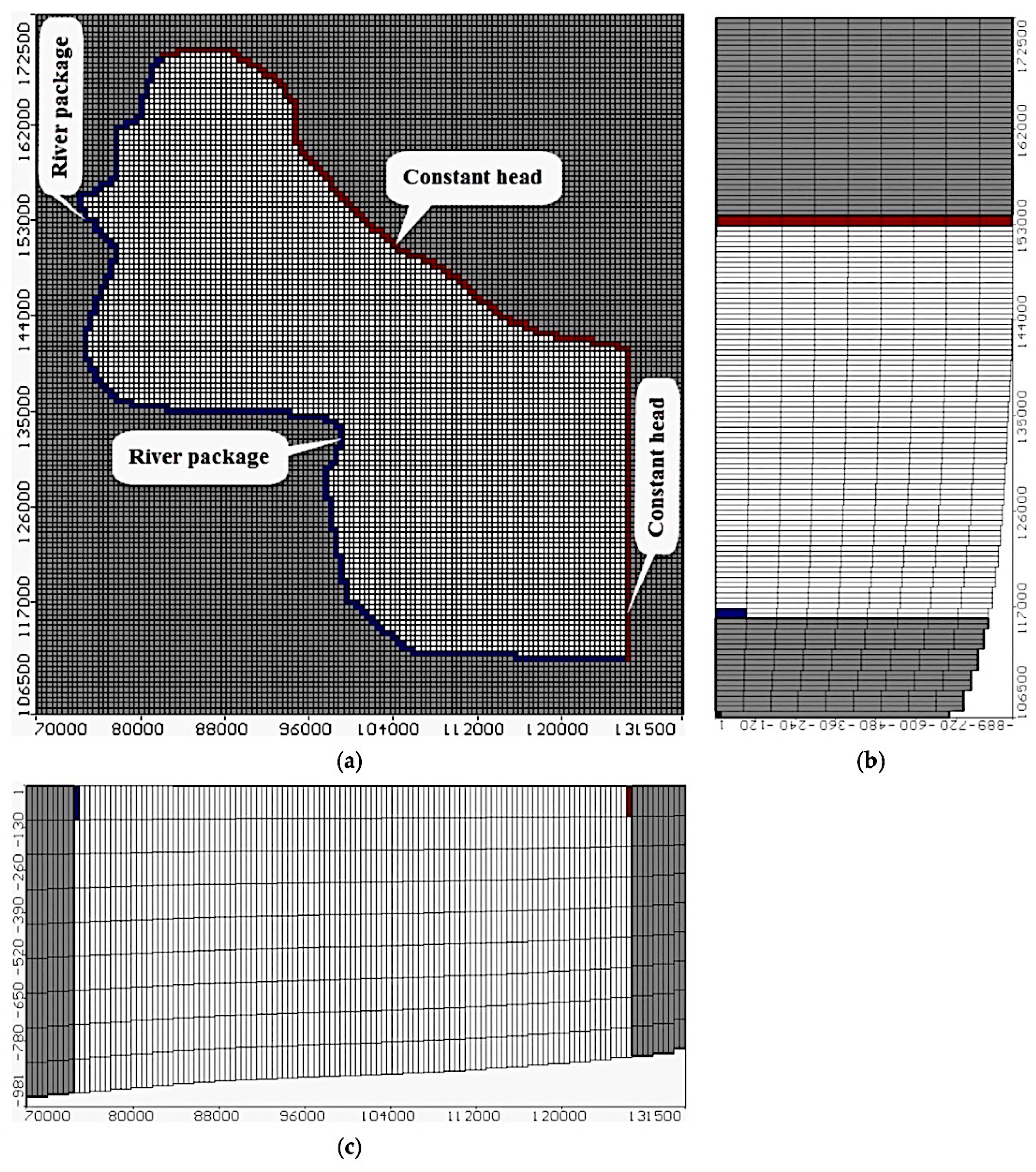
3.1.1. Costal Aquifer Model of the Northeastern Nile Delta

The finite difference code of Visual MODFLOW was applied to the North Eastern part of Nile Delta aquifer to simulate the groundwater flow for rising of sea level by 25 and 50 cm to investigate the impact of SLR on slope stability of the El-Salam Canal. The developed model was carried out using 135 rows and 127 columns for active and inactive cell using square cell dimension of 0.25 km² as shown in Figure 2. The model thickness ranges from 700 m in the South to 950 m in the North including clay cap, this cap kept quaternary aquifer as a semi-confined aquifer. The model was digitized using eleven layers; the first was a clay cap with an average thickness of 50 m, layers two to eleven were divided by equal thickness to represent the quaternary aquifer.

Figure 2 represents sections taken in X-direction from East at Suez Canal to West at Damietta branch, also in Y-direction. The model topography level (ground surface) varies from zero level to 1.00 m above mean sea level (MSL).

3.1.2. Model Boundary Conditions and Hydraulic Parameters

The study area was confined by four boundaries including a zero-specified head along shore line of Mediterranean Sea at the North and Suez Canal at East. The river package was assigned to El-Salam Canal starting from Nile flow in the West to end at Suez Canal in the East based on each reach conductance. The aquifer hydraulic parameters that were used in the simulated model were collected from experimental, field, and previous studied. The hydraulic conductivity of the clay layer ranged from 0.25 to 0.50 m/day while the specific yield and specific storage are 0.10 and 1 × 10⁻⁵ m⁻¹ respectively and the effective porosity between 50 to 60%. Moreover, the quaternary aquifer hydraulic conductivity was between 50 to 150 m/day, the specific yield ranges from 0.15 to 0.20, the specific storage is 1 × 10⁻⁵ m⁻¹ and the effective porosity ranges from 20 to 35%. The recharge process plays a vital role on groundwater flow, the assign model recharge with ranges between zero to 0.80 mm/day.

3.2. Finite Element Model

The finite element software of Phase 2 was applied in this study to simulate the slope stability analysis. This software is a 2-D elasto-plastic finite element program for slope and excavation stability analyses, and it was used to calculate the stresses, displacements, slopes stability, and civil engineering problems. This software supports analysis of elastic and plastic materials but plastic material properties are defined only with isotropic properties. The factor of safety (FOS) in Phase 2 was calculated using the shear strength reduction method (SSRM) that simulated the problem in a just stable state of FOS equal one (Phase 2 version 8, 2011) [34]. Moreover, the failure criterion used in the slope analysis was Mohr-Coulomb failure criterion which was the better agreement with experiment results than the other theories of the slope analysis [35,36]. The selected failure criterion in the finite element model is Mohr-Coulomb criterion due to simply used with the finite element analysis. In addition, the model parameters were the meaningful soil shear strength parameters, soil modulus, Poisson’s ratio, and the angle of dilation. Mohr-Coulomb is an elastic perfectly plastic model without stress softening or hardening. Figure 3 shows a 2-D graphical representation of the slope safety factor using Mohr-Coulomb failure criterion in conjunction with strength reduction method (SRT). The FOS using Mohr-Coulomb failure criterion in conjunction with the strength reduction technique is presented in the following equations:

$$I_1={\sigma }_{xx}+{\sigma }_{yy}+{\sigma }_{zz}$$

(2)

$$J_2=\frac{1}{6}\left[{({\sigma }_{xx}-{\sigma }_{yy})}^2+{({\sigma }_{yy}-{\sigma }_{zz})}^2+{({\sigma }_{zz}-{\sigma }_{xx})}^2\right]+{{\tau }_{xy}}^2+{{\tau }_{yz}}^2+{{\tau }_{zx}}^2$$

(3)

$$\begin{gathered} J_3=({\sigma }_{xx}-\frac{I_1}{3})({\sigma }_{yy}-\frac{I_1}{3})({\sigma }_{zz}-\frac{I_1}{3})+2{\tau }_{xy}{\tau }_{yz}{\tau }_{zx}-({\sigma }_{xx}-\frac{I_1}{3}){{\tau }_{yz}}^2-({\sigma }_{yy}-\frac{I_1}{3}){{\tau }_{zx}}^2 \\ -({\sigma }_{zz}-\frac{I_1}{3}){{\tau }_{xy}}^2 \end{gathered}$$

(4)

$$\theta =\frac{1}{3}si{n}^{-1}\left[-\frac{3\sqrt{3}{J}_3}{2{J_2}^{1.50}}\right]\hspace{1em}-\frac{\pi }{6}<\theta <\frac{\pi }{6}$$

(5)

$$S=\sqrt{J_2}$$

(6)

$$S_{\max }=\frac{\frac{I_1}{3}sin\varphi +ccos\varphi }{cos\theta +\frac{sin\theta sin\varphi }{\sqrt{3}}}$$

(7)

$$\mathrm{Factor}\mathrm{of}\mathrm{safety}\left(\mathrm{FOS}\right)=\frac{S_{\max }}{S}$$

(8)

where: I₁ are the principal stresses invariant [F L⁻²], J₂ and J₃ are deviatoric stresses invariants [F² L⁻⁴], S is the deviator stress [F L⁻²], S_max is the max deviator stress [F L⁻²], C is Cohesion [F L⁻²], ϕ is Friction angle [degree], Ɵ: is inclination angle [degree], τ is shear stress [F L⁻²], and σ is the total stress [F L⁻²].

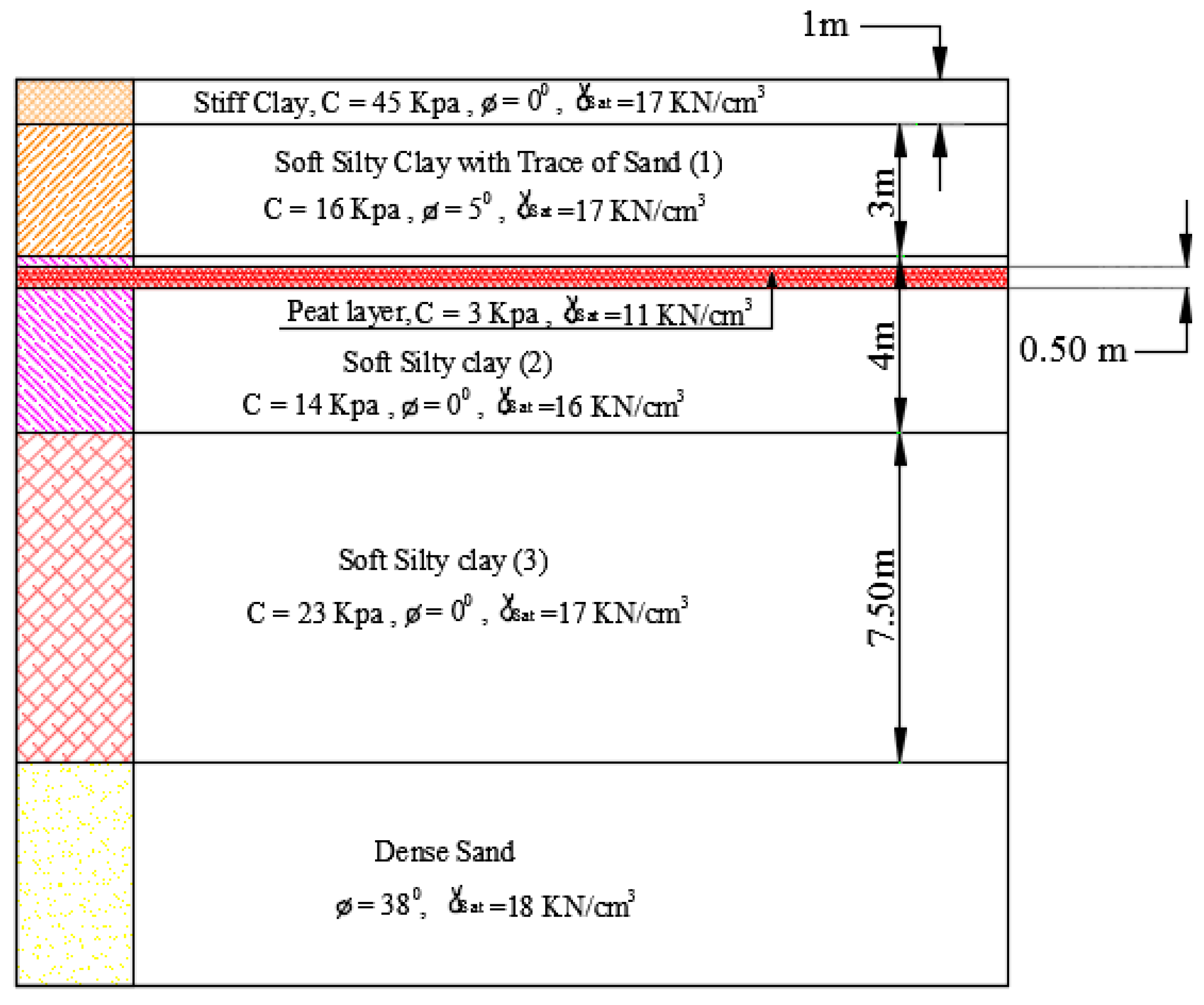
El-Salam Canal Model

Although Egypt is characterized by low seismicity, it has experienced damaging earthquake effects throughout its history. Figure 4 shows a revised catalog of earthquakes for the Eastern Mediterranean region during the period from 2200 BC to 2009 AD, based on information from several international and local seismic catalogs. This catalog was processed through different steps, including the elimination of repetitions and the scale of unifying magnitude [37]. The two critical events affecting Cairo were Ms. 5.8 in 1847 [38] and Ms. 5.4, the Cairo earthquake in October 1992 [39,40]. The earthquake in Cairo is still one of the most painful events and is buried in memory of the Egyptians due to the loss and damage associated with it including; 561 deaths, 10,000 injured, and 3,000 families lost their homes [41].

The numerical model of phase 2 was applied to identify the stability factor of on El-Salam Canal slope under the impact of sea level rise and earthquake. Three scenarios were considered to investigate the FOS of canal side slope under the effect of SLR by 26.70 cm and 51.30 cm (Scenario one), increasing earthquake horizontal acceleration to 0.1 g and 0.2 g (Scenario two), and the combination of scenario one and two (Scenario three). The typical cross section of the canal is presented in Figure 5. This figure is based on the previous studies which applied on this slope starting with a general planning study performed by the Egyptian Ministry of Water Resources and Irrigation. Moreover, Figure 6 presented the soil profile using boreholes which carried out for El-Salam Canal from 8.800 km to 8.850 km [42].

4. Results and Discussion

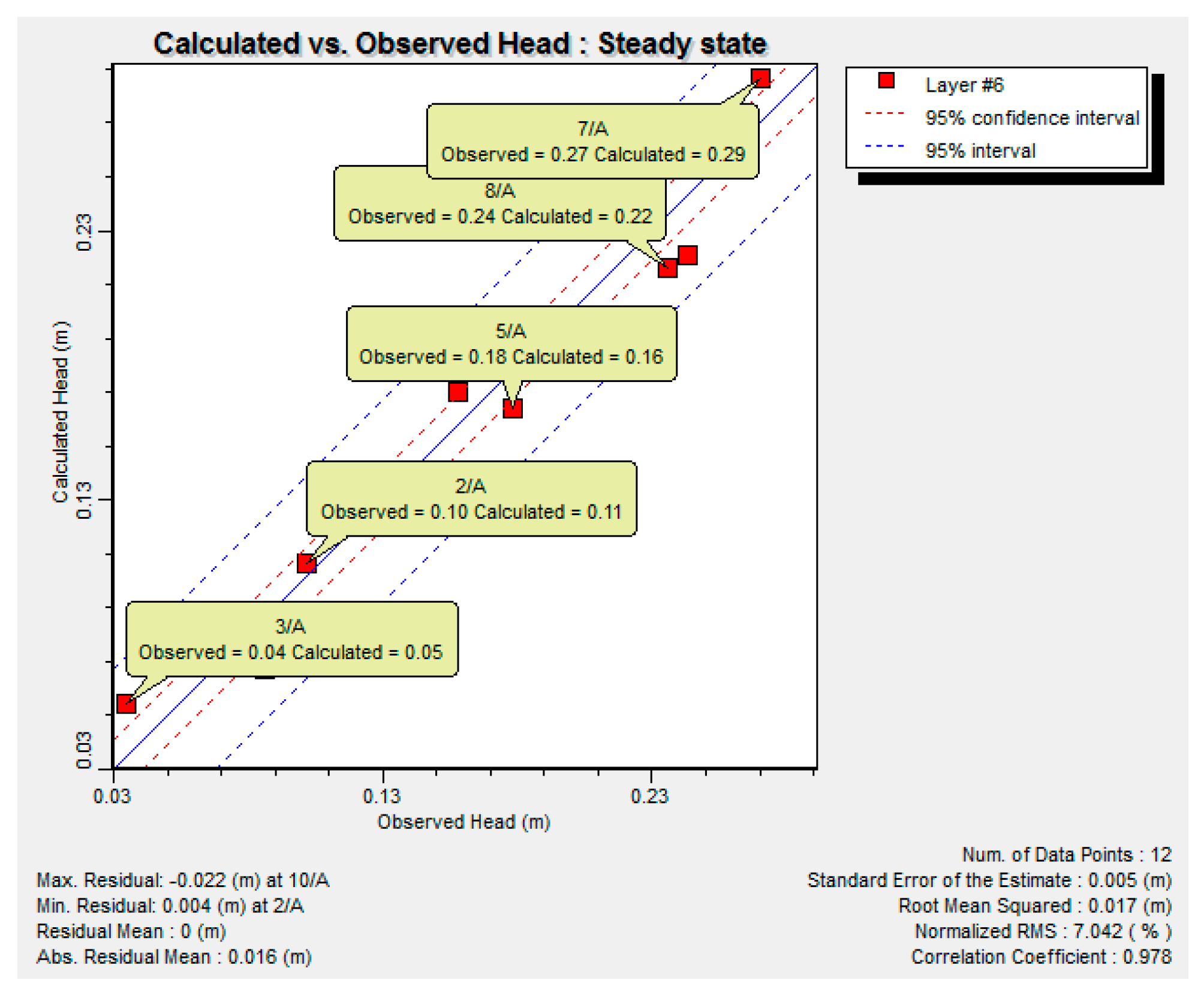
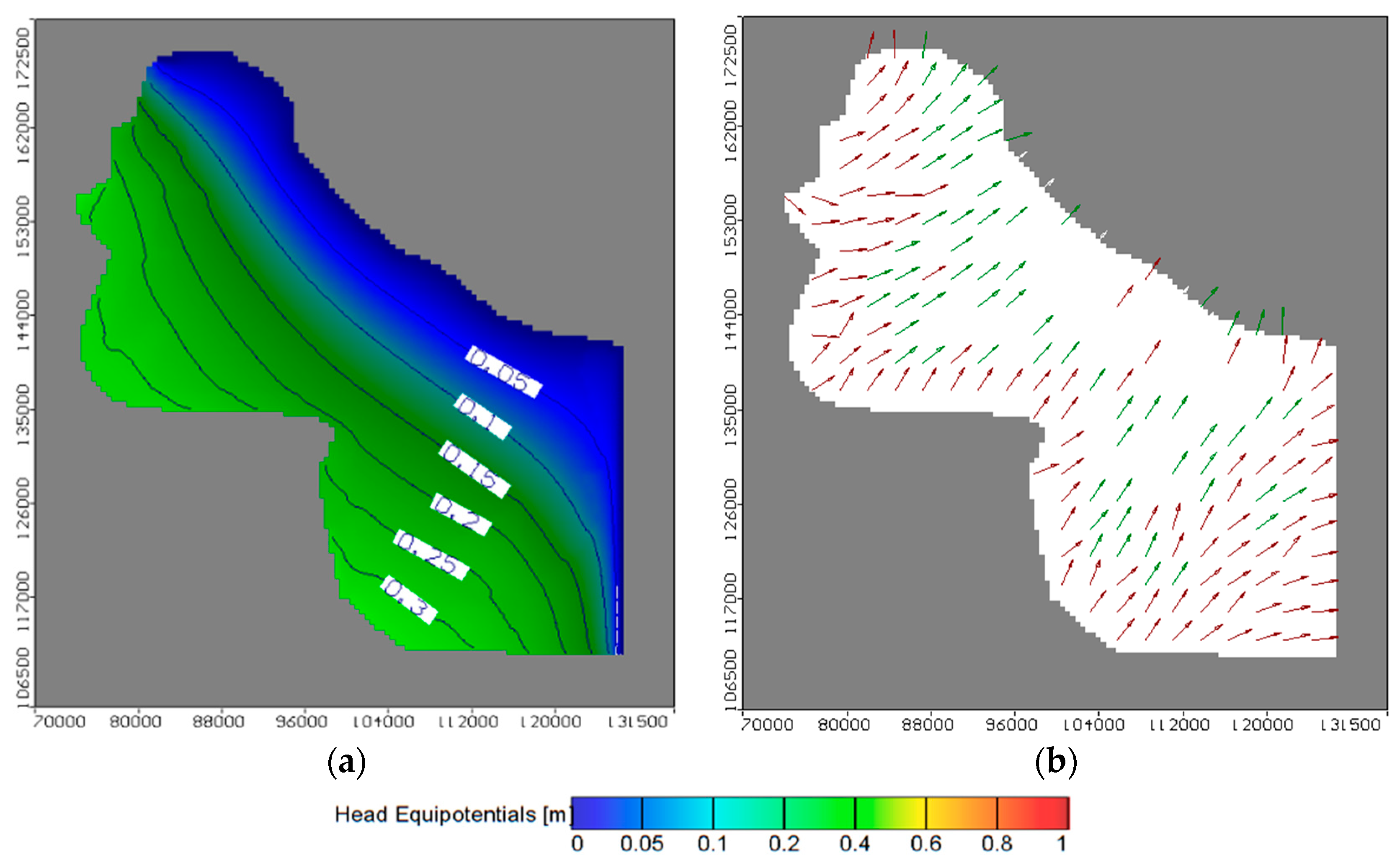
4.1. Calibration of Groundwater Flow Model

The calibration process of groundwater flow model is the critical model step which comparing the calculated model heads with measured in field. This process was conducted before using of the developed model in the future prediction. The simulated model was calibrated by changing the aquifer hydraulic properties using trial and error to get the target of calibration by minimizing difference between the calculated and measured heads. The model was calibrated based on field data which measured by RIGW in 2008 and published by Morsy (2009) [44]. Figure 7 represents the difference between calculated and observed head in the study area for a number of 12 observations well. The residual range is between −0.022 and 0.004 m with root mean square (RMS) of 0.017 m while the normalization RMS is 7.042%. The model calibration target was 10% the difference between maximum and minimum head to be 0.03 m the results are greet satisfactory.

Figure 8 indicates that the groundwater head ranges from a zero value at the North to 0.30 m at the South. Also, the model flow direction is gradually from high head at the Southwestern where the Nile branch of Damietta and El-Salam Canal are located to supply the aquifer while the low head at the North. The groundwater velocity for the clay and quaternary layer are 2.70 × 10⁻⁵ and 0.01 m/d respectively. The model results indicate a great satisfactory between calculated heads compare with the field data; this gives much reality to predict the groundwater level in the future.

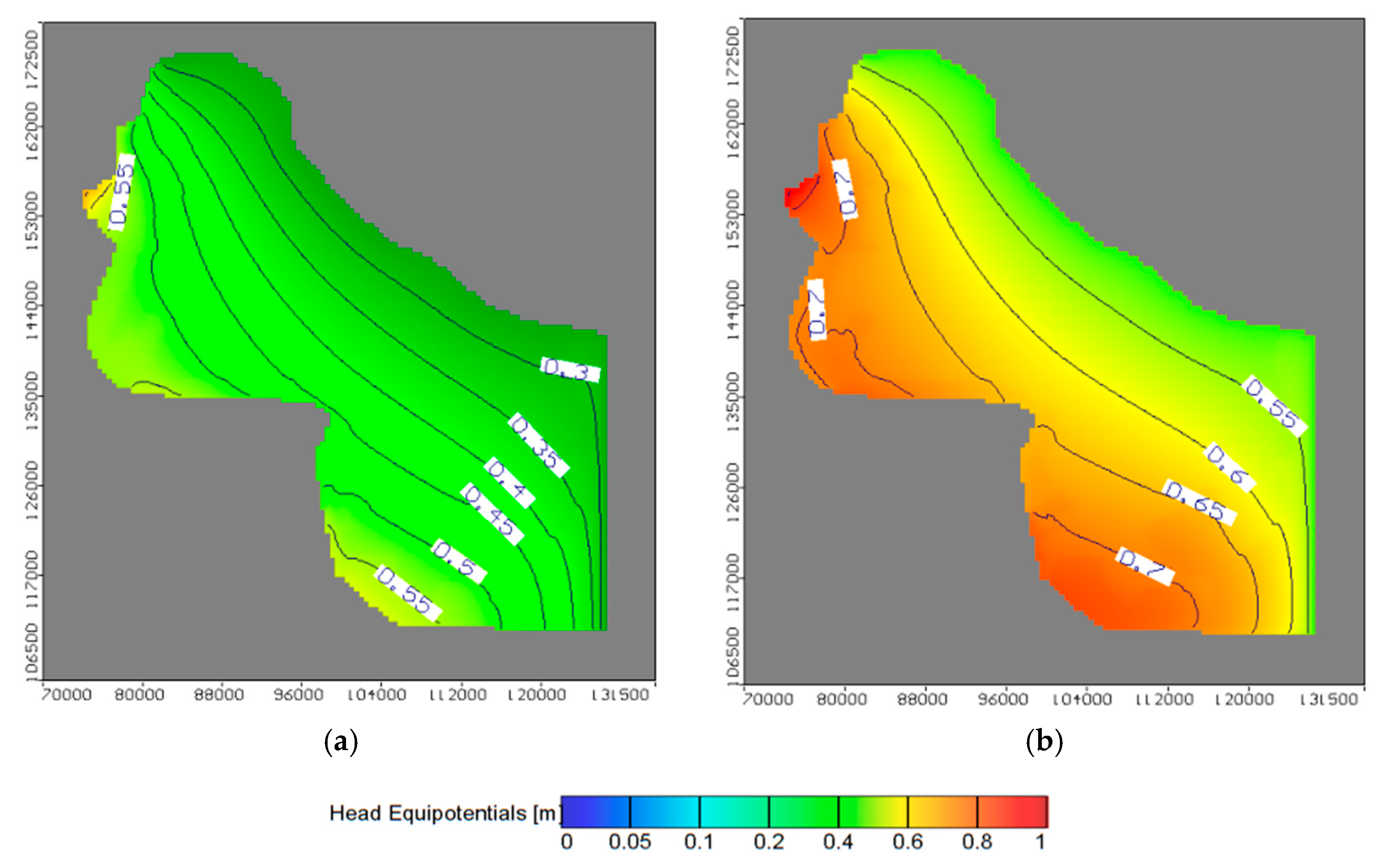
4.2. Impact of Sea Level Rise on Groundwater Level at Project Area

Based on Legeais et al. (2018) [9] estimation, the SLR was calculated for years 2060 and 2090 to be 26.70 and 51.30 respectively (referred to year 2000). Figure 9 presents the results of increase sea level by 26.70 and 51.30 cm, it is clear that SLR leads to increase the aquifer piezometric head. Moreover, the maximum increase occurred along the shore line of Mediterranean Sea at the North and Suez Canal at East, and decreased gradually to West South.

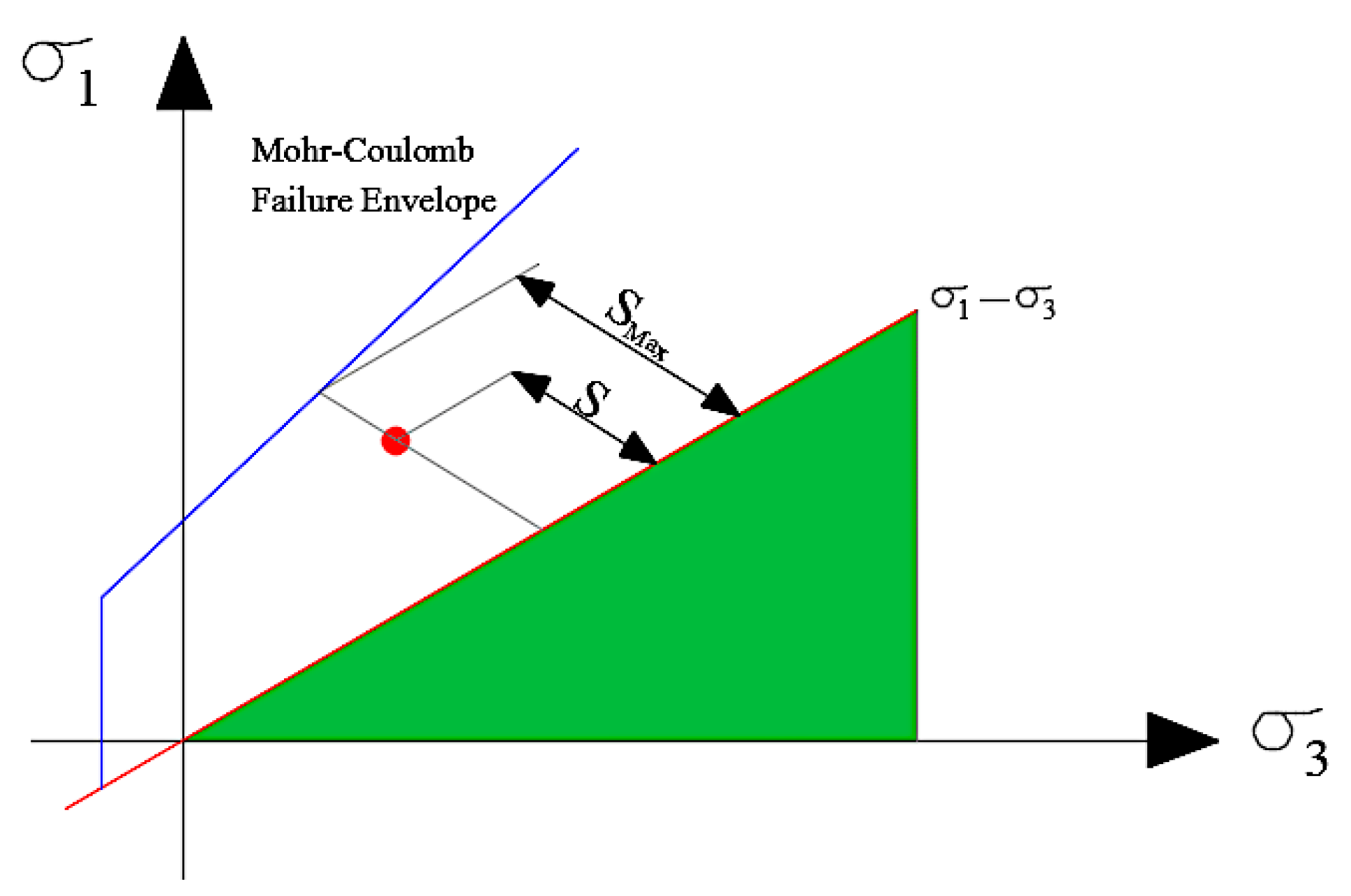
4.3. Verification of Slope Stability Model Using Experimental Model

The current stability model was calibrated using the experimental carried out by Al-Quamhawy (2016) [45]. This models dimensions were 100 cm length with 4 cm width, the right depth was 25 cm to represent the canal and the left depth is 50 cm to represent the embankment while the side slope ratio of 2H (horizontal) to 1V (vertical). The laboratory methods were used to measure the model hydraulic parameter for the internal angle of friction (ø) and the soil porosity to be 30° and 30% respectively while the hydraulic conductivity was calculated using Darcy’s law under the steady state conditions to be 28.50 m/day. The model boundary conditions were assigned using the water depth ratio at embankment side equals 0.80 from total height and the canal water depth is zero. Figure 10a,b presents the failure wedge for numerical and experimental model, the figure prevailed that the failure wedge is near to the toe of slope. Furthermore, the piezometric line and water table show a good agreement between the experimental and numerical models, and the mean relative error was 8.77%.

The model was developed to the case study of El-Salam Canal and used the hydraulic parameters from soil profile that are presented in Figure 6. The model boundary conditions were assigned based on the field data of groundwater head and the canal stage to be 3 and 2.95 m respectively from canal bed. Moreover, the piezometric lines packages were chosen to simulate the water table as shown in Figure 11. The deformations due to the pore water pressure and the effective stress could be calculated.

The failure in soil occurs when the actual shear stresses exceed the soil strength. The results of slope analysis using SRM technique were shown in Figure 12 which shows the shading contours of the maximum shear strain with the slope depth. The sliding surface passed through the peat layer because it is considered the weakest layer in the slope stratification. The calculated safety factor was reached 1.086. Thus, increasing the soil shear strength parameters for the soil cohesion and the internal angle of friction leads to increase the slope safety against shear failure. The maximum values of the embankment displacement were found to be 18.20, 24.30, and 42.16 cm for the horizontal, vertical, and total displacement respectively due to the slope own weight as shown in Figure 13.

4.4. Effect of Sea Level Rise on Factor of Safety of Canal Slope

The effect of SLR on canal embankment was studied. The SLR was increased by 26.70 and 51.30 cm, thus the groundwater level reached 0.60 and 0.70 from MSL. Figure 14 and Figure 15 represent shear strain and total displacement distribution under the variation of SLR by 26.70 and 51.30 cm. Moreover, the canal slope FOS reached 1.083 and 1.072 respectively comparing with original value. Furthermore, the results indicated that the maximum shear strain in the slope was concentrated with the peat layer region and increased with groundwater level increase. Figure 16 describes the decrease of canal slope FOS against sea level rise SLR. It is noticed that for SLR equals 26.70 and 51.30 cm the FOS decreases by 0.3% and 1.3% from the base case respectively.

4.5. Effect of Earthquake Intensity on Factor of Safety of Canal Slope

The earthquake acceleration intensities 0.1 g and 0.2 g were studied. Figure 17 and Figure 18 describe shear strain and total displacement distribution due to change the earthquake acceleration intensities to 0.1 g and 0.2 g. The results indicated that the canal embankment slope safety factors reached 0.436 and 0.204 when the earthquake acceleration changed to 0.1 g and 0.2 g respectively. Moreover, the maximum shear strain increases with depth to reach the last layer of sand. Furthermore, the increase in earthquake acceleration leads to significant deformation increase. Figure 19 represents the relation between the decrease of canal slope FOS and the earthquake intensity increase. It is noticed that for earthquake intensities equal 0.1 g and 0.2 g the FOS decreases by 59.9% and 81.2% from the base case, respectively.

4.6. Effect of Combination Scenario on Factor of Safety of Canal Slope

The following stage of the numerical modeling was carried out to study the effect of the combination of SLR by 26.70 and 51.30 cm with earthquake acceleration of 0.1 g and 0.2 g. The results show that the slope factor of safety reached 0.42 and 0.405 when SLR was 26.70 cm, while it reached 0.2 and 0.196 when SLR was 51.30 cm under earthquake acceleration of 0.1 g and 0.2 g respectively. The maximum shear strain distribution was studied. Moreover, the results of total displacement in the canal slope were presented, as shown in

Table 1. Maximum total displacement for different scenarios.

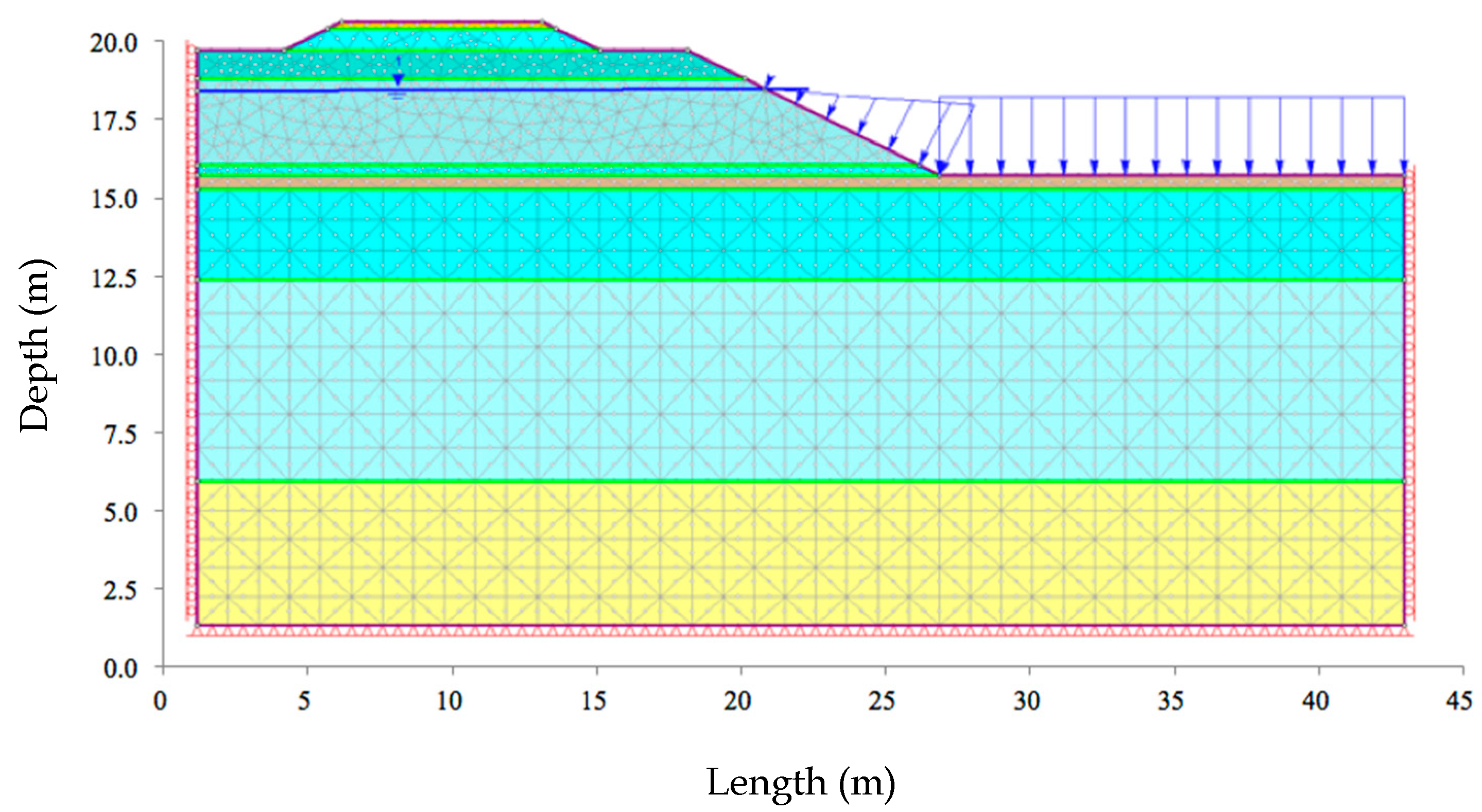
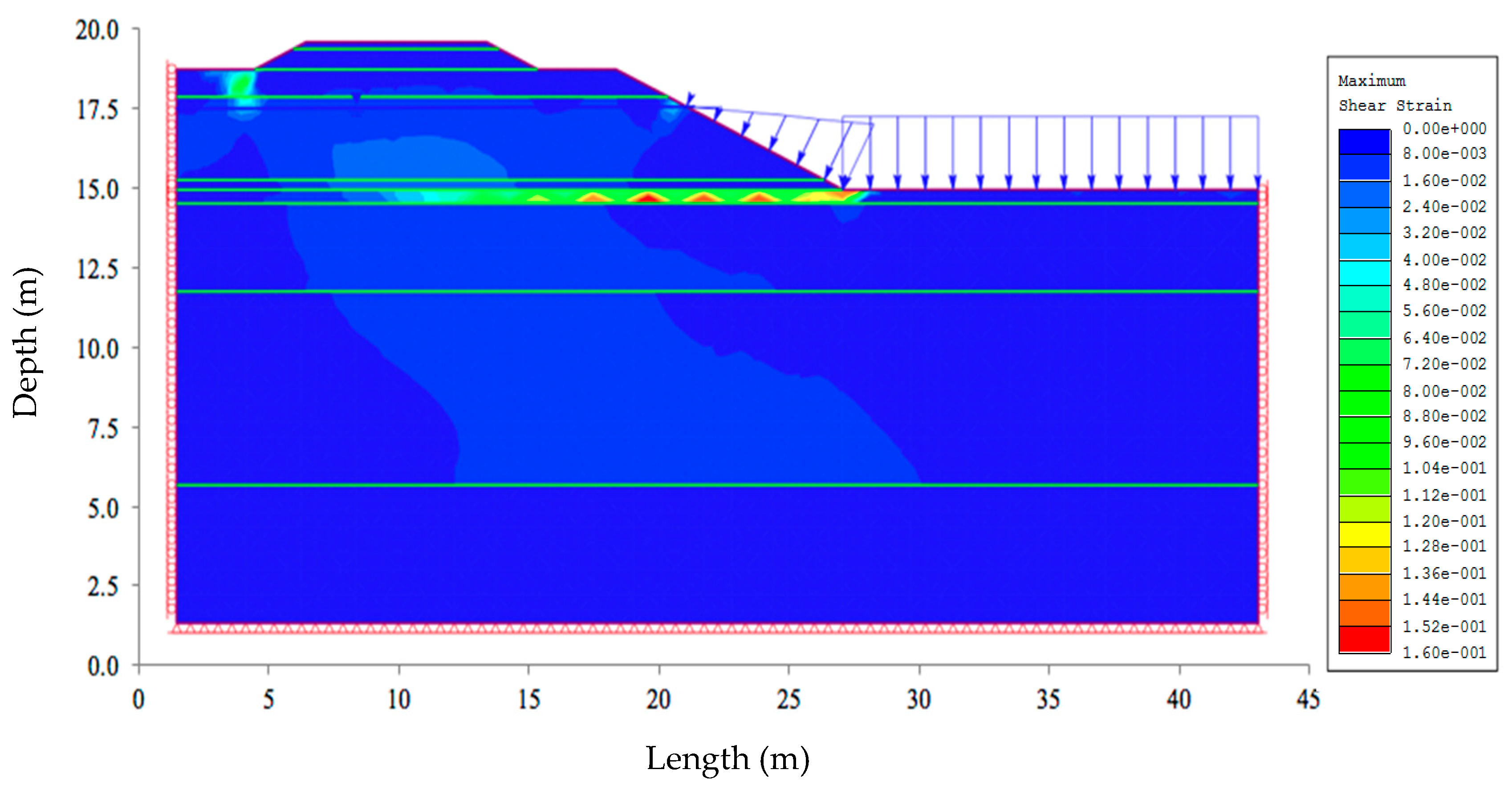
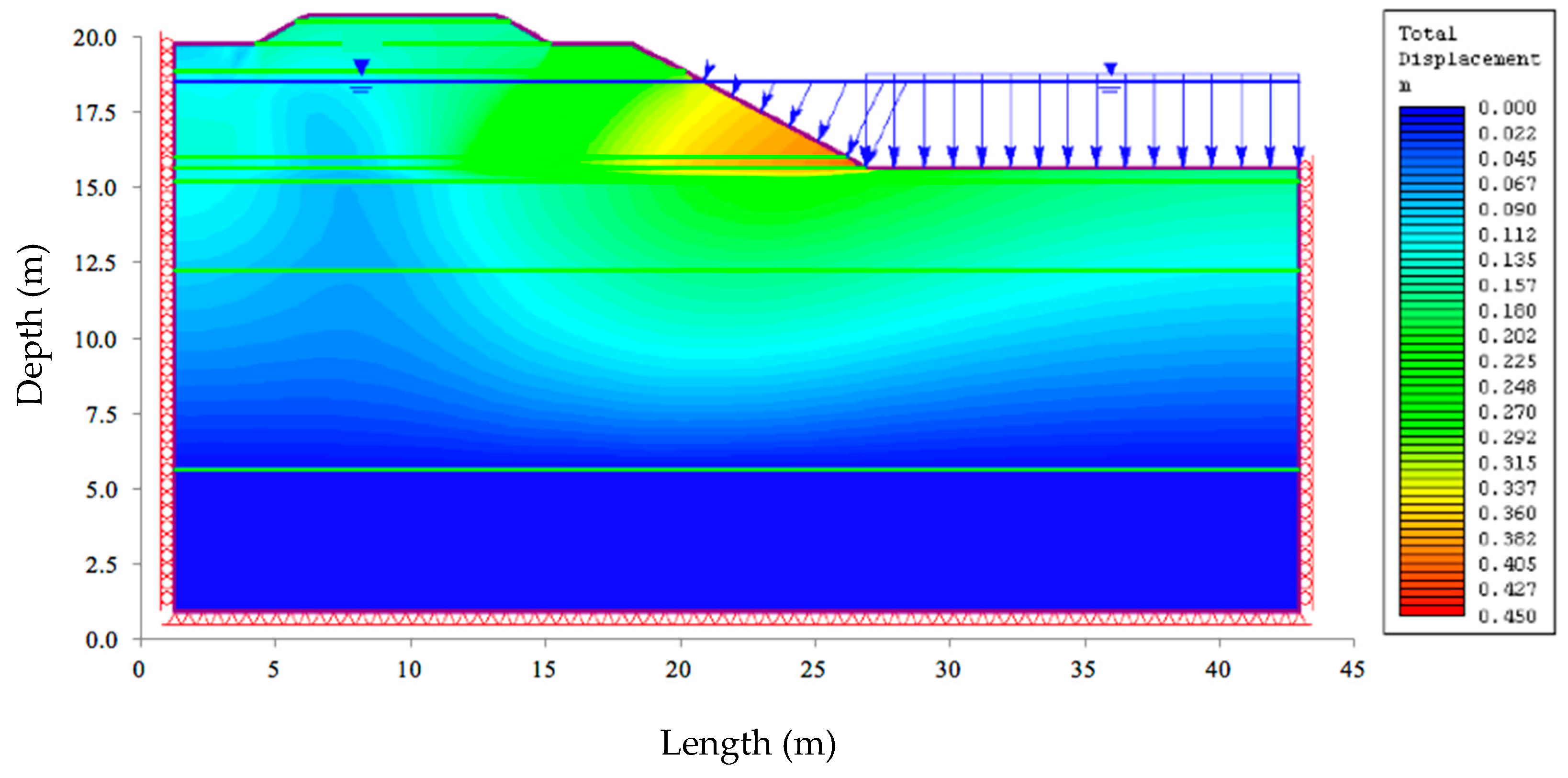
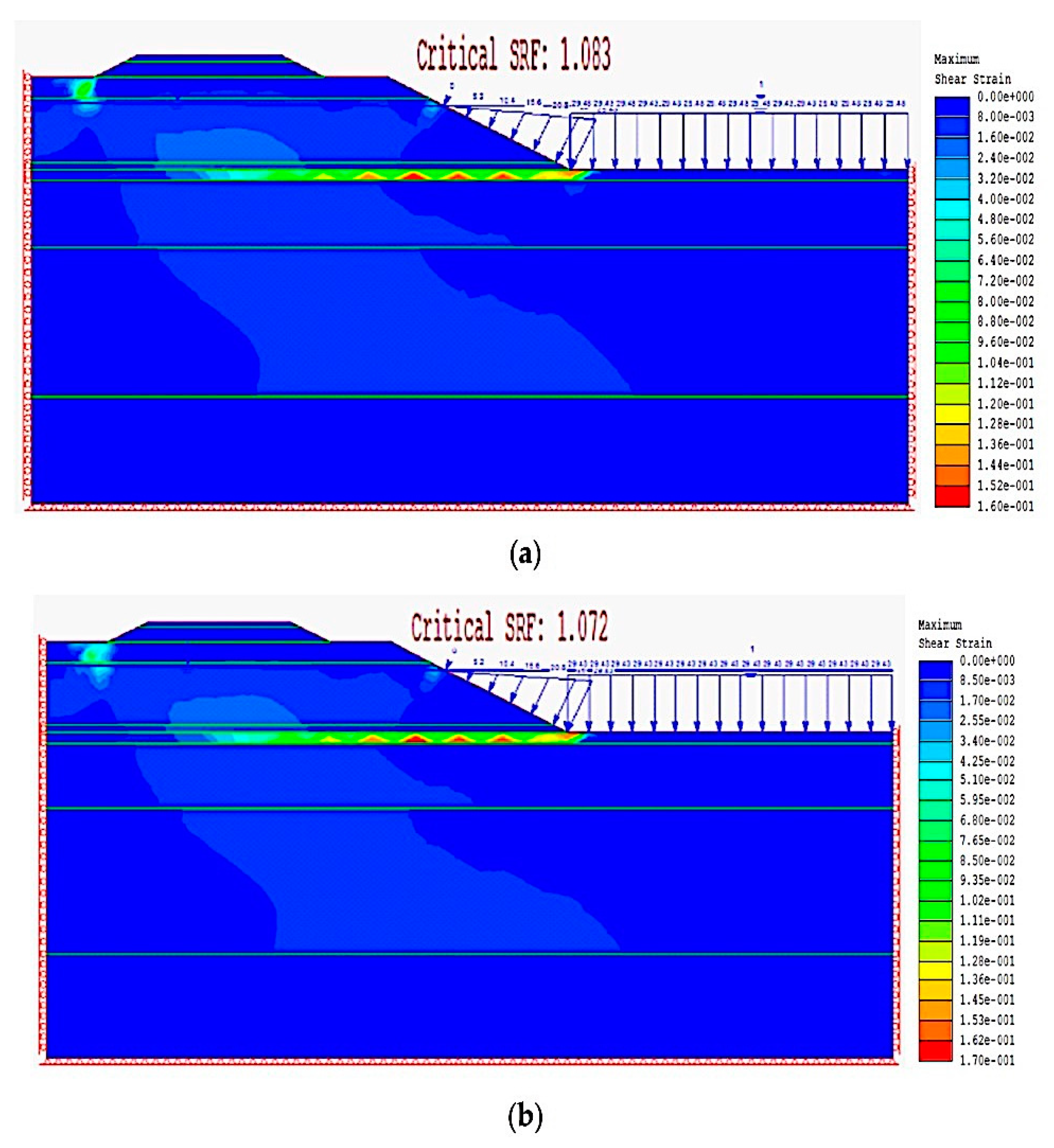
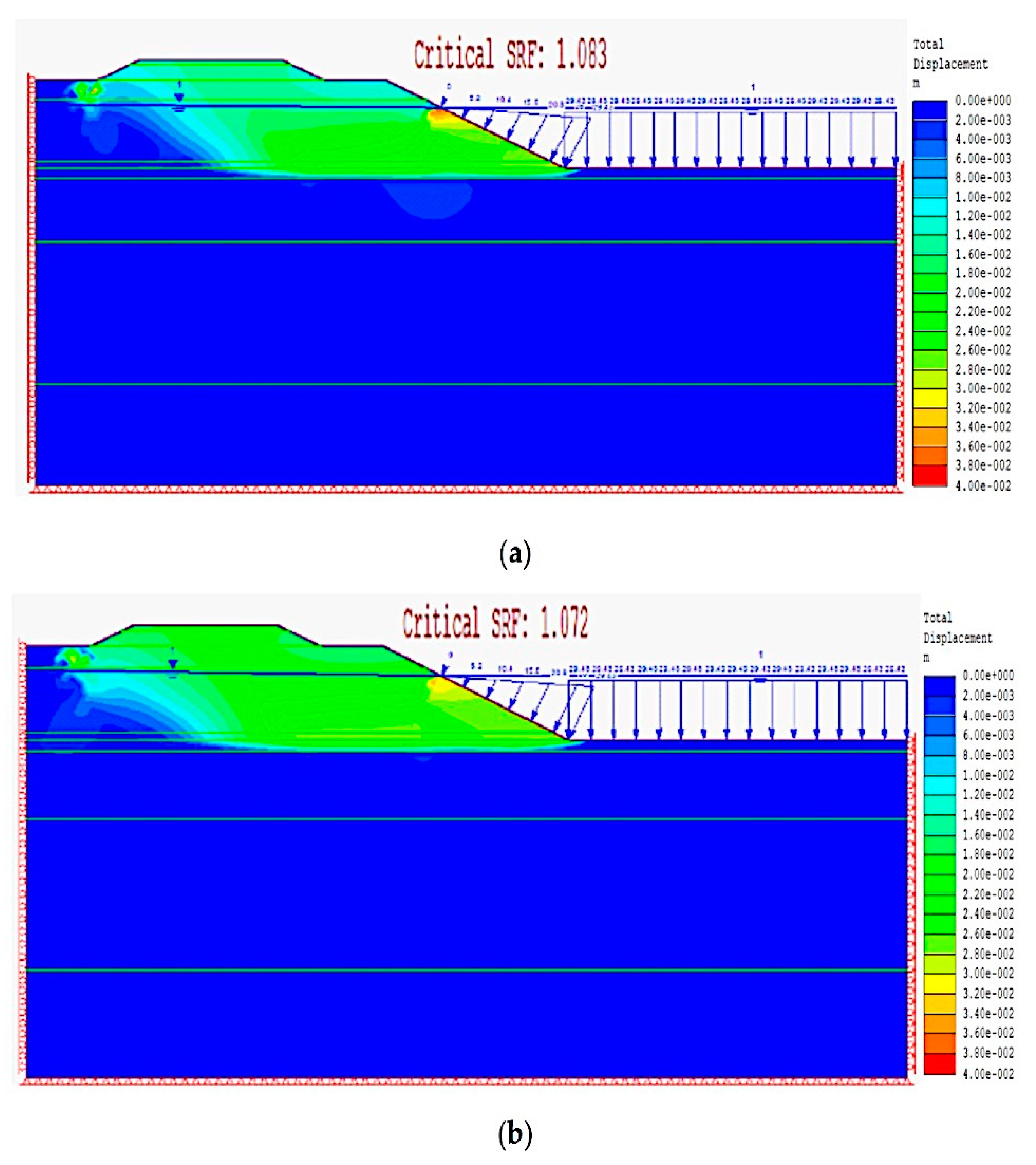
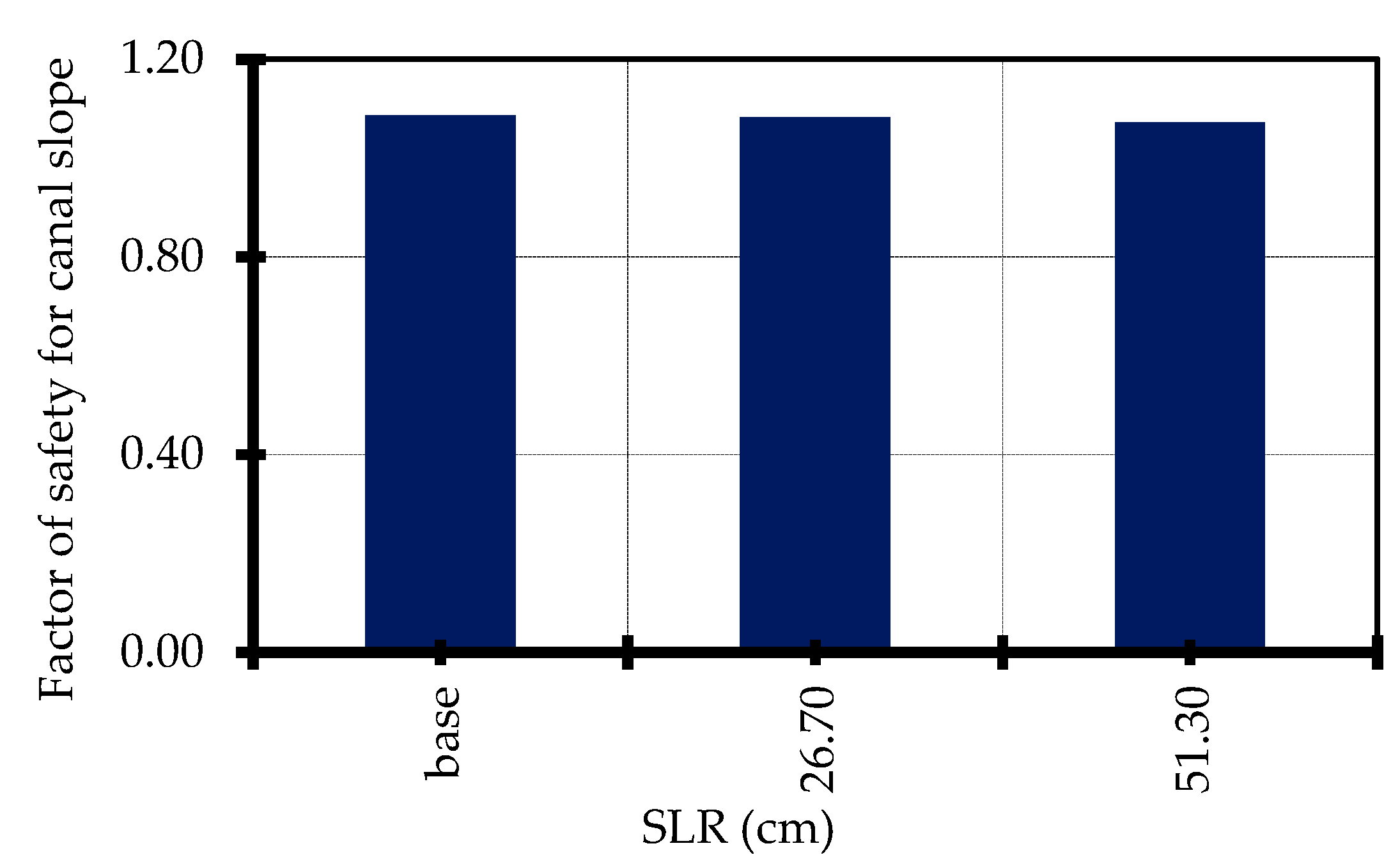
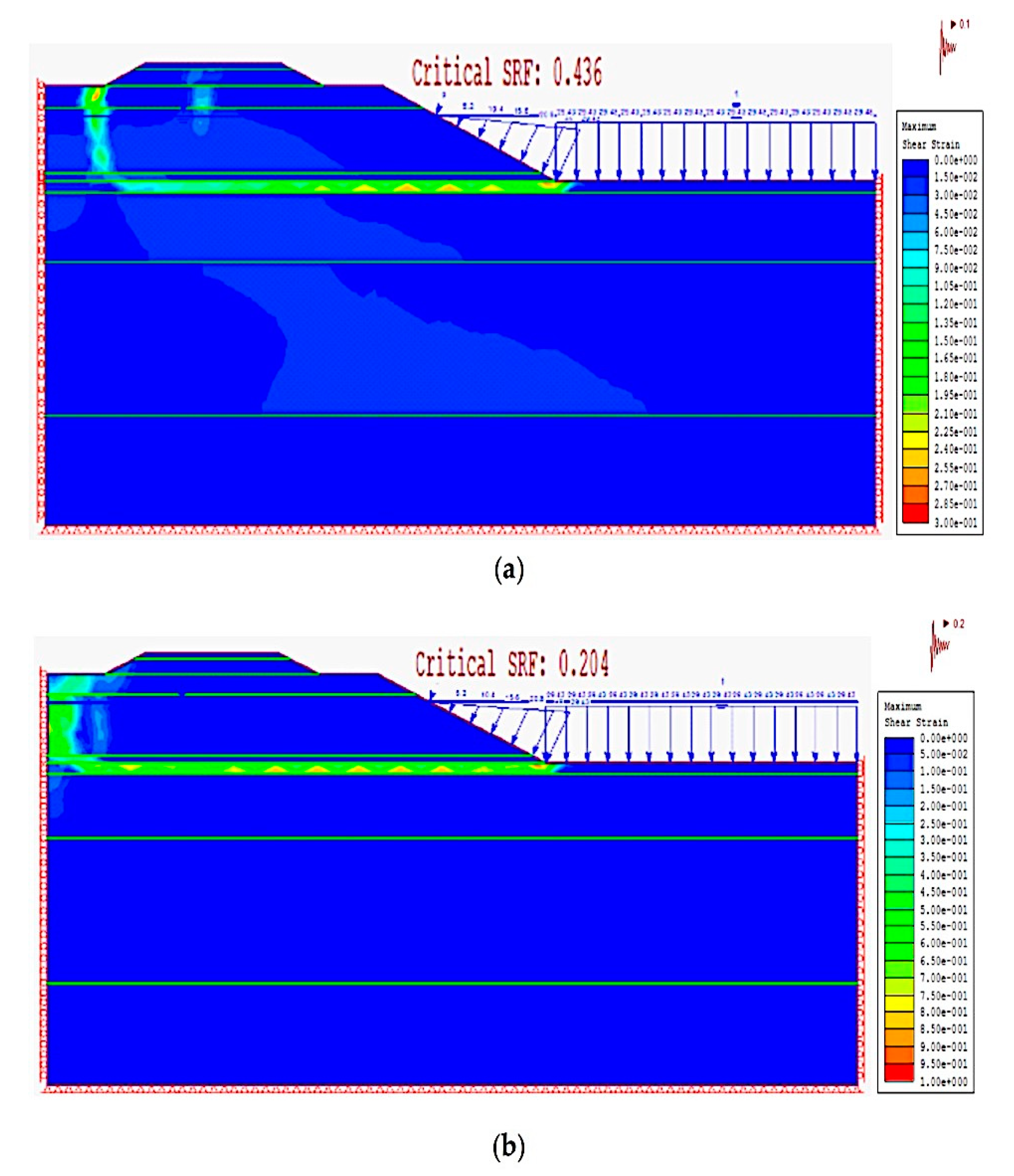
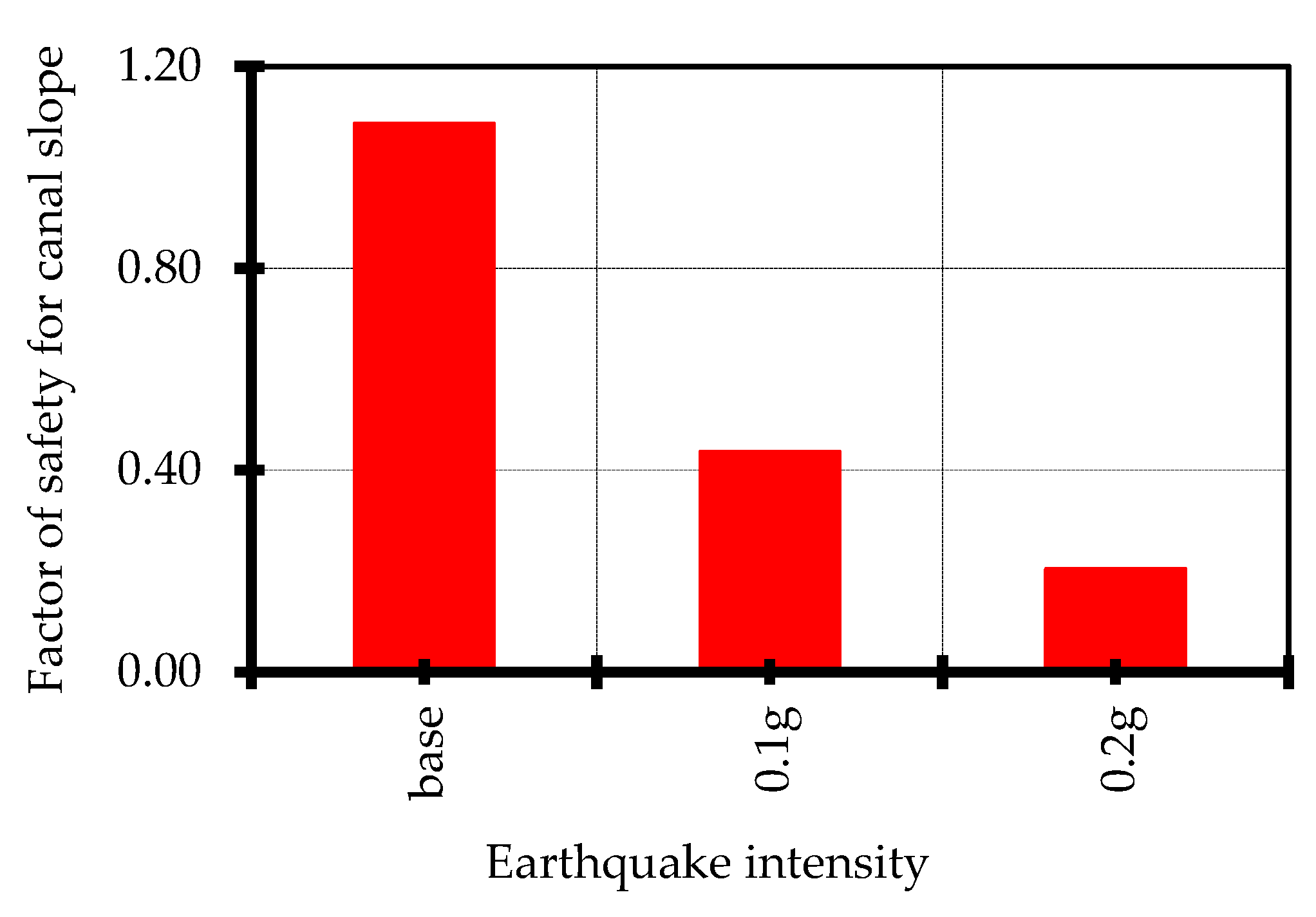
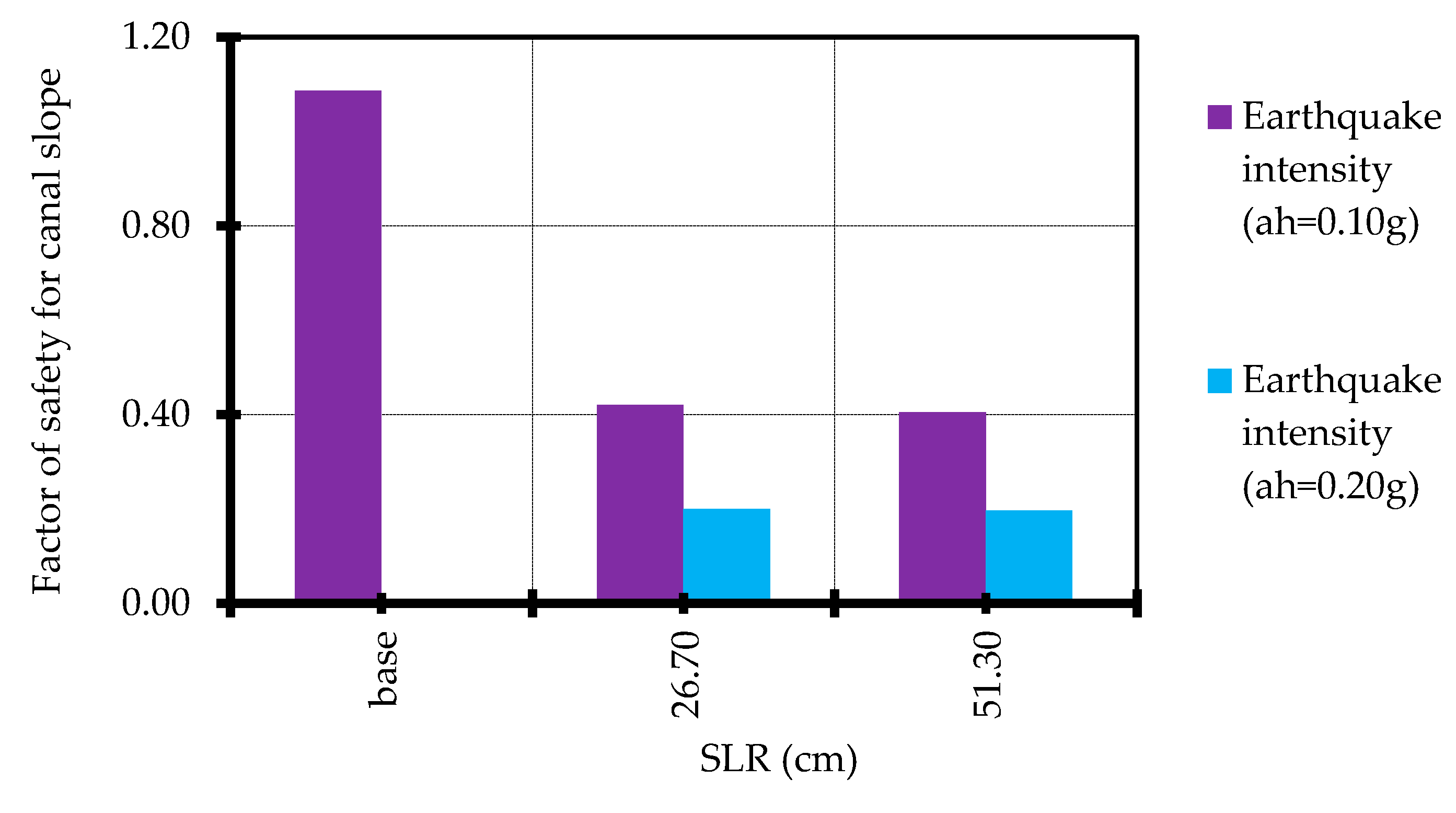
Stage	Scenario	Description	Factor of Safety	Maximum Total Displacement (m)	Total Displacement at Toe (m)
Base case	-	Current situation	1.086	0.038	0.026
SLR	1	SLR 26.70 cm	1.083	0.040	0.030
	2	SLR 51.30 cm	1.072	0.040	0.024
Earthquake Intensity	3	ah 0.1 g	0.436	0.160	0.160
	4	ah 0.2 g	0.204	1.040	0.605
SLR & Earthquake	5	SLR 26.70 cm, ah 0.1 g	0.420	0.170	0.162
	6	SLR 51.30 cm, ah 0.1 g	0.405	0.150	0.142
	7	SLR 26.70 cm, ah 0.2 g	0.200	0.400	0.160
	8	SLR 51.30 cm, ah 0.2 g	0.196	0.400	0.140

and

Table 2. Maximum shear strain for different scenarios.

Stage	Scenario	Description	Factor of Safety	Maximum Shear Strain	Shear Strain at Toe
Base case	-	Current situation	1.086	0.16	0.008
SLR	1	SLR 26.70 cm	1.083	0.16	0.008
	2	SLR 51.30 cm	1.072	0.17	0.009
Earthquake Intensity	3	ah 0.1 g	0.436	0.29	0.015
	4	ah 0.2 g	0.204	0.95	0.050
SLR & Earthquake	5	SLR 26.70 cm, ah 0.1 g	0.420	0.30	0.015
	6	SLR 51.30 cm, ah 0.1 g	0.405	0.30	0.015
	7	SLR 26.70 cm, ah 0.2 g	0.200	0.40	0.040
	8	SLR 51.30 cm, ah 0.2 g	0.196	0.40	0.040

. Figure 20 represents the effect of the combination of SLR and earthquake intensity on canal slope FOS. It is noticed that for SLR 26.70 cm, the FOS decreases by 61.3% and 81.5% from the base case for earthquake intensities equal 0.1 g and 0.2 g respectively. Furthermore, for SLR 51.30 cm, the decrease percentages reach 62.7% and 81.95% from the base case for earthquake intensities equal 0.1 g and 0.2 g respectively.

5. Conclusions

The North Eastern part of Nile Delta aquifer is simulated using the finite difference code (MODFLOW). The groundwater flow under the effect of SLR is investigated to indicate its effect on slope stability of El-Salam Canal, Egypt. The present paper aims to investigate the stability of the canal slopes considering the climate changes through sea level rise and seismic actions. Moreover, the finite element program (Phase 2) is implemented, and FOS are calculated. The models are calibrated and verified through experimental work using permeability and seepage model. As a result of climate changes and sea level rise, the groundwater level raises at the project area, thus led to study two scenarios of SLR by 26.70 cm and 51.30 cm. This action allows the flow of water towards the canal, and reduces the canal slopes stability. Inasmuch of this, the canal slope FOS decreases by about 0.3% and 1.3% respectively. Furthermore, earthquake probability of intensity equals 0.1 g and 0.2 g is studied, it causes a drop in FOS by about 60% and 81% respectively. Finally, it was concluded that the occurrence of earthquake even with small accelerations has a significant effect on the slope stability of El-Salam Canal.