Flood Hazard Scenarios of the Sirba River (Niger): Evaluation of the Hazard Thresholds and Flooding Areas
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Data
2.2.1. Hydrologic Dataset
2.2.2. Topography
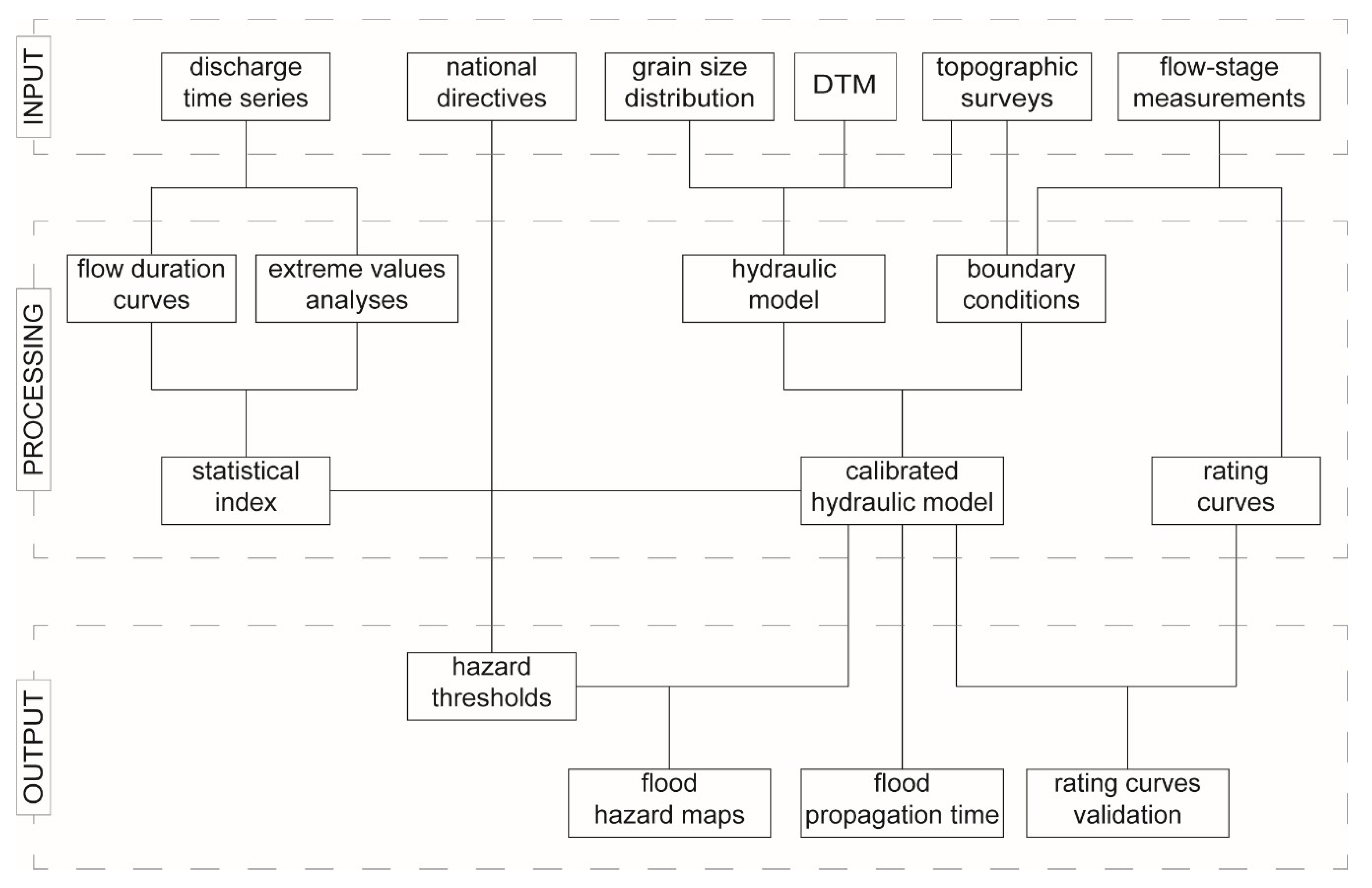
3. Methods
3.1. Hazard Threshold Definition
3.1.1. Field Effects
- -
- Normal condition (green): the characteristic flow of the river with no effects on the riverine activities;
- -
- Yellow alert: frequent flood of the river that slightly affects human activities. It could cause damages to fish nets, water pumps and livestock watering on the river;
- -
- Orange alert: severe flood of the river that has a significant impact on the human life. It can cause damages to the low-altitude houses and avoid access to the wells closest to the river banks;
- -
- Red alert: catastrophic flood that represents a high hazard source for human life. It can cause big damages to a vast portion of the riverine villages with likely human losses.
3.1.2. Statistical Analyses
3.2. Hydraulic Numerical Model
3.2.1. Geometry
3.2.2. Flow and Boundary Conditions
- -
- Steady flow: discharge values corresponding to the different hazard thresholds were used to evaluate the extension of the flood-prone areas. The discharge values are summarized in Table 5;
- -
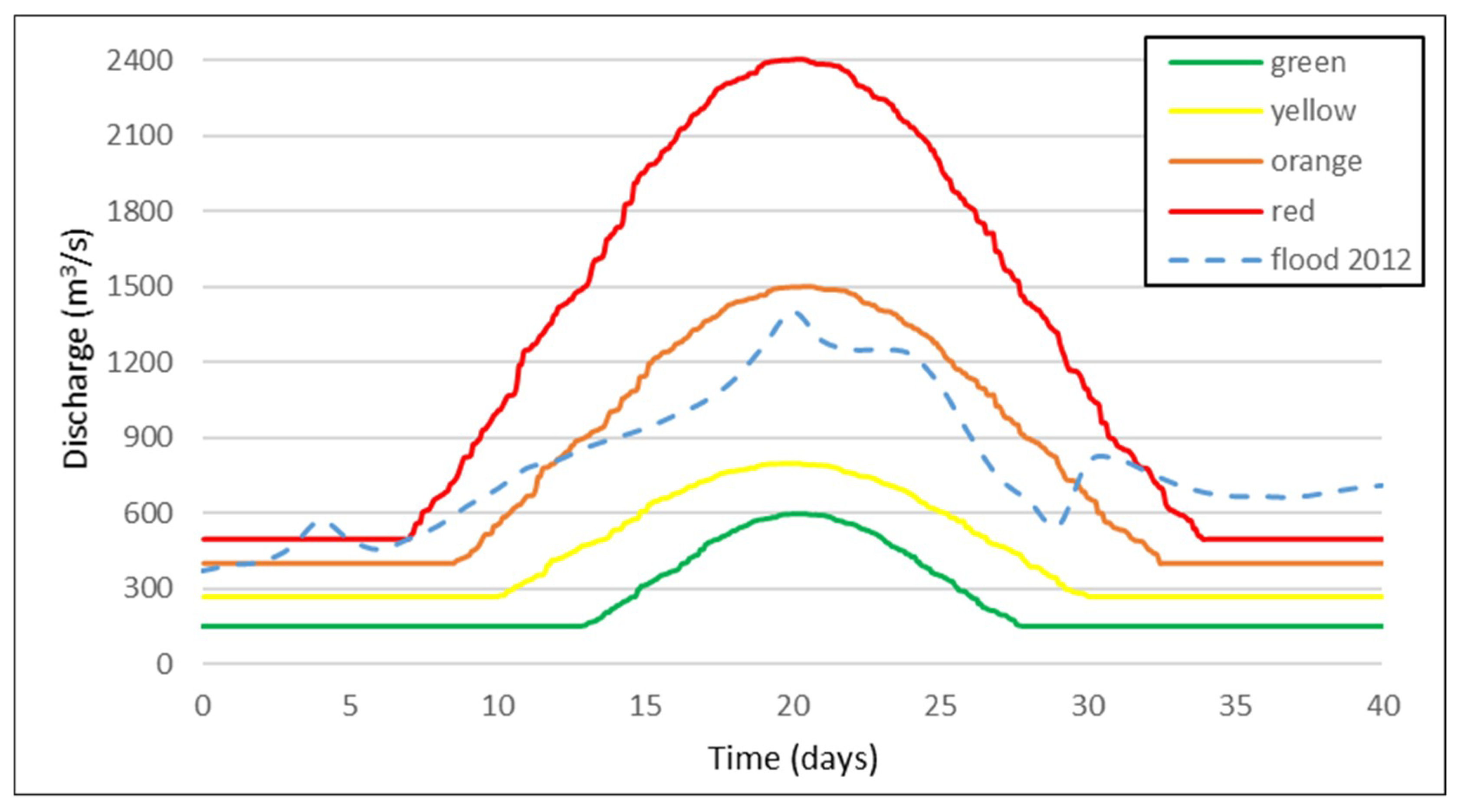
- Unsteady flow: four artificial hydrographs have been run in the hydraulic model to calculate the flood peak propagation time. Each hydrograph was shaped following a gaussian curve according the duration with the temporal extent of 2012 flood event (the highest discharge ever measured) and the peak equal to the hazard thresholds (Figure 6).
3.2.3. Roughness and Calibration
4. Results and Discussion
4.1. Hazard Thresholds
- -
- The normal condition was considered for the flow below the threshold of 600 m3/s that correspond at the Q15 (the discharge meanly exceeded 15 days a year) and the S-RT5;
- -
- The frequent flood comprised the flow in the range 600–800 m3/s where 800 m3/s is related both to FDC (Q5) and GEV analyses (S-RT10 and NS-RT2);
- -
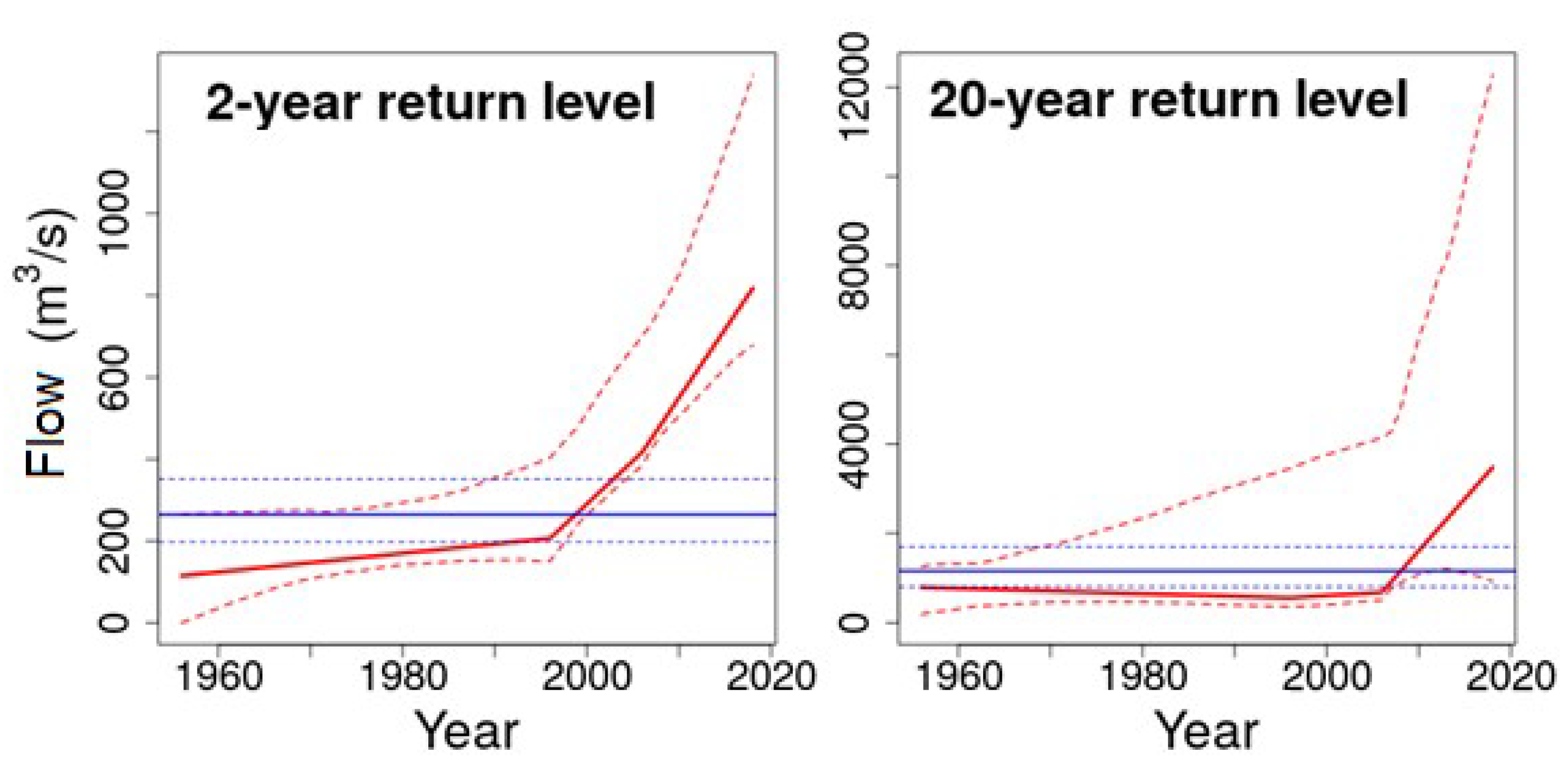
- The severe flood varied from 800 to 1500 m3/s and corresponded to a flood with S-RT30 years that became a NS-RT5, a little greater than the major measured flood event of 2012;
- -
- The catastrophic flood covered up to 2400 m3/s that is the flood event with S-RT equal to 100 years. After the non-stationary analysis, it was ten times more likely (NS-RT10).
4.1.1. Generalized Extreme Value Analysis
4.1.2. Historical Flood Analysis
- most of the events (six out of seven) in recent years (nine out of 18) are emphasizing the increased significance of recent flood events also for the Sirba River;
- adaptation and flood awareness produce a decrease of the damage related to a certain discharge: the flooding event of 2010 (with the maximum recorded discharge until that year) affected more than 20,000 people while the higher event of 2013 affected half of the people (10,000). The same behavior is noticeable compared to the flood of 2007 and the higher event of 2015. The decrease of damages was due to the displacement of settlements after flooding events. The reallocation was noticed both during local surveys and participative meetings with inhabitants.
4.2. Flood Hazard Scenarios
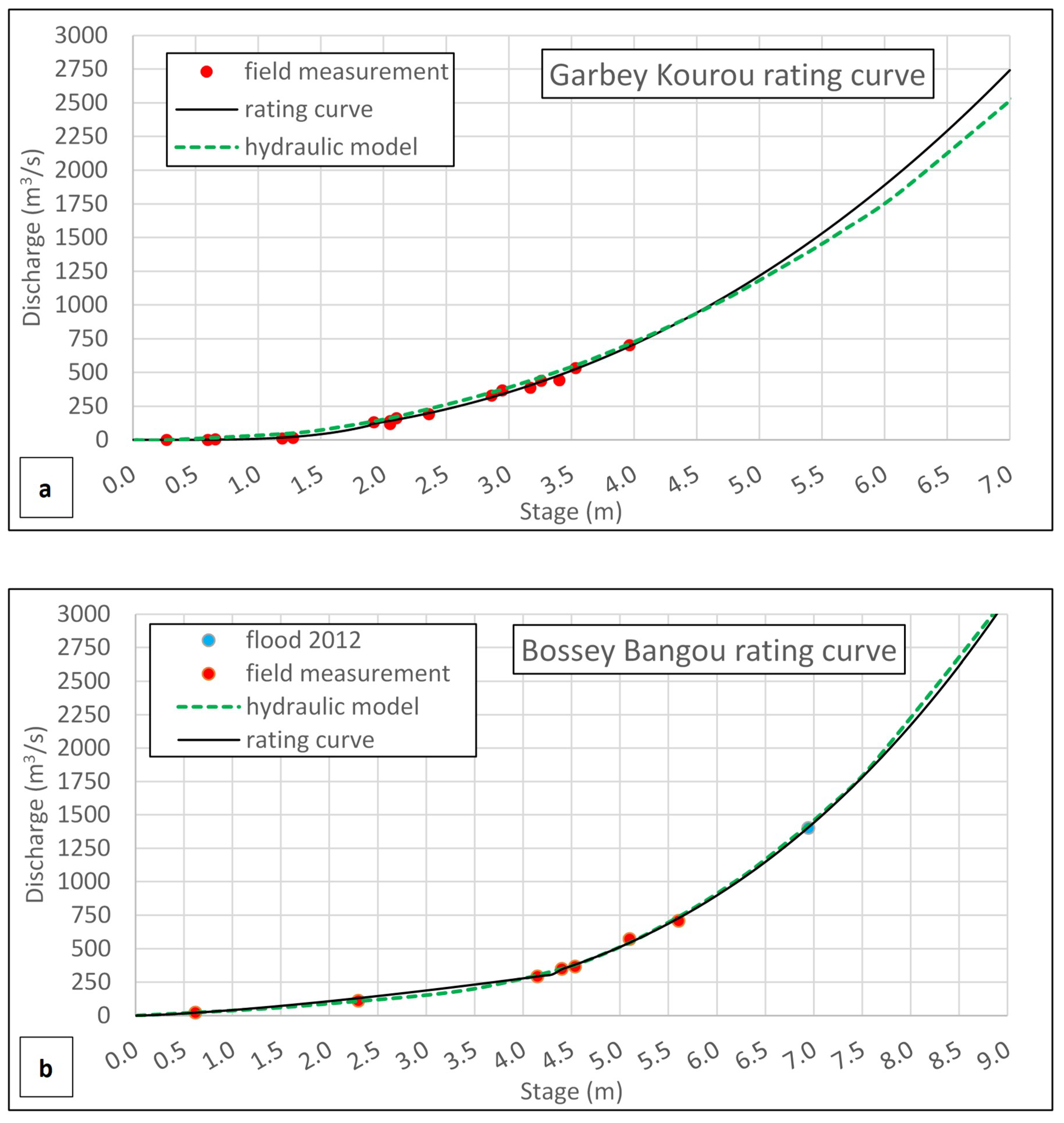
4.3. Evaluation of Hydrometric Station Rating Curves
4.4. Flood Propagation Time
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Berghuijs, W.R.; Aalbers, E.E.; Larsen, J.R.; Trancoso, R.; Woods, R.A. Recent changes in extreme floods across multiple continents. Environ. Res. Lett. 2017, 12, 114035. [Google Scholar] [CrossRef]
- Nka, B.N.; Oudin, L.; Karambiri, H.; Paturel, J.E.; Ribstein, P. Trends in floods in West Africa: Analysis based on 11 catchments in the region. Hydrol. Earth Syst. Sci. 2015, 19, 4707–4719. [Google Scholar] [CrossRef]
- Amogu, O.; Descroix, L.; Yéro, K.S.; Le Breton, E.; Mamadou, I.; Ali, A.; Vischel, T.; Bader, J.-C.; Moussa, I.B.; Gautier, E.; et al. Increasing River Flows in the Sahel? Water 2010, 2, 170–199. [Google Scholar] [CrossRef]
- Descroix, L.; Genthon, P.; Amogu, O.; Rajot, J.L.; Sighomnou, D.; Vauclin, M. Change in Sahelian Rivers hydrograph: The case of recent red floods of the Niger River in the Niamey region. Glob. Planet. Chang. 2012, 98–99, 18–30. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Andersson, J.C.M.; Müller, E.N.; Hattermann, F.F. Climate or land use? - Attribution of changes in river flooding in the Sahel zone. Water Switz. 2015, 7, 2796–2820. [Google Scholar] [CrossRef]
- Descroix, L.; Mahé, G.; Lebel, T.; Favreau, G.; Galle, S.; Gautier, E.; Olivry, J.C.; Albergel, J.; Amogu, O.; Cappelaere, B.; et al. Spatio-temporal variability of hydrological regimes around the boundaries between Sahelian and Sudanian areas of West Africa: A synthesis. J. Hydrol. 2009, 375, 90–102. [Google Scholar] [CrossRef]
- Descroix, L. Processus et enjeux d’eau en Afrique de l’Ouest soudano-sahélienne; Editions des archives contemporaines: Paris, France, 2018; ISBN 978-2-8130-0314-0. [Google Scholar]
- Tarhule, A. Damaging rainfall and flooding: The other Sahel hazards. Clim. Chang. 2005, 72, 355–377. [Google Scholar] [CrossRef]
- Descroix, L.; Guichard, F.; Grippa, M.; Lambert, L.; Panthou, G.; Mahé, G.; Gal, L.; Dardel, C.; Quantin, G.; Kergoat, L.; et al. Evolution of Surface Hydrology in the Sahelo-Sudanian Strip: An Updated Review. Water 2018, 10, 748. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T. Recent trends in the regime of extreme rainfall in the Central Sahel. Int. J. Climatol. 2014, 34, 3998–4006. [Google Scholar] [CrossRef]
- Mahe, G.; Paturel, J.-E.; Servat, E.; Conway, D.; Dezetter, A. The impact of land use change on soil water holding capacity and river flow modelling in the Nakambe River, Burkina-Faso. J. Hydrol. 2005, 300, 33–43. [Google Scholar] [CrossRef]
- Paturel, J.-E.; Ouedraogo, M.; Servat, E.; Mahe, G.; Dezetter, A.; Boyer, J.-F. The concept of rainfall and streamflow normals in West and Central Africa in a context of climatic variability. Hydrol. Sci. J. 2003, 48, 125–137. [Google Scholar] [CrossRef]
- Amani, A.; Paturel, J.-E. Le projet de révision des normes hydrologiques en Afrique de l’Ouest et Afrique Centrale. La Météorologie 2017. [Google Scholar] [CrossRef]
- Aich, V.; Koné, B.; Hattermann, F.F.; Paton, E.N. Time series analysis of floods across the Niger River Basin. Water Switz. 2016, 8, 165. [Google Scholar] [CrossRef]
- Wilcox, C.; Vischel, T.; Panthou, G.; Bodian, A.; Blanchet, J.; Descroix, L.; Quantin, G.; Cassé, C.; Tanimoun, B.; Kone, S. Trends in hydrological extremes in the Senegal and Niger Rivers. J. Hydrol. 2018, 566, 531–545. [Google Scholar] [CrossRef]
- Tiepolo, M.; Tarchiani, V. Risque et adaptation climatique dans la région Tillabéri, Niger; L’Harmattan: Paris, France, 2016; ISBN 978-2-343-08493-0. [Google Scholar]
- Fiorillo, E.; Maselli, F.; Tarchiani, V.; Vignaroli, P. Analysis of land degradation processes on a tiger bush plateau in South West Niger using MODIS and LANDSAT TM/ETM+ data. Int. J. Appl. Earth Obs. Geoinformation 2017, 62, 56–68. [Google Scholar] [CrossRef]
- Fiorillo, E.; Crisci, A.; Issa, H.; Maracchi, G.; Morabito, M.; Tarchiani, V. Recent Changes of Floods and Related Impacts in Niger Based on the ANADIA Niger Flood Database. Climate 2018, 6, 59. [Google Scholar] [CrossRef]
- Erena, S.H.; Worku, H.; De Paola, F. Flood hazard mapping using FLO-2D and local management strategies of Dire Dawa city, Ethiopia. J. Hydrol. Reg. Stud. 2018, 19, 224–239. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Mwale, F.D.; Dulanya, Z. A metric-based assessment of flood risk and vulnerability of rural communities in the Lower Shire Valley, Malawi. Proc. Int. Assoc. Hydrol. Sci. 2015, 370, 139–145. [Google Scholar] [CrossRef]
- Odunuga, S.; Adegun, O.; Raji, S.A.; Udofia, S. Changes in flood risk in Lower Niger–Benue catchments. Proc. Int. Assoc. Hydrol. Sci. 2015, 370, 97–102. [Google Scholar] [CrossRef]
- Ghile, Y.B.; Taner, M.Ü.; Brown, C.; Grijsen, J.G.; Talbi, A. Bottom-up climate risk assessment of infrastructure investment in the Niger River Basin. Clim. Change 2014, 122, 97–110. [Google Scholar] [CrossRef]
- Nkeki, F.N.; Henah, P.J.; Ojeh, V.N. Geospatial Techniques for the Assessment and Analysis of Flood Risk along the Niger-Benue Basin in Nigeria. J. Geogr. Inf. Syst. 2013, 5, 123–135. [Google Scholar] [CrossRef]
- Robi, M.A.; Abebe, A.; Pingale, S.M. Flood hazard mapping under a climate change scenario in a Ribb catchment of Blue Nile River basin, Ethiopia. Appl. Geomat. 2018, 11, 1–14. [Google Scholar] [CrossRef]
- Smith, R. Directive 2008/94/EC of the European Parliament and of the Council of 22 October 2008; Official Journal of the European Union: Bruxelles, Belgium, 2007; pp. 423–426. [Google Scholar]
- Paprotny, D.; Morales-Nápoles, O.; Jonkman, S.N. Efficient pan-European river flood hazard modelling through a combination of statistical and physical models. Nat. Hazards Earth Syst. Sci. 2017, 17, 1267–1283. [Google Scholar] [CrossRef]
- Salman, A.M.; Li, Y. Flood Risk Assessment, Future Trend Modeling, and Risk Communication: A Review of Ongoing Research. Nat. Hazards Rev. 2018, 19, 04018011. [Google Scholar] [CrossRef]
- Alfieri, L.; Salamon, P.; Bianchi, A.; Neal, J.; Bates, P.; Feyen, L. Advances in pan-European flood hazard mapping. Hydrol. Process. 2014, 28, 4067–4077. [Google Scholar] [CrossRef]
- Barredo, J.I.; de Roo, A.; Lavalle, C. Flood risk mapping at European scale. Water Sci. Technol. 2007, 56, 11–17. [Google Scholar] [CrossRef]
- Jha, A.K.; Bloch, R.; Lamond, J. Cities and Flooding: A Guide to Integrated Urban Flood Risk Management for the 21st Century; The World Bank: Washington, DC, USA, 2012; ISBN 978-0-8213-8866-2. [Google Scholar]
- Niger Basin Authority. Available online: http://www.abn.ne/ (accessed on 4 March 2019).
- Tamagnone, P.; Massazza, G.; Pezzoli, A.; Rosso, M. Hydrology of the Sirba River: Updating and Analysis of Discharge Time Series. Water 2019, 11, 156. [Google Scholar] [CrossRef]
- Tiepolo, M.; Bacci, M.; Braccio, S. Multihazard Risk Assessment for Planning with Climate in the Dosso Region, Niger. Climate 2018, 6, 67. [Google Scholar] [CrossRef]
- Bigi, V.; Pezzoli, A.; Rosso, M. Past and Future Precipitation Trend Analysis for the City of Niamey (Niger): An Overview. Climate 2018, 6, 73. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. HydroSHEDS Technical Documentation v1.0; World Wildlife Fund US: Washington, DC, USA, 2006. [Google Scholar]
- Hydrosheds. Available online: https://hydrosheds.cr.usgs.gov/ (accessed on 5 February 2019).
- Niger Data Portal. Available online: http://niger.opendataforafrica.org/ (accessed on 5 February 2019).
- Aich, V.; Koné, B.; Hattermann, F.F.; Müller, E.N. Floods in the Niger basin — analysis and attribution. Nat. Hazards Earth Syst. Sci. Discuss. 2014, 2, 5171–5212. [Google Scholar] [CrossRef]
- Tschakert, P.; Sagoe, R.; Ofori-Darko, G.; Codjoe, S.N. Floods in the Sahel: An analysis of anomalies, memory, and anticipatory learning. Clim. Change 2010, 103, 471–502. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived from Spaceborne Elevation Data. Eos Trans. Am. Geophys. Union 2008, 89, 93. [Google Scholar] [CrossRef]
- Rodríguez, E.; Morris, C.S.; Belz, J.E.; Chapin, E.C.; Martin, J.M.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products; Technical Report; Jet Propulsion Laboratory: Pasadena, CA, USA, 2005. [Google Scholar]
- Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.; Oimoen, M.; Zhang, Z.; Danielson, J.; Krieger, T.; Curtis, B.; Haase, J.; et al. ASTER Global Digital Elevation Model Version 2 – Summary of Validation Results; ASTER GDEM Validation Team: Tokyo, Japan, 2011. [Google Scholar]
- Danielson, J.J.; Gesch, D.B. Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010); US Geological Survey: Reston, VA, USA, 2011; 34.
- International GNSS Service (IGS). Available online: http://www.igs.org/network (accessed on 11 March 2019).
- Bisnath, S.; Wells, D.; Dodd, D. Evaluation of commercial carrier phase-based WADGPS services for marine applications. In Proceedings of the Institute of Navigation GPS/GNSS 2003, Portland, OR, USA, 9–12 September 2003. [Google Scholar]
- Kouba, J.; Héroux, P. GPS Solutions; Wiley: Hoboken, NJ, USA, 2001; ISSN 1080-5370. [Google Scholar]
- Natural Resource Canada. Available online: http://www.nrcan.gc.ca/home (accessed on 13 March 2019).
- Andersson, J.C.M.; Ali, A.; Arheimer, B.; Gustafsson, D.; Minoungou, B. Providing peak river flow statistics and forecasting in the Niger River basin. Phys. Chem. Earth Parts ABC 2017, 100, 3–12. [Google Scholar] [CrossRef]
- Shrestha, S.; Lohpaisankrit, W. Flood hazard assessment under climate change scenarios in the Yang River Basin, Thailand. Int. J. Sustain. Built Environ. 2017, 6, 285–298. [Google Scholar] [CrossRef]
- Zeleňáková, M.; Fijko, R.; Labant, S.; Weiss, E.; Markovič, G.; Weiss, R. Flood risk modelling of the Slatvinec stream in Kružlov village, Slovakia. J. Clean. Prod. 2019, 212, 109–118. [Google Scholar] [CrossRef]
- Chow, Te Ven Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959.
- Ligget, J.A.; Cunge, J.A. Numerical methods of solution of the unsteady flow equations; Water Resources Pubblications: Denver, CO, USA, 1975. [Google Scholar]
- Brunner, G.W. HEC-RAS River Analysis System: Hydraulic Reference Manual Version 5.0; US Army Corps of Engineers-Hydrologic Engineering Center (HEC): Davis, CA, USA, 2016. [Google Scholar]
- Google Earth. Available online: https://earth.google.com/web/ (accessed on 5 February 2019).
- Barnes, H.H. Roughness Characteristics of Natural Channel; United States Geological Survey: Washington, DC, USA, 1967.
- Hicks, D.M.; Mason, P.D. Roughness Characteristics of New Zeland Rivers; Water Resources Survey DSIR Marine and Freshwater: Wellington, New Zeland, 1991; ISBN 0-477-02608-7. [Google Scholar]
- Mays, L.W. Water Resources Engineering; Wiley: Hoboken, NJ, USA, 2010; ISBN 978-0-470-46064-1. [Google Scholar]
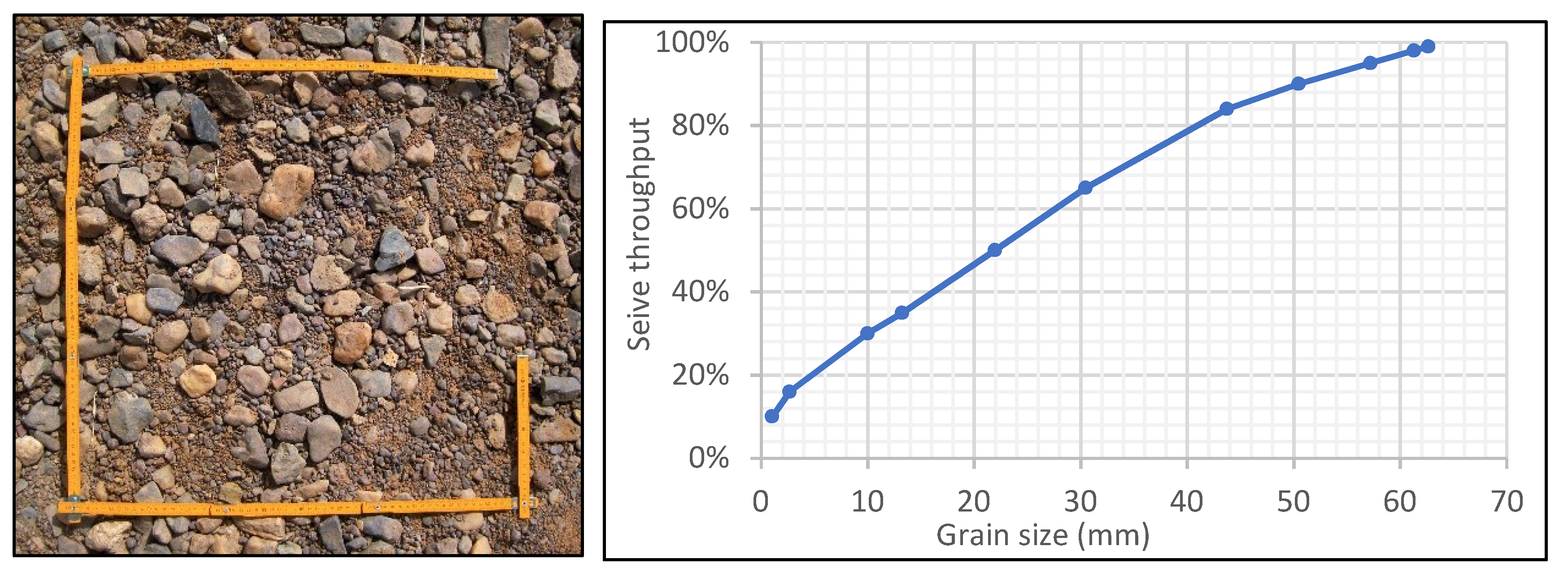
- Detert, M.; Weitbrecht, V. Automatic object detection to analyze the geometry of gravel grains–a free stand-alone tool. In River Flow; Taylor & Francis Group: London, UK, 2012; pp. 595–600. ISBN 978-0-415-62129-8. [Google Scholar]
- Detert, M.; Weitbrecht, V. User guide to gravelometric image analysis by BASEGRAIN. Adv. River Sediment Res. 2013, 1789–1796. [Google Scholar]
- Irmay, S. On steady Flow Formulas in Pipes and Channels. In Proceedings of the IAHR 3rd Congress, Grenoble, France, 5–7 September 1949. [Google Scholar]
- Decreto Legislativo 23 febbraio 2010. Available online: https://www.minambiente.it/sites/default/files/dlgs_23_02_2010_49.pdf (accessed on 5 May 2019).
- Mostert, E.; Junier, S.J. The European flood risk directive: challenges for research. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 4961–4988. [Google Scholar] [CrossRef]
- Tsakiris, G. Critical Technical Issues on the EU Flood Directive. European Water 2009, 29, 39–51. [Google Scholar]
- FANFAR. Available online: http://fanfar.eu/ivp/ (accessed on 5 February 2019).
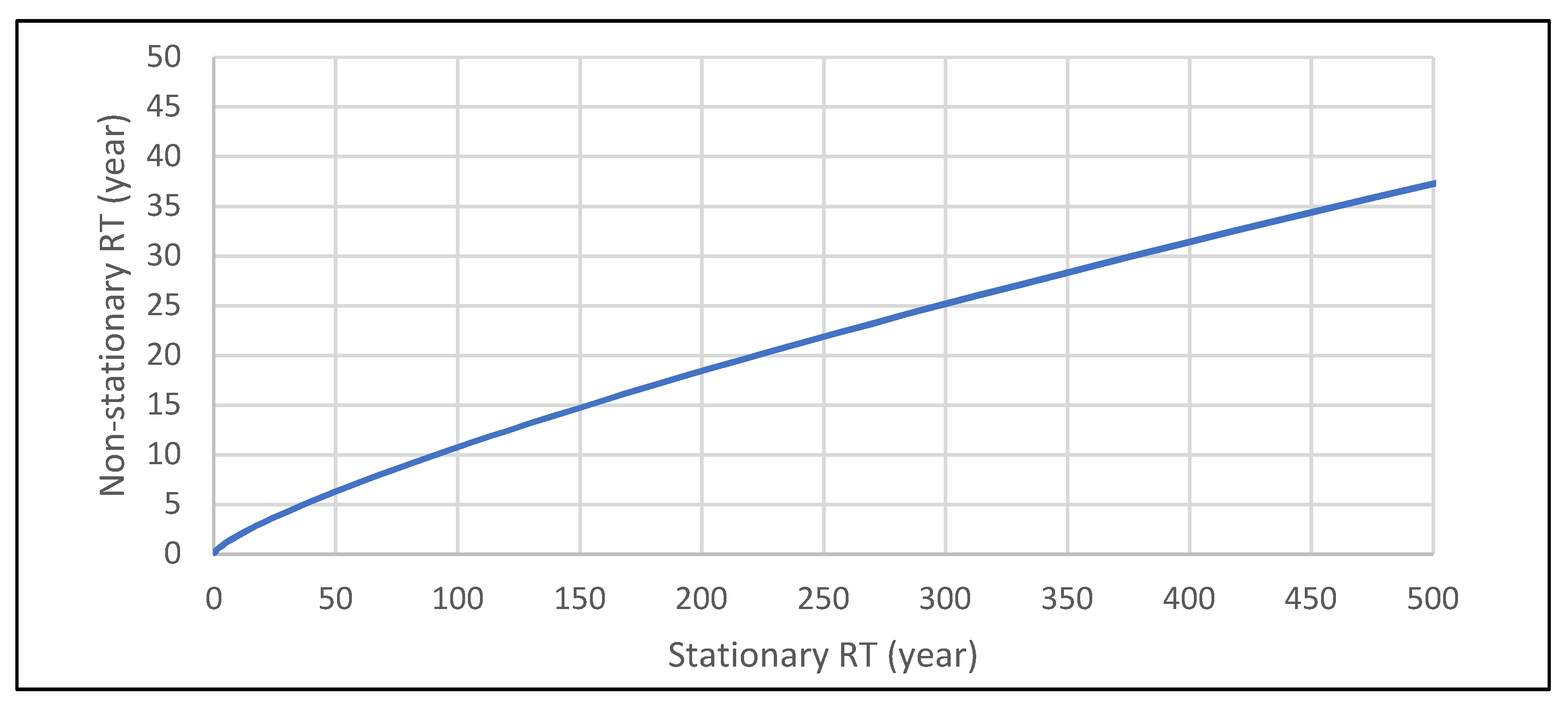
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Bertilsson, L.; Wiklund, K.; de Moura Tebaldi, I.; Rezende, O.M.; Veról, A.P.; Miguez, M.G. Urban flood resilience–A multi-criteria index to integrate flood resilience into urban planning. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Horn, F.; Elagib, N.A. Building socio-hydrological resilient cities against flash floods: Key challenges and a practical plan for arid regions. J. Hydrol. 2018, 564, 125–132. [Google Scholar] [CrossRef]
- Bodoque, J.M.; Díez-Herrero, A.; Amerigo, M.; García, J.A.; Olcina, J. Enhancing flash flood risk perception and awareness of mitigation actions through risk communication: A pre-post survey design. J. Hydrol. 2019, 568, 769–779. [Google Scholar] [CrossRef]
- Sighomnou, D.; Descroix, L.; Genthon, P.; Mahé, G.; Moussa, I.B.; Gautier, E.; Mamadou, I.; Vandervaere, J.P.; Bachir, T.; Coulibaly, B.; et al. La crue de 2012 à Niamey: Un paroxysme du paradoxe du Sahel? Sci. Chang. Planetaires-Secheresse 2013, 24, 3–13. [Google Scholar]
- Arcgis Web Imagery. Available online: http://sampleserver1.arcgisonline.com/ArcGIS/rest/services/Specialty/ESRI_StateCityHighway_USA/MapServer (accessed on 5 February 2019).
- Herschy, R.W. Streamflow Measurement; Taylor & Francis: New York, NY, USA, 2009; ISBN 0-203-9139-4. [Google Scholar]
- Baldassarre, G.D.; Montanari, A. Uncertainty in river discharge observations: a quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913–921. [Google Scholar]
- Juston, J.; Jansson, P.-E.; Gustafsson, D. Rating curve uncertainty and change detection in discharge time series: case study with 44-year historic data from the Nyangores River, Kenya: Rating curve uncertainty and change detection in discharge time series. Hydrol. Process. 2014, 28, 2509–2523. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. GloFAS – global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 12293–12332. [Google Scholar] [CrossRef]
- Andersson, J.C.M.; Arheimer, B.; Traoré, F.; Gustafsson, D.; Ali, A. Process refinements improve a hydrological model concept applied to the Niger River basin. Hydrol. Process. 2017, 31, 4540–4554. [Google Scholar] [CrossRef]
- Douinot, A.; Roux, H.; Dartus, D. Modelling errors calculation adapted to rainfall – Runoff model user expectations and discharge data uncertainties. Environ. Model. Softw. 2017, 90, 157–166. [Google Scholar] [CrossRef][Green Version]
- Koriche, S.A.; Rientjes, T.H.M. Application of satellite products and hydrological modelling for flood early warning. Phys. Chem. Earth Parts ABC 2016, 93, 12–23. [Google Scholar] [CrossRef]



| Sirba River Basin | Sirba River | |||||||
|---|---|---|---|---|---|---|---|---|
| Surface (km2) | Height (meter a.s.l.) | Slope (%) | Length (km) | Slope (%) | ||||
| Total | BF (%) | NE (%) | max | mean | min | Mean | max | Mean |
| 39,138 | 93% | 7% | 444 | 286 | 181 | 1.12 | 439 | 0.02 |
| Parameters | Value | |
|---|---|---|
| surface irregularities | 0.005 | |
| variations of the cross-section | 0 | |
| influence of obstruction | 0 | |
| type of vegetation | 0.005 | |
| degree of meandering | 1 | |
| Type of Channel and Description | Major Stream | Flood Plain | n (s/m1/3) |
|---|---|---|---|
| irregular and rough section | X | 0.033 | |
| regular and rectilinear channel (covered by fine sediments) | X | 0.02 | |
| irregular and rough bedrock | X | 0.045 | |
| light brush and trees (in summer) | X | 0.06 | |
| mature field crops | X | 0.04 | |
| scattered brush, heavy weeds | X | 0.04–0.05 | |
| irregular and rough bedrock | X | 0.08 | |
| heavy stand of timber, a few down trees, little undergrowth | X | 0.1 |
| Description | Bossey Bangou | Touré | Larba Birno | Garbey Kourou | Bridge | Confluence | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| XS | 108 | 107.95 | 107.75 | 38.52 | 15.69 | 9.28 | 9.2 | 8.97 | 8.87 | 2.47 | 2.38 | 0.32 |
| MEAS | 219.12 | 216.58 | 216.52 | 202.1 | 196.09 | 192.22 | 192.33 | 192.02 | 191.95 | 188.57 | 188.51 | 188.30 |
| SIM | 219.09 | 216.62 | 216.58 | 202.05 | 196.17 | 192.40 | 192.33 | 192.14 | 192.06 | 188.62 | 188.58 | 188.30 |
| ∆H (m) | 0.03 | −0.04 | −0.06 | 0.05 | −0.08 | −0.18 | 0 | −0.12 | −0.11 | −0.05 | −0.07 | 0 |
| Color | Q max (m3/s) | Index | Magnitude | Expected Damages | ||
|---|---|---|---|---|---|---|
| FDC (QXX) | SGEV (S-RTXX) | NSGEV (NS-RTXX) | ||||
| green | 600 | 15 | 5 | / | normal condition | / |
| yellow | 800 | 5 | 10 | 2 | frequent flood | fish nets, water pumps, livestock |
| orange | 1500 | / | 30 | 5 | severe flood | wells, boreholes, low-altitude houses, barns, and crops |
| red | 2400 | / | 100 | 10 | catastrophic flood | extended area at medium–low altitude (houses, barns, and crops) |
| Year | Qmax (m3/s) | Number of Villages | Affected Villages | Involved People |
|---|---|---|---|---|
| 1998 | 651 | ND | ND | ND |
| 2007 | 626 | 4 | Garbey Kourou, Larba Birno, Larba Koira Zeno, Tallé | 11,017 |
| 2009 | 618 | ND | ND | ND |
| 2010 | 1216 | 18 | Bossia, Guidere, Koutoume, Larba Birno, Larba Koira Zeno, Tallé, Tchawa, Touré, Bobonbongou, Boksay, Daberou, Dirim Halidou, Dirim Sonrhai, Gawana, Kobaniou, Koutoume B., Larba Touloumbo, Tiaptey T. | 21,325 |
| 2012 | 1403 | ND | ND | ND |
| 2013 | 1349 | 3 | Garbey Kourou, Tallé, Touré | 10,383 |
| 2015 | 1101 | 1 | Larba Birno | 3687 |
| Color | Scenario | A (km2) | Increment |
|---|---|---|---|
| green | normal condition | 30.12 | / |
| yellow | frequent flood | 37.77 | 25% |
| orange | severe flood | 60.13 | 100% |
| red | catastrophic flood | 76.86 | 155% |
| Rating Curve | Validity | Ranges (m) | a | b | R2 |
|---|---|---|---|---|---|
| Bossey Bangou | 2018–now | [0–4.4) | 41.965 | 1.366 | 0.992 |
| [4.4–8] | 3.664 | 3.071 | 0.988 | ||
| Garbey Kourou | 2004–now | [0–1.9) | 8.238 | 4.025 | 0.972 |
| [1.9–5] | 24.769 | 2.419 | 0.986 |
| villages | Bossey Bangou | Goundoulo | Tchawa | Tchambi | Boulkagou | Touré | Guidare | Larba Birno | Garbey Kourou | Tallé | Confluence |
|---|---|---|---|---|---|---|---|---|---|---|---|
| XS | 108 | 86.16 | 81.5 | 65.58 | 56.28 | 39.44 | 25.88 | 16.58 | 8.21 | 4.89 | 0.32 |
| T (h) | 0 | 5 | 7 | 11 | 15 | 20 | 24 | 26 | 28 | 28 | 29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massazza, G.; Tamagnone, P.; Wilcox, C.; Belcore, E.; Pezzoli, A.; Vischel, T.; Panthou, G.; Housseini Ibrahim, M.; Tiepolo, M.; Tarchiani, V.; et al. Flood Hazard Scenarios of the Sirba River (Niger): Evaluation of the Hazard Thresholds and Flooding Areas. Water 2019, 11, 1018. https://doi.org/10.3390/w11051018
Massazza G, Tamagnone P, Wilcox C, Belcore E, Pezzoli A, Vischel T, Panthou G, Housseini Ibrahim M, Tiepolo M, Tarchiani V, et al. Flood Hazard Scenarios of the Sirba River (Niger): Evaluation of the Hazard Thresholds and Flooding Areas. Water. 2019; 11(5):1018. https://doi.org/10.3390/w11051018
Chicago/Turabian StyleMassazza, Giovanni, Paolo Tamagnone, Catherine Wilcox, Elena Belcore, Alessandro Pezzoli, Theo Vischel, Gérémy Panthou, Mohamed Housseini Ibrahim, Maurizio Tiepolo, Vieri Tarchiani, and et al. 2019. "Flood Hazard Scenarios of the Sirba River (Niger): Evaluation of the Hazard Thresholds and Flooding Areas" Water 11, no. 5: 1018. https://doi.org/10.3390/w11051018
APA StyleMassazza, G., Tamagnone, P., Wilcox, C., Belcore, E., Pezzoli, A., Vischel, T., Panthou, G., Housseini Ibrahim, M., Tiepolo, M., Tarchiani, V., & Rosso, M. (2019). Flood Hazard Scenarios of the Sirba River (Niger): Evaluation of the Hazard Thresholds and Flooding Areas. Water, 11(5), 1018. https://doi.org/10.3390/w11051018










