Optimization of Pump Start-Up Depth in Drainage Pumping Station Based on SWMM and PSO
Abstract
1. Introduction
2. Methodology
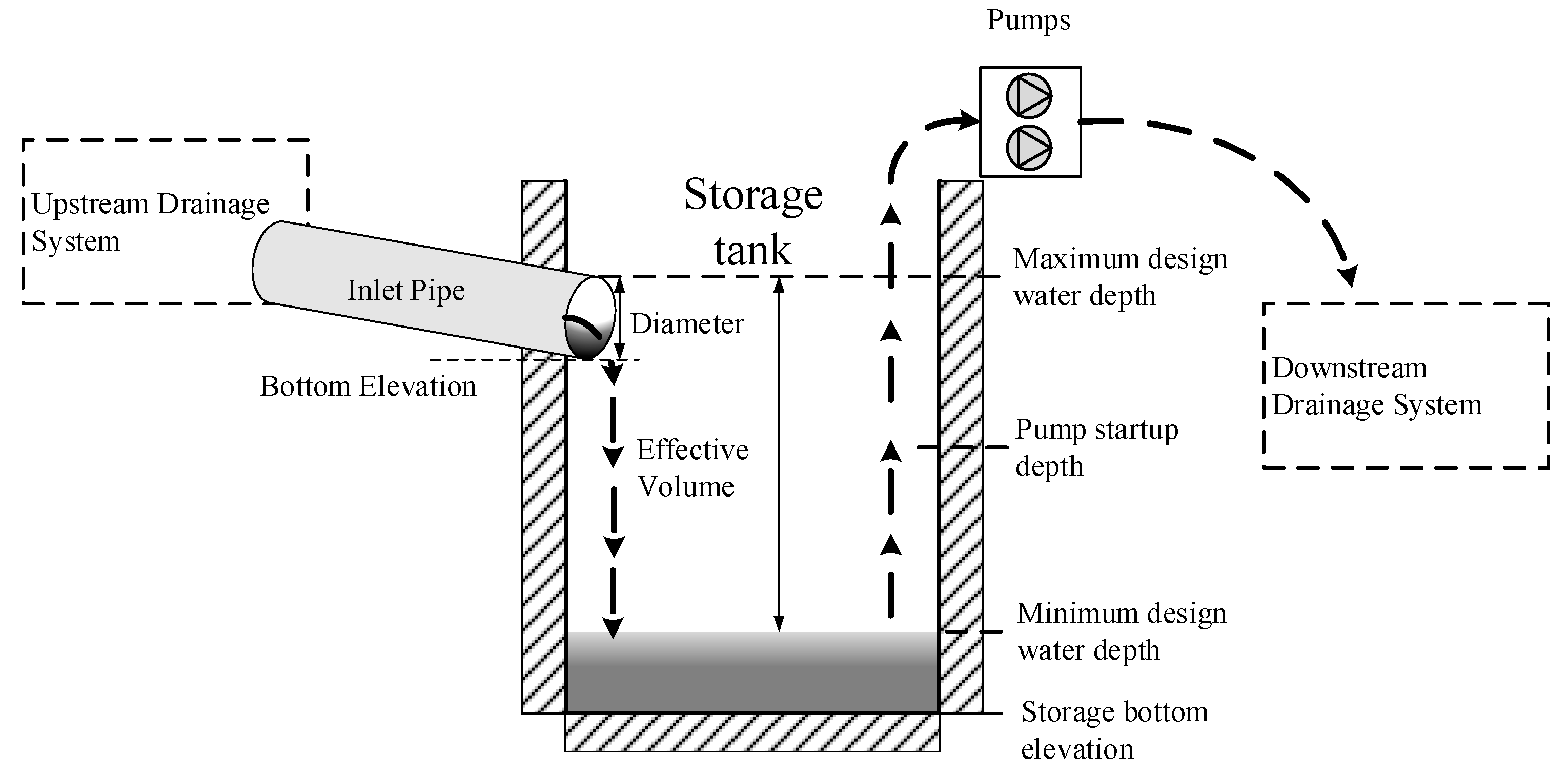
2.1. Operational Optimization of Start-Up and Shutoff of Pumps
- (1)
- The effective volume of the storage tank was calculated according to the upstream and the downstream flow within the pipe network of the pumping station.
- (2)
- The bottom area of the storage tank depended on the actual land use condition.
- (3)
- The total flow of the pump depended on the design flow of the downstream pipe network.
- (4)
- The number of pumps generally ranged from two to eight.
- (5)
- The minimum design water depth of the storage tank depended on the requirements of the suction head of the pumps.
- (6)
- The maximum design water depth of the storage tank was generally equal to the top of the inlet pipe or was set to ensure that the storage tank will not overflow during the operation of the pumping station.
- (7)
- During the operation of the pump, the number of start-up/shutoff times should not exceed six times per hour.
- (1)
- The pump start-up depth was set to ensure that the water depth in the storage tank did not exceed the maximum design water depth during the operation of the pumping station.
- (2)
- The pump start-up depth was set to ensure that the start-up/shutoff times of each pump were not too numerous during the operation of the pumping station, and the phenomenon of frequent start-ups and shutoffs was avoided.
2.2. Optimization Model of the Start-Up Depths of Pumps
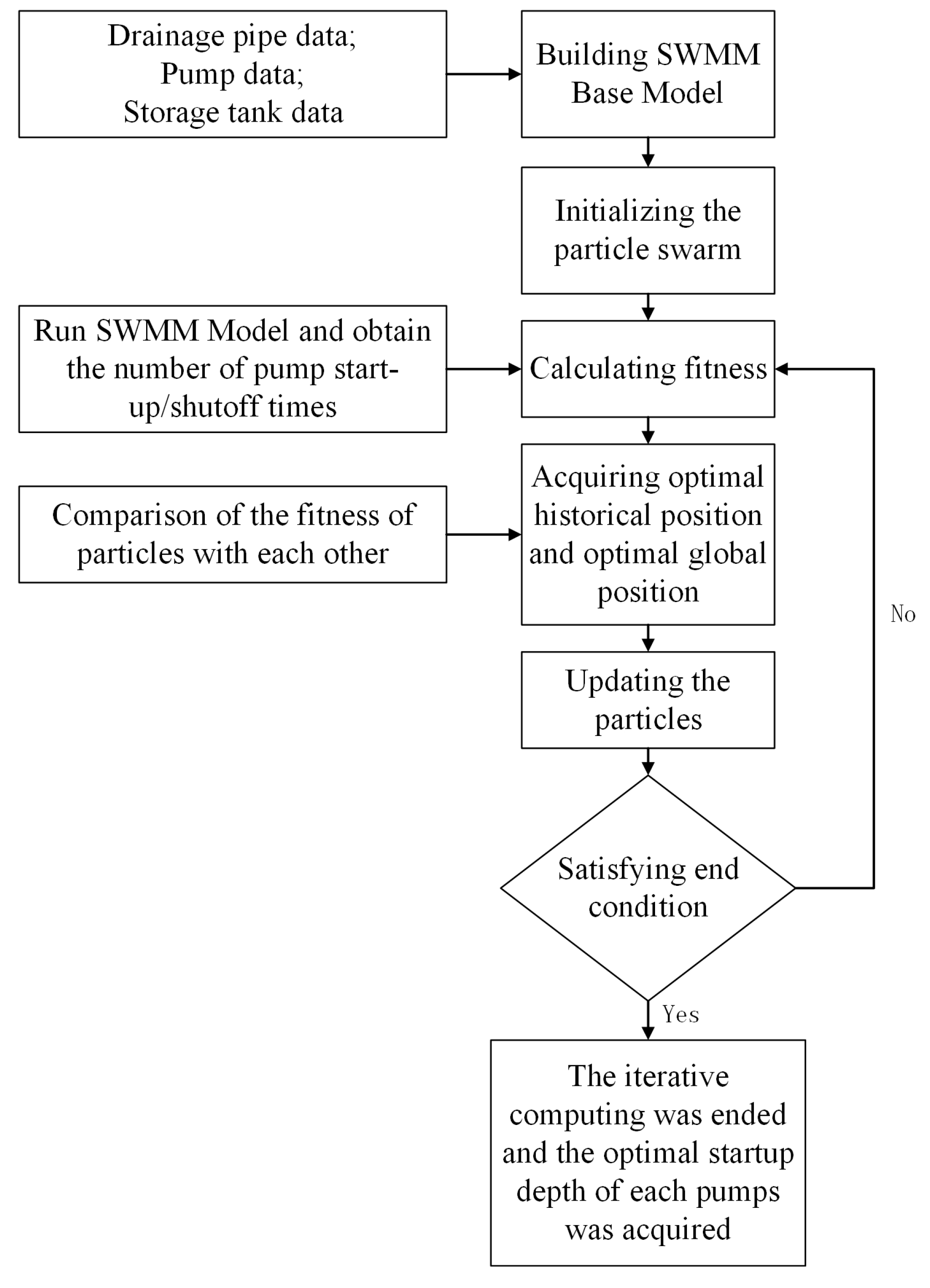
2.3. Solution to the Optimization Model of Start-Up Depths of Pumps
3. Materials and Methods
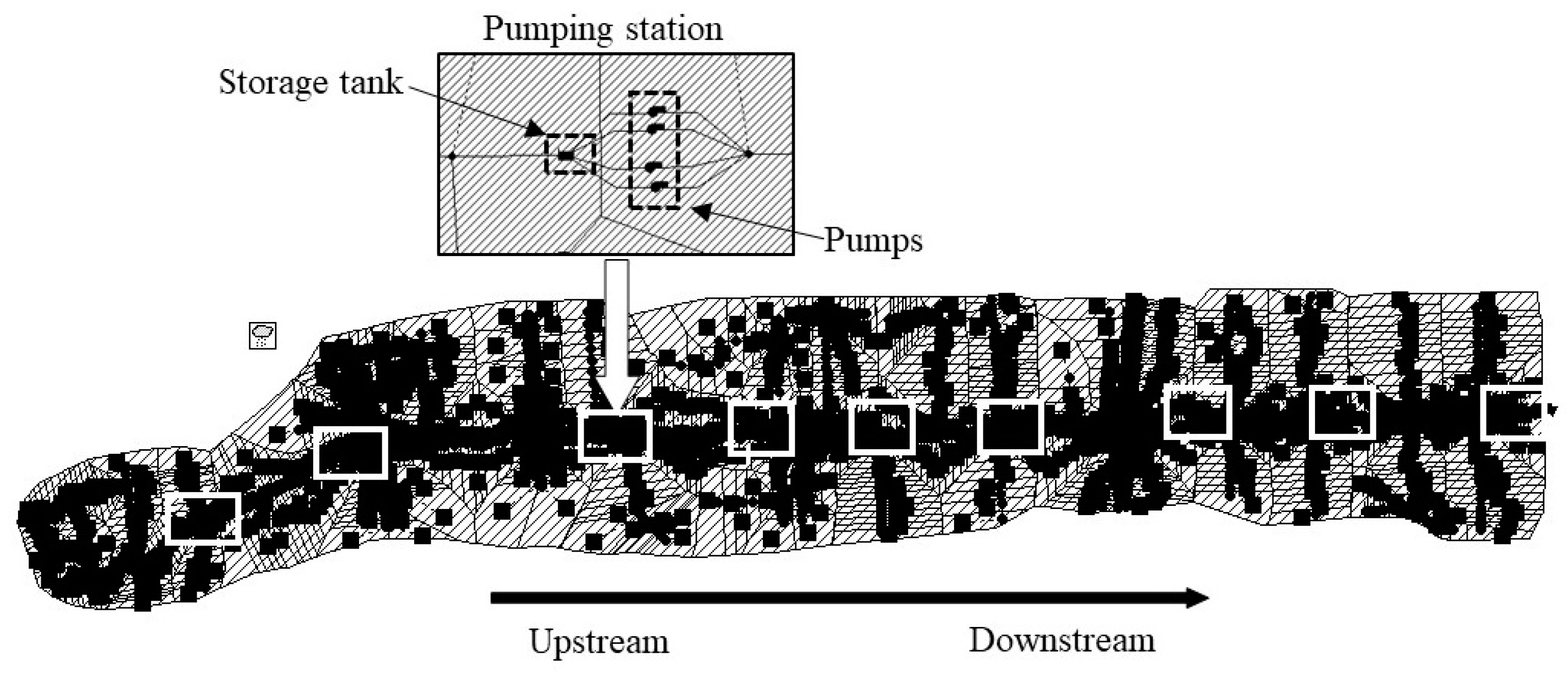
3.1. Optimization of the Start-Up Depths of Pumps for Multistage Drainage Pumping Stations
3.2. Optimization of the Start-Up Depths of Pumps for Each Single Pumping Station
4. Results and Discussion
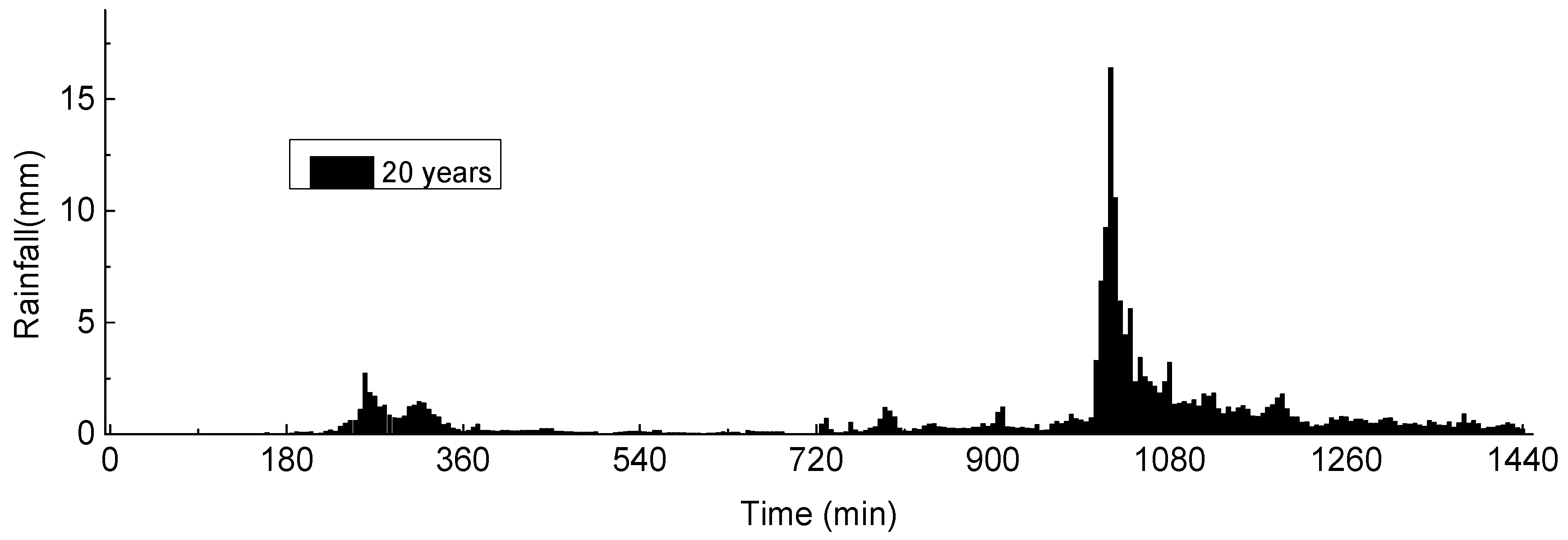
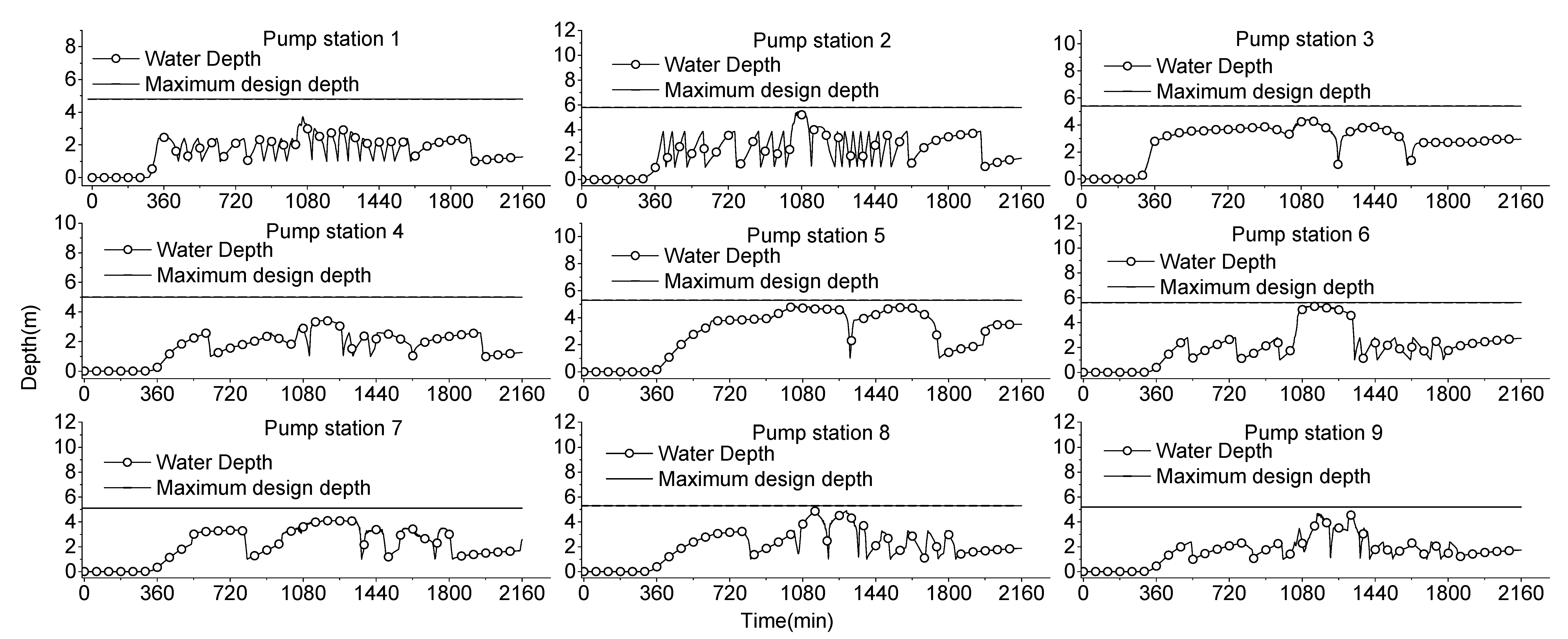
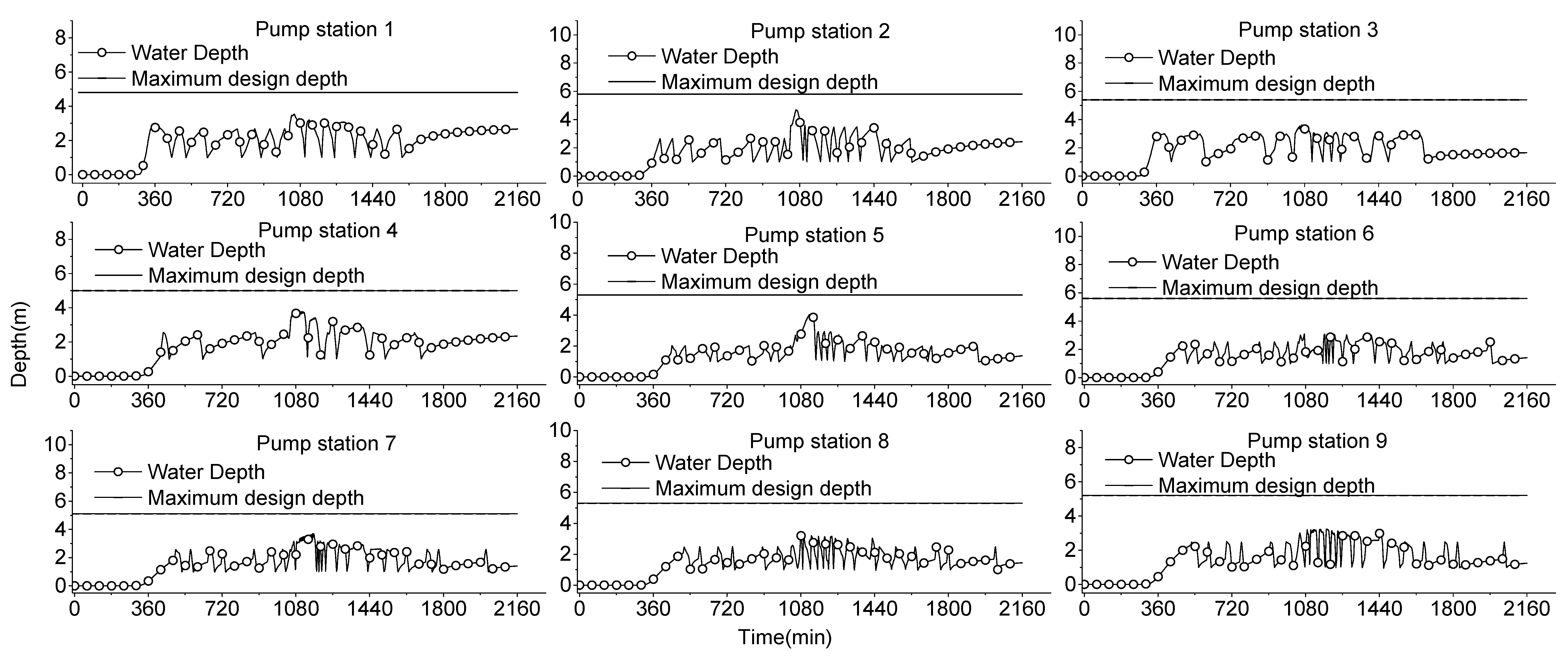
4.1. Verification of the Two Methods
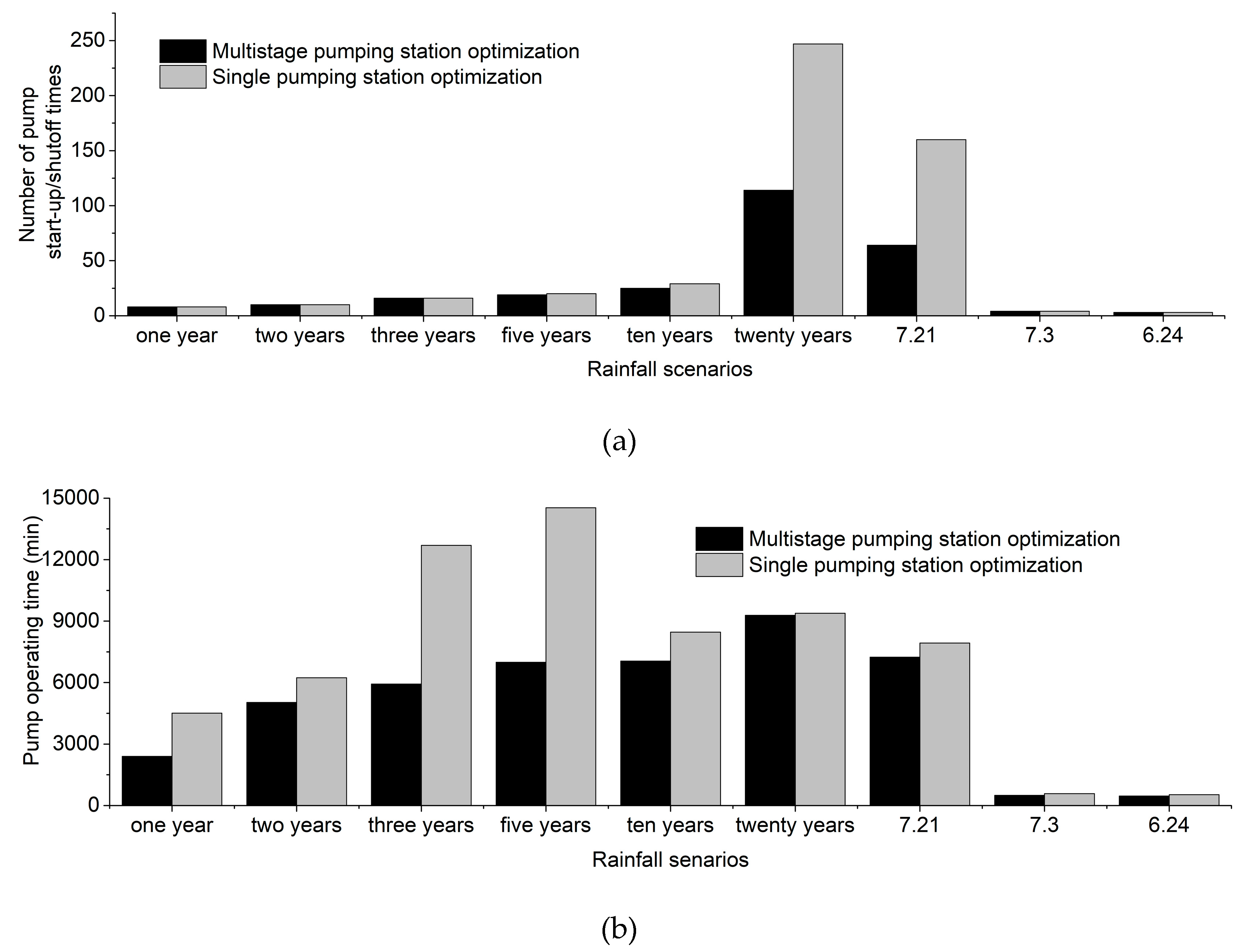
4.2. Comparison of Number of Pump Start-Up/Shutoff Times
4.3. Comparison of Pump Operating Time
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, J.; Forman, B.A.; Davis, A.P. Probabilistic Stormwater Runoff and Water Quality Modeling of a Highway in Suburban Maryland. J. Hydrol. Eng. 2018, 23, 05017034. [Google Scholar] [CrossRef]
- Hsu, M.; Chen, S.; Chang, T.; Chen, A. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef]
- Chen, X.; Ji, P.; Wu, Y.; Zhao, Y.; Zeng, L. Coupling simulation of overland flooding and underground network drainage in a coastal nuclear power plant. Nucl. Eng. Des. 2017, 325, 129–134. [Google Scholar] [CrossRef]
- Markus, I.; Sunela, R.P. A visual tool to calculate optimal control strategy for non-identical pumps working in parallel, taking motor and VSD efficiencies into account. Water Supply 2015, 15, 1115–1122. [Google Scholar] [CrossRef]
- Eui, H.L.; Joong, H.K. Convertible operation techniques for pump stations sharing centralized reservoirs for improving resilience in urban drainage systems. Water 2017, 9, 843. [Google Scholar] [CrossRef]
- Torregrossa, D.; Hansen, J.; Hernández-Sancho, F.; Cornelissen, A.; Schutz, G.; Leopold, U. A data-driven methodology to support pump performance analysis and energy efficiency optimization in Waste Water Treatment Plants. Appl. Energy 2017, 208, 1430–1440. [Google Scholar] [CrossRef]
- Yazdi, J.; Choi, H.; Kim, J. A methodology for optimal operation of pumping stations in urban drainage systems. J. Hydro-Environ. 2016, 11, 101–112. [Google Scholar] [CrossRef]
- Lee, E.H.; Lee, Y.S.; Joo, J.G.; Jung, D.; Kim, J.H. Flood Reduction in Urban Drainage Systems: Cooperative Operation of Centralized and Decentralized Reservoirs. Water 2016, 8, 469. [Google Scholar] [CrossRef]
- Lee, E.H.; Lee, Y.S.; Joo, J.G.; Jung, D.; Kim, J.H. Investigating the Impact of Proactive Pump Operation and Capacity Expansion on Urban Drainage System Resilience. J. Water Resour. Plan. Manag. 2017, 143, 4017024. [Google Scholar] [CrossRef]
- Yazdi, J.; Kim, J.H. Intelligent Pump Operation and River Diversion Systems for Urban Storm Management. J. Hydrol. Eng. 2015, 20, 04015031. [Google Scholar] [CrossRef]
- Wei, C.-C.; Hsu, N.-S.; Huang, C.-L. Two-Stage Pumping Control Model for Flood Mitigation in Inundated Urban Drainage Basins. Water Resour. Manag. 2013, 28, 425–444. [Google Scholar] [CrossRef]
- Hsu, N.-S.; Huang, C.-L.; Wei, C.-C. Intelligent real-time operation of a pumping station for an urban drainage system. J. Hydrol. 2013, 489, 85–97. [Google Scholar] [CrossRef]
- Graber, S. David Generalized method for storm-water pumping station design. J. Hydrol. Eng. 2010, 15, 901–908. [Google Scholar] [CrossRef]
- Graber, S. David Closure to “Generalized method for storm-water pumping station design” by S.David Grabber. J. Hydrol. Eng. 2011, 16, 761–762. [Google Scholar] [CrossRef]
- Duc, C.N.; Moo, Y.H. Rainfall-storage-pump-discharge (RSPD) model for sustainable and resilient flood mitigation. In Proceedings of the International Low Impact Development Conference China 2016—Applications in Sponge City Construction, Beijing, China, 26–29 June 2016. [Google Scholar]
- Uchida, T.; Hamabe, R.; Fukuoka, S. Investigation of Impacts of Discharge from Drainage Pump Stations on Flood Flow in Lowland River Using Unsteady 2D Analysis and Observed Water Surface Profiles. J. Soc. Hydrol. Water Resour. 2012, 25, 201–213. [Google Scholar] [CrossRef][Green Version]
- Wei, C.C. Application of pumping operation models for a drainage system. Appl. Mech. Mater. 2012, 256–259, 2416–2419. [Google Scholar] [CrossRef]
- Tamoto, N.; Endo, J.; Yoshimoto, K.; Yoshida, T.; Sakakibara, T. Forecast-based operation method in minimizing flood damage in urban area. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, Scotland, UK, 31 August–5 September 2008. [Google Scholar]
- Bu, X.; Chen, H.; Li, Y.; Wang, W. Performance optimization of low-specific speed under variable operation conditions. J. Drain. Irrig. Mach. Eng. 2015, 33, 203–208. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Morani, M.C.; Padulano, R. Optimal pump scheduling for urban drainage under variable flow conditions. Resources 2018, 7, 73. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chang, K.-Y.; Chang, L.-C. Counterpropagation fuzzy-neural network for city flood control system. J. Hydrol. 2008, 358, 24–34. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Chang, L.-C.; Tsai, M.-J.; Wang, Y.-F.; Chang, F.-J. Auto-control of pumping operations in sewerage systems by rule-based fuzzy neural networks. Hydrol. Earth Sci. 2011, 15, 185–196. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Yagi, S.; Shiba, S. Application of genetic algorithms and fuzzy control to a combined sewer pumping station. Water Sci. Technol. 1999, 39, 217–224. [Google Scholar] [CrossRef]
- Jafari, F.; Mousavi, S.J.; Yazdi, J.; Kim, J.H. Real-Time Operation of Pumping Systems for Urban Flood Mitigation: Single-Period vs. Multi-Period Optimization. Water Resour. Manag. 2018, 31, 4643–4660. [Google Scholar] [CrossRef]
- Wang, J.Y.; Chang, T.P.; Chen, J.S. An enhanced genetic algorithm for bi-objective pump scheduling in water supply. Expert Syst. Appl. 2009, 36, 10249–10258. [Google Scholar] [CrossRef]
- Ibarra, D.; Arnal, J. Parallel programming techniques applied to water pump scheduling problems. Water Resour. Plan Manag. 2014, 140, 06014002. [Google Scholar] [CrossRef]
- Mahar, P.S.; Singh, R.P. Optimal Design of Pumping Mains Considering Pump Characteristics. J. Pipline Syst. Eng. Pr. 2014, 5, 4013010. [Google Scholar] [CrossRef]
- Reca, J.; García-Manzano, A.; Martinez, J. Optimal Pumping Scheduling for Complex Irrigation Water Distribution Systems. J. Pipline Resour. Plan. Manag. 2014, 140, 630–637. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Giugni, M.; Marini, G.; Pugliese, F. An Application of the Harmony-Search Multi-Objective (HSMO) Optimization Algorithm for the Solution of Pump Scheduling Problem. Procedia Eng. 2016, 162, 494–502. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Giugni, M.; Marini, G.; Pugliese, F. Optimal solving of the pump scheduling problem by using a Harmony Search optimization algorithm. J. Hydroinform. 2017, 19, 879–889. [Google Scholar] [CrossRef]
- Code for Design of Outdoor Wastewater Engineering; 150000; Ministry of Housing and Urban-Rural Development of People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2006; pp. 45–47. (In Chinese)
- Wang, H.; Zhang, Y.X.; Tang, Y.; Liu, Y.; Li, K.X. Optimization of pump start-stops in rainwater pump station. J. Harbin Inst. Technol. 2017, 49, 98–103. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Y.; Yang, T.; Zhao, R.-H.; Li, Y.-B.; Zhao, W.-J.; Ma, X.-Y. Irrigation Canal System Delivery Scheduling Based on a Particle Swarm Optimization Algorithm. Water 2018, 10, 1281. [Google Scholar] [CrossRef]
- Li, Y.H.; Zhan, Z.H.; Lin, S.J. Competitive and cooperative particle swarm optimization with information sharing mechanism for global optimization problems. Inf. Sci. 2015, 293, 370–382. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, X.; Huang, C. Automatic calibration a hydrological model using a master–slave swarms shuffling evolution algorithm based on self-adaptive particle swarm optimization. Expert Syst. Appl. 2013, 40, 752–757. [Google Scholar] [CrossRef]
- Ghoshal, S. Optimizations of PID gains by particle swarm optimizations in fuzzy based automatic generation control. Electric Power Syst. Res. 2004, 72, 203–212. [Google Scholar] [CrossRef]
- Yang, W.N.; Zhou, W.; Liao, W.H. Prediction of drill flank wear using ensemble of co-evolutionary particle swarm optimization based-selective neural network ensembles. J. Intell. Manuf. 2016, 27, 343–361. [Google Scholar] [CrossRef]
- Hassan, W.H.; Nile, B.K.; Al-Masody, B.A. Climate change effect on storm drainage networks by storm water management model. Environ. Eng. 2017, 22, 393–400. [Google Scholar] [CrossRef]
- Chen, W.; Huang, G.; Zhang, H. Urban stormwater inundation simulation based on SWMM and diffusive overland-flow model. Water Sci. Technol. 2017, 76, 3392–3403. [Google Scholar] [CrossRef]
- Gülbaz, S.; Kazezyılmaz-Alhan, C.M. An evaluation of hydrologic modeling performance of EPA SWMM for bioretention. Water Sci. Technol. 2017, 76, 3035–3043. [Google Scholar] [CrossRef] [PubMed]
- Oreste, F.; Armando, C.; Maria, C.M.; Roberta, P. Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions. Resources 2018, 7, 73. [Google Scholar] [CrossRef]

| Design Parameters | Design Parameter Values of Nine Pumping Station | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Storage | Effective volume (m3) | 134.4 | 315 | 553.5 | 592 | 748 | 860 | 769.5 | 874 | 986.7 |
| Bottom area (m2) | 38.4 | 70 | 135 | 160 | 187 | 200 | 202.5 | 218.5 | 253 | |
| Bottom elevation (m) | 42.3 | 44 | 44 | 42.6 | 41.7 | 40.5 | 39.5 | 40 | 40 | |
| Bottom elevation of inlet pipe (m) | 45.1 | 47.8 | 47.4 | 45.6 | 45 | 44.1 | 42.6 | 43.3 | 43.1 | |
| Diameter of inlet pipe (m) | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| Maximum design depth (m) | 4.8 | 5.8 | 5.4 | 5 | 5.3 | 5.6 | 5.1 | 5.3 | 5.2 | |
| Minimum design depth (m) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Pumps | Total flow of pumps (m3/s) | 0.4 | 0.8 | 1.4 | 1.8 | 2 | 2.4 | 2.6 | 3.2 | 3.6 |
| Number of pumps | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| Properties of Drainage System | Value of Properties |
|---|---|
| Pipe diameters | From 0.3 m to 2.5 m |
| Number of pipes | 1136 |
| Total length of pipes in the drainage system | 51 km |
| Elevation of the pipes | From 41.8 m to 54.2 m |
| Methods | One Year | Two Years | Three Years | Five Years | Ten Years | Twenty Years | 7.21 | 7.30 | 6.24 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | T | N | T | N | T | N | T | N | T | N | T | N | T | N | T | N | T | |
| Multistage pumping station optimization | 8 | 2400 | 10 | 5030 | 16 | 5929 | 19 | 6991 | 25 | 7051 | 114 | 9286 | 64 | 7240 | 4 | 500 | 3 | 460 |
| Single pumping station optimization | 8 | 4509 | 10 | 6236 | 16 | 12,694 | 20 | 14,533 | 29 | 8462 | 247 | 9383 | 160 | 7933 | 4 | 582 | 3 | 532 |
| Pumping Station 1 | Pumping Station 2 | Pumping Station 3 | Pumping Station 4 | Pumping Station 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pump Number | h | n | Pump Number | h | n | Pump Number | h | n | Pump Number | h | n | Pump Number | h | n |
| (m) | (m) | (m) | (m) | (m) | ||||||||||
| P1-1 | 2.4 | 18 | P2-1 | 3.9 | 15 | P3-1 | 3.9 | 2 | P4-1 | 2.6 | 7 | P5-1 | 4.8 | 2 |
| P1-2 | 2.8 | 5 | P2-2 | 4 | 5 | P3-2 | 4.1 | 1 | P4-2 | 3.2 | 2 | P5-2 | 4.9 | 1 |
| P1-3 | 3.3 | 1 | P2-3 | 4.3 | 1 | P3-3 | 5 | 0 | P4-3 | 2.9 | 2 | P5-3 | 5.1 | 0 |
| P1-4 | 3 | 4 | P2-4 | 4.5 | 1 | P3-4 | 4.4 | 1 | P4-4 | 4.5 | 0 | P5-4 | 5 | 1 |
| Pumping Station 6 | Pumping Station 7 | Pumping Station 8 | Pumping Station 9 | |||||||||||
| Pump Number | h | n | Pump Number | h | n | Pump Number | h | n | Pump Number | h | n | |||
| (m) | (m) | (m) | (m) | |||||||||||
| P6-1 | 4.8 | 2 | P7-1 | 3.5 | 5 | P8-1 | 4.9 | 1 | P9-1 | 5 | 0 | |||
| P6-2 | 4.7 | 2 | P7-2 | 3.7 | 1 | P8-2 | 3.9 | 1 | P9-2 | 4.8 | 1 | |||
| P6-3 | 2.8 | 10 | P7-3 | 4.6 | 0 | P8-3 | 5 | 0 | P9-3 | 3.5 | 2 | |||
| P6-4 | 5.3 | 1 | P7-4 | 3.6 | 1 | P8-4 | 3.3 | 7 | P9-4 | 2.4 | 11 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Lei, X.; Khu, S.-T.; Song, L. Optimization of Pump Start-Up Depth in Drainage Pumping Station Based on SWMM and PSO. Water 2019, 11, 1002. https://doi.org/10.3390/w11051002
Wang H, Lei X, Khu S-T, Song L. Optimization of Pump Start-Up Depth in Drainage Pumping Station Based on SWMM and PSO. Water. 2019; 11(5):1002. https://doi.org/10.3390/w11051002
Chicago/Turabian StyleWang, Hao, Xiaohui Lei, Soon-Thiam Khu, and Lixiang Song. 2019. "Optimization of Pump Start-Up Depth in Drainage Pumping Station Based on SWMM and PSO" Water 11, no. 5: 1002. https://doi.org/10.3390/w11051002
APA StyleWang, H., Lei, X., Khu, S.-T., & Song, L. (2019). Optimization of Pump Start-Up Depth in Drainage Pumping Station Based on SWMM and PSO. Water, 11(5), 1002. https://doi.org/10.3390/w11051002






