Impact of Climate Change on Water Resources in the Kilombero Catchment in Tanzania
Abstract
1. Introduction
- Assess the possible climatic future of the Kilombero Catchment with an emphasis on precipitation patterns and temperature variations;
- Estimate the impact of these climatic changes on hydrology by analyzing temporal and spatial changes in the water balance;
- Analyze the impact of climate change on hydrological risks, such as floods and droughts, through analyzing extreme flow situations.
2. Materials and Methods
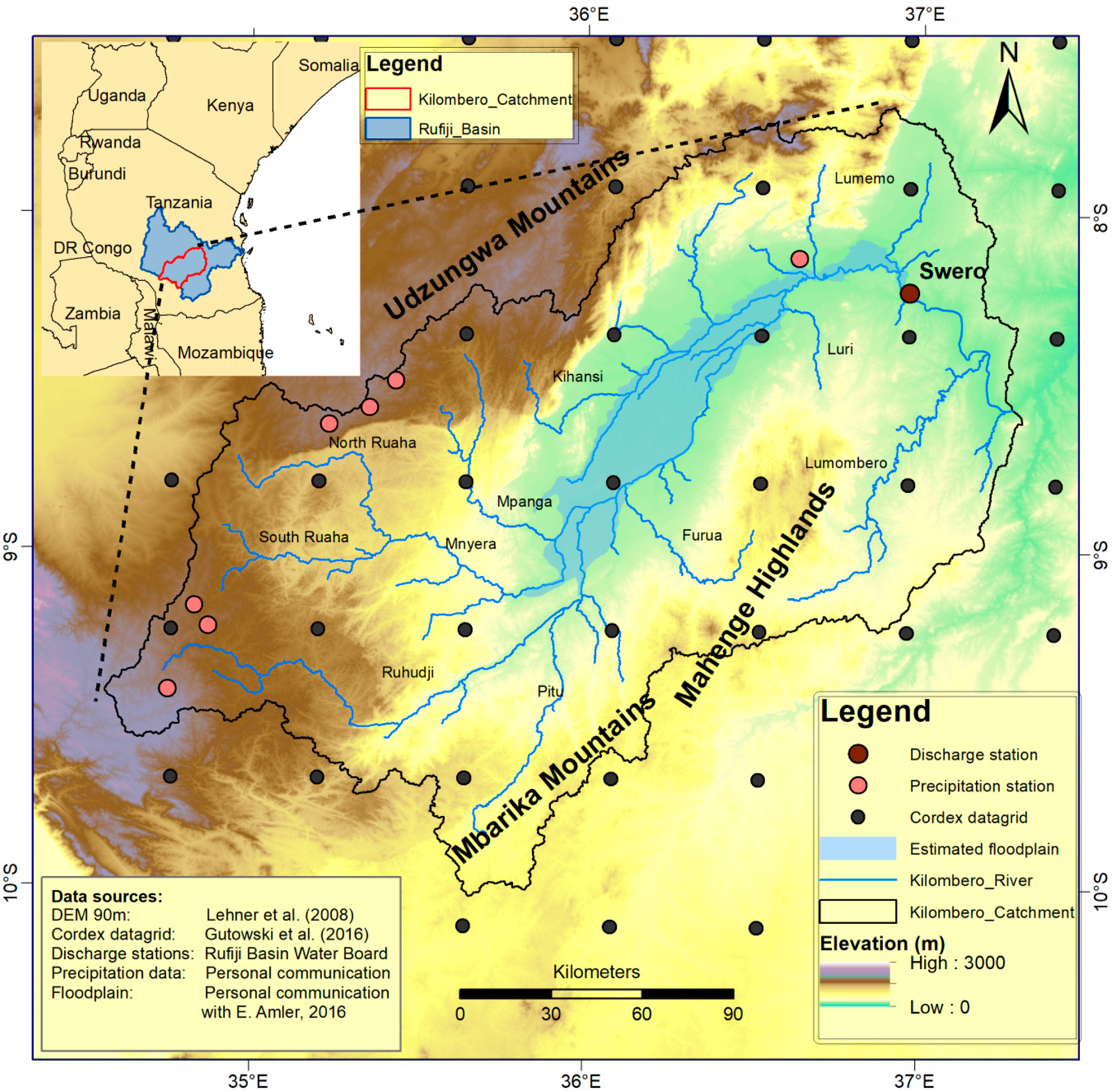
2.1. Study Site
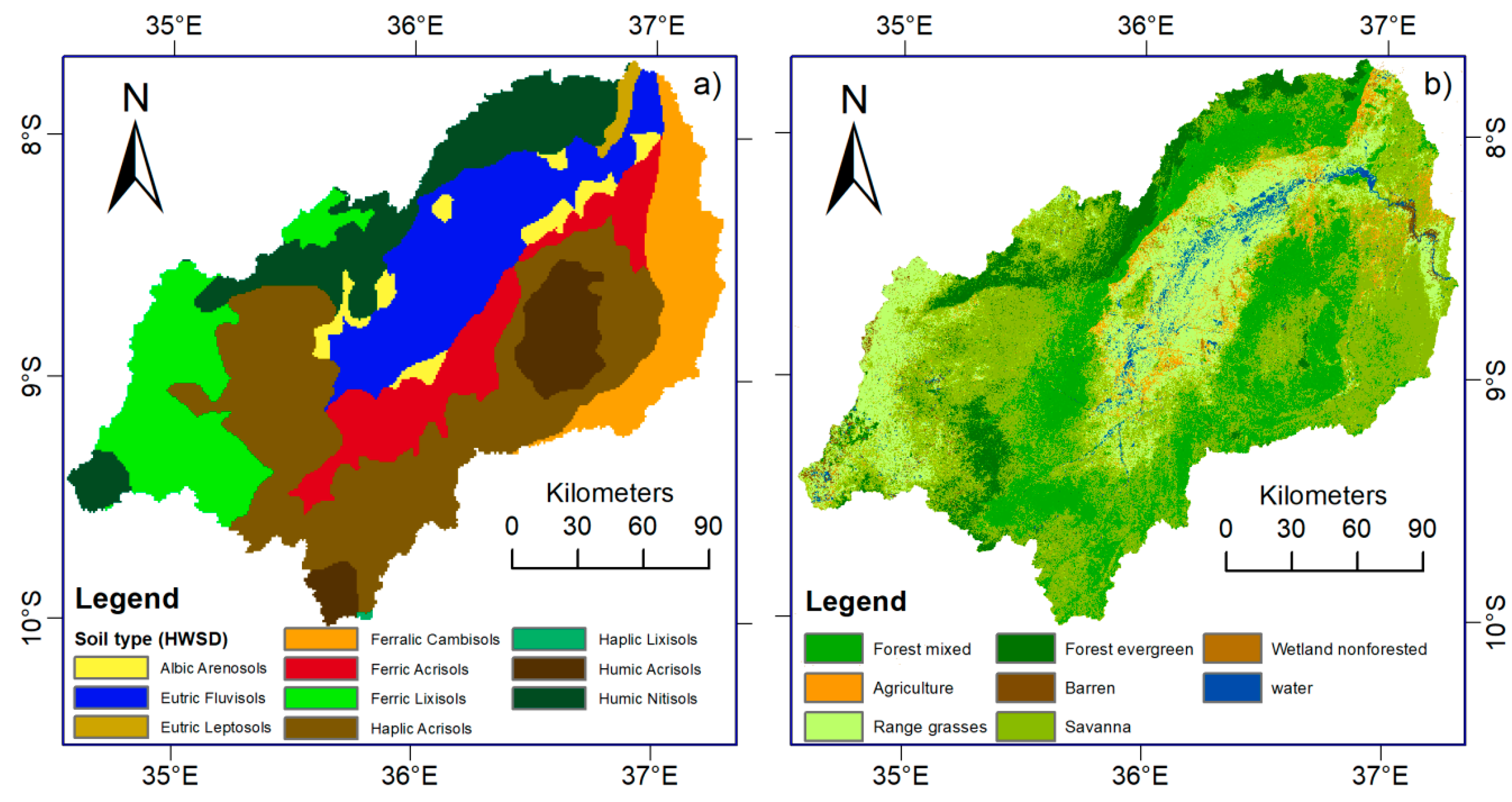
2.2. Input Data
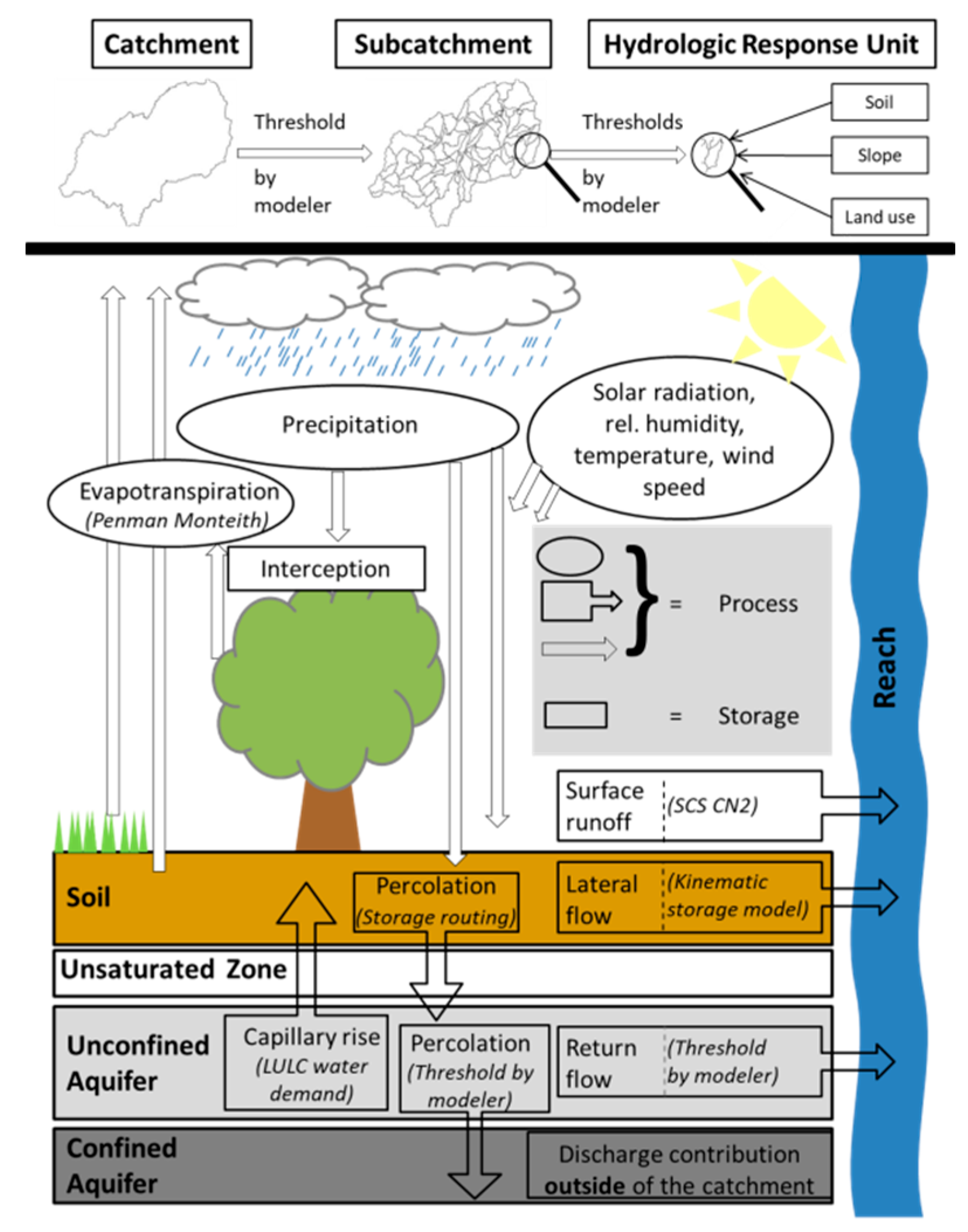
2.3. Model Description (SWAT Model)
2.4. Model Setup and Evaluation (SWAT Model)
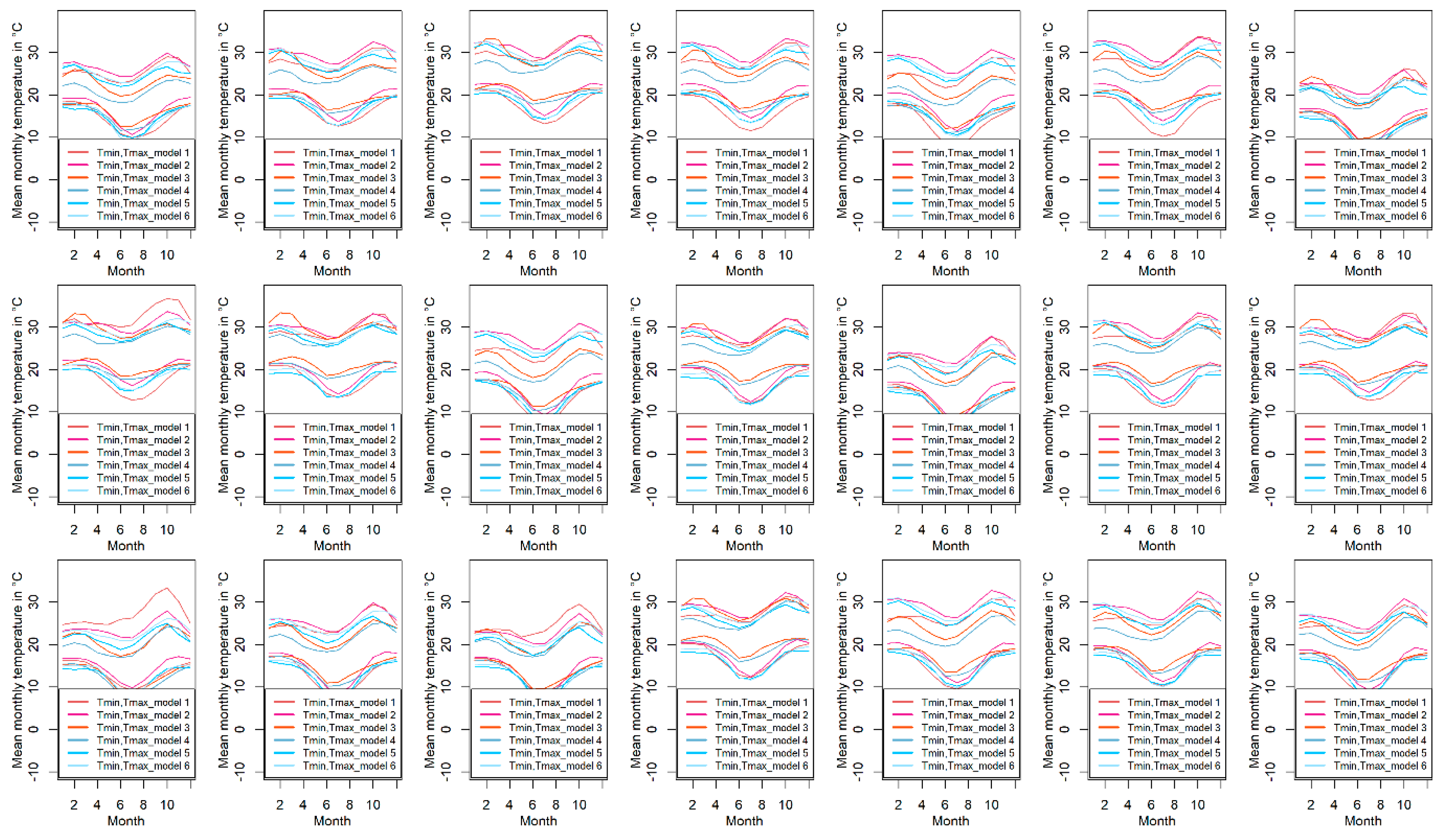
2.5. Climate Change Scenarios and Bias-Correction
- For the bias correction of minimum and maximum temperatures, the simple approach that was already used in a previous study [23] was adopted. In this approach, temperatures from the ERA-Interim reanalysis [55] were used as reference. Using the differences in the mean annual cycles, which were calculated from the 11-day running means of individual years between observations and model data in the period 1979–2005, model data was corrected towards observations. Due to the different representation of orography that results from the different horizontal resolutions of both datasets, i.e., 0.75° for ERA-Interim and 0.44° for CORDEX Africa RCMs, the correction was carried out for 700-hPa potential temperatures. After the correction, the RCM temperatures were transformed back to the initial level.
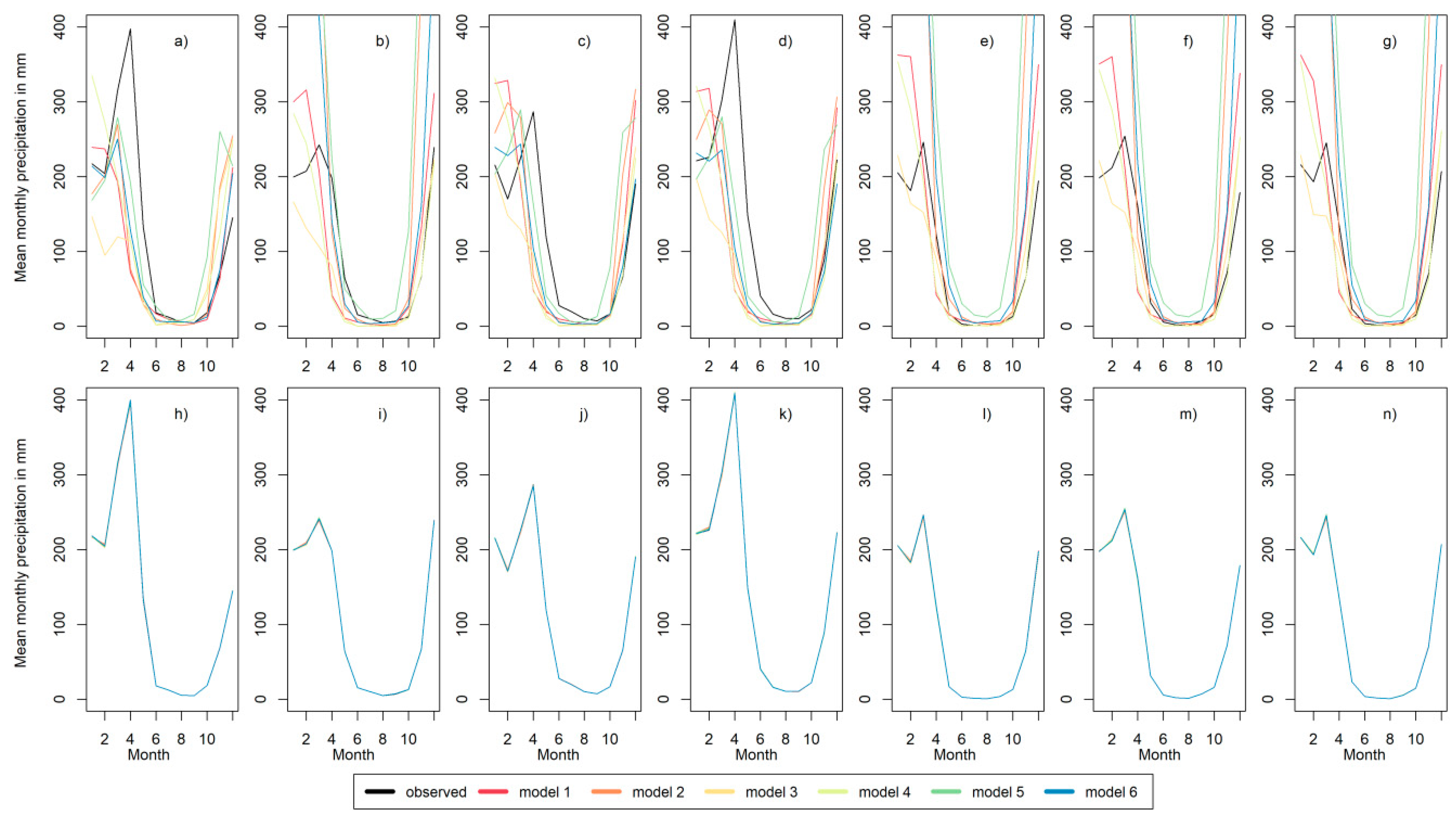
- Due to the non-linear statistical behavior of precipitation, a more comprehensive approach was needed for the bias correction of daily rainfall sums. All available data from seven stations in the Kilombero catchment (Figure 1) in the historical period 1951–2005 were used as reference for an empirical quantile mapping approach. In this approach the cumulative distribution function (CDF) based on simulated precipitation is adjusted towards the observation-based CDF [56]. The nearest CORDEX datagrid to the respective station was thereby utilized for the bias-correction. The usefulness of the distribution-independent quantile mapping method was demonstrated by various previous studies [31,57,58].
2.6. Flood Frequency and Low Flow Analysis
3. Results
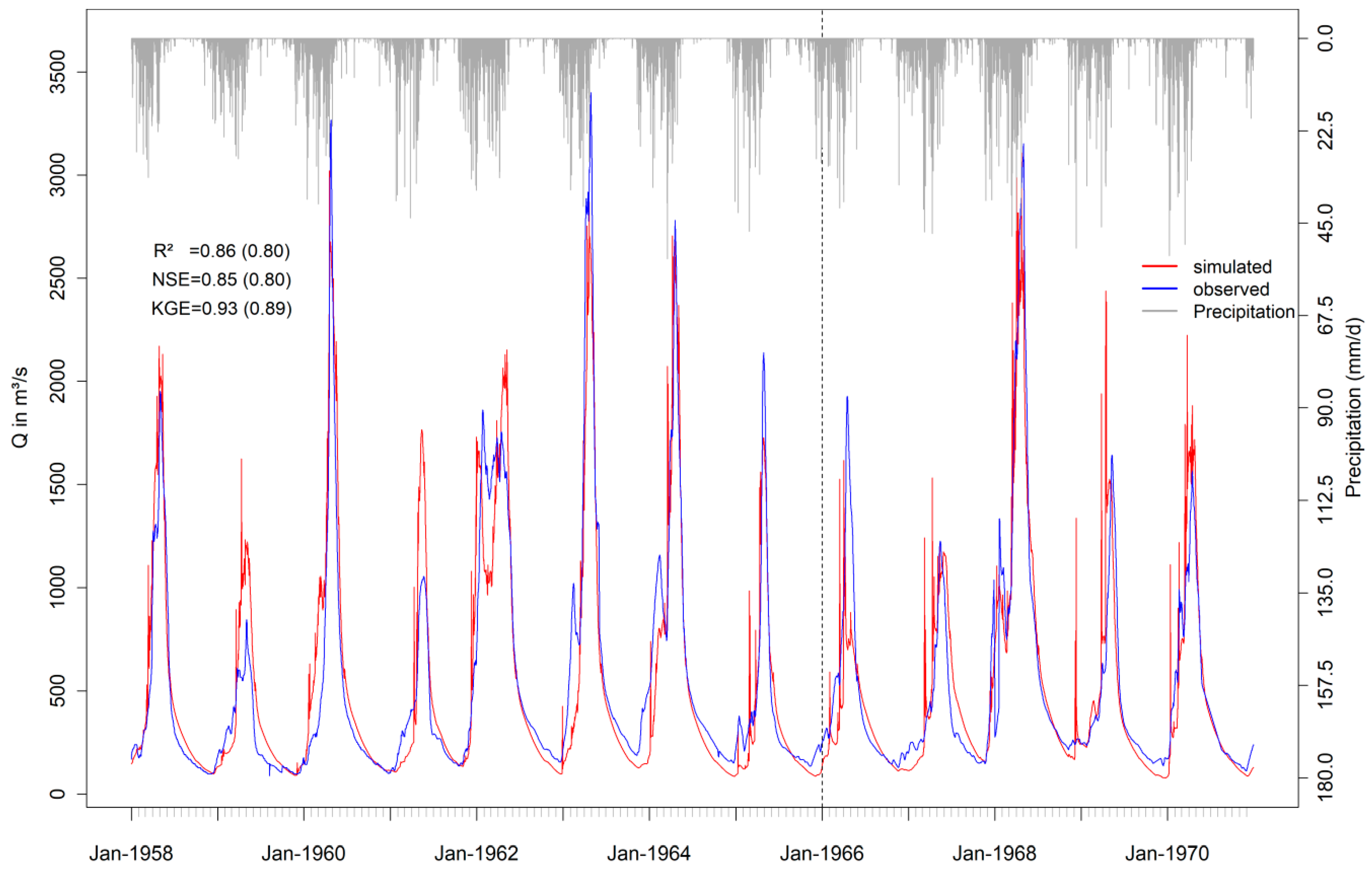
3.1. Model Performance
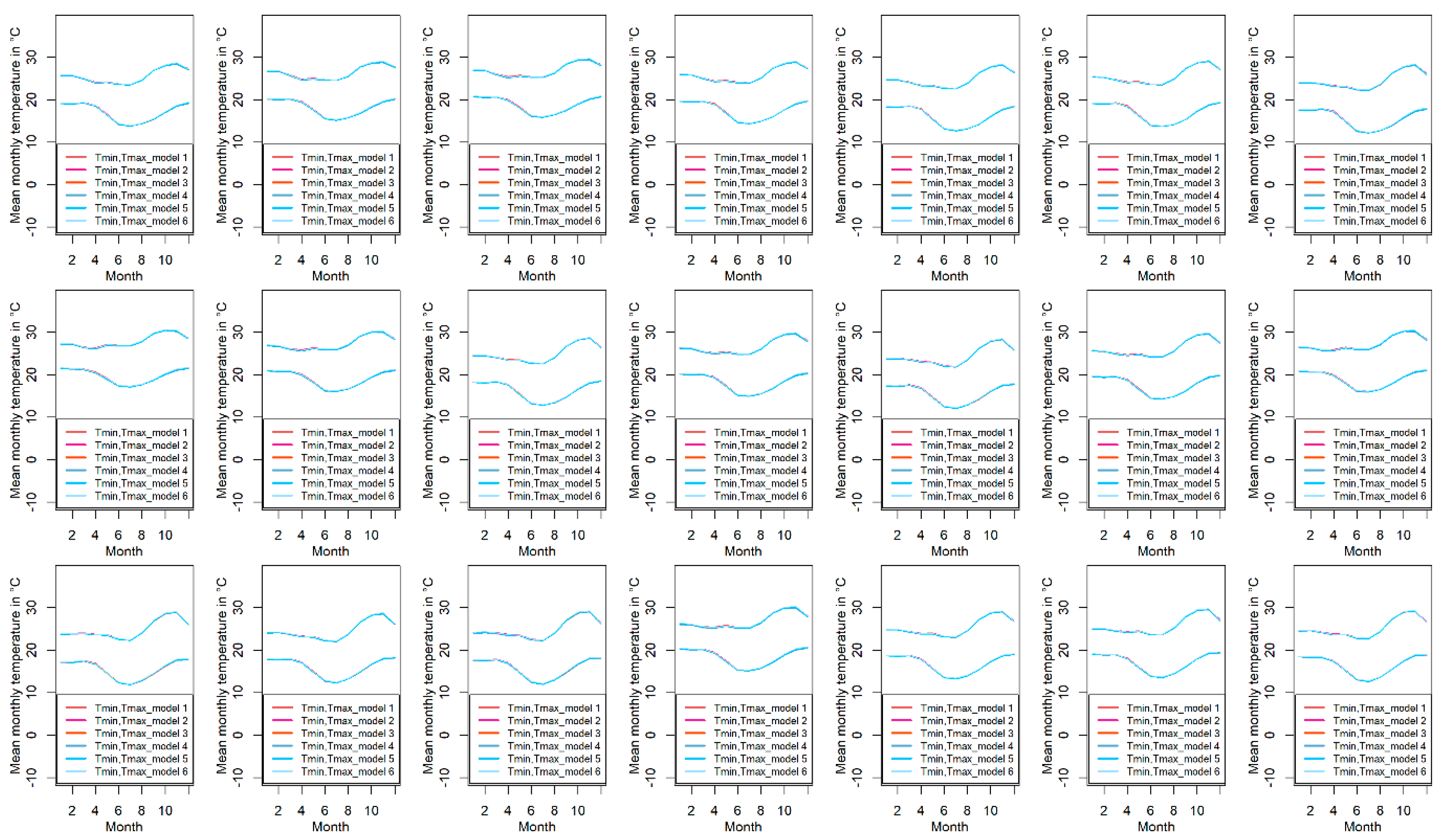
3.2. Bias-Correction
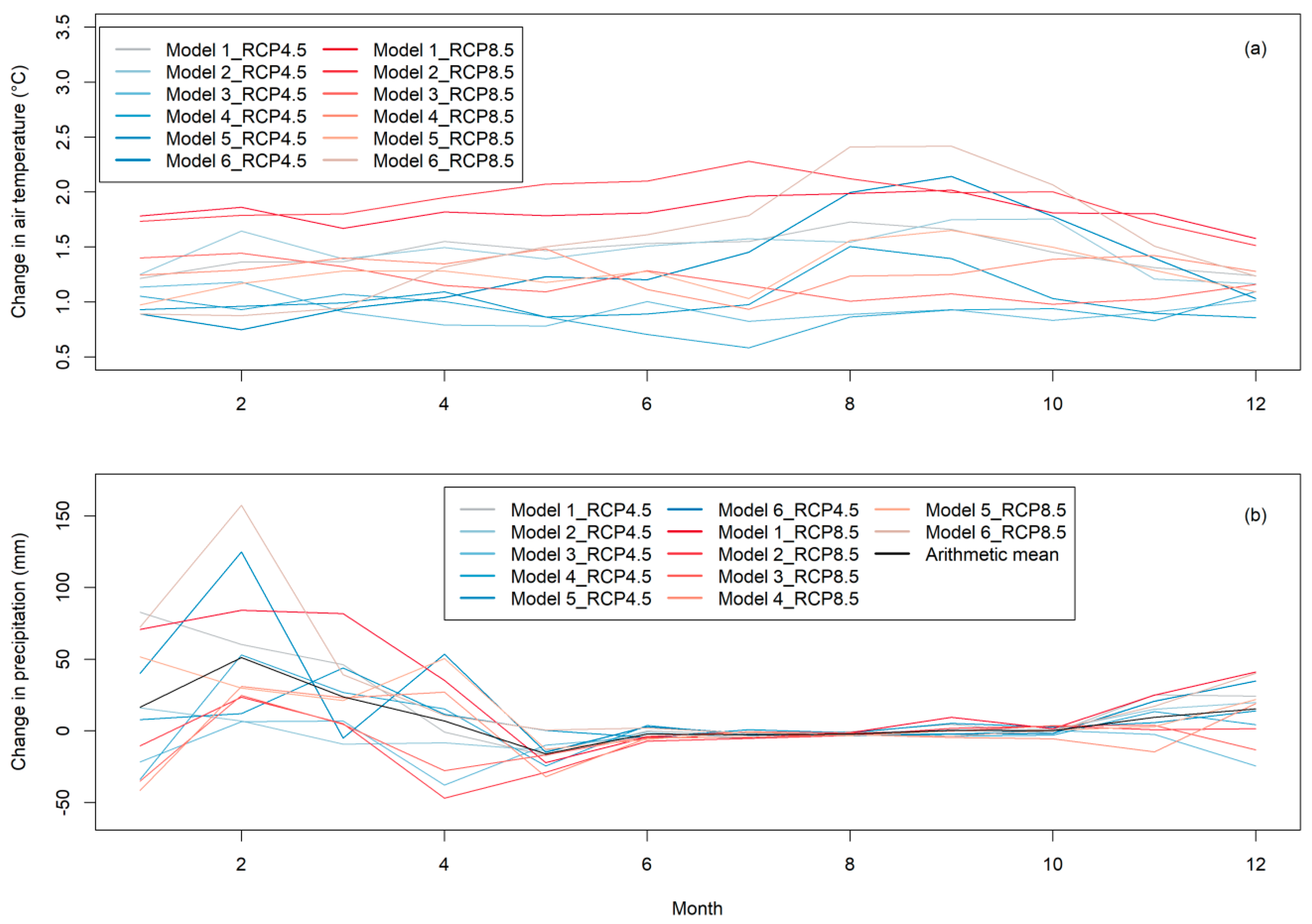
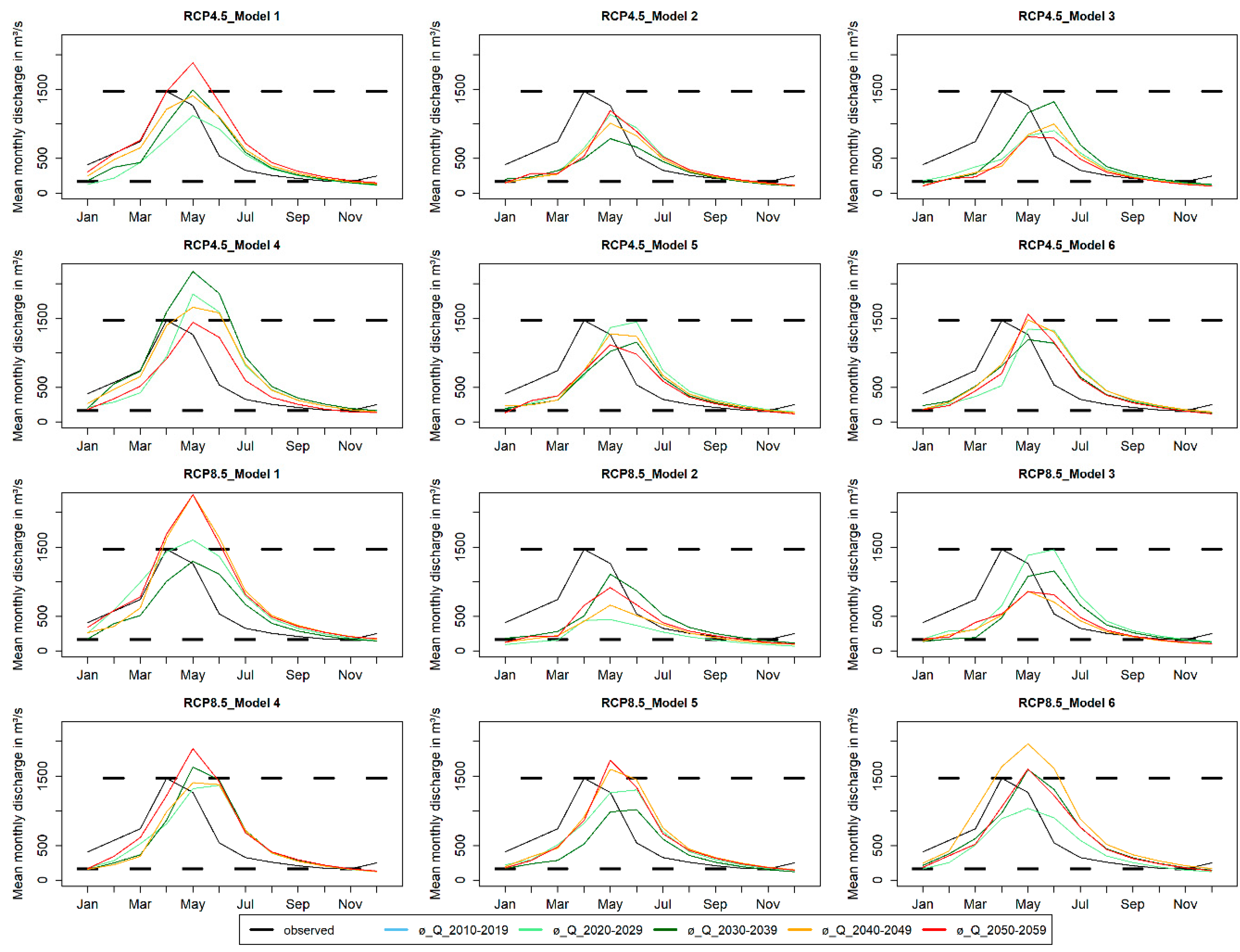
3.3. Climate Change Signal
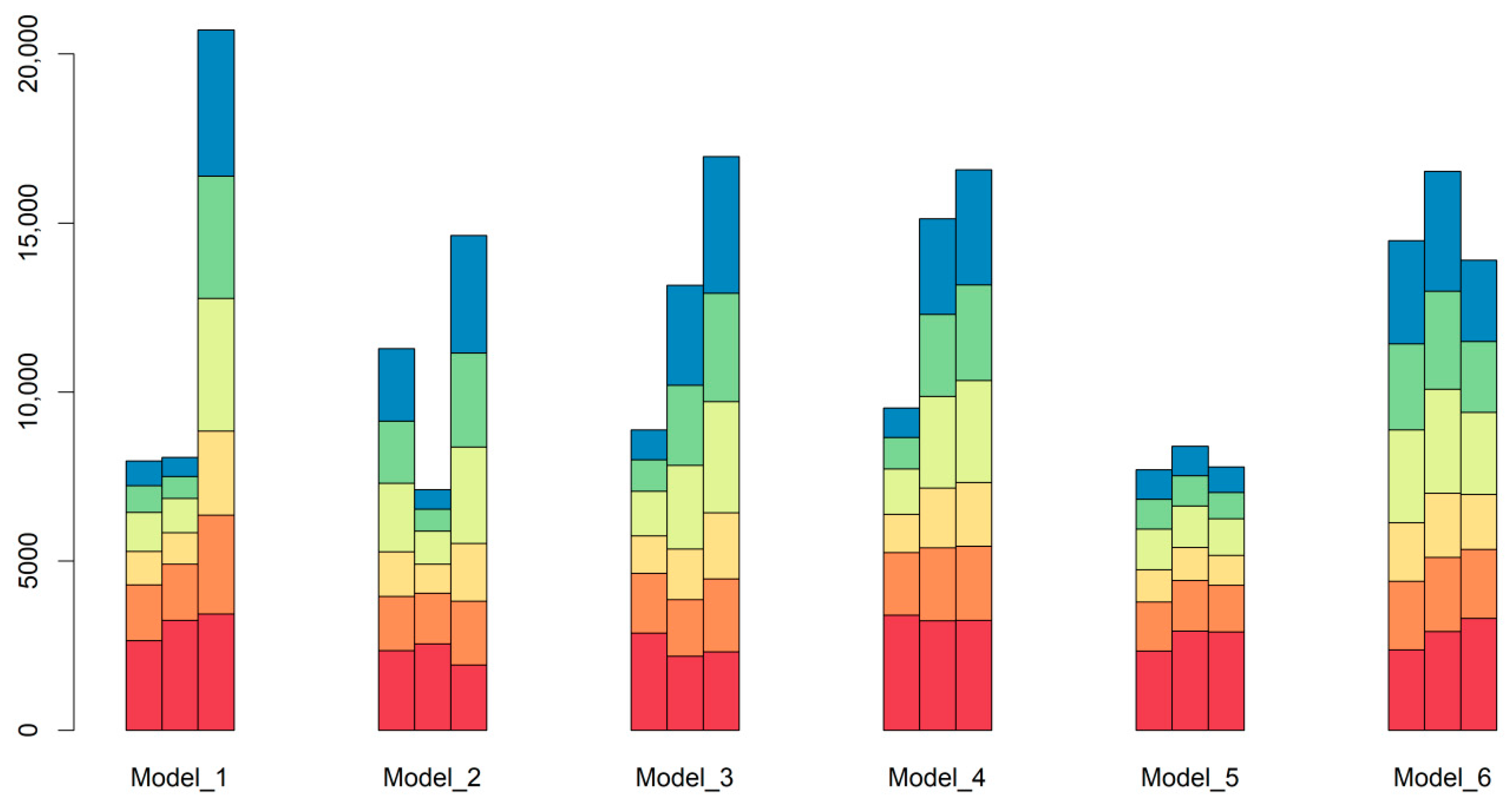
3.4. Impacts of Climate Change on Water Resources
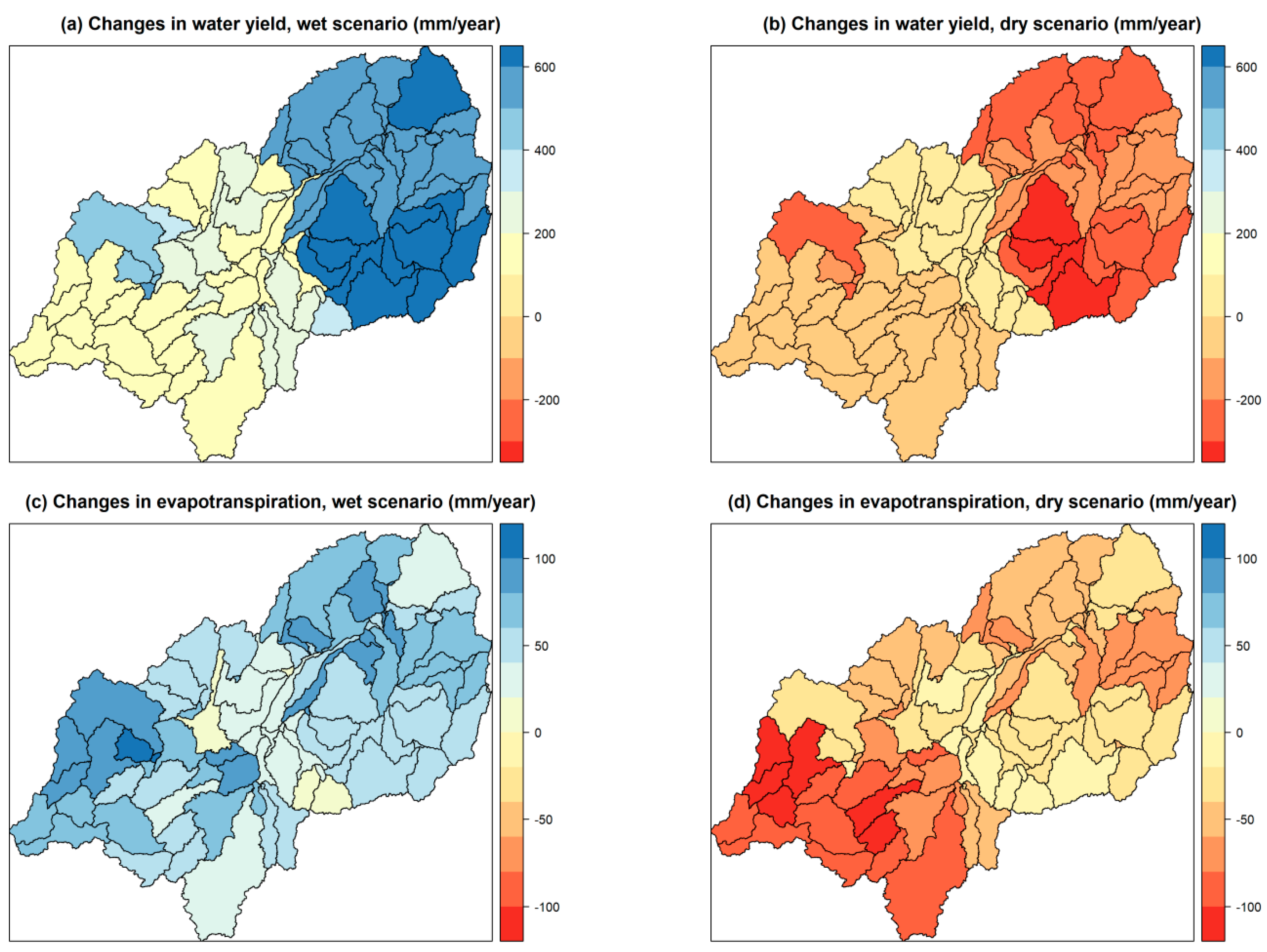
3.4.1. General Trend Analysis
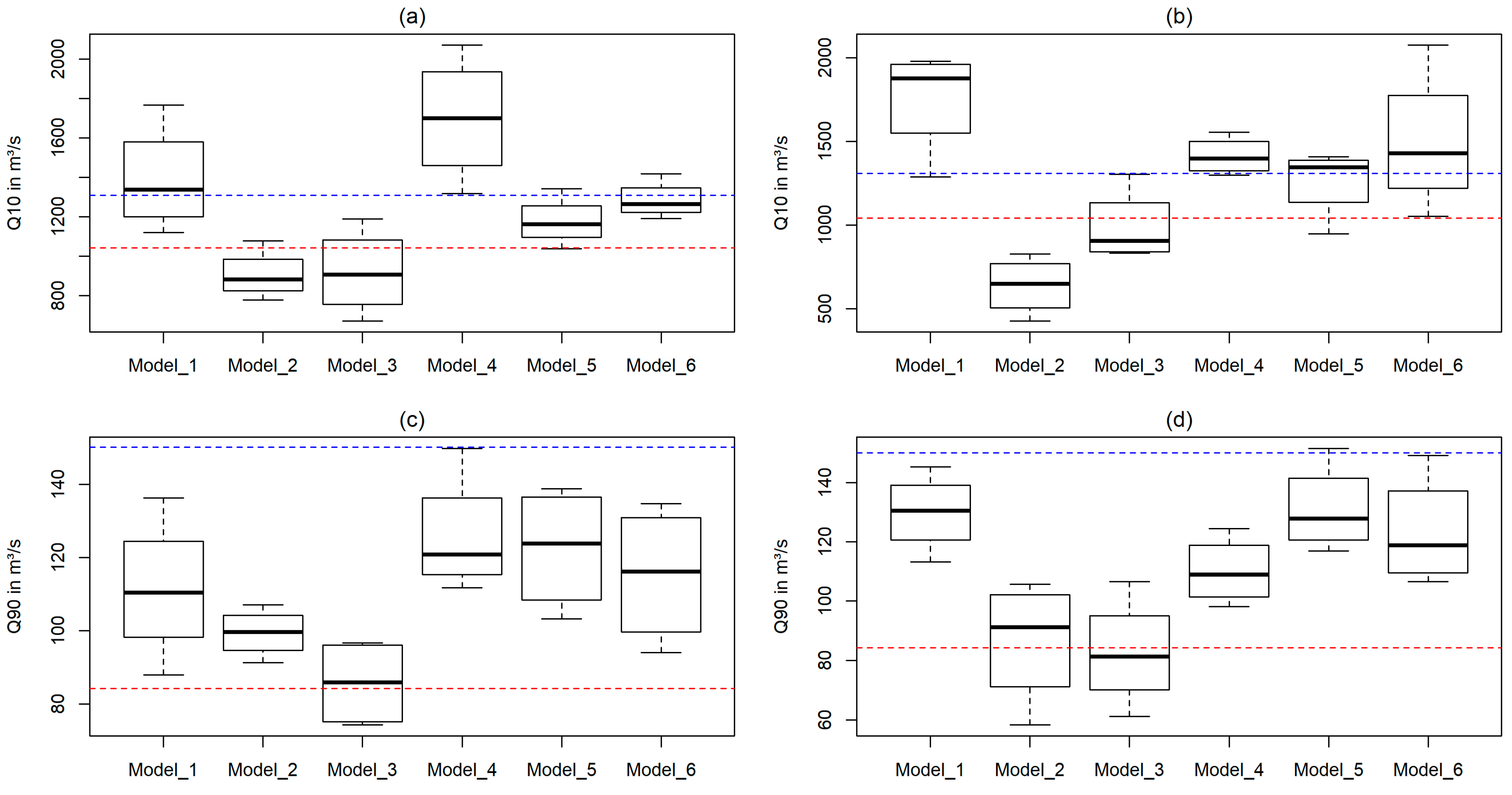
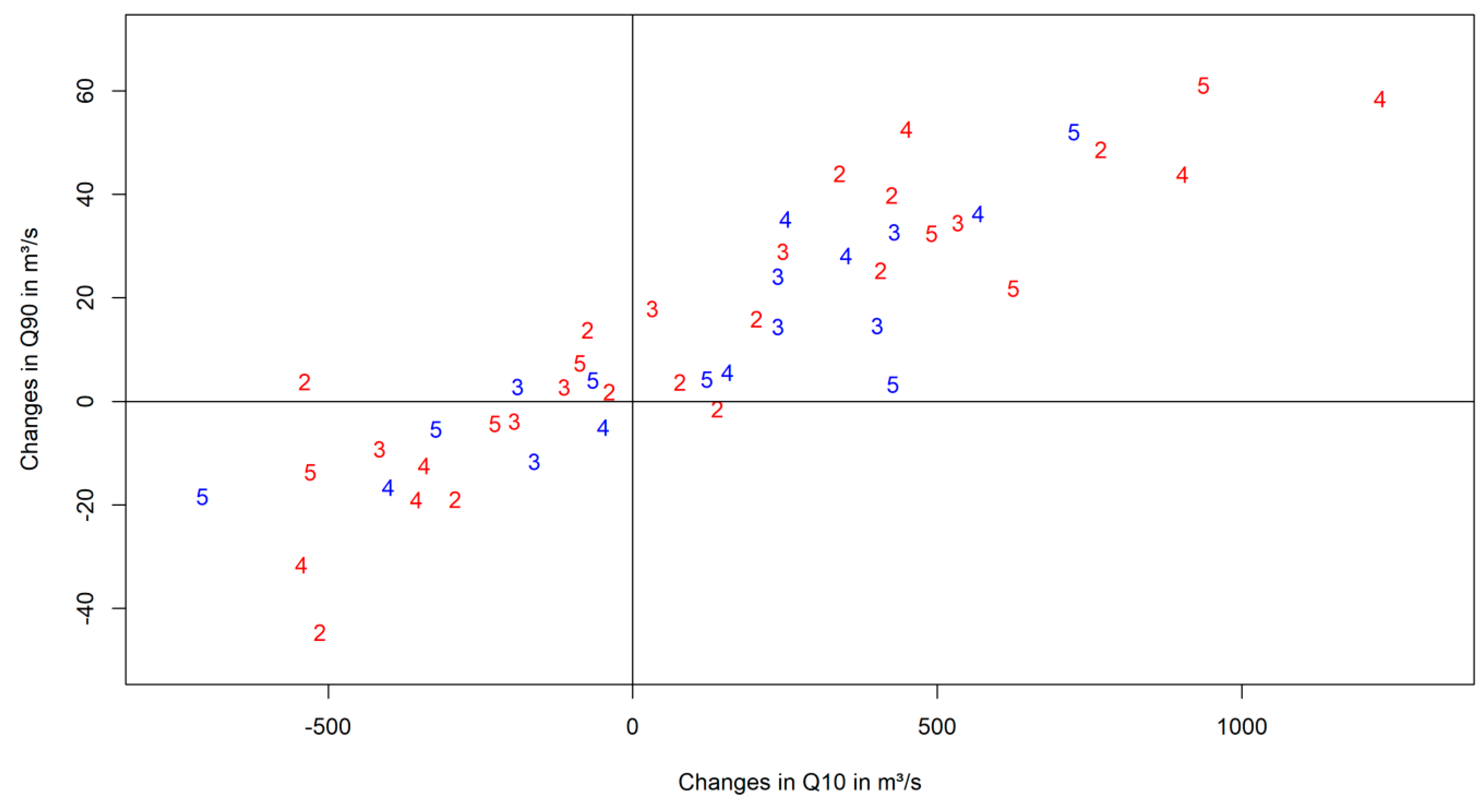
3.4.2. Flood Frequency and Low Flow Analysis
4. Discussion
4.1. Model Performance and Bias-Correction
4.2. Impact of Climate Change on Water Resources
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Leemhuis, C.; Amler, E.; Diekkrüger, B.; Gabiri, G.; Näschen, K. East African wetland-catchment data base for sustainable wetland management. Proc. Int. Assoc. Hydrol. Sci. 2016, 374, 123–128. [Google Scholar] [CrossRef]
- Stevenson, N.; Frazier, S. Review of wetland inventory information in Africa. In Global Review of Wetland Resources and Priorities for Wetland Inventory; Spiers, A.G., Finlayson, C.M., Eds.; Supervising Scientist: Canberra, Australia, 1999; pp. 105–201. [Google Scholar]
- Amler, E.; Schmidt, M.; Menz, G. Definitions and Mapping of East African Wetlands: A Review. Remote Sens. 2015, 7, 5256–5282. [Google Scholar] [CrossRef]
- Heinkel, S.B. Therapeutic Effects of Wetlands on Mental Well-Being. The Concept of Therapeutic Landscapes Applied to an Ecosystem in Uganda. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2018. [Google Scholar]
- Maltby, E.; Acreman, M. Ecosystem services of wetlands: Pathfinder for a new paradigm. Hydrol. Sci. J. 2011, 56, 1341–1359. [Google Scholar] [CrossRef]
- Gardner, R.C.; Finlayson, C.M. Global Wetland Outlook: State of the World’s Wetlands and Their Services to People; The Ramsar Convention Secretariat: Gland, Switzerland, 2018. [Google Scholar]
- Beuel, S.; Alvarez, M.; Amler, E.; Behn, K.; Kotze, D.; Kreye, C.; Leemhuis, C.; Wagner, K.; Willy, D.K.; Ziegler, S.; et al. A rapid assessment of anthropogenic disturbances in East African wetlands. Ecol. Indic. 2016, 67, 684–692. [Google Scholar] [CrossRef]
- Behn, K.; Becker, M.; Burghof, S.; Möseler, B.M.; Willy, D.K.; Alvarez, M. Using vegetation attributes to rapidly assess degradation of East African wetlands. Ecol. Indic. 2018, 89, 250–259. [Google Scholar] [CrossRef]
- Kirimi, F.; Thiong, K.; Gabiri, G.; Diekkrüger, B. Assessing seasonal land cover dynamics in the tropical Kilombero floodplain of East Africa. J. Appl. Remote Sens. 2018, 12, 026027. [Google Scholar] [CrossRef]
- Gabiri, G.; Diekkrüger, B.; Leemhuis, C.; Burghof, S.; Näschen, K.; Asiimwe, I.; Bamutaze, Y. Determining hydrological regimes in an agriculturally used tropical inland valley wetland in central Uganda using soil moisture, groundwater, and digital elevation data. Hydrol. Process. 2017, 32, 349–362. [Google Scholar] [CrossRef]
- Rebelo, L.M.; McCartney, M.P.; Finlayson, C.M. Wetlands of Sub−Saharan Africa: Distribution and contribution of agriculture to livelihoods. Wetl. Ecol. Manag. 2010, 18, 557–572. [Google Scholar] [CrossRef]
- Mombo, F.; Speelman, S.; Huylenbroeck, G.V.; Hella, J.; Moe, S. Ratification of the Ramsar convention and sustainable wetlands management: Situation analysis of the Kilombero Valley wetlands in Tanzania. J. Agric. Ext. Rural Dev. 2011, 3, 153–164. [Google Scholar]
- Munishi-Kongo, S. Ground and Satellite-Based Assessment of Hydrological Responses To Land Cover Change in the Kilombero River Basin, Tanzania. Ph.D. Thesis, University of KwaZulu-Natal, Durban, South Africa, 2013. [Google Scholar]
- Wilson, E.; McInnes, R.; Mbaga, D.P.; Ouedaogo, P. Ramsar Advisory Mission Report: United Republic of Tanzania, Kilombero Valley; The Ramsar Convention Secretariat: Gland, Switzerland, 2017. [Google Scholar]
- Government of Tanzania. Southern Agricultural Growth Corridor of Tanzania (SAGCOT): Environmental and Social Management Framework (ESMF); Government of Tanzania: Dar es Salaam, Tanzania, 2013.
- Lyon, S.W.; Koutsouris, A.; Scheibler, F.; Jarsjö, J.; Mbanguka, R.; Tumbo, M.; Robert, K.K.; Sharma, A.N.; van der Velde, Y. Interpreting characteristic drainage timescale variability across Kilombero Valley, Tanzania. Hydrol. Process. 2015, 29, 1912–1924. [Google Scholar] [CrossRef]
- Koutsouris, A.J.; Chen, D.; Lyon, S.W. Comparing global precipitation data sets in eastern Africa: A case study of Kilombero Valley, Tanzania. Int. J. Climatol. 2016, 36, 2000–2014. [Google Scholar] [CrossRef]
- Burghof, S. Hydrogeology and water quality of wetlands in East Africa. Ph.D. Thesis, University of Bonn, Bonn, Switzerland, 2017. [Google Scholar]
- Daniel, S.; Gabiri, G.; Kirimi, F.; Glasner, B.; Näschen, K.; Leemhuis, C.; Steinbach, S.; Mtei, K. Spatial Distribution of Soil Hydrological Properties in the Kilombero Floodplain, Tanzania. Hydrology 2017, 4, 57. [Google Scholar] [CrossRef]
- Yawson, D.K.; Kongo, V.M.; Kachroo, R.K. Application of linear and nonlinear techniques in river flow forecasting in the Kilombero River basin, Tanzania. Hydrol. Sci. J. 2005, 50, 37–41. [Google Scholar] [CrossRef]
- Gabiri, G.; Burghof, S.; Diekkrüger, B.; Steinbach, S.; Näschen, K. Modeling Spatial Soil Water Dynamics in a Tropical Floodplain, East Africa. Water 2018, 10, 191. [Google Scholar] [CrossRef]
- Leemhuis, C.; Thonfeld, F.; Näschen, K.; Steinbach, S.; Muro, J.; Strauch, A.; López, A.; Daconto, G.; Games, I.; Diekkrüger, B. Sustainability in the food-water-ecosystem nexus: The role of land use and land cover change for water resources and ecosystems in the Kilombero Wetland, Tanzania. Sustainability 2017, 9, 1513. [Google Scholar] [CrossRef]
- Näschen, K.; Diekkrüger, B.; Leemhuis, C.; Steinbach, S.; Seregina, L.; Thonfeld, F.; van der Linden, R. Hydrological Modeling in Data-Scarce Catchments: The Kilombero Floodplain in Tanzania. Water 2018, 10, 599. [Google Scholar] [CrossRef]
- Seregina, L.S.; Fink, A.H.; van der Linden, R.; Elagib, N.A.; Pinto, J.G. A new and flexible rainy season definition: Validation for the Greater Horn of Africa and application to rainfall trends. Int. J. Climatol. 2018, 39, 898–1012. [Google Scholar] [CrossRef]
- Koutsouris, A. Building a coherent hydro-climatic modelling framework for the data limited Kilombero Valley of Tanzania. Ph.D. Thesis, Stockholm University, Stockholm, Sweden, 2017. [Google Scholar]
- Duvail, S.; Mwakalinga, A.B.; Eijkelenburg, A.; Hamerlynck, O.; Kindinda, K.; Majule, A. Jointly thinking the post-dam future: Exchange of local and scientific knowledge on the lakes of the Lower Rufiji, Tanzania. Hydrol. Sci. J. 2014, 59, 713–730. [Google Scholar] [CrossRef]
- Schneider, C.; Laizé, C.L.R.; Acreman, M.C.; Flörke, M. How will climate change modify river flow regimes in Europe? Hydrol. Earth Syst. Sci. 2013, 17, 325–339. [Google Scholar] [CrossRef]
- Eisner, S.; Flörke, M.; Chamorro, A.; Daggupati, P.; Donnelly, C.; Huang, J.; Hundecha, Y.; Koch, H.; Kalugin, A.; Krylenko, I.; et al. An ensemble analysis of climate change impacts on streamflow seasonality across 11 large river basins. Clim. Chang. 2017, 141, 401–417. [Google Scholar] [CrossRef]
- Barnett, T.P.; Pierce, D.W.; Hidalgo, H.G.; Bonfils, C.; Santer, B.D.; Das, T.; Bala, G.; Wood, A.W.; Nozawa, T.; Mirin, A.A.; et al. Human-induced changes in the hydrology of the western United States. Science 2008, 319, 1080–1083. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Yira, Y.; Diekkrüger, B.; Steup, G.; Bossa, A.Y. Impact of climate change on hydrological conditions in a tropical West African catchment using an ensemble of climate simulations. Hydrol. Earth Syst. Sci. 2017, 21, 2143–2161. [Google Scholar] [CrossRef]
- Feng, D.; Beighley, E.; Raoufi, R.; Melack, J.; Zhao, Y.; Iacobellis, S.; Cayan, D. Propagation of future climate conditions into hydrologic response from coastal southern California watersheds. Clim. Chang. 2019, 153, 199–218. [Google Scholar] [CrossRef]
- Gelfan, A.; Gustafsson, D.; Motovilov, Y.; Arheimer, B.; Kalugin, A.; Krylenko, I.; Lavrenov, A. Climate change impact on the water regime of two great Arctic rivers: Modeling and uncertainty issues. Clim. Chang. 2017, 141, 499–515. [Google Scholar] [CrossRef]
- Lalika, M.C.S.; Meire, P.; Ngaga, Y.M.; Chang’a, L. Understanding watershed dynamics and impacts of climate change and variability in the Pangani River Basin, Tanzania. Ecohydrol. Hydrobiol. 2015, 15, 26–38. [Google Scholar] [CrossRef]
- Natkhin, M.; Dietrich, O.; Schäfer, M.P.; Lischeid, G. The effects of climate and changing land use on the discharge regime of a small catchment in Tanzania. Reg. Environ. Chang. 2015, 15, 1269–1280. [Google Scholar] [CrossRef]
- Gutowski, J.W.; Giorgi, F.; Timbal, B.; Frigon, A.; Jacob, D.; Kang, H.S.; Raghavan, K.; Lee, B.; Lennard, C.; Nikulin, G.; et al. WCRP COordinated Regional Downscaling EXperiment (CORDEX): A diagnostic MIP for CMIP6. Geosci. Model Dev. 2016, 9, 4087–4095. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef]
- Nicholson, S.E. The nature of rainfall variability over Africa on time scales of decades to millenia. Glob. Planet. Chang. 2000, 26, 137–158. [Google Scholar] [CrossRef]
- Kangalawe, R.Y.M.; Liwenga, E.T. Livelihoods in the wetlands of Kilombero Valley in Tanzania: Opportunities and challenges to integrated water resource management. Phys. Chem. Earth Parts A/B/C 2005, 30, 968–975. [Google Scholar] [CrossRef]
- Camberlin, P.; Philippon, N. The East African March–May Rainy Season: Associated Atmospheric Dynamics and Predictability over the 1968–97 Period. J. Clim. 2002, 15, 1002–1019. [Google Scholar] [CrossRef]
- Nicholson, S.E. Climate and climatic variability of rainfall over eastern Africa. Rev. Geophys. 2017, 55, 590–635. [Google Scholar] [CrossRef]
- Dewitte, O.; Jones, A.; Spaargaren, O.; Breuning-Madsen, H.; Brossard, M.; Dampha, A.; Deckers, J.; Gallali, T.; Hallett, S.; Jones, R.; et al. Harmonisation of the soil map of Africa at the continental scale. Geoderma 2013, 211, 138–153. [Google Scholar] [CrossRef]
- Zemandin, B.; Mtalo, F.; Mkhandi, S.; Kachroo, R.; McCartney, M. Evaporation Modelling in Data Scarce Tropical Region of the Eastern Arc Mountain Catchments of Tanzania. Nile Basin Water Sci. Eng. J. 2011, 4, 1–13. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived From Spaceborne Elevation Data. Eos Trans. Am. Geophys. Union 2008, 89, 93. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Available online: https/ /Earthexplorer.Usgs.Gov/ (accessed on 8 December 2016).
- RBWO. The Rufiji Basin Water Office (RBWO) Discharge Database; Rufiji Basin Water Office: Iringa, Tanzania, Personal communication; 2014. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Soil Conservation Service (Ed.) Hydrology. In National Engineering Handbook; Soil Conservation Service: Washington, DC, USA, 1972. [Google Scholar]
- Monteith, J.L.; Moss, C.J. Climate and the Efficiency of Crop Production in Britain. Philos. Trans. R. Soc. B Biol. Sci. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Sloan, P.G.; Moore, I.D. Modeling subsurface stormflow on steeply sloping forested watersheds. Water Resour. Res. 1984, 20, 1815–1822. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Neitsch, S.L., Arnold, J.G., Kiniry, J.R., Williams, J.R., Eds.; Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 2011.
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Soil & Water Assessment Tool: Input/Output Documentation; Texas Water Resources Institute: College Station, TX, USA, 2012. [Google Scholar]
- Abbaspour, K.C. SWAT-CUP 2012. SWAT Calibration and Uncertainty Programs; Abbaspour, K.C., Ed.; Eawag: Dübendorf, Switzerland, 2013. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Gilleland, E.; Katz, R.W. extRemes 2.0: An Extreme Value Analysis Package in R. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- van Vliet, M.T.H.; Franssen, W.H.P.; Yearsley, J.R.; Ludwig, F.; Haddeland, I.; Lettenmaier, D.P.; Kabat, P. Global river discharge and water temperature under climate change. Glob. Environ. Chang. 2013, 23, 450–464. [Google Scholar] [CrossRef]
- Bond, N. Hydrostats: Hydrologic Indices for Daily Time Series Data; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Burghof, S.; Gabiri, G.; Stumpp, C.; Chesnaux, R.; Reichert, B. Development of a hydrogeological conceptual wetland model in the data-scarce north-eastern region of Kilombero Valley, Tanzania. Hydrogeol. J. 2017, 26, 267–284. [Google Scholar] [CrossRef]
- Teng, J.; Potter, N.J.; Chiew, F.H.S.; Zhang, L.; Wang, B.; Vaze, J.; Evans, J.P. How does bias correction of regional climate model precipitation affect modelled runoff? Hydrol. Earth Syst. Sci. 2015, 19, 711–728. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Oxford, UK; Chichester, UK; Hoboken, NJ, USA, 2012. [Google Scholar]
- Tang, Q.; Gao, H.; Lu, H.; Lettenmaier, D.P. Remote sensing: Hydrology. Prog. Phys. Geogr. 2009, 33, 490–509. [Google Scholar] [CrossRef]
- Pokorny, J. Evapotranspiration. Encycl. Ecol. 2019, 292–303. [Google Scholar] [CrossRef]
- McClain, M.E. Balancing water resources development and environmental sustainability in Africa: A review of recent research findings and applications. Ambio 2013, 42, 549–565. [Google Scholar] [CrossRef] [PubMed]
- CDM Smith. Environmental Flows in Rufiji River Basin Assessed from the Perspective of Planned Development in Kilombero and Lower Rufiji Sub−Basins. 2016. Available online: https://pdf.usaid.gov/pdf_docs/pa00mkk4.pdf (accessed on 1 February 2019).
- Yanda, P.Z.; Munishi, P.K.T. Hydrologic and Land Use/Cover Change Analysis for the Ruvu River (Uluguru) and Sigi River (East Usambara) Watersheds; WWF/CARE: Dar es Salaam, Tanzania, 2007. [Google Scholar]
- Githui, F.W. Assessing the Impacts of Environmental Change on the Hydrology of the Nzoia Catchment, in the Lake Victoria Basin. Ph.D. Thesis, Vrije Universiteit Brussel, Brussel, Belgium, 2008; p. 203. [Google Scholar]
- Kashaigili, J.J. Impacts of land-use and land-cover changes on flow regimes of the Usangu wetland and the Great Ruaha River, Tanzania. Phys. Chem. Earth Parts A/B/C 2008, 33, 640–647. [Google Scholar] [CrossRef]
- Mwamila, T.B.; Kimwaga, R.J.; Mtalo, F.W. Eco-hydrology of the Pangani River downstream of Nyumba ya Mungu reservoir, Tanzania. Phys. Chem. Earth Parts A/B/C 2008, 33, 695–700. [Google Scholar] [CrossRef]
- Montanari, A.; Young, G.; Savenije, H.H.G.; Hughes, D.; Wagener, T.; Ren, L.L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S.; et al. “Panta Rhei—Everything Flows”: Change in hydrology and society—The IAHS Scientific Decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Giertz, S. Analyse der hydrologischen Prozesse in den sub-humiden Tropen Westafrikas unter besonderer Berücksichtigung der Landnutzung am Beispiel des Aguima-Einzugsgebietes in Benin. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2004. [Google Scholar]
- Zimmermann, B.; Elsenbeer, H.; De Moraes, J.M. The influence of land-use changes on soil hydraulic properties: Implications for runoff generation. For. Ecol. Manag. 2006, 222, 29–38. [Google Scholar] [CrossRef]
- Daconto, G.; Games, I.; Lukumbuzya, K.; Raijmakers, F. Integrated Management Plan for the Kilombero Valley Ramsar Site; Ministry of Natural Resources and Tourism: Dodoma, Tanzania, 2018. [Google Scholar]
- Msofe, N.K.; Sheng, L.; Lyimo, J. Land use change trends and their driving forces in the Kilombero Valley Floodplain, Southeastern Tanzania. Sustainability 2019, 11, 505. [Google Scholar] [CrossRef]
- Op de Hipt, F.; Diekkrüger, B.; Steup, G.; Yira, Y.; Hoffmann, T.; Rode, M.; Näschen, K. Modeling the impact of climate change on water resources and soil erosion in a tropical catchment in Burkina Faso, West Africa. Sci. Total Environ. 2019, 653, 431–445. [Google Scholar] [CrossRef] [PubMed]
- Danvi, A.; Giertz, S.; Zwart, S.J.; Diekkrüger, B. Comparing water quantity and quality in three inland valley watersheds with different levels of agricultural development in central Benin. Agric. Water Manag. 2017, 192, 257–270. [Google Scholar] [CrossRef]



| Data Set | Resolution/Scale | Source | Required Parameters |
|---|---|---|---|
| Digital Elevation Model (DEM) | 90 m | Shuttle Radar Topography Mission (SRTM) [45] | Topographical data |
| Soil map | 1 km | Food and Agriculture Organization of the United Nations (FAO) [42] | Soil classes and physical properties |
| Land use map | 60 m (1970s) | Landsat pre-Collection Level-1 [46] | Land cover and use classes |
| Precipitation | Daily (1958–1970) | Personal communication: RBWB, University of Dar es Salaam (UDSM), Tanzania Meteorological Agency (TMA) | Measured precipitation |
| Climate | Daily/0.44° (1951–2060) | Coordinated Regional Downscaling Experiment (CORDEX) Africa [36] | Temperature, humidity, solar radiation, wind speed, precipitation |
| Discharge | Daily (1958–1970) | RBWB [47] | Discharge |
| GCM | RCM | Institution | URL | In This Study Referred to as |
|---|---|---|---|---|
| CanESM2 | CanRCM4_r2 | Canadian Centre for Climate Modelling and Analysis (CCCma) | http://climate-modelling.canada.ca/ | Model 1 |
| CanESM2 | RCA4_v1 | Rossby Centre, Swedish Meteorological and Hydrological Institute (SMHI) | https://esg-dn1.nsc.liu.se/ | Model 2 |
| CNRM-CM5 | CCLM4-8-17_v1 | Climate Limited-area Modelling Community (CLMcom) | https://esg-dn1.nsc.liu.se/ | Model 3 |
| EC-EARTH | CCLM4-8-17_v1 | Climate Limited-area Modelling Community (CLMcom) | https://esg-dn1.nsc.liu.se/ | Model 4 |
| EC-EARTH | RCA4_v1 | Rossby Centre, Swedish Meteorological and Hydrological Institute (SMHI) | https://esg-dn1.nsc.liu.se/ | Model 5 |
| MIROC5 | RCA4_v1 | Rossby Centre, Swedish Meteorological and Hydrological Institute (SMHI) | https://esg-dn1.nsc.liu.se/ | Model 6 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tmin | 19.2 | 19.1 | 19.2 | 18.5 | 16.4 | 14.3 | 14.0 | 14.6 | 15.9 | 17.7 | 19.0 | 19.5 |
| Tmax | 25.4 | 25.4 | 24.8 | 24.3 | 24.5 | 23.9 | 23.8 | 25.2 | 27.6 | 29.0 | 29.3 | 27.2 |
| Climate Model | Historical Precipitation (After bias-correction) | RCP Precipitation Changes in mm (%) | RCP ET0 Changes in mm (%) | RCP ETp Changes in mm (%) | RCP SQ Changes in mm (%) | RCP WYLD changes in mm (%) |
|---|---|---|---|---|---|---|
| Model 1 (RCP4.5) | 1338 | 195 | 39 | 73 | 23 | 124 |
| (14.5) | (4.4) | (4.7) | (40.2) | (28.7) | ||
| Model 2 (RCP4.5) | 1334 | 3 | −4 | 94 | 7 | −20 |
| (0.2) | (−0.4) | (5.3) | (12.0) | (−4.9) | ||
| Model 3 (RCP4.5) | 1311 | −109 | −10 | 66 | −12 | −103 |
| (−8.3) | (−1.4) | (5.1) | (−18.3) | (−19.8) | ||
| Model 4 (RCP4.5) | 1334 | 22 | −9 | 43 | 7 | 23 |
| (1.7) | (−1.3) | (3.8) | (10.8) | (3.6) | ||
| Model 5 (RCP4.5) | 1355 | 75 | 11 | 54 | 11 | 52 |
| (5.5) | (1.2) | (3.3) | (19.7) | (12.4) | ||
| Model 6 (RCP4.5) | 1345 | 218 | 14 | 81 | 25 | 163 |
| (16.2) | (1.5) | (4.5) | (42.1) | (42.1) | ||
| EM (RCP4.5) | 1335 | 68 | 0 | 70 | 2 | 46 |
| (5.1) | (0.0) | (5.0) | (25.4) | (8.5) | ||
| Model 1 (RCP8.5) | 1338 | 288 | 39 | 96 | 39 | 216 |
| (21.5) | (4.4) | (6.2) | (67.8) | (50.1) | ||
| Model 2 (RCP8.5) | 1334 | −83 | −16 | 136 | −5 | −91 |
| (−6.2) | (−1.8) | (7.8) | (−9.7) | (−22.5) | ||
| Model 3 (RCP8.5) | 1311 | −76 | 11 | 76 | −6 | −85 |
| (−5.8) | (1.5) | (5.9) | (−8.9) | (−16.3) | ||
| Model 4 (RCP8.5) | 1334 | −33 | −28 | 91 | 12 | −28 |
| (−2.4) | (−4.2) | (8.1) | (18.6) | (−4.4) | ||
| Model 5 (RCP8.5) | 1355 | 130 | 1 | 75 | 18 | 102 |
| (9.6) | (0.1) | (4.6) | (31.6) | (24.2) | ||
| Model 6 (RCP8.5) | 1345 | 302 | 25 | 81 | 38 | 239 |
| (22.5) | (2.7) | (4.5) | (63.4) | (61.6) | ||
| EM (RCP8.5) | 1335 | 88 | −2 | 101 | 3 | 60 |
| (6.6) | (−0.2) | (7.2) | (34.6) | (10.9) |
| Statistic Measure | 2-Year | 5-Year | 10-Year | 25-Year | 50-Year | 100-Year |
|---|---|---|---|---|---|---|
| Arithmetic mean | 8.60 | 9.58 | 13.19 | 20.47 | 27.89 | 37.19 |
| Standard deviation | 21.79 | 16.31 | 18.64 | 28.72 | 39.75 | 53.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Näschen, K.; Diekkrüger, B.; Leemhuis, C.; Seregina, L.S.; van der Linden, R. Impact of Climate Change on Water Resources in the Kilombero Catchment in Tanzania. Water 2019, 11, 859. https://doi.org/10.3390/w11040859
Näschen K, Diekkrüger B, Leemhuis C, Seregina LS, van der Linden R. Impact of Climate Change on Water Resources in the Kilombero Catchment in Tanzania. Water. 2019; 11(4):859. https://doi.org/10.3390/w11040859
Chicago/Turabian StyleNäschen, Kristian, Bernd Diekkrüger, Constanze Leemhuis, Larisa S. Seregina, and Roderick van der Linden. 2019. "Impact of Climate Change on Water Resources in the Kilombero Catchment in Tanzania" Water 11, no. 4: 859. https://doi.org/10.3390/w11040859
APA StyleNäschen, K., Diekkrüger, B., Leemhuis, C., Seregina, L. S., & van der Linden, R. (2019). Impact of Climate Change on Water Resources in the Kilombero Catchment in Tanzania. Water, 11(4), 859. https://doi.org/10.3390/w11040859





