Effect of the Concentration of Sand in a Mixture of Water and Sand Flowing through PP and PVC Elbows on the Minor Head Loss Coefficient
Abstract
1. Introduction
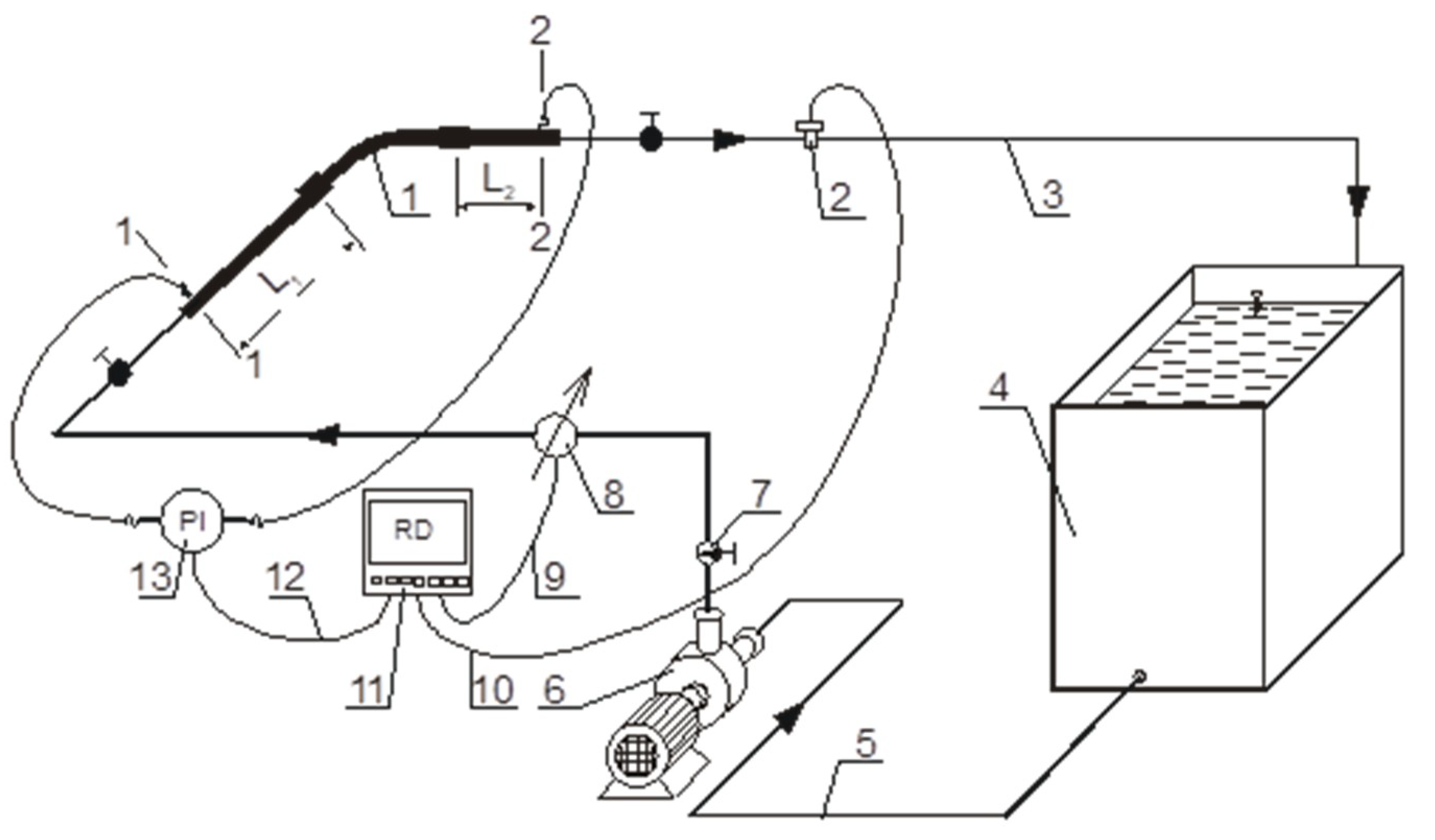
2. Materials and Methods
3. Results
3.1. Hydraulic Conditions of Flow the Mixture Water and Sand
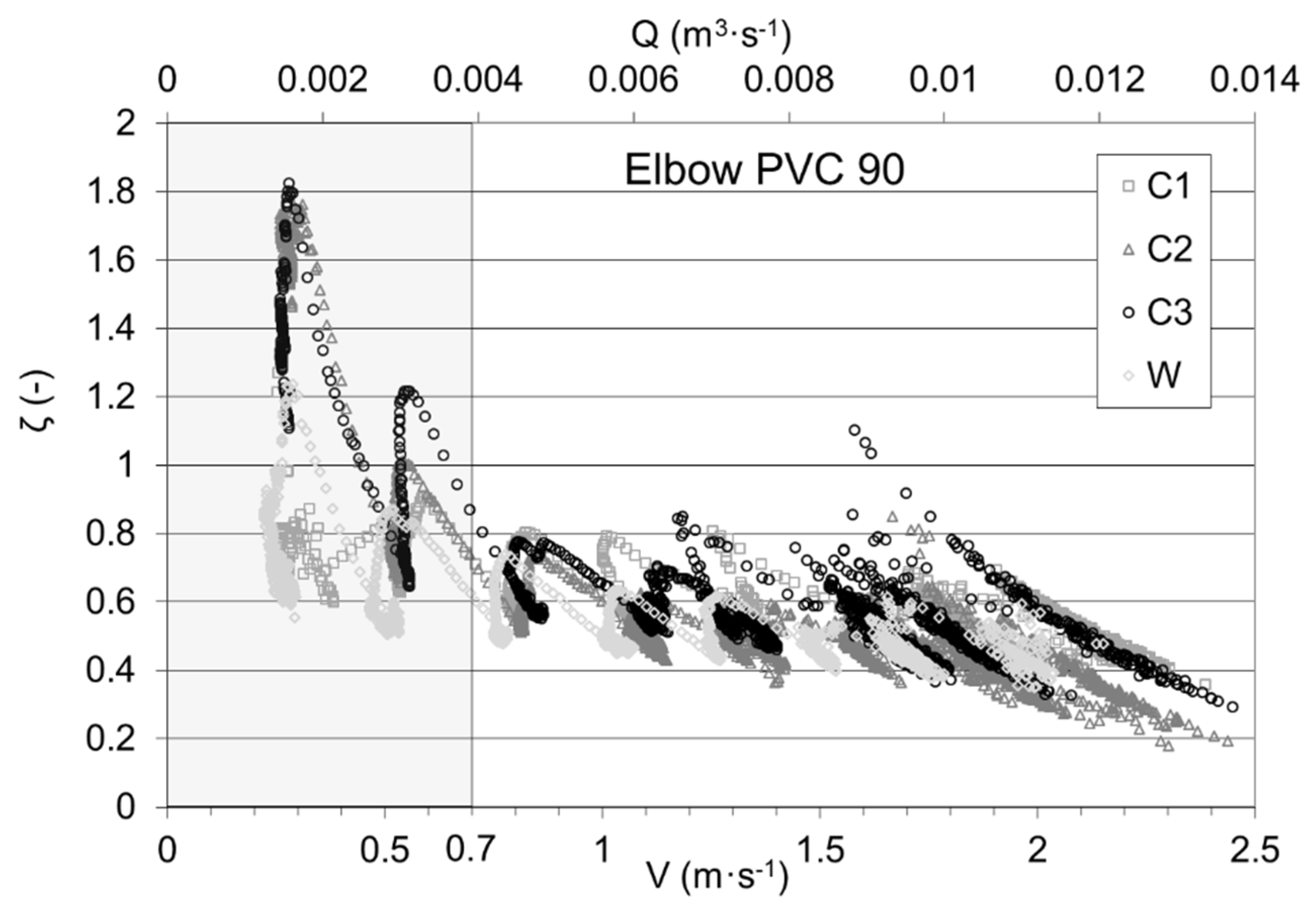
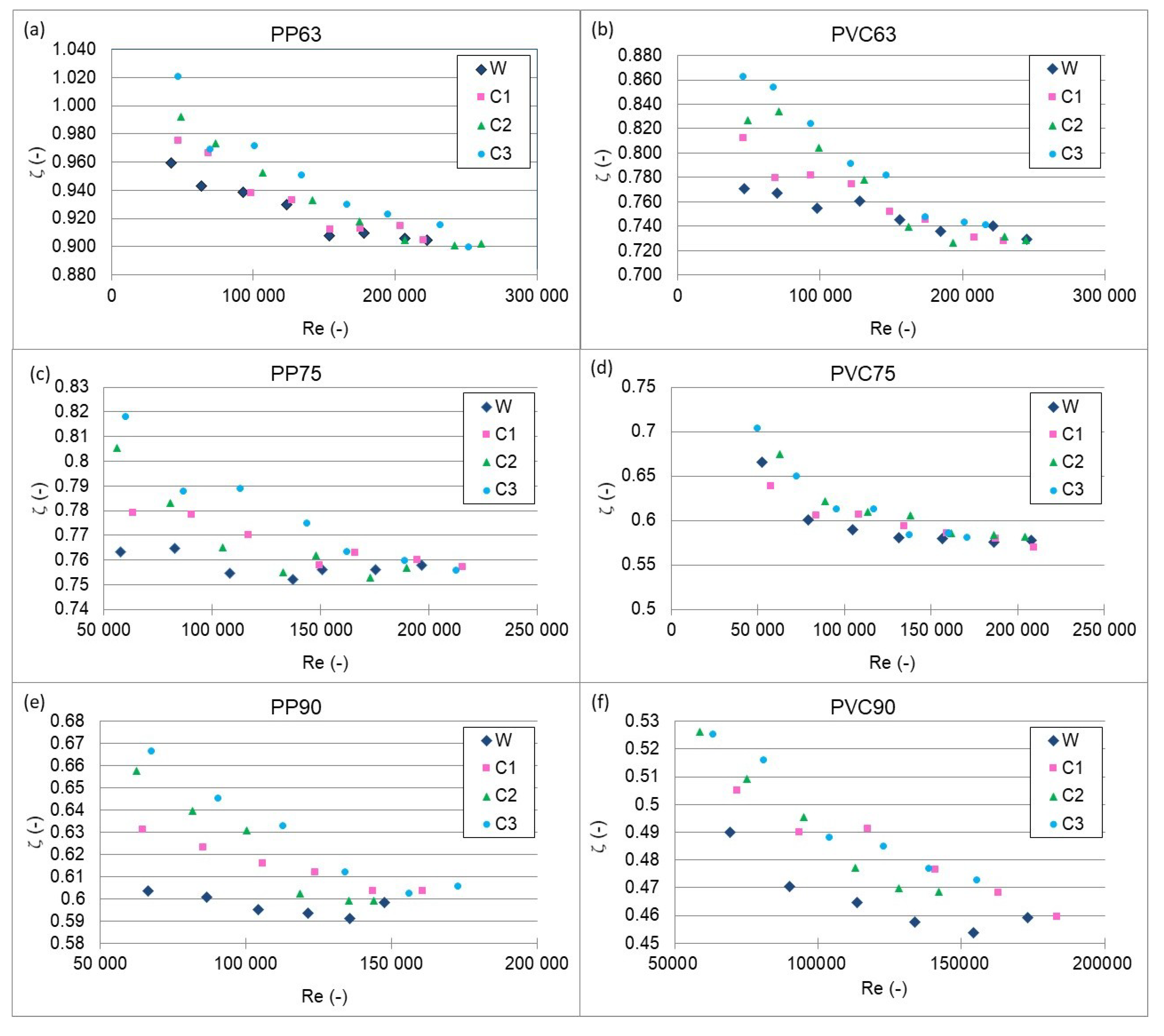
3.2. Results of Measurements
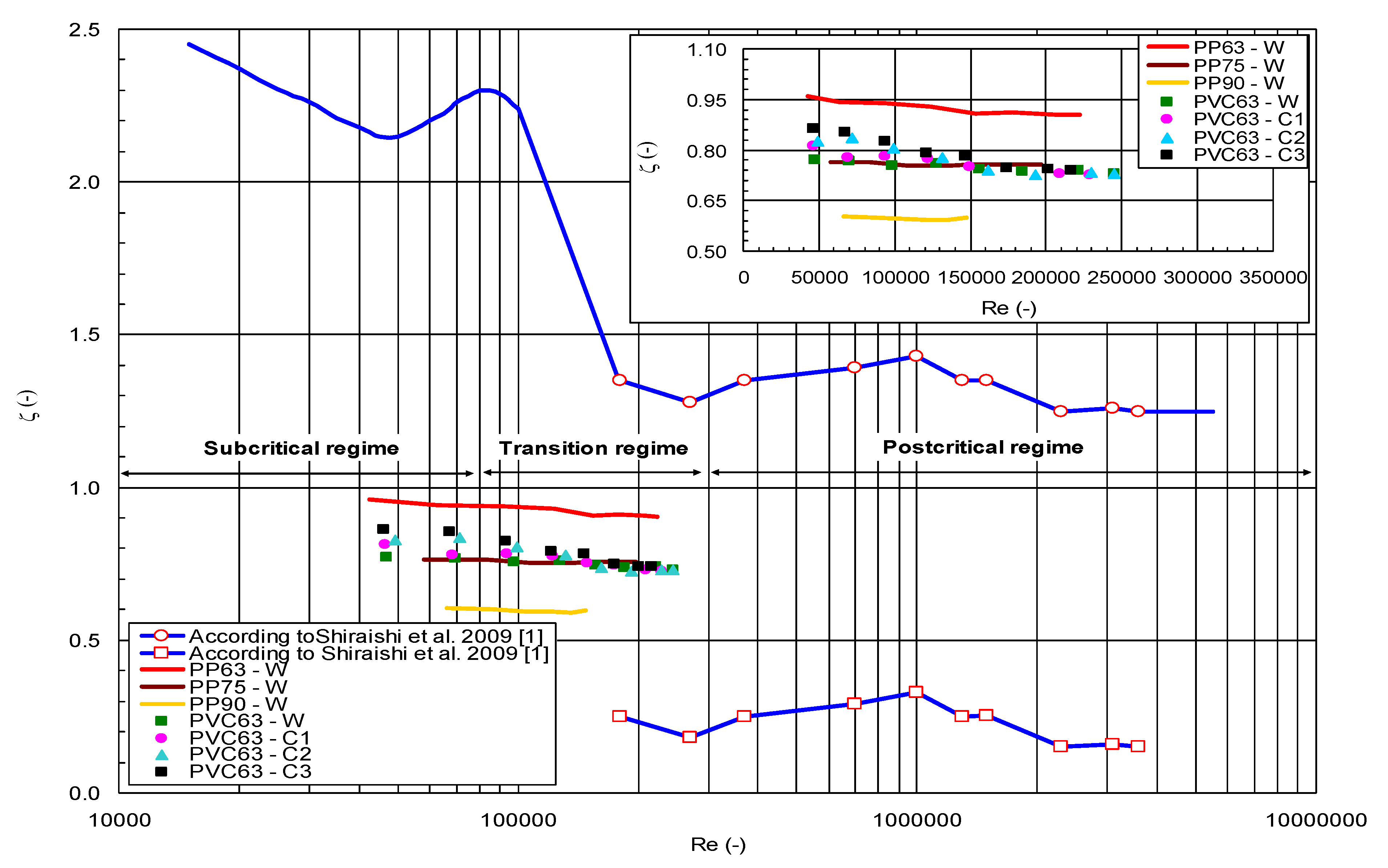
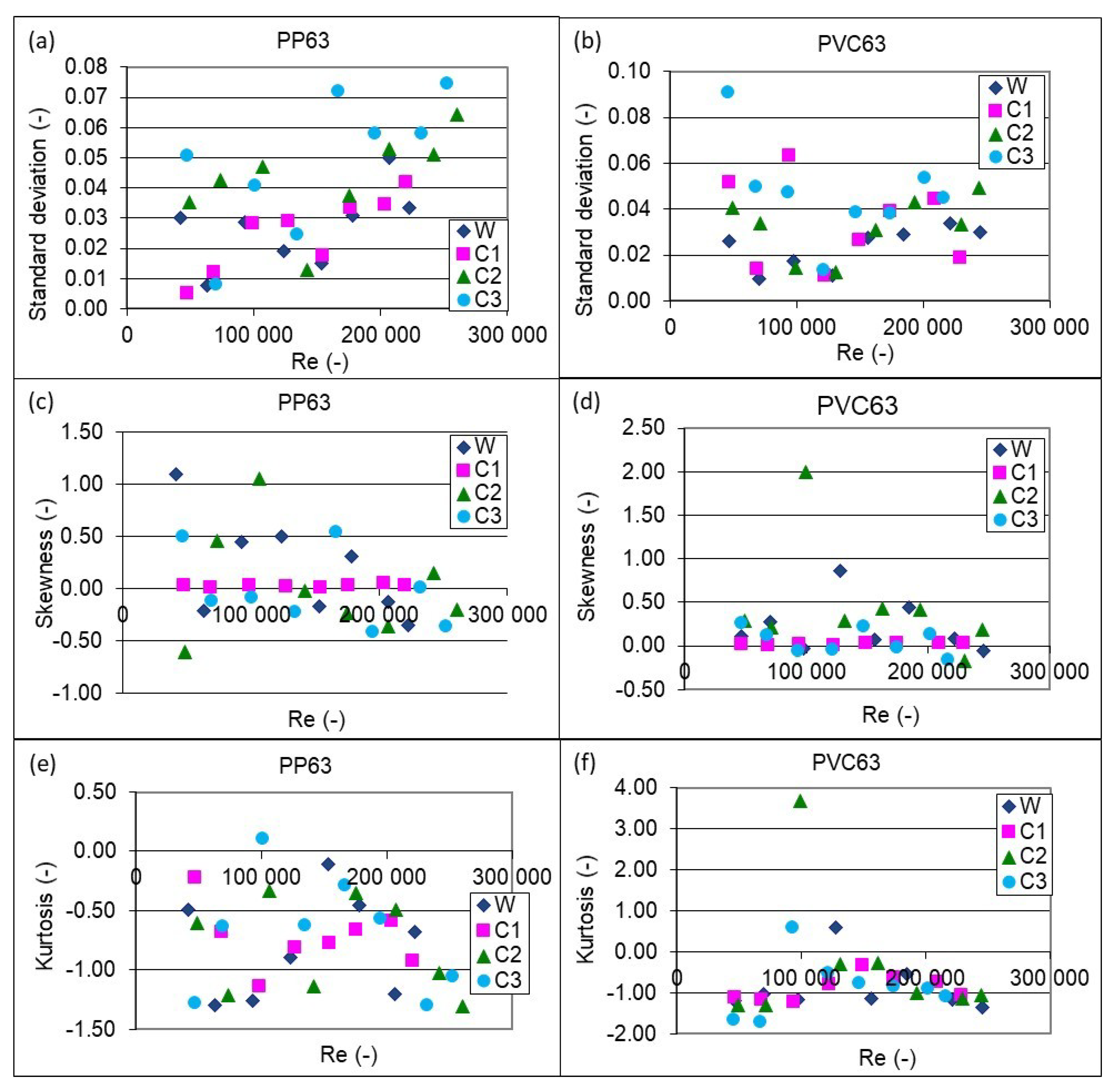
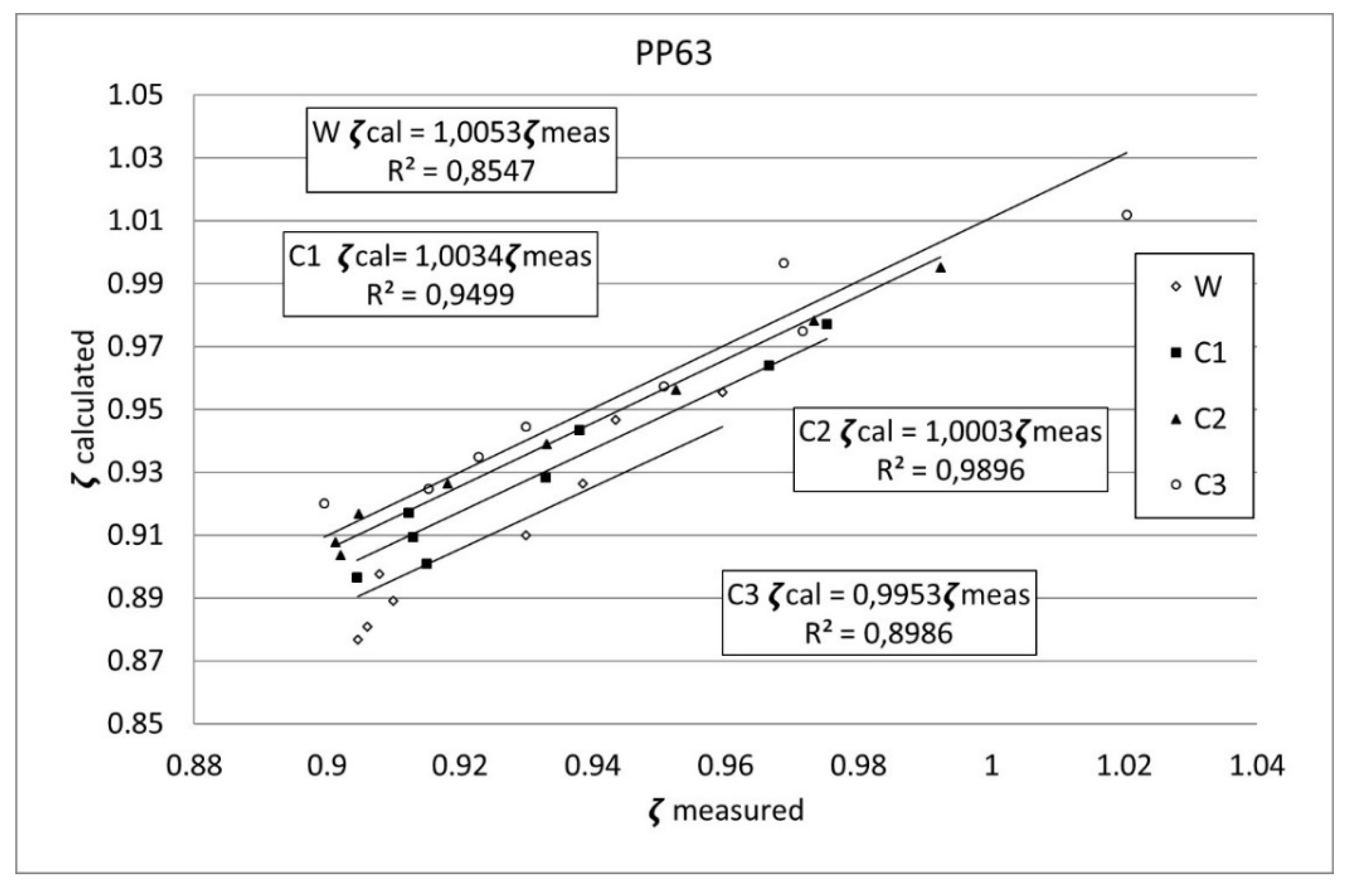
3.3. Statistical Analysis of Results
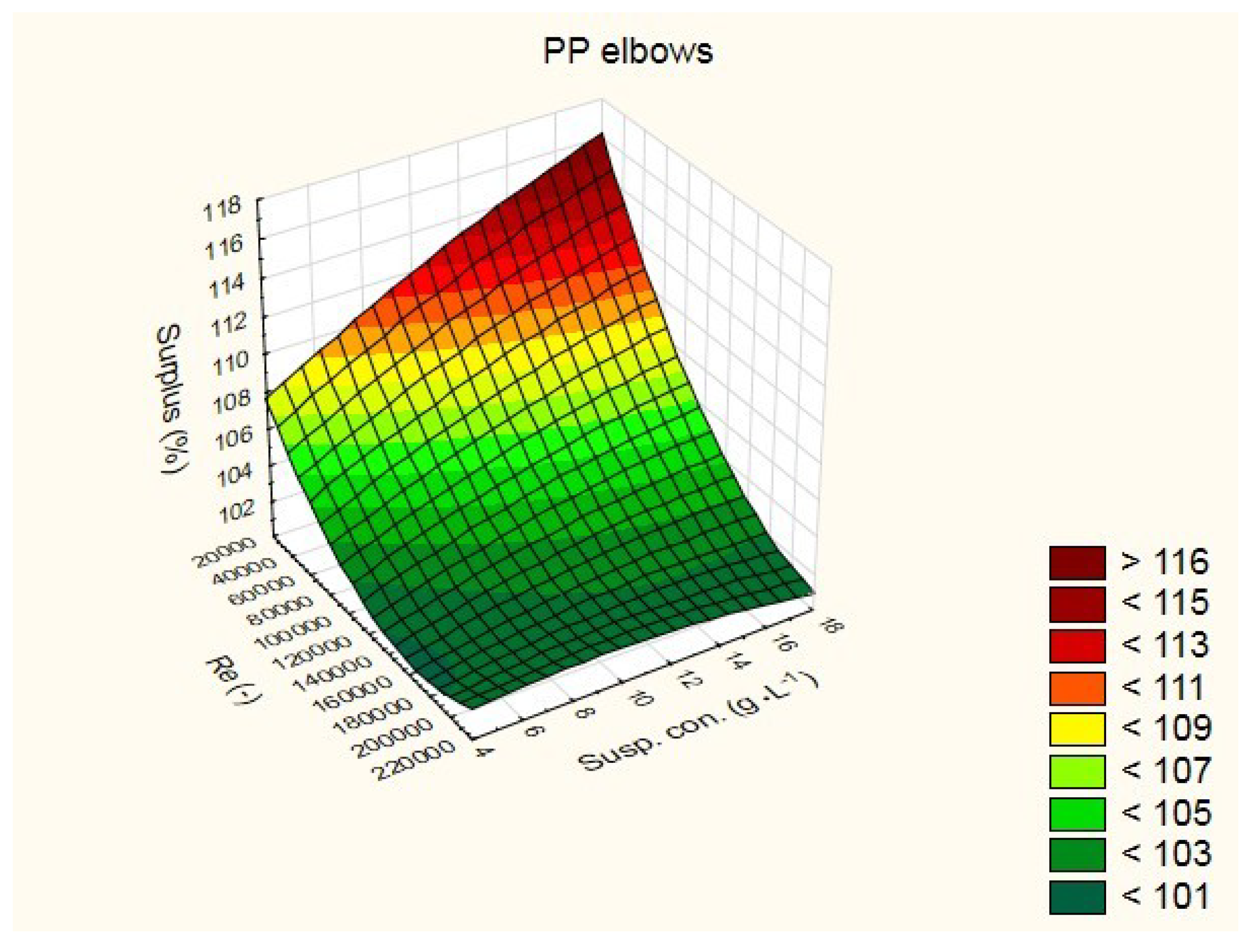
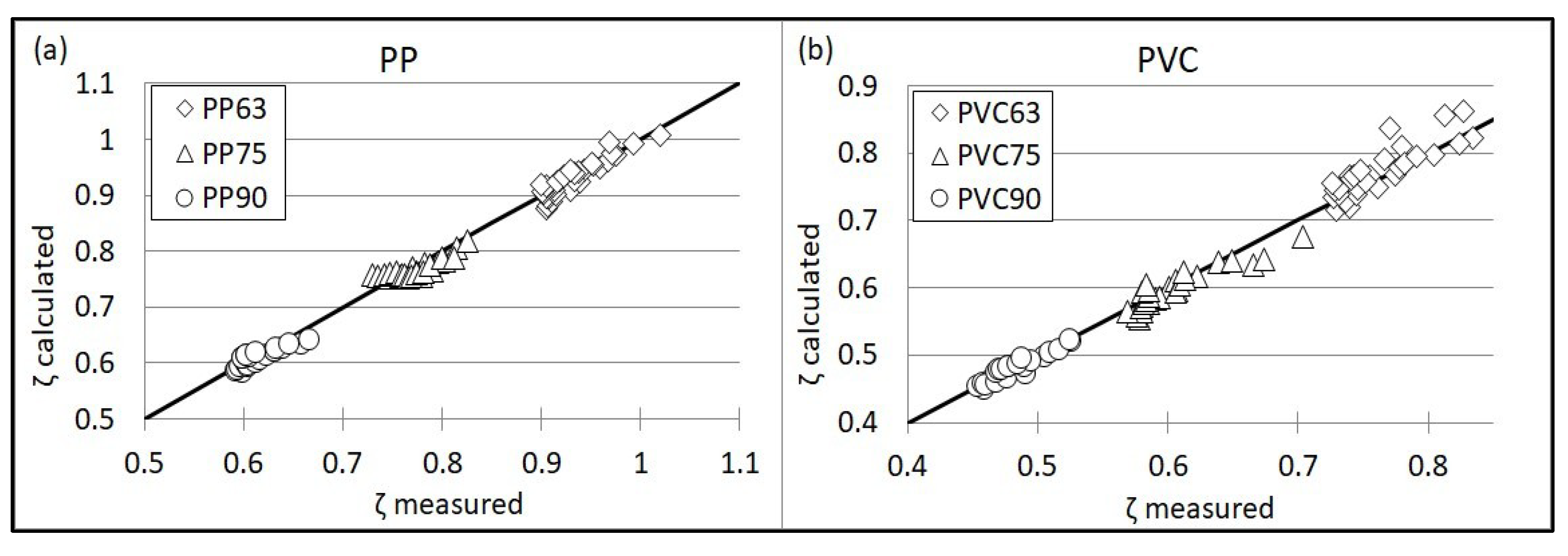
3.4. Appointment of Models for Calculation on the Minor Head Loss Coefficient for Elbows PP and PVC
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shiraishi, T.; Watakabe, H.; Sago, H.; Yamanao, H. Pressure fluctuation characteristics of the short-radius elbow pipe for FBR in the postcritical Reynolds regime. J. Fluid Sci. Technol. 2009, 4, 430–441. [Google Scholar] [CrossRef][Green Version]
- Ma, Z.W.; Zhang, P. Pressure drops and loss coefficients of a phase change material slurry in pipe fittings. Int. J. Refrig. 2012, 35, 991–1002. [Google Scholar] [CrossRef]
- Ono, A.; Kimura, N.; Kamide, H.; Tobita, A. Influence of elbow curvature on flow structure at elbow outlet under high Reynolds number condition. Nucl. Eng. Des. 2011, 241, 4409–4419. [Google Scholar] [CrossRef]
- Shi, X.J.; Zhang, P. Two-phase flow and heat transfer characteristics of tetra-n-butyl aminium bromide clathrate hydrate slurry in horizontal 90° pipe and U-pipe. Int. J. Heat Mass Transf. 2016, 97, 364–378. [Google Scholar] [CrossRef]
- Ikarashi, Y.; Taguchi, S.; Yamagata, T.; Fujisawa, N. Mass and momentum transfer characteristics in and downstream of 90° elbow. Int. J. Heat Mass Transf. 2017, 107, 1085–1093. [Google Scholar] [CrossRef]
- Dutta, P.; Saha, S.K.; Nandi, N.; Pal, N. Numerical study on flow separation in 90° pipe bend under high Reynolds number by k-ε modelling. Eng. Sci. Technol. Int. J. 2016, 19, 904–910. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; Souza, F.J.; de Vasconcelos Salvo, R.; dos Santos, V.F. The role of inter-particle collisions in elbow erosion. Int. J. Multiph. Flow 2017, 89, 1–22. [Google Scholar] [CrossRef]
- Vieira, R.E.; Parsi, M.; Zahedi, P.; McLaury, B.S.; Shirazi, S.A. Ultrasonic measurements of sand particle erosion under upward multiphase annular flow conditions in a vertical-horizontal bend. Int. J. Multiph. Flow 2017, 93, 48–62. [Google Scholar] [CrossRef]
- Kalenik, M. Empirical formulas for calculation of negative pressure difference in vacuum pipelines. Water 2015, 7, 5284–5304. [Google Scholar] [CrossRef]
- Qiao, S.; Kim, S. Interfacial area transport across a 90° vertical-upward elbow in air–water bubbly two-phase flow. Int. J. Multiph. Flow 2016, 85, 110–122. [Google Scholar] [CrossRef]
- Yadaw, M.S.; Kim, S.; Tien, K.; Bajorek, S.M. Experiments on geometric effects of 90-degree vertical-upward elbow in air water two-phase flow. Int. J. Multiph. Flow 2014, 65, 98–107. [Google Scholar] [CrossRef]
- Yadaw, M.S.; Worosz, T.; Kim, S.; Tien, K.; Bajorek, S.M. Characterization of the dissipation of elbow effects in bubbly two-phase flows. Int. J. Multiph. Flow 2014, 66, 101–109. [Google Scholar] [CrossRef]
- Rohring, R.; Jakirlić, S.; Tropea, C. Comparative computational study of turbulent flow in a 90° pipe elbow. Int. J. Heat Fluid Flow 2015, 55, 120–131. [Google Scholar] [CrossRef]
- Yoo, D.H.; Singh, V.P. Explicit design of commercial pipes with secondary losses. J. Hydro-Environ. Res. 2010, 4, 37–45. [Google Scholar] [CrossRef]
- Li, A.; Chen, X.; Chen, L.; Gao, R. Study on local drag reduction effects of wedge-shaped components in elbow and T-junction close-coupled pipes. Build. Simul. 2014, 7, 175–184. [Google Scholar] [CrossRef]
- Yuki, K.; Hasegawa, S.; Sato, T.; Hoshizume, H.; Aizawa, K.; Yamano, H. Matched refractive-index PIV visualization of complex flow structure in a three-dimentionally connected dual elbow. Nucl. Eng. Des. 2011, 241, 4544–4550. [Google Scholar] [CrossRef]
- Ebara, S.; Takamura, H.; Hoshizume, H.; Yamano, H. Characteristics of flow field and pressure fluctuation in complex turbulent flow in the third elbow of a triple elbow piping with small curvature radius in three-dimensional layout. Int. J. Hydrogen Energy 2016, 41, 7139–7145. [Google Scholar] [CrossRef]
- Basset, M.; Winterbone, D.; Pearson, R. Calculation of steady flow pressure loss coefficients for pipe junctions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 861–881. [Google Scholar] [CrossRef]
- Cisowska, I.; Kotowski, A. Studies of hydraulic resistance in polypropylene pipes and pipe fittings. Found. Civ. Environ. Eng. 2006, 8, 37–57. [Google Scholar]
- Gietka, N.N. Experimental analysis of local resistance coefficients on elbows in multilayer duct systems. Acta Sci. Pol. Formatio Circumiectus 2015, 14, 47–56. [Google Scholar] [CrossRef]
- Siwiec, T.; Morawski, D.; Karaban, G. Experimental tests of head losses in welded plastic fittings. Gaz Woda Technika Sanitarna 2002, 2, 49–68. (In Polish) [Google Scholar]
- Nawrot, T.; Matz, R.; Błażejewski, R.; Spychała, M. A case study of a small diameter gravity sewerage system in Zolkiewka Commune, Poland. Water 2018, 10, 1358. [Google Scholar] [CrossRef]
- Gopaliya, M.K.; Kaushal, D.R. Modeling of sand-water slurry flow through horizontal pipe using CFD. J. Hydrol. Hydromech. 2016, 64, 261–272. [Google Scholar] [CrossRef]
- Vlasak, P.; Chara, Z.; Krupička, J.; Konfršt, J. Experimental investigation of coarse particles-water mixture flow in horizontal and inclined pipes. J. Hydrol. Hydromech. 2014, 62, 241–247. [Google Scholar] [CrossRef]
- Assefa, K.M.; Kausha, D.R. A comparative study of friction factor correlations for high concentrate slurry flow in smooth pipes. J. Hydrol. Hydromech. 2015, 63, 13–20. [Google Scholar] [CrossRef]
- Csizmadia, P.; Hos, C. CFD-based estimation and experiments on the loss coefficient for Bingham and power-law fluids through diffusers and elbows. Comput. Fluids 2014, 99, 116–123. [Google Scholar] [CrossRef]
- Kalenik, M.; Witowska, B. Research of local hydraulic resistance in PVC fittings. ACTA Scientiarum Polonorium. Architectura 2007, 6, 15–24. (In Polish) [Google Scholar]
- Weinerowska-Bords, K. Experimental analysis of local energy loss coefficients for selected fittings and connectors in polymeric multilayer pipe systems. Instal 2014, 6, 42–49. (In Polish) [Google Scholar]
- Liu, M.; Duan, Y.F. Resistance properties of coal–water slurry flowing through local piping fittings. Exp. Therm. Fluid Sci. 2009, 33, 828–837. [Google Scholar] [CrossRef]
- Pliżga, O.; Kowalska, B.; Musz-Pomorska, A. Laboratory and numerical studies of water flow through selected fittings installed at copper pipelines. Annu. Set Environ. Prot. 2016, 18, 873–884. [Google Scholar]
- Li, Y.; Wang, C.; Ha, M. Experimental determination of local resistance coefficient of sudden expansion tube. Energy Power Eng. 2015, 7, 154–159. [Google Scholar] [CrossRef][Green Version]
- PN-EN 1267:2012. Industrial Valves—Test of Flow Resistance Using Water as Test Fluid. Polish Standard. Available online: http://sklep.pkn.pl/pn-en-1267-2012e.html (accessed on 18 March 2016).
- PN-EN 12880:2004. Characterization of Sludges. Determination of Dry Residue and Water Content. Polish Standard. Available online: http://sklep.pkn.pl/pn-en-12880-2002e.html (accessed on 18 March 2016).
- Siwiec, T.; Wichowski, P.; Kalenik, M.; Morawski, D. Comparative analyse formulas for calculation head coefficient in plastic pipes with water and wastewater flow. Instal 2012, 7–8, 52–57. (In Polish) [Google Scholar]
- Jeż, P.; Książyński, K.; Gręplowska, Z. Tables for Hydraulic Calculations; Cracow University of Technology: Cracow, Poland, 1998. (In Polish) [Google Scholar]
- Dziubiński, M.; Prywer, J. Mechanics of Two-Phase Fluids; WNT: Warsaw, Poland, 2009. (In Polish) [Google Scholar]
- Wilson, K.C.; Addie, G.R.; Sellgren, A.; Clift, R. Slurry Transport Using Centrifugal Pumps, 3rd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Zięba, A. Data Analysis in Science and Technology; PWN: Warsaw, Poland, 2013. (In Polish) [Google Scholar]
- PN EN 16932-2:2018. Drain and Sewer Systems Outside Buildings.Pumping Systems. Positive Pressure Systems. Available online: http://sklep.pkn.pl/pn-en-16932-2-2018-05e.html (accessed on 18 March 2016).
- Wichowski, P.; Zalewska, K. Experimental studies on removal of mineral suspension from siphons in rain water pipelines. Annu. Set Environ. Prot. 2015, 17, 1642–1659. (In Polish) [Google Scholar]
- Mizutani, J.; Ebara, S.; Hashizume, H. Evaluation of influence of the inlet swirling flow on the flow field in the triple elbow system. Int. J. Hydrogen Energy 2016, 41, 7233–7238. [Google Scholar] [CrossRef]




| Medium | No. | W | C1 | C2 | C3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Elbow | ζav | ζmed | ζσ | ζav | ζmed | ζσ | ζav | ζmed | ζσ | ζav | ζmed | ζσ | |
| PP63 | 1 | 0.905 | 0.909 | 0.034 | 0.905 | 0.915 | 0.042 | 0.902 | 0.915 | 0.064 | 0.899 | 0.920 | 0.075 |
| 2 | 0.906 | 0.910 | 0.050 | 0.915 | 0.912 | 0.035 | 0.901 | 0.904 | 0.051 | 0.915 | 0.916 | 0.058 | |
| 3 | 0.910 | 0.909 | 0.031 | 0.913 | 0.914 | 0.033 | 0.905 | 0.905 | 0.053 | 0.923 | 0.928 | 0.058 | |
| 4 | 0.908 | 0.907 | 0.015 | 0.912 | 0.913 | 0.018 | 0.918 | 0.925 | 0.037 | 0.930 | 0.919 | 0.072 | |
| 5 | 0.930 | 0.924 | 0.019 | 0.933 | 0.938 | 0.029 | 0.933 | 0.932 | 0.013 | 0.951 | 0.952 | 0.025 | |
| 6 | 0.938 | 0.926 | 0.029 | 0.938 | 0.933 | 0.028 | 0.953 | 0.941 | 0.047 | 0.972 | 0.974 | 0.041 | |
| 7 | 0.943 | 0.944 | 0.008 | 0.967 | 0.972 | 0.012 | 0.973 | 0.961 | 0.043 | 0.969 | 0.968 | 0.008 | |
| 8 | 0.960 | 0.945 | 0.030 | 0.975 | 0.975 | 0.005 | 0.992 | 1.011 | 0.035 | 1.020 | 0.982 | 0.051 | |
| PVC63 | 1 | 0.729 | 0.729 | 0.030 | 0.728 | 0.725 | 0.019 | 0.729 | 0.738 | 0.049 | 0.741 | 0.747 | 0.045 |
| 2 | 0.740 | 0.738 | 0.034 | 0.731 | 0.738 | 0.045 | 0.732 | 0.731 | 0.033 | 0.743 | 0.749 | 0.054 | |
| 3 | 0.736 | 0.728 | 0.029 | 0.745 | 0.742 | 0.039 | 0.726 | 0.710 | 0.043 | 0.748 | 0.754 | 0.038 | |
| 4 | 0.745 | 0.739 | 0.027 | 0.752 | 0.754 | 0.027 | 0.739 | 0.740 | 0.031 | 0.782 | 0.777 | 0.039 | |
| 5 | 0.761 | 0.759 | 0.011 | 0.774 | 0.773 | 0.011 | 0.778 | 0.777 | 0.013 | 0.791 | 0.794 | 0.013 | |
| 6 | 0.755 | 0.760 | 0.018 | 0.782 | 0.771 | 0.063 | 0.804 | 0.801 | 0.014 | 0.824 | 0.826 | 0.048 | |
| 7 | 0.767 | 0.765 | 0.010 | 0.779 | 0.783 | 0.014 | 0.834 | 0.830 | 0.034 | 0.854 | 0.836 | 0.050 | |
| 8 | 0.771 | 0.770 | 0.026 | 0.812 | 0.831 | 0.052 | 0.827 | 0.816 | 0.041 | 0.863 | 0.820 | 0.091 | |
| Fitting | m | Value | k | Value | Remin | Remax |
|---|---|---|---|---|---|---|
| PP63 | mPP63zaw | −0.031306 | kPP63zaw | 0.661078 | 4.2 × 104 | 2.6 × 105 |
| PP75 | mPP75zaw | −0.066786 | kPP75zaw | 0.546732 | 5.6 × 104 | 2.15 × 105 |
| PP90 | mPP90zaw | −0.0085 | kPP90zaw | 0.428871 | 6.2 × 104 | 1.7 × 105 |
| PVC63 | mPVC63zaw | −0.004077 | kPVC63zaw | 0.539926 | 4.6 × 104 | 2.5 × 105 |
| PVC75 | mPVC75zaw | −0.00892 | kPVC75zaw | 0.424447 | 4.9 × 104 | 2.1 × 105 |
| PVC90 | mPVC90zaw | −0.00973 | kPVC90zaw | 0.337607 | 5.9 × 104 | 1.8 × 105 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wichowski, P.; Siwiec, T.; Kalenik, M. Effect of the Concentration of Sand in a Mixture of Water and Sand Flowing through PP and PVC Elbows on the Minor Head Loss Coefficient. Water 2019, 11, 828. https://doi.org/10.3390/w11040828
Wichowski P, Siwiec T, Kalenik M. Effect of the Concentration of Sand in a Mixture of Water and Sand Flowing through PP and PVC Elbows on the Minor Head Loss Coefficient. Water. 2019; 11(4):828. https://doi.org/10.3390/w11040828
Chicago/Turabian StyleWichowski, Piotr, Tadeusz Siwiec, and Marek Kalenik. 2019. "Effect of the Concentration of Sand in a Mixture of Water and Sand Flowing through PP and PVC Elbows on the Minor Head Loss Coefficient" Water 11, no. 4: 828. https://doi.org/10.3390/w11040828
APA StyleWichowski, P., Siwiec, T., & Kalenik, M. (2019). Effect of the Concentration of Sand in a Mixture of Water and Sand Flowing through PP and PVC Elbows on the Minor Head Loss Coefficient. Water, 11(4), 828. https://doi.org/10.3390/w11040828







