Assessing the Impact of Terraces and Vegetation on Runoff and Sediment Routing Using the Time-Area Method in the Chinese Loess Plateau
Abstract
1. Introduction
2. Materials and Methods
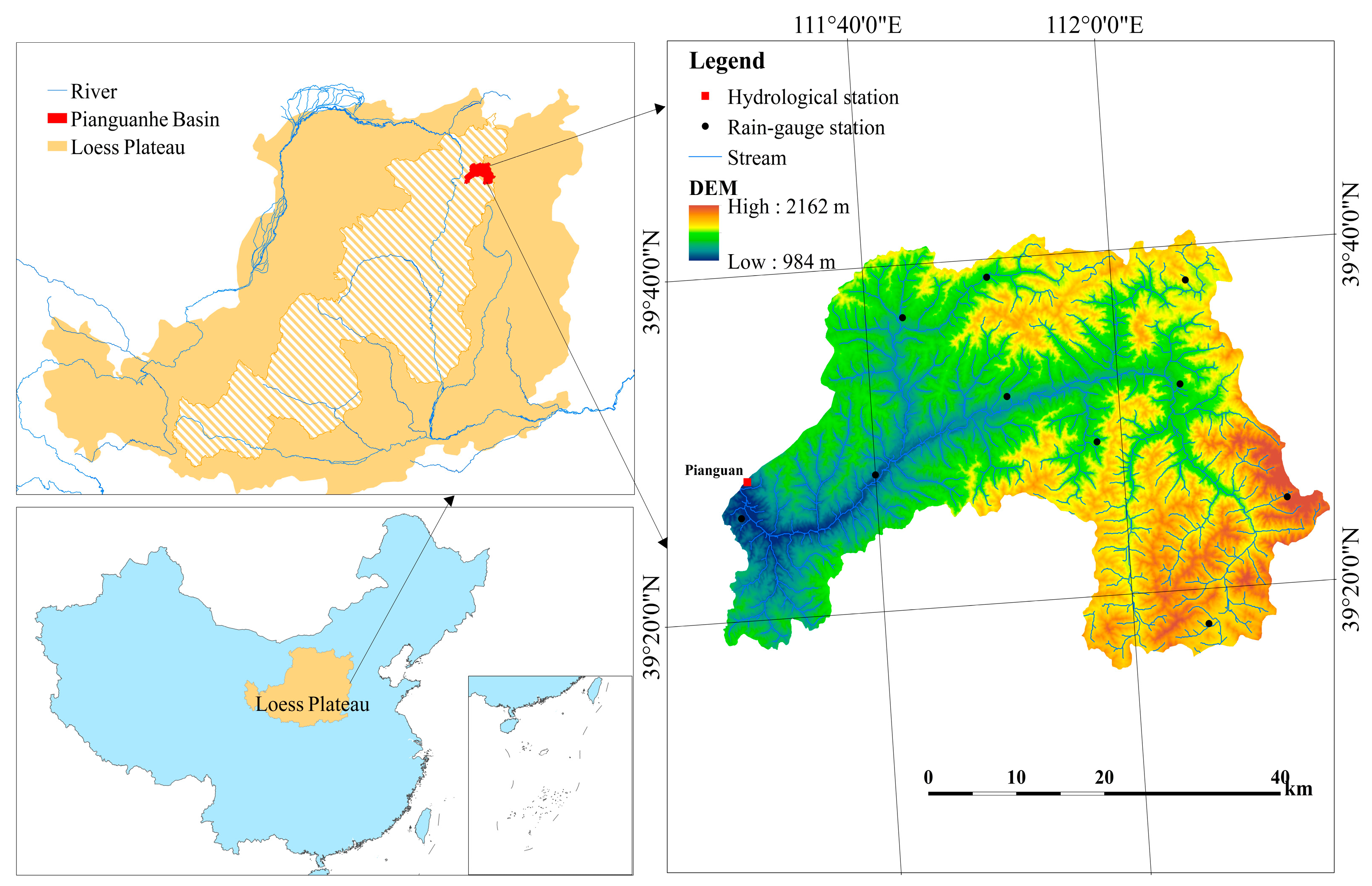
2.1. Study Area
2.2. Methods
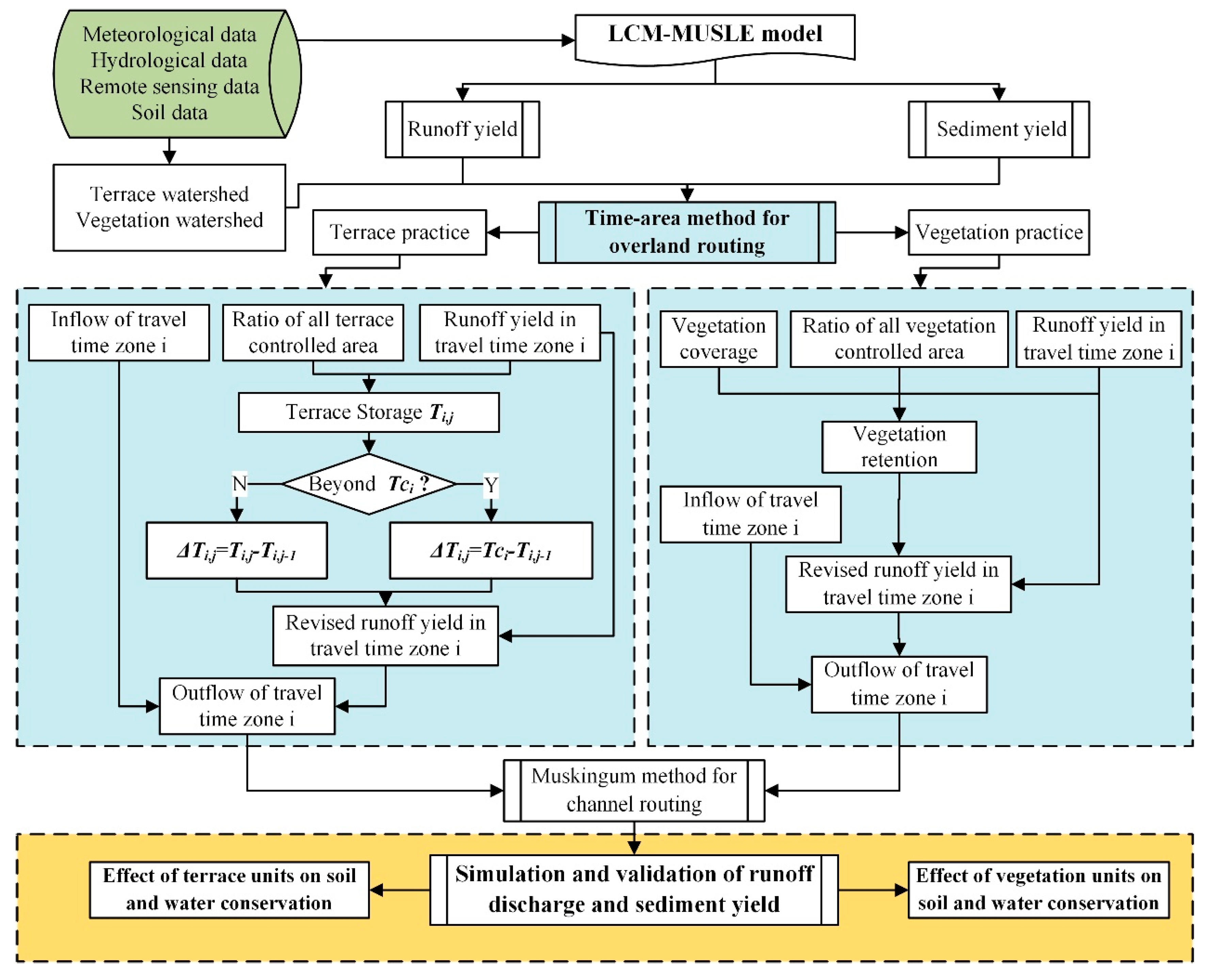
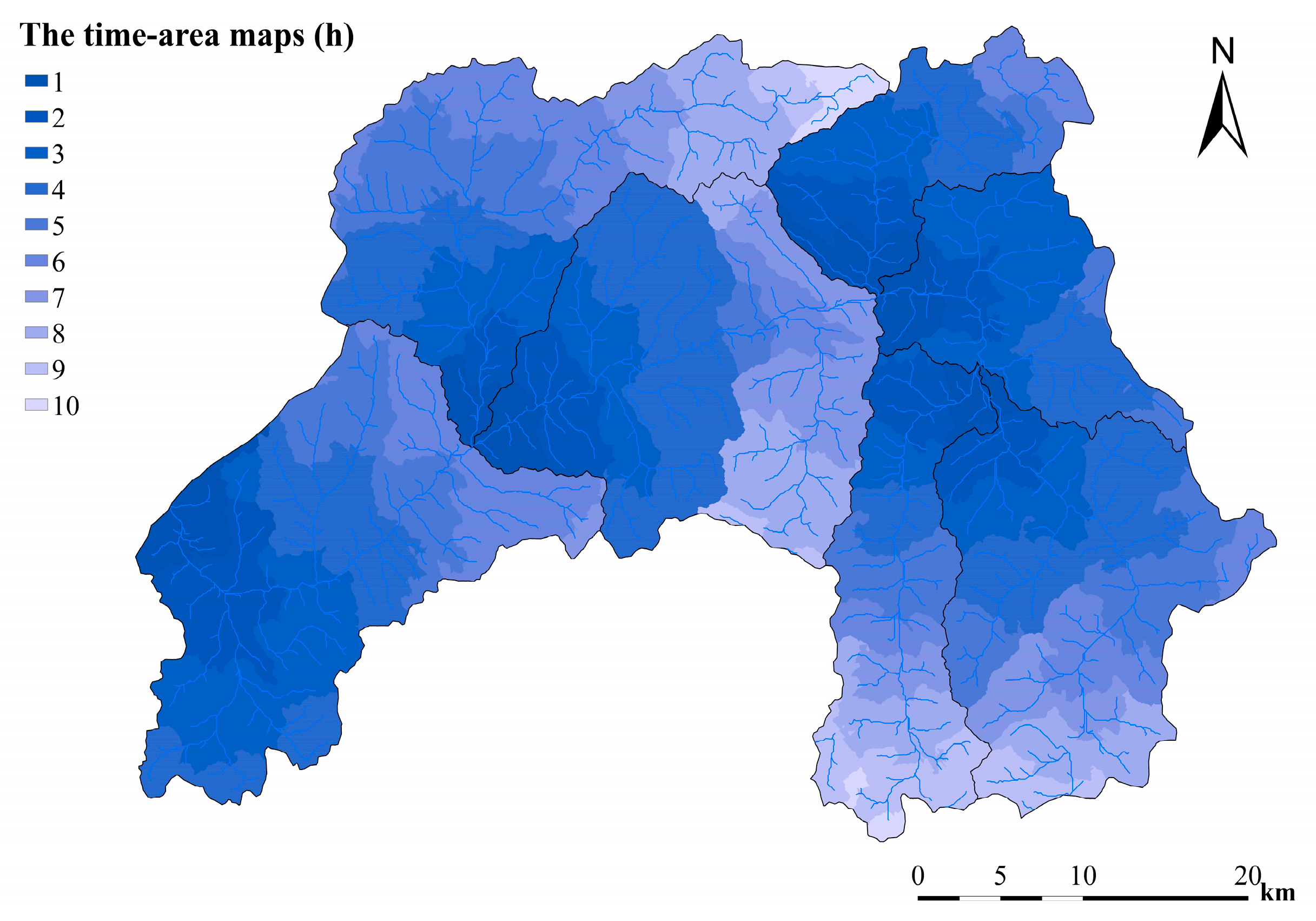
2.2.1. Time-Area Method for Overland Routing
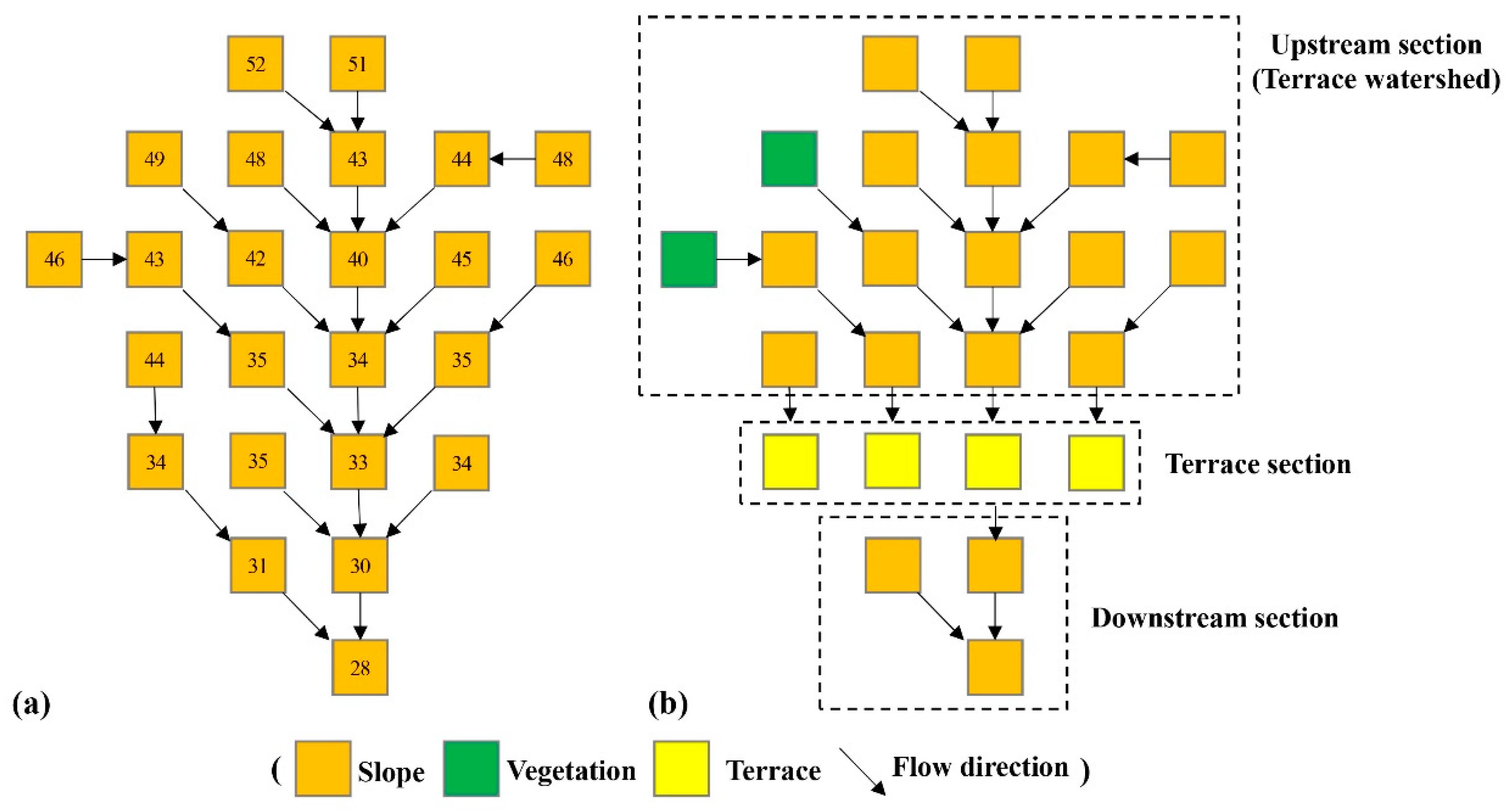
2.2.2. Extraction of the Terrace Units and Vegetation Units Watershed
2.2.3. Consideration of Terrace Units in the Time-Area Method
2.2.4. Consideration of Vegetation Units in the Time-area Method
2.2.5. Model Performance Evaluation Criteria
2.3. Data Source
- (1)
- Hourly precipitation was collected from 10 rain-gauge stations (Figure 1). The gauge data were interpolated by the inverse distance weighted (IDW) method to acquire the spatial data.
- (2)
- Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model (ASTER GDEM) was selected to extract topographical information, river network, sub-basins and isochrones (http://www.gscloud.cn/).
- (3)
- Land use and vegetation coverage were derived from Landsat images (http://www.gscloud.cn/). Land use was classified into 11 types, including cropland (slope < 6°), cropland (6° < slope < 25°), cropland (slope ≥ 25°), forest, shrub, open woodland, immature forest land and orchard, grassland, water area, developed land, and other land. Vegetation coverage was derived based on its relation with normalized difference vegetation index (NDVI) [79], while the vegetation coverage of cropland was not included in routing process. Land use and vegetation coverage data from 1978 and 2010 were used to represent data for 1980s and 2010s, respectively.
- (4)
- Terrace data in 2012 was acquired from the Yellow River Conservancy Commission (YRCC), which was interpreted from ZY-3 images with a spatial resolution of 2.5 m and an accuracy of 94% [78].
- (5)
- The soil types, sand content, silt content, clay content, organic carbon, and gravel content were derived from the Harmonized World Soil Database (HWSD), and the soil saturated moisture of each soil type were determined from the software Soil-Plant-Atmosphere-Water Field & Pond Hydrology (SPAW).
- (6)
- The measured discharge, sediment concentration and median of sediment particle size (D50) at the Pianguanhe hydrological station were acquired from the YRCC.
3. Results
3.1. Watershed of Terrace Unit and Vegetation Unit
3.2. Validation of Runoff Discharge
3.3. Validation of Sediment Discharge
4. Discussion
4.1. Effect of Terraces and Vegetation on Runoff Reduction
4.2. Effect of Terraces and Vegetation on Sediment Reduction
4.3. Reliability Analysis of the Water and Sediment Reduction Efficiency of Terraces and Vegetation
4.4. Limitations and Potential Improvements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schnitzer, S.; Seitz, F.; Eicker, A.; Güntner, A.; Wattenbach, M.; Menzel, A. Estimation of soil loss by water erosion in the Chinese Loess Plateau using Universal Soil Loss Equation and GRACE. Geophys. J. Int. 2013, 193, 1283–1290. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, B.; Gao, G.; Lü, Y.; Liu, Y.; Lü, N.; Wang, S. Effects of precipitation and restoration vegetation on soil erosion in a semi-arid environment in the Loess Plateau, China. Catena 2016, 137, 1–11. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z.; Jia, L.; Li, P.; Xu, G.; Ren, Z.; Pang, G.; Zhao, B. Capacity of soil loss control in the Loess Plateau based on soil erosion control degree. J. Geogr. Sci. 2016, 26, 457–472. [Google Scholar] [CrossRef]
- Shi, H.; Shao, M. Soil and water loss from the Loess Plateau in China. J. Arid Environ. 2000, 45, 9–20. [Google Scholar] [CrossRef]
- Lal, R. Soil erosion and the global carbon budget. Environ. Int. 2003, 29, 437–450. [Google Scholar] [CrossRef]
- Yang, Q.; Zhao, Z.; Chow, T.L.; Rees, H.W.; Bourque, C.P.A.; Meng, F.-R. Using GIS and a digital elevation model to assess the effectiveness of variable grade flow diversion terraces in reducing soil erosion in northwestern New Brunswick, Canada. Hydrol. Process. 2009, 23, 3271–3280. [Google Scholar] [CrossRef]
- Ouyang, W.; Hao, F.; Skidmore, A.K.; Toxopeus, A.G. Soil erosion and sediment yield and their relationships with vegetation cover in upper stream of the Yellow River. Sci. Total Environ. 2010, 409, 396–403. [Google Scholar] [CrossRef]
- Preiti, G.; Romeo, M.; Bacchi, M.; Monti, M. Soil loss measure from Mediterranean arable cropping systems: Effects of rotation and tillage system on C-factor. Soil Tillage Res. 2017, 170, 85–93. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Wei, W.; Fu, B.; Wu, D. Effects of landscape restoration on soil water storage and water use in the Loess Plateau Region, China. For. Ecol. Manag. 2010, 259, 1291–1298. [Google Scholar] [CrossRef]
- Deng, L.; Shangguan, Z.P.; Sweeney, S. “Grain for Green” driven land use change and carbon sequestration on the Loess Plateau, China. Sci. Rep. 2014, 4, 7039. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Liu, Y.; Lü, Y.; He, C.; Zeng, Y.; Wu, B. Assessing the soil erosion control service of ecosystems change in the Loess Plateau of China. Ecol. Complex. 2011, 8, 284–293. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Jiao, J.-Y.; Rayburg, S.; Wang, Q.-L.; Su, Y. Soil erosion resistance of “Grain for Green” vegetation types under extreme rainfall conditions on the Loess Plateau, China. Catena 2016, 141, 109–116. [Google Scholar] [CrossRef]
- Marques, M.J.; Bienes, R.; Jimenez, L.; Perez-Rodriguez, R. Effect of vegetal cover on runoff and soil erosion under light intensity events. Rainfall simulation over USLE plots. Sci. Total Environ. 2007, 378, 161–165. [Google Scholar] [CrossRef]
- Huang, D.; Han, J.G.; Wu, J.Y.; Wang, K.; Wu, W.L.; Teng, W.J.; Sardo, V. Grass hedges for the protection of sloping lands from runoff and soil loss: An example from Northern China. Soil Tillage Res. 2010, 110, 251–256. [Google Scholar] [CrossRef]
- Wu, J.Y.; Huang, D.; Teng, W.J.; Sardo, V.I. Grass hedges to reduce overland flow and soil erosion. Agron. Sustain. Dev. 2010, 30, 481–485. [Google Scholar] [CrossRef]
- Tarolli, P.; Preti, F.; Romano, N. Terraced landscapes: From an old best practice to a potential hazard for soil degradation due to land abandonment. Anthropocene 2014, 6, 10–25. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, Y.; Lu, H.; Yuan, J.; Zhu, Y.; Liang, Y. Grass hedge effects on controlling soil loss from concentrated flow: A case study in the red soil region of China. Soil Tillage Res. 2015, 148, 97–105. [Google Scholar] [CrossRef]
- Lambrechts, T.; François, S.; Lutts, S.; Muñoz-Carpena, R.; Bielders, C.L. Impact of plant growth and morphology and of sediment concentration on sediment retention efficiency of vegetative filter strips: Flume experiments and VFSMOD modeling. J. Hydrol. 2014, 511, 800–810. [Google Scholar] [CrossRef]
- Khatavkar, P.; Mays, L.W. Optimization Models for the Design of Vegetative Filter Strips for Stormwater Runoff and Sediment Control. Water Resour. Manag. 2017, 31, 2545–2560. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, J.E.; Huang, Y.; Wang, G.; Zhang, M. Effects of Vegetation Stems on Hydraulics of Overland Flow Under Varying Water Discharges. Land Degrad. Dev. 2016, 27, 748–757. [Google Scholar] [CrossRef]
- Arabi, M.; Frankenberger, J.R.; Engel, B.A.; Arnold, J.G. Representation of agricultural conservation practices with SWAT. Hydrol. Process. 2008, 22, 3042–3055. [Google Scholar] [CrossRef]
- Yang, Q.; Meng, F.-R.; Zhao, Z.; Chow, T.L.; Benoy, G.; Rees, H.W.; Bourque, C.P.A. Assessing the impacts of flow diversion terraces on stream water and sediment yields at a watershed level using SWAT model. Agric. Ecosyst. Environ. 2009, 132, 23–31. [Google Scholar] [CrossRef]
- Chen, D.; Wei, W.; Chen, L. Effects of terracing practices on water erosion control in China: A meta-analysis. Earth-Sci. Rev. 2017, 173, 109–121. [Google Scholar] [CrossRef]
- Arnáez, J.; Lana-Renault, N.; Lasanta, T.; Ruiz-Flaño, P.; Castroviejo, J. Effects of farming terraces on hydrological and geomorphological processes. A review. Catena 2015, 128, 122–134. [Google Scholar] [CrossRef]
- Ben Khelifa, W.; Hermassi, T.; Strohmeier, S.; Zucca, C.; Ziadat, F.; Boufaroua, M.; Habaieb, H. Parameterization of the effect of bench terraces on runoff and sediment yield by SWAT modeling in a small semi-arid watershed in Northern Tunisia. Land Degrad. Dev. 2017, 28, 1568–1578. [Google Scholar] [CrossRef]
- Berendse, F.; van Ruijven, J.; Jongejans, E.; Keesstra, S. Loss of Plant Species Diversity Reduces Soil Erosion Resistance. Ecosystems 2015, 18, 881–888. [Google Scholar] [CrossRef]
- Pan, C.; Shangguan, Z. Runoff hydraulic characteristics and sediment generation in sloped grassplots under simulated rainfall conditions. J. Hydrol. 2006, 331, 178–185. [Google Scholar] [CrossRef]
- Rogger, M.; Agnoletti, M.; Alaoui, A.; Bathurst, J.C.; Bodner, G.; Borga, M.; Chaplot, V.; Gallart, F.; Glatzel, G.; Hall, J.; et al. Land use change impacts on floods at the catchment scale: Challenges and opportunities for future research. Water Resour. Res. 2017, 53, 5209–5219. [Google Scholar] [CrossRef]
- Liu, S.L.; Dong, Y.H.; Li, D.; Liu, Q.; Wang, J.; Zhang, X.L. Effects of different terrace protection measures in a sloping land consolidation project targeting soil erosion at the slope scale. Ecol. Eng. 2013, 53, 46–53. [Google Scholar] [CrossRef]
- Yao, Y. Analysis of Effects of Bench Terraced Field on Reducing Soil Erosion. Soil Water Conserv. China 1992, 12, 40–41. (In Chinese) [Google Scholar]
- Wu, F. Study on the Benefits of Level Terrace on Soil and Water Conservation. Sci. Soil Water Conserv. 2004, 2, 34–37. (In Chinese) [Google Scholar]
- Huo, Y.P.; Zhu, B.B. Analysis on the Benefits of Level Terrace on Soil and Water Conservation in Loess Hilly Areas. Res. Soil Water Conserv. 2013, 20, 24–28. (In Chinese) [Google Scholar]
- Meng, C.; Zhang, H.; Yang, P. Effects of Simulated Vegetation Types and Spatial Patterns on Hydrodynamics of Overland Flow. J. Soil Water Conserv. 2017, 31, 50–56. (In Chinese) [Google Scholar]
- Kovář, P.; Bačinová, H.; Loula, J.; Fedorova, D. Use of terraces to mitigate the impacts of overland flow and erosion on a catchment. Plant Soil Environ. 2016, 62, 171–177. [Google Scholar] [CrossRef]
- Zhao, H.; Fang, X.; Ding, H.; Josef, S.; Xiong, L.; Na, J.; Tang, G. Extraction of Terraces on the Loess Plateau from High-Resolution DEMs and Imagery Utilizing Object-Based Image Analysis. ISPRS Int. J. Geo-Inf. 2017, 6, 157. [Google Scholar] [CrossRef]
- Wei, W.; Chen, D.; Wang, L.; Daryanto, S.; Chen, L.; Yu, Y.; Lu, Y.; Sun, G.; Feng, T. Global synthesis of the classifications, distributions, benefits and issues of terracing. Earth-Sci. Rev. 2016, 159, 388–403. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool Input/Output File Documentation: Version 2009; Texas Water Resources Institute Technical Report 365; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Chiu, Y.-J.; Lee, H.-Y.; Wang, T.-L.; Yu, J.; Lin, Y.-T.; Yuan, Y. Modeling Sediment Yields and Stream Stability Due to Sediment-Related Disaster in Shihmen Reservoir Watershed in Taiwan. Water 2019, 11, 332. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Wu, Y.-H.; Shen, C.-W.; Chiu, Y.-J. Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan. Water 2018, 10, 1808. [Google Scholar] [CrossRef]
- Panuska, J.C.; Moore, I.D.; Kramer, L.A. Terrain Analysis: Integration into Agricultural Nonpoint Source (AGNPS) Pollution Model. J. Soil Water Conserv. 1991, 46, 59–64. [Google Scholar]
- Gassman, P.W.; Williams, J.R.; Wang, X.; Saleh, A.; Osei, E.; Hauck, L.M.; Izaurralde, R.C.; Flowers, J.D. Invited Review Article: The Agricultural Policy/Environmental eXtender (APEX) Model: An Emerging Tool for Landscape and Watershed Environmental Analyses. Trans. ASABE 2010, 53, 711–740. [Google Scholar] [CrossRef]
- Shao, H.; Baffaut, C.; Gao, J.E.; Nelson, N.O.; Janssen, K.A.; Pierzynski, G.M.; Barnes, P.L. Development and application of algorithms for simulating terraces within SWAT. Trans. ASABE 2013, 56, 1715–1730. [Google Scholar]
- Mishra, S.K.; Singh, V.P. Soil Conservation Service Curve Number (SCS-CN) Methodology. Water Sci. Technol. Libr. 2007, 22, 355–362. [Google Scholar]
- Her, Y.; Heatwole, C. Two-dimensional continuous simulation of spatiotemporally varied hydrological processes using the time-area method. Hydrol. Process. 2016, 30, 751–770. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Tiwari, A.K.; Singh, R. Estimation of temporal variation of sediment yield from small catchments through the kinematic method. J. Hydrol. 1997, 203, 39–57. [Google Scholar] [CrossRef]
- Darvishan, A.V.K.; Sadeghi, S.H.R.; Gholami, L. Efficacy of Time-Area Method in simulating temporal variation of sediment yield in Chehelgazi Watershed, Iran. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2010, 42, 51–60. [Google Scholar] [CrossRef]
- Her, Y.; Heatwole, C. HYSTAR Sediment Model: Distributed Two-Dimensional Simulation of Watershed Erosion and Sediment Transport Using Time-Area Routing. AWRA J. Am. Water Resour. Assoc. 2016, 52, 376–396. [Google Scholar] [CrossRef]
- Melesse, A.M.; Graham, W.D. Storm runoff prediction based on a spatially distributed travel time method utilizing remote sensing and GIS. AWRA J. Am. Water Resour. Assoc. 2004, 40, 863–879. [Google Scholar] [CrossRef]
- Saghafian, B.; Julien, P.Y.; Rajaie, H. Runoff hydrograph simulation based on time variable isochrone technique. J. Hydrol. 2002, 261, 193–203. [Google Scholar] [CrossRef]
- Wang, F.; Mu, X.; Zhang, X.; Li, R. Effect of soil and water conservation on runoff and sediment in Pianguan River. Sci. Soil Water Conserv. 2005, 3, 10–14. (In Chinese) [Google Scholar]
- Liu, C.; Hong, B.; Zeng, M.; Cheng, Y. Experimental study on the relationship between storm and runoff in the Loess Plateau of China. Chin. Sci. Bull. 1965, 10, 158–161. (In Chinese) [Google Scholar]
- Li, J.; Liu, C.M.; Wang, Z.G.; Liang, K. Two universal runoff yield models: SCS vs. LCM. J. Geogr. Sci. 2015, 25, 311–318. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Z.; Zheng, H.; Zhang, L.; Wu, X. Development of Hydro-Informatic Modelling System and its application. Sci. China Ser. E Technol. Sci. 2008, 51, 456–466. [Google Scholar] [CrossRef]
- Liu, C.; Yang, S.; Wen, Z.; Wang, X.; Wang, Y.; Li, Q.; Sheng, H. Development of ecohydrological assessment tool and its application. Sci. China Ser. E Technol. Sci. 2009, 52, 1947–1957. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Yang, S.; Liu, X.; Cai, M.; Dong, G.; Luo, Y. Comparison of LCM hydrological models with lumped, semi-distributed and distributed building structures in typical watershed of Yellow River Basin. Acta Geogr. Sin. 2014, 69, 90–99. (In Chinese) [Google Scholar]
- Williams, J.R. Sediment-yield prediction with Universal Equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; United States Department of Agriculture: Washington, DC, USA, 1975; pp. 244–252. [Google Scholar]
- Ye, A.; Xia, J.; Qiao, Y.; Wang, G. A distributed soil erosion model on the small watershed. J. Basic Sci. Eng. 2008, 16, 328–340. (In Chinese) [Google Scholar]
- Wang, S.P.; Zhang, Z.Q.; Tang, Y.; Guo, J.T. Evaluation of spatial distribution of soil erosion and sediment yield for a small watershed of the Loess Plateau by coupling MIKE-SHE with MUSLE. Trans. Chin. Soc. Agric. Eng. 2010, 26, 92–98. (In Chinese) [Google Scholar]
- Luo, Y.; Yang, S.; Liu, X.; Liu, C.; Zhang, Y.; Zhou, Q.; Zhou, X.; Dong, G. Suitability of revision to MUSLE for estimating sediment yield in the Loess Plateau of China. Stoch. Environ. Res. Risk Assess. 2015, 30, 379–394. [Google Scholar] [CrossRef]
- McCarthy, G.T. The unit hydrograph and flood routing. In Proceedings of the Conference of North Atlantic Division, US Army Corps of Engineers, New London, CT, USA, 24 June 1938; pp. 608–609. [Google Scholar]
- Overton, D.E. Muskingum flood routing of upland streamflow. J. Hydrol. 1966, 4, 185–200. [Google Scholar] [CrossRef]
- Aston, A.R. Rainfall interception by 8 small trees. J. Hydrol. 1979, 42, 383–396. [Google Scholar] [CrossRef]
- Williams, J.R.; Singh, V.P. Chapter 25: The EPIC model. In Computer Models of Watershed Hydrology; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 909–1000. [Google Scholar]
- Liu, B.Y.; Nearing, M.A.; Risse, L.M. Slope Gradient Effects on Soil Loss for Steep Slopes. Trans. ASAE 1994, 37, 1835–1840. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Shi, P.J.; Jia, Z.W. Slope length effects on soil loss for steep slopes. Soil Sci. Soc. Am. J. 2000, 64, 1759–1763. [Google Scholar] [CrossRef]
- Cai, C.F.; Ding, S.W.; Shi, Z.H.; Huang, L.; Zhang, G.Y. Study of Applying USLE and Geographical Information System IDRISI to Predict Soil Erosion in Small Watershed. J. Soil Water Conserv. 2000, 14, 19–24. (In Chinese) [Google Scholar]
- Sabzevari, T. Runoff prediction in ungauged catchments using the gamma dimensionless time-area method. Arab. J. Geosc. 2017, 10. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment routing for agricultural watersheds. AWRA J. Am. Water Resour. Assoc. 1975, 11, 965–974. [Google Scholar] [CrossRef]
- Jenson, S.K. Extracting topographic structure from digital elevation data for geographic information system analysis. Pe Rs 1988, 54, 1593–1600. [Google Scholar]
- Wang, G.Q.; Zhang, C.C.; Liu, J.H.; Wei, J.H.; Xue, H.; Tie-Jian, L.I. Analyses on the variation of vegetation coverage and water/sediment reduction in the rich and coarse sediment area of the Yellow River Basin. J. Sediment Res. 2006, 2, 10–16. (In Chinese) [Google Scholar]
- Cadaret, E.M.; McGwire, K.C.; Nouwakpo, S.K.; Weltz, M.A.; Saito, L. Vegetation canopy cover effects on sediment erosion processes in the Upper Colorado River Basin Mancos Shale formation, Price, Utah, USA. Catena 2016, 147, 334–344. [Google Scholar] [CrossRef]
- Boer, M.; Puigdefabregas, J. Effects of spatially structured vegetation patterns on hillslope erosion in a semiarid Mediterranean environment: A simulation study. Earth Surf. Processes Landf. 2005, 30, 149–167. [Google Scholar] [CrossRef]
- Hua, D.; Wen, Z. Study on Runoff and Sediment Under Simulated Rainstorm Condition of Different Stages of Vegetation Restoration in Loess Hilly Region, China. J. Soil Water Conserv. 2015, 29, 27–31. (In Chinese) [Google Scholar]
- Guo, Y.H.; Zhao, T.N.; Sun, B.P.; Ding, G.D.; Cheng, C.; Hu, F.B. Study on the Dynamic Characteristics of Overland Flow and Resistance to Overland Flow of Grass Slope. Res. Soil Water Conserv. 2006, 13, 264–267. (In Chinese) [Google Scholar]
- Li, M.; Yao, W.; Yang, J.; Chen, J.; Ding, W.; Li, L.; Yang, C. Experimental Study on the Effect of Grass Cover on the Overland Flow Pattern in the Hillslope-gully Side Erosion System. J. Basic Sci. Eng. 2009, 17, 513–523. (In Chinese) [Google Scholar]
- Yu, G.Q.; Li, Z.B.; Pei, L.; Li, P. Difference of Runoff-Erosion-Sediment Yield Under Different Vegetation Type. J. Soil Water Conserv. 2012, 26, 1–5. (In Chinese) [Google Scholar]
- Xiong, Y.; Wang, H.; Bai, Z. Preliminary Study on Benefit Indexes of Runoff and Sediment Reduction by Terraced Field, Forest Land and Grass Land. Soil Water Conserv. China 1996, 8, 10–14. (In Chinese) [Google Scholar]
- Liu, X.Y.; Yang, S.T.; Wang, F.G.; Xing-Zhao, H.E.; Hong-Bin, M.A.; Luo, Y. Analysis on sediment yield reduced by current terrace and shrubs-herbs-arbor vegetation in the Loess Plateau. J. Hydraul. Eng. 2014, 45, 1293–1300. (In Chinese) [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Mao, Y.; Ye, A.; Xu, J.; Ma, F.; Deng, X.; Miao, C.; Gong, W.; Di, Z. An advanced distributed automated extraction of drainage network model on high-resolution DEM. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 7441–7467. [Google Scholar] [CrossRef]
- Liu, X.Y.; Yang, S.T.; Xiaoyu, L.I.; Zhou, X.; Luo, Y.; Dang, S.Z. The current vegetation restoration effect and its influence mechanism on the sediment and runoff yield in severe erosion area of Yellow River Basin. Sci. Sin. 2015, 45, 1052. (In Chinese) [Google Scholar]
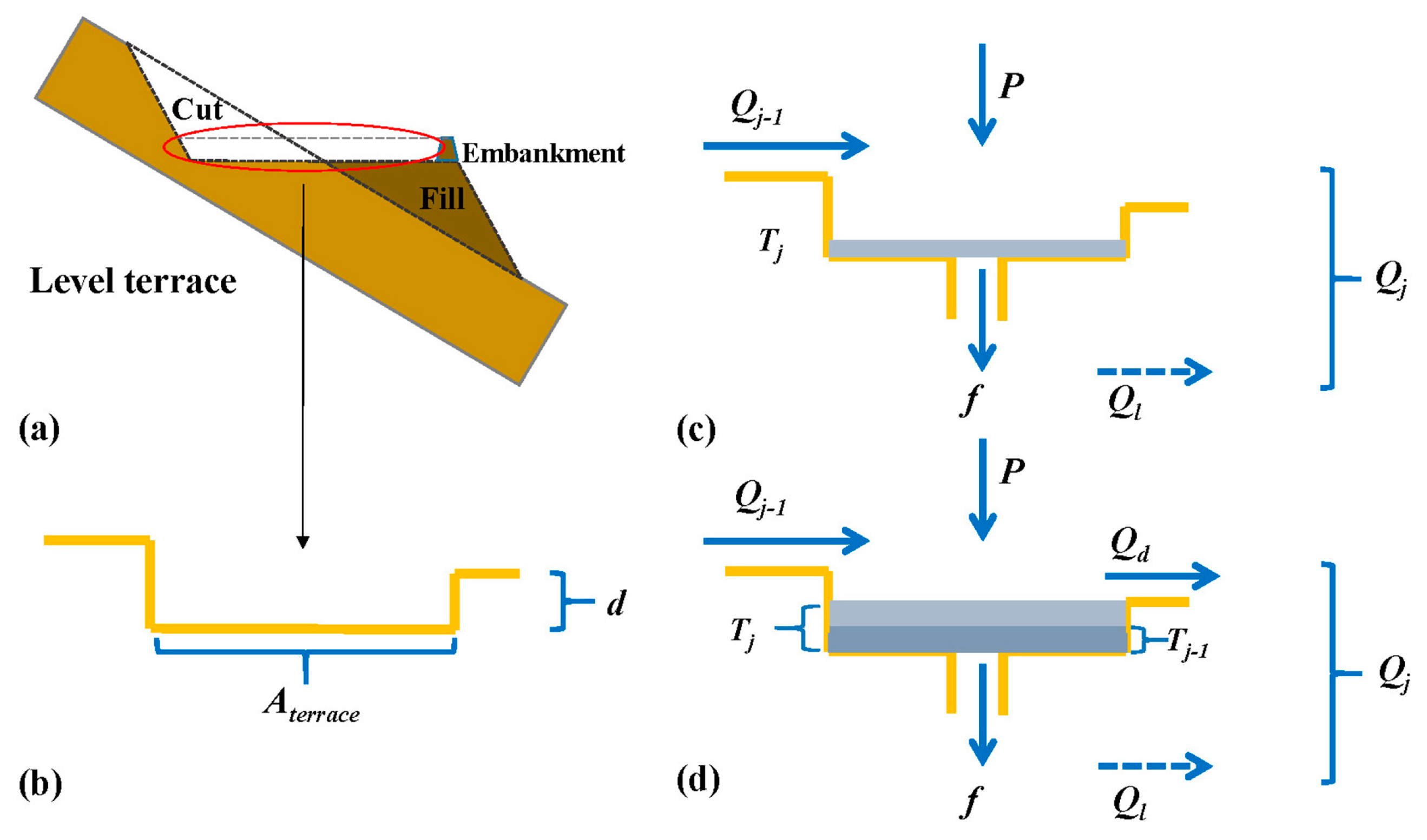

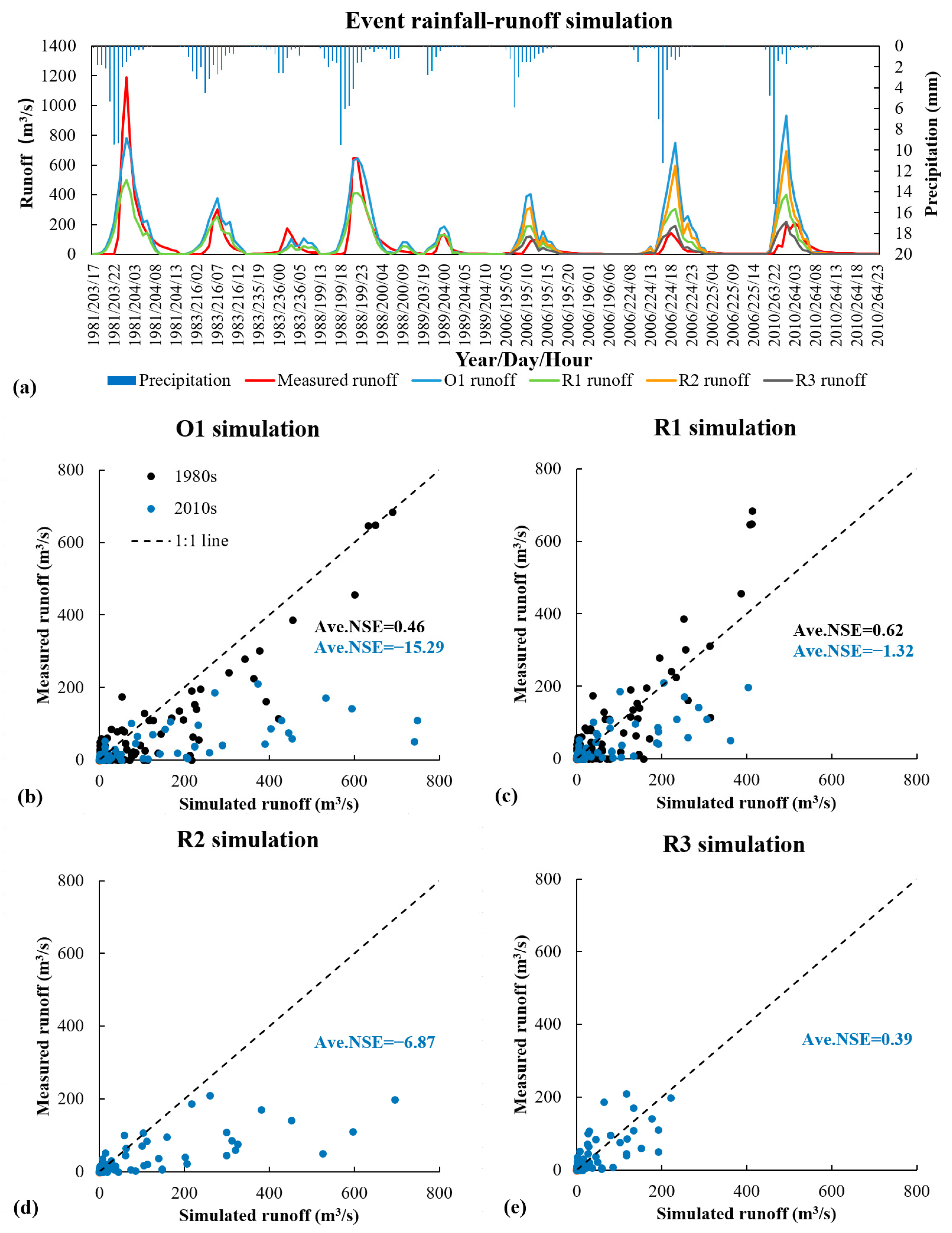

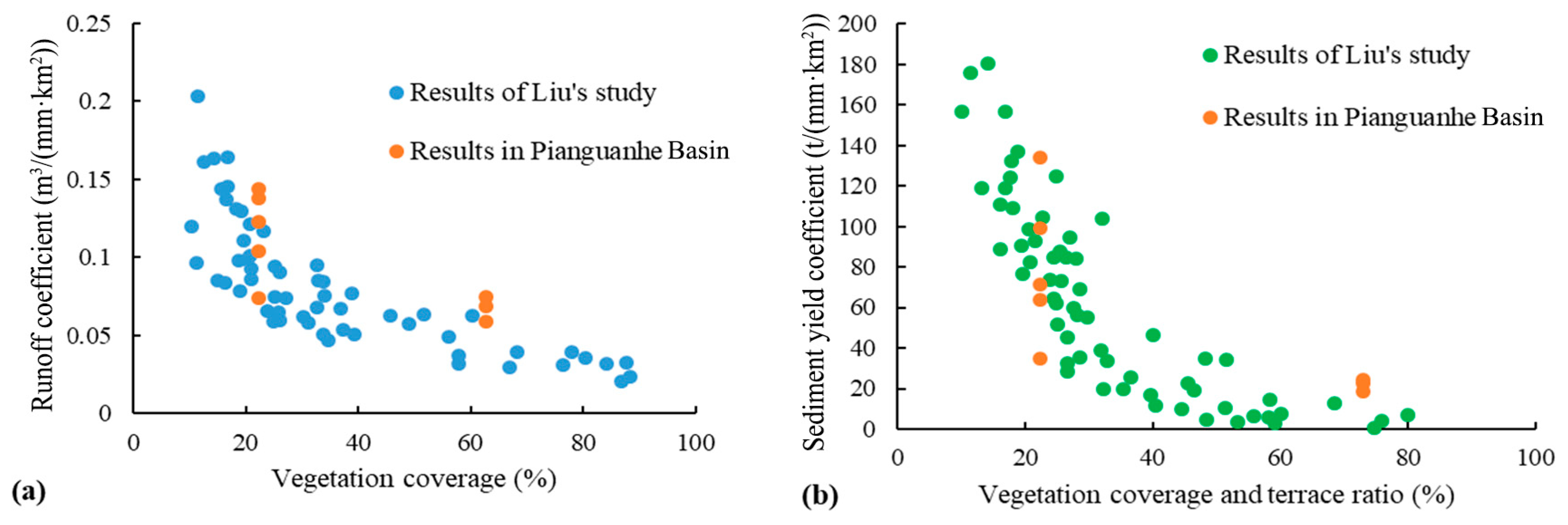
| No. | Module Name | Equations Reference | Equations Reference |
|---|---|---|---|
| 1 | Canopy interception | [62] | |
| 2 | Surface runoff | [51] | |
| 3 | Interflow | [51] | |
| 4 | Base flow | [51] |
| No. | Module Name | Equations Reference | Equations Reference |
|---|---|---|---|
| 1 | Sediment yield | [63] | |
| 2 | Runoff factor | [37] | |
| 3 | Soil erodibility factor | [63] | |
| 4 | Topographic factor | [64,65] | |
| 5 | Cover and management factor | [66] | |
| 6 | Coarse fragment factor | [63] |
| Vegetation Coverage (%) | Dry Year | Normal Year | Wet Year | ||||
|---|---|---|---|---|---|---|---|
| Runoff Reduction (%) | Sediment Reduction (%) | Runoff Reduction (%) | Sediment Reduction (%) | Runoff Reduction (%) | Sediment Reduction (%) | ||
| Forest | 70 | 100 | 100 | 100 | 98 | 76.5 | 57.7 |
| 60 | 100 | 100 | 96.5 | 92.9 | 72.2 | 51 | |
| 50 | 99 | 99 | 90.1 | 86.9 | 64.2 | 46.2 | |
| 40 | 94 | 96 | 73.2 | 69.8 | 48.8 | 33.3 | |
| 30 | 80 | 89 | 52 | 48.2 | 28.4 | 19.2 | |
| 20 | 55 | 73 | 26.7 | 20.2 | 11.1 | 6.4 | |
| Grass | 70 | 100 | 100 | 96.3 | 94.4 | 64.8 | 50 |
| 60 | 100 | 100 | 92.6 | 89.9 | 59.3 | 45.1 | |
| 50 | 98 | 99 | 83.7 | 82.5 | 51.2 | 40 | |
| 40 | 86 | 95 | 67.8 | 66.5 | 37.7 | 30 | |
| 30 | 72 | 85 | 42.7 | 41.8 | 22.1 | 16.9 | |
| 20 | 45 | 69 | 19.5 | 18.6 | 8.2 | 5.9 | |
| Land | Dry Year | Normal Year | Wet Year |
|---|---|---|---|
| Forest | y = 0.3619ln(x) − 0.468 | y = 0.6145ln(x) − 1.557 | y = 0.5551ln(x) − 1.565 |
| Grass | y = 0.4537ln(x) − 0.854 | y = 0.6498ln(x) − 1.748 | y = 0.4733ln(x) − 1.357 |
| Land | Dry Year | Normal Year | Wet Year |
|---|---|---|---|
| Forest | y = 0.2136ln(x) + 0.133 | y = 0.6429ln(x) − 1.701 | y = 0.4239ln(x) − 1.222 |
| Grass | y = 0.2527ln(x) − 0.028 | y = 0.6384ln(x) − 1.721 | y = 0.3669ln(x) − 1.053 |
| No. of Storm (year/day/hour) | Class | Practice | ||||||
|---|---|---|---|---|---|---|---|---|
| Vegetation | Terrace | Vegetation and Terrace | ||||||
| RR1 (%) | AR1 (m3/km2) | RR2 (%) | AR2 (m3/km2) | RR3 (%) | RR1 + RR2 (%) | Difference (%) | ||
| 1981/203/17 | Calibration | 35.95 | 4096.15 | - | - | - | - | - |
| 1983/215/22 | 30.42 | 1642.02 | - | - | - | - | - | |
| 1983/235/16 | 39.60 | 642.21 | - | - | - | - | - | |
| 1988/199/13 | Validation | 35.77 | 3959.85 | - | - | - | - | - |
| 1989/203/19 | 26.18 | 494.47 | - | - | - | - | - | |
| 2006/195/5 | 48.22 | 3318.46 | 26.13 | 9122.72 | 69.02 | 74.35 | −5.33 | |
| 2006/224/8 | 53.17 | 5034.97 | 26.26 | 18,060.69 | 73.26 | 79.43 | −6.17 | |
| 2010/263/20 | 51.66 | 5223.21 | 27.57 | 20,244.11 | 73.30 | 79.23 | −5.93 | |
| No. of Storm (year/day/hour) | Class | Practice | ||||||
|---|---|---|---|---|---|---|---|---|
| Vegetation | Terrace | Vegetation and Terrace | ||||||
| RR1 (%) | AR1 (t/km2) | RR2 (%) | AR2 (t/km2) | RR3 (%) | RR1 + RR2 (%) | Difference (%) | ||
| 1981/203/17 | Calibration | 13.66 | 796.05 | - | - | - | - | - |
| 1983/215/22 | 11.52 | 299.66 | - | - | - | - | - | |
| 1983/235/16 | 17.31 | 96.91 | - | - | - | - | - | |
| 1988/199/13 | 15.37 | 748.46 | - | - | - | - | - | |
| 1989/203/19 | 8.71 | 129.34 | - | - | - | - | - | |
| 2006/224/8 | Validation | 33.22 | 341.94 | 23.62 | 1765.63 | 54.02 | 56.84 | −2.83 |
| 2006/195/5 | 30.36 | 528.25 | 24.08 | 3041.80 | 51.75 | 54.44 | −2.69 | |
| 2010/263/20 | 33.07 | 659.02 | 25.87 | 3743.10 | 55.80 | 58.94 | −3.14 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Yang, S.; Zhang, Y.; Liu, X.; Guan, Y. Assessing the Impact of Terraces and Vegetation on Runoff and Sediment Routing Using the Time-Area Method in the Chinese Loess Plateau. Water 2019, 11, 803. https://doi.org/10.3390/w11040803
Bai J, Yang S, Zhang Y, Liu X, Guan Y. Assessing the Impact of Terraces and Vegetation on Runoff and Sediment Routing Using the Time-Area Method in the Chinese Loess Plateau. Water. 2019; 11(4):803. https://doi.org/10.3390/w11040803
Chicago/Turabian StyleBai, Juan, Shengtian Yang, Yichi Zhang, Xiaoyan Liu, and Yabing Guan. 2019. "Assessing the Impact of Terraces and Vegetation on Runoff and Sediment Routing Using the Time-Area Method in the Chinese Loess Plateau" Water 11, no. 4: 803. https://doi.org/10.3390/w11040803
APA StyleBai, J., Yang, S., Zhang, Y., Liu, X., & Guan, Y. (2019). Assessing the Impact of Terraces and Vegetation on Runoff and Sediment Routing Using the Time-Area Method in the Chinese Loess Plateau. Water, 11(4), 803. https://doi.org/10.3390/w11040803




