Methods of In Situ Assessment of Infiltration Rate Reduction in Groundwater Recharge Basins
Abstract
1. Introduction
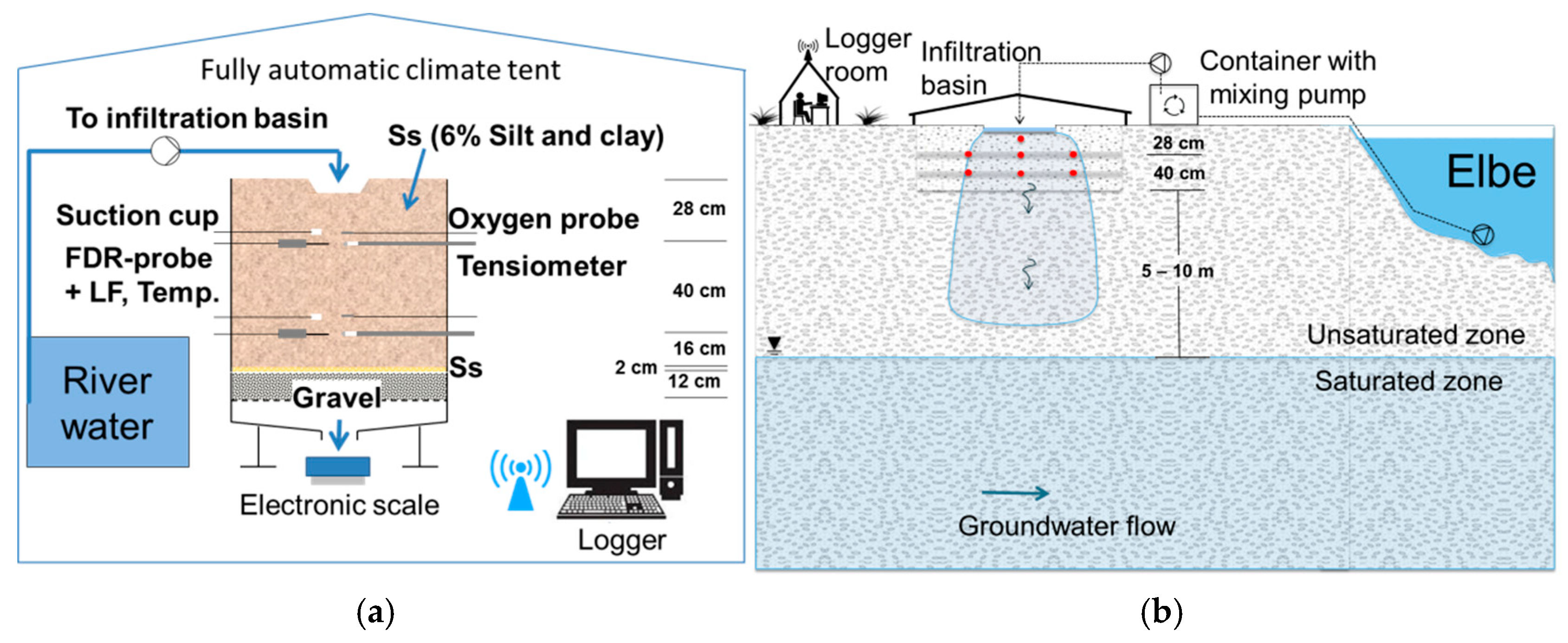
2. Materials and Methods
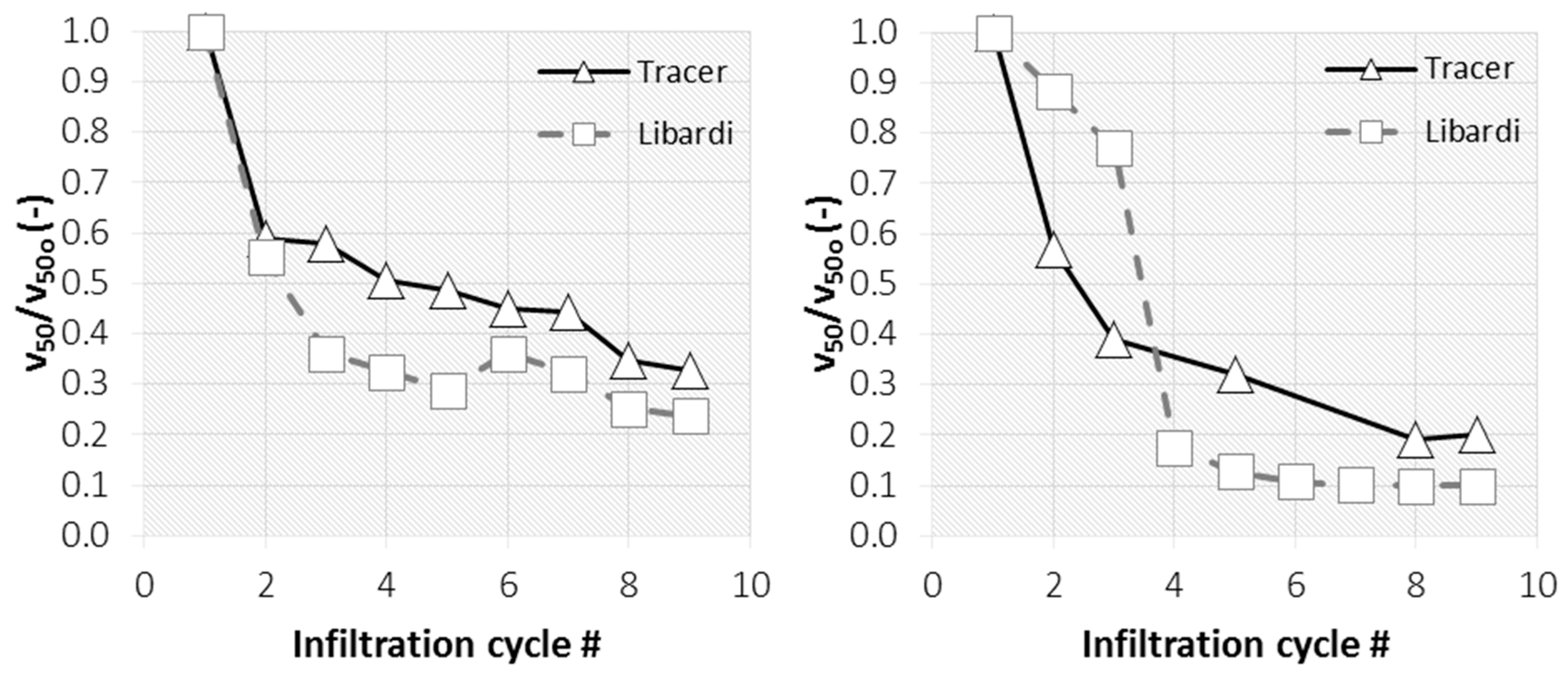
2.1. Tracer Method
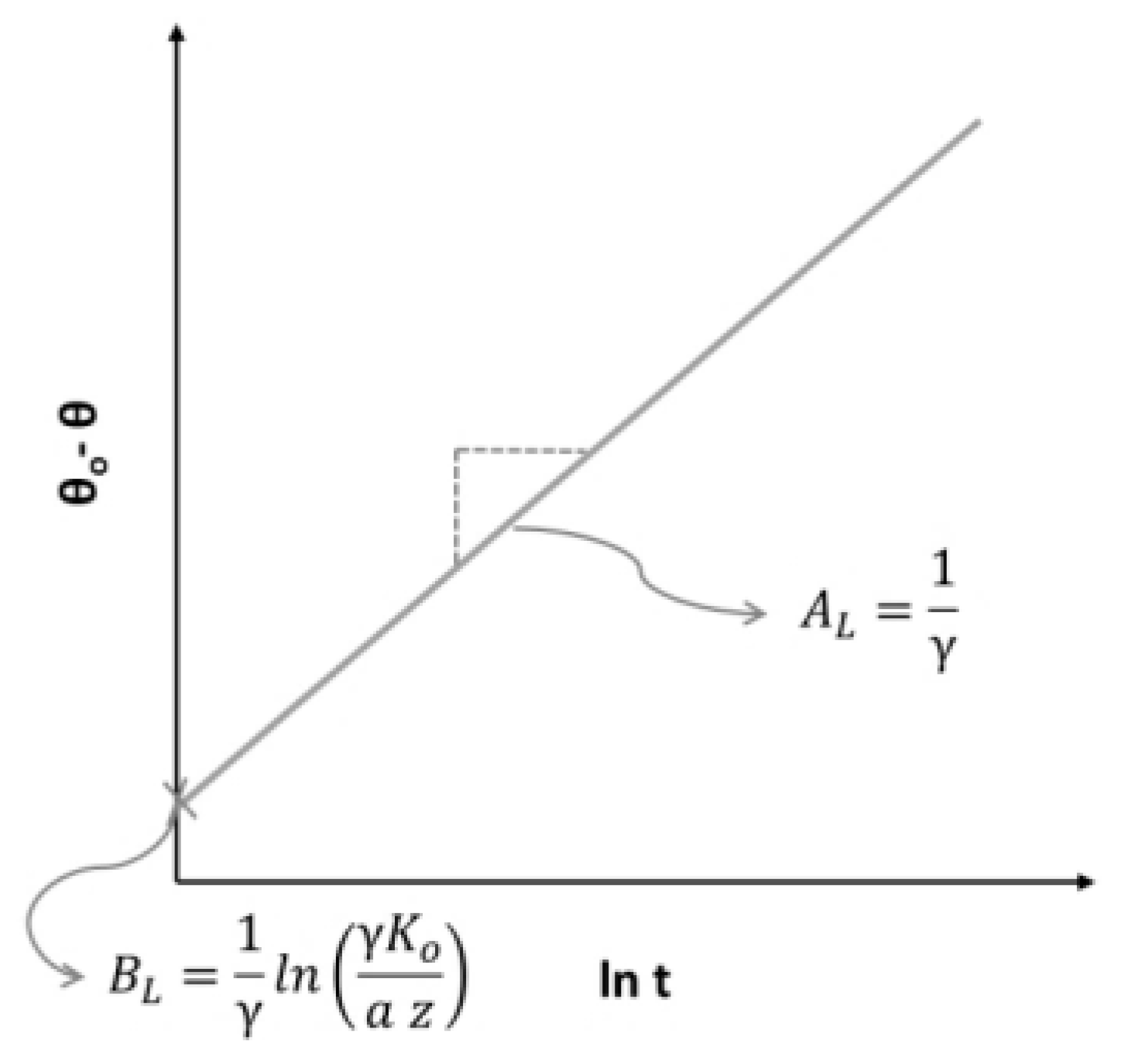
2.2. Libardi Method
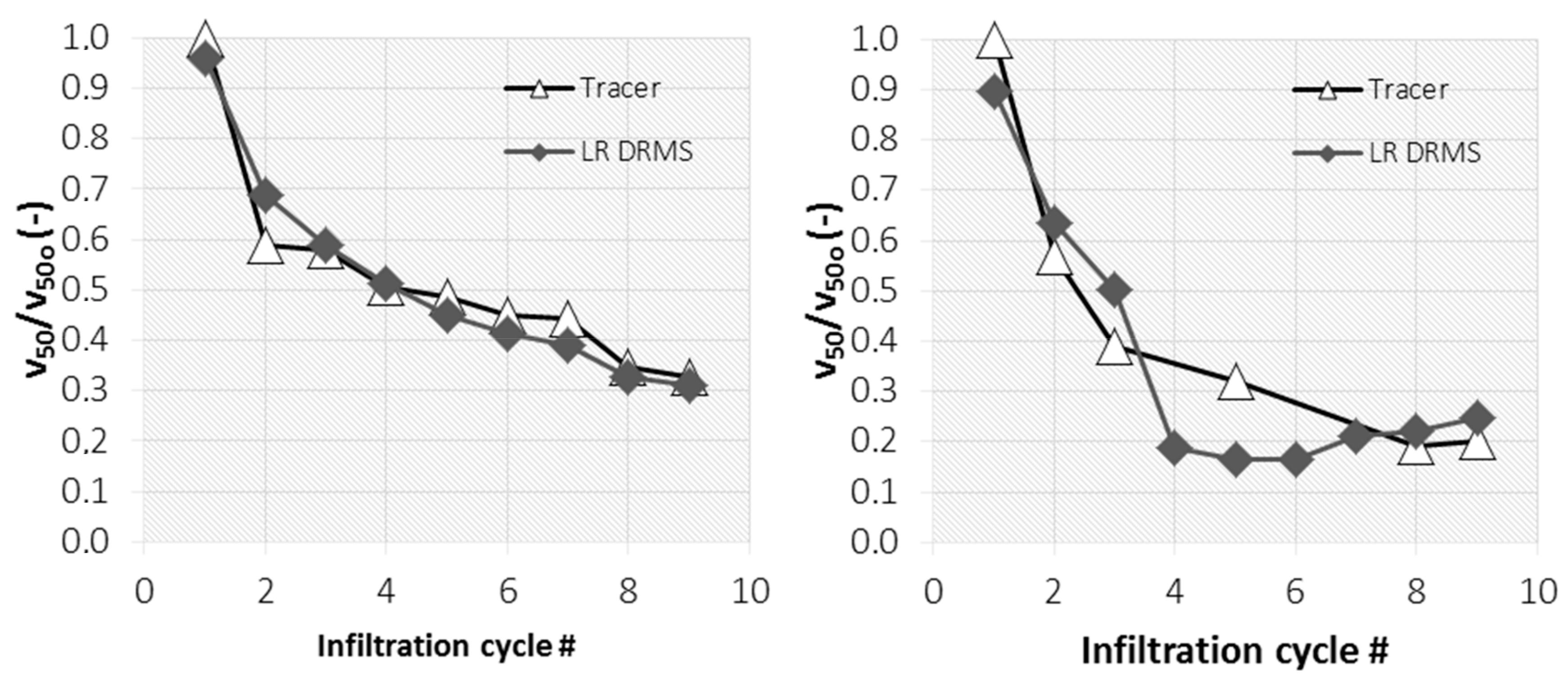
2.3. Root Mean Square Method
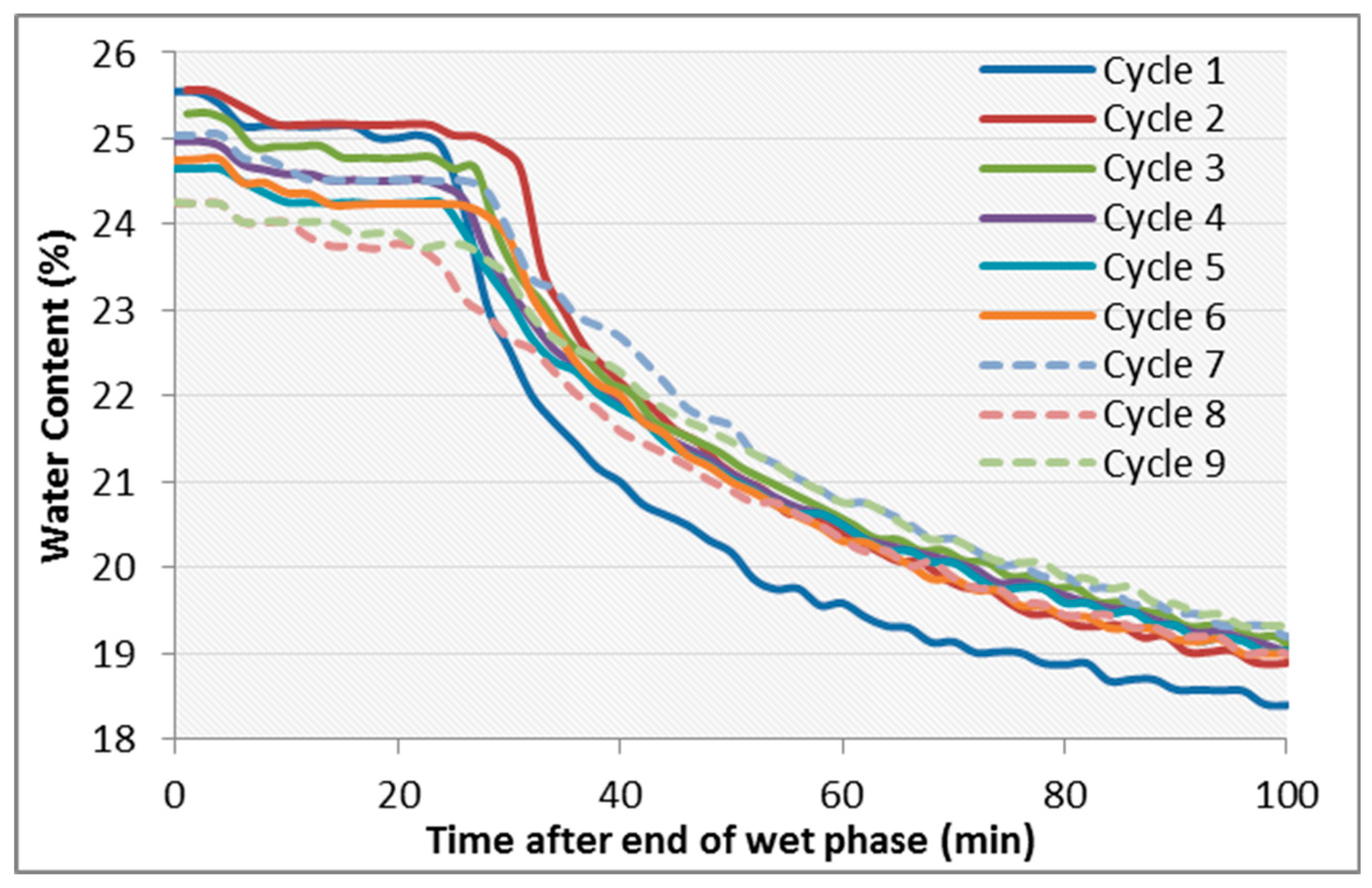
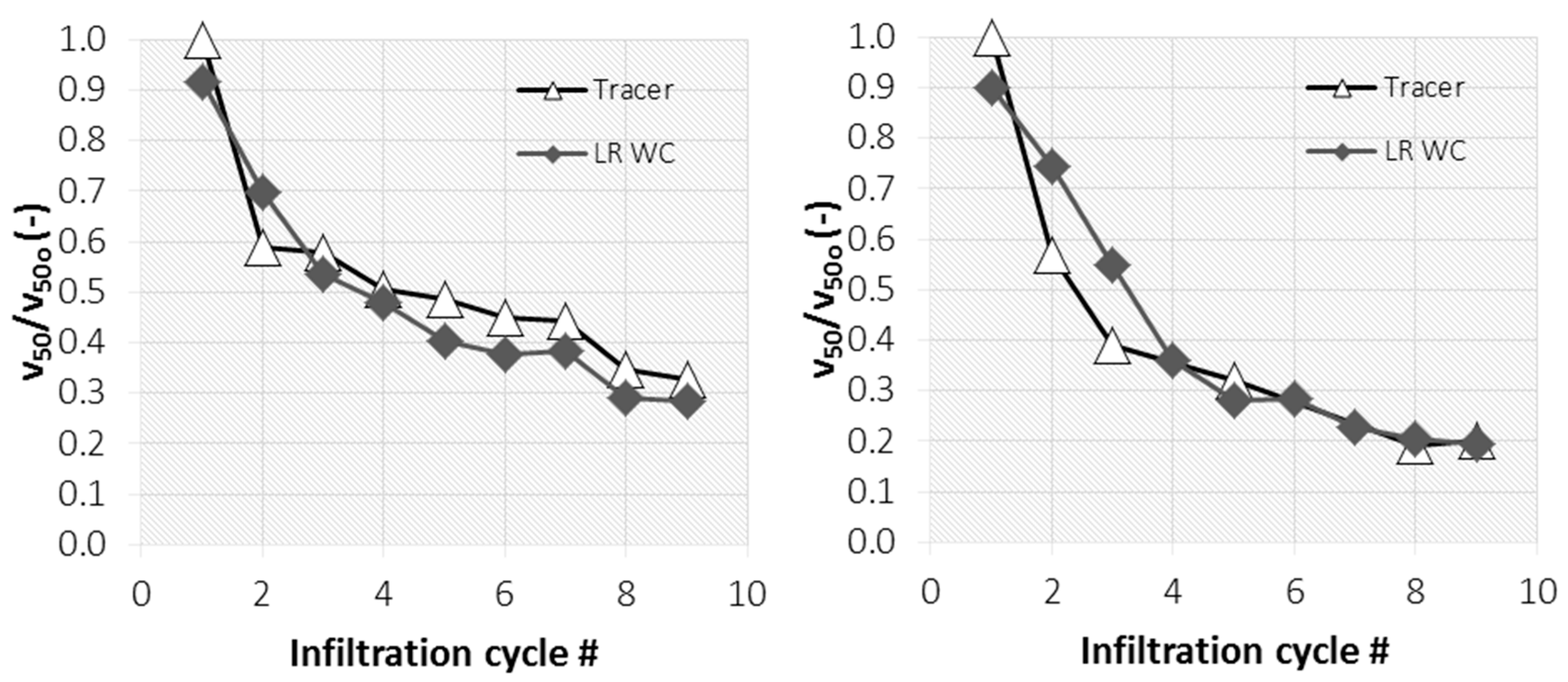
2.4. Water Content Method
2.5. Sensor Trigger Time Method
3. Results and Discussion
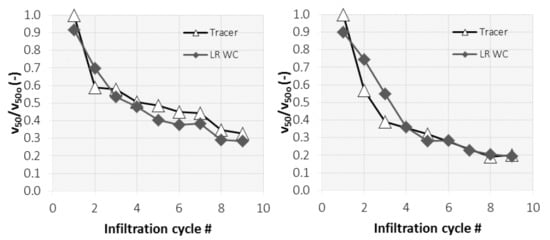
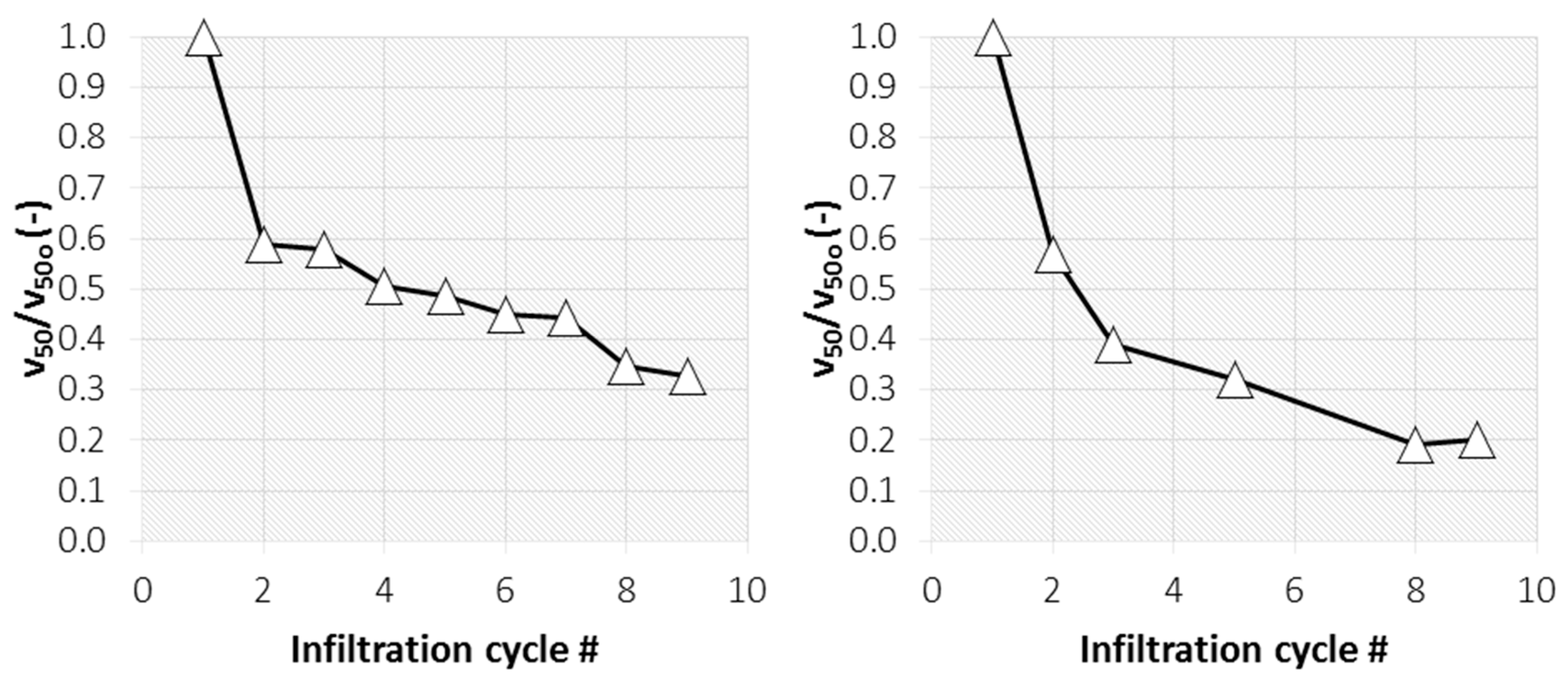
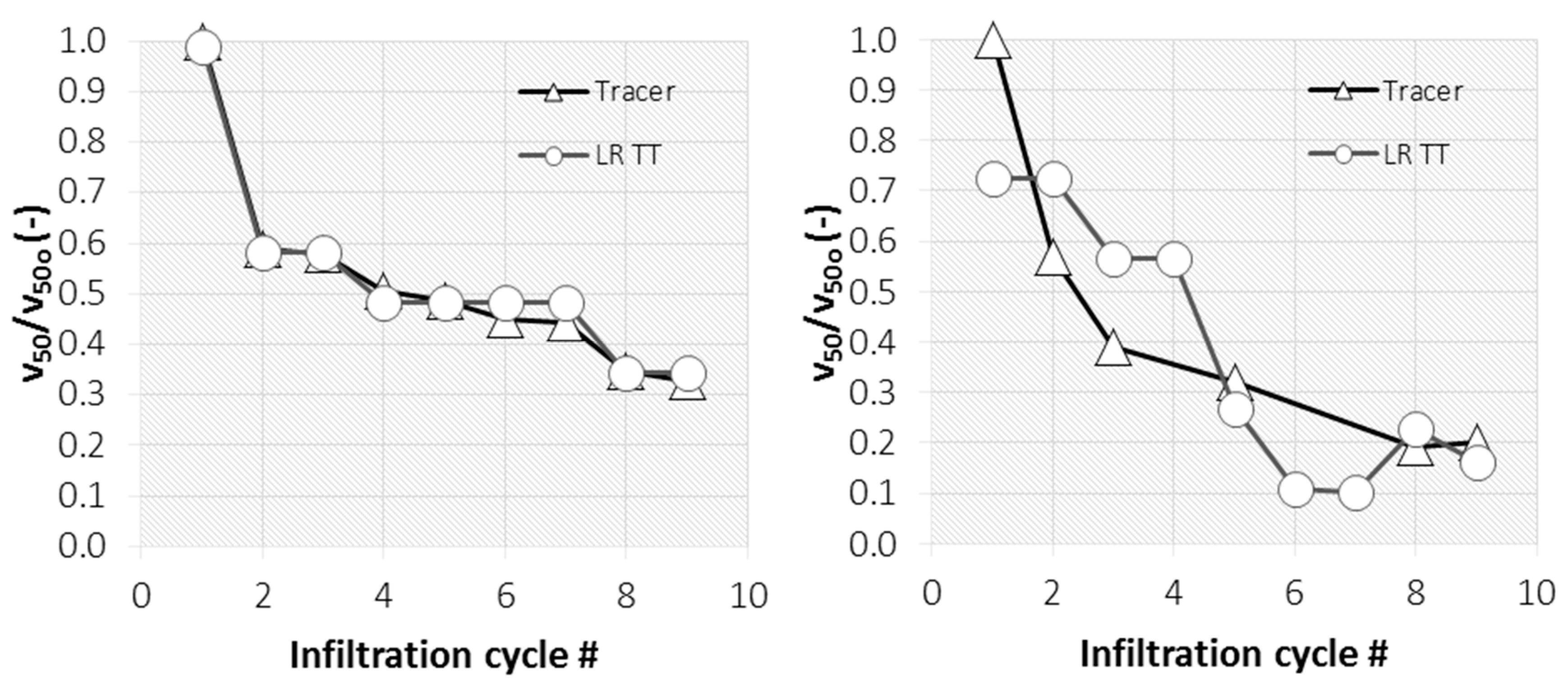
3.1. Tracer Method
3.2. Libardi Method
3.3. Root Mean Square Method
3.4. Water Content Method
3.5. Sensor Trigger Time Method
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bekele, E.B.; Donn, M.J.; Barry, K.E.; Vanderzalm, J.L.; Kaksonen, A.H.; Puzon, G.J.; Wylie, J.; Miotlinski, K.; Cahill, K.; Walsh, T.; et al. Managed Aquifer Recharge and Recycling Options: Understanding Clogging Processes and Water Quality Impacts; Australian Water Recycling Center of Excellence: Brisbane, Australia, 2015. [Google Scholar]
- Laws, B.V.; Dickenson, E.R.V.; Johnson, T.A.; Snyder, S.A.; Drewes, J.E. Attenuation of contaminants of emerging concern during surface-spreading aquifer recharge. Sci. Total Environ. 2011, 409, 1087–1094. [Google Scholar] [CrossRef]
- Arshad, M.; Guillaume, J.; Ross, A. Assessing the Feasibility of Managed Aquifer Recharge for Irrigation under Uncertainty. Water 2014, 6, 2748–2769. [Google Scholar] [CrossRef]
- Rupérez-Moreno, C.; Pérez-Sánchez, J.; Senent-Aparicio, J.; Flores-Asenjo, P.; Paz-Aparicio, C. Cost-Benefit Analysis of the Managed Aquifer Recharge System for Irrigation under Climate Change Conditions in Southern Spain. Water 2017, 9, 343. [Google Scholar] [CrossRef]
- Dillon, P. Future management of aquifer recharge. Hydrogeol. J. 2005, 13, 313–316. [Google Scholar] [CrossRef]
- Bouwer, H. Issues in artificial recharge. Water Sci. Technol. 1996, 33, 381–390. [Google Scholar] [CrossRef]
- Dutta, T.; Carles-Brangarí, A.; Fernàndez-Garcia, D.; Rubol, S.; Tirado-Conde, J.; Sanchez-Vila, X. Vadose zone oxygen (O2) dynamics during drying and wetting cycles: An artificial recharge laboratory experiment. J. Hydrol. 2015, 527, 151–159. [Google Scholar] [CrossRef]
- Sprenger, C.; Hartog, N.; Hernández, M.; Vilanova, E.; Grützmacher, G.; Scheibler, F.; Hannappel, S. Inventory of Managed Aquifer Recharge sites in Europe—Historical development, current situation and perspectives. Hydrogeol. J. 2017, 25, 1909–1922. [Google Scholar] [CrossRef]
- Haaken, K. Applied Hydrogeophysics for Managed Aquifer Recharge; Rheinische Friedrich-Wilhelms-Universität: Bonn, Germany, 2018. [Google Scholar]
- Council, N.R. Ground Water Recharge Using Waters of Impaired Quality; National Academy Press: Washington, DC, USA, 1969; ISBN 978-0-309-05142-2. [Google Scholar]
- Stibinger, J.; Univerzita, J.E. Purkyně v Ústí nad Labem; Fakulta životního prostředí Examples of Determining the Hydraulic Conductivity of Soils: Theory and Applications of Selected Basic Methods: University Handbook on Soil Hydraulics; Jan Evangelista Purkyně University, Faculty of the Environment: Ústí nad Labem, Czech Republic, 2014; ISBN 978-80-7414-837-8. [Google Scholar]
- Wagner, B.; Tarnawski, V.R.; Hennings, V.; Müller, U.; Wessolek, G.; Plagge, R. Evaluation of pedo-transfer functions for unsaturated soil hydraulic conductivity using an independent data set. Geoderma 2001, 102, 275–297. [Google Scholar] [CrossRef]
- Bagarello, V.; Iovino, M.; Elrick, D. A simplified falling-head tecnique for rapid determination of field-saturated hydraulic conductivity. Soil Sci. Soc. Am. J. 2004, 68, 66–73. [Google Scholar]
- Fodor, N.; Sándor, R.; Orfanus, T.; Lichner, L.; Rajkai, K. Evaluation method dependency of measured saturated hydraulic conductivity. Geoderma 2011, 165, 60–68. [Google Scholar] [CrossRef]
- Vienken, T.; Dietrich, P. Field evaluation of methods for determining hydraulic conductivity from grain size data. J. Hydrol. 2011, 400, 58–71. [Google Scholar] [CrossRef]
- Rosas, J.; Lopez, O.; Missimer, T.M.; Coulibaly, K.M.; Dehwah, A.H.A.; Sesler, K.; Lujan, L.R.; Mantilla, D. Determination of hydraulic conductivity from grain-size distribution for different depositional environments. Ground Water 2014, 52, 399–413. [Google Scholar] [CrossRef]
- Askarinejad, A.; Beck, A.; Casini, F.; Springman, S.M. Unsaturated Hydraulic Conductivity of a Silty Sand with the Instantaneous Profile Method. In Proceedings of the Unsaturated Soils: Research and Applications; Mancuso, C., Jommi, C., D’Onza, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 215–220. [Google Scholar]
- Reichardt, K.; Portezan, O.; Libardi, P.L.; Bacchi, O.O.S.; Moraes, S.O.; Oliveira, J.C.M.; Falleiros, M.C. Critical analysis of the field determination of soil hydraulic conductivity functions using the flux-gradient approach. Soil Tillage Res. 1998, 48, 81–89. [Google Scholar] [CrossRef]
- Fichtner, T.; Barquero, F.; Sallwey, J.; Stefan, C. Assessing Managed Aquifer Recharge Processes under Three Physical Model Concepts. Water 2019, 11, 107. [Google Scholar] [CrossRef]
- Irving, J.; Singha, K. Stochastic inversion of tracer test and electrical geophysical data to estimate hydraulic conductivities. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Pollock, D.; Cirpka, O.A. Fully coupled hydrogeophysical inversion of synthetic salt tracer experiments. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- U.S. EPA. The QTRACER2 Program for Tracer-Breakthrough Curve Analysis for Tracer Tests in Karstic Aquifers and Other Hydrologic Systems; National Center for Environmental Assessment—Washington Office, Office of Research and Development, U.S. Environmental Protection Agency: Washington, DC, USA, 2002.
- Armbruster, H.; Mors, K.; Eiswirth, M.; Hoetzl, H.; Merkler, G.-P.; Naegelsbach, E. Leakage detection of sewing pipes by combined geophysical and tracer techniques. In Tracer Hydrol, Proceedings of the 6th International Syposium on Water Tracing, Karlsruhe, Germany, 21–26 September 1992; HötzL, H., Werner, A., Eds.; Balkema: Rotterdam, The Netherlands, 1992; pp. 97–99. [Google Scholar]
- Kollmann, W.; Meyer, J.W.; Supper, R. Geoelectric surveys in determining the direction and velocity of groundwater flow using introduced salt tracer. In Tracer Hydrol, Proceedings of the 6th International Syposium on Water Tracing, Karlsruhe, Germany, 21–26 September 1992; HötzL, H., Werner, A., Eds.; Balkema: Rotterdam, The Netherlands, 1992; pp. 109–113. [Google Scholar]
- Zellweger, G.W. Testing and comparison of four ionic tracers to measure stream flow loss by multiple tracer injection. Hydrol. Process. 1994, 8, 155–165. [Google Scholar] [CrossRef]
- Hoffmann, R.; Dietrich, P. Geoelektrische Messungen zur Bestimmung von Grundwasserfließrichtungen und -geschwindigkeiten. Grundwasser 2004, 9, 194–200. [Google Scholar] [CrossRef]
- Einsiedl, F. Flow system dynamics and water storage of a fissured-porous karst aquifer characterized by artificial and environmental tracers. J. Hydrol. 2005, 312, 312–321. [Google Scholar] [CrossRef]
- Singha, K.; Gorelick, S.M. Saline tracer visualized with three-dimensional electrical resistivity tomography: Field-scale spatial moment analysis. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Abrantes, J.R.C.B.; Moruzzi, R.B.; Silveira, A.; de Lima, J.L.M.P. Comparison of thermal, salt and dye tracing to estimate shallow flow velocities: Novel triple-tracer approach. J. Hydrol. 2018, 557, 362–377. [Google Scholar] [CrossRef]
- Leibundgut, C.; Maloszewski, P.; Külls, C. Tracers in Hydrology; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-119-96501-5. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318. [Google Scholar] [CrossRef]
- Darcy, H. Les fontaines publiques de la ville de Dijon: Exposition et application des principes à suivre et des formules à employer dans les questions de distribution d’eau: ouvrage terminé par un appendice relatif aux fournitures d’eau de plusieurs villes au filtrage des eaux et à la fabrication des tuyaux de fonte, de plomb, de tole et de bitume; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Buckingham, E. Studies on the Movement of Soil Moisture; US Department of Agriculture, Bureau of Soils: Washington, DC, USA, 1907; p. 38.
- Hillel, D.; Krentos, V.D.; Stylianou, Y. Procedure and test of an internal drainage method for measuring soil hydraulic characteristics in situ. Soil Sci. 1972, 114, 395–400. [Google Scholar] [CrossRef]
- Libardi, P.L.; Reichardt, K.; Nielsen, D.R.; Biggar, J.W. Simple field methods for estimating soil hydraulic conductivity. Soil Sci. Soc. Am. J. 1980, 44, 3–7. [Google Scholar] [CrossRef]
- Sisson, J.B.; Ferguson, A.H.; van Genuchten, M.T. Simple Method for Predicting Drainage from Field Plots 1. Soil Sci. Soc. Am. J. 1980, 44, 1147–1152. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geoscientific Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Gibert, O.; Hernandez, M.; Vilanova, E.; Cornella, O. Guidelining Protocol for Soil Column Experiments Assessing Fate and Transport of Trace Organics. Available online: https://demeau-fp7.eu/sites/files/D123a%20Guidelines%20Column%20experiments.pdf (accessed on 14 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barquero, F.; Fichtner, T.; Stefan, C. Methods of In Situ Assessment of Infiltration Rate Reduction in Groundwater Recharge Basins. Water 2019, 11, 784. https://doi.org/10.3390/w11040784
Barquero F, Fichtner T, Stefan C. Methods of In Situ Assessment of Infiltration Rate Reduction in Groundwater Recharge Basins. Water. 2019; 11(4):784. https://doi.org/10.3390/w11040784
Chicago/Turabian StyleBarquero, Felix, Thomas Fichtner, and Catalin Stefan. 2019. "Methods of In Situ Assessment of Infiltration Rate Reduction in Groundwater Recharge Basins" Water 11, no. 4: 784. https://doi.org/10.3390/w11040784
APA StyleBarquero, F., Fichtner, T., & Stefan, C. (2019). Methods of In Situ Assessment of Infiltration Rate Reduction in Groundwater Recharge Basins. Water, 11(4), 784. https://doi.org/10.3390/w11040784