Abstract
Nonstationarity of univariate flood series has been widely studied, while nonstationarity of some multivariate flood series, such as discharge, water stage, and suspended sediment concentrations, has been studied rarely. This paper presents a procedure for using the time-varying copula model to describe the nonstationary dependence structures of two correlated flood variables from the same flood event. In this study, we focus on multivariate flood event consisting of peak discharge (Q), peak water stage (Z) and suspended sediment load (S) during the period of 1964–2013 observed at the Waizhou station in the Ganjiang River, China. The time-varying copula model is employed to analyze bivariate distributions of two flood pairs of (Z-Q) and (Z-S). The main channel elevation (MCE) and the forest coverage rate (FCR) of the basin are introduced as the candidate explanatory variables for modelling the nonstationarities of both marginal distributions and dependence structure of copula. It is found that the marginal distributions for both Z and S are nonstationary, whereas the marginal distribution for Q is stationary. In particular, the mean of Z is related to MCE, and the mean and variance of S are related to FCR. Then, time-varying Frank copula with MCE as the covariate has the best performance in fitting the dependence structures of both Z-Q and Z-S. It is indicated that the dependence relationships are strengthen over time associated with the riverbed down-cutting. Finally, the joint and conditional probabilities of both Z-Q and Z-S obtained from the best fitted bivariate copula indicate that there are obvious nonstationarity of their bivariate distributions. This work is helpful to understand how human activities affect the bivariate flood distribution, and therefore provides supporting information for hydraulic structure designs under the changing environments.
1. Introduction
Flood has been one of most common natural hazards, increasingly posing a significant risk to human life and environment [1]. Flood events can be described in terms of the multivariate characteristic variables of peak discharge, water stage and suspended sediment load, which are all relevant to risk analyses. Univariate frequency analysis for these hydrological variables mentioned above can be found in many literatures [2,3,4,5]. Unlike the common frequency distribution, theoretically derived distributions of flood peak are constructed based on dominant runoff generation mechanisms [6]. Flood frequency curves can also be established by use of a continuous simulation model [7,8]. Yet, the designs of hydraulic structures (e.g., dam spillways, dikes, and river channels), cross drainage structures (e.g., culverts and bridges) and urban drainage systems require not only peak discharge (Q) value but also peak water stage (Z) and suspended sediment load (S). In fact, the multivariate frequency analysis can provide more comprehensive understanding of the flood event than simple univariate analysis [9,10,11,12,13].
Human intervention in river basins (e.g., urbanization), the effect of climatic variability (e.g., Pacific Decadal Oscillation), and increased greenhouse gasses have been suggested to cause the changes in the magnitude and frequency of extreme floods [14]. Therefore, statistical characteristics (e.g., mean and variance) of univariate flood variables as well as their dependence structure could be time-varying under changing environments (climate change and/or human activities) [15]. To better adapt such background, it is essential to identify a reasonable distribution framework to dynamically capture the evolution of statistical characteristics [16]. Under the time-varying moments model, distribution parameters can be expressed as functions of some physical variables including atmospheric and land cover indices [17,18,19]. Thus, it is a feasible way to describe the external effects in the construction of dependence structures. Copulas [20] allow researchers to easily construct the distribution by estimating marginal distributions and their dependence separately [21]. The method could provide a more convenient statistical tool for more flexibility in modeling the marginal distributions and their dependence [22]. In recent years, copula function has become a popular tool for multivariate flood frequency analysis [23,24,25,26,27,28,29].
In this study, we focus on Q, Z and S observed at Waizhou station in the Ganjiang River basin, which has undergone extensive urban and suburban development over the past 50 years. The mean elevation of the main channel dominated by sediment supply deficit or surplus at the bed can exert a direct influence on water stage [30]. The section-cross elevation in the downstream of Ganjiang River displays a change process over the past decades [31]. Forest cover rate is a valuable indicator of forests in a country or region, controlling runoff processes and sediment generation [32]. Forest coverage rate of the Ganjiang River basin has increased from 41% to 69% due to large-scale forest planting of the basin. Given the aforementioned physical correlations, the main channel elevation (MCE) and forest cover rate (FCR) are chosen as explanatory variables for modeling the time variations of Q, Z, and S of the Ganjiang River. Using time-varying copula model with the covariates MCE and FCR, the nonstationary bivariate joint distributions of different flood variables (i.e., Z-Q and Z-S) are constructed to analyze the evolution of the bivariate relationships of both Z-Q and Z-S, including their joint probabilities and conditional probabilities of Q and S given water stage.
This paper is organized as follows. The study region and the available data used in this study are described in the next section. Then, the methodologies including marginal distribution and copula model with time-varying parameters are presented. Based on deriving the best fitted marginal distributions and copulas, the results about the time-variation of joint and conditional probability for both Z-Q and Z-S are calculated. Finally, the main conclusions of the case study are summarized.
2. Study Region and Data
The Ganjiang River, which is the largest tributary of the Poyang Lake basin, is situated in Jiangxi Province (in Southeastern China) with a drainage area of 83,500 km2 (Figure 1). This study area belongs to hilly region with the main land use type of woodland [33]. The Ganjiang River basin is located in the subtropical humid monsoon climate zone with distinct seasonal variations, where the annual mean precipitation is about 1680 mm. The heaviest rainfall occurs in the main flood season from April and June, and often lasts 15 to 20 days due to monsoon and typhoon rainstorms [34].
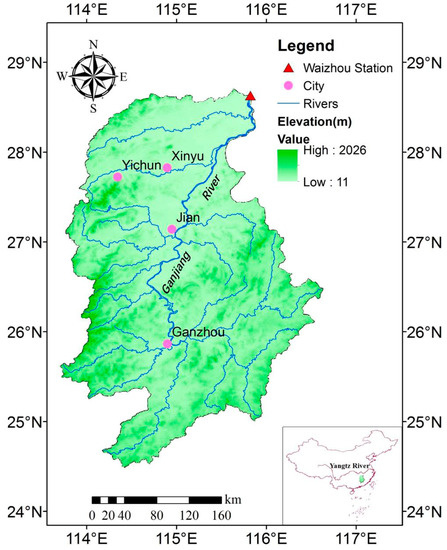
Figure 1.
Topography and river channel of the Ganjiang River basin (GRB) above Waizhou station.
The catchment area upstream of the Waizhou station (115°50′ E, 28°38′ N) accounts for about 97% of the total basin area of the Ganjiang River, and covers an area of 80,948 km2 (Figure 1). The hydrological data used in this study include daily river discharge, daily water stage, daily suspended sediment rate and yearly section-cross elevation at the hydrological station from 1964 to 2013. These data are provided by the Hydrological Bureau of Jiangxi province (http://www.jxsw.cn/). To reflect the capacity of suspended sediment transport in a flood event, suspended sediment load that measures the absolution amount of sediment appears to be more reasonable than suspended sediment rate, since the latter is a relative value for sediment. The daily suspended sediment load (S) is calculated by multiplication between the daily discharge and the corresponding suspended sediment rate. Then, the hydrological series of Q, Z and S are extracted from the same flood event in each year with the maximum discharge value criterion. Besides, the annual forest cover rates of the region are obtained from the book of China Compendium of Statistics 1949–2008 [35] and Jiangxi provincial statistical yearbook from 1983 to 2014 (http://www.jxstj.gov.cn/).
3. Methodology
The time-varying copula model, in which both marginal distributions parameters and copula parameter are expressed as functions of explanatory variables, is constructed to describe the time variations of both marginal distribution and dependence structure of bivariate flood variables. Then, joint probability and conditional probability that are derived from time-varying bivariate copula are illustrated to present nonstationarity of bivariate flood variables over time.
3.1. Calculation of Explanatory Variables
Change in the main channel elevation of alluvial rivers is a normal result about the hydraulic adjustments to adapt the variations of discharge and sediment load. In this study, the observed cross-section elevation data for each year are tabulated and graphed as the profiles of the river cross-section. Then, the main channel elevations of 20 points are extracted from the cross-section digitized graph from left to right bank [36]. To weaken the influence of some distortion/variability points, the point elevations are divided into four quartiles and the 2nd quartile value is considered as the main channel mean elevation (MCE) as follow:
where refers to the median of vector value , which represents the bed elevation value of the selected point.
The forest landscape structure usually contains of the six forest cover classes (i.e., coniferous forest, broadleaf forest, bamboo forest, mixed forest, economic forest, and shrubbery land). Each forest cover with crown cover percent (cp) bigger than 20% has good effects on soil and water conservation [37]. Here, the criterion with this threshold value used in national forest definition is employed to calculate forest area. Thus, the forest cover rate (FCR) is the percentage of six forest cover area to total land area in a region and can be expressed as follow:
where (i = 1,2, …, 6) is the six forest cover classes area with crown cover percent bigger than 20%. AL stands for the total land area of the study region.
3.2. Marginal Distribution with Time-Varying Parameters
To construct the dependence structure of bivariate hydrological variables by copulas, marginal distribution of each variable should be determined firstly. In this study, five probability distributions, including four two-parameter distributions (i.e., Lognormal, Weibull, Logistic, and Gamma) and one three-parameter distributions (Pearson type III distribution) are selected as candidate marginal distributions for Q, Z and S. These distributions have been widely applied in flood frequency analysis [38,39]. The marginal distribution of a flood variable denoted by can be specified through a parametric cumulative distribution function (CDF) , where , and represent location, scale and shape parameters, respectively, and are denoted by the vector [40].
The Generalized Additive Models for Location Scale and Shape (GAMLSS) introduced by Rigby and Stasinopoulos [40] has been widely employed in nonstationary hydrological frequency analysis for its flexibility [15,18,19,41]. If candidate marginal distribution function is chosen to fit the distribution of the variable at any time , parameters of marginal distribution can be expressed as a function of explanatory variables as follow:
where represents the monotonic link function, which depends on the domain of statistical parameter, i.e., if the domain of the distribution parameter is , the link function is , or if , . represents one of marginal distribution parameters (). , , and are the GAMLSS parameters. and represent two candidate explanatory variables. In practice, the shape parameter (if it exists) is often treated as constant since it is quite unstable and difficult to estimate [42], whereas time variations are considered only in location parameter and scale parameter . What’s more, if the parameters are independent from the explanatory variables, it would be a stationary distribution with constant parameters.
The best fitted marginal distribution is determined by the Corrected Akaike Information Criterion (AICc) [43], which is derived from the likelihood function with a penalty determined by the number of model parameters. In addition, because of the potential drawbacks in the quality of the fitting of AICc [44], the goodness-of-fit (GOF), which describes how well the selected distribution fits a set of observations, for candidate distributions is assessed by the Kolmogorov–Smirnov (KS) test and Root Mean Square Error (RMSE). Besides, visual assessment of the residual plot (QQ-plot) [45] is used to examine the best fitted marginal distribution.
3.3. Time-Varying Bivariate Copula Model
In practice, the implementation of the time-varying copula model could be divided into two steps: fitting the time-varying marginal distribution of each variable firstly, and then estimating the time-varying dependence structure of the copula. In other words, both the parameters of marginal distribution and copula dependence parameter could be treated as time variation in building the time-varying copula function. According to the definition of the copula [20], time-varying bivariate copula function for the hydrological variable pairs of and at any time can be expressed as follows:
where represents bivariate copula function with time-varying dependence parameter or . , and represent marginal cumulative distribution functions with corresponding time-varying parameter vectors , , and , respectively. The joint distribution can be constructed by three Archimedean copula functions (i.e., Clayton, Gumbel–Hougaard, and Frank, as shown in Table 1).

Table 1.
The applied time-varying bivariate copulas in this study.
Because of the impacts of external forces on the Ganjiang River basin, the dependence structure of both Z-Q and Z-S could be nonstationary. Similar to the formula expression in Equation (3), the copula dependence parameter could be expressed as a function of the two explanatory variables (FCR and MCE) to reflect the nonstationarity of dependence structure. The totally four scenarios for copula dependence parameter in this paper are listed as follows:
where depends on the domain of copula dependence parameter , i.e., if , the link function is or if , . , and are the model parameters.
The dependence parameter of Archimedean copula family can be estimated by Inference Function for Margins method (IFM) [46]. The IFM method estimates the parameters through maximization of the log-likelihood function of a copula. The most fitted copula function with time-varying dependence parameter is determined by AICc criterion. The Cramér-von Mises test (CM) [47] and RMSE are used to test the GOF of the copula functions. In addition, similar with the test of the univariate distribution, QQ plot is also used to examine the best fitted copula based on the joint probability derived by the selected copula.
3.4. Joint and Conditional Probability under Nonstationary Framework
Joint probability gives the probability that each component falls in any particular range or discrete set of values specified for these variables. Referring to the multivariate frequency analysis, the joint probability of two variables usually includes three cases in general (i.e., KEN, OR, AND). Take AND for the further analysis in this study, AND () means the space in which all the variables exceed corresponding values simultaneously [48]. Under the time-varying copula framework, the joint probability and can be calculated based on the best fitted copula function as follows:
where , , and are the threshold values of Z, Q and S, respectively. In fact, a given joint probability can correspond infinite data couples, among which there exist the most likely combination with the largest probability density [49]. The most likely combinations conditioned on the given joint probability k can be expressed as follows:
where represents copula density function. , and represent the marginal distribution density functions of Z, Q and S, respectively. stands for argument of the maxima, which is the set of points, or , for which the function attains the function’s largest value conditioned on .
To display the time variation of flood variables with given water stage, the conditional probability of peak discharge or suspended sediment load could be derived from the joint probability as Equation (9). The conditional probability based on nonstationary bivariate copula can be expressed as follows:
4. Results
The temporal trends of peak discharge, peak water stage and suspended sediment load are investigated for selection of explanatory variables. Then, the marginal distributions of three flood variables are described by time-varying distributions, and time-varying copulas are applied to construct joint distributions of both Z-Q and Z-S. Finally, joint probability and conditional probability of bivariate flood variables are estimated to display time variation of their joint distributions over time. The details of the results are provided in the following sub-sections.
4.1. Temporal Trend Analysis
The nonstationarities of the flood series Q, Z and S at Waizhou station are examined by three trend analysis methods, including the MK test, Spearman test and Kendall test. Results of the trend analysis for Q, Z, and S are shown in Table 2. It is seen that the series of Z and S have undergone significant decreasing trends at the 1% significance level during 1964–2013. Peak discharge Q has presented some degree of negative trends, but cannot pass the trend tests at the 5% significance level. The change of forest cover does not have strong effects on flood peak discharge during large storm events, especially for large basins [50].

Table 2.
Trend analysis of the three flood peak series at the Waizhou station during 1964–2013.
The suspended sediment load has undergone significant decreasing trend, particularly after 2003 because of projects implementation about afforestation and conservation measures [51]. The river elevation has undergone significant decrease due to river sand mining [31], which has intensified obviously since 2003. In order to display the sharp changes of Q, Z, and S in the period of last decades, the year of 2003 is chosen as a separated point from the inherent physical cause-effect connection. The annual mean values of Z and S are about 23.25 m and 418.22 × 103 kg/day from 1964 to 2003, and then decrease to 20.96 m and 123.90 × 103 kg/day for the last decade. Through the aforementioned analysis, it is reasonable to conclude that both Z and S display significant nonstationarity during the period from 1964 to 2013, whereas Q is stationary. The trend identification of Q, Z and S are consistent with some previous research conclusions [52,53].
4.2. Nonstationary Marginal Distributions
According to the cause-effect analysis, MCE and FCR could be two potential physical driving forces for the nonstationarity of Z and S. MCE series (Figure 2a) at Waizhou station have presented an obvious decreasing trend from 1964 to 2013, especially during last ten years. FCR series (Figure 2b) of Ganjiang River basin displays a slight decreasing trend before 1980s, but it expands rapidly from 1980s to 2010s due to artificial afforestation and forest conservation in Jiangxi province. Figure 2c,d illustrate significant positive correlation between Z and MCE, and significant negative correlation between S and FCR, respectively. Considering their inherent physical connection as well as statistical correlation, MCE and FCR are separately used as explanatory variables of the nonstationarity of Z and S.
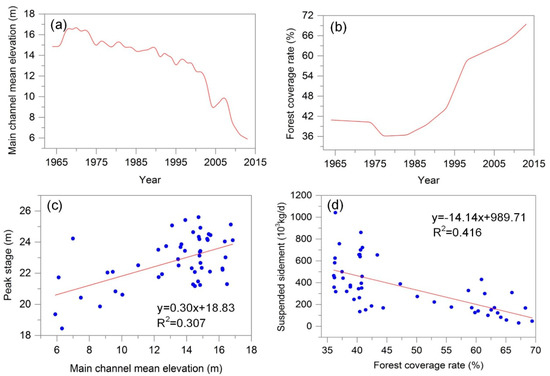
Figure 2.
Data analyses of four variable series in the Ganjiang River basin (GRB) during 1964–2013. (a) is evolution of the main channel mean elevation (MCE) at Waizhou station, (b) is evolution of forest coverage rate (FCR) of the GRB, and two correlation plots are between peak water stage (Z) and MCE (c) and suspended sediment load (S) and FCR (d), respectively. R2 value is the square of the correlation coefficient.
Since annual peak discharge displays stationarity during 1964–2013, Q is fitted by five candidate distributions with all parameters treated as constants. In fitting Z and S series by nonstationary models, there are three main possible situations for each candidate distribution: (1) only the location parameter is time-varying, (2) only the scale parameter is time-varying and (3) both the location and scale parameters are time-varying. The final distribution model for each candidate is determined from the three models above by the selection criterion of AICc (i.e., model with the minimum AICc is the best). For the three flood variables Q, Z and S, the estimated parameters and the results of the GOF test of all candidate marginal distributions are summarized in Table 3. The P-value of the KS test was simulated using the Monte Carlo method. All the distributions pass the KS test at the 0.01 significance level. According to AICc, the most appropriate marginal distributions of Q, Z and S are Gamma distribution. The location parameter of the Gamma distribution for describing Z is positively related to MCE, whereas the scale parameter is constant. Meanwhile, both location and scale parameters of the Gamma distribution for describing S are positively related to FCR. The QQ plot (Figure 3a) of the best fitted distribution indicates that these selected distributions have a quite good fitting quality.

Table 3.
Parameters and goodness-of-fit of the candidate marginal distributions fitted to Q, Z, and S at the Waizhou station during 1964–2013, respectively.
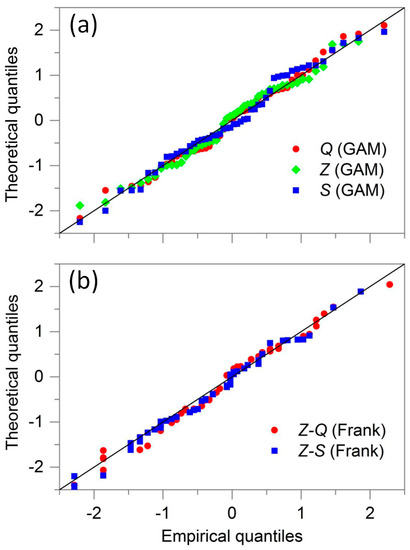
Figure 3.
Quantiles–Quantiles (QQ) plot of the selected marginal distributions (a) and bivariate copula (b).
Due to the balance of riverbed erosion and deposition during 1964–1994, the mean value of Z at Waizhou station is about 23.26 m. In the period of 1995–2013, the value of MCE has underwent a sharp decrease from 12.74 to 5.90 m, thus the variable value for Z has dropped obviously as well. Similarly, the mean and coefficient of variation (Cv) of the suspended sediment load at Waizhou station are 469.81 × 103 kg/day and 0.47 during 1964–1994. After 1995, the mean and Cv of S are getting smaller significantly, because massive afforestation activities have been implemented in the study basin with growth rate of forest cover at 1.17% year by year.
4.3. Nonstationary Dependence of Bivariate Flood Variables
Bivariate copulas under stationary and nonstationary conditions are constructed based on the estimated marginal distributions. In modelling time-varying copula, selection of the explanatory variables (i.e., MCE and FCR) is determined by the two corresponding marginal variables. In detail, about the link function of copula parameter, MCE is selected as covariate expressed in Equation (6) for Z-Q, while MCE and/or FCR are chosen as covariates described in Equations (7) and (8) for Z-S.
The results of the estimated parameters and GOF are summarized in Table 4. The P-value of the CM test is simulated using the Monte Carlo method. All the applied copula functions pass the CM test at the significance level of 0.01. Then, RMSE and AICc, which claim that the model with smaller values is the better, are used as selected criteria [54]. Performances of the candidate copulas are not different obviously from RMSE because of a little difference between them. But the optimum time-varying copulas perform better than stationary ones for Z-Q and Z-S in terms of AICc. Frank is found to be the more appropriate bivariate copula for both Z-Q and Z-S, and parameters expressed in Equations (12) and (13), respectively, as below:

Table 4.
Parameters and goodness-of-fit of the candidate bivariate copulas fitted to Z-Q and Z-S at the Waizhou station during 1964–2013, respectively.
Figure 3b shows the QQ plot of the two bivariate copulas above. It displays a good agreement between empirical distribution and theoretical distribution. In addition, graphical GOF of the selected Frank copulas for both Z-Q and Z-S are shown in Figure 4. The simulation series of Q, Z, and S, which are 30 scatters per year from 1964 to 2013, are generated by Monte Carlo method. Data are transformed to the real space by use of the corresponding marginal distributions. This graphical GOF also demonstrates that the selected time-varying copula functions have satisfactory fitting performances.
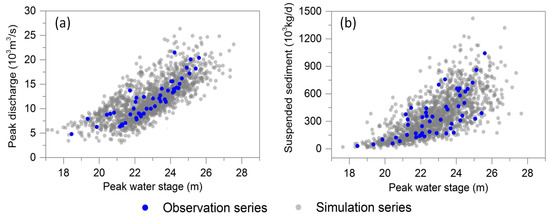
Figure 4.
Scatter plots of Z-Q (a) and Z-S (b) shown comparison of observed data with sets of 1500 generated random samples based on the selected bivariate copulas. Solid circles in blue color are observed data and gray dots are simulated samples.
Therefore, evolutions of the correlation parameters (i.e., , ) present the overall upward trend significantly from 1964 to 2013, which can demonstrate that the dependence structures of Z-Q and Z-S are nonstationary. These results demonstrate that riverbed down-cutting instead of forest coverage is the main external effect for both Z-Q and Z-S at Waizhou station. It is possible to analyze the multivariate flood frequency in the future through the prediction of explanatory variables at Waizhou station based on their relationships [55,56]. Furthermore, it can give supporting information for the flood control design of hydraulic structures under the changing environments [14,39].
4.4. Temporal Variation in Joint and Conditional Probabilities
Contours for various joint probabilities denoted in Figure 5 are calculated by using the selected copulas with parameters in the years of 1970, 1990 and 2010. With the same probability, Z maintains generally higher and almost equivalent value before 1990, whereas moves downward greatly from 1990 to 2010 due to the decrease in mean of the peak water stage. Similarly, the value of S falls rapidly in last ten years due to the significant decrease in mean and Cv of S after 1995. For example, the contours for 0.2 in 2010 for both Z and S are lower than lines for 0.7 in 1970 and 1990, which indicates that the nonstationarity play a great influence on joint probability in the last decade. Upon closer inspection, due to the strengthening in dependence for both Z-Q and Z-S, the corner of contour with the same joint probability becomes angular, especially for the lower probability.
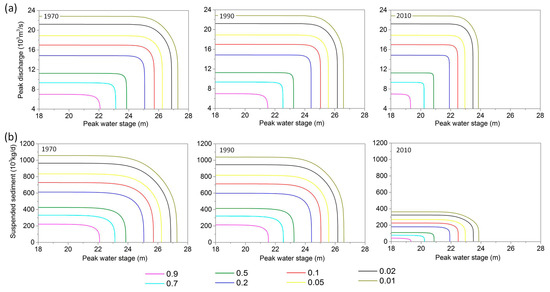
Figure 5.
Joint probability contours with the given (AND) of Z-Q (a) and Z-S (b) using the best fitted bivariate copulas at the Waizhou station in the years of 1970, 1990 and 2010.
As shown in Figure 6, the temporal variations of joint probability as Equation (9) are assessed for each time step from 1964 to 2013. Meanwhile, the magenta dots on the probability contours represent the corresponding the most likely combination derived from Equation (10). The probability contours cover a broad range, with marginal values ranging from 22.12 m to 25.06 m for Z and 721.78 × 103 kg/day to 151.58 × 103 kg/day for S. It can be seen that the suspended sediment load is more sensitive to flood event than the peak water stage from comparison of their value ranges. For the most likely combination, the peak discharge at Waizhou station in the Ganjiang River displays a slight increasing trend from 15.97 × 103 m3/s to 16.41 × 103 m3/s over time, while the values of peak water stage and suspended sediment load have obviously decreased, especially in the last decade. As shown in Figure 6b,d, it is indicated that Z and S in the most likely combination are obviously affected by riverbed down-cutting and the change of forest cover, respectively. Moreover, since the dependence structure of Z-Q is nonstationary as Equation (12), Q in the most likely combination is impacted by riverbed down-cutting as well.
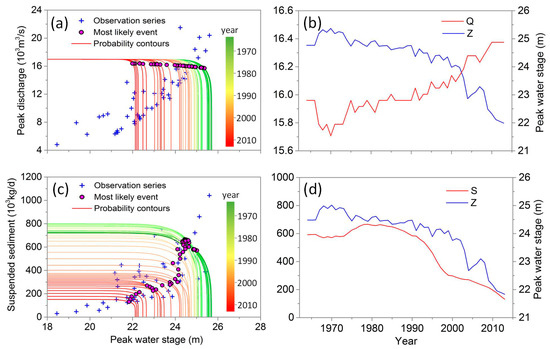
Figure 6.
Time variation of joint probability contours for Z-Q (a) and Z-S (c) and corresponding the most likely combinations for Z-Q (b) and Z-S (d) derived from the best fitted bivariate copula at the Waizhou station from 1964 to 2013.
The conditional probability as Equation (11) is calculated by the best fitted copula function for both Z-Q and Z-S. In practice, flood control planners and managers usually focus on the water stage rather than discharge and suspended sediment load in severe flood flow. Given the warning water stage (23.5 m) at Waizhou station, the time variations of conditional probability () from 1964 to 2013 are presented in Figure 7. The result can be of great important and noteworthy for spillway design and flood control. It can be seen that for the fixed discharge has increased over time, while has decreased during last fifty years. That’s to say, even if Z maintains the same value at Waizhou station, the fact should attract more attention that probabilities of inundation and riverbed erosion are getting higher from 1964 to 2013.
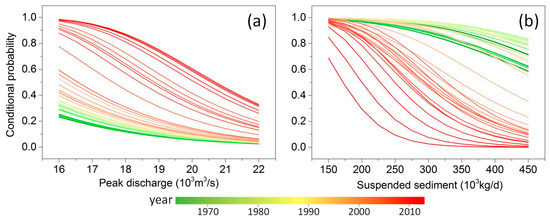
Figure 7.
Time variation of conditional probability (a) and (b) with the given warning water stage (Z ≥ 23.5 m) at the Waizhou station from 1964 to 2013.
What is more, the proposed method also allows us to obtain more information concerning the conditional probabilities under various given water stages. Figure 8 has shown the results, where MCE and FCR are assumed to be 6 m and 70%, respectively. The conditional probabilities become bigger for both Q and S with the higher peak water stage. When values of Q and S become bigger, the differences of conditional probabilities are getting smaller under various given water stages, especially for (Figure 8b). In addition, the conditional probability is more sensitive than on condition of various water stages at Waizhou station. Those results can give us quantitative information about temporal variation of flood variables under the changing environments in the Ganjiang River basin.
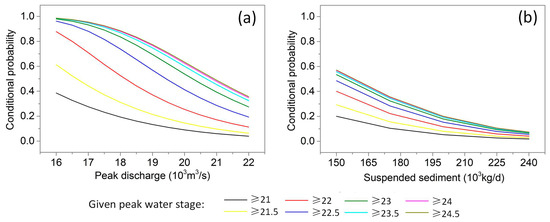
Figure 8.
Conditional probability (a) and (b) with various given water stages when main channel elevation and forest coverage rate are assumed to be 6 m and 70%, respectively.
5. Conclusions
This study employs time-varying copula model to investigate the evolution of the relationships of Z-Q and Z-S depending on main channel elevation (MCE) and forest coverage ratio (FCR) in the Ganjiang River basin during 1964–2013. The main conclusions are presented as follows:
- It is obvious that both the mean and variance of S have significantly decreased, while only the mean has reduced for Z, particularly in the recent decades. Furthermore, Gamma distribution with location parameter expressed as a function of MCE is best fitted distribution for Z, and Gamma with parameters of location and scale expressed as functions of FCA is for S, while the best fitted distribution of Q is the Gamma with constant parameters.
- It is found that the most fitted bivariate copulas for both Z-Q and Z-S are Frank copula, the parameters of which are expressed as the function of MCE. Therefore, riverbed down-cutting at Waizhou station plays the dominant role in strengthening dependences of both Z-Q and Z-S from 1964 to 2013.
- The results of joint probability and conditional probability show that the corner of contour lines enhanced more greatly due to the strengthening dependences over time, especially for the lower probability. In addition, it can be seen that values of Z and S fall rapidly in the last ten years due to the decreasing mean of these two variables.
Author Contributions
Data curation, T.W. and X.X.; Methodology, C.J. and T.W.; Software, T.W.; Formal analysis, T.W.; Writing, review and editing, T.W. and C.J.; Funding acquisition, C.J. All authors reviewed the manuscript.
Funding
This research is financially supported jointly by the National Natural Science Foundation of China (NSFC Grant 51809243), Water Resources Science and Technology Project of Jiangxi, China (201821ZDKT07, KT201704, KT201601, KT201508, KT201501), Science and Technology Project of Jiangxi, China (2015ZBBF60006), the Fundamental Research Funds for the Central Universities (Grant CUG170679), Natural Science Foundation of Hubei Province (Project NO. 2018CFB270), all of which are greatly appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhong, Y.X.; Guo, S.L.; Liu, Z.J.; Wang, Y.; Yin, J.B. Quantifying differences between reservoir inflows and dam site floods using frequency and risk analysis methods. Stoch. Environ. Res. Risk Assess. 2017, 32, 1–15. [Google Scholar] [CrossRef]
- Tena, A.; Batalla, R.J.; Vericat, D.; Lopez-Tarazon, J.A. Suspended sediment dynamics in a large regulated river over a 10-year period (the lower Ebro, NE Iberian Peninsula). Geomorphology 2011, 125, 73–84. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, W.; Kim, T.; Shin, H.; Heo, J.-H. Flood frequency analysis for the annual peak flows simulated by an event-based rainfall-runoff model in an urban drainage basin. Water 2014, 6, 3841–3863. [Google Scholar] [CrossRef]
- Benkhaled, A.; Higgins, H.; Chebana, F.; Necir, A. Frequency analysis of annual maximum suspended sediment concentrations in Abiodwadi, Biskra (Algeria). Hydrol. Process. 2014, 28, 3841–3854. [Google Scholar] [CrossRef]
- Xu, W.T.; Jiang, C.; Yan, L.; Li, L.Q.; Liu, S.N. An adaptive metropolis-hastings optimization algorithm of Bayesian estimation in non-stationary flood frequency analysis. Water Resour. Manag. 2018, 32, 1343–1366. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency prediction for data limited catchments in the Czech Republic using a stochastic rainfall model and TOPMODEL. J. Hydrol. 1997, 195, 256–278. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M.; Gioia, A.; Manfreda, S. Best fit and selection of theoretical flood frequency distributions based on different runoff generation mechanisms. Water 2010, 2, 239–256. [Google Scholar] [CrossRef]
- Gioia, A.; Manfreda, S.; Iacobellis, V.; Fiorentino, M. Performance of a theoretical model for the description of water balance and runoff dynamics in Southern Italy. J. Hydrol. Eng. 2014, 19, 1123–2014. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A. Design event selection in bivariate hydrological frequency analysis. Hydrol. Sci. J. 2012, 57, 1506–1515. [Google Scholar] [CrossRef]
- Shafaei, M.; Fakheri-Fard, A.; Dinpashoh, Y.; Mirabbasi, R.; De Michele, C. Modeling flood event characteristics using D-vine structures. Theor. Appl. Climatol. 2017, 130, 713–724. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; De Michele, C.; Bernardi, M. Hazard assessment under multivariate distributional change-points: Guidelines and a flood case study. Water 2018, 10, 751. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Vezzoli, R.; Pecora, S. Multivariate assessment of droughts: Frequency analysis and dynamic return period. Water Resour. Res. 2013, 49, 6985–6994. [Google Scholar] [CrossRef]
- Vezzoli, R.; Salvadori, G.; Michele, C.D. A distributional multivariate approach for assessing performance of climate-hydrology models. Sci. Rep. 2017, 7, 12071. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.H.; Xu, C.-Y.; Guo, S.L. Bivariate frequency analysis of nonstationary low-flow series based on the time-varying copula. Hydrol. Process. 2014, 29, 1521–1534. [Google Scholar] [CrossRef]
- Gilroy, K.L.; Mccuen, R.H. Anonstationary flood frequency analysis method to adjust for future climate change and urbanization. J. Hydrol. 2012, 414, 40–48. [Google Scholar] [CrossRef]
- Steinschneider, S.; Brown, C. Influences of North Atlantic climate variability on low-flows in the Connecticut River Basin. J. Hydrol. 2011, 409, 212–224. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Palmer, R.N. Use of a nonstationary copula to predict future bivariate low flow frequency in the Connecticut River basin. Hydrol. Process. 2016, 30, 3518–3532. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kwon, H.H.; Lall, U. A copula-based nonstationary frequency analysis for the 2012–2015 drought in California. Water Resour. Res. 2016, 52, 5662–5675. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Bezak, N.; Mikoš, M.; Šraj, M. Trivariate frequency analyses of peak discharge, hydrograph volume and suspended sediment concentration data using copulas. Water Resour. Manag. 2014, 28, 2195–2212. [Google Scholar] [CrossRef]
- Xing, Z.Q.; Yan, D.H.; Zhang, C.; Wang, G.; Zhang, D.D. Spatial Characterization and Bivariate Frequency Analysis of Precipitation and Runoff in the Upper Huai River Basin, China. Water Resour. Manag. 2015, 29, 3291–3304. [Google Scholar] [CrossRef]
- Sarhadi, A.; Burn, D.H.; Wiper, M.P. Time varying nonstationary multivariate risk analysis using a dynamic Bayesian copula. Water Resour. Res. 2016, 52, 2327–2349. [Google Scholar] [CrossRef]
- Guo, A.J.; Chang, J.X.; Wang, Y.M.; Huang, Q.; Guo, Z.H.; Zhou, S. Bivariate frequency analysis of flood and extreme precipitation under changing environment: Case study in catchments of the Loess Plateau, China. Stoch. Environ. Res. Risk Assess. 2007, 32, 2057–2074. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Multivariate multiparameter extreme value models and return periods: A copula approach. Water Resour. Res. 2010, 46, 219–233. [Google Scholar] [CrossRef]
- PappadàElisa, R.; Perrone, E.; Fabrizio, D.; Salvadori, G. Spin-off extreme value and Archimedean copulas for estimating the bivariate structural risk. Stoch. Environ. Res. Risk Assess. 2016, 30, 327–342. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Estimating strategies for multiparameter multivariate extreme value copulas. Hydrol. Earth Syst. Sci. 2011, 15, 141–150. [Google Scholar] [CrossRef]
- Parodi, U.; Ferraris, L. Influence of stage discharge relationship on the annual maximum discharge statistics. Nat. Hazards. 2004, 31, 603–611. [Google Scholar] [CrossRef]
- Lai, X.J.; Shankman, D.; Huber, C.; Yesou, H.; Huang, Q.; Jiang, J.H. Sand mining and increasing Poyang Lake’s discharge ability: A reassessment of causes for lake decline in China. J. Hydrol. 2014, 519, 1698–1706. [Google Scholar] [CrossRef]
- Hua, X.S.; Wu, C.Z.; Hong, W.; Qiu, R.Z.; Li, J.; Hong, T. Forest cover change and its drivers in the upstream area of the Minjiang River, China. Ecol. Indic. 2014, 46, 121–128. [Google Scholar] [CrossRef]
- Du, J.K.; Zheng, D.P.; Xu, Y.P.; Hu, S.F.; Xu, C.-Y. Evaluating functions of reservoirs’ storage capacities and locations on daily peak attenuation for Ganjiang River Basin using Xinanjiang model. Chin. Geogr. Sci. 2016, 26, 789–802. [Google Scholar] [CrossRef]
- Hu, Q.F.; Yang, D.W.; Wang, Y.; Wang, Y.T.; Yang, H.B. Accuracy and spatio-temporal variation of high resolution satellite rainfall estimate over the Ganjiang River Basin. China Technol. Sci. 2013, 56, 853–865. [Google Scholar] [CrossRef]
- Department of Comprehensive Statistics of National Bureau of Statistics. China Compendium of Statistics 1949–2008; China Statistics Press: Beijing, China, 2010.
- Paige, A.D.; Hickin, E.J. Annual bed-elevation regime in the alluvial channel of Squamish River, Southwestern British Columbia, Canada. Earth Surf. Proc. Landf. 2000, 25, 991–1009. [Google Scholar] [CrossRef]
- Magdon, P.; Kleinn, C. Uncertainties of forest area estimates caused by the minimum crown cover criterion--a scale issue relevant to forest cover monitoring. Environ. Monit. Assess. 2013, 185, 5345–5360. [Google Scholar] [CrossRef]
- Kamal, V.; Mukherjee, S.; Singh, P.; Sen, R.; Vishwakarma, C.A.; Sajadi, P. Flood frequency analysis of Ganga River at Haridwar and Garhmukteshwar. Appl. Water Sci. 2016, 7, 1979–1986. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.H.; Liu, D.D.; Hu, T.S.; Xu, C.-Y. Frequency analysis of nonstationary annual maximum flood series using the time-varying two-component mixture distributions. Hydrol. Process. 2017, 31, 69–89. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Rahman, A.; Charron, C.; Ouarda, T.B.M.J.; Chebana, F. Development of regional flood frequency analysis techniques using generalized additive models for Australia. Stoch. Environ. Res. Risk Assess. 2017, 32, 123–139. [Google Scholar] [CrossRef]
- Adlouni, S.E.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobée, B. Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour. Res. 2007, 43, 455–456. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Hipel, K.W. Geophysical model discrimination using the Akaike Information Criterion. IEEE Autom. Control 1981, 26, 358–378. [Google Scholar] [CrossRef]
- Djurovic, Z.; Kovacevic, B.; Barroso, V. QQ-plot based probability density function estimation. In Proceedings of the IEEE Workshop Statistical Signal and Array Processing, Pocono Manor, PA, USA, 16 August 2000. [Google Scholar]
- Joe, H. Multivariate Models and Dependence Concepts; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Bender, J.; Wahl, T.; Jensen, J. Multivariate design in the presence of non-stationarity. J. Hydrol. 2014, 514, 123–130. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Berg, M.J.V.D.; Gräler, B.; Petroselli, A. Joint return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Olang, L.O.; Furst, J. Effects of land cover change on flood peak discharges and runoff volumes: Model estimates for the Nyando River Basin, Kenya. Hydrol. Process. 2011, 25, 80–89. [Google Scholar] [CrossRef]
- Zheng, H.J.; Fang, S.W.; Yang, J.; Xie, S.H.; Chen, X.A. Analysis on evolution characteristics and impacting factors of annual runoff and sediment in the Ganjiang river during 1970–2009. J. Soil Water Conserv. 2012, 26, 28–32. (In Chinese) [Google Scholar]
- Ye, X.C.; Zhang, Q.; Liu, J.; Li, X.H.; Xu, C.-Y. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Luo, W.; Zhang, X.; Deng, Z.M.; Chen, L. Runoff and sediment load transport and cause analysis in Poyang Lake basin over the period 1956–2008. Adv. Water Sci. 2014, 25, 658–667. (In Chinese) [Google Scholar]
- Chen, X.H.; Shao, Q.X.; Xu, C.-Y.; Zhang, J.M.; Zhang, L.G.; Ye, C.Q. Comparative study on the selection criteria for fitting flood frequency distribution models with emphasis on upper-tail behavior. Water 2017, 9, 320. [Google Scholar] [CrossRef]
- Cooley, D. Return Periods and Return Levels under Climate Change. Extremes in a Changing Climate; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).