Numerical Analysis of Recharge Rates and Contaminant Travel Time in Layered Unsaturated Soils
Abstract
1. Introduction
2. Materials and Methods
2.1. General Assumptions
2.2. Structure and Hydraulic Properties of Soils
2.3. Initial and Boundary Conditions
2.4. Numerical Discretization
2.5. Steady-State Methods for Contaminant Travel Time
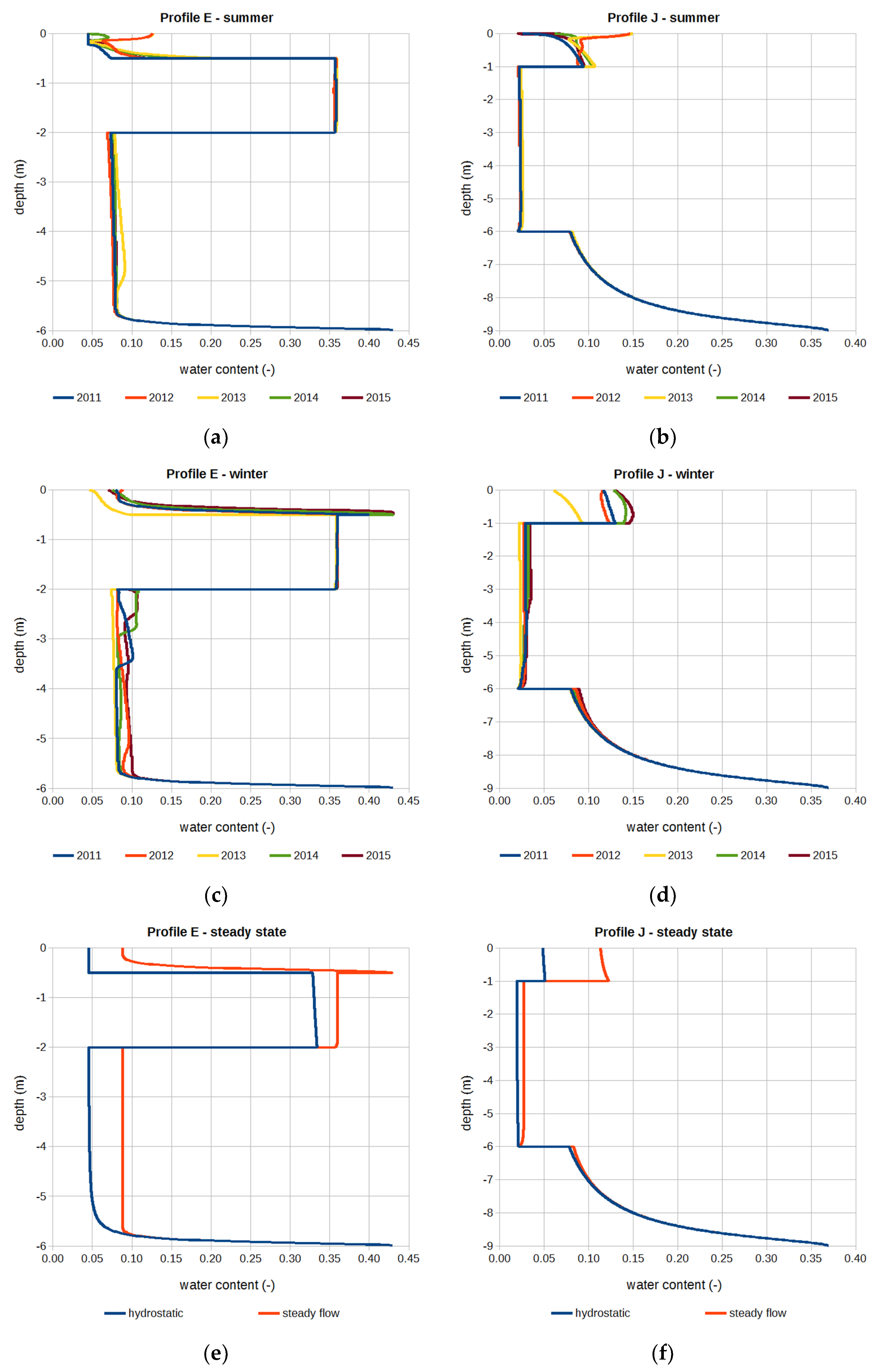
3. Results
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scanlon, B.R.; Christman, M.; Reedy, R.C.; Porro, I.; Simunek, J.; Flerchinger, G.N. Intercode comparisons for simulating water balance of surficial sediments in semiarid regions. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Keese, K.E.; Scanlon, B.R.; Reedy, R.C. Assessing controls on diffuse groundwater recharge using unsaturated flow modeling. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Ordens, C.M.; Post, V.E.; Werner, A.D.; Hutson, J.L. Influence of model conceptualisation on one-dimensional recharge quantification: Uley South, South Australia. Hydrogeol. J. 2014, 22, 795–805. [Google Scholar] [CrossRef]
- Vero, S.E.; Ibrahim, T.G.; Creamer, R.E.; Grant, J.; Healy, M.G.; Henry, T.; Kramers, G.; Richards, K.G.; Fenton, O. Consequences of varied soil hydraulic and meteorological complexity on unsaturated zone time lag estimates. J. Contam. Hydrol. 2014, 170, 53–67. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Franz, T.E.; Zlotnik, V.A. Controls of soil hydraulic characteristics on modeling groundwater recharge under different climatic conditions. J. Hydrol. 2015, 521, 470–481. [Google Scholar] [CrossRef]
- Fenton, O.; Vero, S.; Ibrahim, T.G.; Murphy, P.N.C.; Sherriff, S.C.; Ó hUallacháin, D. Consequences of using different soil texture determination methodologies for soil physical quality and unsaturated zone time lag estimates. J. Contam. Hydrol. 2015, 182, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Vero, S.E.; Healy, M.G.; Henry, T.; Creamer, R.E.; Ibrahim, T.G.; Richards, K.G.; Mellander, P.-E.; McDonald, N.T.; Fenton, O. A framework for determining unsaturated zone water quality time lags at catchment scale. Agric. Ecosyst. Environ. 2017, 236, 234–242. [Google Scholar] [CrossRef]
- Batalha, M.S.; Barbosa, M.C.; Faybishenko, B.; van Genuchten, M.T. Effect of temporal averaging of meteorological data on predictions of groundwater recharge. J. Hydrol. Hydromech. 2018, 66, 143–152. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Šimůnek, J.; Leterme, B.; Beegum, S.; Jaworska-Szulc, B.; Pruszkowska-Cacers, M.; Gorczewska-Langner, W.; Jacques, D. Simulations of freshwater lens recharge and salt/freshwater interfaces using the HYDRUS and SWI2 packages for MODFLOW. J. Hydrol. Hydromech. 2018, 66, 246–256. [Google Scholar] [CrossRef]
- Bashir, R.; Pastora Chevez, E. Spatial and seasonal variations of water and salt movement in the vadose zone at salt-impacted sites. Water 2018, 10, 1833. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, X.S.; Han, P.F. Depth-dependent seasonal variation of soil water in a thick vadose zone in the Badain Jaran Desert, China. Water 2018, 10, 1719. [Google Scholar] [CrossRef]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Implementation of solute transport in the vadose zone into the ‘HYDRUS package for MODFLOW’. Groundwater 2018. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Version 4.0; HYDRUS Software Series 3; University of California: Riverside, CA, USA, 2008. [Google Scholar]
- Kroes, J.G.; van Dam, J.C.; Bartholomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Mulder, H.M.; Supit, I.; van Walsum, P.E.V. SWAP Version 4. Theory Description and User Manual; Report 2780; Wageningen University & Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Fayer, M.J.; Jones, T.L. UNSAT-H Version 2.0: Unsaturated Soil Water and Heat Flow Model (No. PNL-6779); Pacific Northwest Lab.: Richland, WA, USA, 1990.
- Schroeder, P.R.; Dozier, T.S.; Zappi, P.A.; McEnroe, B.M.; Sjostrom, J.W.; Peton, R.L. The Hydrologic Evaluation of Landfill Performance (HELP) Model: Engineering Documentation for Version 3; EPA/600/R-94/168b; US. Environmental Protection Agency, Risk Reduction Engineering Laboratory: Cincinnati, OH, USA, 1994.
- Charbeneau, R.J. Groundwater Hydraulics and Pollutant Transport; Waveland Press: Long Grove, IL, USA, 2006; ISBN 1478608315. [Google Scholar]
- Fenton, O.; Schulte, R.P.; Jordan, P.; Lalor, S.T.; Richards, K.G. Time lag: A methodology for the estimation of vertical and horizontal travel and flushing timescales to nitrate threshold concentrations in Irish aquifers. Environ. Sci. Policy 2011, 14, 419–431. [Google Scholar] [CrossRef]
- Sousa, M.R.; Jones, J.P.; Frind, E.O.; Rudolph, D.L. A simple method to assess unsaturated zone time lag in the travel time from ground surface to receptor. J. Contam. Hydrol. 2013, 144, 138–151. [Google Scholar] [CrossRef]
- Potrykus, D.; Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Szymkiewicz, A. Assessing groundwater vulnerability to pollution in the Puck region (denudation moraine upland) using vertical seepage method. E3S Web Conf. 2018, 44, 00147. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Potrykus, D.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W. Estimation of conservative contaminant travel time through vadose zone based on transient and steady flow approaches. Water 2018, 10, 1417. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Simulation Monographs; Pudoc: Wageningen, The Netherlands, 1978. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Lewandowska, J. Unified macroscopic model for unsaturated water flow in soils of bimodal porosity. Hydrol. Sci. J. 2006, 51, 1106–1124. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Von Hoyningen-Hüne, J. Die Interception des Niederschlags in landwirtschaftlichen Beständen. Schr. DVWK 1983, 57, 1–53. [Google Scholar]
- Braden, H. Ein Energiehaushalts- und Verdunstungsmodell für Wasser und Stoffhaushaltuntersuchungen landwirtschaftlich genutzer Einzugsgebiete. Mitt. Deutsch.Bodenkd. Geselschaft 1985, 42, 294–299. (In German) [Google Scholar]
- Szymkiewicz, A. Approximation of internodal conductivities in numerical simulation of one-dimensional infiltration, drainage, and capillary rise in unsaturated soils. Water Resour. Res. 2009, 45, W10403. [Google Scholar] [CrossRef]
- Charbeneau, R.J.; Daniel, D.E. Contaminant transport in unsaturated flow. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Witczak, S.; Żurek, A. Wykorzystanie map glebowo-rolniczych w ocenie ochronnej roli gleb dla wód podziemnych (Use of soil-agricultural maps in the evolution of protective role of soil for groundwater). In Metodyczne Podstawy Ochrony Wód Podziemnych; Methodical Principles of Groundwater Protection; Kleczkowski, A., Ed.; AkademiaGórniczo-Hutnicza: Kraków, Poland, 1994. (In Polish) [Google Scholar]
- Duda, R.; Winid, B.; Zdechlik, R.; Stępień, M. Metodyka Wyboru Optymalnej Metody Wyznaczania Zasięgu Stref Ochronnych Ujęć Zwykłych Wód Podziemnych z Uwzględnieniem Warunków Hydrogeologicznych Obszaru RZGW w Krakowie; Methodology of Selecting the Optimal Method of the Wellhead Protection Area Delineation Taking into Account the Hydrogeological Conditions in Areas Administered by the Regional Water Management Board in Cracow; Akademia Górniczo-Hutnicza: Kraków, Poland, 2013; ISBN 9788388927294. (In Polish) [Google Scholar]
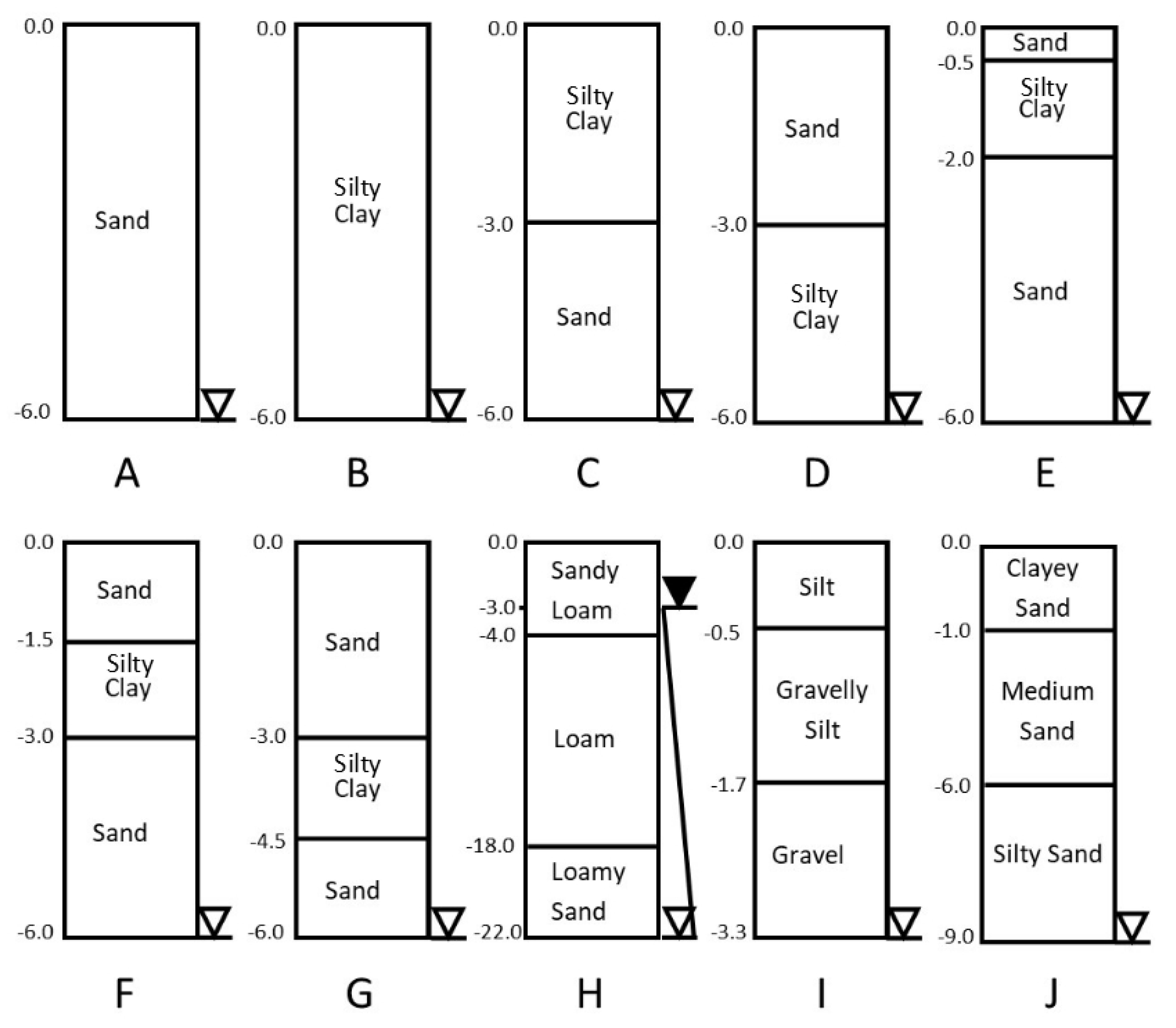
| Soil Type | θr (-) | θs (-) | α (m−1) | ng (-) | ks (m s−1) | θfield Range (-) |
|---|---|---|---|---|---|---|
| Sand [25] | 0.045 | 0.430 | 14.50 | 2.68 | 8.25 × 10−5 | 0.07−0.10 |
| Silty clay [25] | 0.07 | 0.36 | 0.50 | 1.09 | 5.56 × 10−8 | 0.24−0.38 |
| Sandy loam [25] | 0.065 | 0.41 | 7.50 | 1.89 | 1.22 × 10−5 | 0.18−0.26 |
| Loam [25] | 0.078 | 0.43 | 3.60 | 1.56 | 2.89 × 10−6 | 0.24−0.38 |
| Loamy sand [25] | 0.057 | 0.41 | 12.40 | 2.28 | 4.05 × 10−5 | 0.18−0.26 |
| Silt [19] | 0.021 | 0.43 | 0.66 | 1.68 | 8.00 × 10−8 | 0.30−0.36 |
| Gravelly silt [19] | 0.016 | 0.41 | 2.67 | 1.45 | 1.00 × 10−6 | 0.18−0.36 |
| Gravel [19] | 0.001 | 0.28 | 49.30 | 2.19 | 5.00 × 10−2 | 0.05−0.10 |
| Clayey sand [19] | 0.020 | 0.40 | 3.48 | 1.75 | 5.00 × 10−5 | 0.18−0.26 |
| Medium sand [19] | 0.019 | 0.36 | 3.52 | 3.18 | 5.00 × 10−3 | 0.07−0.10 |
| Silty sand [19] | 0.018 | 0.37 | 3.48 | 1.75 | 5.00 × 10−4 | 0.18−0.26 |
| Name | Reference | Method to Calculate θ(z) |
|---|---|---|
| hydrostatic | [19] | θ variable in each soil layer,θ(z) = θ(h(z)), h(z) corresponds to hydrostatic equilibrium above the groundwater table |
| steady flow | [19] | θ variable in each soil layer,θ(z) = θ(h(z)), h(z) obtained from the solution of steady flow equation with uniform flux equal to the average groundwater recharge |
| Charbeneau and Daniel | [17,30] | θ uniform in each soil layer, calculated from Equation (6) |
| Witczak and Żurek | [31,32] | θ uniform in each soil layer, chosen from a range of typical field values θfield provided in Reference [29,30] |
| Quantity | Mean Annual Recharge (mm/year) | Recharge/Precipitation Ratio (-) | Arrival Time c = 0.01 mg/cm3 (days) | Arrival Time c = 0.99 mg/cm3 (days) |
|---|---|---|---|---|
| Profile A | 312 | 0.57 | 424 | 661 |
| Profile B | 62 | 0.11 | 7962 | 10010 |
| Profile C | 61 | 0.11 | 4460 | 6198 |
| Profile D | 325 | 0.59 | 895 | 1535 |
| Profile E | 316 | 0.57 | 746 | 1030 |
| Profile F | 319 | 0.58 | 736 | 1022 |
| Profile G | 320 | 0.58 | 738 | 1020 |
| Profile H | 247 | 0.45 | 10512 | 12642 |
| Profile I | 98 | 0.18 | 808 | 1524 |
| Profile J | 195 | 0.35 | 794 | 1308 |
| Method | Hydrostatic | Steady Flow | Charbeneau & Daniel [28] | Witczak & Żurek [29] |
|---|---|---|---|---|
| Profile A | 383 | 655 | 629 | 491–702 |
| Profile B | 12,011 | 12,650 | 11,445 | 8477–11,303 |
| Profile C | 7106 | 7948 | 7164 | 5565–7539 |
| Profile D | 1325 | 1545 | 1453 | 1044–1415 |
| Profile E | 849 | 1124 | 1030 | 758–1044 |
| Profile F | 879 | 1155 | 1057 | 780–1074 |
| Profile G | 880 | 1141 | 1045 | 770–1163 |
| Profile H | 12,512 | 12,747 | 12,590 | 12,728–13,078 |
| Profile I | 1334 | 2121 | 1419 | 1661–2875 |
| Profile J | 1111 | 1310 | 830 | 2003–2883 |
| Quantity | Mean Annual Recharge (mm/year) | Recharge/Precipitation Ratio (-) | Arrival Time c = 0.01 mg/cm3 (days) | Arrival Time c = 0.99 mg/cm3 (days) |
|---|---|---|---|---|
| Profile A | 220 | 0.40 | 531 | 806 |
| Profile B | 38 | 0.07 | 11,782 | 13,555 |
| Profile C | 38 | 0.07 | 6336 | 8706 |
| Profile D | 223 | 0.42 | 1480 | 1876 |
| Profile E | 215 | 0.39 | 851 | 1526 |
| Profile F | 224 | 0.41 | 834 | 1503 |
| Profile G | 224 | 0.41 | 830 | 1501 |
| Profile H | 195 | 0.35 | 12,956 | 15,477 |
| Profile I | 52 | 0.09 | 963 | 1852 |
| Profile J | 156 | 0.28 | 1314 | 1660 |
| Method | Hydrostatic | Steady Flow | Charbeneau & Daniel [28] | Witczak & Żurek [29] |
|---|---|---|---|---|
| Profile A | 543 | 892 | 857 | 697–995 |
| Profile B | 19,598 | 20,550 | 18,392 | 13,832–21,900 |
| Profile C | 11,407 | 12,630 | 11,271 | 8933–13,832 |
| Profile D | 1880 | 2170 | 2027 | 1482–2295 |
| Profile E | 1283 | 1661 | 1514 | 1146–1732 |
| Profile F | 1241 | 1598 | 1457 | 1100–1662 |
| Profile G | 1257 | 1598 | 1457 | 1100–1662 |
| Profile H | 15,849 | 16,120 | 15,926 | 16,116–16,565 |
| Profile I | 2513 | 3905 | 2454 | 3131–5419 |
| Profile J | 1388 | 1623 | 1011 | 2504–3603 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymkiewicz, A.; Savard, J.; Jaworska-Szulc, B. Numerical Analysis of Recharge Rates and Contaminant Travel Time in Layered Unsaturated Soils. Water 2019, 11, 545. https://doi.org/10.3390/w11030545
Szymkiewicz A, Savard J, Jaworska-Szulc B. Numerical Analysis of Recharge Rates and Contaminant Travel Time in Layered Unsaturated Soils. Water. 2019; 11(3):545. https://doi.org/10.3390/w11030545
Chicago/Turabian StyleSzymkiewicz, Adam, Julien Savard, and Beata Jaworska-Szulc. 2019. "Numerical Analysis of Recharge Rates and Contaminant Travel Time in Layered Unsaturated Soils" Water 11, no. 3: 545. https://doi.org/10.3390/w11030545
APA StyleSzymkiewicz, A., Savard, J., & Jaworska-Szulc, B. (2019). Numerical Analysis of Recharge Rates and Contaminant Travel Time in Layered Unsaturated Soils. Water, 11(3), 545. https://doi.org/10.3390/w11030545




