Abstract
The clarification process removes colloidal particles that are suspended in waste water. The efficiency of this process is influenced by a series of inputs or parameters of the coagulation process, of which the most commonly used are initial turbidity, natural coagulant dosage, temperature, mixing speed and mixing time. The estimation of the natural coagulant dosage that is required to effectively remove these total suspended solids is usually determined by a jar test. This test seeks to achieve the highest efficiency of removal of the total suspended solids while reducing the final turbidity of waste water. This is often configured in iterative fashion, and requires significant experimentation and coagulant. This paper seeks to identify regression models that relate the clarification process parameters to the process outputs (final turbidity and total suspend solid) by the Response Surface Methodology (RSM) based on experiments of Central Composite Design (CCD) of experiments that involve three emerging natural coagulants. Several clarification process scenarios also were proposed and demonstrated using the Multi-Response Surface (MRS) with desirability functions. The experimental results were found to be in close agreement to what are provided by the regression models. This validates the use of the MRS-based methodology to achieve satisfactory predictions after minimal experimentation.
1. Introduction
The management of waste water impacts directly aquatic ecosystems’ biological diversity and affects significantly our life support systems. The management of waste water is an important component of the ecosystem and functions in all sectors. These include fresh water and marine water. The fresh water is exposed to all types of human activity, the water is captured, diverted, treated and reused to sustain communities and their economies. The water that is used in most human is not returned to the watershed from which it is caned. Instead, 80–90 percent of the waste water of developing countries is discharged into surface water, which contains dissolved suspended matter or dissolved solids that are harmful. Waste water discharges that are not regulated are harmful to the biological diversity and the planet’s resilience and its capacity to provide basic ecosystem services. This affects the rural and urban populations. It affects various sectors of human activity, ranging from agriculture, fisheries, industry to health [1]. Coagulation–flocculation is a commonly used chemical treatment process for water [2] and waste water [3]. It has a wide range of application in water and waste water facilities, because it is efficient and simple to operate [4]. Domestic waste water usually contains pathogens, suspended solids, nutrients and organic materials [5]. Waste water treatment is undertaken to satisfy the requirements for discharging treated water into the environment [6]. The processes of coagulation–flocculation followed by sedimentation and filtration are used globally in the treatment process before discharging the treated water into the river. Solid–liquid separation by a coagulation process is considered to be an important process in primary waste water treatment. Coagulation is a term that is used to describe the process of aggregation of colloidal particles into large aggregates to attain better stability. Aggregation of the particles occurs by two distinct mechanisms—charge neutralization and a sweep-floc mechanism. The charge neutralization may be caused by a specific chemical reaction between positively charged coagulants and negatively charged colloids, and natural organic matter. Alternatively, it may be caused by the shielding of the negatively charged sites, resulting in precipitation [7]. The coagulation process is an effective, efficient and simple method of treating water and waste water and is widely used in treating industrial effluent or water waste. The selection process and the coagulant dose that is added to the waste water are extremely important. Inorganic coagulants are frequently used in the coagulation process. In this regard, many researchers have conducted research of inorganic coagulant (aluminum ferric sulfate and chloride), synthetic organic polymers (polyacrylamide derivatives and polyethylene amine) [8,9]. However, prolonged and excessive usage of them can have detrimental effects on human health and living organisms. In addition, these inorganic coagulants can be ineffective in low-temperature water, result in a high procurement cost and generate significant amounts of toxic sludge. In contrast, natural coagulants, which are favored, are biodegradable, low in toxicity, cheaper and produce less sludge [10,11]. Because natural organic coagulants have proved to be effective in removing colloidal particles and are less expensive than other synthetic and inorganic coagulants [12], their use has been rising in recent years. In addition, organic coagulants do not contain metallic elements or reduce the alkalinity of the medium, because it is not subject to hydrolysis in solutions. Due to these characteristics, this coagulant is an ideal coagulant. The efficiency of the coagulation process is governed by various factors. These include the type, dosage and alkalinity of the coagulant [13,14,15], effluent pH [16,17], mixing speed and time [18] and temperature [19]. Therefore, optimization of these factors or inputs is crucial in increasing the coagulation treatment efficiency. Consequently, before application of natural coagulants for the clarification process, these factors must be optimized in order to increase the efficiency of the treatment. In this regard, the traditional method of experimentation, which is termed one-variable-at-a-time, involves changing one factor at a time to obtain the optimal conditions. However, it fails to resolve the relationship between multi-variables due to the complex influences of these factors. Further, this approach is time-consuming, laborious, and expensive because it requires a large number of experiments to be carried out [20,21]. To find a solution to this problem, Design of Experiments (DoE) and Response Surface Methodology (RSM) have been employed to study the effect of variables and their responses using a minimum number of experiments. RSM is an effective and efficient mathematical statistical method to build regression models, evaluate the effects of multiple variables and determine the optimal conditions that will provide desirable responses that successfully overcome the limitations of the conventional method [19,22,23,24,25,26,27]. Estimating the amount of coagulant that is necessary to remove the colloidal particles is normally accomplished by experiment using a jar test. The jar testing, which was developed almost 100 years ago, is still used to determine the optimal coagulation condition. Additionally, in solving waste water treatment engineering problems, soft computing and machine learning-based methods have proved their usefulness [22]. To treat and purify waste water, researchers have modelled and optimized many factors that influence the coagulation–flocculation process by means of regression models that were based on machine learning techniques. Baxter et al. [28], for example, modelled water quality with Artificial Neural Networks (ANNs) considering the water’s turbidity and final color as outputs variables. In addition, the optimum dose of chemical flocculants that were necessary for maximum clarification of the waste water was found. Multiple Linear Regression (MLR) and ANN were used by other researchers [29] to model turbidity and aluminum in treated water. Many factors or inputs were considered in this work including hardness, pH, color, silica, conductivity and turbidity. More recently [30], two types of Support Vector Machine (SVM) that employed different kernel functions were examined for use in predicting with K-Nearest Neighbors (KNN) the necessary coagulant dosage in water treatment plants for various levels of water turbidity. The input parameters in this study were the dosage, pH and temperature. In this case, the differential functions were radial basis functions and polynomial functions.
Several researchers have used also the RSM to obtain the optimal combination of inputs or process variables in the clarification process. However, most of their work is based on the modelling and optimization of relatively few output and input variables. This makes the optimization problem much easier. For example, Trinh and Kang [31] used the RSM technique to optimize the coagulation process in treatment of drinking water. In this case, the input parameters were pH and coagulant dose, whereas the output variables were turbidity and dissolved organic carbon. Other authors, such as Khayet et al. [32], investigated the effects of aluminium sulphate for coagulation/flocculation in removing dye from highly concentrated solutions at different temperatures and initial pH values. Li et al. [33] recently implemented a Multiple Response Surface (MRS) to optimize the coagulation process using polyferric chloride and optimizing three process parameters. They were coagulant dosage, pH and basicity. Subramonian et al. [10] applied RSM based on Central Composite Design (CCD) to investigate the effects of the main process variables, which included the coagulant dosage, pH and mixing time, in optimizing the coagulation process using Cassia obtusifolia seed gum and alum.
In the present study, final turbidity (finTurb) and total suspended solids (TSS), as the outputs of the clarification process, were considered. Meanwhile, the inputs or parameters of the coagulation process were initial turbidity (iniTurb), dosage of natural coagulant (cuaDose), process temperature (T), mixing speed (s) and mixing time (t). The main objective of this work was to conduct a comprehensive optimization study on three different and emerging natural coagulants in the treatment of raw domestic waste water. Regression models that relate the clarification process parameters to the outputs of the process were obtained with the use of RSM based on experiments of a CCD. Five clarification process scenarios were proposed and achieved using the MRS with desirability functions. The work is focused on the following ranges of input parameters, in which the regression models and the optimization achieved with MRS were valid: mixing time (t) (30–120 sec), mixing speed (s) (50–100 rpm), water temperature (T) (10–20 °C), initial turbidity (iniTurb) (40–140 NTU) and coagulant dosage (cuaDose) (1–6 mL). The experimental results were found to be close to the prediction that was derived from the regression models.
2. Materials and Methods
2.1. Materials
The samples of waste water that was used in this study were collected from the Water Waste Treatment Plant (WWTP) in Logroño (Spain). The waste water samples were transported to the laboratory within 15 minutes and then characterized (see Table 1). Three different coagulants were used in this study. They were ECOTAN BIO 90D, ECOTAN BIO 100 and ECOTAN BIO G150 (Servyeco Group, Castellón, Spain). The three coagulants that were studied were cationic organic polymers of essentially vegetal origin and strongly coagulating and flocculating action that act on the systems of colloidal particles. They neutralize charges and create bridges between these particles. This is the process that is responsible for the floc formation and consequently the separation by decantation. None of the coagulants that were used in the research modify the pH of the treated water, because they did not reduce the alkalinity of the medium. However, they were effective in a pH range of 4.5–8.0. The three emerging natural coagulants can be dosed directly to the water to be treated. Their application must be carried out at a point where the agitation guarantees the correct homogenization of the water with the product, to favor the reaction of the polymer with the finest particles and allow for the formation of flocs. The jar test that was used in the experiments involved a programmable apparatus (FLOCUMATIC, Selecta, Spain [34]) according to the standard American Society of Testing Materials (ASTM) D2035-13 [35]. The apparatus consisted of six paddles on a bench. The paddles were connected to each other by a gear mechanism, and were rotated simultaneously by the same motor at a controlled speed and time. A jar test procedure was established at different temperatures for each experimental run. Waste water samples with a volume of 1000 mL each were transferred to the jars. Then, the required doses of different coagulants were added to each beaker during the flash mixing stage (the speed of the jar test and the time were varied throughout each experiment). Finally, the treated waste water was left to settle for 30 min. After the jar test had been completed, the treated waste water was analyzed to determine the finTurb, TSS and hence the extent of pollutant removal. The finTurb measurement was conducted with a 2100Q Turbidimeter (HACH, Loveland, CO, USA) according to the ASTM D1889-00 [36] standard, and TSS was performed following the standard ASTM D5907-10 method [37].

Table 1.
Waste water characterization.
Response Surface Method for Optimizing the Clarification Process
The RSM method determines the relationships between input variables and one or more output variables. It was introduced by Box and Wilson in 1951 [38] for experimental data to be used for a model or optimal response. RSM was developed initially to model experimental responses. However, it has found use in optimizing industrial processes and products [39,40]. RSM often appears as a series of statistical techniques that require a regression model that depends on a low-degree polynomial function (Equation (1)):
where Y is an experimental response, f consists of cross products of polynomial’s terms, X1, X2, X3, …, Xk are input vectors, and e is the error. The quadratic (second-order) model is a polynomial function that is frequently used, and is written as Equation (2):
where the linear part constitutes the first summation, the quadratic part forms the second part, and the third part is the product of the pairs of variables. Regression analysis is used to determine the values of the coefficients b0, bi, bii, and bi. However, good results are not always possible with these functions, if the problem is complex and involves many inputs and nonlinearities. The reason is that the coefficients cannot be adjusted if the data are sparse-like continuous functions that are described by polynomials. The p-value (or Prob. > F) is the probability that the result that will equal or exceed the value that was actually observed assuming that the model produces results that are accurate. The p-value can be determined by analysis of the variance (ANOVA). If the model’s Prob. > F and no term exceeds the level of significance (e.g., α = 0.05), one can consider the model to be acceptable within a (1 − α) confidence interval. Some investigators have used ANOVA to study the effect of inputs or process variables on process outputs [41,42]. If a problem has more than one outputs, the latter is termed MRS. Normally, it causes conflicting solutions, as the optimal configuration may vary significantly from one output to another. A compromise was suggested by Harrington [43]. It involves desirability functions for each output, Equations (3) and (4). It also involves an overall desirability. The latter is the mean value of the desirability (D) of each output (Equation (5)). Equations (3)–(5) can be described as:
where A and B are limiting values, s indicates the importance of reaching the target value, X is the input vector, and fr is the model for prediction. It is beneficial to use a second-higher-degree polynomial to optimize responses [44]. In the desirability approach, each estimated response is transformed into a unit-less utility that is bounded by 0 < dr < 1. A higher value of dr signifies a more desirable response value. The optimization function of the R package v.1.6 [45] searches for a combination of importance factors (or weights of 1, 2 or −3) that satisfy the process criteria for each response and input.
2.2. Experiments Design
In order to create accurate models with the minimum amount of data that is necessary to support the initial hypotheses, RSM must establish a DoE [46]. There are several methods available. However, they require the construction of a design matrix (inputs) to measure the responses or outputs. In this case, a CCD [47] that involved three factors and three levels was chosen. The input variables that were selected to develop the DoE were time (t), temperature (T), speed (S), initial turbidity (iniTurb), and coagulant dosage (cuaDose). The factors that were selected by experiment for optimization and their respective ranges were: mixing time (30–120 sec), mixing speed (50–100 rpm), water temperature (10–20 °C), initial turbidity (40–140 NTU) and coagulant dosage (1–6 mL). The model was valid only inside the region of the parameters studied. The variable ranges that are provided in Table 2 were adopted to cover the intervals that are commonly utilized in the literature [48,49,50].

Table 2.
Parameters of the coagulation process and levels.
After the parameters of the coagulation process and levels were set as in Table 1, the design matrix (Table 3) was generated by the R Statistical Software [45]. In order to provide for all possibilities and to select the optimum process of clarification, 54 experiments were required in this case.

Table 3.
Design matrix for clarification of waste water.
After establishing the inputs or parameters of the coagulation process from the DoE, the output variables of the process were determined experimentally (Table 4).

Table 4.
Experimental design matrix for the clarification process in waste water treatment.
3. Results and Discussion
This methodology was found to be an efficient and direct way to obtain the optimal dose of coagulant with which finTurb and TSS were reduced, when several inputs or process parameters of the coagulation process were considered. The inputs were: initial turbidity (iniTurb), dosage of natural coagulant (cuaDose), process temperature (T), mixing speed (s) and mixing time (t). The proposed method has been applied to three emerging natural coagulants. The proposed method has been applied to various types of natural coagulants.
3.1. Experimental Results
3.2. Analysis of Variance
The data that appear in Table 2 were used in fitting Equation (2) to obtain by the R Base package regression equations for the responses [48]. Second-order polynomial models then were constructed for each response. Then, several criteria (p-value, Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and Correlation (Corr.)) were used in the selection of the model that provided the greatest accuracy.
Equations (6)–(11) show the reduced quadratic regression models that were obtained to model finTurb and TSS for each coagulant tested. These equations show how a combination of second-order polynomials is formed by combining the input variables that provide the output. An ANOVA was used to reduce the size of these regression models by removing the insignificant terms of the polynomial [49]. This method, called step-wise regression, automatically removes the features of no significance for each model [50].
finTurb = 36.7506673 − 0.9446782·t + 0.0039169·t² - 0.2203728 ·s + 0.000966·t·s + 3.5979252·T + 0.0096595·t·T − 0.1570211·T² + 0.009553·T·iniTurb − 0.0005356·iniTurb² + 0.0102462·t·cuaDose + 0.0183188·s·cuaDose − 0.1771652·T·cuaDose − 0.0170971·iniTurb·cuaDose + 0.2285438·cuaDose²
TSS = −107.42648 − 36.95502·t + 0.16738·t² + 0.06127·t·s − 0.04981·s² + 195.53517·T + 0.23366·t·T − 6.46003·T² + 13.57065·iniTurb − 0.07392·iniTurb² − 101.30295·cuaDose + 1.00312·t·cuaDose + 0.90183·s·cuaDose − 3.98293·T·cuaDose
finTurb = −94.889721 − 0.065567·t + 3.138794·s − 0.021709·s² + 0.023985·s·T + 0.336475·iniTurb − 0.002649·s·iniTurb − 0.013975·T·iniTurb + 6.61089·cuaDose − 0.049384·S·cuaDose − 0.280453·T·cuaDose + 0.025552·iniTurb·cuaDose
TSS = 2301.0174 + 19.1258·t − 0.1315·t² − 67.1235·s + 0.4737·s² − 0.1496·T·iniTurb − 0.9338·S·cuaDose + 4.391·T·cuaDose + 0.8546·iniTurb·cuaDose − 17.0285·cuaDose²
finTurb = −18.290656 − 1.140292·t + 0.007104·t² + 3.264461·s − 0.01929·s² − 0.021824·s·T − 0.454037·iniTurb + 0.012343·T·iniTurb − 0.025762·s·cuaDose + 0.04546·iniTurb·cuaDose
TSS = 75.98257 − 15.657·t + 0.08411·t² + 46.44557·s − 0.30951·s² − 150.0361·T + 0.17174·t·T + 4.19307·T² + 5.53688·iniTurb − 0.0266·iniTurb² + 211.01884·cuaDose − 0.67333·s·cuaDose − 28.27164·cuaDose²
In addition, an ANOVA test was conducted in order to determine whether the variables used in the regression models are statistically significant. It is well known that p-value (or Prob. > F) is the probability of receiving a result that equals or exceeds what was observed. If the Prob. is greater than the F value of the model, and the model has no term with a level of significance that exceeds, for example, α = 0.05, then the model is acceptable at a confidence interval of (1 – α). In this case, most of the variables have a p-value that is less than 0.05. This indicates that the variables that were used on the quadratic models are statistically significant. Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 show the results of the ANOVA test for each of the final quadratic models for each coagulant that was tested.

Table 5.
ANOVA values for the “finTurb” quadratic model for ECOTAN BIO 90D.

Table 6.
ANOVA values for the “TSS” quadratic model for ECOTAN BIO 90D.

Table 7.
ANOVA values for the “finTurb” quadratic model for ECOTAN BIO 100.

Table 8.
ANOVA values for the “TSS” quadratic model for ECOTAN BIO 100.

Table 9.
ANOVA values for the “finTurb” quadratic model for ECOTAN BIO G150.

Table 10.
ANOVA values for the “TSS” quadratic model for ECOTAN BIO G150.
From Table 5, it is observed that for ECOTAN BIO 90D, there is a notable influence of t (p-value = 8.428 × 10–6) on finTurb, whereas for s (p-value = 0.18584) and for T (p-value = 0.30660), its influence is much smaller. On the other hand, iniTurb has a certain influence on finTurb when it interacts with itself (p-value = 0.00484), as well as when it interacts with T (p-value = 0.00013). Finally, cuaDose has a notable influence on finTurb when it interacts with iniTurb (p-value = 0.00751) and with T (p-value = 0.00013). From Table 6, it is observed that for ECOTAN BIO 90D, there is no significant influence of any input on TSS, at least when the variables do not interact. However, Table 5 also shows that cuaDose has a notable influence when it interacts with t (p-value = 0.00041) and s (p-value = 0.05395). In addition, t has a notable influence when it interacts with s (p-value = 0.03045), and with T as well when it interacts with itself (p-value = 0.00699). From Table 7, it is observed that for ECOTAN BIO 100, there is a notable influence of s (p-value = 0.053178) on finTurb, whereas for t (p-value = 0.203000) its influence is limited. In addition, this table also shows that s has an important influence when it interacts with itself (p-value = 2.943 × 10−5) and when it interacts with cuaDose (p-value = 0.047805). On the other hand, iniTurb also has a notable influence when it interacts with T (p-value = 0.011558). In the same manner that occurs with ECOTAN BIO 90D, Table 8 shows that for ECOTAN BIO 100, there is no significant influence of any input on TSS, at least when the variables do not interact. However, in Table 8, it is observed that t and s have a notable influence on TSS when it interacts with itself (p-value = 0.02714 and p-value = 0.00619, respectively). These two variables also have a notable influence on cuaDose, which is also significantly influenced when it interacts with s (p-value = 0.00026), with iniTurb (p-value = 0.00137), and with itself (p-value = 0.01175). Finally, regarding ECOTAN BIO G150 (Table 9), it is observed that t, s and iniTurb have an important influence on finTurb (p-value = 0.03742, p-value = 0.04282 and p-value = 0.00116, respectively), and on cuaDose, where very low values are obtained for p-value (for s·cuaDose: p-value = 0.00077; and for iniTurb·cuaDose: p-value = 7.74 × 10−5). For this same coagulant, it is also observed that s and cuaDose have a significant influence on TSS (p-value = 0.04463 and p-value = 0.00141, respectively), while t also influences TSS when it is interacting with itself (p-value = 0.01602). T has no influence on TSS in any way.
Once the results of the ANOVA were presented, it was concluded that the input T has no influence on any of the coagulants for finTurb as well as for TSS. Thus, T can be eliminated from this study, while t and s are the most influential variables. By contrast, in ECOTAN BIO G150, iniTurb and cuaDose have a very important influence on finTurb and TSS, in addition to the aforementioned s and t.
MAE and RMSE were calculated to determine the generalization capacity of the quadratic models using the samples shown in Table 4 according to Equations (12) and (13):
In this case, Yk Experiment are the experimentally obtained responses and Yk Model are responses from the quadratic models that RSM and m experiments produced. The prediction errors are shown in Table 11. The maximum error corresponds to TSS (the MAE equals to 0.14905 and the RMSE equals to 0.17981). The minimum error corresponds to finTurb (the MAE equals to 0.09261 and the RMSE equals to 0.11363).

Table 11.
Results of the errors in FinTurb and TSS using the quadratic models.
In order to test the proposed models, 11 new experiments that had not been used during the training process were conducted. They were used to test the proposed second-order regression models with previously unused regression model parameters. These new 11 experiments were generated randomly. Table 12 shows the test matrix for the clarification process in waste water treatment.

Table 12.
Test matrix for clarification process in waste water treatment.
Once the 11 new experiments had been completed, the errors that arose during the testing stage were calculated (see Table 13). This table shows that the maximum error corresponds to TSS (an MAE of 0.1741 and an RMSE of 0.2342), whereas the minimum error corresponds to finTurb (an MAE of 0.1206 and an RMSE of 0.1630). The errors indicate that the adjustment of the regression models and the results of the experiments are relatively accurate.

Table 13.
Results of the errors in finTurb and TSS using the second-order regression models.
After determining the errors in the prediction from the regression models of the training and test data, a scatter diagram of the variables was created. Figure 1 shows the scatter diagrams or relationships between the actual values that were obtained experimentally and the values of finTurb that were predicted by the quadratic models of (Figure 1a,c and e) and TSS (Figure 1b,d and f) for each of the tested coagulants—ECOTAN BIO 90D, ECOTAN BIO 100 and ECOTAN BIO G150. The blue points relate to the 54 data points that appear in Table 2. The red points relate to the 11 additional experiments that the regression models used. They appear in Table 11. If the variables in this case are correlated, the points will follow the diagonal line or curve. The better the correlation, the closer the points will be to the line. Because all of the red dots (test data) are closer to the diagonal line than are most blue dots (training data), their correlation is greater. Because there are fewer test data points than training data points, the MAE and RMSE errors in the testing analysis and training analysis are similar (see Table 11 and Table 12).
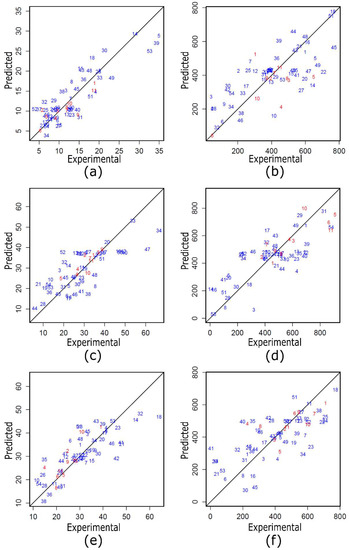
Figure 1.
Scatter diagrams of ECOTAN BIO 90D: (a) finTurb and (b) TSS; ECOTAN BIO 100: (c) finTurb and (d) TSS; and ECOTAN BIO G150: (e) finTurb and (f) TSS.
3.3. Multi-Response Optimization
Table 14, Table 15, Table 16, Table 17 and Table 18 show the combination of parameters of the coagulation and outputs of the process that were studied when examining the clarification process in waste water treatment by desirability functions. The examination involved the desirability package [51] for three different emerging natural coagulants and five different criteria. The first column of each table shows the coagulant that was used in the tests. The second and third columns show, respectively, the parameters of the coagulation and the outputs of the process that were studied, as well as the goal that was established for the optimization process. The fourth column indicates the degrees of importance considered in the optimization process. For all cases studied, it was assumed that all objectives had an importance level of 1.0. The fifth column shows the optimized values that were obtained. The desirability values that were obtained appear in the sixth column. Table 14 shows the results when all coagulation parameters and process outputs are equally important and the design requirements are based on minimizing t, s, T, iniTurb, finTurb and TSS. In this case, the values of the overall desirability were 0.841 for ECOTAN BIO 90D, 0.797 for ECOTAN BIO 100, and 0.774 for ECOTAN G150. Table 15 shows the results when the design requirements were based on minimizing the energy that the coagulation process consumes (the energy is a function of t, s, and T) and obtaining the highest removal efficiency of turbidity (minimizing finTurb) while minimizing TSS. The overall desirability values that were obtained were 0.88 for ECOTAN BIO 90D, 0.791 for ECOTAN BIO 100, and 0.768 for ECOTAN G150. Table 16 provides the results when the design requirements were based on minimizing the energy that was consumed to obtain the highest removal efficiency of turbidity (minimizing finTurb) and minimize TSS, when the waste water has a high degree of turbidity (iniTurb is maximum). In this case, the overall desirability values that were obtained for the natural coagulants were 0.857 for ECOTAN BIO 90D, 0.716 for ECOTAN BIO 100, and 0.794 for ECOTAN G150. Table 17 shows the results when the design requirements are based on maximizing the efficiency in removing turbidity (minimizing the finTurb) and minimizing TSS, while the waste water has a high degree of turbidity (iniTurb is maximum) and a very low temperature (T is minimum). The overall desirability values that were obtained were 0.986 for ECOTAN BIO 90D, 0.754 for ECOTAN BIO 100, and 0.774 for ECOTAN G150. Finally, Table 18 shows the results when the design requirements are based on maximizing the efficiency in removing turbidity (minimizing the finTurb) and minimizing TSS, when the waste water has a high degree of turbidity (iniTurb is maximum) and a high temperature (T is maximum). The overall desirability values obtained were 0.976 for ECOTAN BIO 90D, 0.941 for ECOTAN BIO 100, and 0.774 for ECOTAN G150. Additionally, the results that appear in Table 14, Table 15, Table 16, Table 17 and Table 18 indicate that the outputs of the process that was studied (cuaDose and TSS) are very similar for all different optimization scenarios in a range of inputs or parameters of the coagulation process that was considered. For example, the ranges of values for the cuaDose of the different optimization scenarios that considered for the natural coagulants extend from 3.007 to 5.455 for the ECOTAN BIO 90D, from 1.000 to 5.441 for the ECOTAN BIO 100, and from 1.062 to 5.422 for the ECOTAN G150. In addition, the ranges of values for the TSS of the different optimization scenarios for each natural coagulant extend from 0.000 to 51.901 for the ECOTAN BIO 90D, from 0.000 to 441.478 for the ECOTAN BIO 100, and from 194.109 to 343.679 for the ECOTAN G150. From these results, it appears that the optimal parameters of coagulation for different clarification optimization scenarios are found in a relatively narrow range.

Table 14.
The first clarification optimization scenario: all variables are considered to be equally important.

Table 15.
The second clarification optimization scenario: the energy consumption is minimized to obtain the highest efficiency of turbidity removal and TSS.

Table 16.
The third clarification optimization scenario: the energy consumption is minimized to obtain the highest efficiency of turbidity removal and TSS, when the sample water is very turbid.

Table 17.
The fourth clarification optimization scenario: the turbidity and TSS are minimized when sample water is very cold and turbid.

Table 18.
The fifth clarification optimization scenario: the turbidity and TSS are minimized when the sample water is turbid and hot.
After the different clarification optimization scenarios were obtained, five new experiments were conducted using the combination of process variables that appear in Table 14, Table 15, Table 16, Table 17 and Table 18 prepared in order to determine the accuracy of the proposed methodology. Table 19, Table 20 and Table 21 show the values of different outputs variables (finTurb and TSS) according to the five clarification optimization scenarios that were studied for each of the three emerging coagulants. These tables show that the experimentally obtained values for the five clarification optimization scenarios for the different coagulants that were studied do not differ significantly from those of the MRS methodology produced (see the results of Table 14, Table 15, Table 16, Table 17 and Table 18). To compare the different errors that arise in predicting outputs in this case in accordance with the five design requirements, the normalized data provide MAE and RMSE. Normalizing the data in statistical processes is a common practice. This ensures that the same scale is used by all variables (i.e., 0–1). To normalize the data in this case, the minimum value was subtracted from each original value and the result was divided by the range of each variable, as seen in Equation (14):
where Yk,norm are the normalized, experimental outputs of the models that were developed using RSM. The errors in the last columns concern the MAE and RMSE that were normalized for each variable in each clarification optimization scenario to be studied. The normalized MAE and RMSE that appear in the last two rows relate to the errors in the outputs variables that were examined. For example, Table 19, Table 20 and Table 21 show that the output variable that produce the greatest error in prediction for each of the three natural coagulants studied is the TSS variable (ECOTAN BIO 90D: MAE = 0.08, ECOTAN BIO 100: MAE = 0.08 and ECOTAN BIO G150: MAE = 0.29). These values correspond to the errors that appear in Table 13. In the latter table, the maximum MAE corresponds to the output variable TSS for the three natural coagulants that were studied. However, in Table 19, Table 20 and Table 21, the third optimization scenario has the highest MAE and RMSE values for the three studied coagulants. The reason for this may be that the samples of raw water in this optimization scenario required a high turbidity to analyze each of the natural coagulants to obtain the highest efficiency of turbidity removal and TSS. In this case, a greater initial turbidity of the raw water sample, also as a greater requirement in turbidity removal, could produce this maximum MAE for this scenario.

Table 19.
Experimental outputs that were obtained according to the five clarification optimization scenarios for ECOTAN BIO 90D.

Table 20.
Experimental outputs that were obtained according to the five clarification optimization scenarios for ECOTAN BIO 100.

Table 21.
Experimental outputs that were obtained according to the five clarification optimization scenarios for ECOTAN G150.
4. Conclusions
Physical–chemicals methods are usually used for waste water treatment processes. One such physical–chemical method is coagulation, and determining the amount of coagulant that is necessary to clarify a waste water sample is a complicated task that is usually done with a jar test. This article describes a methodology to obtain the optimal combination of the clarification process parameters for efficient removal of turbidity (finTurb), and TSS from a waste water sample collected from the WWTP in Logroño (Spain). In this case, the clarification process parameters considered were: initial turbidity (iniTurb), dosage of natural coagulant (cuaDose), process temperature (T), mixing speed (s) and mixing time (t). The methodology proposed is based on the RSM with desirability functions, and was applied to three natural coagulants (ECOTAN BIO 90D, ECOTAN BIO 100 and ECOTAN G150). A CCD was used to study the effects of the process parameters and inputs variables on the water clarification process through quadratic regression models. An ANOVA test was performed on the regression models obtained, and it was observed that the process parameter T has no influence on finTurb or on TSS for the studied coagulants. Thus, these parameters could be eliminated in this study. For the natural coagulant ECOTAN BIO G150, iniTurb and cuaDose exercise a strong influence on finTurb and TSS, in addition to those variables mentioned above: s and t. Finally, the optimal combination of process parameters according to five optimization scenarios was determined by applying MRS based on desirability functions. The optimization study reveals that ECOTAN BIO 90D is more efficient than ECOTAN BIO 100 and ECOTAN G150 for removal of turbidity. ECOTAN BIO 90D is recommended for clarification of high-turbidity water. For water that is turbid and hot, both ECOTAN BIO 90D and ECOTAN BIO 100 should be considered. A compromise was made of the removal efficiencies of turbidity and TSS, along with the coagulant dose required. If other parameters are taken into account, such as the low water temperature of samples with high turbidity, the ECOTAN BIO 90D is the coagulant that will demonstrate greatest efficiency in removal of turbidity and TSS. Of the five optimization scenarios that were analyzed, ECOTAN G150 is the natural coagulant that is least efficient in eliminating both turbidity and TSS. This paper has demonstrated that using RMS with desirability functions can be an efficient method for use in selecting and adjusting the parameters of a clarification process using different coagulants, in a short period of time and with the minimal experimentation necessary.
Author Contributions
Experimental work: M.C.B., R.L.L., F.S.G., and E.P.V.G. Contributions to development of predictive models and optimization: R.E.G. Results analysis, revision and improvement of the manuscript: all authors.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank Servyeco Group for partial support of this study (https://www.servyeco.com/).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Corcoran, E.; Nellemann, C.; Baker, E.; Bos, R.; Osborn, D.; Savelli, H. Sick Water? The Central Role of Wastewater Management in Sustainable Development. A Rapid Response Assessment; UNEP: Nairobi, Kenya, 2010. [Google Scholar]
- Choy, S.Y.; Prasad, K.M.N.; Wu, T.Y.; Ramanan, R.N. A review on common vegetables and legumes as promising plant-based natural coagulants in water clarification. Int. J. Environ. Sci. Technol. 2015, 12, 367–390. [Google Scholar] [CrossRef]
- Teh, C.Y.; Budiman, P.M.; Shak, K.P.Y.; Wu, T.Y. Recent advancement of coagulation–flocculation and its application in wastewater treatment. Ind. Eng. Chem. Res. 2016, 55, 4363–4389. [Google Scholar] [CrossRef]
- Lee, K.E.; Morad, N.; Teng, T.T.; Poh, B.T. Development, characterization and the applica-tion of hybrid materials in coagulation/flocculation of wastewater: A review. Chem. Eng. J. 2012, 203, 370–386. [Google Scholar] [CrossRef]
- Boisvert, J.P.; To, T.C.; Berrak, A.; Jolicoeur, C. Phosphate adsorption in flocculation processes of aluminum sulphate and poly-aluminum-silicate-sulphate. Water Res. 1997, 31, 1939–1946. [Google Scholar] [CrossRef]
- Dawood, A.S.; Li, Y. Modeling and optimization of new flocculant dosage and pH for flocculation: Removal of pollutants from wastewater. Water 2013, 5, 342–355. [Google Scholar] [CrossRef]
- Ahmad, A.; Ismail, S.; Bhatia, S. Optimization of coagulation-flocculation process for palm oil mill effluent using response surface methodology. Environ. Sci. Technol. 2005, 39, 2828–2834. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.Y.; Yue, Q.Y.; Wang, B.J.; Chu, Y.B. Poly-aluminum-silicate-chloride (PASiC) a new type of composite inorganic polymer coagulant. Colloids Surf. A Physicochem. Eng. Asp. 2003, 229, 121–127. [Google Scholar] [CrossRef]
- Sinha, S.; Yoon, Y.; Amy, G.; Yoon, J. Determining the effectiveness of conventional and alternative coagulants through effective characterization schemes. Chemosphere 2004, 57, 1115–1122. [Google Scholar] [CrossRef] [PubMed]
- Subramonian, W.; Wu, T.Y.; Chai, S.P. An application of response surface methodology for optimizing coagulation process of raw industrial effluent using Cassia obtusifolia seed gum together with alum. Ind. Crops Prod. 2015, 70, 107–115. [Google Scholar] [CrossRef]
- Wang, J.P.; Chen, Y.Z.; Wang, Y.; Yuan, S.J.; Yu, H.Q. Optimization of the coagulation-flocculation process for pulp mill wastewater treatment using a combination of uniform design and response surface methodology. Water Res. 2014, 45, 5633–5640. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.L.; Yasin, N.M.; Derek, C.J.C.; Lim, J.K. Optimization of microalgae coagulation process using chitosan. Chem. Eng. J. 2011, 173, 879–882. [Google Scholar] [CrossRef]
- Hu, C.Z.; Liu, H.J.; Qu, J.H.; Wang, D.S.; Ru, J. Coagulation Behavior of Aluminum Salts in Eutrophic Water: Significance of Al13 Species and pH Control. Environ. Sci. Technol. 2006, 40, 325–331. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.S.; Tang, H.X.; Gregory, J. Relative Importance of Charge Neutralization and Precipitation on Coagulation of Kaolin with PACl: Effect of Sulfate Ion. Environ. Sci. Technol. 2002, 36, 1815–1820. [Google Scholar] [CrossRef] [PubMed]
- Teh, C.Y.; Wu, T.Y.; Juan, J.C. Potential use of rice starch in coagulation-flocculation process of agro-industrial wastewater: Treatment performance and flocs characterization. Ecol. Eng. 2014, 71, 509–519. [Google Scholar] [CrossRef]
- Miller, S.M.; Fugate, E.J.; Craver, V.O.; Smith, J.A.; Zimmerman, J.B. Toward Understanding the Efficacy and Mechanism of Opuntia spp. as a Natural Coagulant for Potential Application in Water Treatment. Environ. Sci. Technol. 2008, 42, 4274–4279. [Google Scholar] [CrossRef] [PubMed]
- Syu, M.; Chen, B.; Chou, S. A Study on the Sedimentation Model and Neural Network Online Adaptive Control of a Benzoic Acid Imitated Wastewater Oxidation Process. Ind. Eng. Chem. Res. 2003, 42, 6862–6871. [Google Scholar] [CrossRef]
- Yu, W.Z.; Gregory, J.; Campos, L.; Li, G.B. The role of mixing conditions on floc growth, breakage and re-growth. Chem. Eng. J. 2011, 171, 425–430. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.; Mo, L.; Li, J.; Xu, J. Optimization of coagulation-flocculation process for papermaking-reconstituted tobacco slice wastewater treatment using response surface methodology. J. Ind. Eng. Chem. 2014, 20, 391–396. [Google Scholar] [CrossRef]
- Wu, T.Y.; Mohammad, A.W.; Jahim, J.M.; Anuar, N. Optimized reused and bioconversion from retentate of pre-filtered palm oil mill effluent (POME) into microbial protease by Aspergillus terreus using response surface methodology. J. Chem. Technol. Biotechnol. 2009, 84, 1390–1396. [Google Scholar] [CrossRef]
- Teh, C.Y.; Wu, T.Y. The potential use of natural coagulants and flocculants in the treatment of urban waters. Chem. Eng. Trans. 2014, 39, 1603–1608. [Google Scholar]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; de Marinis, G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Shak, K.P.Y.; Wu, T.Y. Optimized use of alum together with unmodified Cassia obtusifolia seed gum as a coagulant aid in treatment of palm oil mill effluent under natural pH of wastewater. Ind. Crop. Prod. 2015, 76, 1169–1178. [Google Scholar] [CrossRef]
- Witek-Krowiak, A.; Chojnacka, K.; Podstawczyk, D.; Dawiec, A.; Pokomeda, K. Application of response surface methodology and artificial neural network methods in modelling and optimization of biosorption process. Bioresour. Technol. 2014, 160, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Sedano, J.; Curiel, L.; Corchado, E.; de la Cal, E.; Villar, J. A soft computing method for detecting lifetime building thermal insulation failures. Integr. Comput. Aided Eng. 2010, 17, 103–115. [Google Scholar] [CrossRef]
- Lostado, R.; Fernández, R.; Mac Donald, B.J.; Villanueva, P.M. Combining soft computing techniques and the finite element method to design and optimize complex welded products. Integr. Comput. Aided Eng. 2015, 22, 153–170. [Google Scholar] [CrossRef]
- Ratnaweera, H.; Fettig, J. State of the art of online monitoring and control of the coagulation process. Water 2015, 7, 6574–6597. [Google Scholar] [CrossRef]
- Baxter, C.W.; Zhang, Q.; Stanley, S.J.; Shariff, R.; Tupas, R.R.; Stark, H.L. Drinking water quality and treatment: The use of artificial neural networks. Can. J. Civ. Eng. 2001, 28, 26–35. [Google Scholar] [CrossRef]
- Juntunen, P.; Liukkonen, M.; Pelo, M.; Lehtola, M.J.; Hiltunen, Y. Modelling of water quality: An application to a water treatment process. Appl. Comput. Intell. Soft Comput. 2012, 4, 14. [Google Scholar] [CrossRef]
- Zhang, K.; Achari, G.; Li, H.; Zargar, A.; Sadiq, R. Machine learning approaches to predict coagulant dosage in water treatment plants. Int. J. Syst. Assur. Eng. Manag. 2013, 4, 205–214. [Google Scholar] [CrossRef]
- Trinh, T.K.; Kang, L.S. Response surface methodological approach to optimize the coagulation–flocculation process in drinking water treatment. Chem. Eng. Res. Des. 2011, 89, 1126–1135. [Google Scholar] [CrossRef]
- Khayet, M.; Zahrim, A.Y.; Hilal, N. Modelling and optimization of coagulation of highly concentrated industrial grade leather dye by response surface methodology. Chem. Eng. J. 2011, 167, 77–83. [Google Scholar] [CrossRef]
- Li, N.; Hu, Y.; Lu, Y.Z.; Zeng, R.J.; Sheng, G.P. Multiple response optimization of the coagulation process for upgrading the quality of effluent from municipal wastewater treatment plant. Sci. Rep. 2016, 6, 26115. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://www.grupo-selecta.com/es/catalogo/subcategorias/5/AGITADORES (accessed on 10 June 2018).
- ASTM D2035-13 Standard Practice for Coagulation-Flocculation Jar Test of Water. Available online: https://www.astm.org/Standards/D2035.htm (accessed on 10 March 2018).
- ASTM D1889-00 Standard Test Method for Turbidity of Water (Withdrawn 2007). Available online: https://www.astm.org/Standards/D1889.htm (accessed on 10 March 2018).
- ASTM D5907-10 Standard Test Methods for Filterable Matter (Total Dissolved Solids) and Nonfilterable Matter (Total Suspended Solids) in Water. Available online: https://www.astm.org/Standards/D5907.htm (accessed on 15 March 2018).
- Box, G.E; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Lostado, R.; García, R.E.; Martinez, R.F. Optimization of operating conditions for a double-row tapered roller bearing. Int. J. Mech. Mater. Des. 2016, 12, 353–373. [Google Scholar] [CrossRef]
- Lostado, R.; Escribano, R.; Martínez, M.A.; Múgica, R. Improvement in the Design of Welded Joints of EN 235JR Low Carbon Steel by Multiple Response Surface Methodology. Metals 2016, 6, 205. [Google Scholar] [CrossRef]
- Moussaoui, K.; Mousseigne, M.; Senatore, J.; Chieragatti, R.; Lamesle, P. Influence of Milling on the Fatigue Lifetime of a Ti6Al4V Titanium Alloy. Metals 2015, 5, 1148–1162. [Google Scholar] [CrossRef]
- Gopalsamy, B.M.; Mondal, B.; Ghosh, S. Taguchi method and ANOVA: An approach for process parameters optimization of hard machining while machining hardened steel. J. Sci. Ind. Res. India 2009, 68, 686–695. [Google Scholar]
- Harrington, E.C. The desirability function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Kuhn, M. Desirability: Desirability Function Optimization and Ranking. R package v.1.6. Available online: http://CRAN.R-project.org/package=desirability (accessed on 25 August 2016).
- R Core Team R: A Language and Environment for Statistical Computing. R foundation for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 22 January 2018).
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Box, G.E.; Behnken, D.W. Some new three level designs for the study of quantitative variables. Technometrics 1960, 2, 455–475. [Google Scholar] [CrossRef]
- Lenth, R.V. Response-Surface Methods in R, Using RSM. J. Stat. Softw. 2009, 32, 1–17. [Google Scholar] [CrossRef]
- Sathiya, P.; Aravindan, S.; Haq, A.N. Optimization for friction welding parameters with multiple performance characteristics. Int. J. Mech. Mater. Des. 2006, 3, 309–318. [Google Scholar] [CrossRef]
- Wilkinson, L.; Dallal, G.E. Tests of significance in forward selection regression with an F-to enter stopping rule. Technometrics 1981, 23, 377–380. [Google Scholar]
- Max, K. Desirability Function Optimization and Ranking. R package Version 1.9. 2015. Available online: https://CRAN.R-project.org/package=desirability (accessed on 28 March 2017).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).