Update of Early Warning Indicators of Flash Floods: A Case Study of Hunjiang District, Northeastern China
Abstract
1. Introduction
2. Material and Methods
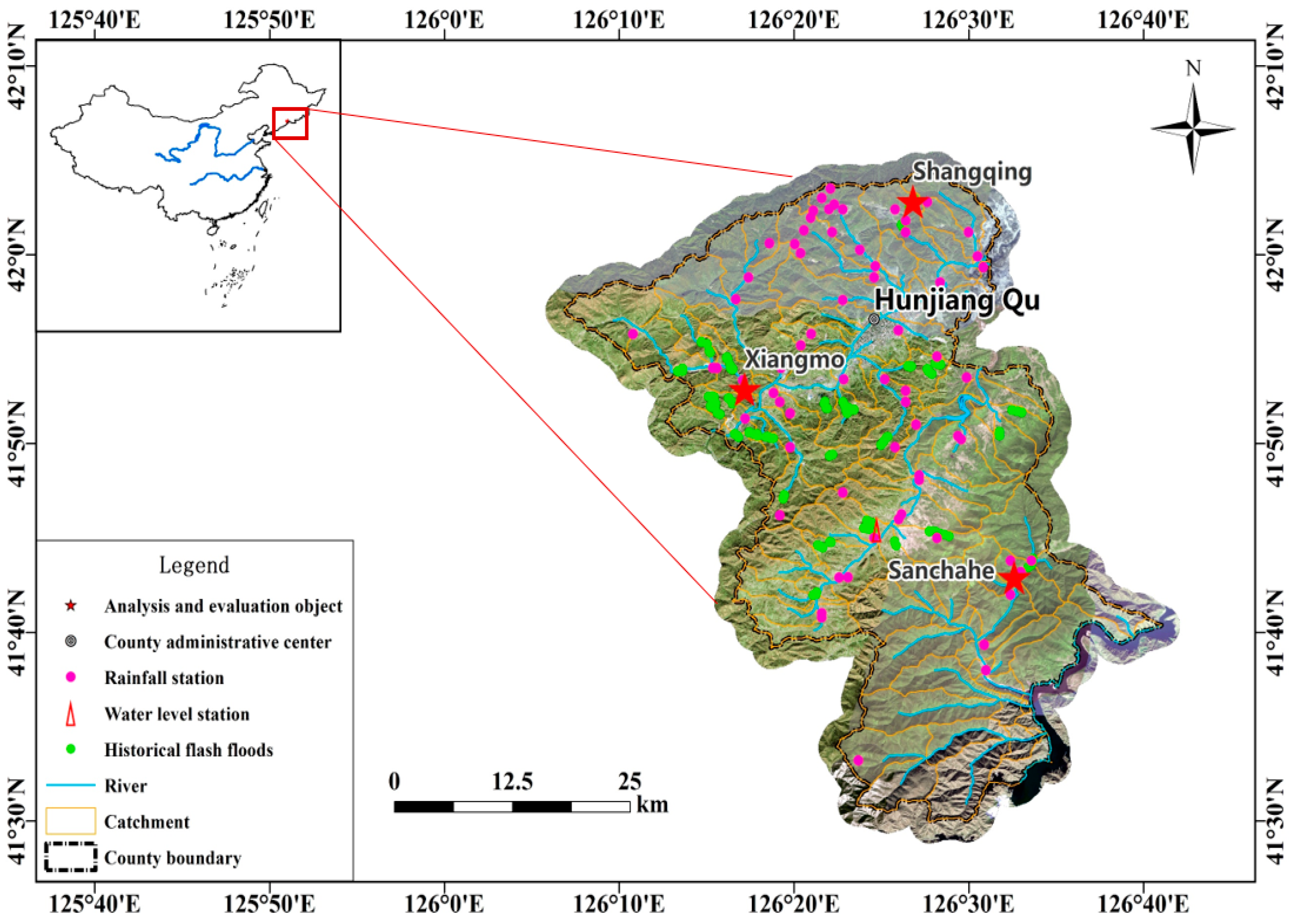
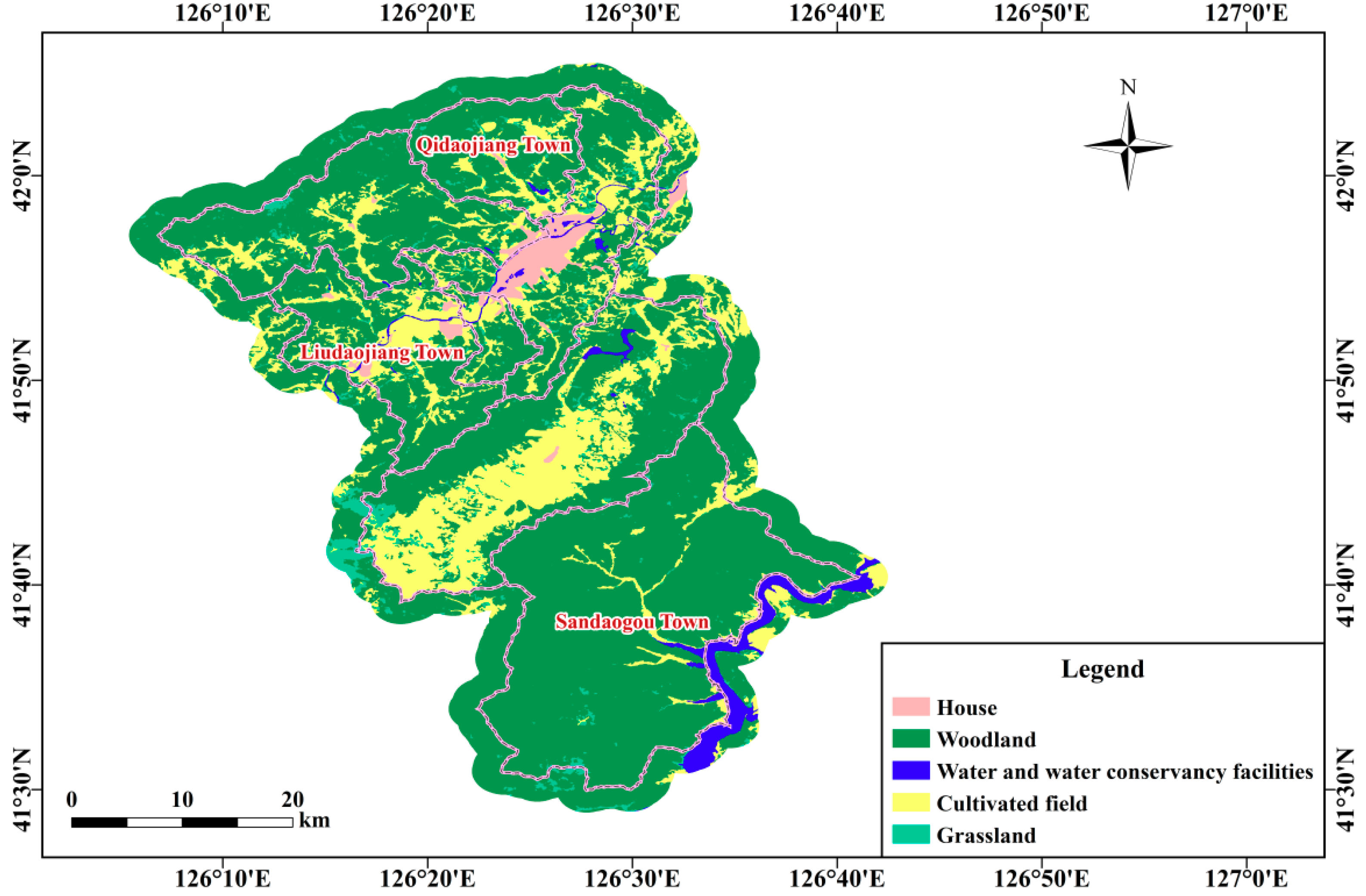
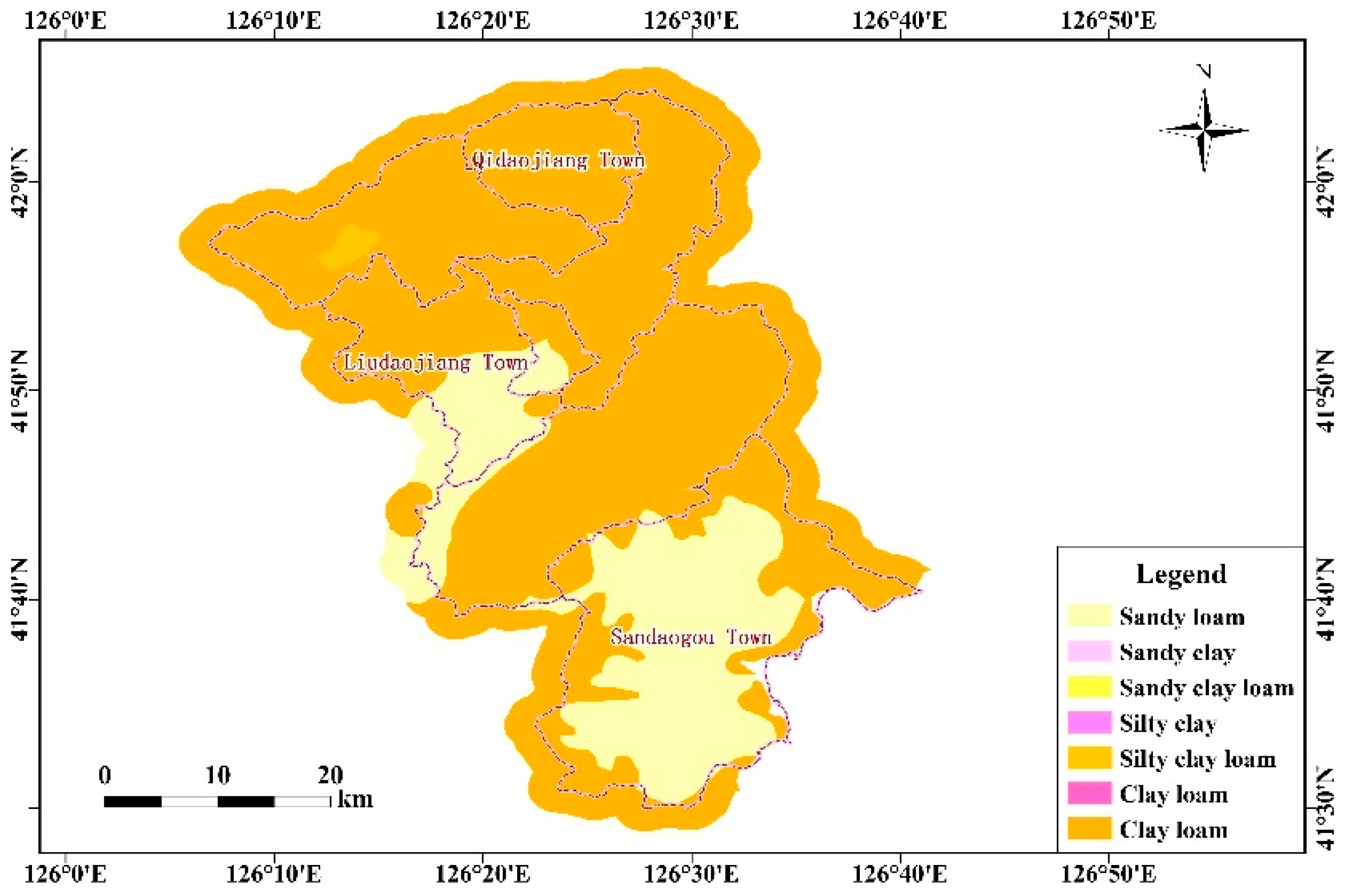
2.1. Study Area
2.2. Methodology
2.2.1. Design Rainstorm Calculation
2.2.2. Runoff Generation Calculation
2.2.3. Confluence Calculation
- (i)
- The water–surface ratio determined by the flood marks of the latest floods should be selected.
- (ii)
- The comprehensive gradient (no sudden change at the bottom of the river) or the partial gradient (sudden change, for example, the gradient of the upstream section of the dam must be the gradient of the upstream water–surface, and the additional gradient caused by the river congestion should be eliminated.
2.3. Data Sources
3. Results and Discussion
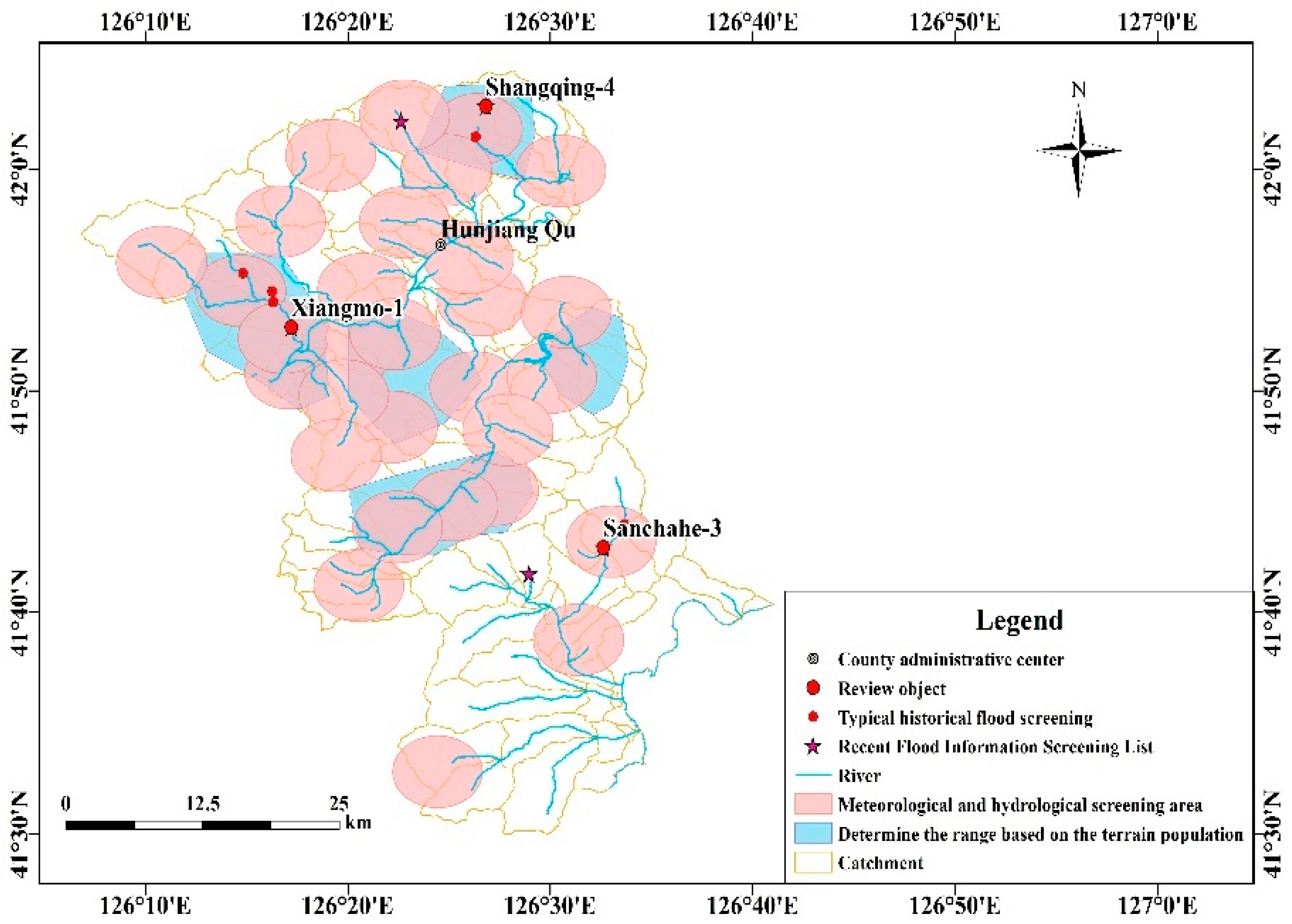
3.1. Determine Updating Object
- (1)
- Meteorological and hydrological data. Due to the flash flood watershed is mostly less than 200 km2, one of the screening conditions is the watershed area is less than 1000 km2 (considering the original disaster prevention objects, hydrometeorological data, and station distribution). Moreover, taking into account the short-duration characteristics of heavy rainfall, and the rapid convergence of the slopes, and the rapid convergence of the river on the slope, both the areas with smaller upstream watersheds and better rainfall data are considered.
- (2)
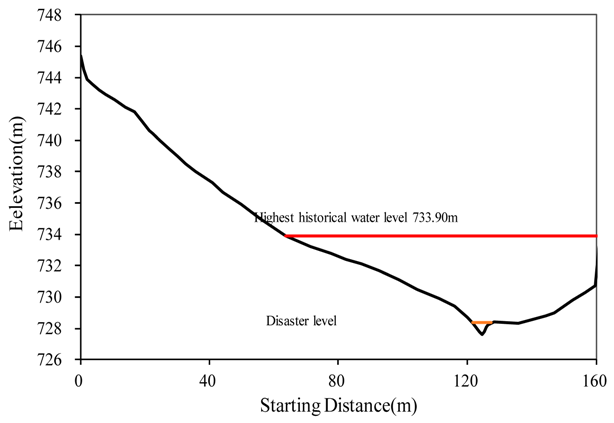
- Typical historical flash flood. Since the convergence time of flash flood is usually less than 12 h, considering the spatial–temporal distribution, frequency, the average value and variation coefficient of heavy rain, the northern Hunjiang district is the key prevention area, which mainly distributes in the central region from west to east. In the northeast hilly area, the upstream is prone to trigger flash flood disasters due to the small catchment area. Combined with the recent flash flood disaster data and expert scoring, Figure 4 is the Distribution map of the review objects in Hunjiang. Table 1 is the watershed attribute information. Among them, Xiangmu-1 and Sanchahe-3 are located in the lower reaches of the river, mainly affected by upstream rainfall, and are typical villages that cause floods due to the fluctuation of river floods.
3.2. Design Flood
3.2.1. Water Level-Discharge Curves
3.2.2. Inference Formula
3.3. Early Warning Indicators
4. Conclusions
- (1)
- Based on the survey data, such as recent flash flood data, meteorological hydrological data, and topographical population data, the three typical riverside villages of Shangqing-4, Xiangmo-1, and Sanchahe-3 were comprehensively screened by expert scoring method.
- (2)
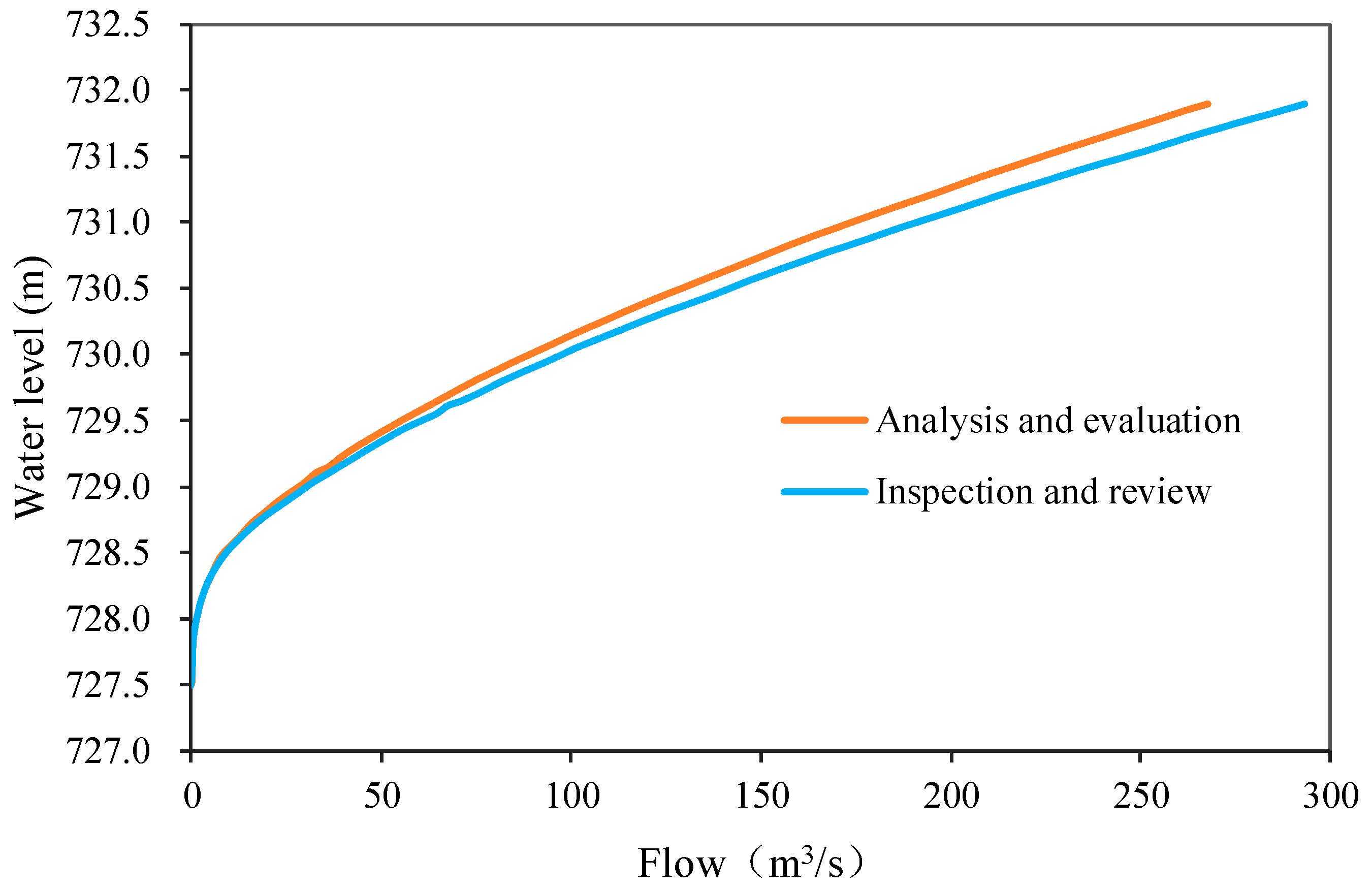
- Using the inference formula method and the water level-discharge curves respectively, the maximum error of the flood peak is 10.6%, which has high reliability and can be applied to the inspection and verification of early warning indicators. The measurement results along the river section are consistent with the actual measurement results, but the roughness of the main channel and the two banks are high.
- (3)
- The calculation method of the design rainstorm and the relevant parameters of the early warning indicator are reasonable. Both the gradient and the roughness in CFFIED are larger than the measured. When the same water level condition, the peek flow value is smaller than the rechecked value.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Destro, E.; Amponsah, W.; Nikolopoulos, E.I.; Marchi, L.; Marra, F.; Zoccatelli, D.; Borga, M. Coupled prediction of flash flood response and debris flow occurrence: Application on an alpine extreme flood event. J. Hydrol. 2018, 558, 225–237. [Google Scholar] [CrossRef]
- Palik, B.J.; Michener, W.K.; Mitchell, R.J.; Edwards, D. The effects of landform and plant size on mortality and recovery of longleaf pine during a 100-year flood. Écoscience 1999, 6, 255–263. [Google Scholar] [CrossRef]
- French, J.; Ing, R.; von Allen, S.; Wood, R. Mortality from flash floods: A review of national weather service reports, 1969–81. Public Health Rep. 1983, 98, 584. [Google Scholar]
- Jonkman, S.N.; Kelman, I. An analysis of the causes and circumstances of flood disaster deaths. Disasters 2005, 29, 75–97. [Google Scholar] [CrossRef] [PubMed]
- Borga, M.; Stoffel, M.; Marchi, L.; Marra, F.; Jakob, M. Hydrogeomorphic response to extreme rainfall in headwater systems: Flash floods and debris flows. J. Hydrol. 2014, 518, 194–205. [Google Scholar] [CrossRef]
- Gruntfest, E.; Handmer, J. Coping with Flash Floods; Springer Science & Business Media: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Ashley, S.T.; Ashley, W.S. Flood Fatalities in the United States. J. Appl. Meteorol. Climatol. 2008, 47, 805–818. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical assessment of Chinese and Japanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. Glofas—global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. 2013, 17, 1161–1175. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, W.B.; Hsu, M.H.; Fu, J.C. Dynamic routing modeling for flash flood forecast in river system. Nat. Hazard. 2010, 52, 519–537. [Google Scholar] [CrossRef]
- Clark, R.A.; Gourley, J.J.; Flamig, Z.L.; Hong, Y.; Clark, E. CONUS-Wide Evaluation of National Weather Service Flash Flood Guidance Products. Weather Forecast. 2014, 29, 377–392. [Google Scholar] [CrossRef]
- Reed, S.; Schaake, J.; Zhang, Z. A distributed hydrologic model and threshold frequency-based method for flash flood forecasting at ungauged locations. J. Hydrol. 2007, 337, 402–420. [Google Scholar] [CrossRef]
- Gourley, J.J.; Hong, Y.; Flamig, Z.L.; Arthur, A.; Clark, R.; Calianno, M.; Ruin, L.; Ortel, T.; Wieczorek, M.E.; Kirstetter, P.-E.; et al. A Unified Flash Flood Database across the United States. Bull. Am. Meteorol. Soc. 2013, 94, 799–805. [Google Scholar] [CrossRef]
- Lee, M. Overview of Debris-Flow Monitoring and Warning System in Taiwan. Res. Soil Water Conserv. 2009, 16, 239–242. [Google Scholar]
- Alfieri, L.; Thielen, J.; Pappenberger, F. Ensemble hydro-meteorological simulation for flash flood early detection in southern Switzerland. J. Hydrol. 2012, 424–425, 143–153. [Google Scholar] [CrossRef]
- Liu, Z. Research and application of mountain flood warning and forecasting technology. Chin. Flood Drought Manag. 2012, 22, 41–45. [Google Scholar]
- Guo, L.; He, B.; Ma, M.; Chang, Q.; Li, Q.; Zhang, K.; Hong, Y. A comprehensive flash flood defense system in China: Overview, achievements, and outlook. Nat. Hazard. 2018, 92, 727–740. [Google Scholar] [CrossRef]
- Guo, L.; Ding, L.; Sun, D.; Liu, C.; He, B.; Liu, R. Key techniques of flash flood disaster prevention in China. J. Hydraul. Eng. 2018, 49, 1123–1136. [Google Scholar]
- Luo, P.; Zhou, M.; Deng, H.; Lyu, J.; Cao, W.; Takara, K.; Nover, D.; Schladow, S.G. Impact of forest maintenance on water shortages: Hydrologic modeling and effects of climate change. Sci. Total Environ. 2018, 615, 1355–1363. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Duan, W.; Takara, K.; Nover, D. Impact assessment of rainfall scenarios and land-use change on hydrologic response using synthetic Area IDF curves. J. Flood Risk Manag. 2018, 11, S84–S97. [Google Scholar] [CrossRef]
- Liu, C.; Guo, L.; Ye, L.; Zhang, S.; Zhao, Y.; Song, T. A review of advances in China’s flash flood early-warning system. Nat. Hazard. 2018, 92, 619–634. [Google Scholar] [CrossRef]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
| Prevention Object | Rainfall Collection Area (km2) | Slope (‰) | Roughness | Design Peak Flow (m3/s) | Runoff Concentration-Time (h) | Peak Flow/104 m3 | Flood Duration (h) | Flood Stage (m) | Cause Disaster (m) | Earling Warning Period (h) | Soil Moisture (%) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Left Bank | Main Channel | Right Bank | |||||||||||
| Shangqing-4 | 1.2 | 51 | 0.05 | 0.035 | 0.05 | 18.1 | 0.5 | 4.8 | 10 | 728.8 | 728.4 | 1 January | 0.2 Wm |
| Xiangmo-1 | 80.5 | 11 | 0.06 | 0.04 | 0.06 | 280 | 7.4 | 339.3 | 47 | 472.8 | 471.8 | 12 January | 0.5 Wm |
| Sanchahe-3 | 51.4 | 42 | 0.05 | 0.035 | 0.05 | 266.7 | 6.3 | 323.7 | 53 | 477.8 | 477.2 | 6 January | 0.8 Wm |
| Name of Village | Roughness of the Left Bank | Rroughness of the Right Bank | Roughness of the Main Channel | Slope (‰) | Diagram of Water Level-Flow Relation |
|---|---|---|---|---|---|
| Shangqing-4 | 0.043 | 0.043 | 0.032 | 51 | 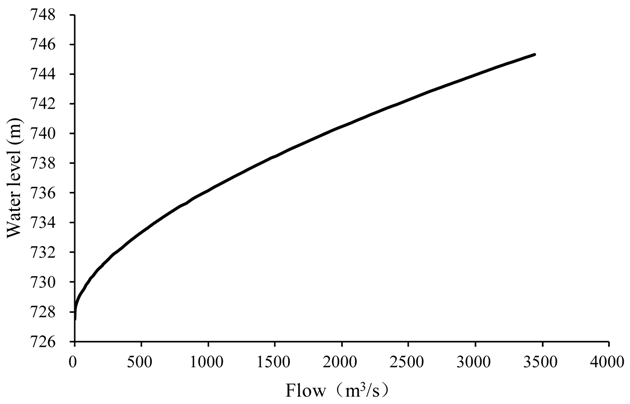 |
 | |||||
| Xiangmo-1 | 0.048 | 0.048 | 0.035 | 11 | 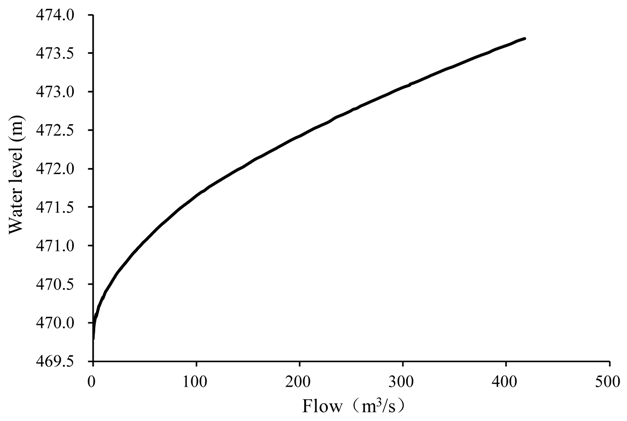 |
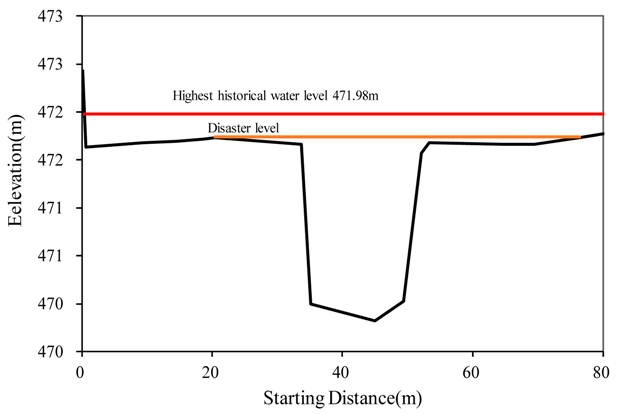 | |||||
| Sanchahe-3 | 0.045 | 0.045 | 0.035 | 42 |  |
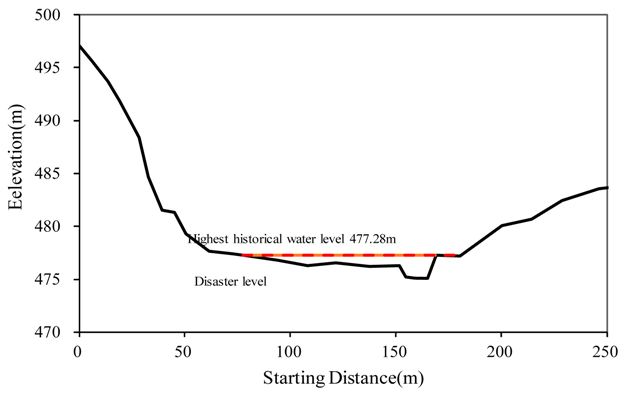 | |||||
| Prevention Object | Confluence Time (h) | Peak Flow (104 m3) | Flood Duration (h) | Flood-Peak Stage (m) | Design Peak Flow (m3/s) | ||
|---|---|---|---|---|---|---|---|
| Inference Formula | Water Level-Flow Relation | PB (%) | |||||
| Shangqing-4 | 0.5 | 4.8 | 10 | 728.75 | 18.1 | 16.19 | 10.6 |
| Xiangmo-1 | 7.4 | 339.3 | 47 | 472.84 | 170.1 | 168.66 | 0.8 |
| Sanchahe-3 | 6.3 | 323.7 | 53 | 477.76 | 266.7 | 274.02 | 2.6 |
| Reviewing Object | Early Warning Period (h) | Antecedent Precipitation Index (Wm) | Characteristic Rainfall (mm) | Updated Critical Rainfall (mm) | PB (%) | Early Warning Index (mm) | |
|---|---|---|---|---|---|---|---|
| Prepare to Transfer | Transfer Now | ||||||
| Shangqing-4 | 1 | 0.8 | 30 | 26 | 13.3 | 19 | 26 |
| Xiangmo-1 | 1 | 26 | 45 | 15.4 | 32 | 45 | |
| 2 | 28 | 59 | 7.1 | 42 | 59 | ||
| 3 | 34 | 69 | 5.8 | 51 | 69 | ||
| Sanchahe-3 | 1 | 62 | 80 | 29 | 56 | 80 | |
| 2 | 81 | 88 | 8.6 | 62 | 88 | ||
| 3 | 104 | 97 | 6.5 | 69 | 97 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Zhang, J.; Su, H.; Wang, D.; Wang, Z. Update of Early Warning Indicators of Flash Floods: A Case Study of Hunjiang District, Northeastern China. Water 2019, 11, 314. https://doi.org/10.3390/w11020314
Ma M, Zhang J, Su H, Wang D, Wang Z. Update of Early Warning Indicators of Flash Floods: A Case Study of Hunjiang District, Northeastern China. Water. 2019; 11(2):314. https://doi.org/10.3390/w11020314
Chicago/Turabian StyleMa, Meihong, Jingnan Zhang, Huidong Su, Dacheng Wang, and Zhongliang Wang. 2019. "Update of Early Warning Indicators of Flash Floods: A Case Study of Hunjiang District, Northeastern China" Water 11, no. 2: 314. https://doi.org/10.3390/w11020314
APA StyleMa, M., Zhang, J., Su, H., Wang, D., & Wang, Z. (2019). Update of Early Warning Indicators of Flash Floods: A Case Study of Hunjiang District, Northeastern China. Water, 11(2), 314. https://doi.org/10.3390/w11020314




