1. Introduction
Coastal and ocean engineering is generally under the influence of extreme wind wave, which has a high risk of damage. Extreme ocean waves belong to multidimensional random variable that is of interdependence. In recent years, with the requirement of ocean engineering structure reliability and the environmental design standard improving, extreme value distributions of single variables can no longer meet the need of researchers [
1,
2,
3,
4]. Researchers pay more and more attention to the theory of multivariate distribution [
5,
6,
7], such as the joint distributions of wave heights, wave periods, and corresponding wind speeds [
8,
9]. Actually, the damage of coastal and ocean engineering are usually the result of their combined effect. Currently, the theory of multivariate distribution has been applied in many fields [
10,
11,
12,
13,
14,
15,
16]. Many application examples have also shown that the design parameters derived from a joint probability distribution can better meet the design need of ocean engineering [
17,
18,
19,
20], reduce the building cost of ocean engineering more reasonably, explore return periods of multivariable waves, and calculate joint design level values more accurately. Additionally, all of these are of great significance for the design and risk management of related projects [
21].
Currently, the commonly used two-dimensional joint distribution models are the mixed Gumbel, bivariate Logistic, Gumbel-Logistic, and two-dimensional Pearson joint distributions. Yue [
22] used the mixed Gumbel distribution to analyze the rainstorm frequency; Zhou and Duan [
23] used Gumbel-Logistic model to analyze the joint distribution of extreme wind speed and significant wave height; Dong et al. [
24] used the two-dimensional Pearson joint distribution to analyze the joint design parameter estimation of annual extreme winds and waves. However, it is usually necessary to meet certain constraints when using these traditional joint distributions. That is, the marginal distribution model should be the same as the marginal distribution model of the traditional joint distribution [
25,
26,
27,
28,
29]. For example, the mixed Gumbel distribution requires the marginal distribution to be Gumbel distribution. In order to solve this limitation, Copula function has gradually become the focus of researchers. The Copula function describing multivariate correlation structure promotes the application of multivariate joint distribution and its risk probability in coastal and ocean engineering. Additionally, the Copula function was first proposed by Sklar [
30] in 1959, and it has been applied in many fields [
31,
32,
33,
34]. The Copula function used in constructing the two two-dimensional joint distribution is able to describe both the non-normality of a single factor (such as wave height, wind speed, water level, etc.), and the complex relationship between different wave elements. For example, the joint distribution of wind speed and wave height or wave height and period can be constructed by Archimedes Copula function that describes the joint distribution of two variables. Currently, the concept of Copula has been abstracted into theory [
35,
36,
37,
38]. The Copula function can connect multiple ocean wave elements with non-normal properties and correlation, thus constructing a joint distribution of multiple ocean wave elements. The two-dimensional joint distribution constructed by the Copula function has no strict requirements on the form of the marginal distribution. For this reason, it is more suitable for practical applications.
This paper will analyze the correlation between the annual extreme wave height and the corresponding wind speed by an engineering example, and study the joint distribution models of the two. Then, we will select Gumbel-Hougaard (GH) Copula function and Clayton Copula function, suitable for describing the annual extreme wave height and the corresponding wind speed, to establish two-dimensional joint distribution functions of the extreme wave height and the corresponding wind speed. The established distributions will be compared with the mixed Gumbel distribution and Gumbel-Logistic distribution. Finally, the joint return period analysis and conditional probability analysis of annual extreme wave height and wind speed will be carried out.
2. Common Copula Functions and Distribution Characteristics
Copula theory was first proposed by Sklar in 1959 when the relationship between low dimensional marginal distribution numbers, low dimensional marginal distribution function, and multi-dimensional joint distribution function was studied. With the concept of Copula put forward and its theory gradually improved, Nelsen [
39] made a strict definition of Copula in 1999, and presented the Sklar theorem that is important in the application of Copula theory. The Sklar theorem stated that if
F(
x,
y) is the joint distribution function of the random vector (
X,
Y), and
Fx(
x) and
Fy(y) are corresponding marginal distributions, there must be a correlation structure function
C that enables Equation (1) true.
Additionally, when the marginal distributions are continuous distribution functions, C is unique.
Gumbel-Hougaard (GH) Copula function and Clayton Copula function are two Copula functions suitable for describing the positive correlation between variables, which are widely used in the fields of ocean engineering and hydrometeorology. Its distribution function and density function are as follows:
First, the Gumbel-Hougaard (GH) Copula function:
where
u and
v are corresponding marginal distributions,
θ is the parameter of Copula function.
The corresponding density function is:
Gumbel-Hougaard (GH) Copula is only suitable for the condition in which variables are of positive correlation, and mainly describes the upper tail correlation between random variables.
Second, the Clayton Copula function:
The corresponding density function is:
Like the Gumbel-Hougaard (GH) Copula function, the Clayton Copula function is only suitable for the condition in which variables are of positive correlation, and mainly describes the lower tail correlation between random variables in the joint distribution. In addition to the above two two-dimensional Copula functions, the other two common Copula functions are as follows:
Third, Ali-Mikhail-Haq (AMH) Copula function:
The AMH function can describe the random variables with positive or negative correlation, but it is not suitable for the variables with high positive or negative correlation. AMH Copula structure is symmetrical.
Fourth, the Frank Copula function:
It is similar to AMH Copula function, but has no restriction on the degree of correlation. Frank Copula structure is of symmetry, that is, the correlation between the variables increases symmetrically at the upper tail and lower tail of its distribution.
In order to understand Copula functions intuitively, the diagrams of scatter, functions and probability functions are used to describe the distribution characteristics of the above two Copula functions.
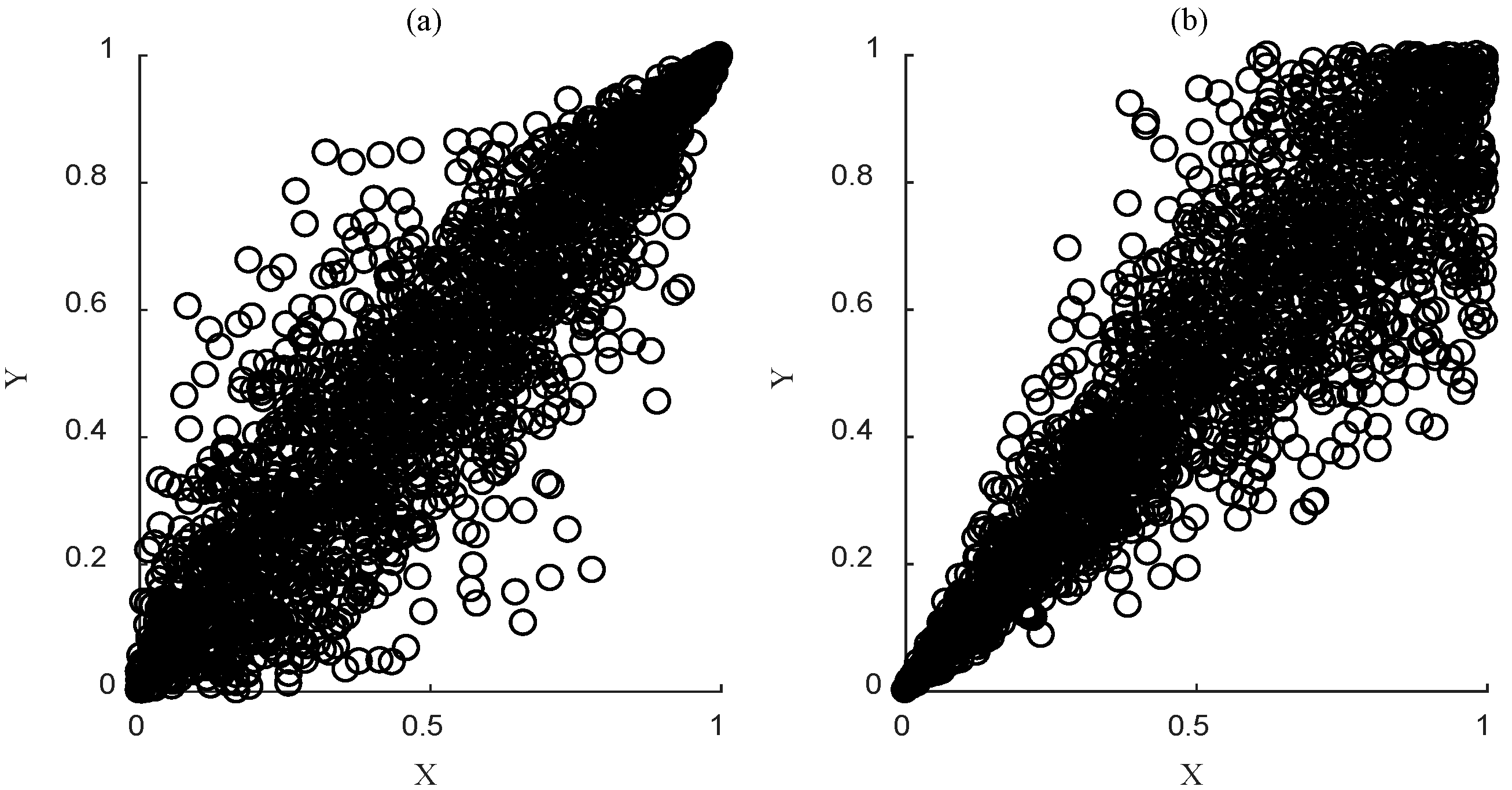
Figure 1a,b are the scatter diagrams of the Gumbel-Hougaard (GH) Copula function and the Clayton Copula function after 2000 times of stochastic simulation (the value of parameter
θ is 4 for GH Copula function, and 6 for Clayton Copula function), respectively.
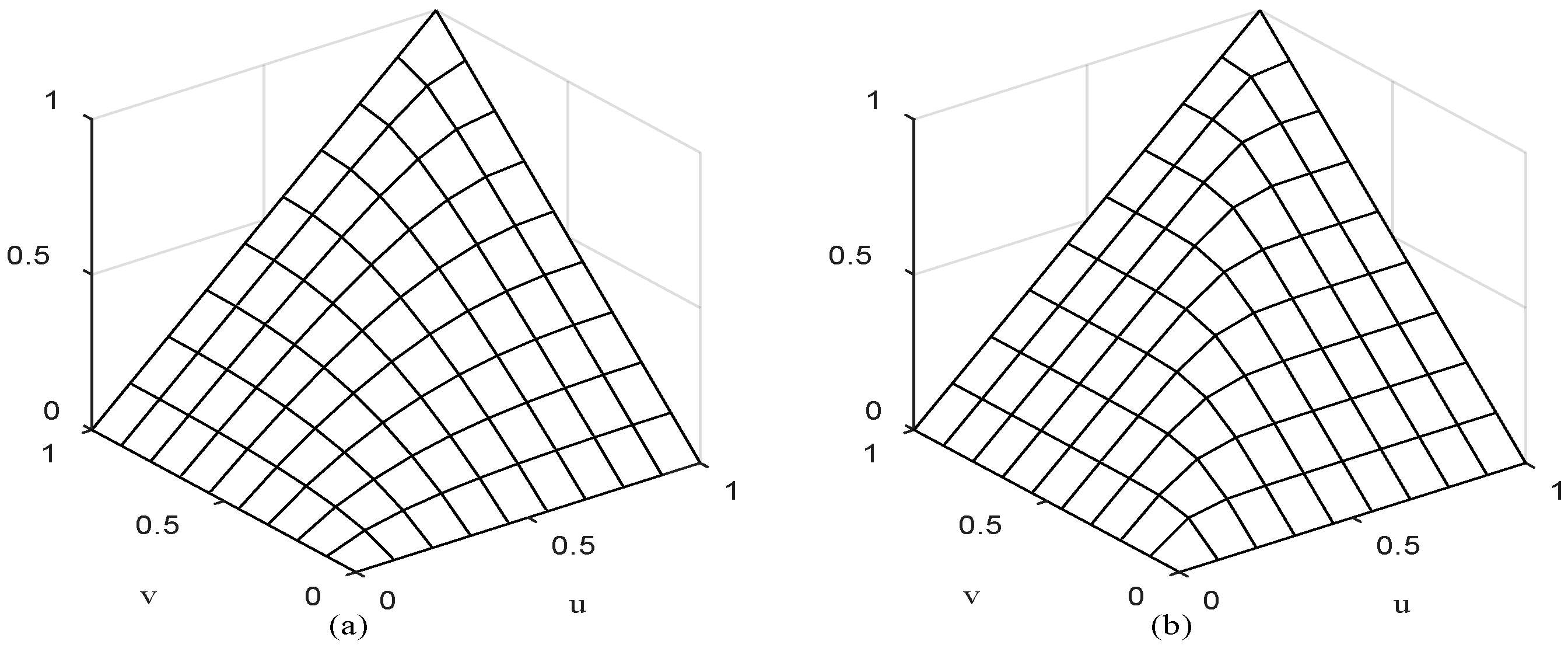
Figure 2a,b are the diagrams of the Gumbel-Hougaard (GH) Copula function when
θ is two and four, respectively.
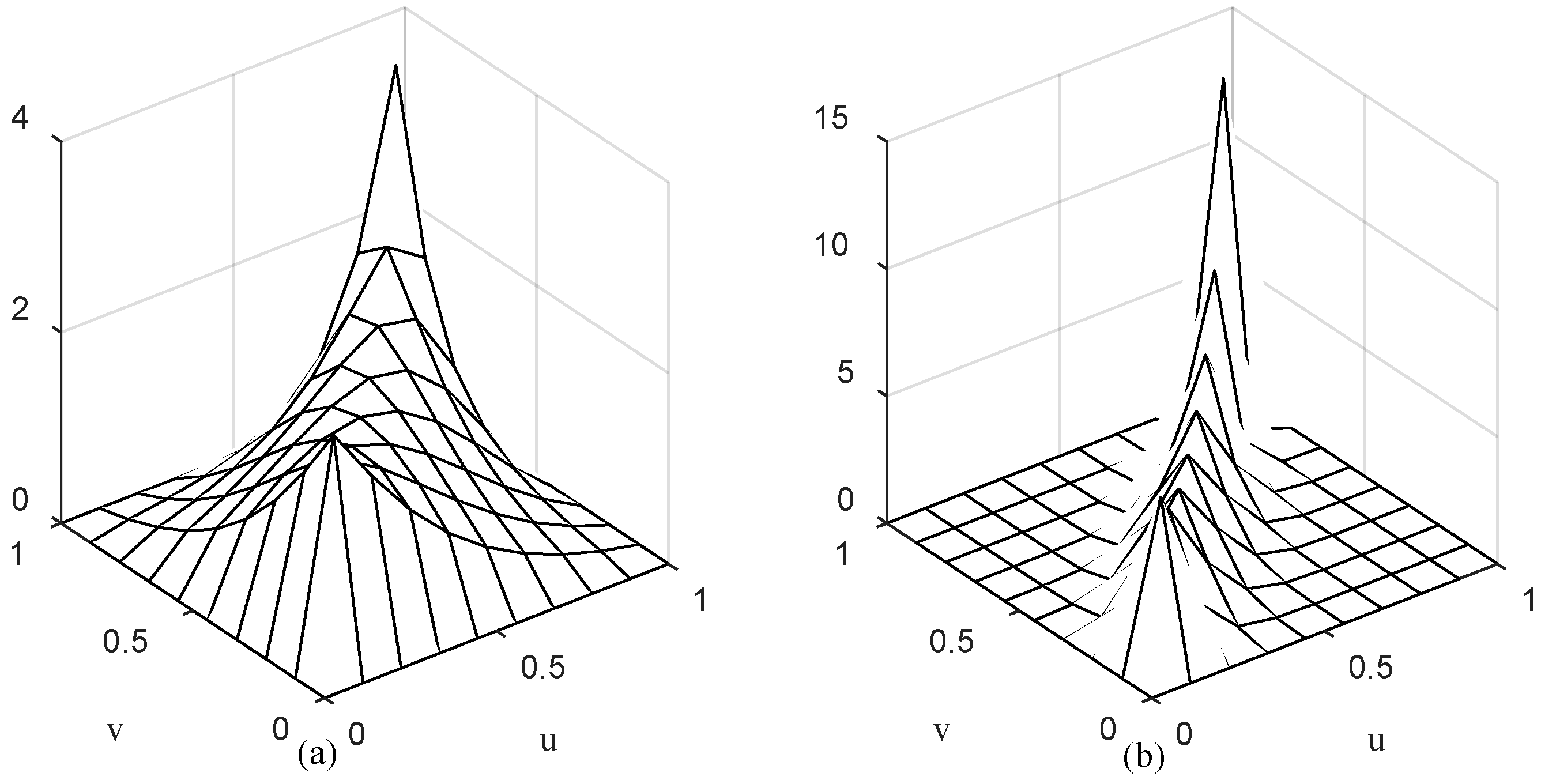
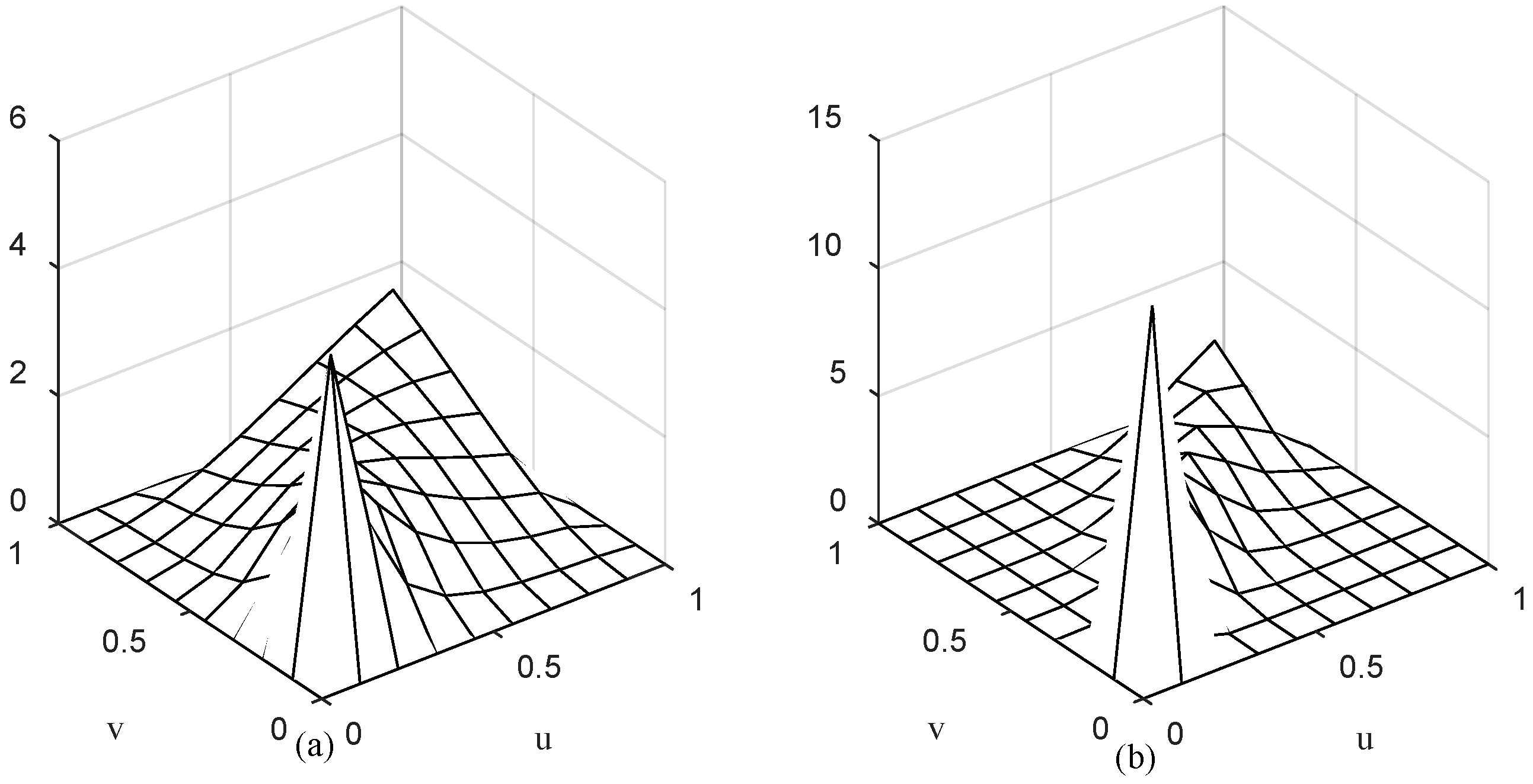
Figure 3a,b are the diagrams of the Gumbel-Hougaard (GH) Copula density function when
θ is two and four, respectively.
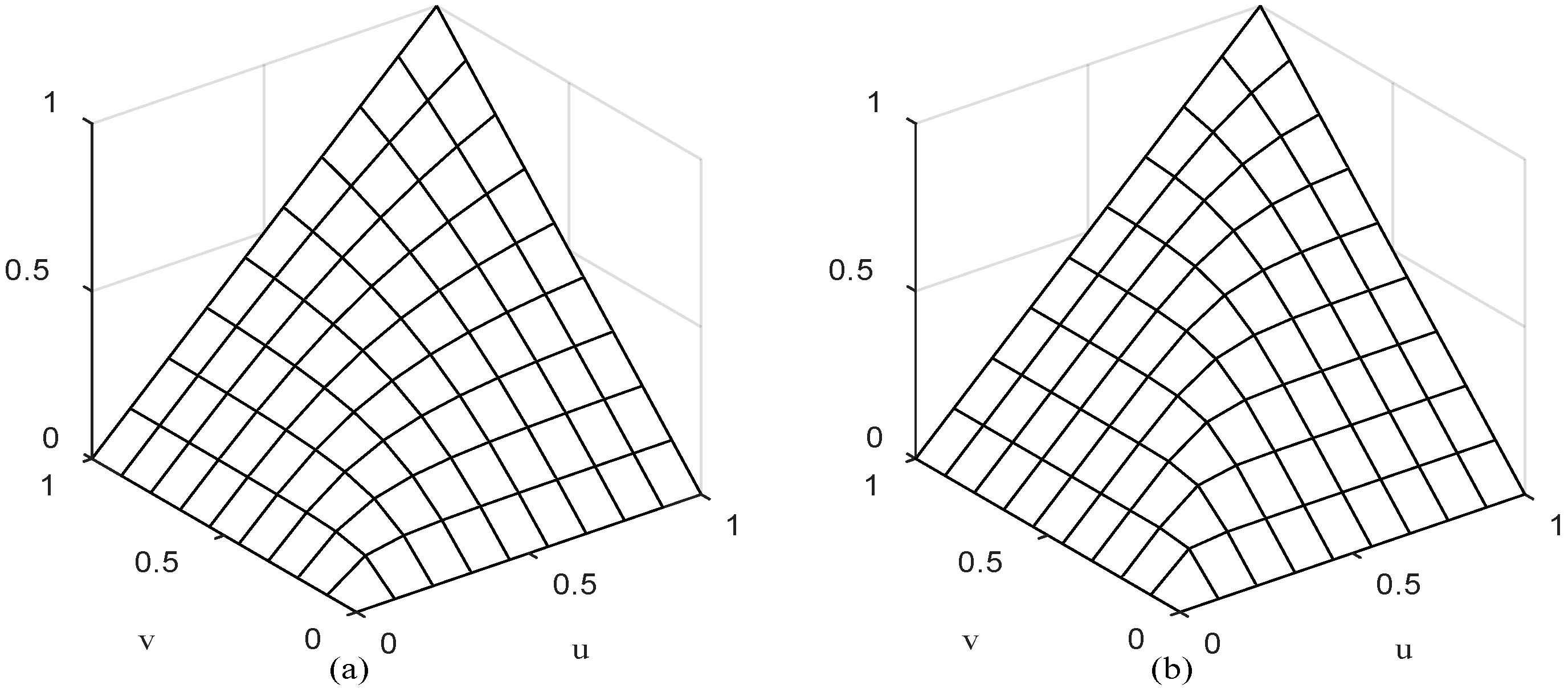
Figure 4a,b are the diagrams of the Clayton Copula function when
θ is two and four, respectively.
Figure 5a,b are the diagrams of the Clayton Copula density function when
θ is two and four, respectively.
As shown in
Figure 1, after 2000 times of stochastic simulation, the Gumbel-Hougaard (GH) Copula function shows more obvious tendency of a fat upper tail, while Clayton Copula function is more intensive in the lower tail, and scattered in the upper tail. The similar characteristics can be seen from
Figure 3 and
Figure 5. When
θ is two and four, the Gumbel-Hougaard (GH) Copula density function appears as a J-shaped distribution, namely, the upper tail is higher than the lower tail. Thus, Gumbel-Hougaard (GH) Copula function is very sensitive to the correlation of the upper tail among variables. For Clayton Copula function, the tail behavior is quite the opposite. When
θ is two and four, Clayton Copula density function tends towards an L-shaped distribution. That is, the lower tail is higher than the upper tail, and the Copula function is very sensitive to the correlation of the lower tail among variables.
3. Examples of the Application of the Copula Function
Taking the time series of the annual extreme wave height and corresponding wind speed measured at the Weizhou Island Ocean Station as an example, this paper discussed the validity of two-dimensional joint distribution constructed by Copula functions, when used in ocean engineering. Weizhou Island Ocean station (196°20′ E, 10°90′ N) is located in the South China Sea area. We used the data of the annual extreme wave heights and corresponding wind speeds during 1970–1990 as an example. Its linear correlation coefficient
ρ and rank correlation coefficient
τ are shown in
Table 1.
Table 1 shows the linear correlation coefficient of the data is 0.4992 and the rank correlation coefficient is 0.383. The linear correlation coefficient is well known, and can be expressed as,
where
xi stands for the
ith observation value of
X and
is the mean value of
X;
yi stands for the
ith observation value of
Y and
is the mean value of
Y.
It reflects the linear correlation between two random variables
X and
Y. The rank correlation coefficient is also called the relational coefficient of gradation, and its expression is:
where
di is the corresponding rank difference and
n represents the number of the data in the dataset. The rank correlation coefficient reflects the correlation between the annual extreme wave height and corresponding wind speed.
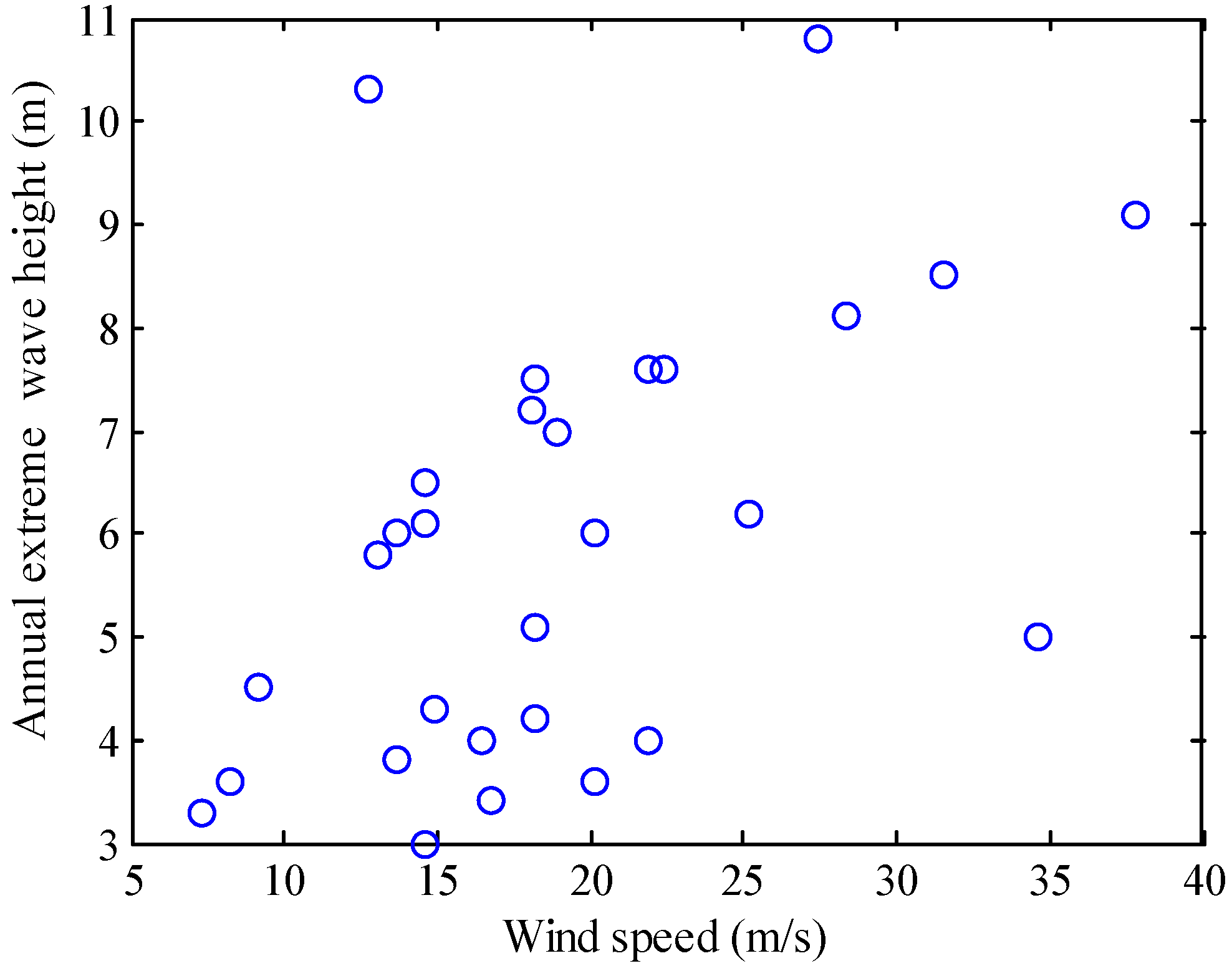
Figure 6 is a scatter plot of wind speed and annual extreme wave height. The scatter plot of the two is shown below:
Table 1 presents the correlation coefficient analysis, and results there is positive correlation between the annual extreme wave height and wind speed. Therefore, it is reasonable to use the Gumbel-Hougaard Copula function and Clayton Copula function to construct the two-dimensional joint distribution of annual extreme wave height and wind speed. As for the parameter estimation of the Copula function, the most common and concise method is the rank correlation coefficient. The rank correlation coefficient and the parameters meets:
The parameters of the above two Copula functions are easily calculated as 1.6207 and 1.2415, respectively, through the rank correlation coefficient shown in
Table 1.
To construct the two-dimensional joint distribution by Copula function, the marginal distribution need to be determined, namely, the single variable extreme distributions of annual extreme wave height and wind speed are in need of determination, respectively. The two-dimensional mixed Gumbel distribution was first proposed by Gumbel, and the Gumbel density function and distribution function of its marginal distribution are:
where
x stands for the observation value,
σ and
μ are two undetermined parameters,
f(
x;
μ,
σ) is the Gumbel density function and
F(
x;
μ,
σ) is the Gumbel distribution function.
Two-dimensional mixed Gumbel joint probability density function (PDF) and distribution function (CDF) are expressed as follows:
where
and
ρ is linear correlation coefficient:
where
c,
d,
σ1 and
σ2 are four undetermined parameters,
g(
x,
y) is two-dimensional mixed Gumbel joint probability density function and
G(
x,
y) is the corresponding distribution function.
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
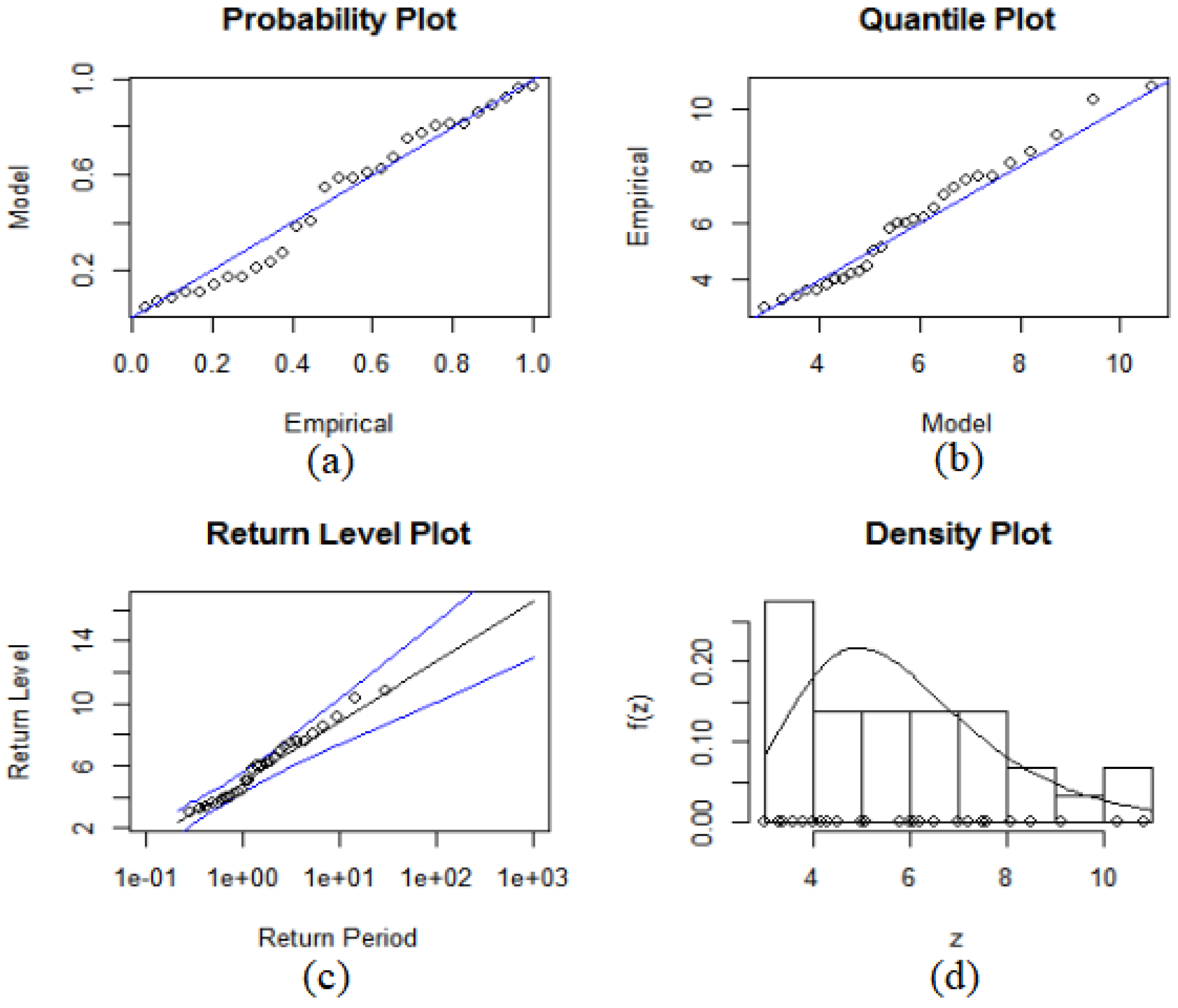
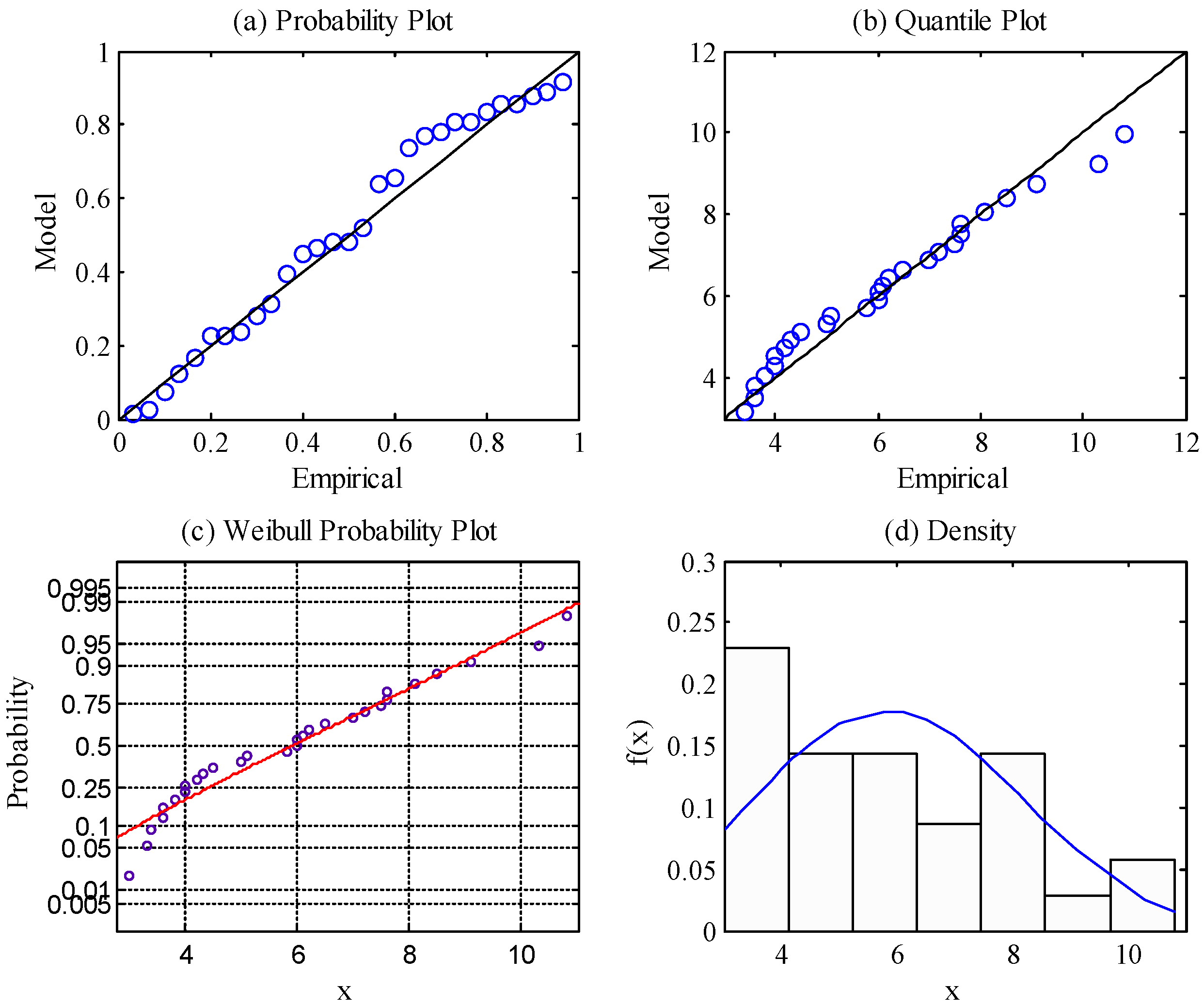
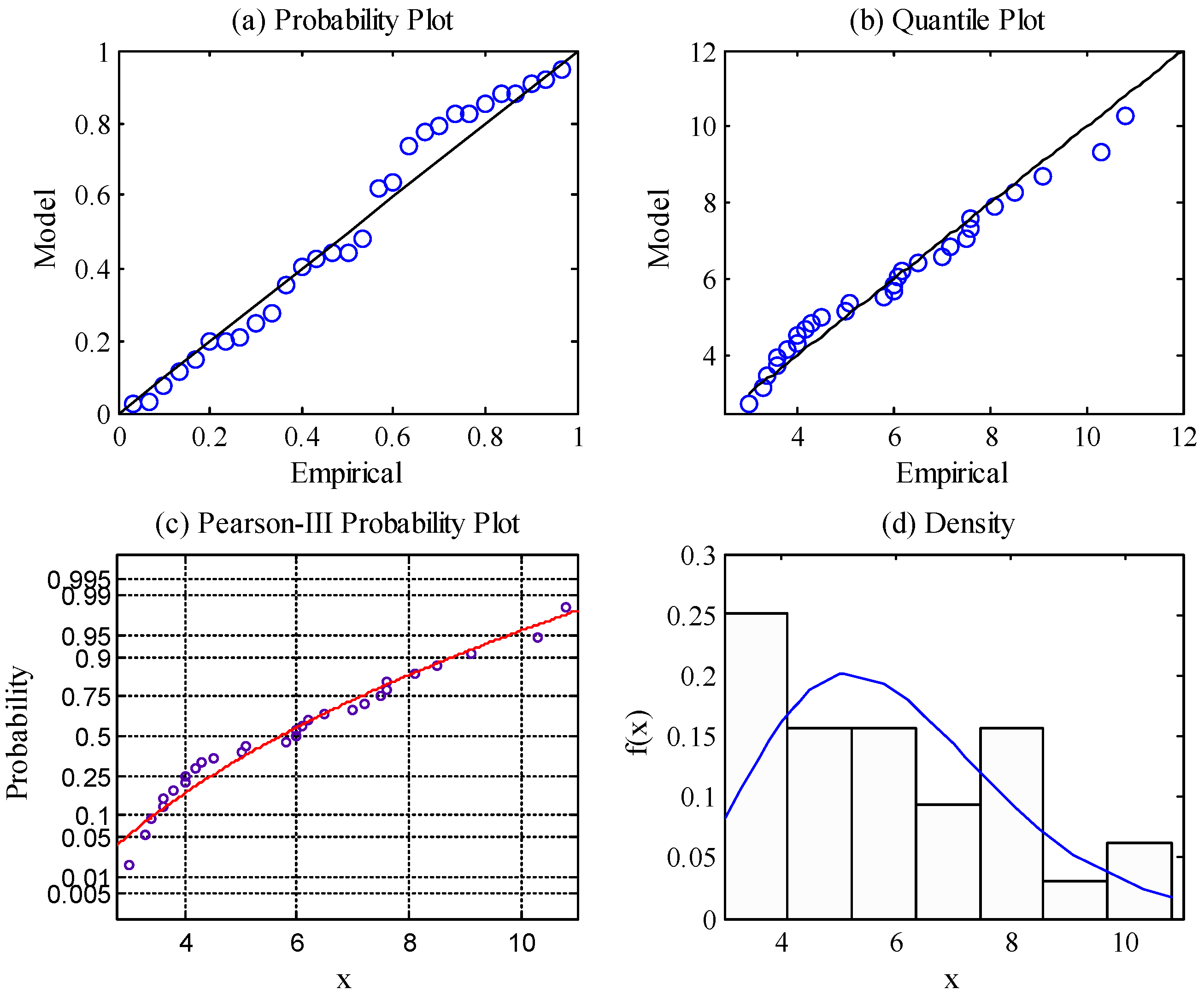
Figure 12 show diagnostic tests including charts of probability, quantile, and return level (or a probability distribution plot) and a density histogram when using the Gumbel, Weibull, and Pearson-III distributions fitting of the annual extreme wave height and wind speed. The circles in the figures represent data points and solid lines that represent model curves.
The results of the corresponding diagnostic tests show that the annual extreme wave height and wind speed observation data comply with the Gumbel, Weibull, and Pearson-III distributions, and thus, the data can be used as analysis samples of the corresponding extreme value distribution.
Table 2 and
Table 3 present interval estimates of the 95% confidence levels when using the Gumbel, Weibull, and Pearson-III distributions fitting of the annual extreme wave height and wind speed.
As shown in
Table 2 and
Table 3, it can be seen that, when the maximum entropy distribution is used to describe the annual extreme wave height, the P-Value is the maximum. Additionally, when describing the wind speed with Gumbel distribution, the P-Value is the maximum. Therefore, it is most appropriate to use the maximum entropy distribution to describe the annual extreme wave height, and use Gumbel distribution to describe the wind speed.
According to this, the two-dimensional joint distribution functions constructed by Gumbel-Hougaard Copula function and Clayton Copula function can be obtained. The joint distribution functions are as follows:
When the joint distribution of annual extreme wave height and wind speed is described with the mixed Gumbel distribution and Gumbel-Logistic distribution as well as Equations (14) and (15), three-dimensional contour plot of the corresponding distribution function is shown in
Figure 13. The corresponding two-dimensional contour plot is shown in
Figure 14.
As shown in
Figure 13, it can be seen that the shape of the four distribution function plots has little difference. Considering that mixed Gumbel and Gumbel-logistic distributions have been applied many times to different hydrological probabilistic analysis, the two established joint distributions based on Copula functions are similar to them, which are of a certain practical value in engineering application as well.
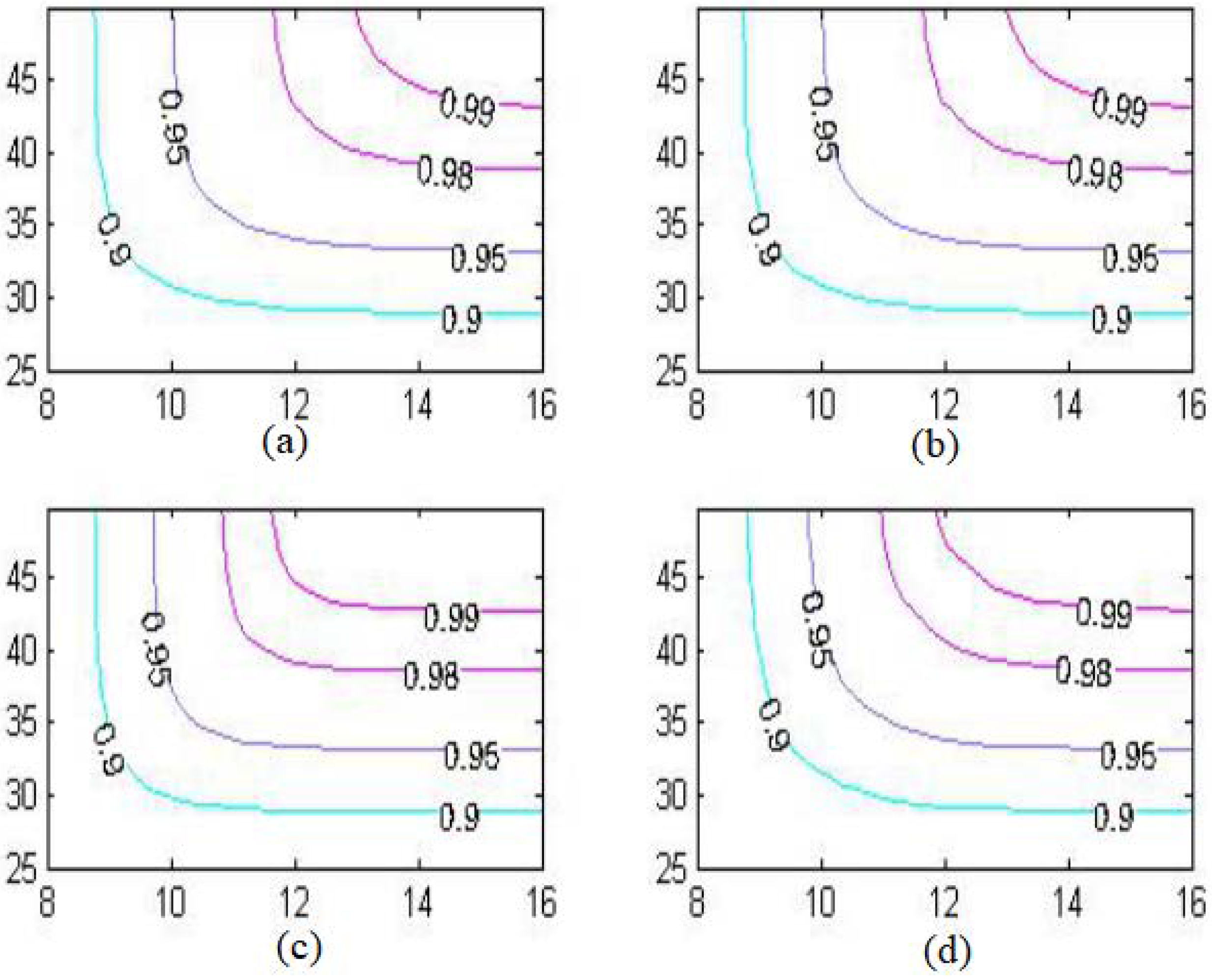
Figure 14 shows a certain difference, especially when the joint probability exceeds 0.95, there are some differences between their contour. The mixed Gumbel distribution and Gumbel-Logistic distributions are steeper than the two distributions based on the Gumbel-Hougaard Copula function and Clayton Copula function. That means that when comparing with the established joint distributions, the traditional joint distributions can not fit the tail data very well. Namely, the multiyear return values calculated by the traditional joint distributions will be slightly larger. In the actual projects, the design parameters in the traditional joint distributions will bring a lot of unnecessary economic cost, and that the newly established joint distributions will be more reasonable and directly improve the economic benefits of projects.
4. The Joint Return Period Analysis
When analyzing two wave elements, we usually pay attention to the following two events, {
X >
x} and {
Y >
y}. Therefore, the joint return period can be defined as:
When the joint distribution of annual extreme wave height and wind speed is described with the mixed Gumbel distribution and Gumbel-Logistic distribution, as well as Equations (14) and (15), the multiyear design value and its joint return period of a single factor can be calculated, respectively.
Table 4,
Table 5,
Table 6 and
Table 7 shows them, respectively.
Table 4,
Table 5,
Table 6 and
Table 7 present the joint return period calculated by the above four joint distributions, respectively, with the design wave height values and design wind speed values in 100, 200, 500, and 1000 year return periods. Obviously, the joint return periods of annual extreme wave height and wind speed are larger than that of single variable. The joint return periods calculated by the joint distributions that was constructed by the Gumbel-Hougaard Copula function and Clayton Copula function are lower than that calculated by the mixed Gumbel distribution and the Gumbel-Logistic distribution. In terms of the conservation of ocean engineering construction, the joint distribution of the Gumbel-Hougaard Copula function and Clayton Copula function are more reasonable.
After constructing the joint distribution of annual extreme wave height and wind speed with the Copula function, some design criteria for ocean engineering can be determined through joint return period analysis and conditional probability analysis. This provides a theoretical basis for the construction of ocean engineering, which can well control the construction cost of ocean engineering and ensure its safety in theory.