Effects of Different Spatial Configuration Units for the Spatial Optimization of Watershed Best Management Practice Scenarios
Abstract
:1. Introduction
2. Materials and Methods
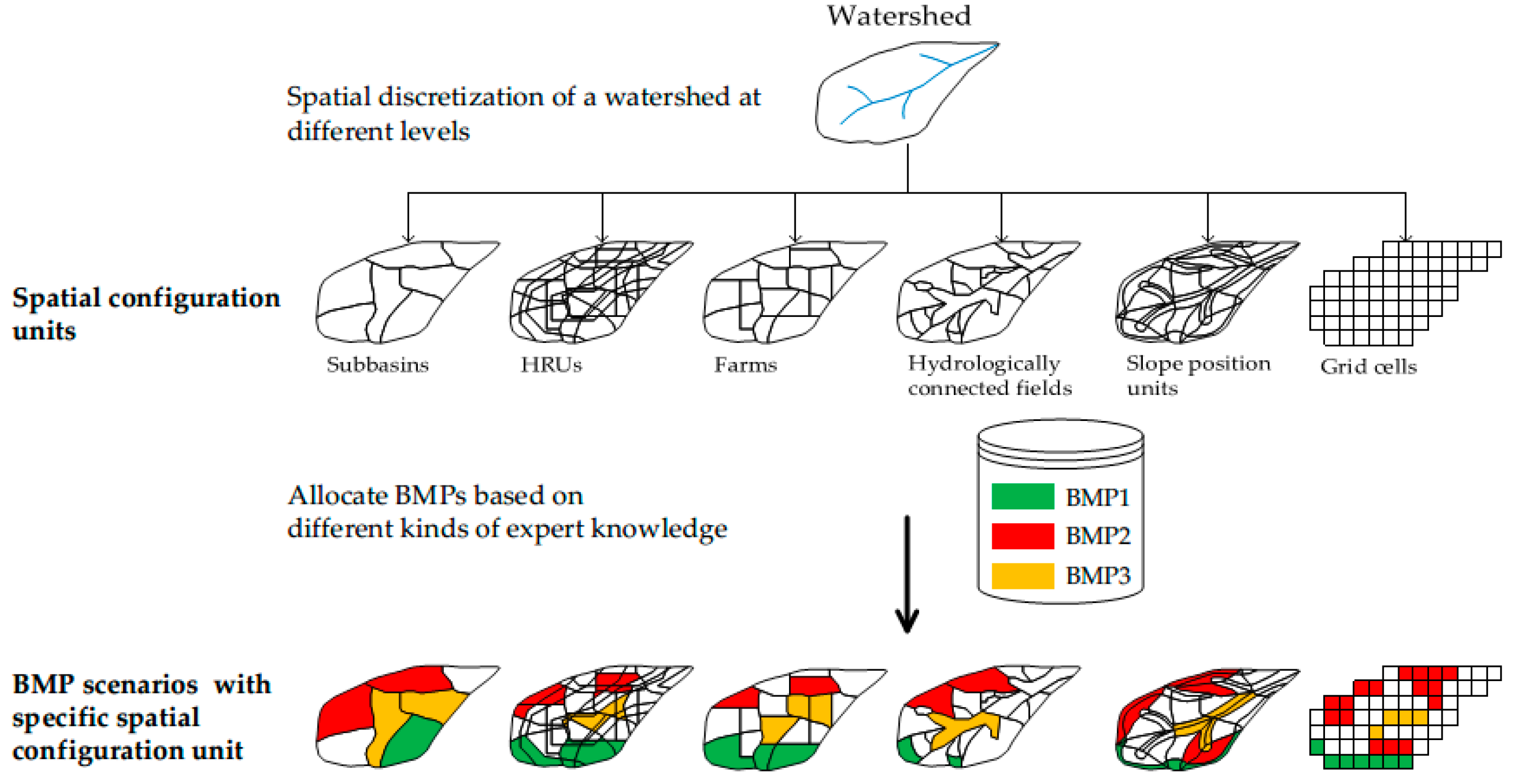
2.1. Methodology
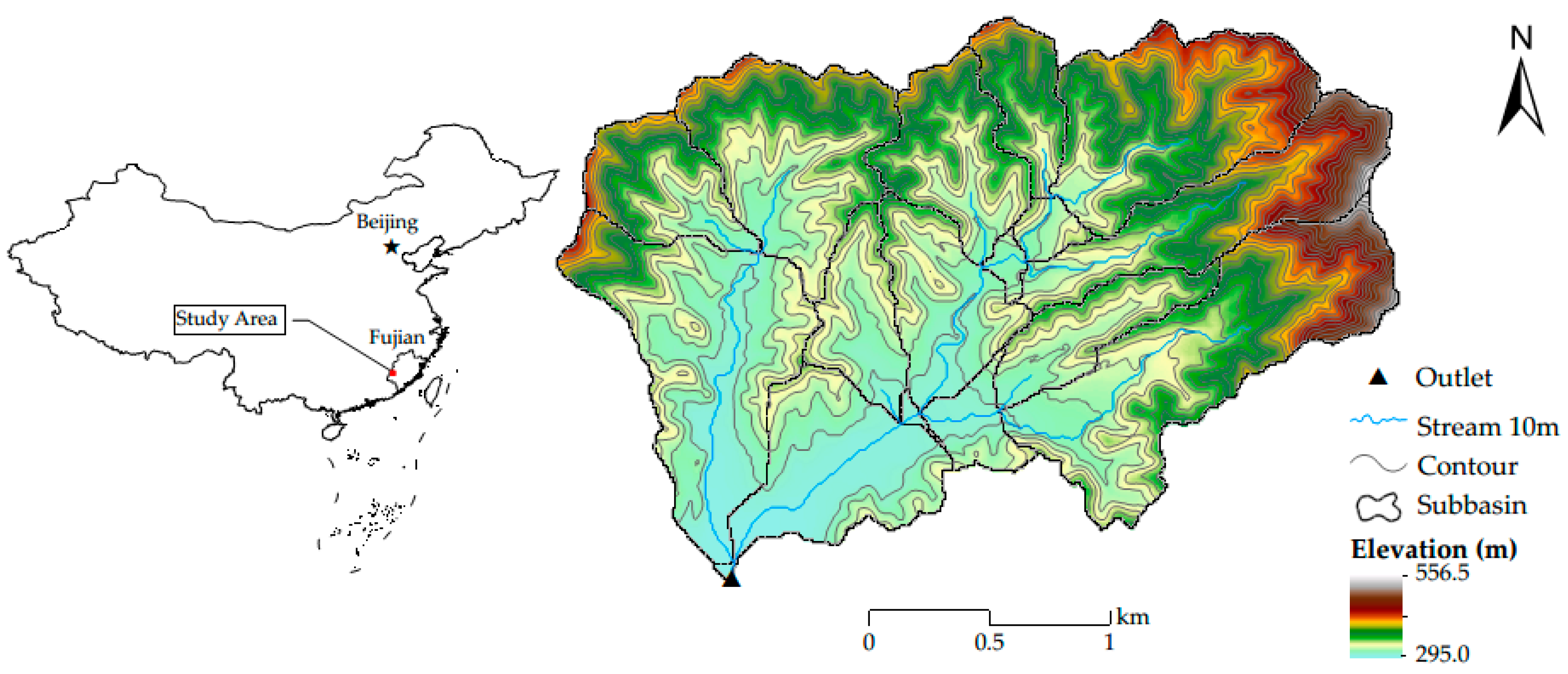
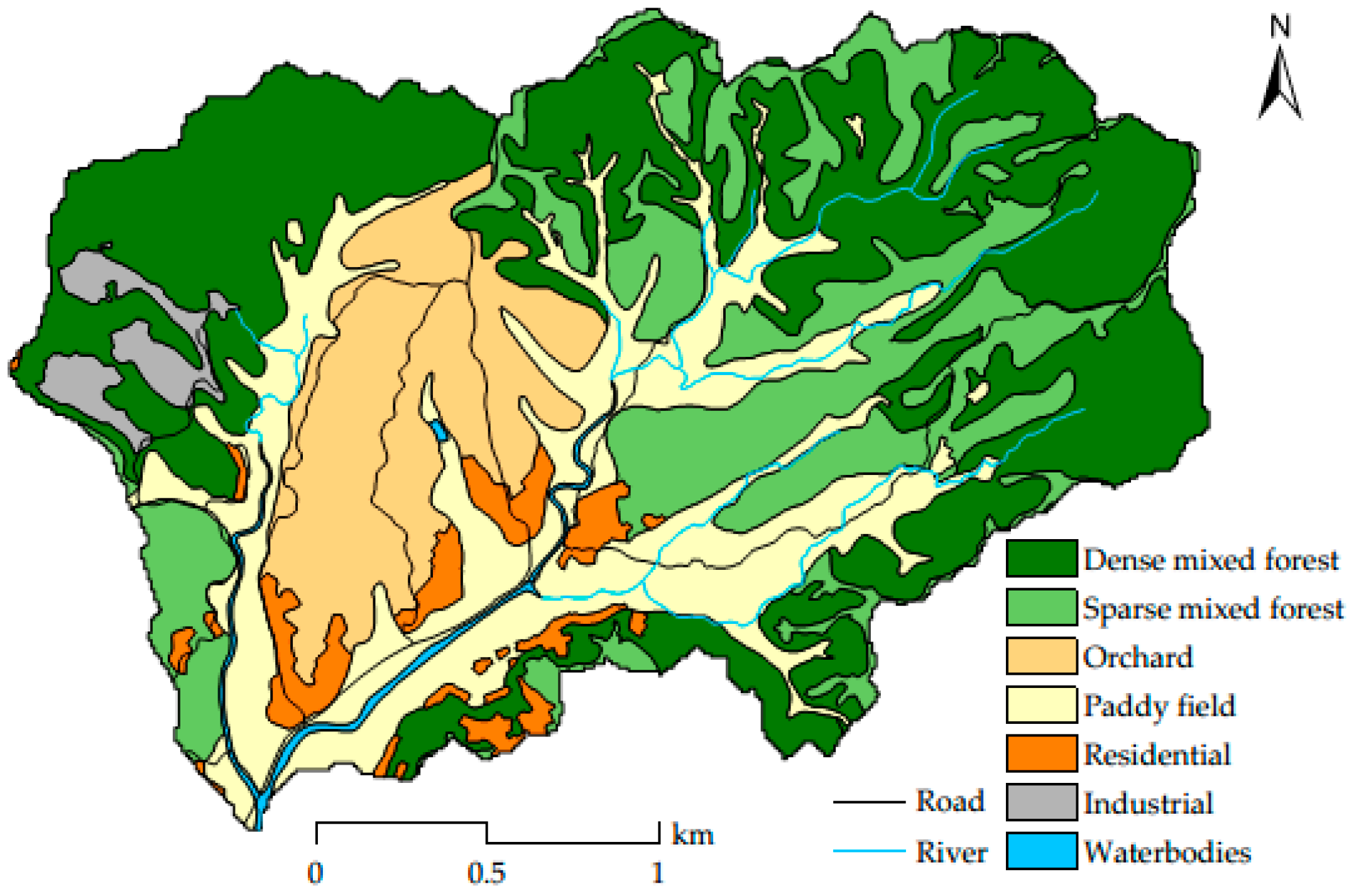
2.2. Study Area and Dataset
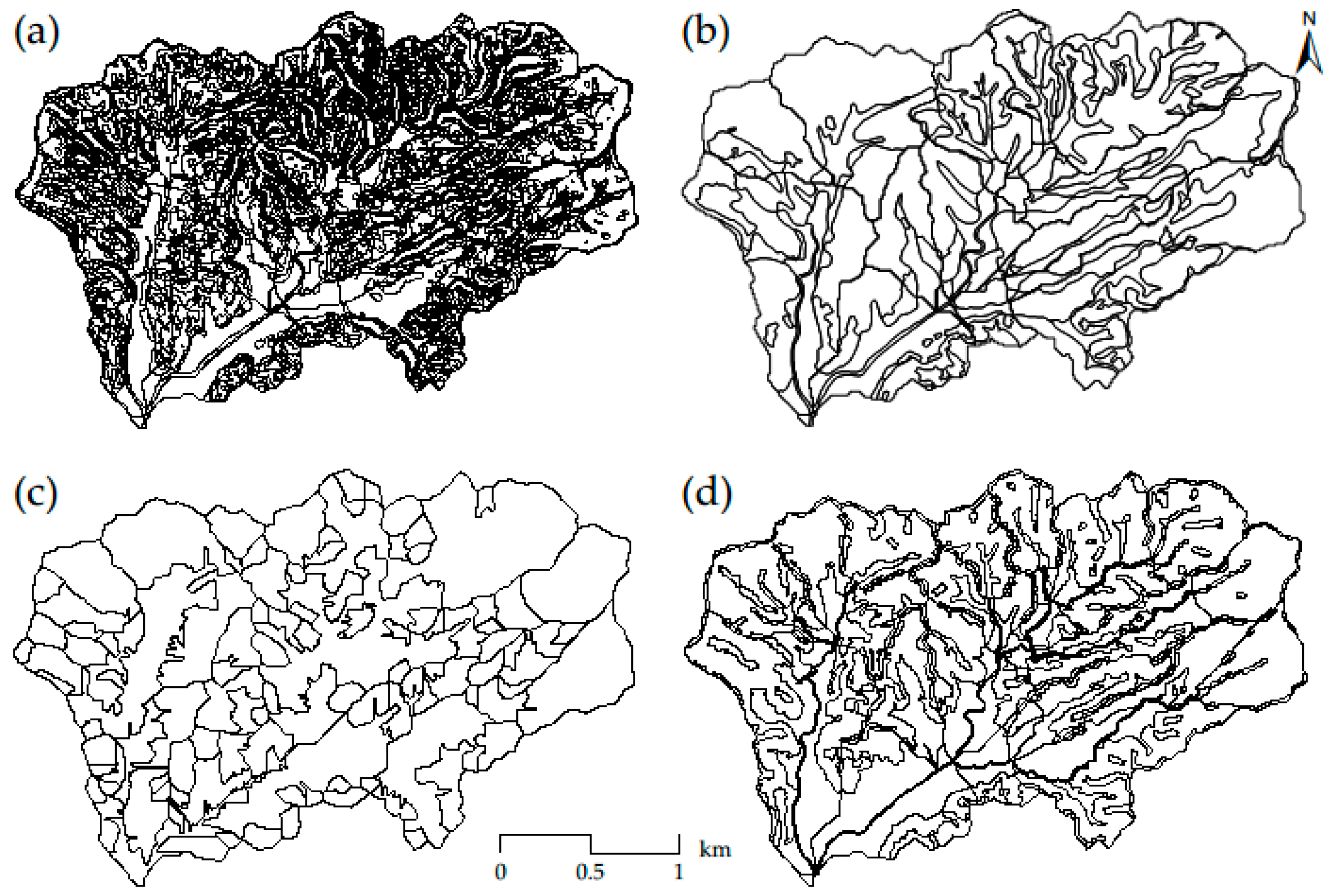
2.3. Delineation of BMP Configuration Units
2.3.1. HRUs
2.3.2. Spatially Explicit HRUs
2.3.3. Hydrologically Connected Fields
2.3.4. Slope Position Units
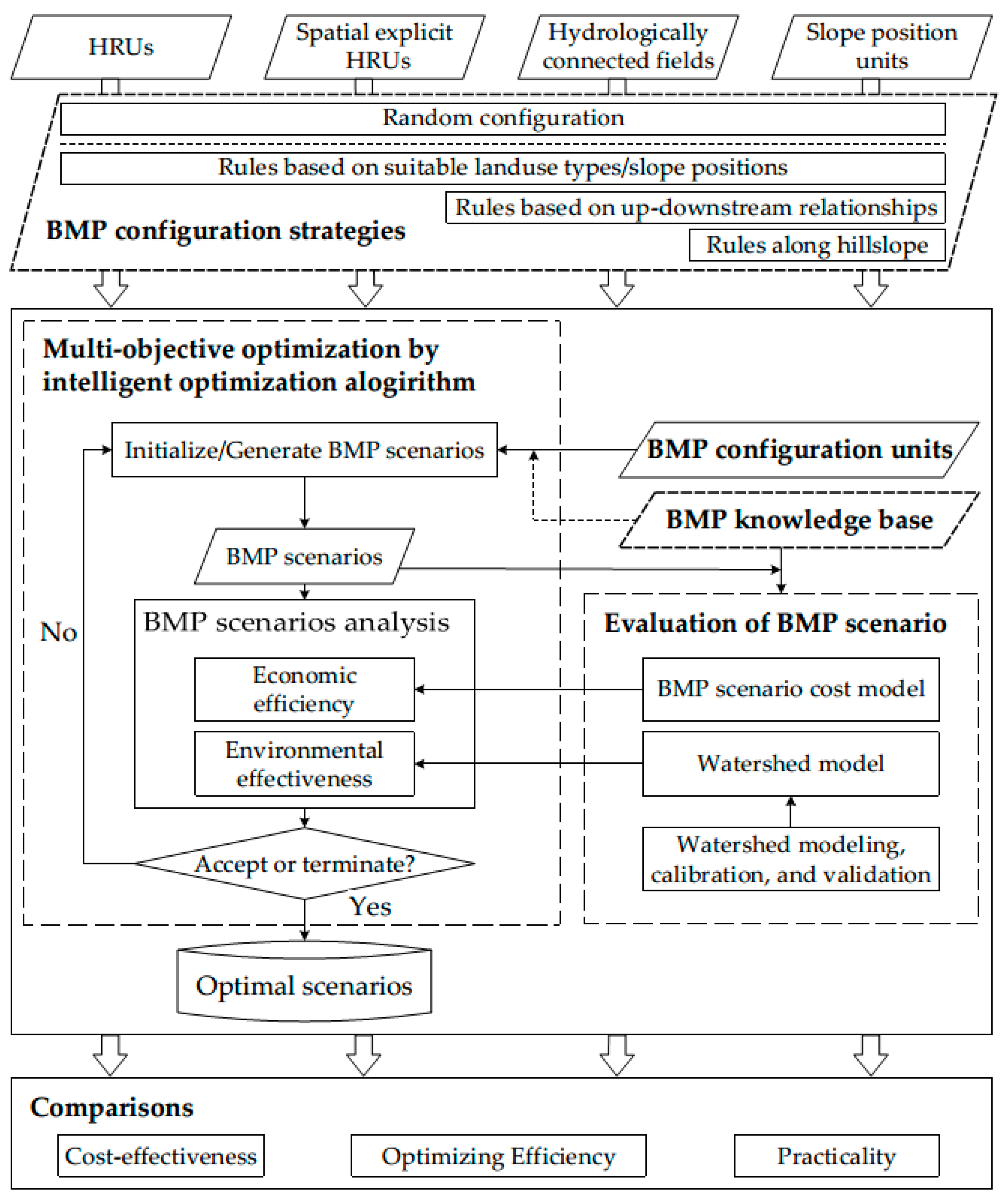
2.4. BMP Knowledge Base and BMP Configuration Strategies
- Random configuration strategy (RAND for short). Without knowledge used, the RAND strategy randomly selects and allocates one of the four BMPs on the BMP configuration units. Thus, it can be used for any type of BMP configuration unit considered in this study.
- Strategy with knowledge on the suitable landuse types/slope positions of individual BMPs (SUIT for short). The SUIT strategy is to randomly select and allocate one of the suitable BMPs according to its suitable landuse type and/or slope position to the BMP configuration unit. This strategy is applicable for any BMP configuration units with landuse type and/or slope position type.
- Strategy based on expert knowledge of upstream–downstream relationships [5] (UPDOWN for short). Extended from the SUIT strategy, the UPDOWN strategy applies the expert rules of BMP interactions (“if–then” rules) based on the upstream–downstream relationships between BMP configuration units to generating BMP scenarios. That is, if a field has been configured with one BMP, its adjacent upstream fields should not be configured with a BMP; otherwise the BMP will be randomly selected and configured on the adjacent upstream fields according to their landuse types. This strategy is available for hydrologically connected fields and slope position units.
- Strategy with expert knowledge on the spatial relationships between BMPs and slope positions along the hillslope [2] (HILLSLP for short). The HILLSLP strategy further extends the SUIT strategy to consider spatial constraints among BMPs on different slope positions along the hillslope from upstream to downstream. Such expert knowledge used in this study was adapted from Qin et al. [2], i.e., the effectiveness grade of the BMP configured on the downstream unit of a hillslope should be greater than or equal to that of the BMP configured on the upstream unit of the same hillslope. For example, according to the knowledge in Table 3, if the backslope unit has been configured with ABHMP, the downstream valley unit of the same hillslope may be configured with ABHMP or without BMP, while the upstream ridge unit has three configuration options (i.e., CM, ABHMP, and without BMP).
2.5. Watershed Model and BMP Scenario Cost Model
2.6. Multi-Objective Optimization by an Intelligent Optimization Algorithm
2.7. Design of Comparison Experiment
3. Results
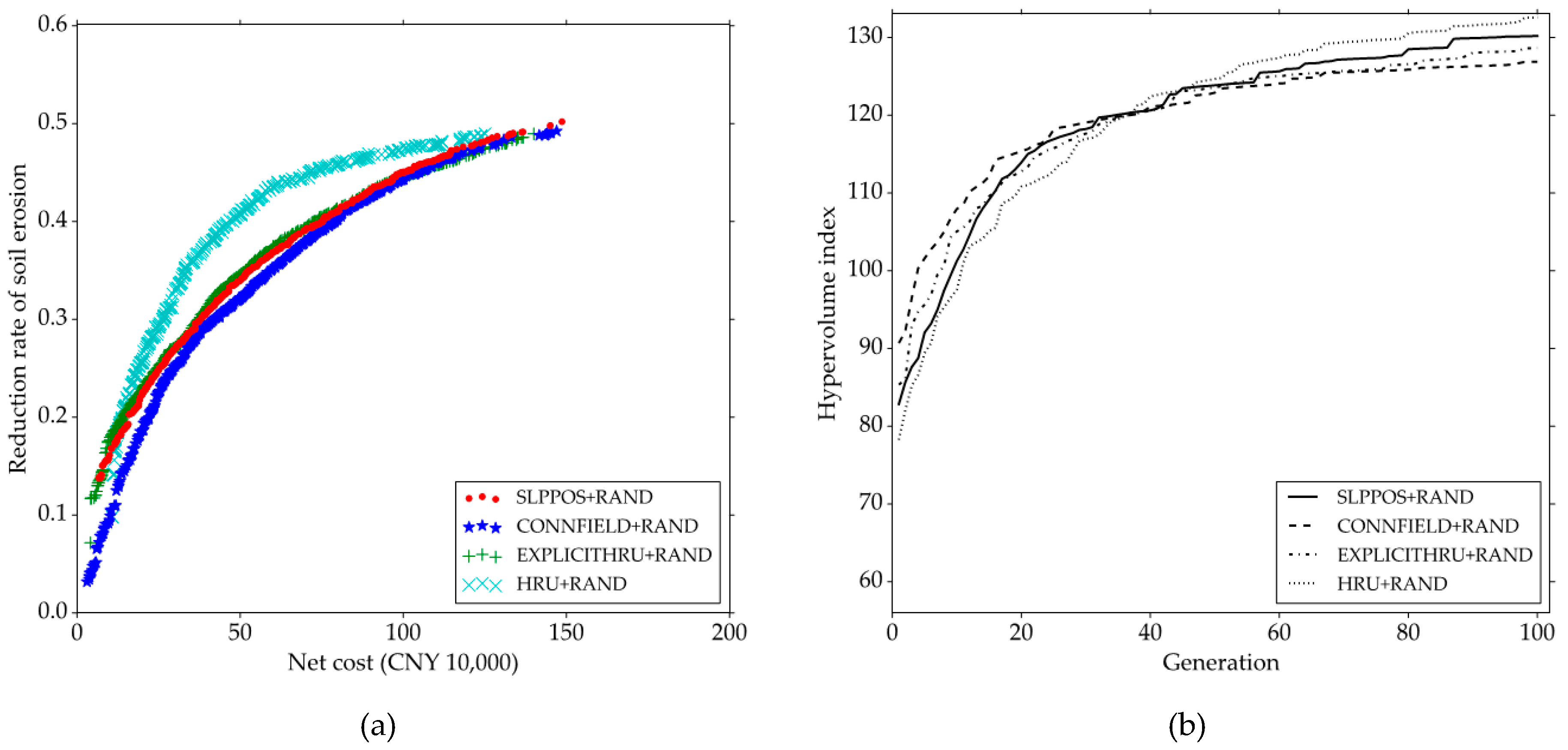
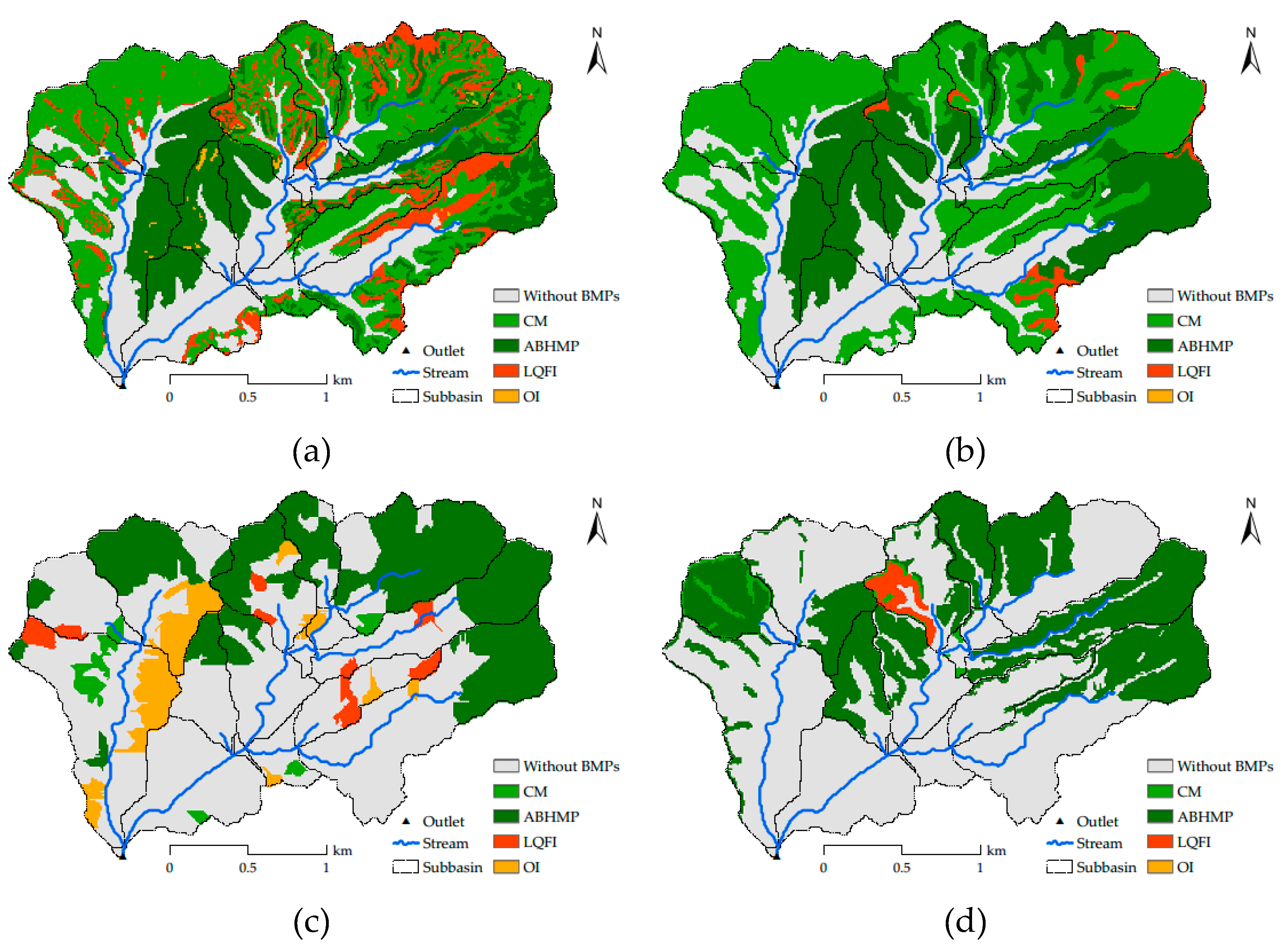
3.1. Comparison among Different BMP Configuration Units with the RAND Strategy
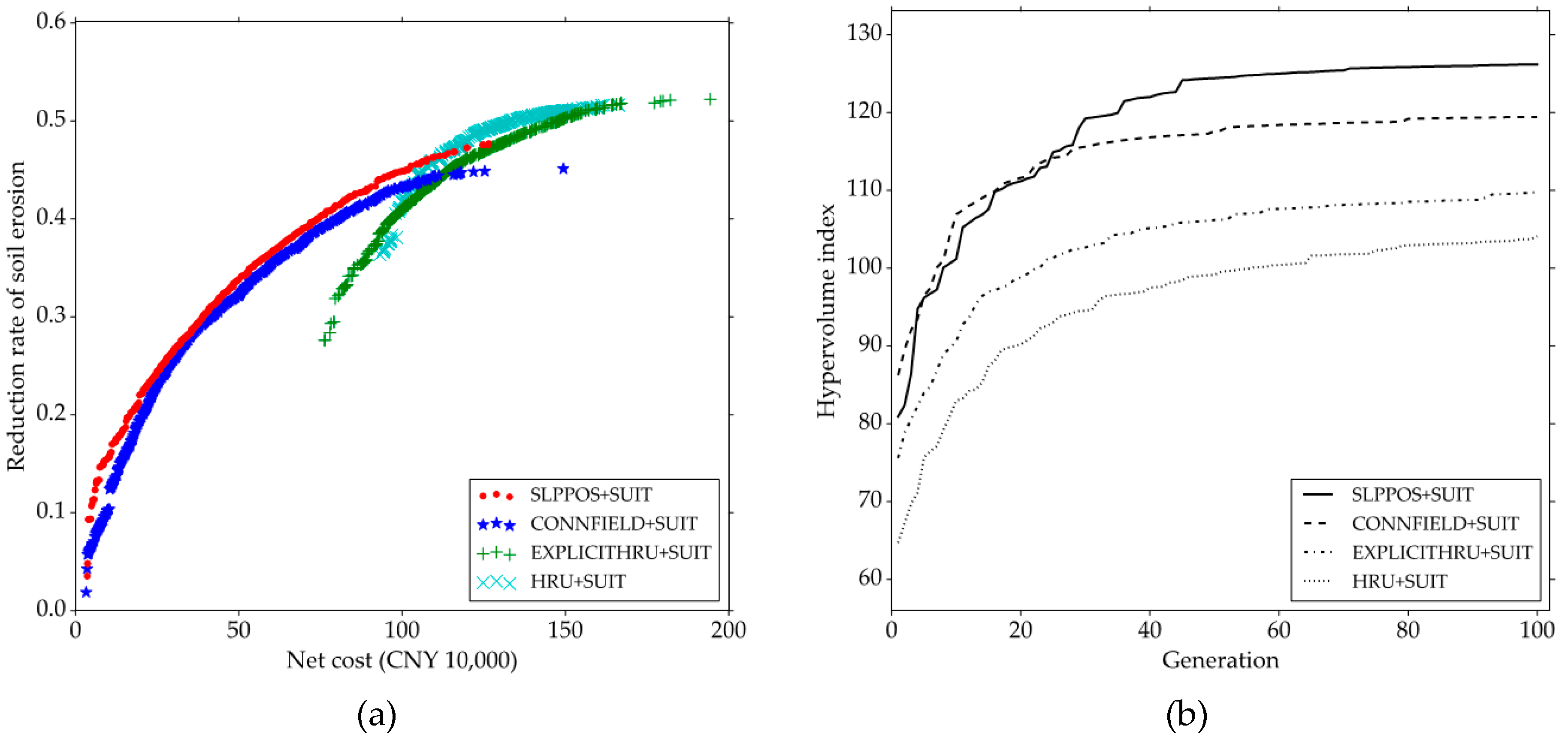
3.2. Comparison among Different BMP Configuration Units with the SUIT Strategy
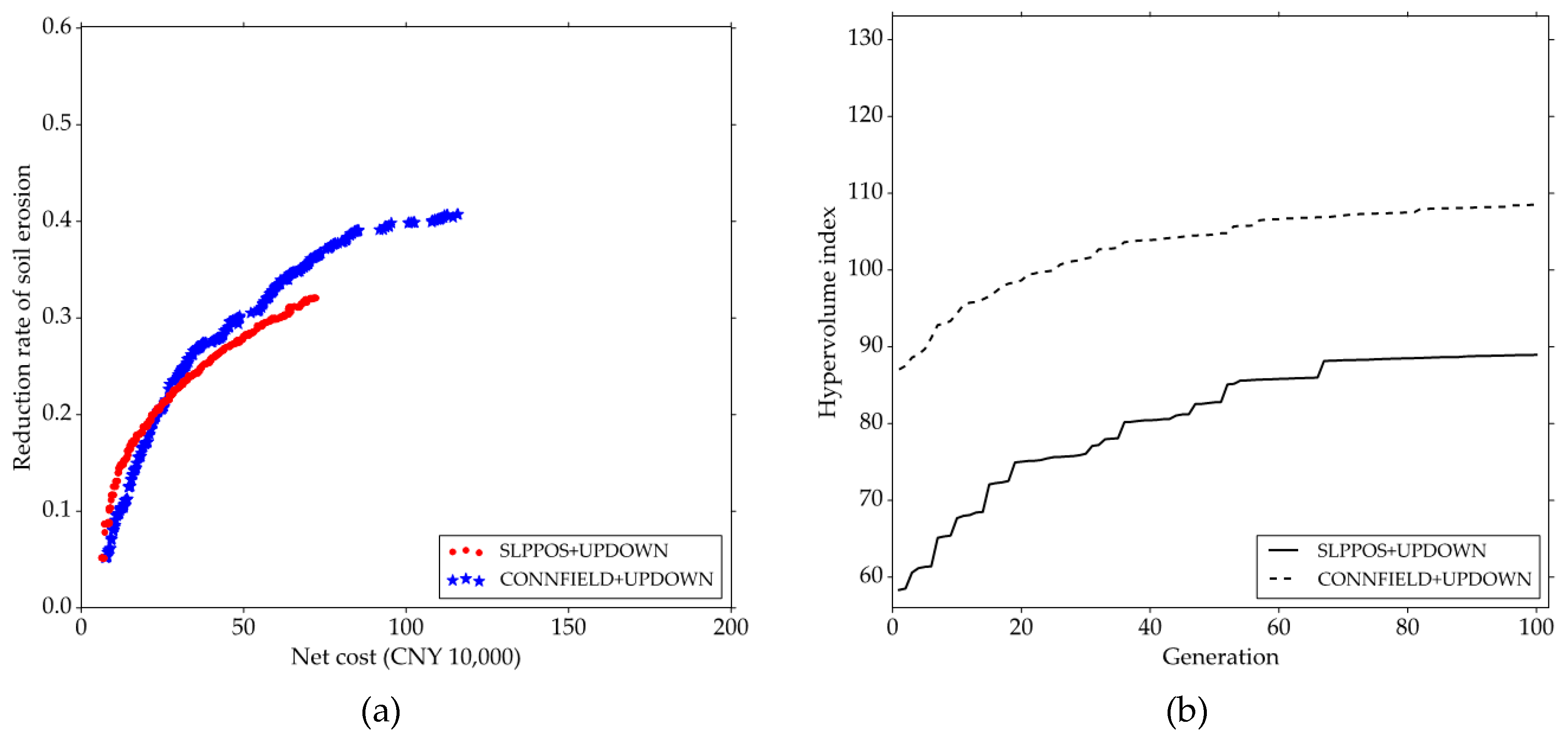
3.3. Comparison between Feasible BMP Configuration Units with the UPDOWN Strategy
3.4. Comparison among Different BMP Configuration Units with the Corresponding Optimal Configuration Strategies
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kalcic, M.M.; Frankenberger, J.; Chaubey, I. Spatial Optimization of Six Conservation Practices Using Swat in Tile-Drained Agricultural Watersheds. J. Am. Water Resour. Assoc. JAWRA 2015, 51, 956–972. [Google Scholar] [CrossRef]
- Qin, C.-Z.; Gao, H.-R.; Zhu, L.-J.; Zhu, A.-X.; Liu, J.-Z.; Wu, H. Spatial optimization of watershed best management practices based on slope position units. J. Soil Water Conserv. 2018, 73, 504–517. [Google Scholar] [CrossRef]
- Sahu, M.; Gu, R.R. Modeling the effects of riparian buffer zone and contour strips on stream water quality. Ecol. Eng. 2009, 35, 1167–1177. [Google Scholar] [CrossRef]
- Veith, T.L.; Wolfe, M.L.; Heatwole, C.D. Optimization Procedure for Cost Effective Bmp Placement at a Watershed Scale. J. Am. Water Resour. Assoc. JAWRA 2003, 39, 1331–1343. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, A.-X.; Liu, J.; Liu, Y.; Jiang, J. Best Management Practices Optimization at Watershed Scale: Incorporating Spatial Topology among Fields. Water Resour. Manag. 2018, 32, 155–177. [Google Scholar] [CrossRef]
- Wang, X.; Amonett, C.; Williams, J.R.; Wilcox, B.P.; Fox, W.E.; Tu, M.-C. Rangeland watershed study using the Agricultural Policy/Environmental eXtender. J. Soil Water Conserv. 2014, 69, 197–212. [Google Scholar] [CrossRef]
- Duriancik, L.F.; Bucks, D.; Dobrowolski, J.P.; Drewes, T.; Eckles, S.D.; Jolley, L.; Kellogg, R.L.; Lund, D.; Makuch, J.R.; O’Neill, M.P. The first five years of the Conservation Effects Assessment Project. J. Soil Water Conserv. 2008, 63, 185A–197A. [Google Scholar] [CrossRef]
- Turpin, N.; Bontems, P.; Rotillon, G.; Bärlund, I.; Kaljonen, M.; Tattari, S.; Feichtinger, F.; Strauss, P.; Haverkamp, R.; Garnier, M.; et al. AgriBMPWater: Systems approach to environmentally acceptable farming. Environ. Model. Softw. 2005, 20, 187–196. [Google Scholar] [CrossRef]
- Xie, H.; Chen, L.; Shen, Z.; Xie, H.; Chen, L.; Shen, Z. Assessment of Agricultural Best Management Practices Using Models: Current Issues and Future Perspectives. Water 2015, 7, 1088–1108. [Google Scholar] [CrossRef]
- Arabi, M.; Govindaraju, R.S.; Hantush, M.M. Cost-effective allocation of watershed management practices using a genetic algorithm. Water Resour. Res. 2006, 42, W10429. [Google Scholar] [CrossRef]
- Gitau, M.W.; Veith, T.L.; Gburek, W.J. Farm-level optimization of BMP placement for cost-effective pollution reduction. Trans. ASAE 2004, 47, 1923–1931. [Google Scholar] [CrossRef]
- Maringanti, C.; Chaubey, I.; Arabi, M.; Engel, B. Application of a multi-objective optimization method to provide least cost alternatives for NPS pollution control. Environ. Manag. 2011, 48, 448–461. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, P.; Hamlett, J.M.; Robillard, P.D.; Day, R.L. Watershed optimization of best management practices using AnnAGNPS and a genetic algorithm. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Chang, C.L.; Chiueh, P.T.; Lo, S.L. Effect of spatial variability of storm on the optimal placement of best management practices (BMPs). Environ. Monit. Assess. 2007, 135, 383–389. [Google Scholar] [CrossRef] [PubMed]
- Chichakly, K.J.; Bowden, W.B.; Eppstein, M.J. Minimization of cost, sediment load, and sensitivity to climate change in a watershed management application. Environ. Model. Softw. 2013, 50, 158–168. [Google Scholar] [CrossRef]
- Qiu, J.; Shen, Z.; Huang, M.; Zhang, X. Exploring effective best management practices in the Miyun reservoir watershed, China. Ecol. Eng. 2018, 123, 30–42. [Google Scholar] [CrossRef]
- Yang, G.X.; Best, E.P.H. Spatial optimization of watershed management practices for nitrogen load reduction using a modeling-optimization framework. J. Environ. Manag. 2015, 161, 252–260. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Makropoulos, C.; Mimikou, M. Decision support for diffuse pollution management. Environ. Model. Softw. 2012, 30, 57–70. [Google Scholar] [CrossRef]
- Rodriguez, H.G.; Popp, J.; Maringanti, C.; Chaubey, I. Selection and placement of best management practices used to reduce water quality degradation in Lincoln Lake watershed. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Band, L.E. Spatial hydrography and landforms. In GIS: Management Issues and Applications; Longley, P., Goodchild, M., Maguire, D., Rhind, D., Eds.; John Wiley & Sons: Hoboken, NI, USA, 1999; pp. 527–542. [Google Scholar]
- Jiang, P.; Anderson, S.H.; Kitchen, N.R.; Sadler, E.J.; Sudduth, K.A. Landscape and conservation management effects on hydraulic properties of a claypan-soil toposequence. Soil Sci. Soc. Am. J. 2007, 71, 803–811. [Google Scholar] [CrossRef]
- Mudgal, A.; Baffaut, C.; Anderson, S.H.; Sadler, E.J.; Thompson, A.L. APEX model assessment of variable landscapes on runoff and dissolved herbicides. Trans. ASABE 2010, 53, 1047–1058. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. JAWRA 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Volk, M.; Williams, J.R.; Bosch, D.D. Assessment of Different Representations of Spatial Variability on SWAT Model Performance. Trans. ASABE 2010, 53, 1433–1443. [Google Scholar] [CrossRef]
- Kalcic, M.M.; Chaubey, I.; Frankenberger, J. Defining Soil and Water Assessment Tool (SWAT) hydrologic response units (HRUs) by field boundaries. Int. J. Agric. Biol. Eng. 2015, 8, 69–80. [Google Scholar]
- Teshager, A.D.; Gassman, P.W.; Secchi, S.; Schoof, J.T.; Misgna, G. Modeling Agricultural Watersheds with the Soil and Water Assessment Tool (SWAT): Calibration and Validation with a Novel Procedure for Spatially Explicit HRUs. Environ. Manag. 2016, 57, 894–911. [Google Scholar] [CrossRef]
- Gaddis, E.J.B.; Voinov, A.; Seppelt, R.; Rizzo, D.M. Spatial Optimization of Best Management Practices to Attain Water Quality Targets. Water Resour. Manag. 2014, 28, 1485–1499. [Google Scholar] [CrossRef]
- Limbrunner, J.F.; Vogel, R.M.; Chapra, S.C.; Kirshen, P.H. Optimal Location of Sediment-Trapping Best Management Practices for Nonpoint Source Load Management. J. Water Resour. Plan. Manag. 2013, 139, 478–485. [Google Scholar] [CrossRef]
- Perez-Pedini, C.; Limbrunner, J.F.; Vogel, R.M. Optimal Location of Infiltration-Based Best Management Practices for Storm Water Management. J. Water Resour. Plan. Manag. 2005, 131, 441–448. [Google Scholar] [CrossRef]
- Qin, C.-Z.; Zhu, A.-X.; Shi, X.; Li, B.-L.; Pei, T.; Zhou, C.-H. Quantification of spatial gradation of slope positions. Geomorphology 2009, 110, 152–161. [Google Scholar] [CrossRef]
- Zhu, L.-J.; Zhu, A.-X.; Qin, C.-Z.; Liu, J.-Z. Automatic approach to deriving fuzzy slope positions. Geomorphology 2018, 304, 173–183. [Google Scholar] [CrossRef]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, A Completely Restructured Version of the Soil and Water Assessment Tool. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 115–130. [Google Scholar] [CrossRef]
- Zhu, L.-J.; Liu, J.; Qin, C.-Z.; Zhu, A.-X. A modular and parallelized watershed modeling framework. Environ. Model. Softw. under review.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Chen, Z.-B.; Chen, Z.-Q.; Yue, H. Comprehensive Research on Soil and Water Conservation in Granite Red Soil Region: A Case Study of Zhuxi Watershed, Changting County, Fujian Province; Science Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Shi, X.; Yang, G.; Yu, D.; Xu, S.; Warner, E.D.; Petersen, G.W.; Sun, W.; Zhao, Y.; Easterling, W.E.; Wang, H. A WebGIS system for relating genetic soil classification of China to soil taxonomy. Comput. Geosci. 2010, 36, 768–775. [Google Scholar] [CrossRef]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Soil and Water Assessment Tool 2012 Input/Output Documentation; Texas Water Resources Institute: College Station, TX, USA, 2012. [Google Scholar]
- Chen, S.; Zha, X. Evaluation of soil erosion vulnerability in the Zhuxi watershed, Fujian Province, China. Nat. Hazards 2016, 82, 1589–1607. [Google Scholar] [CrossRef]
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a new open source GIS user interface for the SWAT model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Chen, Z.-Q.; Chen, Z.-B.; Bai, L.; Zeng, Y. A catastrophe model to assess soil restoration under ecological restoration in the red soil hilly region of China. Pedosphere 2017, 27, 778–787. [Google Scholar] [CrossRef]
- Fujian Soil and Water Conservation Monitoring Station; Fujian Agriculture and Forestry University; Fujian Normal University; Changting Soil and Water Conservation Monitoring Station. Monitoring Report of Soil and Water Loss in Changting County; Fuzhou, Fujian, China, 2010. (In Chinese) [Google Scholar]
- Liu, Y.; Engel, B.A.; Flanagan, D.C.; Gitau, M.W.; McMillan, S.K.; Chaubey, I.; Singh, S. Modeling framework for representing long-term effectiveness of best management practices in addressing hydrology and water quality problems: Framework development and demonstration using a Bayesian method. J. Hydrol. 2018, 560, 530–545. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, A.-X.; Qin, C.-Z.; Wu, H.; Jiang, J. A two-level parallelization method for distributed hydrological models. Environ. Model. Softw. 2016, 80, 175–184. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; U.S. Department of Agriculture: Washington, DC, USA, 1975; Volume ARS-S-40, pp. 244–252. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]

| BMP | Photo | Brief Description |
|---|---|---|
| Closing measures (CM) |  | Closing the ridge area and/or upslope positions from human disturbance (e.g., ban on felling tree and grazing) to facilitate afforestation. |
| Arbor–bush–herb mixed plantation (ABHMP) |  | Planting trees (e.g., Schima superba and Liquidambar formosana), bushes (e.g., Lespedeza bicolor), and herbs (e.g., Paspalum wettsteinii) in level trenches with compound fertilizer on hillslopes. |
| Low-quality forest improvement (LQFI) |  | Improving the infertile forest located in the upslope and steep backslope positions by applying compound fertilizer to the hole with a size of 40 cm × 40 cm × 40 cm in the uphill position of crown projection. |
| Orchard improvement (OI) |  | Improving orchards on the middle and down slope positions under better water and fertilizer conditions by constructing level terraces, drainage ditches, storage ditches, irrigation facilities, and roads, planting economic fruit, and interplanting grasses and Fabaceae (Leguminosae) plants. |
| BMP | Environmental Effectiveness 1 | Cost-Benefit (CNY 10,000/km2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| OM | BD | PORO | SOL_K | USLE_K | USLE_P | Initial | Maintain/yr | Benefit/yr | |
| CM | 1.22 | 0.98 | 1.02 | 0.81 | 1.01 | 0.90 | 15.5 | 1.5 | 2.0 |
| ABHMP | 1.45 | 0.93 | 1.07 | 1.81 | 0.82 | 0.50 | 87.5 | 1.5 | 6.9 |
| LQFI | 1.05 | 0.87 | 1.13 | 1.71 | 1.71 | 0.50 | 45.5 | 1.5 | 3.9 |
| OI | 2.05 | 0.96 | 1.03 | 1.63 | 1.63 | 0.75 | 420 | 20 | 60.3 |
| BMP | Suitable Landuse Types | Suitable Slope Positions | Effectiveness Grade |
|---|---|---|---|
| CM | forest | ridge, backslope | 3 |
| ABHMP | forest, orchard | ridge, backslope, and valley | 5 |
| LQFI | forest | backslope | 4 |
| OI | forest, orchard | valley | 4 |
| Constituent | Calibration Period (2014–2015) | Validation Period (2013) | ||||
|---|---|---|---|---|---|---|
| NSE | RSR | PBIAS (%) | NSE | RSR | PBIAS (%) | |
| Streamflow (m3 s−1) | 0.50 | 0.71 | 13.55 | 0.57 | 0.65 | −14.71 |
| Sediment export (kg) | 0.30 | 0.84 | 13.93 | 0.45 | 0.74 | −42.39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.-J.; Qin, C.-Z.; Zhu, A.-X.; Liu, J.; Wu, H. Effects of Different Spatial Configuration Units for the Spatial Optimization of Watershed Best Management Practice Scenarios. Water 2019, 11, 262. https://doi.org/10.3390/w11020262
Zhu L-J, Qin C-Z, Zhu A-X, Liu J, Wu H. Effects of Different Spatial Configuration Units for the Spatial Optimization of Watershed Best Management Practice Scenarios. Water. 2019; 11(2):262. https://doi.org/10.3390/w11020262
Chicago/Turabian StyleZhu, Liang-Jun, Cheng-Zhi Qin, A-Xing Zhu, Junzhi Liu, and Hui Wu. 2019. "Effects of Different Spatial Configuration Units for the Spatial Optimization of Watershed Best Management Practice Scenarios" Water 11, no. 2: 262. https://doi.org/10.3390/w11020262
APA StyleZhu, L.-J., Qin, C.-Z., Zhu, A.-X., Liu, J., & Wu, H. (2019). Effects of Different Spatial Configuration Units for the Spatial Optimization of Watershed Best Management Practice Scenarios. Water, 11(2), 262. https://doi.org/10.3390/w11020262







