Effects of Residue Cover on Infiltration Process of the Black Soil Under Rainfall Simulations
Abstract
1. Introduction
- (1)
- To determine the optimal infiltration model for bare black soil;
- (2)
- To establish the infiltration model combined with the effect of residue cover for black soil.
2. Materials and Methods
2.1. Design of Rainfall Simulation Experiments
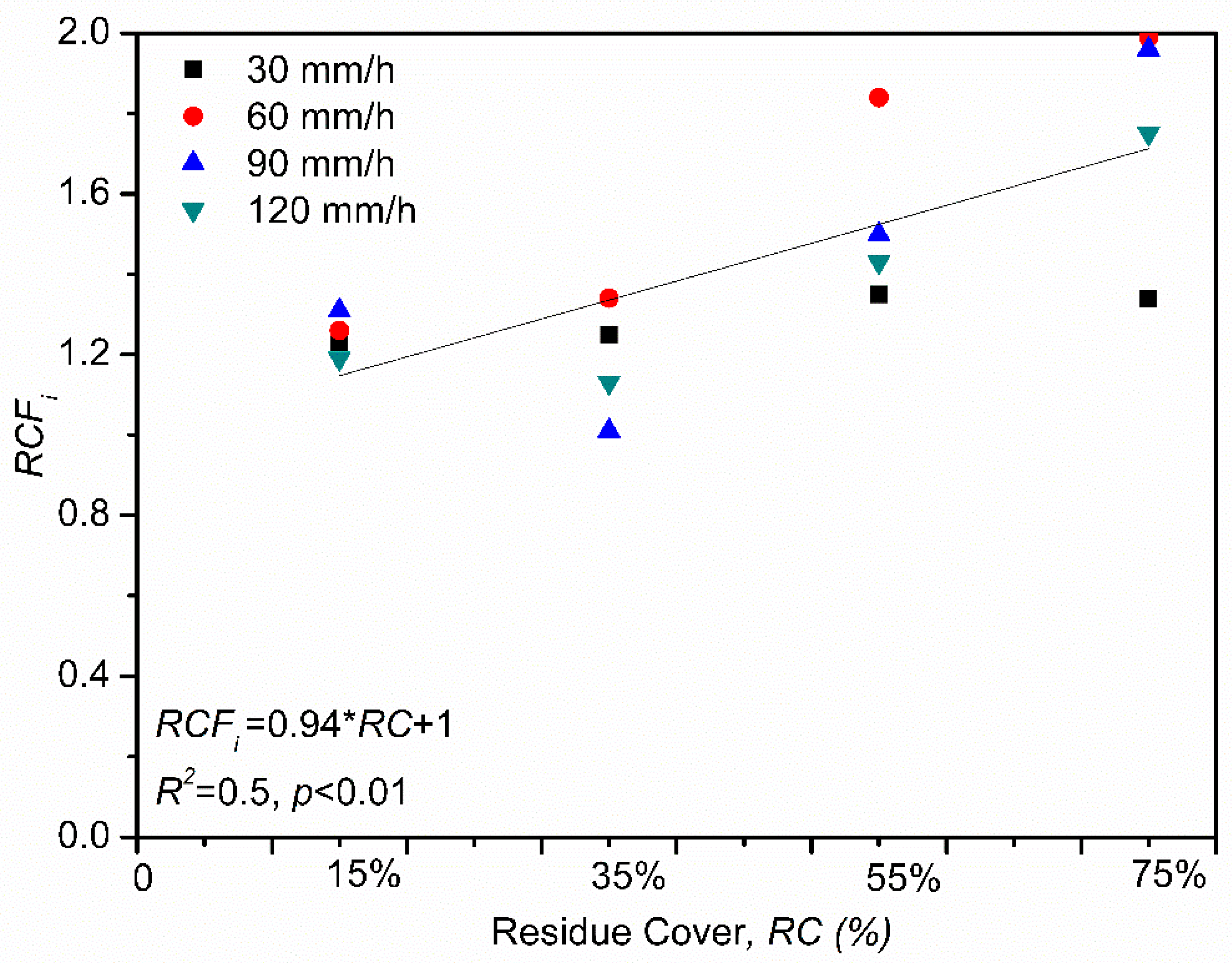
2.2. The Residue Cover Factor for Model Validation
2.3. Accuracy Assessment Methods
3. Results
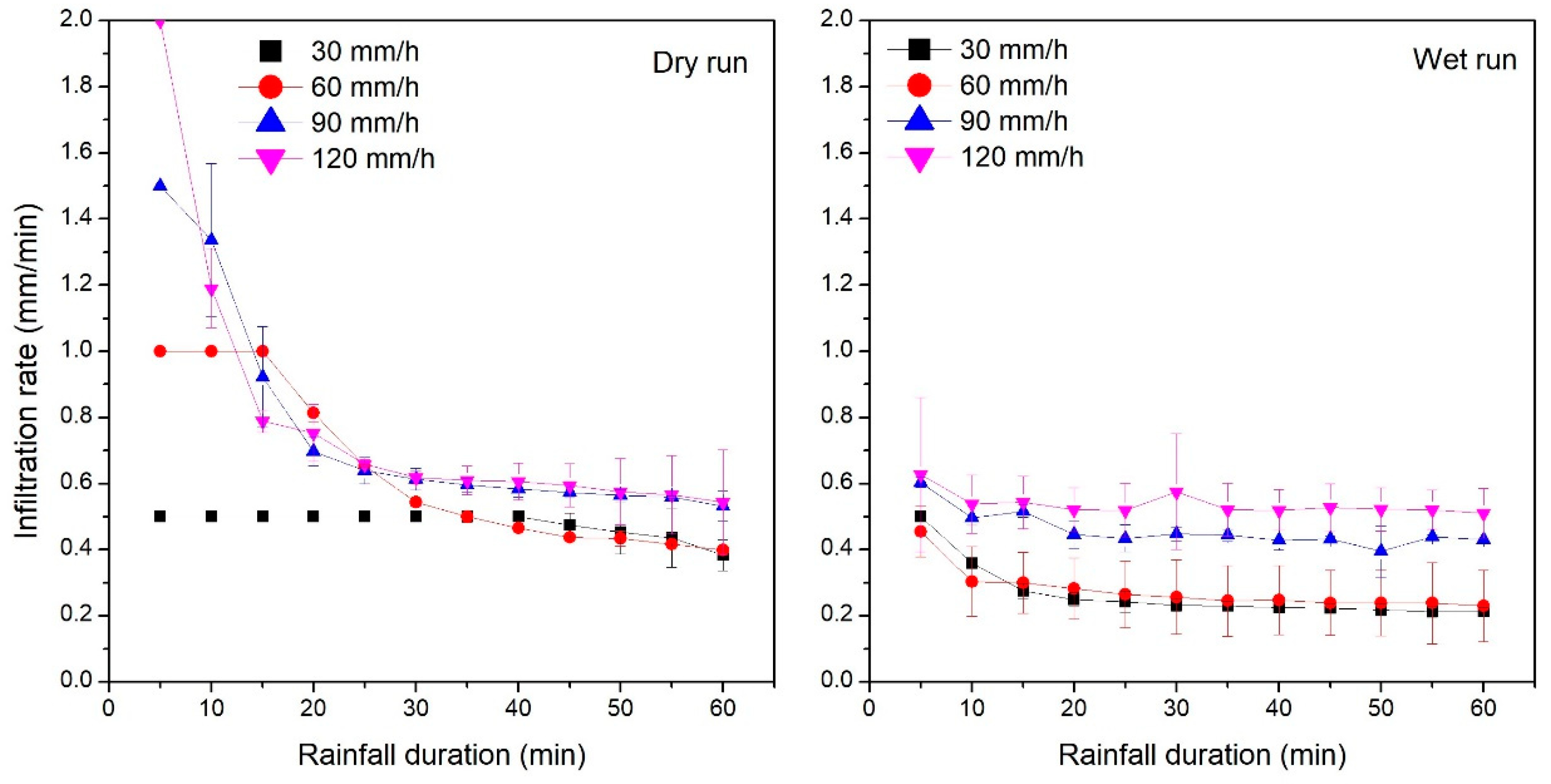
3.1. Infiltration Rates of Bare Black Soil Under Various Rainfall Events
3.2. Estimation of the Infiltration Model Parameters
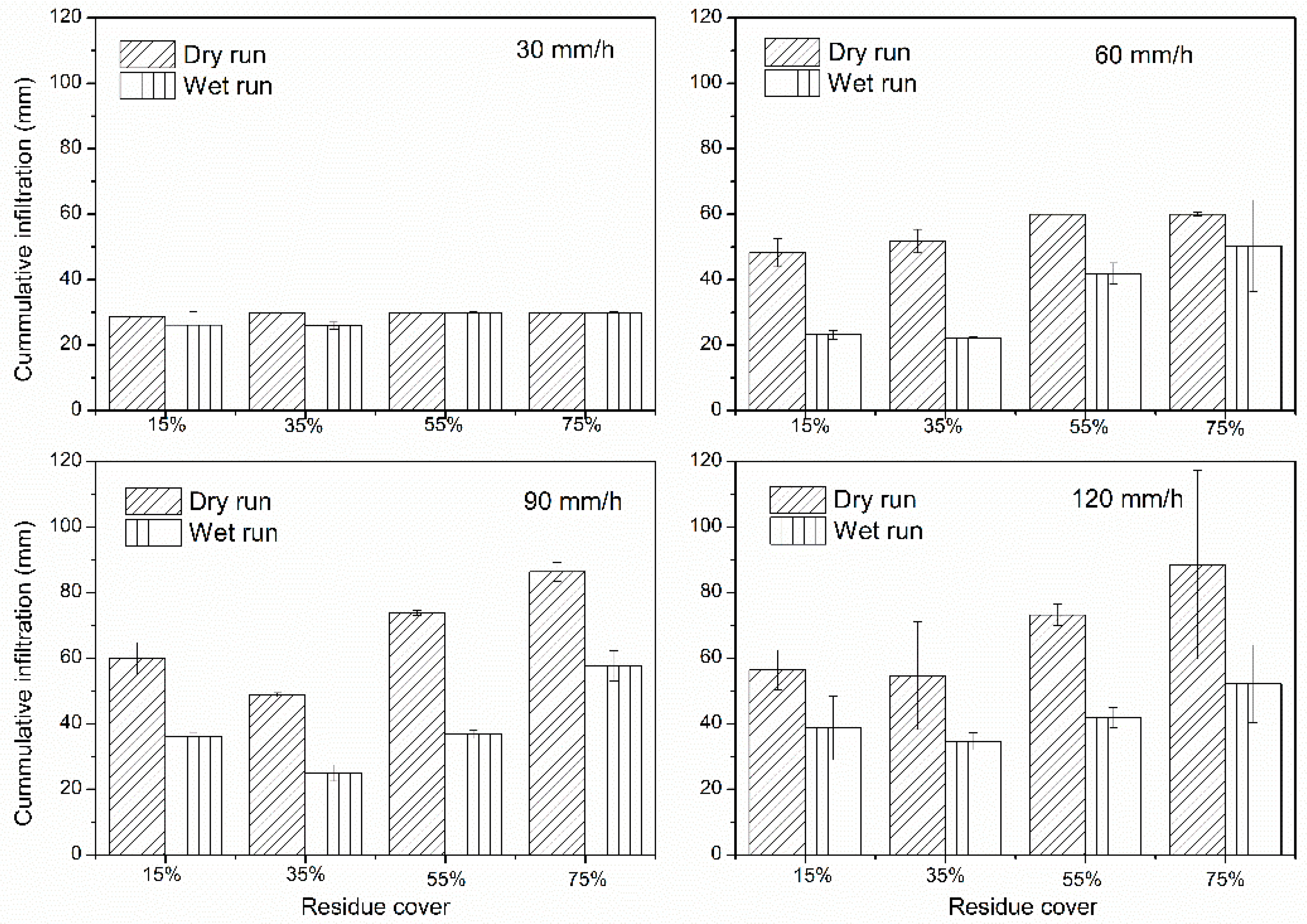
3.3. Cumulative Infiltration Amounts for the Residue-Covered Black Soil under Various Rainfall Events
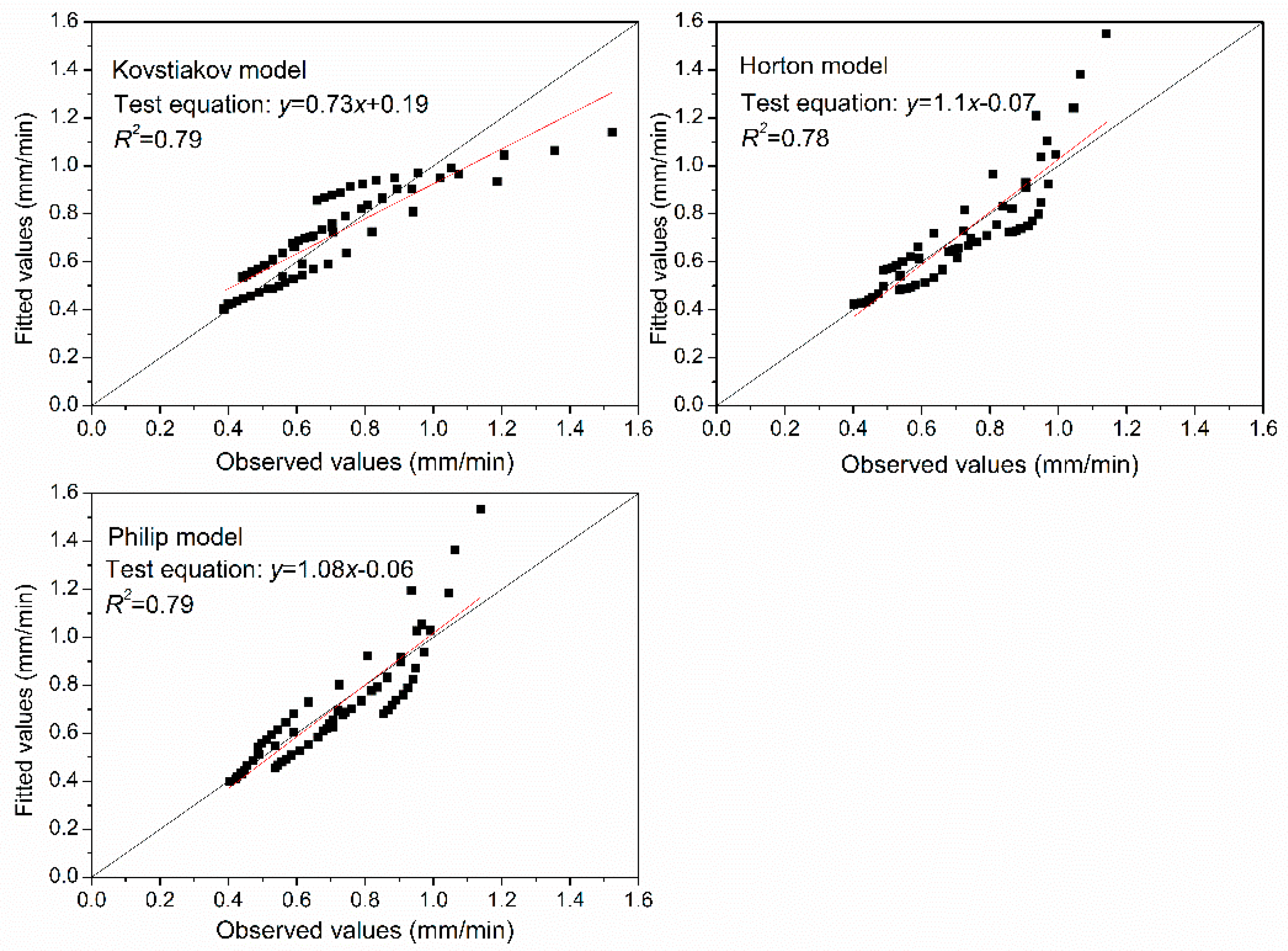
3.4. Performance of the Models for the Residue-Covered Black Soil
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hillel, D. Environmental Soil Physics; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Zhang, J.; Lei, T.; Yin, Z.; Hu, Y.; Xiusheng Yang, X. Effects of time step length and positioning location on ring-measured infiltration rate. Catena 2017, 157, 344–356. [Google Scholar] [CrossRef]
- Philip, J.R. Hillslope infiltration: Divergent and convergent slopes. Water Resour. Res. 1991, 27, 1035–1040. [Google Scholar] [CrossRef]
- Herrada, M.A.; Gutiérrez-Martin, A.; Montanero, J.M. Modeling infiltration rates in a saturated/unsaturated soil under the free draining condition. J. Hydrol. 2014, 515, 10–15. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Govindaraju, R.S. Role of slope on infiltration: A review. J. Hydrol. 2018, 557, 878–886. [Google Scholar] [CrossRef]
- Wang, K.; Yang, X.; Liu, X.; Liu, C. A simple analytical infiltration model for short-duration rainfall. J. Hydrol. 2017, 555, 141–154. [Google Scholar] [CrossRef]
- Green, W.; Ampt, G. Studies on soil physics, part I: The flow of air and water through soils. J. Agric. Sci. 1991, 4, 1–24. [Google Scholar]
- Kostiakov, A.N. On the dynamics of the coefficient of water percolation in soils and on the necessity of studying it from a dynamic point of view for purposes of amelioration. Trans. Sixth Comm. Int. Soc. Soil Sci. Part A 1932, 1, 7–21. [Google Scholar]
- Horton, R. The role of infiltration in the hydrologic cycle. Am. Geophys. Union Trans. 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Holtan, H.N. A Concept for Infiltration Estimates in Watershed Engineering; USDA-ARS Bull. 41–51; United States Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1961.
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–357. [Google Scholar] [CrossRef]
- Soil Conservation Service. SCS National Engineering Handbook; Section 4, Hydrology; United States Department of Agriculture: Washington, DC, USA, 1972.
- Smith, R.E.; Parlange, J.Y. A parameter-efficient hydrologic infiltration model. Water Resour. Res. 1978, 14, 533–538. [Google Scholar] [CrossRef]
- Corradini, C.; Melone, F.; Smith, R.E. Modeling infiltration during complex rainfall sequences. Water Resour. Res. 1994, 30, 2777–2784. [Google Scholar] [CrossRef]
- Van Den Putte, A.; Govers, G.; Leys, A.; Langhans, C.; Clymans, W.; Diels, J. Estimating the parameters of the Green–Ampt infiltration equation from rainfall simulation data: Why simpler is better. J. Hydrol. 2013, 476, 332–344. [Google Scholar] [CrossRef]
- Mein, R.G.; Larson, C.L. Modeling infiltration during a steady rain. Water Resour. Res. 1973, 9, 384–394. [Google Scholar] [CrossRef]
- Chu, X.; Mariño, M.A. Determination of ponding condition and infiltration into layered soils under unsteady rainfall. J. Hydrol. 2005, 313, 195–207. [Google Scholar] [CrossRef]
- Chen, L.; Young, M.H. Green-Ampt infiltration model for sloping surfaces. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Derpsch, R.; Franzluebbers, A.J.; Duiker, S.W.; Reicosky, D.C.; Koeller, K.; Friedrich, T.; Sturny, W.G.; Sá, J.C.M.; Weiss, K. Why do we need to standardize no-tillage research? Soil Till. Res. 2014, 137, 16–22. [Google Scholar] [CrossRef]
- Gavin, K.; Xue, J. A simple method to analyze infiltration into unsaturated soil slopes. Comput. Geotech. 2008, 35, 223–230. [Google Scholar] [CrossRef]
- Gong, Z.T.; Chen, Z.C.; Shi, X.Z. Chinese Soil Taxonomy; Science Press: Beijing, China, 1999. [Google Scholar]
- Gu, Z.; Xie, Y.; Gao, Y.; Ren, X.; Cheng, C.; Wang, S. Quantitative assessment of soil productivity and predicted impacts of water erosion in the black soil region of northeastern China. Sci Total Environ. 2018, 637-638, 706–716. [Google Scholar] [CrossRef]
- Wang, J.; Xie, Y.; Liu, G.; Zhao, Y.; Zhang, S. Soybean root development under water stress in eroded soils. Acta Agric. Scand. Sect. B Soil Plant Sci. 2015, 65, 374–382. [Google Scholar] [CrossRef]
- Zhao, X.N.; Wu, P.; Gao, X.D.; Tian, L.; Li, H.C. Changes of soil hydraulic properties under early-stage natural vegetation recovering on the Loess Plateau of China. Catena 2014, 113, 386–391. [Google Scholar] [CrossRef]
- Xin, Y.; Xie, Y.; Liu, Y.; Liu, H.; Ren, X. Residue cover effects on soil erosion and the infiltration in black soil under simulated rainfall experiments. J. Hydrol. 2016, 543, 651–658. [Google Scholar] [CrossRef]
- Bamutaze, Y.; Tenywa, M.M.; Majaliwa, M.J.G.; Vanacker, V.; Bagoora, F.; Magunda, M.; Obando, J.; Wasige, J.E. Infiltration characteristics of volcanic sloping soils on Mt. Elgon, Eastern Uganda. Catena 2010, 80, 122–130. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wu, L.Z.; Zhou, Y.; Sun, P.; Shi, J.S.; Liu, G.G.; Bai, L.Y. Laboratory characterization of rainfall-induced loess slope failure. Catena 2017, 150, 1–8. [Google Scholar] [CrossRef]
- Meyer, L.D.; Wischimeier, W.H.; Foster, G.R. Mulch rates required for erosion control on steep slopes. Soil Sci. Soc. Am. J. 1970, 34, 928–931. [Google Scholar] [CrossRef]
- Naeth, M.A.; Bailey, A.W.; Chanasyk, D.S.; Pluth, D.J. Water holding capacity of litter and soil organic matter in mixed prairie and fescue grassland ecosystems of Alberta. J. Range Manag. 1991, 44, 13–17. [Google Scholar] [CrossRef]
- De Almeida, W.S.; Panachuki, E.; de Oliveira, P.T.S.; Da Silva Menezes, R.; Sobrinho, T.A.; de Carvalho, D.F. Effect of soil tillage and vegetal cover on soil water infiltration. Soil Till. Res. 2018, 175, 130–138. [Google Scholar] [CrossRef]
- Mohammadzadeh-Habili, J.; Heidarpour, M. Application of the Green–Ampt model for infiltration into layered soil. J. Hydrol. 2015, 527, 824–832. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, Q.; Zhang, Y.; Liu, B.; Cheng, H.; Wang, Y. Development of gullies and sediment production in the black soil region of northeastern China. Geomorphology 2008, 101, 683–691. [Google Scholar] [CrossRef]
- Bouwer, H. Infiltration into increasingly permeable soils. J. Irrig. Drain. Eng. 1976, 102, 127–136. [Google Scholar]

| Model | Year | Equation | Symbols |
|---|---|---|---|
| Kostiakov [8] | 1932 | , fitting parameters | |
| Horton [9] | 1933 | f0, initial rate fc, constant rate k, decay constant | |
| Philip [11] | 1957 | S, sorptivity Ks, saturated hydraulic conductivity | |
| Mein and Larson (GAML) [16] | 1973 | F, cumulative infiltration Ke, effective hydraulic conductivity S, suction at the wetting front M, hydrological parameter of difference between saturated and initial volumetric moisture content |
| Kostiakov | Horton | Philip | GAML | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | n | R2 | fc | f0 | k | R2 | S | Ks | R2 | Ke | S·M | R2 |
| 1.511 | 0.352 | 0.494 | 0.421 | 1.199 | 0.096 | 0.511 | 3.185 | 0.290 | 0.509 | 0.507 | −0.572 | 0.553 |
| RMSE | NSE | |
|---|---|---|
| Horton | 0.112 | 0.666 |
| Philip | 0.105 | 0.699 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Y.; Xie, Y.; Liu, Y. Effects of Residue Cover on Infiltration Process of the Black Soil Under Rainfall Simulations. Water 2019, 11, 2593. https://doi.org/10.3390/w11122593
Xin Y, Xie Y, Liu Y. Effects of Residue Cover on Infiltration Process of the Black Soil Under Rainfall Simulations. Water. 2019; 11(12):2593. https://doi.org/10.3390/w11122593
Chicago/Turabian StyleXin, Yan, Yun Xie, and Yuxin Liu. 2019. "Effects of Residue Cover on Infiltration Process of the Black Soil Under Rainfall Simulations" Water 11, no. 12: 2593. https://doi.org/10.3390/w11122593
APA StyleXin, Y., Xie, Y., & Liu, Y. (2019). Effects of Residue Cover on Infiltration Process of the Black Soil Under Rainfall Simulations. Water, 11(12), 2593. https://doi.org/10.3390/w11122593




