A Data-Driven Probabilistic Rainfall-Inundation Model for Flash-Flood Warnings
Abstract
1. Introduction
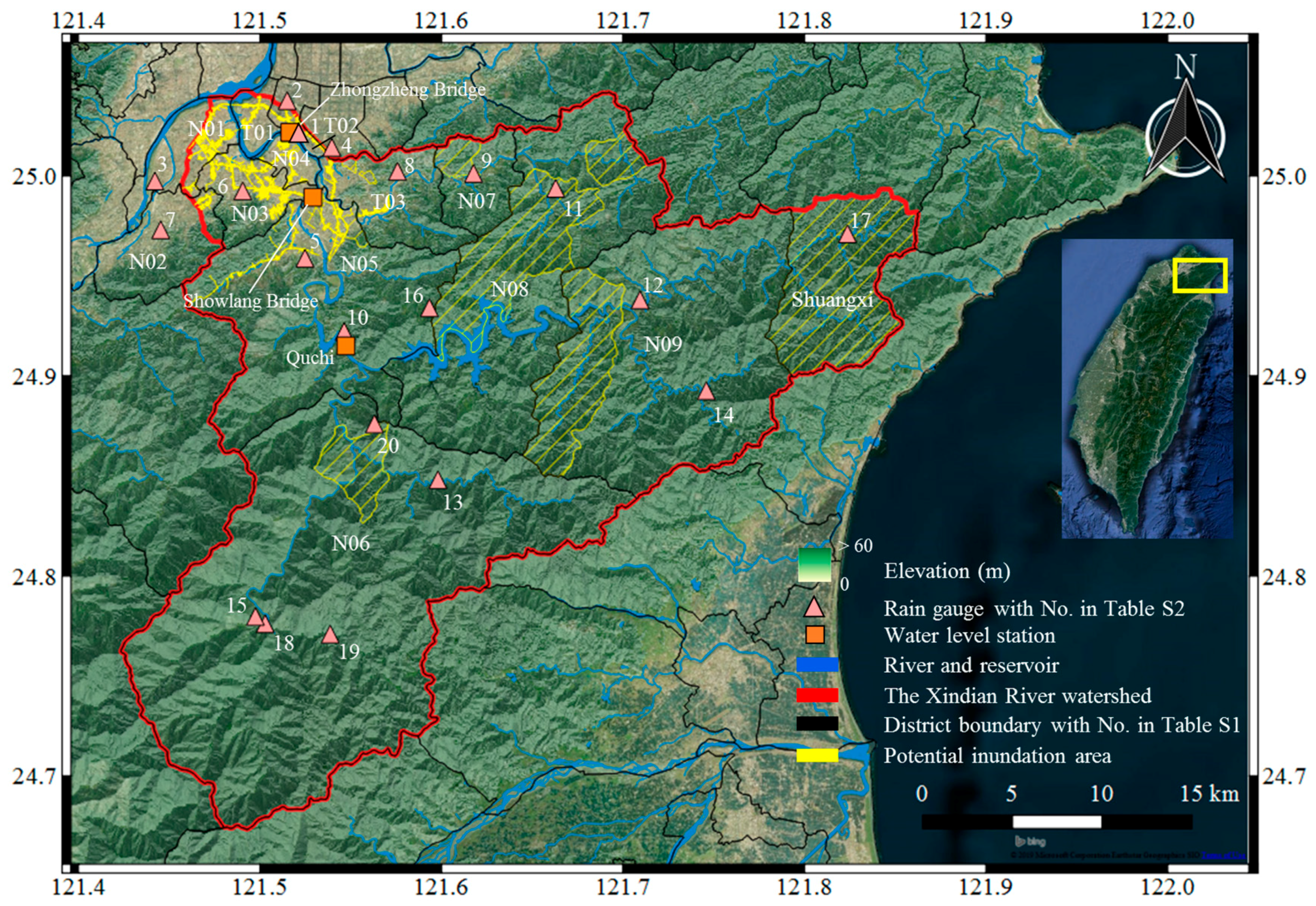
2. Study Area and Data Used
2.1. Xindian River and Its Flood Disaster Events
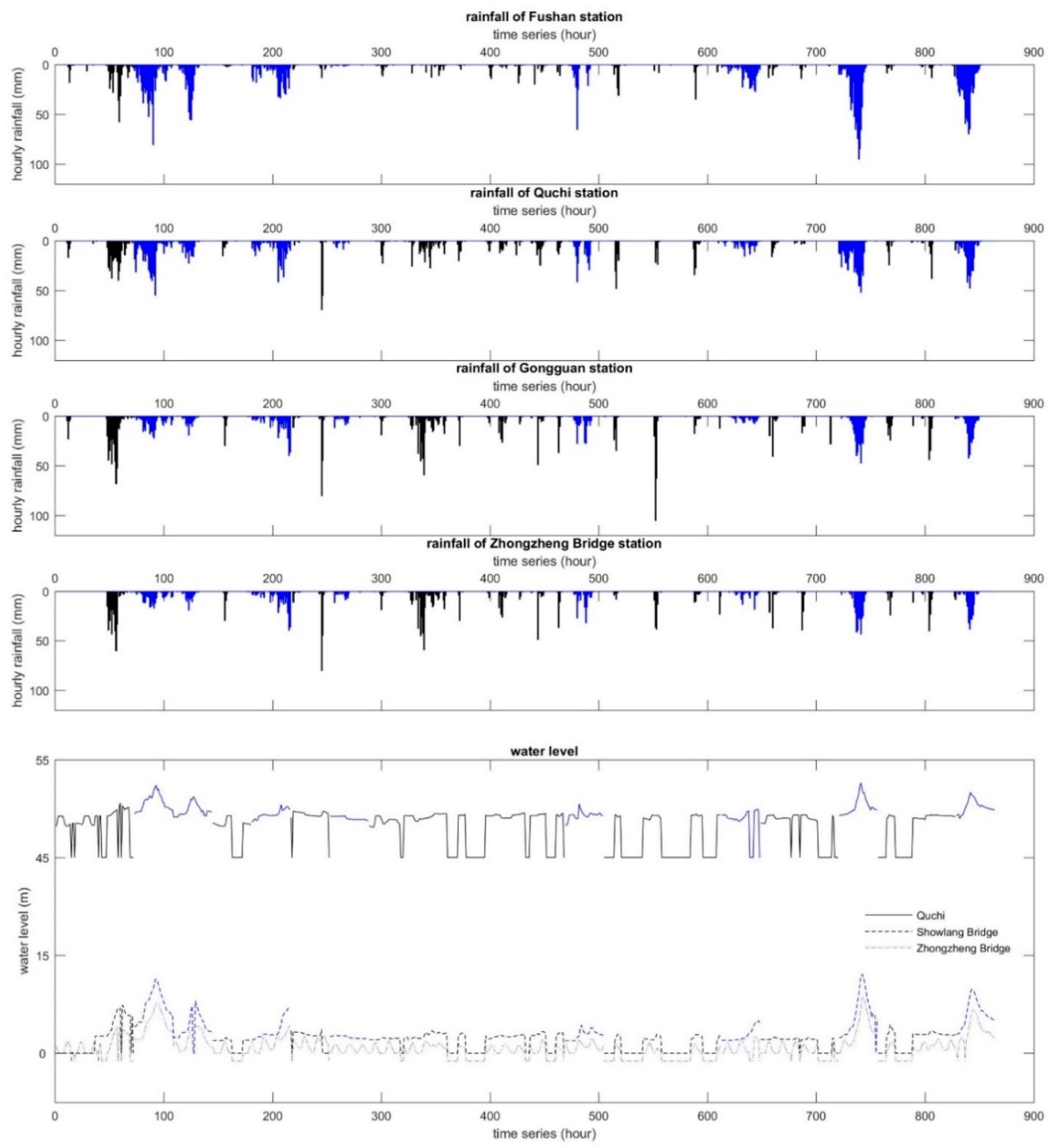
2.2. Dataset
3. Methodology
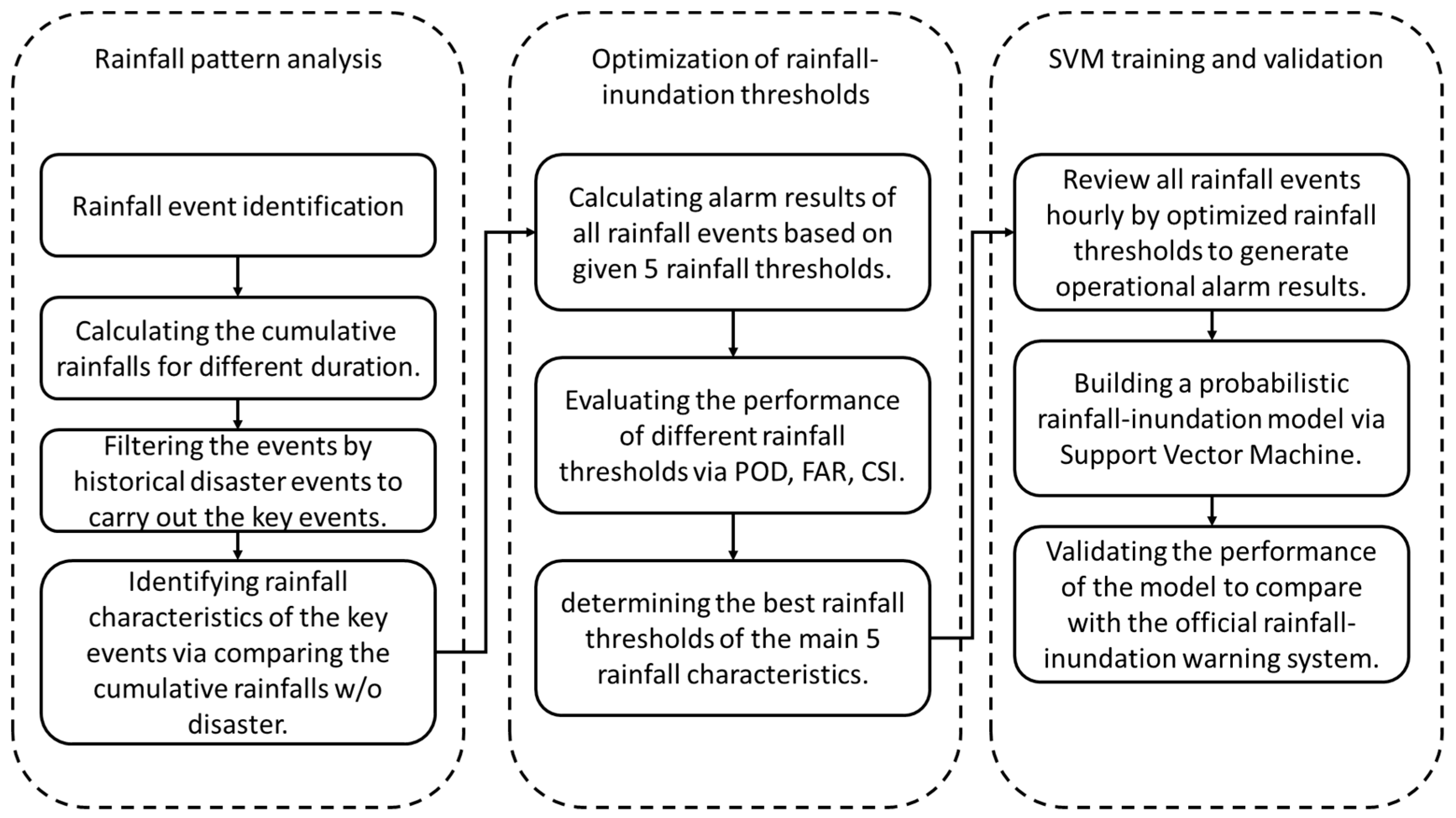
3.1. Model Development Process
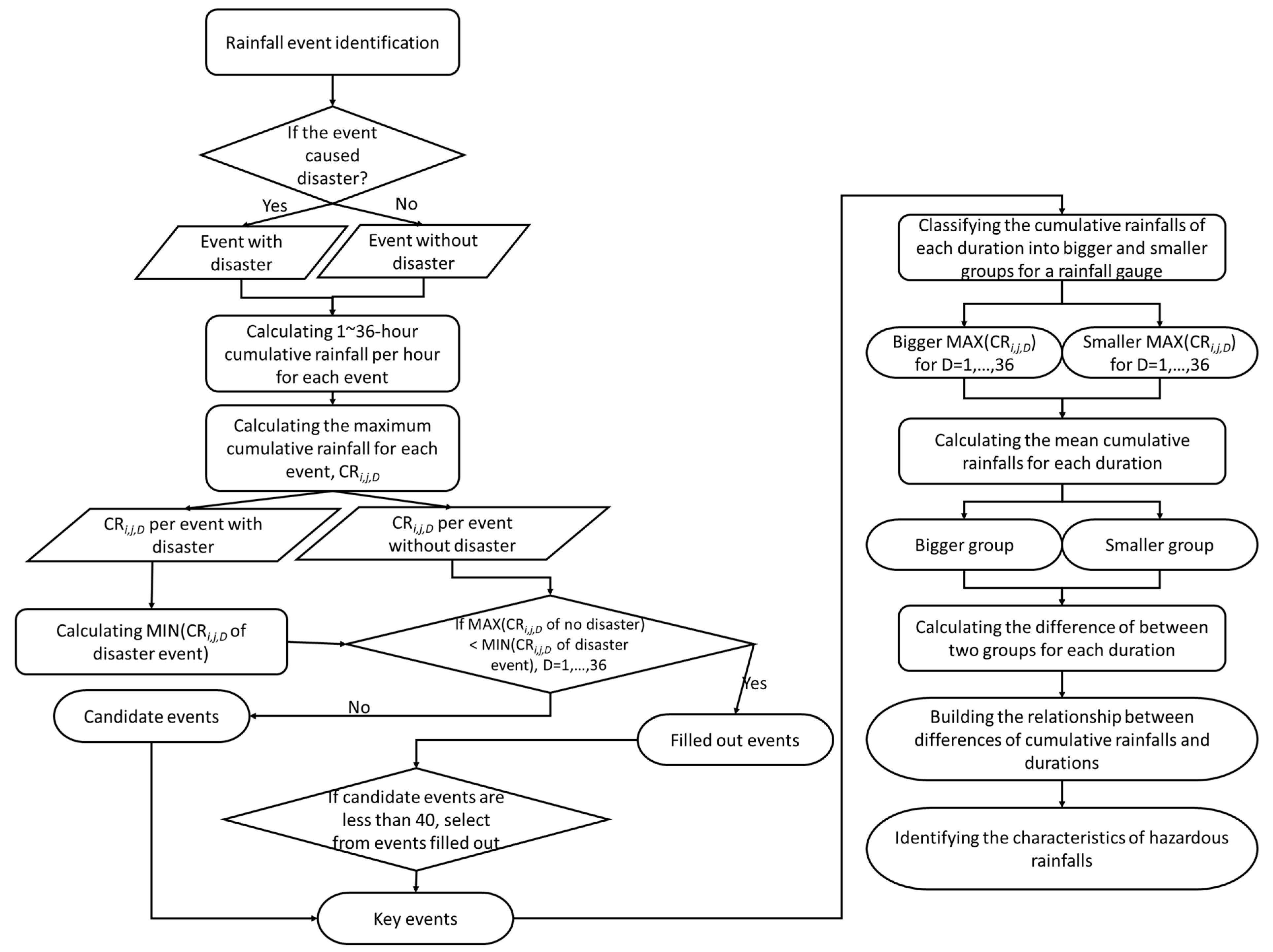
3.2. Rainfall Pattern Analysis
3.3. Optimization of Rainfall-Inundation Thresholds
3.4. Support Vector Machine and Its Supervised Data Generation
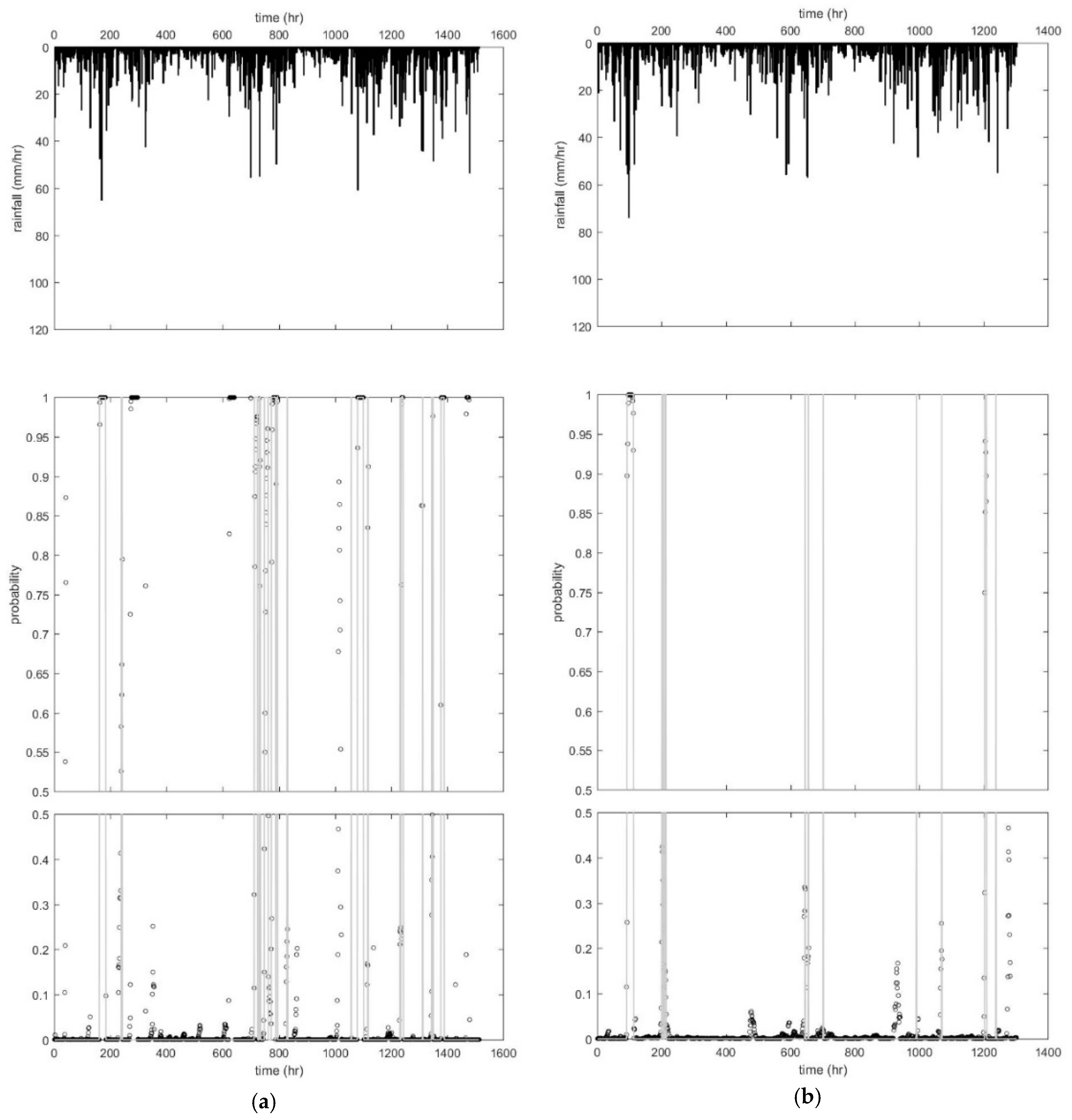
4. Results and Discussion
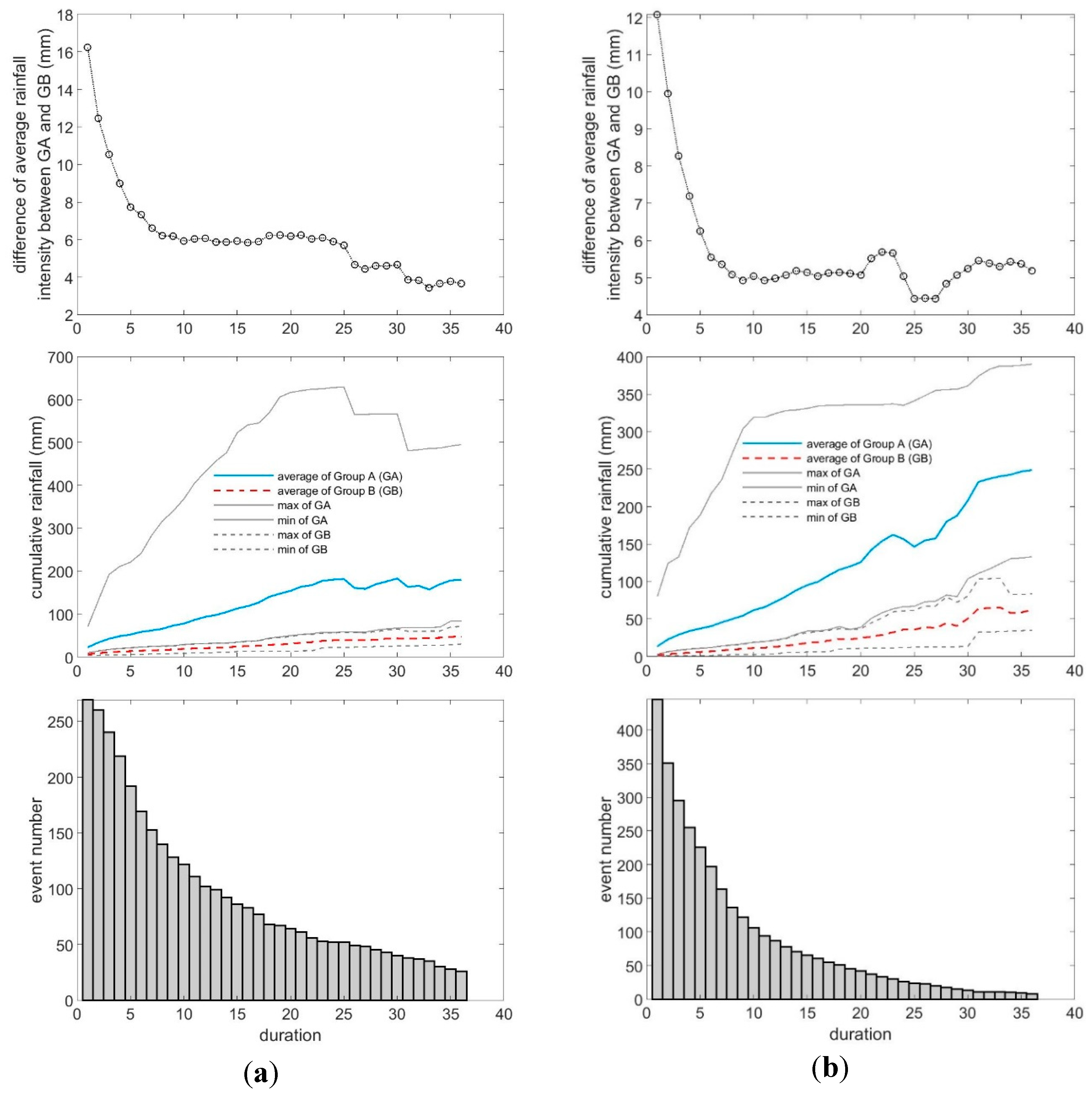
4.1. Identifying the Characteristics of Extreme Rainfalls
4.2. Optimization of Rainfall-Inundation Thresholds
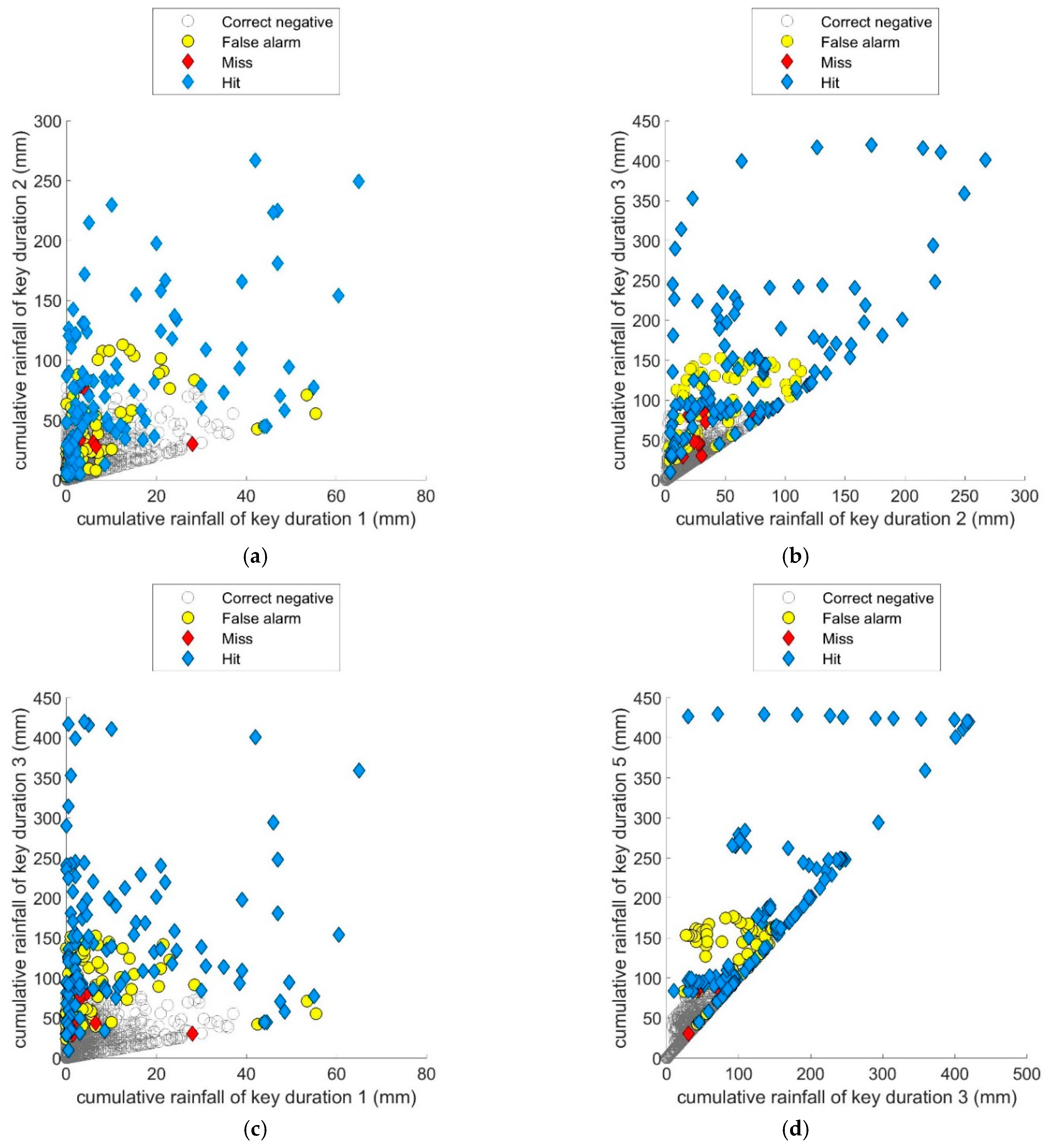
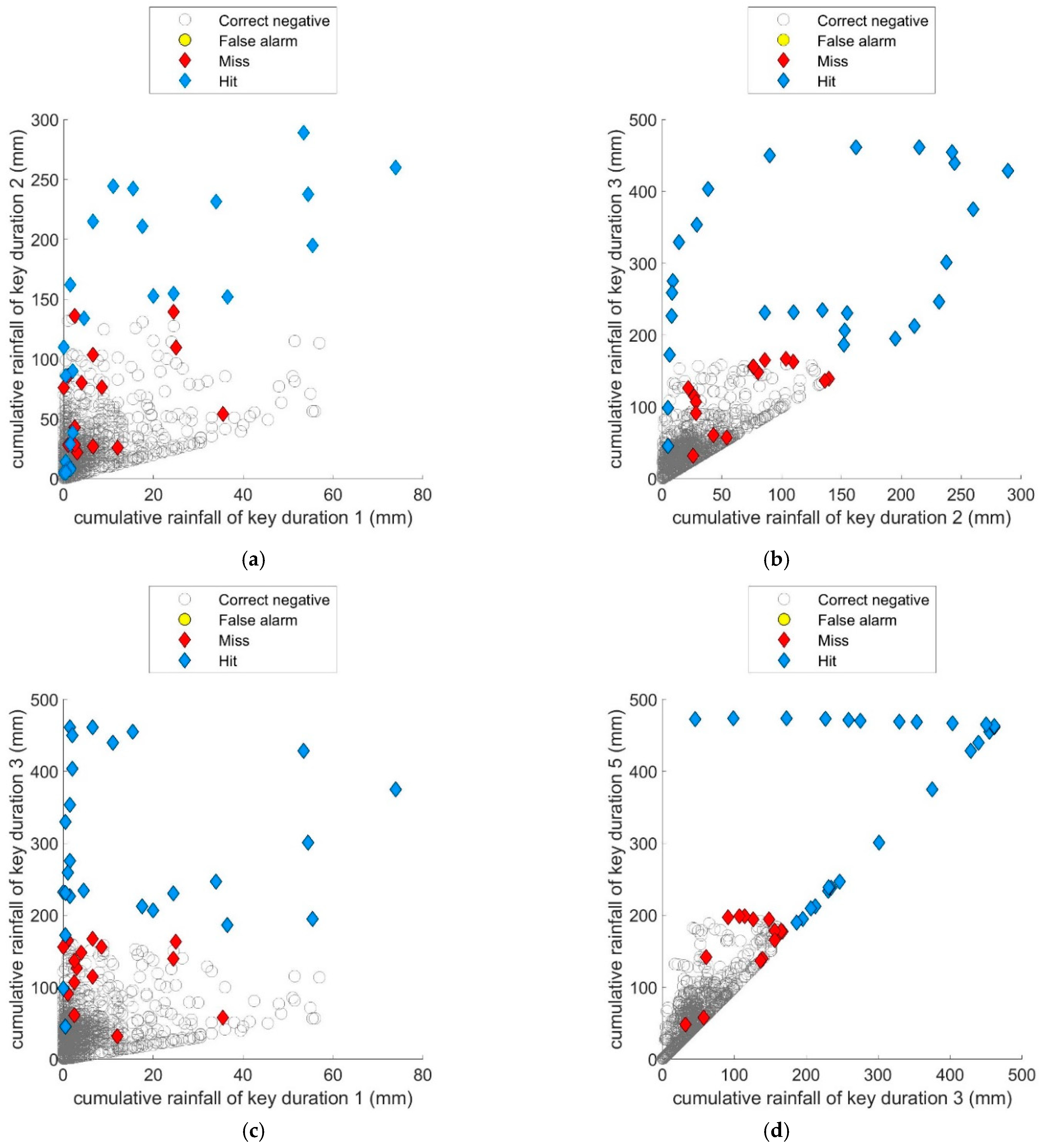
4.3. Building a Probabilistic Rainfall-Inundation Model Based on SVM
5. Conclusions and Recommendations
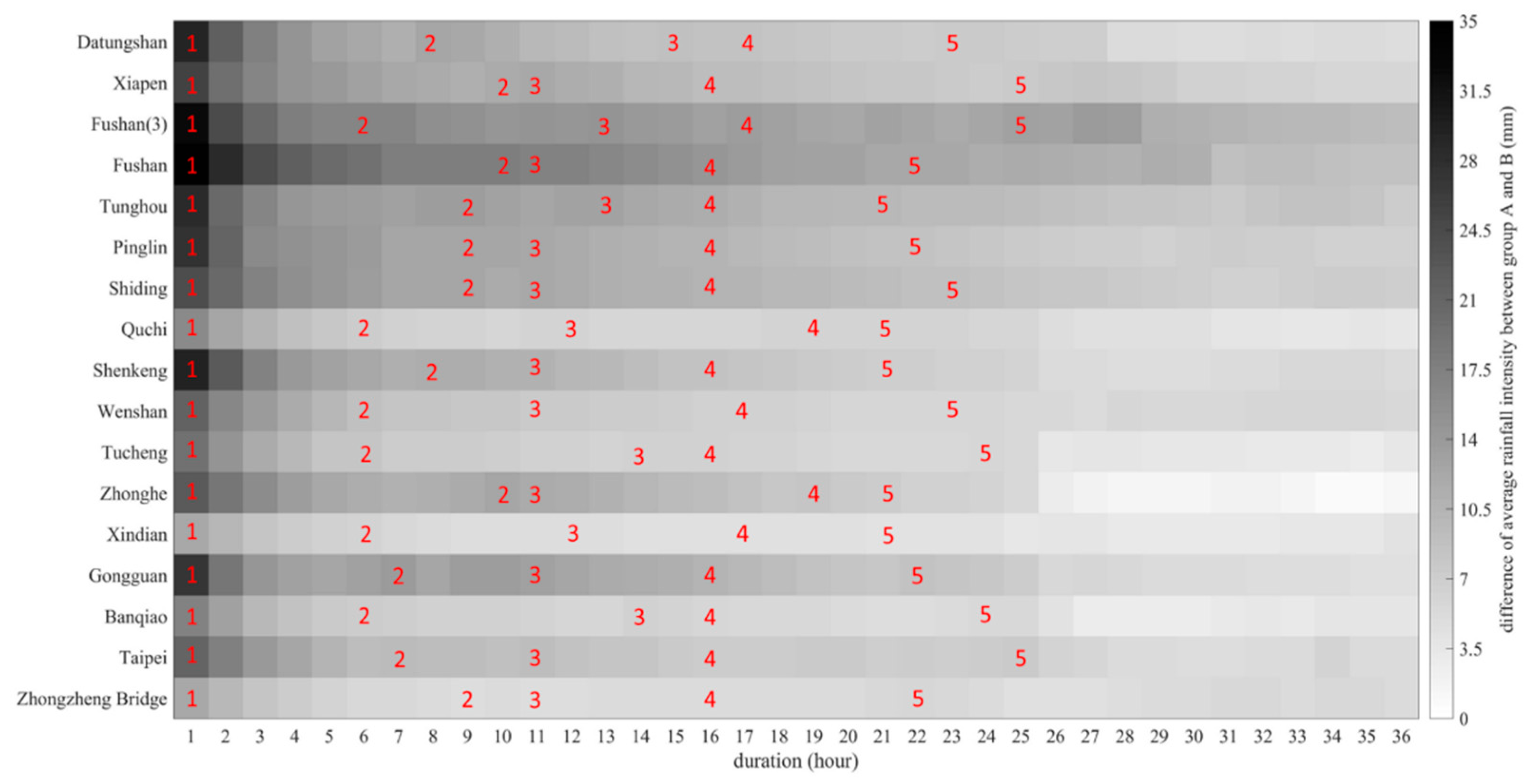
- The rainfall patterns obtained by the rain gauges depend on the geographical and hydrological environment. Therefore, the key durations of the extreme rainfalls related to disaster events, identified by rainfall pattern analysis of the multi-duration cumulative rainfalls at the rain gauges, can improve the hazardous event identification.
- Because the developed probabilistic rainfall-inundation model is a data-driven model, its performance is highly sensitive to the quality of the supervised data. Here, satisfactory supervised data were generated by screening the hourly historical rainfalls using optimized flood warning thresholds.
- Regarding the characteristics of extreme rainfalls, the rainfall patterns showed that most of the disasters in the plain areas are induced by brief, high intensity rainfall events, whereas those in mountainous areas are caused by longer-duration typhoons or frontal systems. Furthermore, the key durations of the first (1–5 h), second (6–10 h), and fifth (21–25 h) intervals are more critical than those of the third (11–15 h) and fourth (16–20 h) intervals.
- The rainfall thresholds of each duration were optimized by the trial-and-error method, which is time consuming but guarantees a global optimum. The optimized rainfall thresholds were related to the capacities of the drainage systems in the study area. For practical operation, rounding the estimated values of rainfall thresholds at least till integer or 5 mm values would be appropriate due to local measurements of rainfall with complicated structure. Moreover, they ensured adequate supervised data for developing the data-driven probabilistic rainfall-inundation model of flash-flood warnings.
- Among four approaches, applying the rainfall-inundation thresholds established by trial and error to the officially designed durations, and applying the key durations obtained in the rainfall pattern analysis significantly improved the official warning system. Furthermore, determining the key durations by rainfall pattern analysis only slightly affected the probability of disaster detection but significantly improved the FAR and CSI by reducing the number of false alarms. Moreover, although the supervised data were generated from similar optimized rainfall-inundation thresholds, the flash-flood warning performance was significantly higher in the proposed model than in the official warning system.
- Most rainfall-inundation warning systems only provide a Boolean description, but our data-driven probabilistic rainfall-inundation model exports the probability of floods. The modified SVM model can provide 1- to 3-h advance warnings when the probability is approaching 0.5. Through such probabilistic warning, the model not only quantifies the potential risk of impacts for decision makers, but also provides early warnings based on probability changes.
- This analysis was conducted on the station (point) scales. It means local rain gauges only. Therefore, the spatial impacts by considering the whole stations together need to be addressed to check such outputs changes over the whole region for further study.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yin, J.; Yu, D.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef]
- Candela, A.; Aronica, G.T. Rainfall thresholds derivation for warning pluvial flooding risk in urbanised areas. In Proceedings of the 3rd European Conference on Flood Risk Management, Lyon, France, 17–21 October 2016; Volume 7, p. 18016. [Google Scholar] [CrossRef]
- Douinot, A.; Roux, H.; Garambois, P.A.; Larnier, K.; Labat, D.; Dartus, D. Accounting for rainfall systematic spatial variability in flash flood forecasting. J. Hydrol. 2016, 541, 359–370. [Google Scholar] [CrossRef]
- Clark, C. Saving lives: Timely flash flood warnings in the UK. J. Geosci. Environ. Prot. 2017, 5, 60–74. [Google Scholar] [CrossRef]
- Forestieri, A.; Caracciolo, D.; Arnone, E.; Noto, L.V. Derivation of rainfall thresholds for flash flood warning in a Sicilian basin using a hydrological model. Procedia Eng. 2016, 154, 818–825. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Degli Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: an assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Golian, S.; Saghafian, B.; Elmi, M.; Maknoon, R. Probabilistic rainfall thresholds for flood forecasting: evaluating different methodologies for modelling rainfall spatial correlation (or dependence). Hydrol. Process. 2011, 25, 2046–2055. [Google Scholar] [CrossRef]
- Gourley, J.J.; Erlingis, J.M.; Hong, Y.; Wells, E.B. Evaluation of tools used for monitoring and forecasting flash floods in the United States. Weather Forecast 2012, 27, 158–173. [Google Scholar] [CrossRef]
- Diakakis, M. Rainfall thresholds for flood triggering. The case of Marathonas in Greece. Nat. Hazards 2012, 60, 789–800. [Google Scholar] [CrossRef]
- Seo, D.; Lakhankar, T.; Mejia, J.; Cosgrove, B.; Khanbilvardi, R. Evaluation of operational national weather service gridded flash flood guidance over the Arkansas Red River Basin. J. Am. Water Resour. Assoc. 2013, 49, 1296–1307. [Google Scholar] [CrossRef]
- Clark, R.A.; Gourley, J.J.; Flamig, Z.L.; Hong, Y.; Clark, E. CONUS-wide evaluation of national weather service flash flood guidance products. Weather Forecast 2014, 29, 377–392. [Google Scholar] [CrossRef]
- Bezak, N.; Šraj, M.; Mikoš, M. Copula-based IDF curves and empirical rainfall thresholds for flash floods and rainfall-induced landslides. J. Hydrol. 2016, 541, 272–284. [Google Scholar] [CrossRef]
- Marra, F.; Nikolopoulos, E.I.; Creutin, J.D.; Borga, M. Space–time organization of debris flows-triggering rainfall and its effect on the identification of the rainfall threshold relationship. J. Hydrol. 2016, 541, 246–255. [Google Scholar] [CrossRef]
- Miao, Q.; Yang, D.; Yang, H.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef]
- Liao, H.-Y.; Pan, T.-Y.; Chang, H.-K.; Hsieh, C.-T.; Lai, J.-S.; Tan, Y.-C.; Su, M.-D. Using Tabu Search Adjusted with Urban Sewer Flood Simulation to Improve Pluvial Flood Warning via Rainfall Thresholds. Water 2019, 11, 348. [Google Scholar] [CrossRef]
- Fan, J.C.; Liu, C.H.; Wu, M.F.; Yu, S.K. Determination of critical rainfall thresholds for debris-flow occurrence in central Taiwan and their revision after the 1999 Chi-Chi great earthquake. In Proceedings of the 3rd International DFHM Conference, Davos, Switzerland, 10–12 September 2003; Volume 1, pp. 103–114. [Google Scholar]
- Shieh, C.L.; Chen, Y.S.; Tsai, Y.J.; Wu, J.H. Variability in rainfall threshold for debris flow after the Chi-Chi earthquake in central Taiwan, China. Int. J. Sediment Res. 2009, 24, 177–188. [Google Scholar] [CrossRef]
- Yang, T.H.; Yang, S.C.; Ho, J.Y.; Lin, G.F.; Hwang, G.D.; Lee, C.S. Flash flood warnings using the ensemble precipitation forecasting technique: A case study on forecasting floods in Taiwan caused by typhoons. J. Hydrol. 2015, 520, 367–378. [Google Scholar] [CrossRef]
- Wu, D.S.; Wang, Y.F. A research on using critical precipitation value for Taiwan inundation warning system. In Proceedings of the 2009 Conference for Disaster Management in Taiwan, Taipei, Taiwan, 2009. (In Chinese). [Google Scholar]
- Pan, T.Y.; Yang, Y.T.; Kuo, H.C.; Tan, Y.C.; Lai, J.S.; Chang, T.J.; Lee, C.S.; Hsu, K.H. Improvement of statistical typhoon rainfall forecasting with ANN-based southwest monsoon enhancement. Terr. Atmos. Ocean. Sci. 2011, 22, 633–645. [Google Scholar] [CrossRef]
- Pan, T.Y.; Chang, L.Y.; Lai, J.S.; Chang, H.K.; Lee, C.S.; Tan, Y.C. Coupling typhoon rainfall forecasting with overland-flow modeling for early warning of inundation. Nat. Hazards 2014, 70, 1763–1793. [Google Scholar] [CrossRef]
- Buizza, R. The value of probabilistic prediction. Atmos. Sci. Lett. 2008, 9, 36–42. [Google Scholar] [CrossRef]
- Verkade, J.S.; Werner, M.G.F. Estimating the benefits of single value and probability forecasting for flood warning. Hydrol. Earth Syst. Sci. 2011, 15, 3751–3765. [Google Scholar] [CrossRef]
- Pappenberger, F.; Cloke, H.L.; Parker, D.J.; Wetterhall, F.; Richardson, D.S.; Thielen, J. The monetary benefit of early flood warnings in Europe. Environ. Sci. Policy 2015, 51, 278–291. [Google Scholar] [CrossRef]
- Arnal, L.; Ramos, M.H.; Coughlan de Perez, E.; Cloke, H.L.; Stephens, E.; Wetterhall, F.; Van Andel, S.J.; Pappenberger, F. Willingness-to-pay for a probabilistic flood forecast: a risk-based decision-making game. Hydrol. Earth Syst. Sci. 2016, 20, 3109–3128. [Google Scholar] [CrossRef]
- New, M.; Lopez, A.; Dessai, S.; Wilby, R. Challenges in using probabilistic climate change information for impact assessments: an example from the water sector. Philos. Trans. R. Soc. A 2007, 365, 2117–2131. [Google Scholar] [CrossRef] [PubMed]
- Siccardi, F.; Boni, G.; Ferrais, L.; Rudari, R. A hydrometeorological approach for probabilistic flood forecast. J. Geophys. Res. 2005, 110, D5. [Google Scholar] [CrossRef]
- Pappenberger, F.; Bartholmes, J.; Thielen, J.; Cloke, H.L.; Buizza, R.; de Roo, A. New dimensions in early flood warning across the globe using grand-ensemble weather predictions. Geophys. Res. Lett. 2008, 35, L10404. [Google Scholar] [CrossRef]
- Alfieri, L.; Velasco, D.; Thielen, J. Flash flood detection through a multi-stage probabilistic warning system for heavy precipitation events. Adv. Geosci. 2011, 9, 69–75. [Google Scholar] [CrossRef]
- Dale, M.; Wicks, J.; Mylne, K.; Pappenberger, F.; Laeger, S.; Taylor, S. Probabilistic flood forecasting and decision-making: an innovative risk-based approach. Nat. Hazards 2014, 70, 159–172. [Google Scholar] [CrossRef]
- Hardy, J.; Gourley, J.J.; Kirstetter, P.E.; Hong, Y.; Kong, F.; Flamig, Z.L. A method for probabilistic flash flood forecasting. J. Hydrol. 2016, 541, 480–494. [Google Scholar] [CrossRef]
- Buahin, C.A.; Sangwan, N.; Fagan, C.; Maidment, D.R.; Horsburgh, J.S.; Nelson, E.J.; Merwade, V.; Rae, C. Probabilistic flood inundation forecasting using rating curve libraries. J. Am. Water Resour. Assoc. 2017, 53, 300–315. [Google Scholar] [CrossRef]
- Todini, E. A model conditional processor to assess predictive uncertainty in flood forecasting. Int. J. River Basin Manag. 2008, 6, 123–137. [Google Scholar] [CrossRef]
- Biondi, D.; Todini, E. Comparing hydrological postprocessors including ensemble predictions into full predictive probability distribution of streamflow. Water Resour. Res. 2018, 54, 9860–9882. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef]
- Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2004, 40, W01106. [Google Scholar] [CrossRef]
- Todini, E.; Coccia, G.; Ortiz, E. On the proper use of Ensembles for Predictive Uncertainty assessment. In Proceedings of the European Geosciences Union General Assembly 2015, Vienna, Austria, 12–17 April 2015; Volume 17. EGU2015-10365. [Google Scholar]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.T. Learning from Data: A Short Course; AMLBook: New York, NY, USA, 2012. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: a gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Platt, J. Probabilistic outputs for support vector machines and comparison to regularized likelihood methods. In Advances in Large Margin Classifiers; Smola, A., Bartlett, P., Sch¨olkopf, B., Schuurmans, D., Eds.; MIT Press: Cambridge, MA, USA, 2000; Volume 10, pp. 61–74. [Google Scholar]
- Capital Engineering Corporation. The improvement plan of upper and middle reaches of Xin-dian River system; The Tenth River Management Office, Water Resources Agency, MOEA: Taipei, Taiwan, 2009. [Google Scholar]
- Arnaud, P.; Bouvier, C.; Cisneros, L.; Dominguez, R. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 2002, 260, 216–230. [Google Scholar] [CrossRef]
- Burian, S.; Shepherd, J.M. Effect of urbanization on the diurnal rainfall pattern in Houston. Hydrol. Process. 2005, 19, 1089–1103. [Google Scholar] [CrossRef]
- Segond, M.L.; Wheater, H.S.; Onof, C. The significance of spatial rainfall representation for flood runoff estimation: A numerical evaluation based on the Lee catchment. J. Hydrol. 2007, 347, 116–131. [Google Scholar] [CrossRef]
- Cheng, K.S.; Hueter, I.; Hsu, E.C.; Yeh, H.C. A scale-invariant Gauss-Markov model for design storm hyetographs. J. Am. Water Resour. Assoc. 2001, 37, 723–735. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A practical guide to support vector classification; Technical report; Department of Computer Science, National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Lin, H.T.; Lin, C.J.; Weng, R.C. A note on Platt’s probabilistic outputs for support vector machines. Mach. Learn. 2007, 68, 267–276. [Google Scholar] [CrossRef]
| City | District | Reference Rain Gauge | Official Cumulative Rainfall Threshold of Each Duration | ||||
|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 12 h | 24 h | |||
| Taipei | Wanhua | Taipei | 70 | 140 | 180 | 340 | 400 |
| Zhongzheng | Gongguan | 70 | 130 | 180 | 250 | 350 | |
| Taipei | 70 | 130 | 180 | 250 | 350 | ||
| Zhongzheng Bridge | 70 | 130 | 180 | 250 | 350 | ||
| Wenshan | Wenshan | 60 | 120 | 170 | 240 | 350 | |
| New Taipei | Banqiao | Banqiao | 50 | 120 | 150 | 200 | 300 |
| Tucheng | 50 | 120 | 150 | 200 | 300 | ||
| Tucheng | Banqiao | 60 | 110 | 150 | 210 | 300 | |
| Tucheng | 50 | 110 | 150 | 210 | 300 | ||
| Zhonghe | Zhonghe | 50 | 110 | 150 | 230 | 300 | |
| Yonghe | Zhongzheng Bridge | 60 | 120 | 170 | 230 | 300 | |
| Xindian | Quchi | 50 | 130 | 180 | 250 | 350 | |
| Xindian | 50 | 130 | 180 | 250 | 350 | ||
| Wulai | Fushan | 70 | 140 | 270 | 310 | 450 | |
| Tunghou | - | - | - | - | - | ||
| Xiapen | - | - | - | - | - | ||
| Fushan(3) | 70 | 140 | 270 | 310 | 450 | ||
| Datungshan | 70 | 140 | 270 | 310 | 450 | ||
| Shenkeng | Shenkeng | 60 | 150 | 230 | 350 | 450 | |
| Shiding | Shiding | 80 | 150 | 230 | 350 | 450 | |
| Pinglin | Pinglin | 80 | 150 | 230 | 330 | 400 | |
| Observation | |||
|---|---|---|---|
| Yes | No | ||
| Warning | Yes | Hit | False alarm |
| No | Miss | Correct negative | |
| Rain Gauge Name | 1–5 h | 6–10 h | 11–15 h | 16–20 h | 21–25 h |
|---|---|---|---|---|---|
| Zhongzheng Bridge | 1 | 9 | 11 | 16 | 22 |
| Taipei | 1 | 7 | 11 | 16 | 25 |
| Banqiao | 1 | 6 | 14 | 16 | 24 |
| Gongguan | 1 | 7 | 11 | 16 | 22 |
| Xindian | 1 | 6 | 12 | 17 | 21 |
| Zhonghe | 1 | 10 | 11 | 19 | 21 |
| Tucheng | 1 | 6 | 14 | 16 | 24 |
| Wenshan | 1 | 6 | 11 | 17 | 23 |
| Shenkeng | 1 | 8 | 11 | 16 | 21 |
| Quchi | 1 | 6 | 12 | 19 | 21 |
| Shiding | 1 | 9 | 11 | 16 | 23 |
| Pinglin | 1 | 9 | 11 | 16 | 22 |
| Tunghou | 1 | 9 | 13 | 16 | 21 |
| Fushan | 1 | 10 | 11 | 16 | 22 |
| Fushan(3) | 1 | 6 | 13 | 17 | 25 |
| Xiapen | 1 | 10 | 11 | 16 | 25 |
| Datungshan | 1 | 8 | 15 | 17 | 23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, T.-Y.; Lin, H.-T.; Liao, H.-Y. A Data-Driven Probabilistic Rainfall-Inundation Model for Flash-Flood Warnings. Water 2019, 11, 2534. https://doi.org/10.3390/w11122534
Pan T-Y, Lin H-T, Liao H-Y. A Data-Driven Probabilistic Rainfall-Inundation Model for Flash-Flood Warnings. Water. 2019; 11(12):2534. https://doi.org/10.3390/w11122534
Chicago/Turabian StylePan, Tsung-Yi, Hsuan-Tien Lin, and Hao-Yu Liao. 2019. "A Data-Driven Probabilistic Rainfall-Inundation Model for Flash-Flood Warnings" Water 11, no. 12: 2534. https://doi.org/10.3390/w11122534
APA StylePan, T.-Y., Lin, H.-T., & Liao, H.-Y. (2019). A Data-Driven Probabilistic Rainfall-Inundation Model for Flash-Flood Warnings. Water, 11(12), 2534. https://doi.org/10.3390/w11122534




