1. Introduction
Groundwater is a crucial water resource for domestic use in arid and semi-arid regions because of its relatively stable and large storage capacity, easy extraction, and low vulnerability to contamination as compared to surface water resources [
1]. However, due to the growth of population, leading to an increase in agricultural activities, sewage disposal, and industrial wastewater, the pollution of groundwater is now a vital issue for groundwater resource sustainability [
2,
3]. Contaminated groundwater treatment is costly, and the prevention of groundwater pollution is, thus, an effective solution to protect groundwater resources [
4]. The assessment of groundwater vulnerability (GV) is recognized as an efficient approach to determine the potential zones of contamination linked to natural and social–economic conditions [
5].
The concept of GV was proposed for decades, and the vulnerability maps are critical references in decision-making for land-use planning, groundwater management, monitoring, and remediation [
6]. Previous investigations proposed three basic approaches to evaluate GV for specific groundwater basins. These approaches can be categorized as (1) index-overlay methods, (2) process-based physical methods, and (3) statistical methods [
4]. Among these approaches, the index-overlay methods are recognized to be efficient and useful to identify GV and are especially proper for utilization with a geographical information system (GIS), which provides useful tools to overlay and integrate the different multiple maps [
2,
3,
7,
8].
The DRASTIC model is the most efficient and widely used index-overlay method for quantifying GV because of its ease of use, minimal data demand, and good definition of GV. With the development of GIS and the associated database, the simple calculations of the DRASTIC model are physically meaningful and well-suited for large-scale problems. Investigators took into account the correlation between the vulnerability index and contaminant concentration in combination with the sensitivity analysis of DRASTIC parameters for vulnerability assessment [
7,
8,
9,
10]. However, the GV maps obtained from the DRASTIC model might be unreliable because the feature ratings and weights in the model are site-specific, and the accuracy highly depends on the experience of the investigators. Recently, many studies proposed the modification of the conventional DRASTIC model for mapping groundwater vulnerability zones, including (i) geostatistics [
11,
12], (ii) an artificial neural network (ANN) [
13,
14], and (iii) the analytical hierarchy process (AHP) [
7,
8,
15]. Among them, the AHP revealed that the modification based on the local hydrogeological setting shows better and more accurate results. Optimizing the weights of DRASTIC using AHP was more effective [
15]. Additionally, the DRASTIC model with the AHP also shows a high correlation between the GV map and the contaminants as compared to field measurements [
16].
The DRASTIC method is flexible, and it can be integrated with other parameters such as lineament, land use/land cover, aquifer thickness, and impact of contaminant, depending on the local hydrogeological conditions and data availability in specific areas [
2,
7,
17]. Recent studies considered land use in a DRASTIC model to improve GV maps [
18,
19,
20]. In general, the change in land use might influence the net recharge in the study areas [
21]. Land use may directly influence the groundwater recharge process, and it plays a critical role in the prediction of the impacts of human activities on groundwater quality. Ribeiro [
22] assessed the impact of the land use on groundwater pollution potential for an agricultural coastal plain using the susceptibility index (SI) method. Lima et al. [
17] applied a modified DRASTIC model and Dynamic Conversion of Land-Use (Dyna-CLUE) model to predict the effect of future agricultural expansion on GV. The factors in GV models typically use fixed groundwater levels and average precipitation to quantify the impact of land use on the variations of GV maps. Li and Merchant [
23] further analyzed the impact of projected land-use change on the vulnerability of groundwater to pollution. They considered that DRASTIC factors such as depth to water, recharge, and land-use conditions might change in response to future changes in climate and socio-economic conditions. The model was used to evaluate groundwater pollution risks under future climate and land-use changes in North Dakota. Results showed that high GV would expand northward and northwestward in eastern North Dakota under different scenarios. Unlike previous studies, this study is the first to consider temporal variations of GV that are connected to future climate and socio-economic conditions.
The critical implementation of the GV map is to quantify the water-related health risks that are induced by different anthropogenic activities. Groundwater pollution risk is defined as the process of estimating the possibility that a particular event may occur under a given set of circumstances [
24]. The groundwater risk assessment integrates information from the aquifer vulnerability, the pollution loads, and the probability of contaminant occurrence. With recent developments in the risk analysis models, Kazakis and Voudouris [
25] employed the DRASTIC model and a nitrogen loss method to assess the GV and pollution risk in porous aquifers. They replaced qualitative parameters such as aquifer type, soil, and impact of the vadose zone with quantitative parameters, including aquifer thickness, nitrogen losses from the soil, and hydraulic resistance. Results of the modified DRASTIC models enabled the estimation of the pollution risk to nitrates. Goudarzi et al. [
26] combined the DRASTIC and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method to map the zones of groundwater pollution risk caused by agricultural practices. The results from their study efficiently identified the area with high-risk levels, which might need emergency recovery action plans. However, the data without long-term observations of climate and land-use data limit the implementation of GV and risk maps to account for temporal variations in a specific groundwater basin. The spatial and temporal evolution of the health risk to groundwater pollution is critical to support decision-making for local development plans.
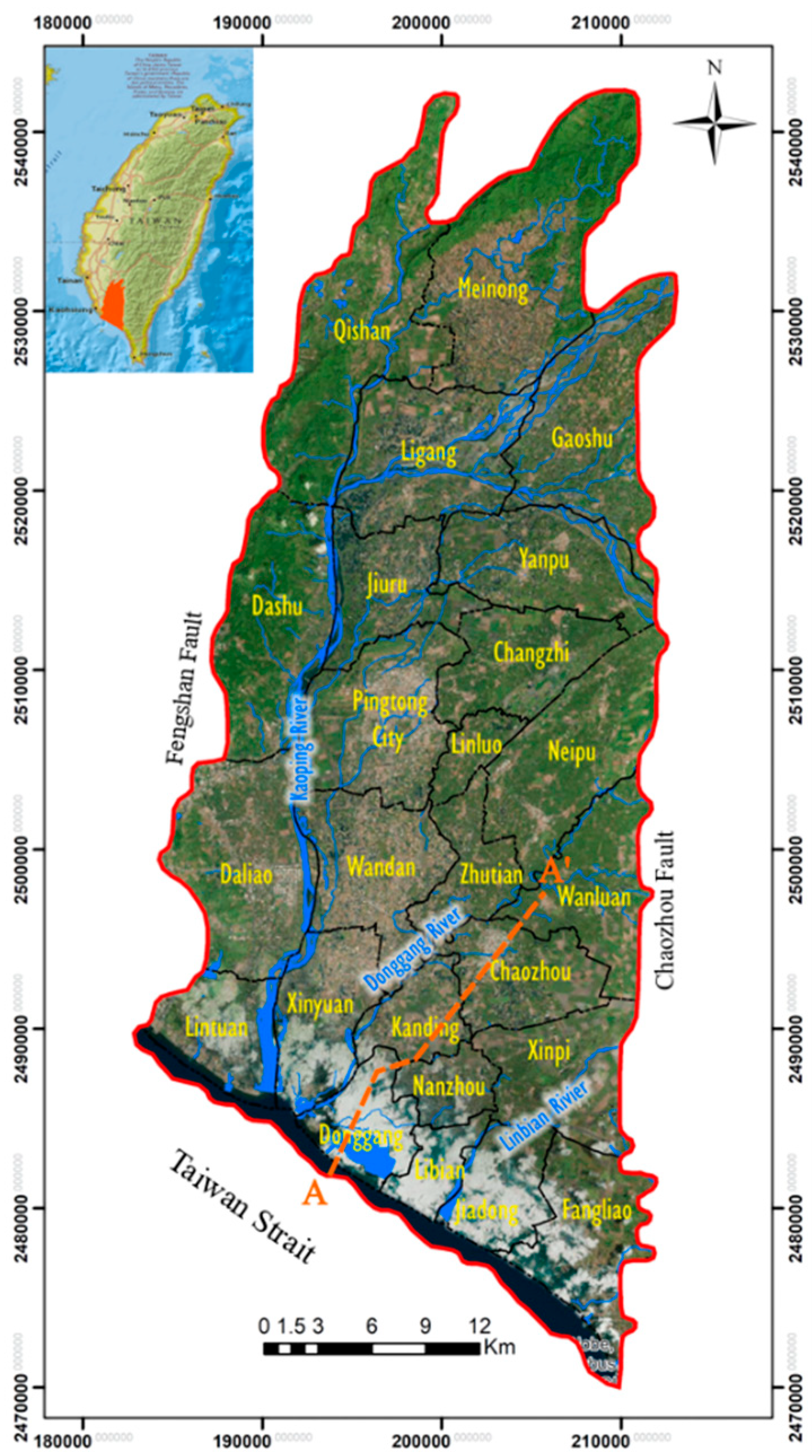
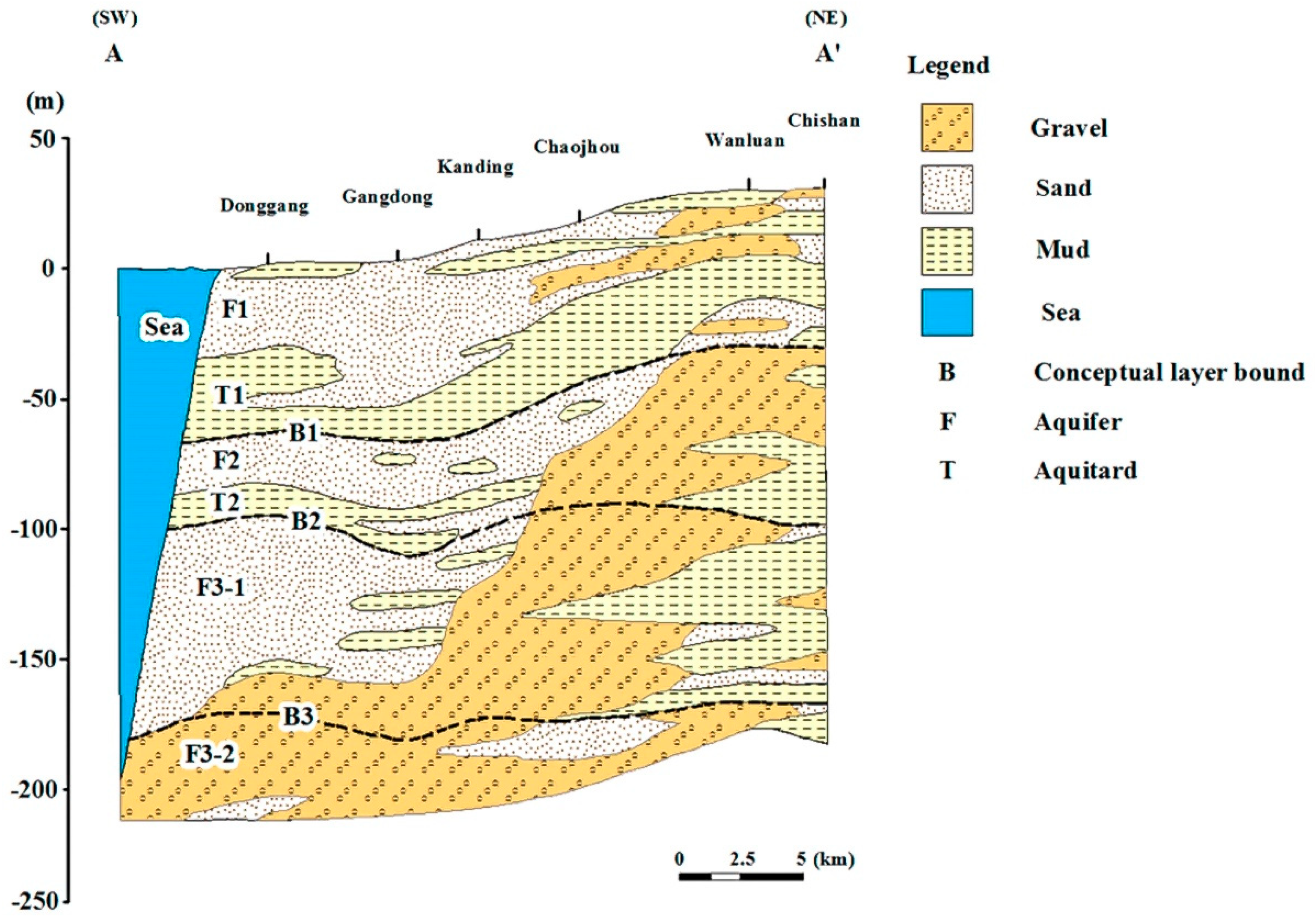
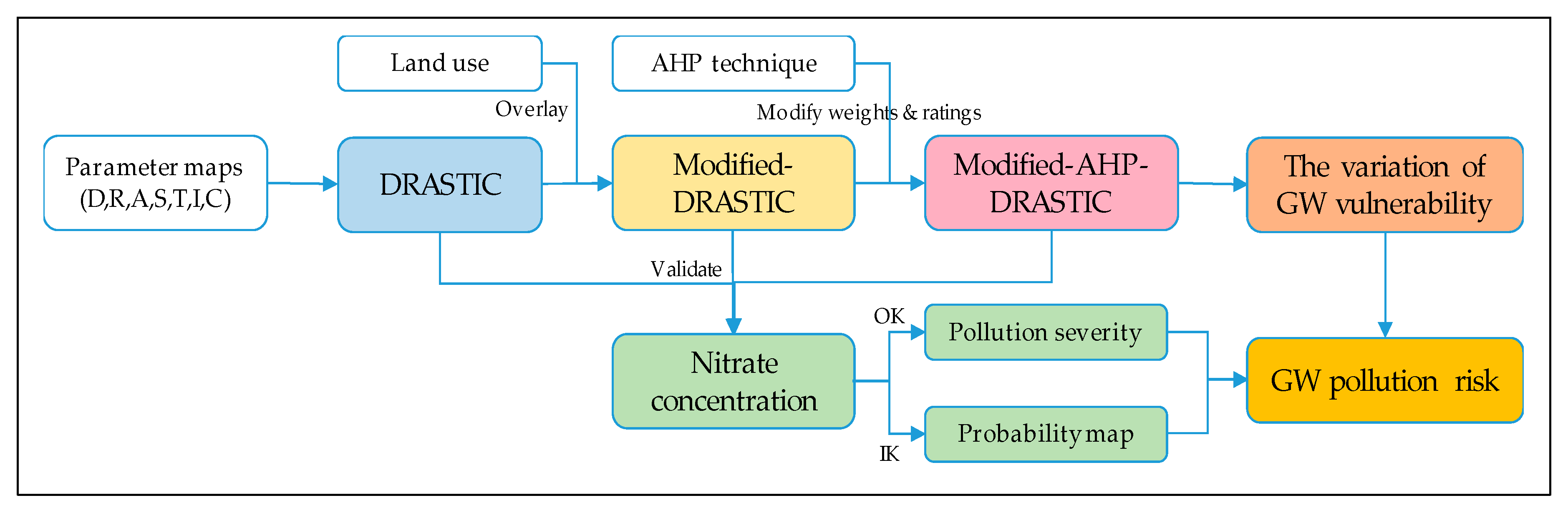
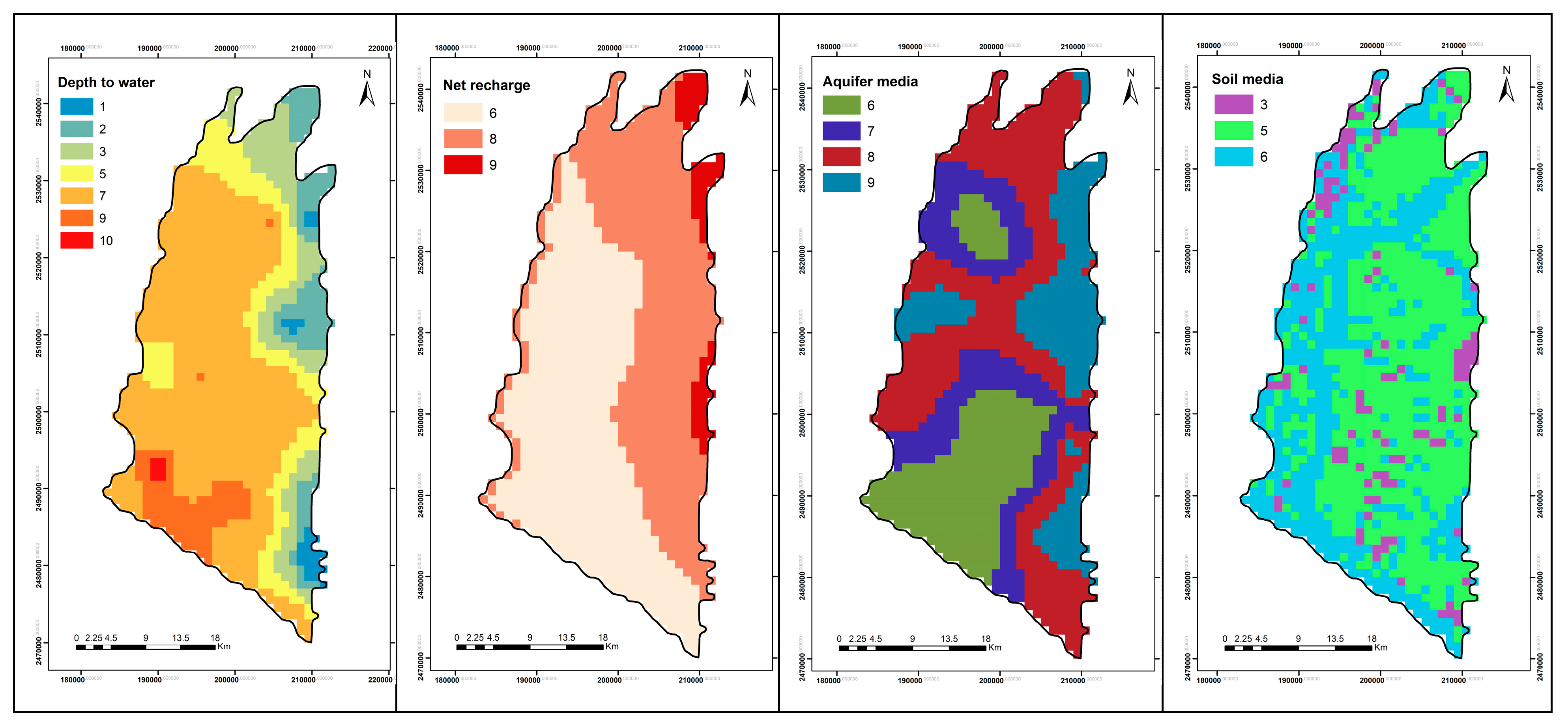
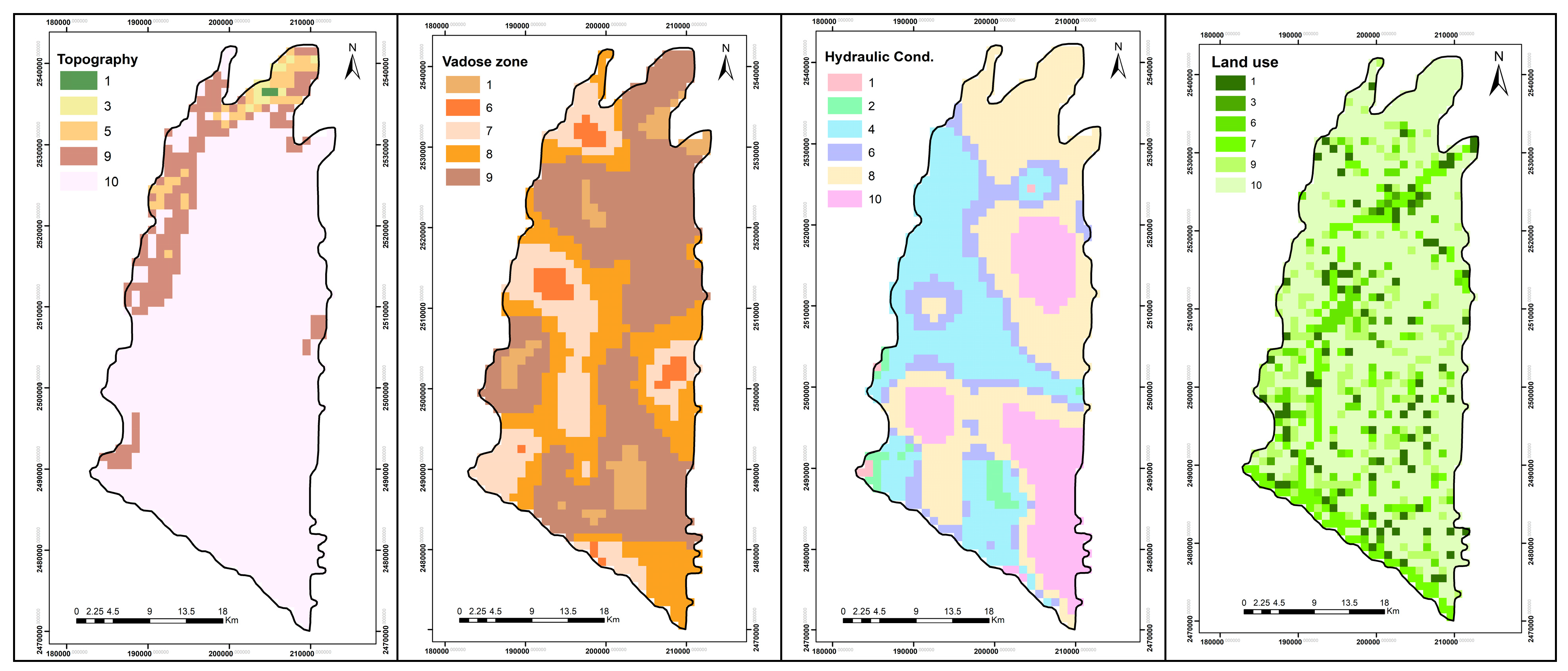
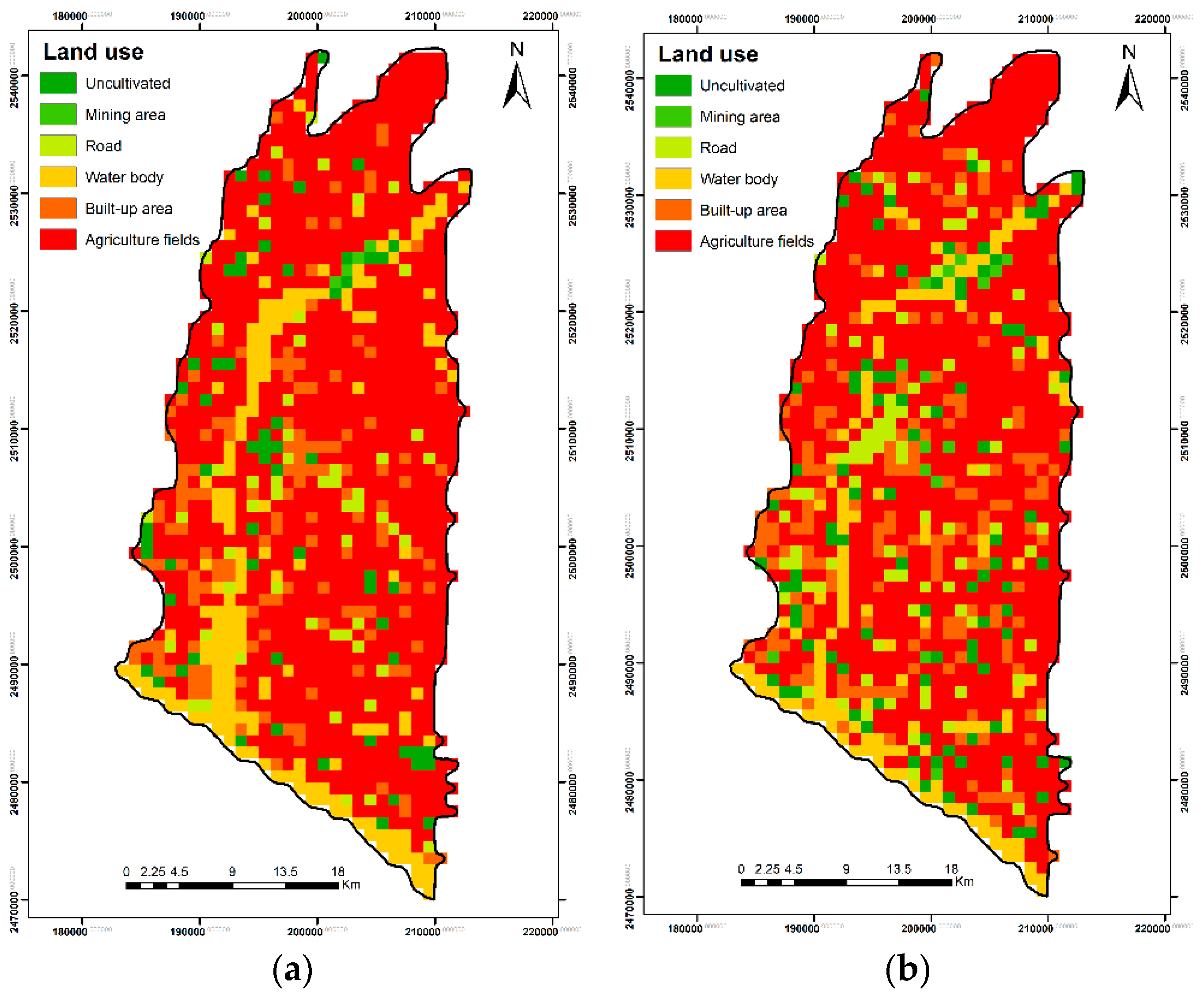
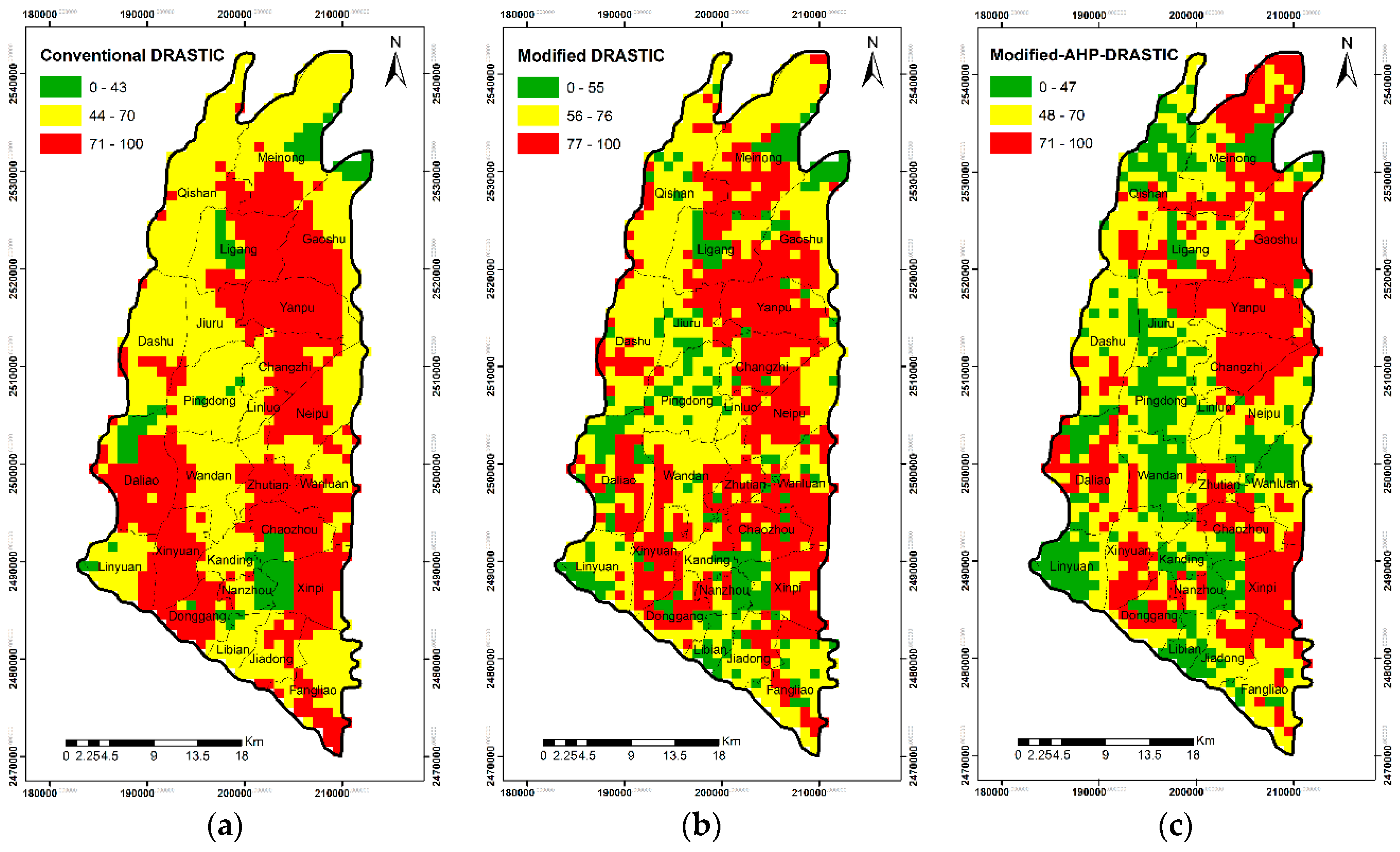
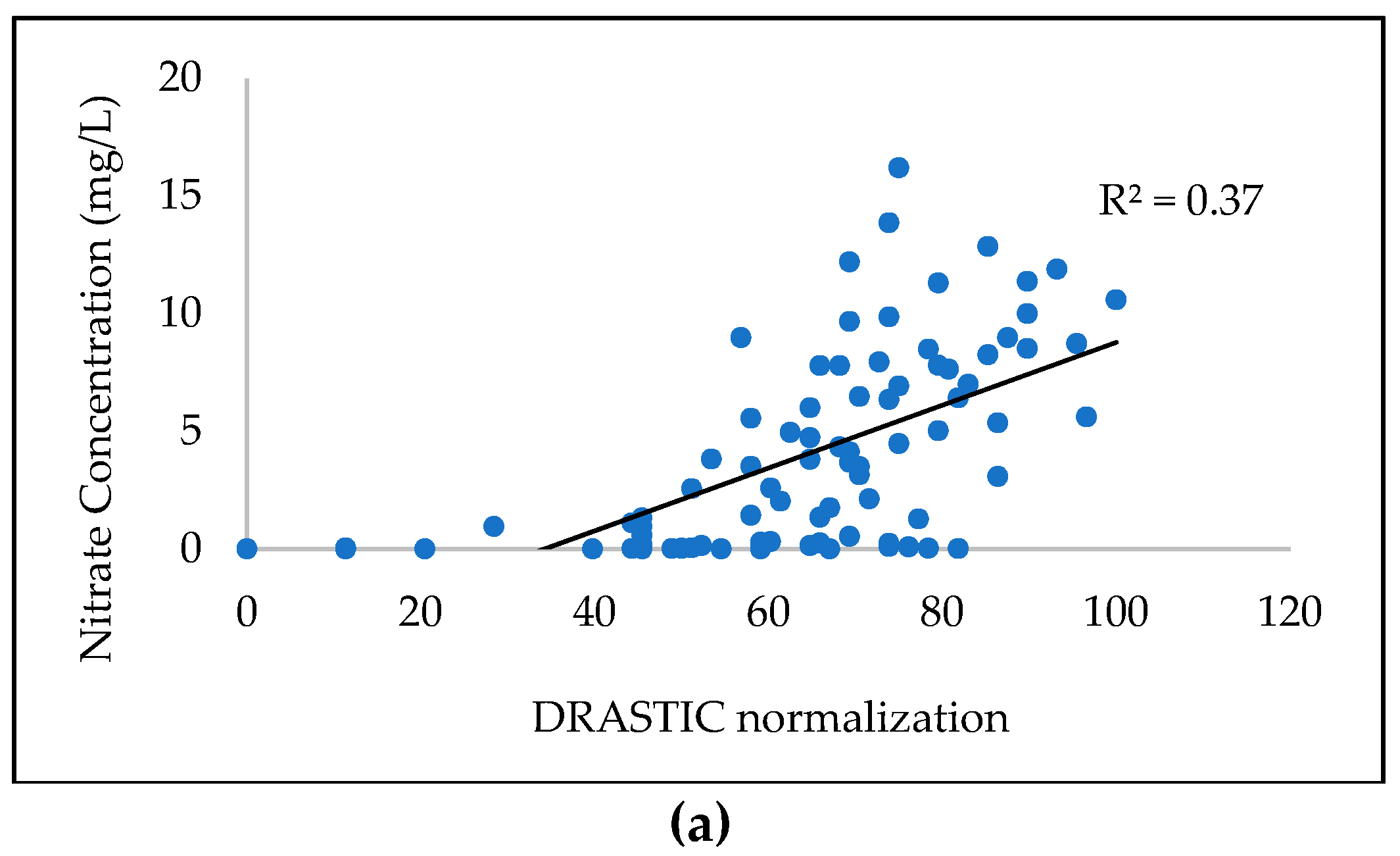
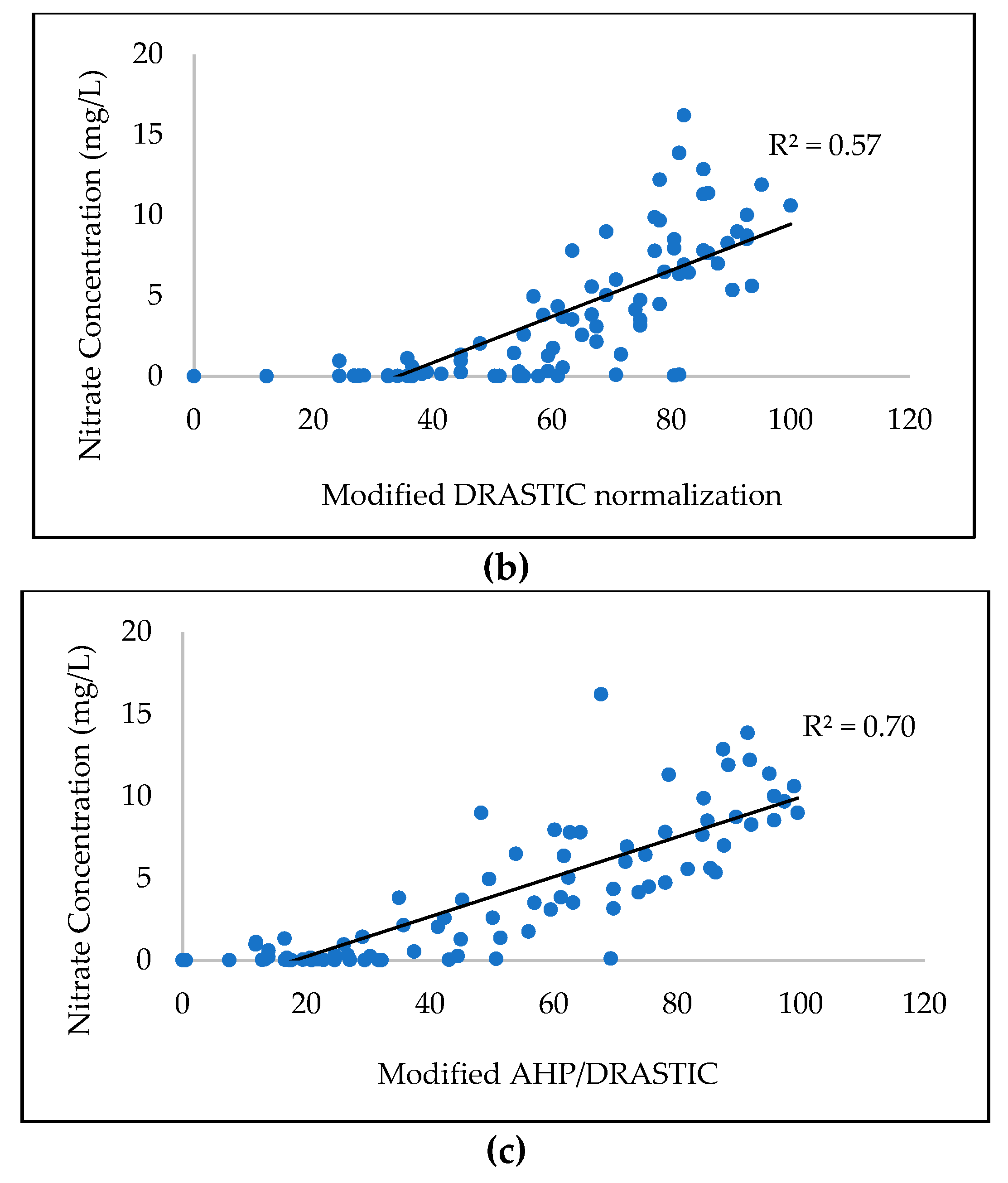
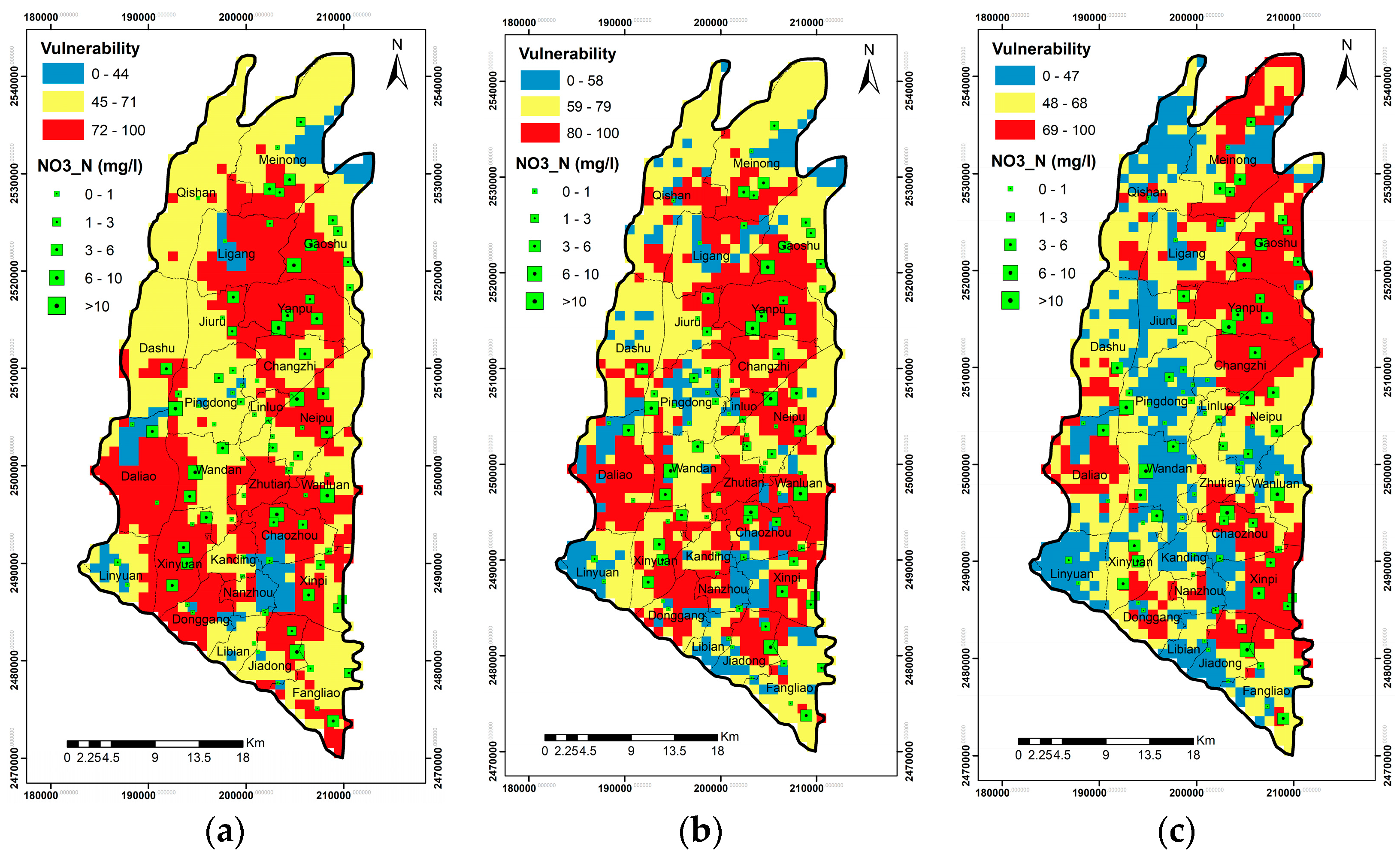
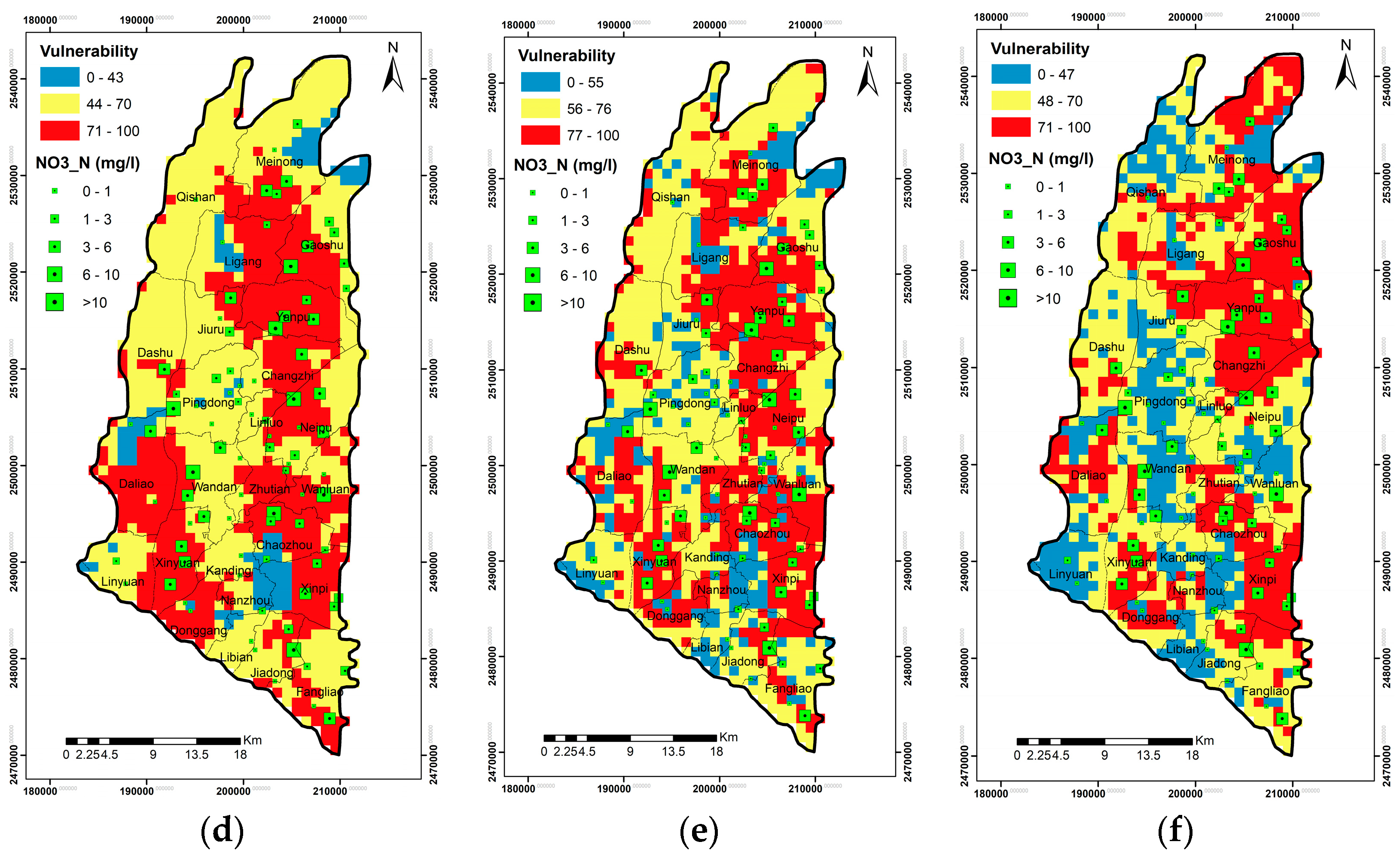
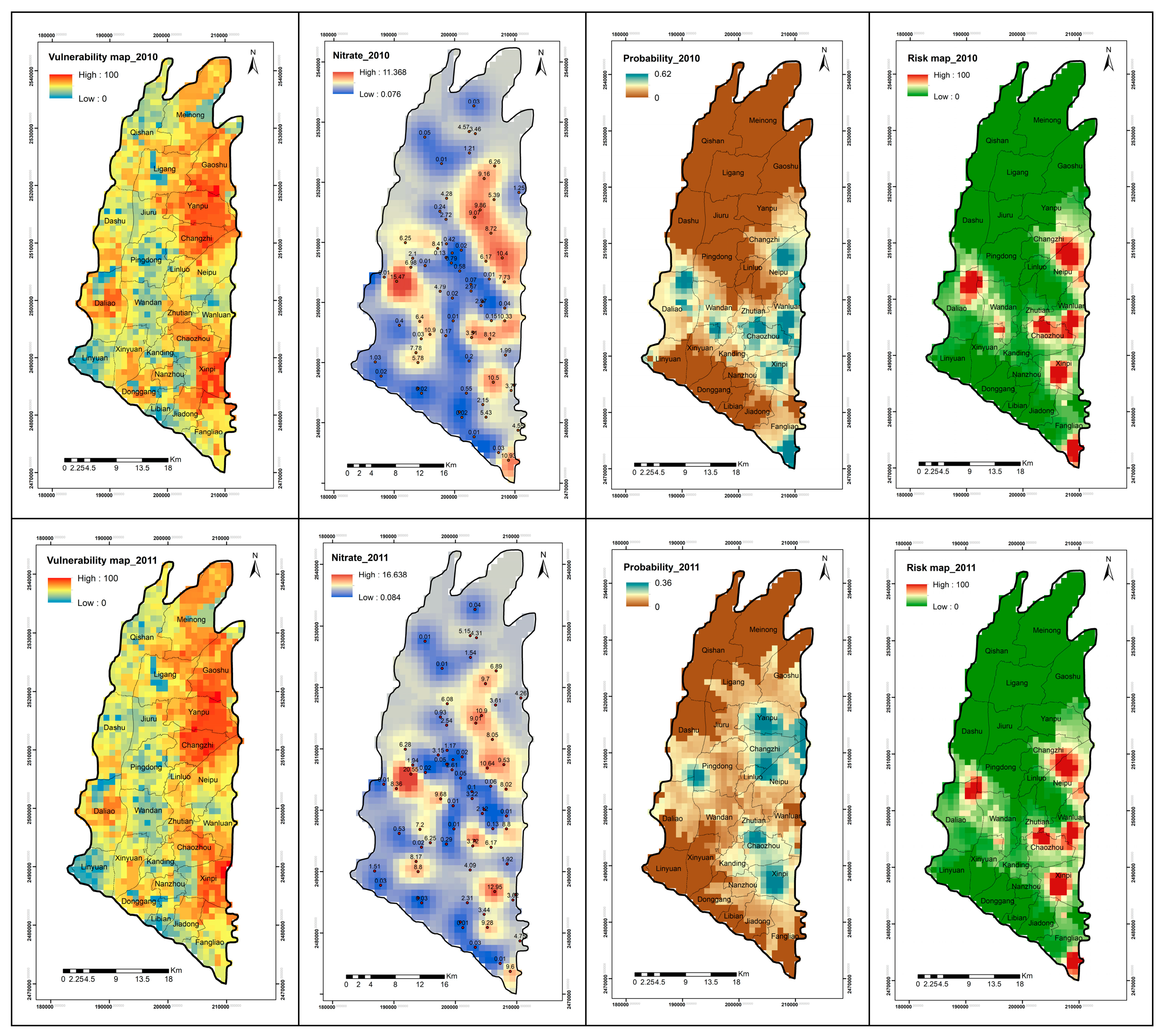
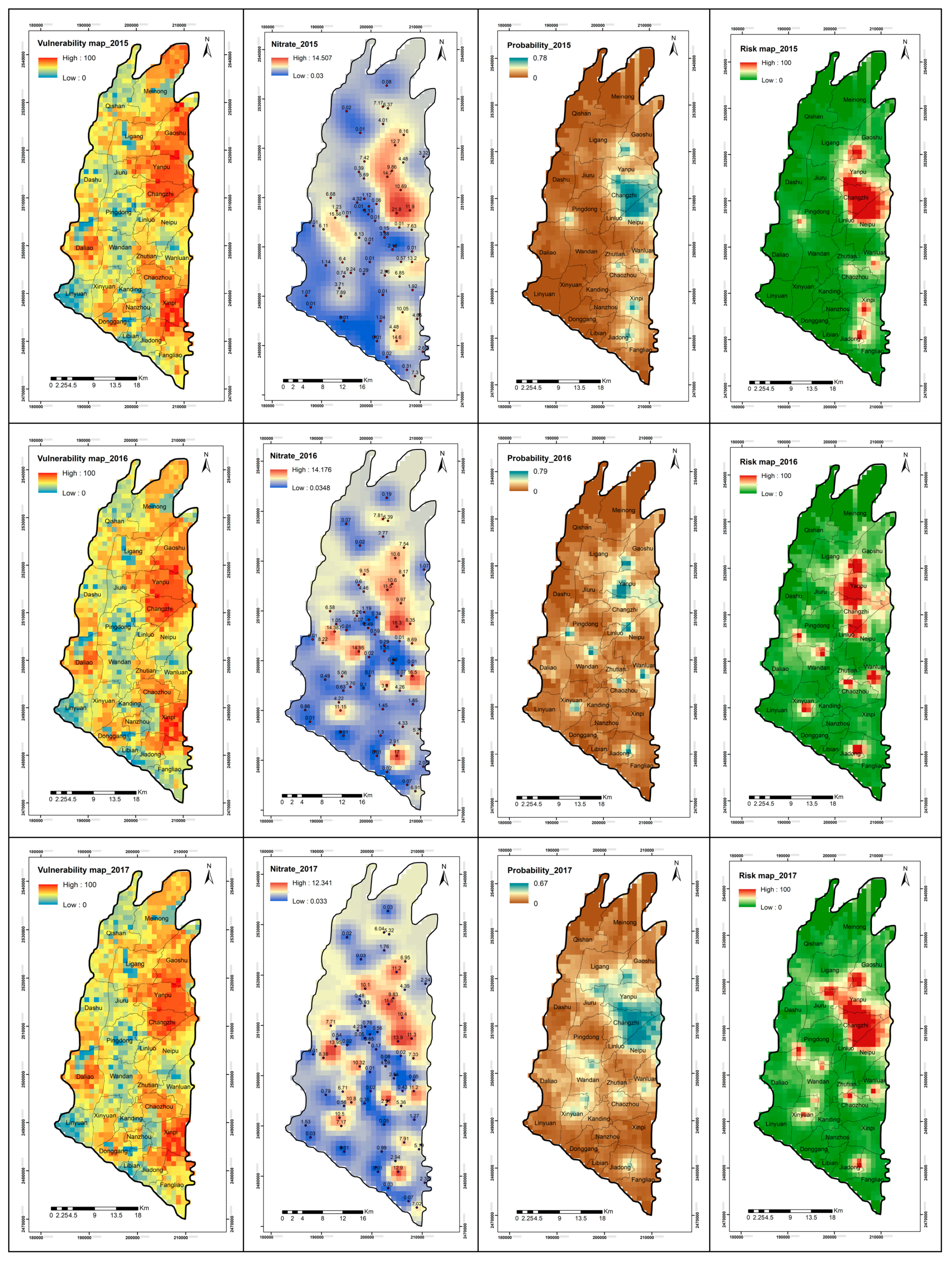
Based on long-term observations of groundwater quality data and available data of land use in Taiwan, this study aimed to quantify the spatial and temporal evolution of GVs and zones of groundwater contamination in the Pingtung groundwater basin in southern Taiwan. More specifically, the DRASTIC model, coupled with the factor of land use and the AHP theory, was employed to calculate the variations of GV. The results of GV were validated with site-specific nitrate concentration values obtained from 2010–2017. The comparison of GV for different land-use maps aimed to quantify the influence of land use on the results of different DRASTIC models. The year-averaged risk maps were then obtained by integrating the validated GV maps, the pollution severity interpolated by ordinary kriging (OK), and the probability of occurrence calculated by indicator kriging (IK). Additionally, the study conducted sensitivity analysis to determine significant input variables that influence the reliability of GV mapping. The results of this study are expected to support policy-makers to adopt the strategies of sustainable development for groundwater resources such as the mitigation of groundwater pollution, the planning of land-use patterns and practices, and the allocation of groundwater resources in local areas.
4. Conclusions
With long-term observations of groundwater quality data in Taiwan, this study assessed and quantified the evolution of GV and zones of groundwater pollution risk in the Pingtung plain groundwater basin in southern Taiwan. The results suggested that the modified AHP/DRASTIC model performed the best in terms of estimating GV, which was highly consistent with the site-specific nitrate observations. The land use is one of the crucial factors that directly reflect the effect of anthropogenic activities on GVs. The newest parameter LU can enhance the reliability of GV mapping because the LU reflects the state of the land use in the study area. The estimations of the spatial–temporal variations of GV and groundwater pollution risk enabled the identification of variable agriculture activities in the study period. In recent years, the increase of specific agriculture zones (or agriculture parks) and other anthropogenic activities yielded an increase in vulnerability to groundwater pollution. Because of the water demands, all these specific agriculture zones (or agriculture parks) are mainly developed by rivers.
Over two decades (1995–2017), the groundwater vulnerability in Pingtung plain slightly decreased due to the change in land-use types such as built-up areas, traffic, and mining areas. The changes in land-use patterns, which are highly related to the land development policy in Pingtung plain, can lead to variations in GV and, therefore, influence the strategies of groundwater resource protection and management. The groundwater contamination risk showed that Jiuru and Ligang counties recorded no risk of groundwater contamination in the past; however, in recent years, these counties exhibited a high risk of groundwater contamination, indicating that agricultural activities increased considerably in recent years. The counties of Yanpu, Changzhi, Gaoshu, and several small areas in Pingtung plain recorded high pollution risk from 2010 up to now. With farmland conditions and changes in plant type, these high-risk areas excluded Fangliao county after 2016. These variations in contamination risk are essential for decision-making and policies of regional development plans.
The concept of spatial–temporal variations in GV and pollution risk shows the importance of human activities on the groundwater environment. In this study, a land-use map was created in 2017, which might not be suitable for estimating GVs from 2010 to 2016 and in the years after 2017. Taking advantage of satellite and imaging technologies, detailed and high-frequency land-use maps can be obtained for any specific area. It is possible to monitor the dynamic variations of GV or pollution risk to track the impact of real-time human activities on the groundwater environment and the influence of health for groundwater usage. Additionally, the prediction of GV and pollution risk can also be possible if the GV estimations are coupled with real-time groundwater monitoring networks and physical groundwater models. Lastly, the physical models can predict and quantify the DRASTIC parameters that correspond to the development plans or strategies for water resources.