Effect of Deficit Irrigation on Nitrogen Uptake of Sunflower in the Low Desert Region of California
Abstract
:1. Introduction
2. Material and Methods
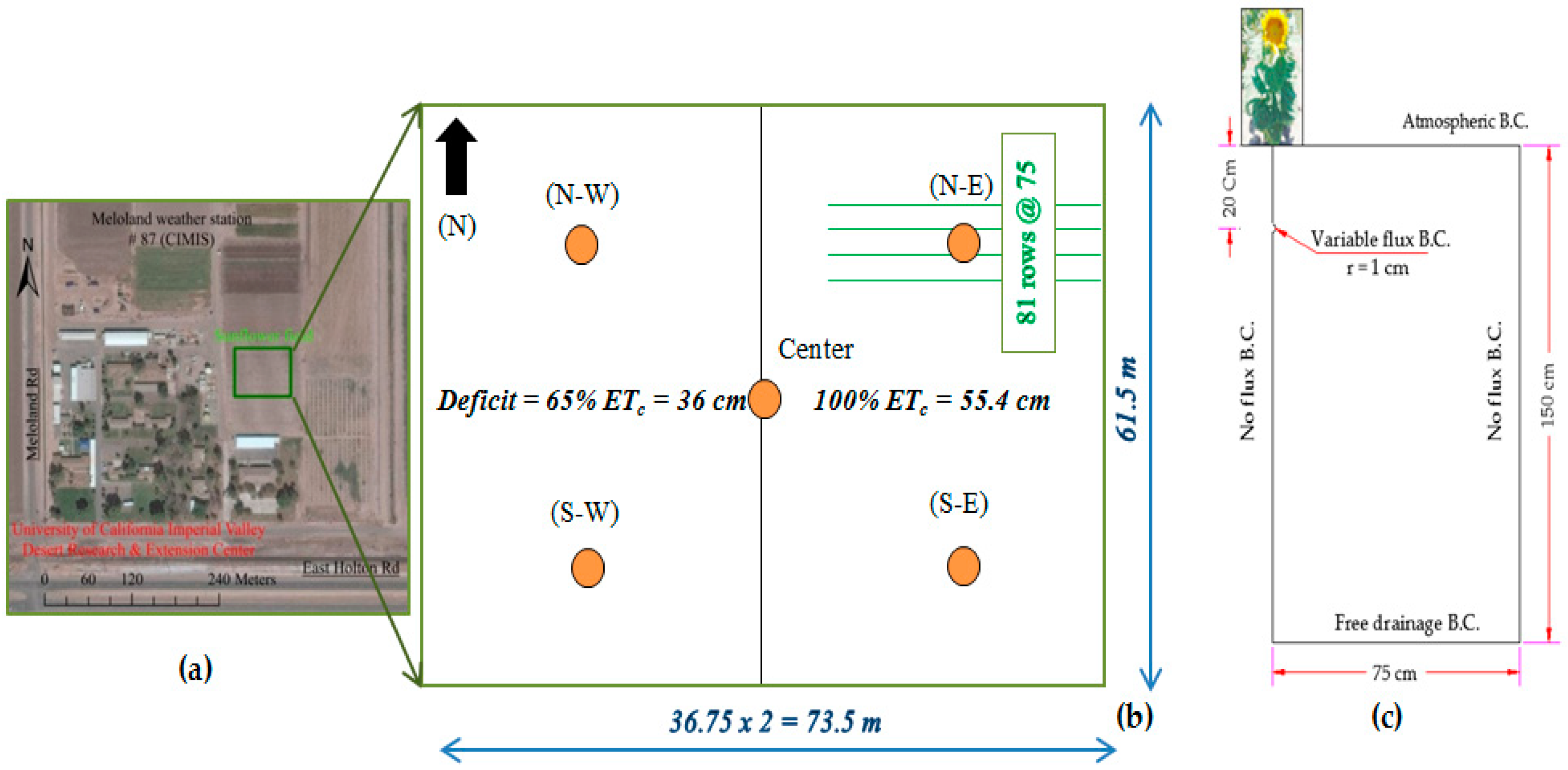
2.1. Study Area and Sunflower Water Use
2.2. Planting, Irrigation, and Fertigation Scheduling
2.3. Transformation Processes and Mass Balance
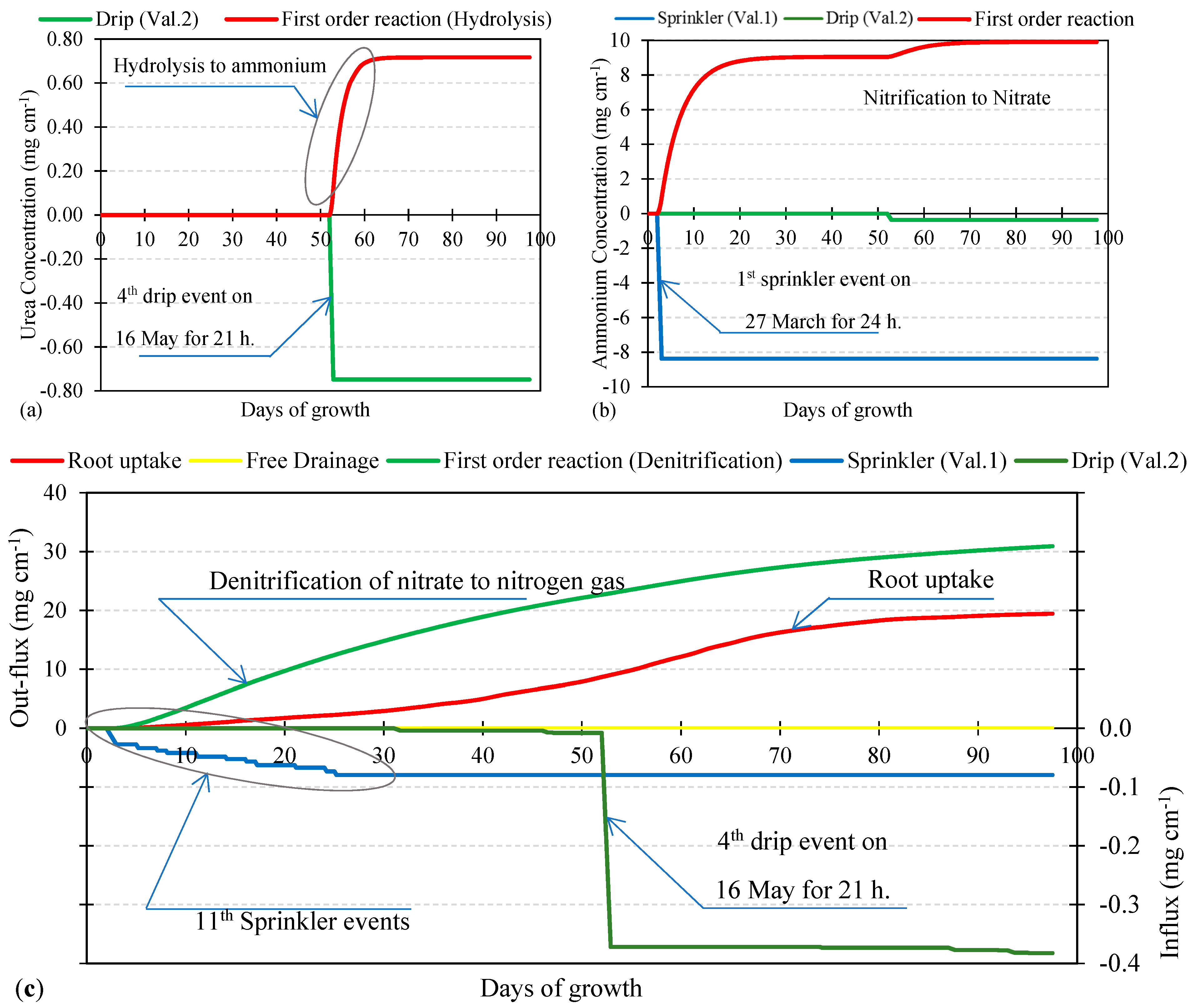
3. Results
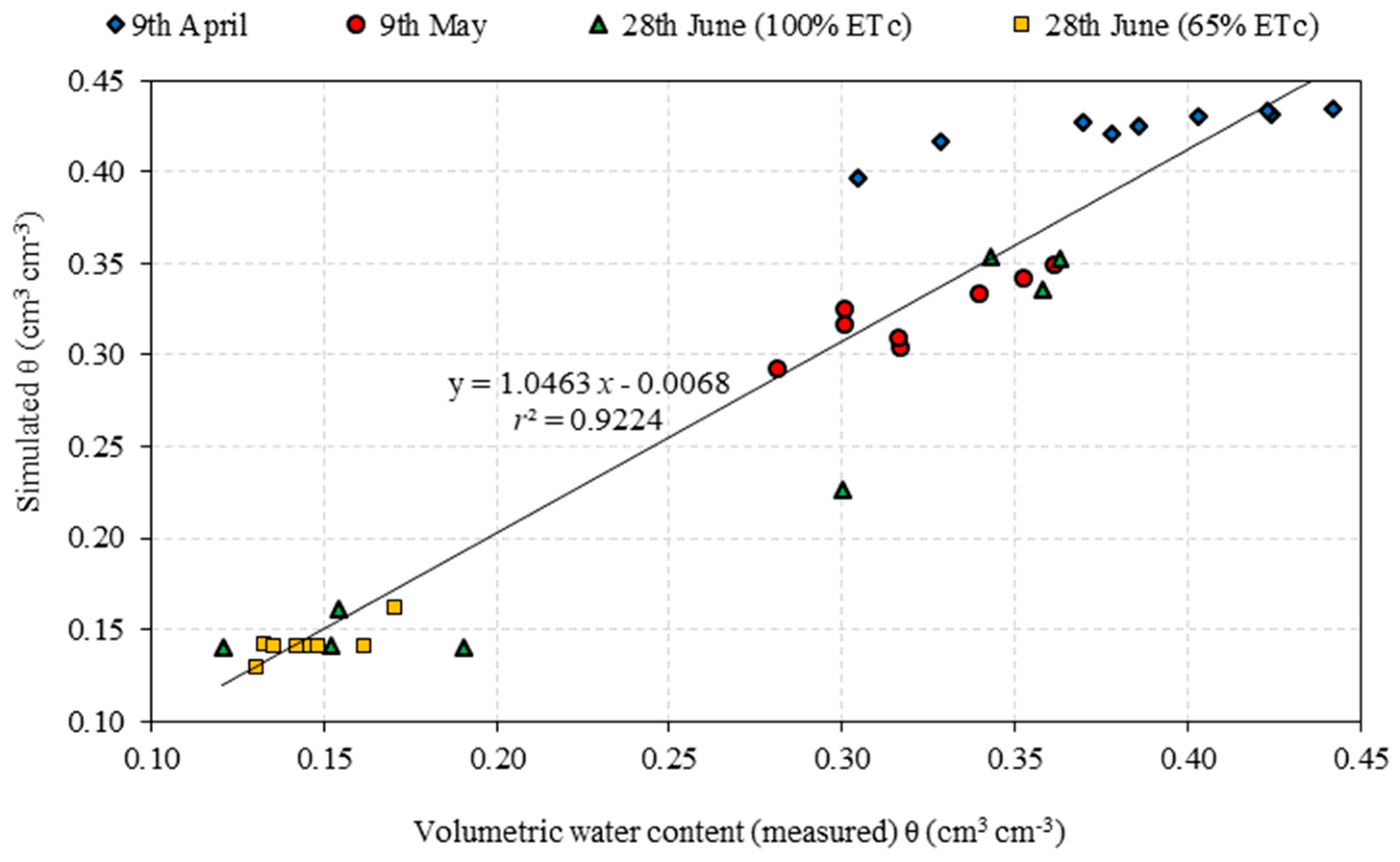
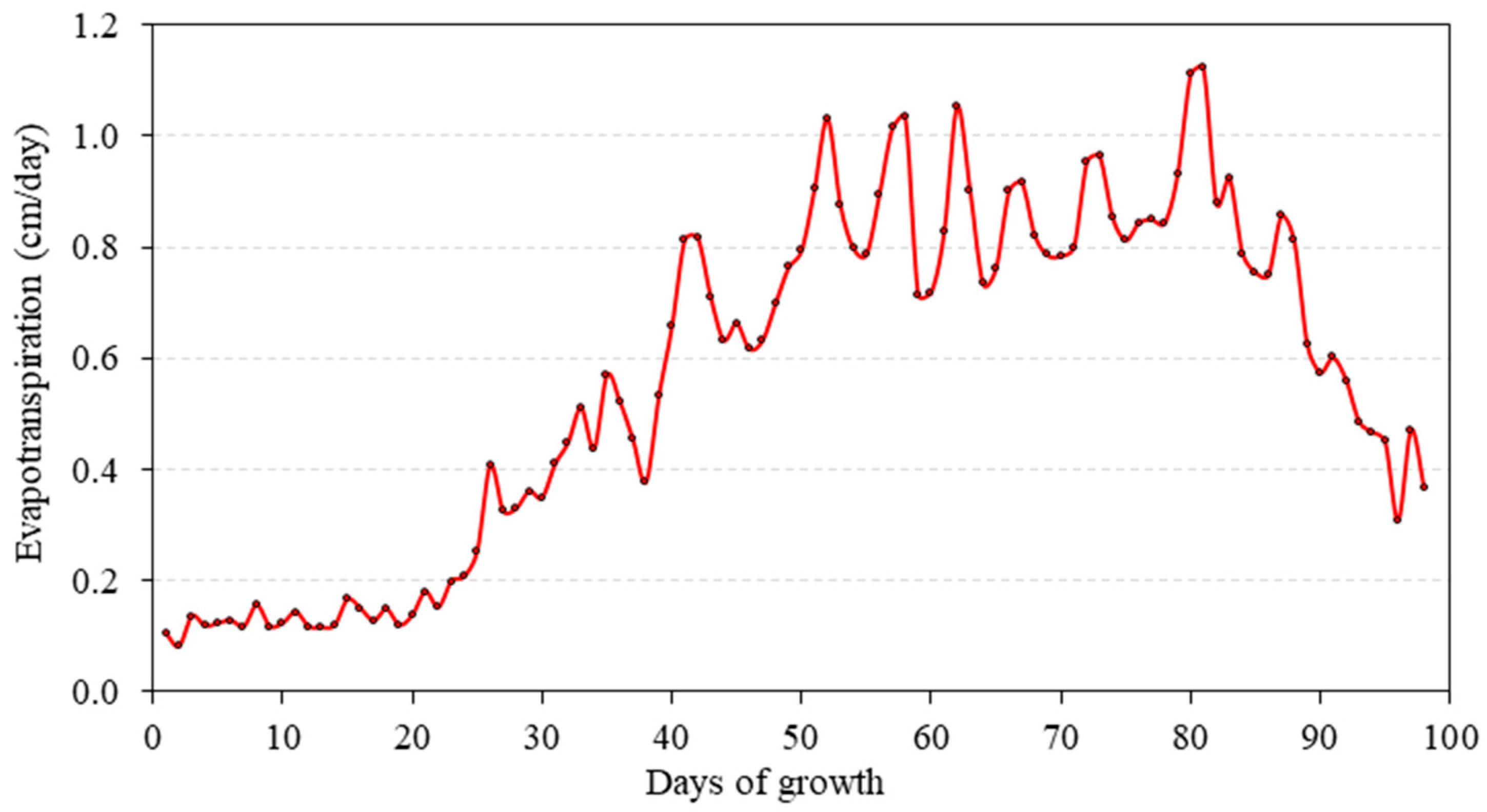
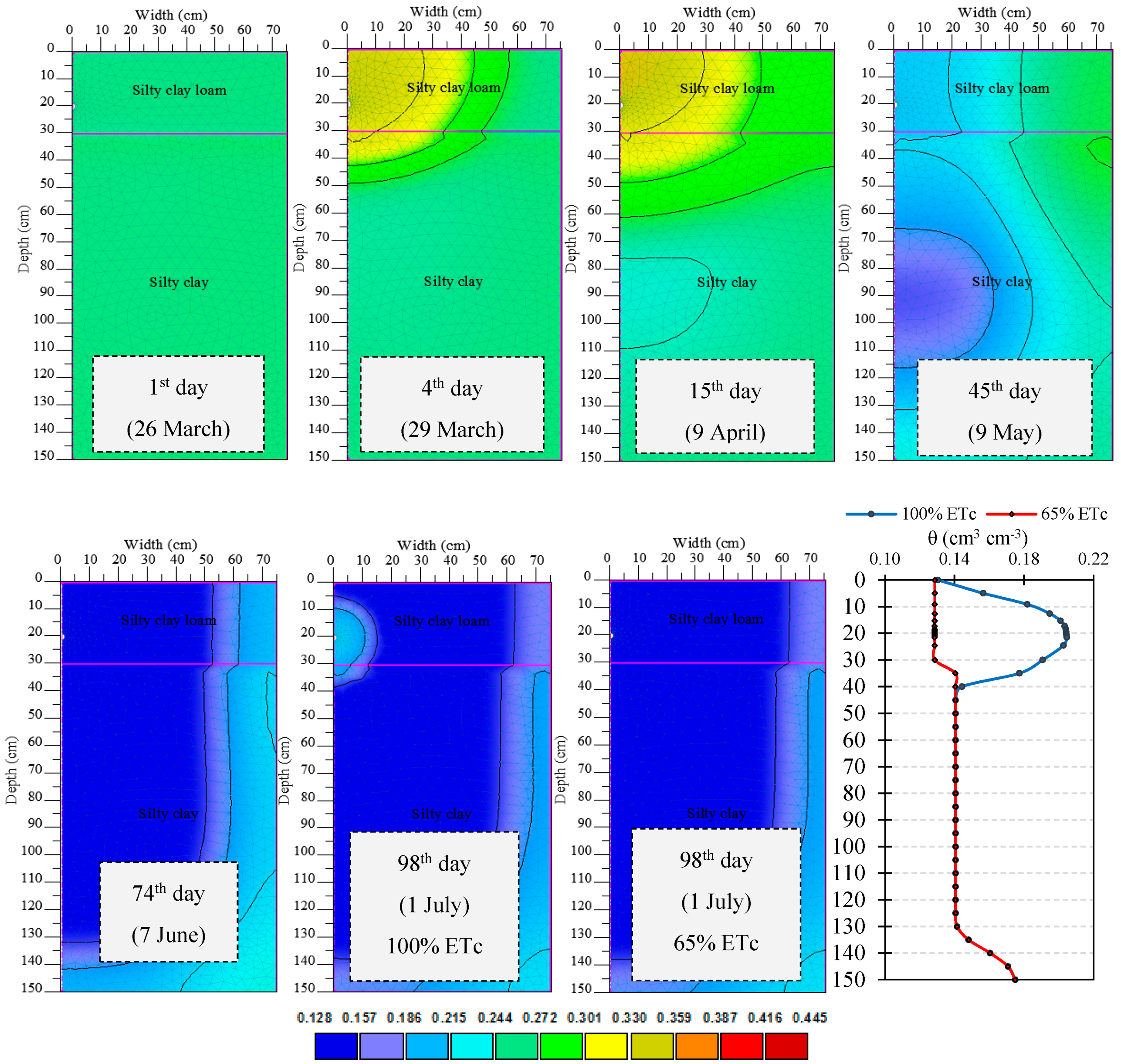
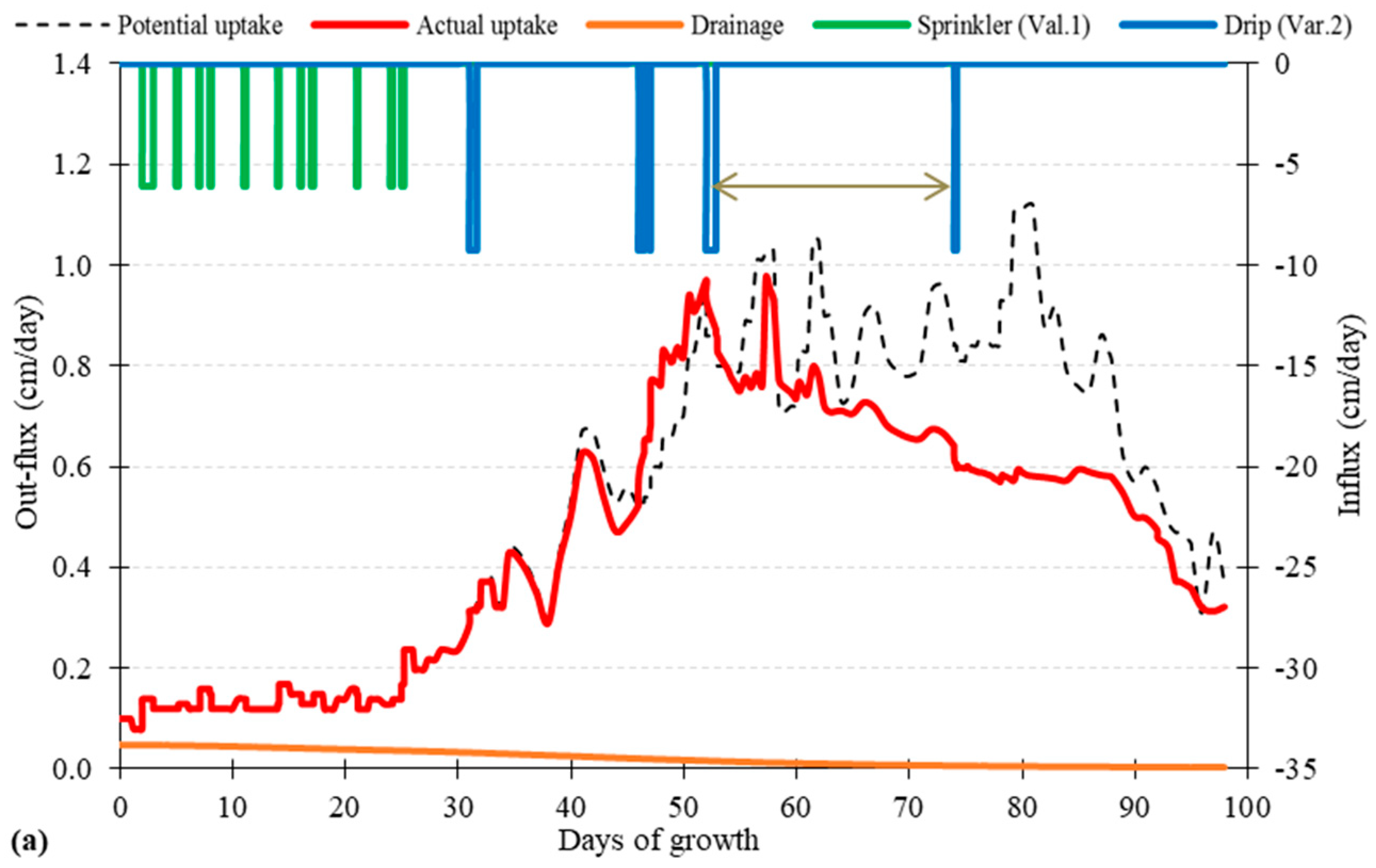
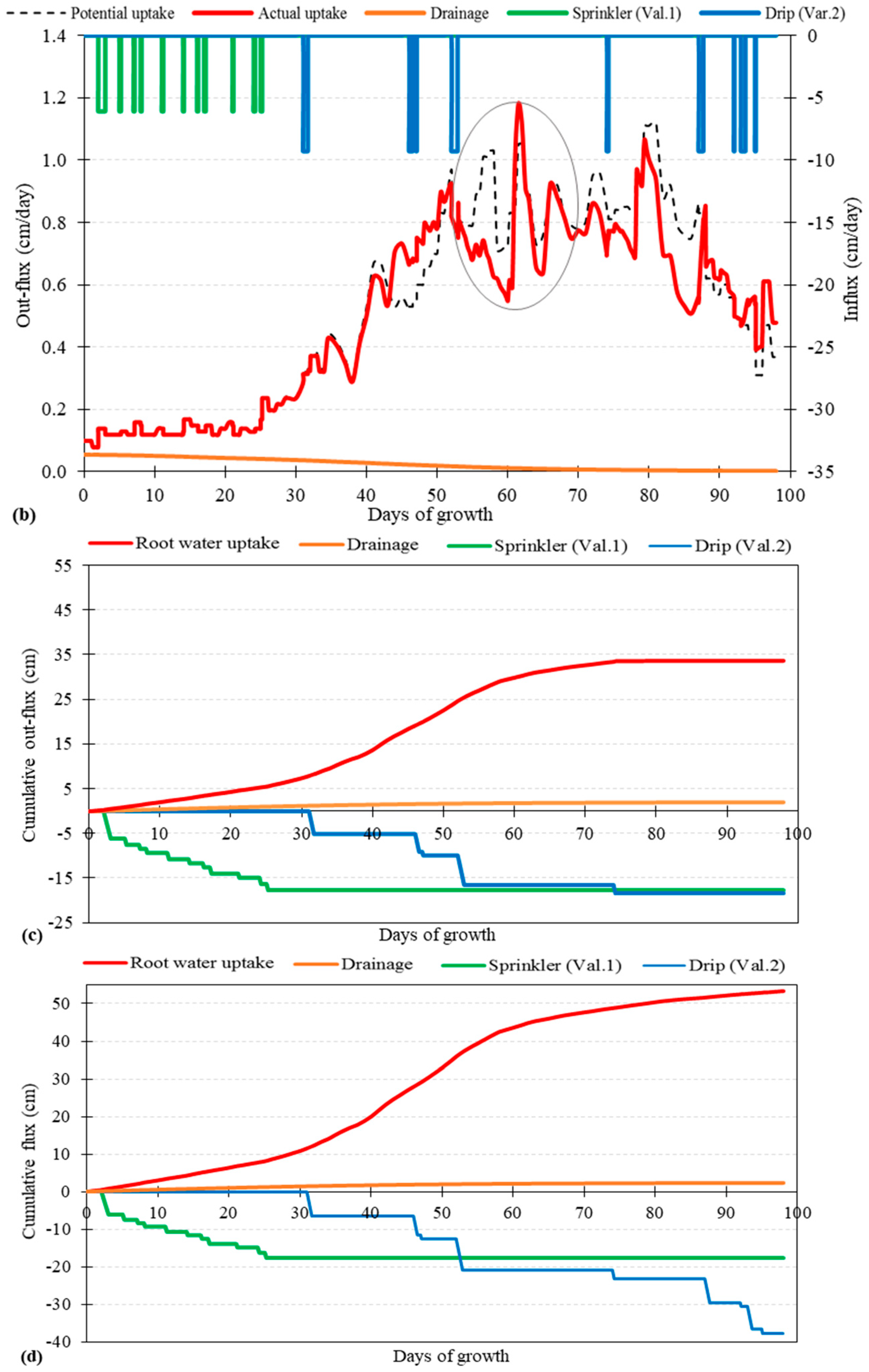
3.1. Root Water Uptake and Model Calibration
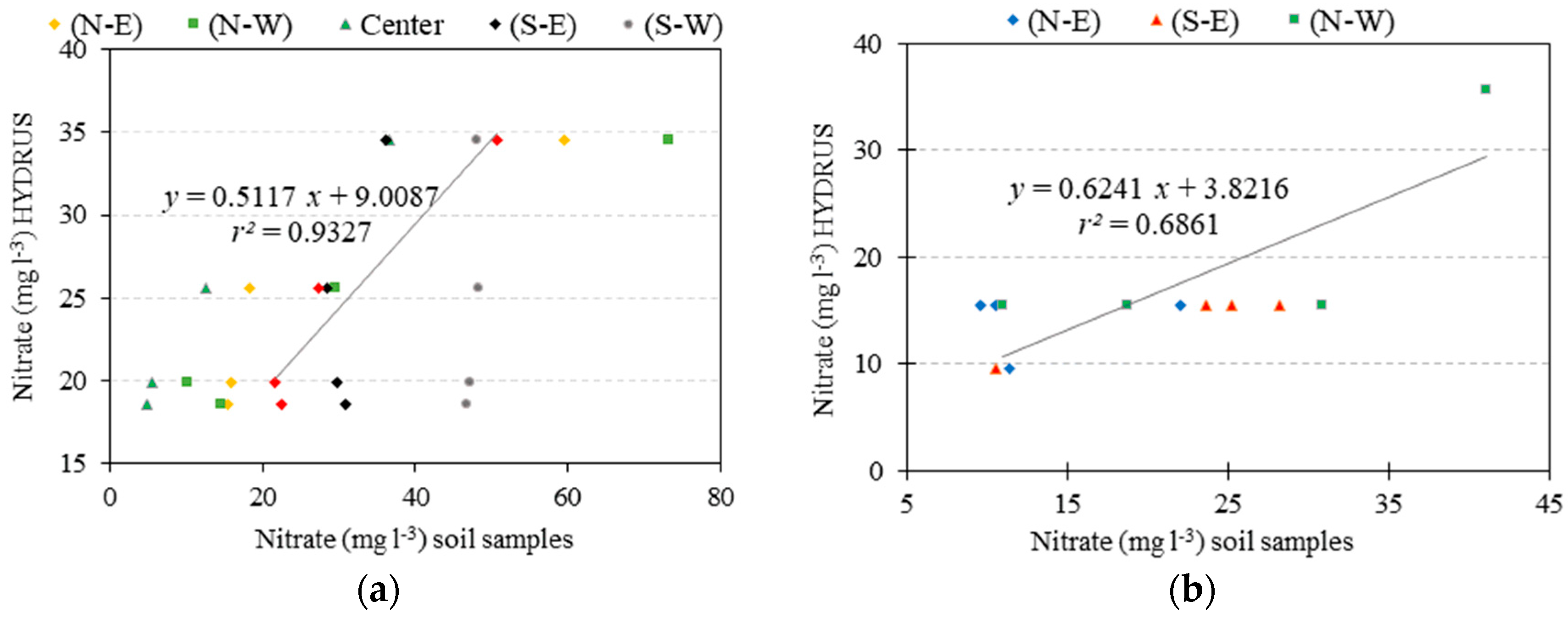
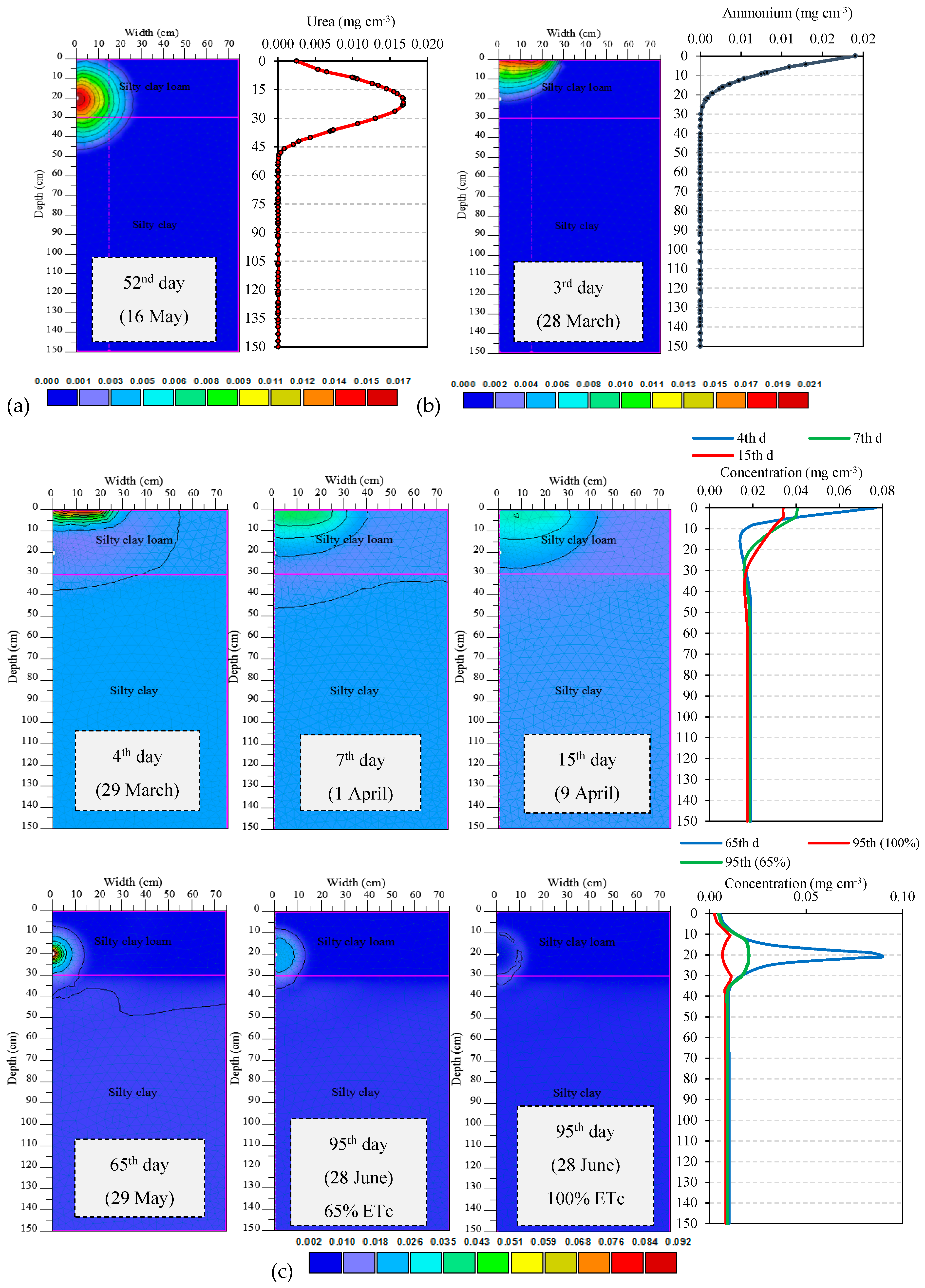
3.2. Nutrient Uptake and Calibration of Transformation Parameters
4. Discussion
5. Conclusions and Recommendations
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Razaq, M.; Zhang, P.; Shen, H.L. Influence of nitrogen and phosphorus on the growth and root morphology of Acer mono. PLoS ONE 2017, 12, e0171321. [Google Scholar] [CrossRef] [PubMed]
- Mullins, G. Phosphorus, Agriculture & the Environment. Virginia Cooperative Extension. 2009. Available online: https://efotg.sc.egov.usda.gov/references/public/va/PhosphorousAgEnv.pdf (accessed on 20 November 2013).
- He, M.; Dijkstra, F.A. Drought effect on plant nitrogen and phosphorus: A meta-analysis. New Phytol. 2014, 204, 924–931. [Google Scholar] [CrossRef] [PubMed]
- Demir, A.O.; Goksoy, A.T.; Buyukcangaz, H.; Turan, Z.M.; Köksal, E.S. Deficit irrigation of sunflower (Helianthus annuus L.) in a sub-humid climate. Irrig. Sci. 2006, 24, 279. [Google Scholar] [CrossRef]
- Rouphael, Y.; Cardarelli, M.; Schwarz, D.; Franken, P.; Colla, G. Effects of drought on nutrient uptake and assimilation in vegetable crops. In Plant Responses to Drought Stress; Aroca, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 171–195. [Google Scholar]
- Sardans, J.; Penuelas, J. The role of plants in the effects of global change on nutrient availability and stoichiometry in the plant-soil system. Plant Physiol. 2012, 160, 1741–1761. [Google Scholar] [CrossRef] [PubMed]
- Farooq, M.; Hussain, M.; Wahid, A.; Siddique, K.H.M. Drought stress in plants: An Overview. In Plant Responses to Drought Stress; Aroca, R., Ed.; Springer Press: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Schimel, J.P.; Balser, T.C.; Wallenstein, M. Microbial stress response physiology and its implications for ecosystem function. Ecology 2007, 88, 1386–1394. [Google Scholar] [CrossRef] [PubMed]
- Lambers, H.; Chapin, F.S.; Pons, T.L. Plant Physiological Ecology; Springer: New York, NY, USA, 2008. [Google Scholar]
- Farooq, M.; Aziz, T.; Wahid, A.; Lee, D.J.; Siddique, K.H.M. Chilling tolerance in maize: Agronomic and physiological approaches. Crop Pasture Sci. 2009, 60, 501–516. [Google Scholar] [CrossRef]
- Austin, A.T.; Yahdjian, L.; Stark, J.M.; Belnap, J.; Porporato, A.; Norton, U.; Ravetta, D.A.; Schaeffer, S.M. Water pulses and biogeochemical cycles in arid and semiarid ecosystems. Oecologia 2004, 141, 221–235. [Google Scholar] [CrossRef]
- Delgado-Baquerizo, M.; Maestre, F.T.; Gallardo, A.; Bowker, M.A.; Wallenstein, M.D.; Quero, J.L.; Ochoa, V.; Gozalo, B.; García-Gómez, M.; Soliveres, S.; et al. Decoupling of soil nutrient cycles as a function of aridity in global drylands. Nature 2013, 502, 672–676. [Google Scholar] [CrossRef]
- Zeng, W.; Xu, C.; Huang, J.; Wu, J.; Ma, T. Emergence rate, yield, and nitrogen-use efficiency of sunflowers (Helianthus annuus) vary with soil salinity and amount of nitrogen applied. Commun. Soil Sci. Plant Anal. 2015, 46, 1006–1023. [Google Scholar] [CrossRef]
- Lazicki, P.A.; Geisseler, D. Soil nitrate testing supports nitrogen management in irrigated annual crops. Calif. Agric. 2016, 71, 90–95. [Google Scholar] [CrossRef]
- Mathers, A.C.; Stewart, B.A. Sunflower nutrient uptake, growth, and yield as affected by nitrogen or manure, and plant populations. Agron. J. 1982, 74, 911–915. [Google Scholar] [CrossRef]
- Schneekloth, J.P. Response of Irrigated Sunflowers to Water Timing. Central Great Plains Research Station 2002 Annual Report. Colorado State University: Akron, CO, USA 4 pgs. Available online: https://www.ksre.k-state.edu/irrigate/oow/p05/Schneekloth1.pdf (accessed on 1 June 2019).
- Zeng, W.; Xu, C.; Wu, J.; Huang, J. Sunflower seed yield estimation under the interaction of soil salinity and nitrogen application. Field Crop. Res. 2016, 198, 1–15. [Google Scholar] [CrossRef]
- Abbadi, J.; Gerendás, J.; Sattelmacher, B. Effects of nitrogen supply on growth, yield and yield components of safflower and sunflower. Plant Soil 2008, 306, 167–180. [Google Scholar] [CrossRef]
- Vigil, M.F.; Benjamin, J.; Schepers, J. Yield response and fertilizer nitrogen recovery by dry land sunflowers in a no-till rotation. In Proceedings of the 23rd Sunflower Production Workshop, Fargo, ND, USA, 17–18 January 2001; Vol. 23, pp. 90–94. [Google Scholar]
- Rachael, L.; Gulya, T.; Light, S.; Bali, K.; Mathesius, K.; Meyer, R. Sunflower Hybrid Seed Production in California. 2019. Available online: https://anrcatalog.ucanr.edu/Details.aspx?itemNo=8638 (accessed on 1 June 2019).[Green Version]
- Eltarabily, M.G.A.; Negm, A.M.; Valeriano, O.C.S.; Gafar, K.E. Effects of di-ammonium phosphate on hydraulic, compaction, and shear strength characteristic of sand and clay soils. Arab. J. Geosci. 2015, 8, 10419–10432. [Google Scholar] [CrossRef]
- Blamey, F.P.C.; Chapman, J. Protein, Oil, and Energy Yields of Sunflower as Affected by N and P Fertilization1. Agron. J. 1981, 73, 583. [Google Scholar] [CrossRef]
- Davidson, E.A.; Seitzinger, S. The enigma of progress in denitrification research. Ecol. Appl. 2006, 16, 2057–2063. [Google Scholar] [CrossRef]
- Gentry, L.E.; David, M.B.; Below, F.E.; Royer, T.V.; McIsaac, G.F. Nitrogen Mass Balance of a Tile-drained Agricultural Watershed in East-Central Illinois. J. Environ. Qual. 2009, 38, 1841–1847. [Google Scholar] [CrossRef] [Green Version]
- Jaynes, D.; Colvin, T.; Karlen, D.; Cambardella, C.; Meek, D. Nitrate loss in subsurface drainage as affected by nitrogen fertilizer rate. J. Environ. Qual. 2001, 30, 1305–1314. [Google Scholar] [CrossRef]
- Webb, J.; Ellis, S.; Harrison, R.; Thorman, R. Measurement of N fluxes and soil N in two arable soils in the UK. Plant Soil 2004, 260, 253–282. [Google Scholar] [CrossRef]
- Hama, T.; Nakamura, K.; Kawashima, S.; Kaneki, R.; Mitsuno, T. Effects of cyclic irrigation on water and nitrogen mass balances in a paddy field. Ecol. Eng. 2011, 37, 1563–1566. [Google Scholar] [CrossRef] [Green Version]
- Letey, J.; Vaughan, P. Soil type, crop and irrigation technique affect nitrogen leaching to groundwater. Calif. Agric. 2013, 67, 231–241. [Google Scholar] [CrossRef]
- Prasad, R.; Hochmuth, G.J.; Boote, K.J. Estimation of Nitrogen Pools in Irrigated Potato Production on Sandy Soil Using the Model SUBSTOR. PLoS ONE 2015, 10, e0117891. [Google Scholar] [CrossRef] [PubMed]
- Negm, A.M.; Yoshimura, C.; Saavedra, O.C.; Eltarabily, M.G. Modeling the impact of nitrate fertilizers on groundwater quality in the southern part of the Nile Delta, Egypt. Water Supply 2016, 17, 561–570. [Google Scholar]
- Follet, R.F. Transformation and transport processes of nitrogen in agricultural systems. In Nitrogen in the Environment: Sources, Problems, and Management; Hatfield, J.L., Follet, R.F., Eds.; Academic Press: San Diego, CA, USA, 2008; Available online: http://digitalcommons.unl.edu/usdaarsfacpub/261 (accessed on 1 June 2019).
- Robertson, G.P.; Groffman, P.M. Nitrogen transformation. In Soil Microbiology, Biochemistry, and Ecology; Paul, E.A., Ed.; Springer: New York, NY, USA, 2007; pp. 341–364. [Google Scholar]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Version 4.0; HYDRUS Software Series 3; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2008. [Google Scholar]
- Baram, S.; Couvreur, V.; Harter, T.; Read, M.; Brown, P.; Kandelous, M.; Smart, D.; Hopmans, J. Estimating Nitrate Leaching to Groundwater from Orchards: Comparing Crop Nitrogen Excess, Deep Vadose Zone Data-Driven Estimates, and HYDRUS Modeling. Vadose Zone J. 2016, 15, 11. [Google Scholar] [CrossRef]
- Jha, R.K.; Sahoo, B.; Panda, R.K. Modeling the water and nitrogen transports in a soil–paddy–atmosphere system using HYDRUS-1D and lysimeter experiment. Paddy Water Environ. 2017, 15, 831–846. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, 15. [Google Scholar] [CrossRef]
- Eltarabily, M.G.; Bali, K.M.; Negm, A.M.; Yoshimura, C. Evaluation of Root Water Uptake and Urea Fertigation Distribution under Subsurface Drip Irrigation. Water 2019, 11, 1487. [Google Scholar] [CrossRef]
- Ullah, H.; Santiago-Arenas, R.; Ferdous, Z.; Attia, A.; Datta, A. Chapter Two—Improving water use efficiency, nitrogen use efficiency, and radiation use efficiency in field crops under drought stress: A review. Adv. Agron. 2019, 156, 109–157. [Google Scholar]
- Galloway, J.N.; Townsend, A.R.; Erisman, J.W.; Bekunda, M.; Cai, Z.; Freney, J.R.; Martinelli, L.A.; Seitzinger, S.P.; Sutton, M.A. Transformation of the Nitrogen Cycle: Recent Trends, Questions, and Potential Solutions. Science 2008, 320, 889–892. [Google Scholar] [CrossRef] [Green Version]
- Gastal, F.; Lemaire, G. N uptake and distribution in crops: An agronomical and ecophysiological perspective. J. Exp. Bot. 2002, 53, 789–799. [Google Scholar] [CrossRef]
- Huang, T.; Ju, X.; Yang, H. Nitrate leaching in a winter wheat-summer maize rotation on a calcareous soil as affected by nitrogen and straw management. Sci. Rep. 2017, 7, 42247. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://websoilsurvey.nrcs.usda.gov/app/WebSoilSurvey.aspx (accessed on 1 June 2019).
- Available online: https://cimis.water.ca.gov/Stations.aspx (accessed on 1 July 2019).
- Snyder, L.; Orang, M.; Bali, K.; Basic Irrigation Scheduling Program (BISe). Oakland: University of California Land, Air, and Water Resources Biomet Website. 2014. Available online: http://biomet.ucdavis.edu/irrigation_scheduling/bis/BIS.htm (accessed on 1 June 2019).
- Available online: https://www.iid.com/water/library/qsa-water-transfer (accessed on 1 July 2019).
- Miller, J. Hybrid selection and production practices. In Sunflower Production; Berglund, D.R., Ed.; North Dakota State University (NDSU): Fargo, ND, USA, 2007; p. 117, Extension Publication A-1331; Available online: https://www.ag.ndsu.edu/pubs/plantsci/rowcrops/a1331-04.pdf (accessed on 15 July 2019).
- Antonopoulos, V.Z. Modelling of water and nitrogen balances in the ponded water and soil profile of rice fields in Northern Greece. Agric. Water Manag. 2010, 98, 321–330. [Google Scholar] [CrossRef]
- Hanson, B.R.; Simunek, J.; Hopmans, J.W. Evaluation of urea–ammonium–nitrate fertigation with drip irrigation using numerical modeling. Agric. Water Manag. 2006, 86, 102–113. [Google Scholar] [CrossRef]
- Jansson, P.-E.; Karlberg, L. Coupled Heat and Mass Transfer Model for Soil-Plant-Atmosphere Systems; Department of Civil and Environmental Engineering, KTH Royal Institute of Technology: Stockholm, Sweden, 2001; p. 321. [Google Scholar]
- Zeng, W.; Lei, G.; Zha, Y.; Fang, Y.; Wu, J.; Huang, J. Sensitivity and uncertainty analysis of the HYDRUS-1D model for root water uptake in saline soils. Crop. Pasture Sci. 2018, 69, 163. [Google Scholar] [CrossRef]
- Ventura, F.; Snyder, R.L.; Bali, K.M. Estimating Evaporation from Bare Soil Using Soil Moisture Data. J. Irrig. Drain. Eng. 2006, 132, 153–158. [Google Scholar] [CrossRef]
- Vanaja, M.; Yadav, S.; Archana, G.; Lakshmi, N.J.; Reddy, P.R.; Vagheera, P.; Razak, S.A.; Maheswari, M.; Venkateswarlu, B. Response of C4 (maize) and C3 (sunflower) crop plants to drought stress and enhanced carbon dioxide concentration. Plant Soil Environ. 2011, 57, 207–215. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Shao, D.; Gu, W.; Liu, H. Field analysis of water and nitrogen fate in lowland paddy fields under different water managements using HYDRUS-1D. Agric. Water Manag. 2015, 150, 67–80. [Google Scholar] [CrossRef]
- Carr, M.K.V. Crop yield response to water. In FAO Irrigation and Drainage Paper 66; Steduto, P., Hsiao, T.C., Fereres, E., Raes, D., Eds.; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012; p. 500. Available online: http://www.fao.org/docrep/016/i2800e/i2800e00.htm (accessed on 20 July 2019).
- Oosterbaan, R.J. Agricultural drainage criteria. In Drainage Principles and Applications; Ritzema, H.P., Ed.; International Institute for Land Reclamation and Improvement (ILRI): Wageningen, The Netherlands, 1994; ISBN 9070754339. [Google Scholar]
- Neshat, A.; Nasiri, S. Finding the optimal distance of emitters in the drip irrigation in loam-sandy soil in the Ghaeme Abad plain of Kerman. Iran. Middle-East J. Sci. Res. 2012, 11, 426–434. [Google Scholar]
- Wu, J.; Zhang, R.; Gui, S. Modeling soil water movement with water uptake by roots. Plant Soil 1999, 215, 7–17. [Google Scholar] [CrossRef]
- Simunek, J.; Hopmans, J.W. Modeling compensated root water and nutrient uptake. Ecol. Model. 2009, 220, 505–521. [Google Scholar] [CrossRef]
- Wagenet, R.J.; Biggar, J.W.; Nielsen, D.R. Tracing the Transformations of Urea Fertilizer during Leaching1. Soil Sci. Soc. Am. J. 1977, 41, 896. [Google Scholar] [CrossRef]
- Selim, H.M.; Iskandar, I.K. Modeling nitrogen transport and transformations in soils: 2. Validation. Soil Sci. 1981, 131, 303–312. [Google Scholar] [CrossRef]
- Kirda, C.; Topcu, S.; Kaman, H.; Ulger, A.; Yazici, A.; Cetin, M.; Derici, M. Grain yield response and N-fertiliser recovery of maize under deficit irrigation. Field Crop. Res. 2005, 93, 132–141. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Jensen, L.S.; de Neergaard, A.; Jensen, C.R. Alternate partial root-zone irrigation improves fertilizer-N use efficiency in tomatoes. Irrig. Sci. 2013, 31, 589–598. [Google Scholar] [CrossRef]
- Li, F.; Liang, J.; Kang, S.; Zhang, J. Benefits of alternate partial root-zone irrigation on growth, water and nitrogen use efficiencies modified by fertilization and soil water status in maize. Plant Soil 2007, 295, 279–291. [Google Scholar] [CrossRef]
- Chai, Q.; Gan, Y.; Zhao, C.; Xu, H.; Waskom, R.M.; Niu, Y.; Siddique, K.H.M. Regulated deficit irrigation for crop production under drought stress. A review. Agron. Sustain. Dev. 2016, 36, 3. [Google Scholar] [CrossRef]
| Stage | Days | Period | KC | ETo (cm) | ETC (cm) | Irrigation (mm-ha/ha) | Fertilizers |
|---|---|---|---|---|---|---|---|
| Initial | 20 | 26 March–14 April | 0.2 | 12.76 | 2.55 | Sprinkler 27/3—19/4 (175) SDI 19/4—1/7 65% ETc (185) 100% ETc (379) | 350 kg ha−1 MAP on 26 March prior to the first sprinkler application of 275 m3 103 kg ha−1 UAN-32 on 16 May with 353 m3 of 4 SDI event |
| Crop development | 29 | 15 April–13 May | 0.2–1.1 | 21.25 | 14.07 | ||
| Mid-season | 34 | 14 May–16 June | 1.1 | 27.22 | 29.94 | ||
| Late season | 16 | 17 June–1 July | 1.1–0.4 | 12.31 | 8.81 | ||
| Total | 98 | 26 March–1 July | KC avg. = 0.75 | 73.54 | 55.37 |
| Basic Physical Soil Properties of the Experimental Field [42] | ||||||||||||||||||||
| USDA a Texture | Soil Layer | Composition Sand, Silt, Clay | ρb (g cm−3) | θf (cm3 cm−3) | Parameters of the Water Retention Equation (Van Genuchten Model) | |||||||||||||||
| θr (cm3 cm−3) | θs (cm3 cm−3) | α (cm−1) | n | Ks (cm day−1) | ||||||||||||||||
| Silty clay loam 1 | 0.0–0.30 m | 17%, 48%, 35% | 1.50 | 0.325 | 0.084 | 0.424 * (0.41–0.44) | 0.009 | 1.451 | 5.28 * (4.0–7.0) | |||||||||||
| Silty clay 2 and clay | 0.30–1.50 m | 18%, 42%, 40% | 1.45 | 0.351 | 0.089 | 0.445 * (0.41–0.44) | 0.012 | 1.403 | 6.99 * (4.0–7.0) | |||||||||||
| Initial and Calibrated N Transport and Transformation Parameters for the Model Simulation | ||||||||||||||||||||
| DL (cm) | (day−1) | (day−1) | (day−1) | (day−1) | (day−1) | (day−1) | (day−1) | (day−1) | Kd | |||||||||||
| 5.0 | (0.3–0.8) | (0.02–0.07) | (0.02–0.72) | (0.02–0.72) | (0.01–0.24) | (0.01–0.24) | (0.001–0.04) | (0.001–0.04) | 3–4 | |||||||||||
| Soil 1 | 5.0 | 0.45 | 0.02 | 0.20 | 0.20 | 0.020 * | 0.020 * | 0.001 | 0.001 | 3.50 | ||||||||||
| Soil 2 | 5.0 | 0.45 | 0.02 | 0.20 | 0.20 | 0.010 * | 0.010 * | 0.001 | 0.001 | 3.50 | ||||||||||
| Vrugt Model for Sunflower Root Distribution Parameters [52] | ||||||||||||||||||||
| z1m (cm) | z1 (cm) | Pz | x1m (cm) | x1 (cm) | Px | |||||||||||||||
| 150 | 120 | 1 | 75 | 30 | 1 | |||||||||||||||
| Feddes’ Parameters (Root Water Uptake Parameters for Sunflower) [50] | ||||||||||||||||||||
| P0 (cm) | Popt (cm) | P2H (cm) | P2L (cm) | P3 (cm) | r2H (cm day−1) | r2L (cm day−1) | ||||||||||||||
| −1 | −5 | −400 | −500 | −10,000 | 0.5 | 0.1 | ||||||||||||||
| Depth (cm) | 9 April | 9 May | 28 June | |||||
|---|---|---|---|---|---|---|---|---|
| 100% ETC | 65% ETC | |||||||
| Soil Samples | HYDRUS | Soil Samples | HYDRUS | Soil Samples | HYDRUS | Soil Samples | HYDRUS | |
| 15.0 | 0.305 | 0.396 | 0.281 | 0.293 | 0.363 | 0.352 | 0.130 | 0.129 |
| 30.0 | 0.328 | 0.417 | 0.317 | 0.305 | 0.343 | 0.354 | 0.133 | 0.141 |
| 45.0 | 0.378 | 0.420 | 0.317 | 0.309 | 0.358 | 0.335 | 0.145 | 0.141 |
| 60.0 | 0.386 | 0.425 | 0.301 | 0.317 | 0.300 | 0.226 | 0.142 | 0.141 |
| 75.0 | 0.370 | 0.428 | 0.301 | 0.325 | 0.191 | 0.141 | 0.162 | 0.141 |
| 90.0 | 0.403 | 0.430 | 0.340 | 0.333 | 0.121 | 0.141 | 0.135 | 0.141 |
| 105.0 | 0.424 | 0.432 | 0.353 | 0.342 | 0.152 | 0.141 | 0.148 | 0.141 |
| 120.0 | 0.423 | 0.433 | 0.361 | 0.349 | 0.154 | 0.161 | 0.171 | 0.161 |
| 150.0 | 0.442 | 0.435 | - | - | - | - | - | - |
| Depth (cm) | Samples on 9 April (Day 15 in Simulation) | Samples on 28 June (Day 95 in Simulation) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (N-E) | (N-W) | Center | (S-E) | (S-W) | Avg. | HYDRUS | (N-E) | (S-E) | Avg. | HYDRUS (100% ETC) | (N-W) | HYDRUS (65% ETC) | |
| 0–30 | 59.6 | 73.2 | 36.6 | 36.1 | 48.0 | 50.7 | 34.5 | 11.4 | 10.6 | 11.0 | 9.5 | 41.1 | 35.6 |
| 30–60 | 18.2 | 29.5 | 12.5 | 28.5 | 48.2 | 27.4 | 25.6 | 22.0 | 25.2 | 23.6 | 15.5 | 30.9 | 15.5 |
| 60–90 | 15.8 | 10.2 | 5.5 | 29.8 | 47.2 | 21.7 | 19.9 | 10.6 | 23.6 | 17.1 | 15.5 | 11.0 | 15.5 |
| 90–105 | 15.4 | 14.6 | 4.8 | 30.8 | 46.8 | 22.5 | 18.6 | 9.6 | 28.2 | 18.9 | 15.5 | 18.7 | 15.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltarabily, M.G.; Burke, J.M.; Bali, K.M. Effect of Deficit Irrigation on Nitrogen Uptake of Sunflower in the Low Desert Region of California. Water 2019, 11, 2340. https://doi.org/10.3390/w11112340
Eltarabily MG, Burke JM, Bali KM. Effect of Deficit Irrigation on Nitrogen Uptake of Sunflower in the Low Desert Region of California. Water. 2019; 11(11):2340. https://doi.org/10.3390/w11112340
Chicago/Turabian StyleEltarabily, Mohamed Galal, John M. Burke, and Khaled M. Bali. 2019. "Effect of Deficit Irrigation on Nitrogen Uptake of Sunflower in the Low Desert Region of California" Water 11, no. 11: 2340. https://doi.org/10.3390/w11112340





