A Rainwater Harvesting Accounting Tool for Water Supply Availability in Colorado
Abstract
:1. Introduction
2. Methods
2.1. Accounting Tool Concept
2.2. Model Selection
2.3. Sensitivity Analysis Methods
2.3.1. Soil Parameter Sensitivity Analysis
2.3.2. Precipitation Sensitivity Analysis
2.4. WQ-COSM Infiltration Modeling
3. Results and Discussion
3.1. Sensitivity Results
3.1.1. Sensitivity to Soil Parameters
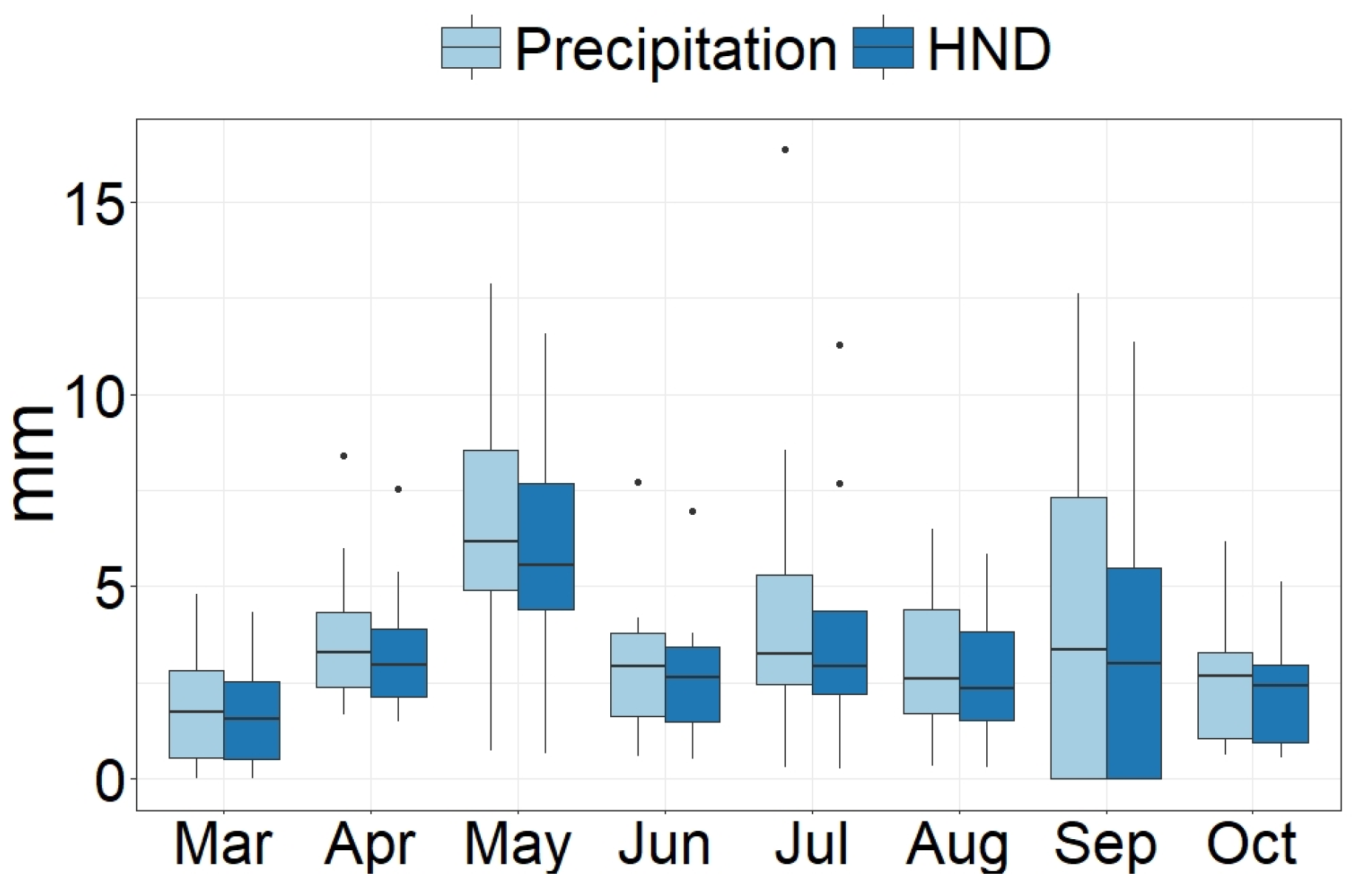
3.1.2. Sensitivity to Precipitation
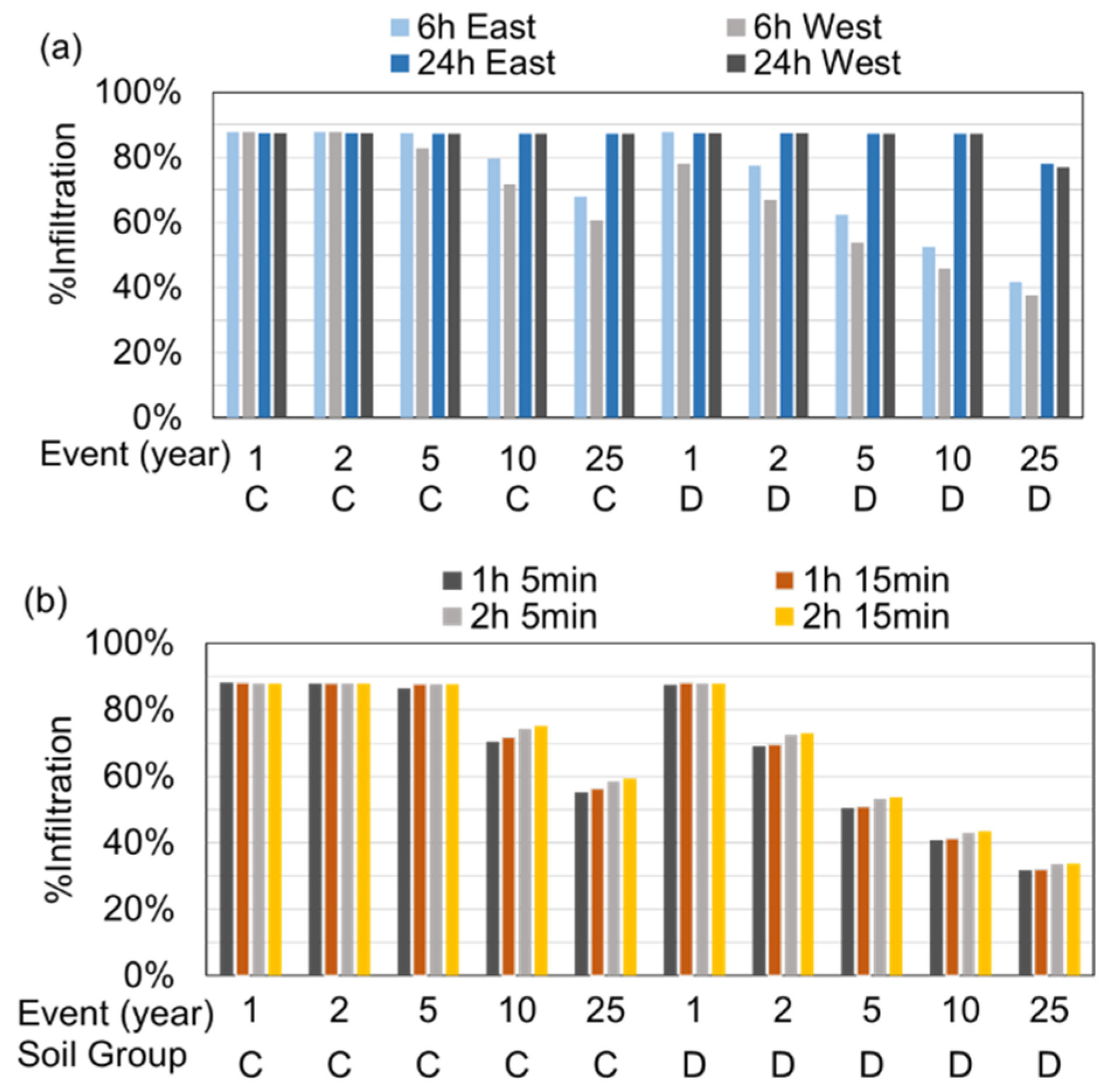
3.2. WQ-COSM Infiltration Modeling Results
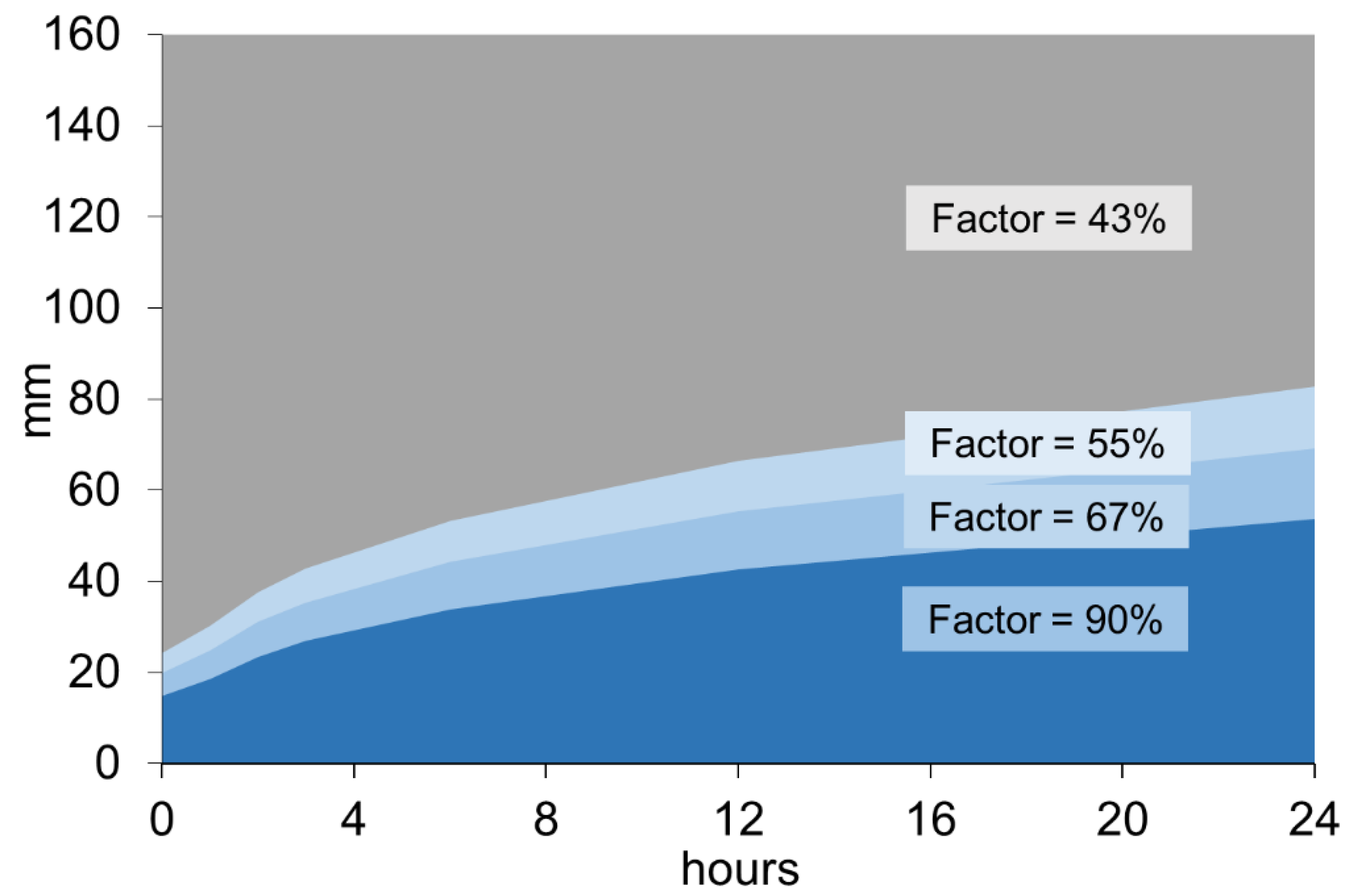
4. Integrating Factors in Accounting Tool
5. Example Application of HND Factors
5.1. HND Factor Application
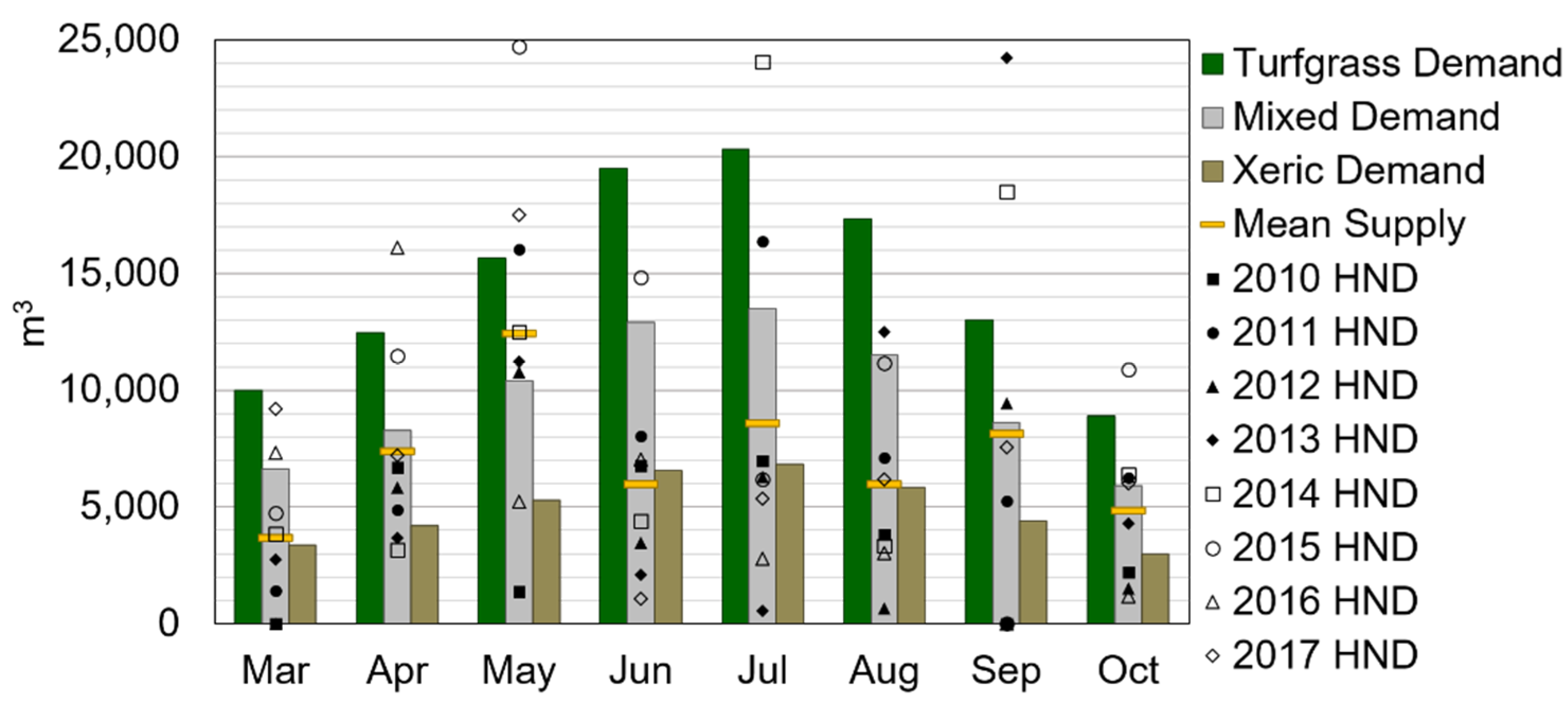
5.2. Example Allowable Harvest and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Udall, B.; Overpeck, J. The twenty-first century Colorado River hot drought and implications for the future. Water Resour. Res. 2017, 53, 2404–2418. [Google Scholar] [CrossRef] [Green Version]
- Rygaard, M.; Binning, P.J.; Albrechtsen, H.-J. Increasing urban water self-sufficiency: New era, new challenges. J. Environ. Manag. 2011, 92, 185–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nel, N.; Jacobs, H.E.; Loubser, C.; Du Plessis, K. Supplementary household water sources to augment potable municipal supply in South Africa. Water SA 2017, 43, 553–562. [Google Scholar] [CrossRef]
- Beal, C.D.; Sharma, A.; Gardner, T.; Chong, M. A Desktop Analysis of Potable Water Savings from Internally Plumbed Rainwater Tanks in South-East Queensland, Australia. Water Resour. Manag. 2012, 26, 1577–1590. [Google Scholar] [CrossRef] [Green Version]
- Haque, M.M.; Rahman, A.; Samali, B. Evaluation of climate change impacts on rainwater harvesting. J. Clean. Prod. 2016, 137, 60–69. [Google Scholar] [CrossRef]
- Alamdari, N.; Sample, D.J.; Liu, J.; Ross, A. Assessing climate change impacts on the reliability of rainwater harvesting systems. Resour. Conserv. Recycl. 2018, 132, 178–189. [Google Scholar] [CrossRef]
- Sample, D.J.; Liu, J.; Wang, S. Evaluating the Dual Benefits of Rainwater Harvesting Systems Using Reliability Analysis. J. Hydrol. Eng. 2013, 18, 1310–1321. [Google Scholar] [CrossRef]
- Ennenbach, M.W.; Larrauri, P.C.; Lall, U. County-Scale Rainwater Harvesting Feasibility in the United States: Climate, Collection Area, Density, and Reuse Considerations. J. Am. Water Resour. Assoc. 2018, 54, 255–274. [Google Scholar] [CrossRef]
- Steffen, J.; Jensen, M.; Pomeroy, C.A.; Burian, S.J. Water Supply and Stormwater Management Benefits of Residential Rainwater Harvesting in U.S. Cities. J. Am. Water Resour. Assoc. 2013, 49, 810–824. [Google Scholar] [CrossRef]
- Leonard, B.; Libecap, G.D. Collective Action by Contract: Prior Appropriation and the Development of Irrigation in the Western United States. J. Law Econ. 2019, 62, 67–115. [Google Scholar] [CrossRef]
- Loper, S.; Anderson, C. Rainwater Harvesting State Regulations and Technical Resources; Pacific Northwest National Laboratory: Richland, WA, USA, 2019.
- Benson, R.D. Alive but Irrelevant: The Prior Appropriation Doctrine in Today’s Western Water Law; Social Science Research Network: Rochester, NY, USA, 2011. [Google Scholar]
- Courtney, B. Rainwater and Snowmelt Harvesting in Colorado; Headwaters Corporation: Kearney, NE, USA, 2008. [Google Scholar]
- Colorado General Assembly. House Bill 09-1129: Concerning an Authorization of Pilot Projects for the Beneficial Use of Captured Precipitation in New Real Estate Developments, and Making an Appropriation in Connection Therewith. 2009. Available online: https://legisource.net/wp-content/uploads/2012/09/1129_enr.pdf (accessed on 22 October 2019).
- Leonard Rice Engineers, Inc.; Meurer & Associates; Ryley Carlock & Applewhite. Holistic Approach to Sustainable Water Management in Northwest Douglas County. 2007. Available online: https://www.conservationfund.org/images/cln_events-resources/2015_WQM_Workshop/WQM-Resources/6_Water_Quality/4_-_CWCBDouglasCountyWaterSustainability2007.pdf (accessed on 22 October 2019).
- Panos, C.; Hogue, T.; Gilliom, R.; McCray, J. High-Resolution Modeling of Infill Development Impact on Stormwater Dynamics in Denver, Colorado. J. Sustain. Water Built Environ. 2018, 4, 04018009. [Google Scholar] [CrossRef]
- Bell, C.D.; Tague, C.L.; McMillan, S.K. Modeling Runoff and Nitrogen Loads from a Watershed at Different Levels of Impervious Surface Coverage and Connectivity to Storm Water Control Measures. Water Resour. Res. 2019, 55, 2690–2707. [Google Scholar] [CrossRef]
- Miller, J.D.; Kim, H.; Kjeldsen, T.R.; Packman, J.; Grebby, S.; Dearden, R. Assessing the impact of urbanization on storm runoff in a peri-urban catchment using historical change in impervious cover. J. Hydrol. 2014, 515, 59–70. [Google Scholar] [CrossRef] [Green Version]
- MacDonnell, L.J. Out-of-Priority Water Use: Adding Flexibility to the Water Appropriation System. Neb. Law Rev. 2004, 83, 485. [Google Scholar] [CrossRef]
- Colorado General Assembly. House Bill 15-1016: Concerning Incentives for Precipitation Harvesting, and, in Connection Therewith, Making an Appropriation; 2015. Available online: http://www.colorado.gov/clics/clics2015a/csl.nsf/fsbillcont/20107829C4AE827F87257D9000782721?Open&file=1016_enr.pdf (accessed on 22 October 2019).
- USDA NRCS Web Soil Survey. Available online: https://websoilsurvey.sc.egov.usda.gov/App/HomePage.htm?TARGET_APP=Web_Soil_Survey_application_bokjab35ulogju0oausikvpj (accessed on 15 August 2019).
- Gilliom, R.L. HB 15-1016 Rainwater Harvesting Pilot Project Regional Factors; Colorado Division of Water Resources: Denver, CO, USA, 2019. [Google Scholar]
- Dunkerley, D. How is overland flow produced under intermittent rain? An analysis using plot-scale rainfall simulation on dryland soils. J. Hydrol. 2018, 556, 119–130. [Google Scholar] [CrossRef]
- Martínez-Mena, M.; Albaladejo, J.; Castillo, V.M. Factors influencing surface runoff generation in a Mediterranean semi-arid environment: Chicamo watershed, SE Spain. Hydrol. Process. 1998, 12, 741–754. [Google Scholar] [CrossRef]
- Mishra, S.K.; Chaudhary, A.; Shrestha, R.K.; Pandey, A.; Lal, M. Experimental Verification of the Effect of Slope and Land Use on SCS Runoff Curve Number. Water Resour. Manag. 2014, 28, 3407–3416. [Google Scholar] [CrossRef]
- Leonard Rice Engineers, Inc. Proposed Regional Factor Methodology for Rainwater Harvesting from the Sterling Ranch Pilot Study; Leonard Rice Engineers, Inc.: Denver, CO, USA, 2019. [Google Scholar]
- Stomph, T.J.; De Ridder, N.; Steenhuis, T.S.; Van de Giesen, N.C. Scale effects of Hortonian overland flow and rainfall-runoff dynamics: Laboratory validation of a process-based model. Earth Surf. Process. Landf. 2002, 27, 847–855. [Google Scholar] [CrossRef]
- Urbonas, B.; Guo, J.; MacKenzie, K. Description of the WQ-COSM Computer Model to Generate a Water Quality Capture Volume for Stormwater BMPs. N.D. 2011. Available online: https://udfcd.org/wp-content/uploads/uploads/resources/technical%20memos/Description_of_the_WQ_COSM_Computer_Model.pdf (accessed on 22 October 2019).
- Urbonas, B.; Rapp, D.N. WQ-COSM: Water Quality Capture Optimization and Statistics Model v3.1; Urban Watersheds Research Institute: Denver, CO, USA, 2018. [Google Scholar]
- Urban Watersheds Research Institute. WQ-COSM User’s Manual: Water Quality Capture Optimization and Statistics Model (WQ-COSM) v3.0; Urban Watersheds Research Institute: Denver, CO, USA, 2017. [Google Scholar]
- Green, I.R.A. An explicit solution of the modified Horton equation. J. Hydrol. 1986, 83, 23–27. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration (NOAA) Cooperative Observer Network (COOP) National Centers for Environmental Information (NCEI) formerly known as National Climatic Data Center (NCDC). Available online: https://www.ncdc.noaa.gov/data-access/land-based-station-data/land-based-datasets/cooperative-observer-network-coop (accessed on 22 August 2019).
- MetStat, Inc.; MGS Engineering Consultants, Inc.; Applied Climate Services. Colorado-New Mexico Regional Precipitation-Frequency Estimation Study Summary Report Volume III; Colorado Division of Water Resources: Denver, CO, USA, 2018. [Google Scholar]
- National Oceanic and Atmospheric Administration NOAA Atlas 14 Point Precipitation Frequency Estimates. Available online: https://hdsc.nws.noaa.gov/hdsc/pfds/pfds_map_cont.html?bkmrk=co (accessed on 19 July 2019).
- Shrestha, S.; Fang, X.; Li, J. Mapping the 95th Percentile Daily Rainfall in the Contiguous U.S. In Proceedings of the World Environmental and Water Resources Congress 2013, Cincinnati, OH, USA, 19–23 May 2013; pp. 219–229. [Google Scholar]
- Colorado Water Conservation Board. Criteria and Guidelines for the Rainwater Harvesting Pilot Project Program; Colorado Water Conservation Board: Denver, CO, USA, 2019; Available online: https://drive.google.com/file/d/1BLMvgtYCZunSDCQUaQxLF1IuDNLXhBhO/view?usp=sharing (accessed on 22 October 2019).
- Colorado Division of Water Resources. Rainwater Collection & Storm Water Management. Available online: http://water.state.co.us/SurfaceWater/RainwaterCollection/Pages/default.aspx (accessed on 9 September 2019).
- Keystone Policy Center. Colorado Water and Growth Dialogue Final Report; Keystone Policy Center: Keystone, CO, USA, 2018; Available online: http://www.keystone.org/wp-content/uploads/2018/10/CO-Water-and-Growth-Dialogue-Final-Report_September-2018.pdf (accessed on 22 October 2019).
- Thompson, K.L. Colorado Division of Water Resource Technical Memorandum: Evaporation and Evapotranspiration Estimates for Colorado; Colorado Division of Water Resources: Denver, CO, USA, under review.
- Hilaire, R.S.; Arnold, M.A.; Wilkerson, D.C.; Devitt, D.A.; Hurd, B.H.; Lesikar, B.J.; Lohr, V.I.; Martin, C.A.; McDonald, G.V.; Morris, R.L.; et al. Efficient Water Use in Residential Urban Landscapes. HortScience 2008, 43, 2081–2092. [Google Scholar] [CrossRef]
- Hart, S.S. EG-07 Potentially Swelling Soil and Rock in the Front Range Urban Corridor, Colorado; Colorado Geological Survey: Denver, CO, USA, 1974. [Google Scholar]
- Denver Water. 2019 Residential Water Rates. Available online: https://www.denverwater.org/residential/billing-and-rates/2019-rates (accessed on 8 October 2019).
- Bossong, C.R.; Caine, J.S.; Stannard, D.I.; Flynn, J.L.; Stevens, M.R.; Heiny-Dash, J.S. USGS Water-Resources Investigations Report 03-4034—Hydrologic Conditions and Assessment of Water Resources in the Turkey Creek Watershed; Jefferson County, CO, USA; U.S. Geological Survey: Reston, VA, USA, 2003.


| Soil Group | Soil Type | Initial Infiltration Rate (mm/h) | Final Infiltration Rate (mm/h) | Infiltration Decay Rate (h−1) |
|---|---|---|---|---|
| A | Sand | 43.2 | 38.1 | 2 |
| B | Sandy loam | 35.6 | 30.5 | 3 |
| C | Loamy sand | 25.4 | 5.1 | 3 |
| D | Clay | 7.6 | 2.5 | 3 |
| Parameter | Value | %Infiltration | Change |
|---|---|---|---|
| Initial Infiltration Rate (mm/h) | 7.6 | 65% | −13 |
| 50.8 | 78% | 0 | |
| 127.0 | 89% | +11 | |
| Final Infiltration Rate (mm/h) | 0.3 | 70% | −8 |
| 2.5 | 78% | - | |
| 50.8 | 91% | +13 | |
| Infiltration Decay Rate (h−1) | 2 | 88% | +10 |
| 5 | 78% | - | |
| 6 | 77% | −1 |
| Event Frequency (year) | Event Duration (h) | Event Depth (mm) | Event Intensity (mm/h) | Soil Group A | Soil Group B | Soil Group C | Soil Group D |
|---|---|---|---|---|---|---|---|
| 0.25 | 0.25 | 2.4 | 9.7 | 100% | 100% | 100% | 100% |
| 0.25 | 0.5 | 3.3 | 6.6 | 96% | 96% | 96% | 96% |
| 0.25 | 1 | 4.1 | 4.1 | 95% | 95% | 95% | 95% |
| 0.25 | 2 | 5.0 | 2.5 | 94% | 94% | 94% | 94% |
| 0.25 | 6 | 6.8 | 1.1 | 93% | 93% | 93% | 93% |
| 0.5 | 0.25 | 4.8 | 19.3 | 94% | 94% | 94% | 94% |
| 0.5 | 0.5 | 6.6 | 13.2 | 93% | 93% | 93% | 93% |
| 0.5 | 1 | 8.3 | 8.3 | 92% | 92% | 92% | 92% |
| 0.5 | 2 | 9.9 | 5.0 | 92% | 92% | 92% | 92% |
| 0.5 | 6 | 13.6 | 2.3 | 91% | 91% | 91% | 91% |
| 0.75 | 0.25 | 7.2 | 29.0 | 93% | 93% | 93% | 93% |
| 0.75 | 0.5 | 9.9 | 19.8 | 92% | 92% | 92% | 92% |
| 0.75 | 1 | 12.4 | 12.4 | 92% | 92% | 92% | 92% |
| 0.75 | 2 | 14.8 | 7.4 | 91% | 91% | 91% | 91% |
| 0.75 | 6 | 20.4 | 3.4 | 91% | 91% | 91% | 91% |
| 1 | 0.25 | 9.7 | 38.6 | 92% | 92% | 92% | 92% |
| 1 | 0.5 | 13.2 | 26.4 | 92% | 92% | 92% | 80% |
| 1 | 1 | 16.5 | 16.5 | 91% | 91% | 91% | 72% |
| 1 | 2 | 19.8 | 9.9 | 91% | 91% | 91% | 72% |
| 1 | 6 | 27.2 | 4.5 | 91% | 91% | 91% | 78% |
| 1 | 24 | 42.2 | 1.8 | 90% | 90% | 90% | 90% |
| 2 | 0.25 | 12.2 | 48.8 | 92% | 92% | 92% | 79% |
| 2 | 0.5 | 16.6 | 33.3 | 91% | 91% | 91% | 63% |
| 2 | 1 | 20.7 | 20.7 | 91% | 91% | 90% | 58% |
| 2 | 2 | 24.8 | 12.4 | 91% | 91% | 91% | 58% |
| 2 | 6 | 33.0 | 5.5 | 91% | 91% | 91% | 66% |
| 2 | 24 | 49.8 | 2.1 | 90% | 90% | 90% | 90% |
| 5 | 0.25 | 16.5 | 65.9 | 91% | 91% | 76% | 58% |
| 5 | 0.5 | 22.5 | 44.9 | 91% | 91% | 68% | 47% |
| 5 | 1 | 28.0 | 28.0 | 91% | 91% | 67% | 43% |
| 5 | 2 | 33.3 | 16.6 | 91% | 91% | 70% | 43% |
| 5 | 6 | 43.4 | 7.2 | 90% | 90% | 81% | 51% |
| 5 | 24 | 63.0 | 2.6 | 90% | 90% | 90% | 81% |
| 10 | 0.25 | 20.2 | 80.8 | 88% | 79% | 62% | 47% |
| 10 | 0.5 | 27.4 | 54.9 | 91% | 84% | 56% | 38% |
| 10 | 1 | 34.0 | 34.0 | 91% | 91% | 55% | 35% |
| 10 | 2 | 40.6 | 20.3 | 90% | 90% | 58% | 35% |
| 10 | 6 | 52.3 | 8.7 | 90% | 90% | 71% | 42% |
| 10 | 24 | 74.9 | 3.1 | 90% | 90% | 90% | 71% |
| 25 | 0.25 | 25.4 | 101.6 | 70% | 62% | 50% | 38% |
| 25 | 0.5 | 34.5 | 69.1 | 78% | 67% | 44% | 30% |
| 25 | 1 | 42.9 | 42.9 | 90% | 84% | 43% | 28% |
| 25 | 2 | 51.3 | 25.7 | 90% | 90% | 46% | 28% |
| 25 | 6 | 65.5 | 10.9 | 90% | 90% | 58% | 34% |
| 25 | 24 | 92.2 | 3.8 | 90% | 90% | 90% | 60% |
| Total Area (km2) | Dwellings (Units) | Density (Units/km2) | Unit Pervious Area (m2/unit) | Total Pervious Area (km2) | Total Impervious (km2) | Turfgrass Demand (L/m2) | Mixed Demand (L/m2) | Xeric Demand (L/m2) |
|---|---|---|---|---|---|---|---|---|
| 0.405 | 1000 | 2471 | 191 | 0.191 | 0.213 | 611 | 407 | 204 |
| Demand | March | April | May | June | July | August | September | October | Season |
|---|---|---|---|---|---|---|---|---|---|
| Turfgrass (m3) | 9993 | 12,453 | 15,672 | 19,487 | 20,326 | 17,343 | 13,008 | 8899 | 117,181 |
| Mixed (m3) | 6627 | 8258 | 10,393 | 12,923 | 13,479 | 11,501 | 8626 | 5901 | 77,709 |
| Xeric (m3) | 3366 | 4195 | 5279 | 6564 | 6847 | 5842 | 4382 | 2997 | 39,471 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilliom, R.L.; Bell, C.D.; Hogue, T.S.; McCray, J.E. A Rainwater Harvesting Accounting Tool for Water Supply Availability in Colorado. Water 2019, 11, 2205. https://doi.org/10.3390/w11112205
Gilliom RL, Bell CD, Hogue TS, McCray JE. A Rainwater Harvesting Accounting Tool for Water Supply Availability in Colorado. Water. 2019; 11(11):2205. https://doi.org/10.3390/w11112205
Chicago/Turabian StyleGilliom, Ryan L., Colin D. Bell, Terri S. Hogue, and John E. McCray. 2019. "A Rainwater Harvesting Accounting Tool for Water Supply Availability in Colorado" Water 11, no. 11: 2205. https://doi.org/10.3390/w11112205
APA StyleGilliom, R. L., Bell, C. D., Hogue, T. S., & McCray, J. E. (2019). A Rainwater Harvesting Accounting Tool for Water Supply Availability in Colorado. Water, 11(11), 2205. https://doi.org/10.3390/w11112205





